电子科技大学DSP课件
DSP课件第1章

第 1章DSP 概念绪论结构 特点DSP原理 理及应用I电子信 信息工程TI的 DSP设计 流程CCS 软件1第 1章DSP 概念绪论正在学习:DSP概念¾DSP概念:① Digital Signal Processin ng 数字信号处理(理论 论和方法) ② Digital Signal Processor 数字信号处理器(实现数字信号处理的微处理器 实 )结构 特点TI的 DSPx’(t) x (t) 放大器x(t)抗混叠 滤波器 输入通道ADCx(n)其它数字系统设计 流程DSP硬件 输出通道CCS 软件放大器 重建 y(t) 滤波器 y’(t y (t) DAC y(n) 其它数字系统 2第 1章DSP 概念绪论正在学习:DSP概念结构 特点¾微处理器发展的几个 个方向: ① 通用CPU ② 微控制器MCU/AR RM ③ DSP处理器 ④ FPGATI的 DSP设计 流程CCS 软件3第 1章DSP 概念绪论正在学习:DSP结构¾ DSP处理器结构特点 ①采用哈佛结构 ②采用多总线结构 ②采用多 线结构 ③采用硬件乘累加(MAC)单元 单 ④采用流水线技术 ⑤采用特殊的程序控制方式 式(如零开销循环) ⑥采用特殊的寻址方式(如 如循环寻址、位倒序寻址)和高效的特 殊指令 ⑦采用丰富的片内外设结构 特点TI的 DSP设计 流程CCS 软件4第 1章DSP 概念绪论正在学习:DSP结构①采用哈佛结构地 地址总线结构 特点冯诺依曼结构存储器: 数据和指令CPU数据 据总线TI的 DSP哈佛结构程序存储器: 仅存放指令地 地址总线地址总线CPU程序 序总线 数据总线数据存储器: 仅存放数据设计 流程改进的哈佛结构CCS 软件地 程序存储器: 地址总线 存放指令和 数据 程序 序总线地址总线CPU缓存 数据总线数据存储器: 仅存放数据5第 1章DSP 概念 取指 结构 特点绪论正在学习:DSP结构②采用流水技术译码 取指 寻址 译码 取指 取数 寻址 译码 取指 第五级流水 运算 算 取数 数 寻址 址 译码 码 取指 指 存储 运算 取数 寻址 译码 取指 第一级流水 存储 运算 取数 寻址 译码 第二级流水 存储 运算 取数 寻址 第三级流水 存储 运算 取数 第四级流水 存储 运算 存储TI的 DSP设计 流程第六级流水 水综合来看 每条指令都是在 综合来看,每条指令都是在 在 个指令周期内执行的。
电子科技大学DSP技术讲稿

讲 稿
课 程 名 称:DSP 处理技术及应用 授 课 学 时:12 授 课 班 级:大学四年级第一学期 任 课 教 师: 教............................................................................................................................................... I 第一章 DSP 技术概述 .................................................................................................................. 1 1.1 DSP 基本概念 .................................................................................................................... 1 1.2 DSP 实现方法 .................................................................................................................... 1 1.3 DSP 发展历程 .................................................................................................................... 2 1.4 典型的 DSP 系统举例 ........................................
DSP教程(电子科技大学,张鹰)(精)
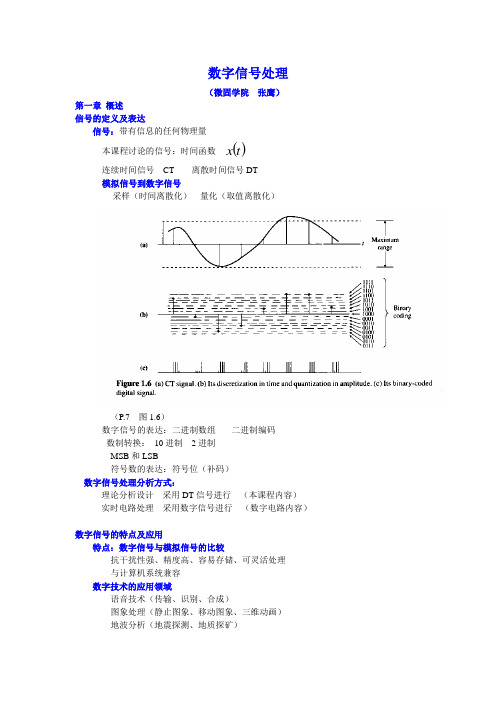
数字信号处理(微固学院张鹰)第一章概述信号的定义及表达信号:带有信息的任何物理量本课程讨论的信号:时间函数()t x连续时间信号CT 离散时间信号DT模拟信号到数字信号采样(时间离散化)量化(取值离散化)(P.7 图1.6)数字信号的表达:二进制数组----二进制编码数制转换:10进制---2进制MSB和LSB符号数的表达:符号位(补码)数字信号处理分析方式:理论分析设计采用DT信号进行(本课程内容)实时电路处理采用数字信号进行(数字电路内容)数字信号的特点及应用特点:数字信号与模拟信号的比较抗干扰性强、精度高、容易存储、可灵活处理与计算机系统兼容数字技术的应用领域语音技术(传输、识别、合成)图象处理(静止图象、移动图象、三维动画)地波分析(地震探测、地质探矿)谐振分析(高层建筑、桥梁、机翼等)自动控制实时检测本课程的主要教学安排:主要内容:(50学时)数字信号的频率分析:定义、变换与计算(22学时)频率定义、CTFS与DTFS、CTFT与DTFT、DFT与FFT数字信号的频率处理:滤波器设计(26学时)LTI系统分析理想滤波器与低阶数字滤波;FIR滤波器设计、IIR滤波器设计数字滤波器结构与误差分析教材与参考书:教材:《Digital Signal Processing –spectral computation and filterdesign 》(Third edition)(美) Chi-Tsong Chen电子工业出版社2002版《数字信号处理基础》(加)Joyce Van de Vegte 著侯正信王国安等译电子工业出版社2003版《信号与系统计算机练习—利用MA TLAB》John R.Buck刘树棠译西安交通大学出版社2000版主要工具:MATLAB :信号波形图、频谱计算与分析滤波器设计及系统频率特性分析考核方式:平时作业30%考试(笔试、开卷)70%MATLAB的基本应用方法命令窗口(Command window)的使用:输入各类变量或函数名称,按回车即得到当前变量或函数值;输入各类命令,按回车即得到该命令执行结果;若需要输入多行命令或程序,各行间用“;”间隔;M文件的编制与调试执行打开空白文件或已经有的文件,进行程序文件的输入编辑;各行间用“;”间隔;一行中“%”以后内容为注释部分,不影响程序执行;程序编制完毕后,可以按“F5”键保存执行,注意根据屏幕提示建立文件名称;如果出现错误,可在命令窗口看到错误类型及位置,根据错误检测信息对程序进行调试;MATLAB命令及函数信号的表达方式及作图在MA TLAB中,任何变量或函数均表现为向量,任何向量的元素编号均从1开始;序列(向量)表达方式设定坐标向量n和信号向量x;x和n为长度相同的向量,向量的编号从1开始;n=[-2 :0.1:2]坐标向量可以直接逐点写出:n=[2 3 4 5 6 7];也可以采用起点,终点和步长的形式写出:n=[-2 :0.1:2] ;信号向量可以直接逐点写出:x=[1 2 3 4 3 2];也可以采用与n 有关的函数运算形式写出:例如: x=3*n x=exp(j*(pi/8)*n)作图: 采用stem (n ,x ) 作出离散图形 DT 信号采用plot (n ,x ) 作出连续图形(折线连接) CT 信号作图时主要通过合理设置n 的范围及步长来保证变量坐标的正确性;可以利用title ,axis等函数为图形设置说明和坐标范围;特别注意:作图时必须保证坐标向量与信号向量长度完全一致;0101:离散序列的作图直接表现离散序列n=[2 3 4 5 6 7];x=[1 2 3 4 3 2];stem(n,x);0102:将图形表现为连续曲线n=[2 3 4 5 6 7];x=[1 2 3 4 3 2];plot(n,x);0203:信号表现为坐标向量的函数n=[2 3 4 5 6 7];x=exp(j*(pi/8)*n);plot(n,x);0204:图形说明和坐标范围的设置n=[-20:0.5:20];x=exp(j*(pi/8)*n);plot(n,x),title('n=[-20:0.5:20];x=exp(j*(pi/8)*n);plot(n,x)');axis([-20,20,-2,2]);第二章 DTFS 和CTFS---周期信号的频率分量信号的时域表达形式:连续时间信号CT 离散时间信号DTDT 信号由CT 信号采样得出CT 信号()t x 采样信号()nT x DT 信号 []n x周期信号:每隔一段时间重复的信号 ()(),...2,1±±=+=k kT t x t x 信号变化快慢的描述:周期T :信号重复的时间间隔频率0ω:单位时间内信号重复的次数频域表达形式人类接受的自然信号主要以频率形式表达:声音 色彩信号分析的重要任务:从时域信号得出频域信号频率的定义----单频率时间信号CT 信号的频率与周期性密切相关标准信号 ()t t x 01s in ω= ()t t x 02c o s ω=()t j t e t x t j 003sin cos 0ωωω+==上述信号均为周期信号,周期为T ;频率均为 0ω;周期与频率的关系 02ωπ=T 0ω 取值范围 ()∞∞-,DT 信号的频率 (仿照CT 信号定义)DT 信号由CT 信号采样得到;周期信号的采样不一定为周期信号;对于DT 信号,频率与周期没有直接对应关系;仿照CT 信号定义基本信号()Tn nT x 01sin ω= ()Tn nT x 02cos ω=()Tn j Tn e nT x Tn j 003sin cos 0ωωω+==上述信号频率均为 )在主值区域内的对应值T d 0(ωω=要点:信号nT j e 0ω的时域性质:非周期性频率性质:多重性频率范围 d ω 取值范围 ]/,/(T T ππ-Nyquist frequency ranged ω与采样频率有关CT 与DT 信号频率之间的关系:P. 29f d 与采样频率有关,位于]5.0,5.0(s s f f -范围内;将高频按周期折合到低频(主值区);例 p.27 2.1 2.2付氏级数及频率分量一般周期时间信号的频率:采用单频率信号表达CTFS (连续时间付氏级数)定义式 (周期信号:周期为P )()∑∞-∞==m t jm m e c t x 0ω P /20πω=()⎰-=Pt jm m dt e t x P c 01ω 存在条件:()t x 绝对可积,而且在一个周期内间断点和极值点有限;频率分量:CTFS coefficient / frequency component 通常为复数: Magnitude phase phase 的范围],(ππ- 共轭对称性:奇偶性()k FS a t x -**−→←()t x k areal {}k k a a Re :even{}k k a a ∠Im : oddreal and even real and evenreal and odd imaginary and odd周期信号频率分量的计算 (例 P.38)要点:P /20πω=2.4 利用简单分解求m c⎩⎨⎧≠==−→←000(m m A c A m FS常数) ⎩⎨⎧≠==−→←nm n m B c Be m FS t jn 00ω 2.5 利用公式求矩形脉冲的m c ()P m a m c ta t t x m FS 00sin 201ωω=−→←⎩⎨⎧≤=其余 2.6 利用公式求冲激串(sampling function )的m c()()Tc kT t t r m FS k 1=−→←-=∑∞-∞=δ 周期信号的时间范围:),(∞-∞ 双边信号一般周期信号的频率范围:),(∞-∞若对于所有的0,=>m c M m ,则称为带限信号;频率分量的意义:平均功率: 只与magnitude 有关phase 的影响:对信号波形的影响对视频有影响,对音频没有影响DTFS (离散时间付氏级数)定义式[]∑==N m nT jm md e c n x 0ω []∑=-=Nn nT jm md e n x N c 01ω 频率分量讨论:md c 的周期性 只有N 个独立系数共轭对称性:奇偶性m 的取值范围:应使 NT m m /20πω=的范围为]/,/(T T ππ-时移的影响: 线性相位变化例 p.48—542.8 利用公式直接计算系数 N=32.9 利用公式直接计算系数 N=42.10 时移的作用时移不影响DTFS 系数的幅度,只在系数中加入线性相位;利用MATLAB 计算频率分量DTFS 系数的FFT 计算重要函数 c=(1/N)*fft(x) x=N*ifft(c)应用要点:x和c的序列都为N个元素,下标排列都为[ 1 …..N],分别对应于离散时间n [0….N-1]和离散频率m [0….N-1];DTFS可以利用任何一个周期进行计算;在采用FFT的时候,输入数据必须从n=0到N-1;利用shift()函数(P.56)可以使频率向量排布在对称区间内:N为odd时,下标0在正中,N为even时,下标0偏左;利用m=ceil(-(N-1)/2):ceil((N-1/2)可以得到对应的横坐标;注意:c为周期序列,周期为N;例:2.8 2.9 程序P2.2 (P.57 )例2.8题的求解N=3;T=0.5; x=[-2 1 –0.6];例2.9题的求解N=4;T=1; x=[ 2.5 -0.4 1 -2];%program 2.2N=3;T=0.5; x=[-2 1 –0.6];D=2*pi/(N*T);X=fft(x/N);m=ceil(-(N-1)/2):ceil((N-1)/2);w=m*D;subplot(2,1,1),stem(w,abs(shift(X))),title('(a)');subplot(2,1,2),stem(w,angle(shift(X))*180/pi),title('(b)');CTFS系数的FFT计算问题:x为连续信号;m取值范围为无限大区间;方案:在一个周期内取N点对x进行采样(离散化);求出DTFS系数---周期序列;取主值范围内的序列即为对应CTFS系数;当x为带限信号时,在满足采样定理条件下可以得出准确的CTFS系数;例2.4题的求解 2.12%program 2.2P=2*pi/0.3;N=11;T=P/N;D=2*pi/P;n=0:N-1;x=-1.2+0.8*sin(0.6*n*T)-1.6*cos(1.5*n*T);X=fft(x/N);m=ceil(-(N-1)/2):ceil((N-1)/2);w=m*D;subplot(2,1,1),stem(w,abs(shift(X))),title('(a)');subplot(2,1,2),stem(w,angle(shift(X))*180/pi),title('(b)');对于带限信号,在满足采样定理的条件下,不同大小的N值(采样数量)得到的幅频分量相同;若采样周期不够小,则将产生频率混叠失真;例2.3 频率混叠的影响例2.5题的求解通过改变采样点数量N,可以比较混叠的影响大小%program 2.4hold on;N=42;P=4;T=P/N;D=2*pi/P;x=[ones(1,q+1) zeros(1,N-2*q-1) ones(1,q)];X=fft(x/N);m=ceil(-(N-1)/2):ceil((N-1)/2);stem(m*D,shift(X),'b','fill');对于在足够逼近条件下,magnetude 可以得到足够良好近似值;(能量逼近);但计算出的phase 不会得出良好近似值(通常不采用);关键:N 的选取(足够大以获得良好近似,足够小以减少运算量)根据设定的精确度,求出最小的N :令N=2n ,选定n 的特定值,再逐1增加;重复计算在Nyquist 范围内的系数差,直到系数差小于设定值为止;例2.6 根据设定最大误差,自动选取最小采样点数量,并求出满足要求的频谱例2.5题的求解% program 2.6a=1;b=100;P=4;D=2*pi/P;beta=1;while b>betaN1=2^a;T1=P/N1;q1=floor(1/T1);x1=[ones(1,q1+1) zeros(1,N1-2*q1-1) ones(1,q1)];X1=fft(x1/N1);N2=2*N1;T2=P/N2;q2=floor(1/T2);x2=[ones(1,q2+1) zeros(1,N2-2*q2-1) ones(1,q2)];X2=fft(x2/N2);m1p=0:N1/2;d=max(abs(abs(X1(m1p+1))-abs(X2(m1p+1))));mm=max(abs(X1(m1p+1)));b=d/mm*100;a=a+1;endN2,bm=-N2/2+1:N2/2;stem(m*D,abs(shift(X2)));对此程序作少数改动可以得到对其他信号的计算:P.73 例2.14平均功率计算CT 信号 ∑∞-∞==m m av c P 2 DT 信号 ∑-==102N m md av c P例2.15分别采用时域序列和频谱序列求信号平均功率例2.4题的信号功率P=2*pi/0.3;N=11;T=P/N;n=0:N-1;x=-1.2+0.8*sin(0.6*n*T)-1.6*cos(1.5*n*T);P1=sum(x.^2)*T/PX=fft(x/N);P2=sum(abs(X).^2)例2.16采用频谱序列求信号平均功率例2.5题的信号功率%program 2.9N=1024;D=2*pi/4;x=[ones(1,257) zeros(1,511) ones(1,256)];X=fft(x/N);mu=floor(5/D);m=2:mu+1;p=abs(X(1))^2+2*sum(abs(X(m)).^2)第三章 CTFT 和DTFT---一般信号的频谱实际信号都是非周期信号(非双边信号)周期信号对应于离散频率分量(离散频谱)非周期信号对应于连续频谱CTFT 连续时间信号的付氏变换 定义式()()⎰∞∞-=ωωπωd e X t x t j 21 ()()⎰∞∞--=dt e t x X t j ωω 频谱存在条件:()t x 绝对可积,而且在一个周期内间断点和极值点有限;例 3.1 e at u(t) 的频谱()()01<-−→←=a a j t u e t x FT at ωP.85 图3.1例3.2 w a (t )的频谱:时域窗口函数()()ωωa at a t t w t x FTa sin 201−→←⎩⎨⎧>≤==P.87 图3.2主瓣:高2a ,宽2π/a旁瓣:宽π/a 零点:n π/a窗口宽度与主瓣/旁瓣宽度成反比;窗口的时移不改变幅频特性,只引入线性相位; 例3.3 模拟理想低通滤波器 :频域窗口函数()()⎩⎨⎧≤=−→←==ωωωωωπωπω其余01sin sin cFTc c c H t c t t t xP.89 图3.3CT 周期信号的频谱()020ωωπδω-−−→←FTt j e步骤:将CT 周期信号先展开为CTFS ,再进行逐项变换; 若干常用信号的频谱(P.91 图3.4)()ωπδ21−→←FT()()000s in ωωπδωωπδω++--−→←j j t FT()()000c o s ωωπδωωπδω++-−→←FT t()()ωωπδj t u FT1+−→←例 3.4 冲激串的CTFT()()∑∑∞-∞=∞-∞=-−→←=m FTk tjm m Tet r 020ωωδπω频谱的性质()()ωj X t x F−→←连续有界:若()t x 绝对可积,则()ωX 有界并连续;奇偶性:()()ωj X t xF -−→←**P.94 表3.1时间实函数----幅频偶、相频奇 时间实偶----频谱实偶 时间实奇----频谱虚奇 时移与频移:()()ωωj X e t t x t j F00-−→←-()()()00ωωω-−→←j X t x e Ft j时移引入线性相位,频移对应复指数调制 时间尺度变换:()⎪⎭⎫⎝⎛−→←a j X a at x Fω1()()ωj X t x F-−→←-时间压缩对应频谱扩展Parseval’s relation 能量的频率分布()()ωωπd j X dt t x E 2221⎰⎰∞+∞-∞+∞-==能量只与幅频特性有关,时移不影响信号能量分布周期信号与非周期信号的能量对比 周期信号能量为无限大,平均功率为∑∞-∞==m mavc P 2,非零功率只存在于离散频率点;绝对可积的非周期信号能量为()()ωωπd j X dt t x E2221⎰⎰∞+∞-∞+∞-==,在任何特定频率点能量为零,能量分布于频率区间上;连续时间信号截断对于频谱的影响只有极少数信号可以求出频谱的解析表达式; 绝大多数实际信号只能采用数值方式求解频谱;对无限长时间连续信号,在实际计算时必须考虑截断并离散化;时域截断模型:以窗口函数乘以时间函数 ()()t w t x a ⋅时域乘积对应于频域卷积:()()()()⎰∞∞--=*ϖϖωϖπωωd X W W X a a 21其中 ()ωωωa W asin 2=单频率信号的截断效果 (P.104 图3.8)使单频率展宽,出现主瓣(高L=2a 、宽4π/L )和旁瓣(高<0.2L 、宽2π/L ); 对于有限带宽信号,截断导致带外泄露(能量)和纹波现象; L 越小,上述效应越显著;对于连续信号,增大L 可以将上述效应削弱到可以忽略的程度; 例3.5()()t u e t x t 1.0-=的频谱:采用不同宽度的窗口截断;(P.104 图3.8)Gibbs 现象用付氏变换表达时间函数时,当频谱信号含有不连续点时,频谱的纹波将会变窄并靠近该点,但纹波不会随L 的无限增大而消失,而是趋于一个常量(宽度无限小,高度约为不连续变化量的9%);(P.105 图3.9)将频谱变换为时间函数时存在相同的现象; 采用矩形窗口截断信号必然出现Gibbs 现象。
DSP技术与应用-第一章-绪论PPT课件

2021/6/7
8
1.1 DSP概述
▪ DSP与DSP技术 ▪ DSP技术发展的两个领域 ▪ 数字信号处理的实现方法 ▪ DSP系统的特点
2021/6/7
9
▪ 1. DSP与DSP技术
☉DSP(Digital Signal 理论和方法。
☉DSP(Digital Signal Processor) ----用于数字信号处理的可编程微处理器。
☉集成方便。因为DSP芯片内除DSP芯片还有一 定的外围电路。
2021/6/7
16
1.2 可编程DSP芯片
▪ DSP芯片的结构特点 ▪ DSP芯片的分类 ▪ DSP芯片的发展及趋势 ▪ DSP芯片的应用
2021/6/7
17
▪ 1. DSP芯片的结构特点
(1) 改进的哈佛结构
2021/6/7
18
(2)多总线结构 多总线结构可以保证在一个机器周期内多次访问程
2021/6/7
11
▪ 2. DSP技术发展的两个领域
☉理论:数字信号处理的理论和方法近二十年来得到迅 速的发展,为各种实时处理的应用提供了方法基础。 如:声音图像压缩编码,加密解密,调制解调,智能 天线。
☉应用:为了满足市场需求,随着微电子科学与技术的 进 步 , DSP 的 性 能 在 迅 速 提 高 。 如 : 时 钟 频 率 达 到 1.1GHZ;处理速度每秒90亿次,32位浮点运算,吞吐 率达到2Gbit/s
序空间和数据空间。
如:TMS320C54x内部有P、C、D、E 4条总线(每条 总线又包括地址总线和数据总线),可以在一个机器周期 内从程序存储器取1条指令、从数据存储器读2个操作数 和向数据存储器写1个操作数,大大提高了DSP的运行速 度。
DSP技术课程(第一章)1.

MOTOROLA HCS05/011/08
3. DSP(Digital Signal Processor)
TI的TMS320系列 ADI的ADSP2100系列 Lucent的DSP16xxx系列 Motorola的DSP56xxx系列 ......
该FTP上,欢迎下载。 E-MAIL:qguan@
第一章 概论
DSP技术
Digital Signal Processing 数字信号处理
Digital Signal Processor 数字信号处理器
第一章中,我们将介绍的内容:
数字信号处理框图 DSP的组成特点 DSP的应用 TI的DSP系列 定点与浮点DSP
DSP 技术
电子科技大学DSPs技术/培训中心 2001年9月
DSP技术课程讲述内容
第一章 DSP概述:在这一章中,我们将 介绍我们数字信号处理的基本框图、 DSP的组成特点 、 DSP的应用、 TI的 DSP系列等。
第二章 和第三章分别介绍DSP的硬件结 构与指令系统。在这两章中我们将介绍 TI的DSP系列中的C2X,C3X,C54X和 C6X系列。重点讲解C54X的硬件结构和 指令系统。
在TMS320C54x中,有RC、BRC、RSA和 REA共四个寄存器。其中,RC用于单指令 循环,BRC、RSA和REA用于块循环。
ST #99,BRC RPTB end_block-1 ... ... end_block:
用DSP实现FIR滤波
利用前面讲到的这些硬件资源,在 TMS320C2xx中实现FIR滤波器的程序可 以简化成:
• 中频采样软件无线电
LNA
DSP技术原理及应用(课件)

DSP的分类
⑵ 按数据格式分:DSP对数据的处理有两种格式:定点数据格式 和浮点数据格式。
①定点DSP芯片:数据以定点格式参加运算。 ②浮点DSP芯片:数据以浮点格式参加运算。不同浮点DSP所 采用的浮点格式可能不同。
⑶按用途分: ①通用型:适合普通的DSP应用。 ②专用型:为特定的功能、运算而设计的。如数字滤波、卷 积、FFT等。如TMS320C24x适合自动控制;MOTOLORA公 司的DSP56200专用于数字滤波。
滤 波
抗混叠滤波器将输入信号X(t)中比主要频率高的信号分量滤除, 避免产生信号频谱的混叠现象。 A/D——将输入的模拟信号转换为DSP芯片可接收的数字信号。 DSP芯片——对A/D输出的信号进行某种形式的数字处理。 D/A——经过DSP芯片处理的数字样值经D/A转换为模拟量,然 后进行平滑滤波得到连续的模拟信号。
DSP的分类
DSP的分类有三种方式:按基础特性分、按数据格式分、按用途分
⑴按基础特性分:DSP芯片的工作时钟(主频)和指令类型
①静态DSP芯片:该类型在某时钟频率范围内都能正常工作,除计 算速度有变化外,没有性能上的下降。如日本OKI电器公司的DSP 和TI公司的TMS320C2XX系列;
②一致性DSP:两种或更多的DSP芯片,其指令集、机器代码及管 脚结构相互兼容。如美国TI公司的TMS320C54X。
时钟 取指
N N+1 N+2 N+3
如四级流水线的操作图: 译码
N-1
N
N+1 N+2
取操作数
N-2 N-1
N
N+1
执行
N-3 N-2 N-1 N
利用这种流水线结构,加上执行重复操作,保证了数字信号处 理中用得最多的乘法累加运算可以在单个指令周期内完成。
DSP完整课件第3章 共29页

fin
CLKOUT
PLL选择 (SCSR1.11:9)
1500pF PLFF2
退出
2)外部滤波器电路回路
3.2.1 锁相环(PLL)
PLL有2个外接滤波输入引脚:PLLF,PLLF2 PLL模块使用外部滤波电路回路来抑制信号抖动和电磁干 扰,使信号抖动和干扰影响最小。
1 1Ω 0.68μ F
PLLF
(3)当未检测到累加器溢出时,其值为0;当溢出发生时, OV位被置1。
(4)根据被测试位的结果,测试控制标志位(TC)位被置1或0。
2019
退出
3.1.4 累加器(ACC)
存放CALU中的运算结果,其存放的数据可以执行单一的移位 或循环操作。其中的高位或低位字可以进入输出定标移位器进行 移位后再存放进数据存储器。与ACC有关的状态位有: 1)进位标志位C ① 当累加器中的数据相加时,结果有进位或减法无借位时C=1; 相减时,结果有借位或或加法无进位时,C=0 。 ② 当累加器中的数据被移动1位时,累加器中的最低位或最高位 进入C。
(2)外部时钟方式
最小和最大的CLKIN频率分别为4MHz和30MHz(2407A 为40MHz)。
2019
退出
3.2.2 看门狗定时器时钟
当CPU工作于低功耗模式下,看门狗能持续计数 WDCLK引脚为看门狗电路的时钟输入端。 WDCLK的时钟来自于时钟输出引脚CLKOUT。
WDCLK=CLKOUT/512 当CPU的挂起信号有效时,WDCLK将被停止。
2019
退出
3.1.6 状态寄存器ST0和ST1
1) 状态寄存器ST0
OV:溢出标志位。当中央算术逻辑单元发生溢出时,OV=1, 直到发生复位、执行以OV(溢出)或NOV(不溢出)为条件的转 移指令、或执行LST指令时被清0。
DSP课件第2章硬件结构

5、电源
采用高性能静态CMOS技术,供电电压为3.3V。 可用IDLE指令进入低功耗模式。
6、在片仿真接口
具有符合IEEEll49.1标准的在片仿真接口(JTAG)。
7、速度
单周期定点指令的执行时间为50ns、35ns或25ns(20MIPS,28.5MIPS, 或40MIPS)。
2.2 TMS320LF240x的总线结构
INTM:中断模式位
用来允许(INTM=0)或禁止(INTM=1)所有的可屏蔽中断。用 SETC OVM或CLRC OVM可将该位置1或清0。LST指令不影响OVM位。
DP:数据页面指针
当使用直接寻址方式时,DP存放存储器的数据页,DP与指令代 码的最低7位构成16位存储器地址。
数据存储器地址
SARAM的地址可以用于数据存储器和程序存储器。可通过软件配置 为外部存储器或内部SARAM。
SARAM在一个机器周期内只能访问一次。当CPU要求多次访问时, SARAM会向CPU提供一个未准备好的信号,然后在每个周期内执行一次 访问。
闪速存储器(Flash) 是电可擦除的、可编程的、可长期保存数据的存储器。
CPU的基本组成包括: 32位中央算术逻辑运算单元(CALU); 32位累加器(ACC);输入与输出数据比例移位器; 16位×16位的乘 法器(MUL)以及乘积比例移位器。
CPU功能结构图
2、输入比例部分
功能:将来自存储器的16位数据左移0~16位送往中央算术逻辑单元 (CALU)。
移位方法:左移后有使用的低位LSB填0,高位MSB填0或用符号 扩展,取决于状态寄存器ST1的符号扩展模式位SXM(D10)。 SXM=0 填0 SXM=1 符号扩展
中央算术逻辑单元
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§2 Discrete-Time Signals And LTI Systems
In Time-Domain §2.1 Discrete-Time Signals
2.1.1 Sequences And Representation [ n] (Commonly used) 1.The Unit Impulse
2. Time-Domain Characterization of LTI Discrete-Time System
Input-Output Relationship
Impulse and Step Responses
• The response of a discrete-time system to a unit sample sequence {[n]} is called the unit impulse response or simply, the impulse response, and is denoted by {h[n]} • The response of a discrete-time system to a unit step sequence {[n]} is called the unit step response or simply, the step response, and is denoted by {s[n]}
x=K*exp(c*n);
Figure 2.16
§2.2 Discrete-Time Systems • • • • Linear System Shift-Invariant System Causal System Stable System
x[n]
y[n]
Discrete-time systme
• Example - The impulse response {h[n]} of the factor-of-2 interpolator
y[n]
1 xu [n] Байду номын сангаас( xu [n 1] xu [n 1]) 2
is obtained by setting xu[n]=[n] and is given by
• The impulse response is thus a finite-length
sequence of length 3:
1 h[n] [n] ( [n 1] [n 1]) 2
{h[n]} {0.5, 1 0.5}
3.
FIR And IIR System (recursive and nonrecursive)
x a (t )
S/H A/D
x[n] y[n]
Digital Processor Fig. 1.47
D/A LPF
ya (t )
x a (t )
ya (t )
y[n]
: analog signals :digital signals(binary)
x[n]
12 8 4
12 8 4
0 2
4 6 8 10 12 14 16 Time in sec (a)
x[n]
m
x[m] [n m] x[n] [n]
2.1.3 Sequence Generation Using MATLAB Program 2-1(read and excercise)
n=1:N; stem(n,real(x)); stem(n,imag(x));
0
5
10
20
...
n
1
xd [ n] x[ nM ]
1
0
5
...
Fig 2.9
and 2.10
10
n
1
Note: The Sampling Process If a continuous signal xa (t ) A cos(2f 0t ) A cos(0t ) ,the sampling frequency isFT 1 / T .The discrete signal is: x[n] xa (nT ) A cos( 0 nT ) (or x[n] A cos( 0 n ) ). Where 0 0T is digital angular frequency. If 0 / 2 f 0 / 2FT m / N ( 0 / 2 is not rational),X[n] is not periodic. 3.An arbitrary sequence can be represented as the sum of impulses :
§1 Introduction 1.What’s DSP?How to DSP? DSP----Processing signals in digital form. The scheme for the digital processing of an analog signal (fig 1.47)
(FIR)
Example 2.3
y[n] 1x[n] 2 x[n 1] 3 x[n 2] 4 x[n 3]
Example 2.4 (IIR)
y[n] b0 x[n] b1 x[n 1] b2 x[n 2] a1 y[n 1] a2 y[n 2]
1
n
0 N-1
4.The Exponential(Causal) sequence
a [n]
n
0
a [ n]
n
...
n
5.Sinusoidal and Exponential Sequence Sinusoidal: Exponential: x[ n]
n
x[n] A cos( 0 n ), n
must
be a rational number) .
example
1 f [n] cos n sin n 8 2 6
Its period is 48 which is the lease common mutiple of 16 and 12. Because
e
j0n
e
j (0 2 k ) n
(k is integer ),the discrete sinusoidal signal has the highest angular frequency .
Note: some classification of sequences (a) Left-sided,right-sided,two-sided, finite-duration; (b) Even,odd; (c) Periodic,aperiodic(energy or power signal)
N dk k 0
y[n k ]
M k 0
pk x[n k ]
(2.82)
Note: Up-sampling
x[n / L], n 0,1,2,... y[n] 0, otherwise
is a time-varying system,so does Down-sampling.
Reference books: 1. A.V.Oppenheim and R.W.Schafer,Digital Signal Processing,1975 2. S.J.Orfanidis ,Introduction of Signal Processing,Prentice Hall,1998, 3. 彭启综等 ,《DSP 与实时数字信号处理》, 电子科大出版社,1995 4.程佩青,《数字信号处理教程》,清华大学 出版社,1997年 5.胡广书,《数字信号处理-理论、算法与 实现》,清华大学出版社,1997年 6.皇甫堪等,《现代数字信号处理》,电 子工业出版社,2003年
0 2 4 6 8 10 12 14 16 Time in sec (b)
0 2
4 6 8 10 12 14 16 Time in sec (c)
0 2 4 6 8 10 12 14 16 Time in sec (d) 12 8 4
12 8 4
0 2 4 6 8 10 12 14 16 Time in sec (e)
0 2 4 6 8 10 12 14 16 Time in sec (f)
Fig 1.48:Typical waveforms of signals
A digital processor :Hardwares(VLSI) and Softwares.
2. Why DSP? Advantage to ASP: more reliable(less sensitive to tolerances such as temperature,noise),higher accurate,can be integrated on a single chip. Limit: A/D D/A rates are not enough available in some applications.
Digital Signal Processing
The Textbook:Digital Signal Processing----A Computer- Based Approach, Sanjit K.Mitra,Second Edition,McGraw-Hill,2001
Website:
http://202.115.21.138/wlxt/listcourse.asp?courseid=0003
1
n
2.The Unit Step
