高三数学直线平面简单几何体PPT优秀课件
合集下载
高考数学复习 第九章 直线、平面、简单几何体(B)9(B)-3课件

(1)求证:BC⊥面D1DB; (2)求D1B与平面D1DCC1所成角的大小. 答案: 解法一: (1) 证明: ∵ ABCD - A1B1C1D1 为直四棱柱, ∴DD1⊥平面ABCD ∴BC⊥D1D ∵AB∥CD,AB⊥AD, ∴四边形ABCD为直角梯形. 又∵AB=AD=1,CD=2, ∴BC⊥DB. ∵D1D∩DB=D, ∴BC⊥平面D1DB.
PC的中线, ∴DE⊥PC,①又由PD⊥平面ABCD,得PD⊥BC. ∵底面ABCD是正方形,CD⊥BC, ∴BC⊥平面PDC.
而DE⊂平面PDC.∴BC⊥DE.②
由①和②推得DE⊥平面PBC.而PB⊂平面PBC, ∴DE⊥PB,又DF⊥PB且DE∩DF=D, 所以PB⊥平面EFD.
【例2】 已知:正方体ABCD-A1B1C1D1中(如图).
⑤若m⊥α,α∥β,则m⊥β(√)
⑥若m⊥α,n⊥α,则m∥n(√)
⑦若α∩β=l,α⊥γ,β⊥γ,则l⊥γ(√)
⑧若α⊥β,m∥β,则m⊥α(×)
⑨若线段 AB 、 CD 在同一平面 α 内的射影相等.则 AB =CD(×) ⑩在平面α内总能找到一条直线与直线m垂直(√)
2.(2009·北京丰台一模)已知直线m⊂平面α,直线n⊂
(1)求证:B1D⊥BC1; (2)求证:B1D⊥面ACD1; (3)若B1D与面ACD1交于O,求证:DO OB1=1 2.
[证明] (1)∵ABCD-A1B1C1D1为正方体,
∴ DC⊥ 面 BCC1B1 , B1D 在 面 BCC1B1 内 的 射 影 为
B1C.∵BCC1B1为正方形,∴BC1⊥B1C. ∴BC1⊥B1D,即B1D⊥BC1.(三垂线定理) (2)(1)中证明了体对角线B1D与面对角线BC1垂直, 同理可证:B1D⊥AD1,B1D⊥AC.∴B1D⊥平面ACD1.
高三数学第一轮复习 第十章《直线、平面、简单几何体A》课件10A5

由(Ⅰ)有 PQ∥DC,又 PQ=12EB=DC, 所以四边形 CQPD 为平行四边形,故 DP∥CQ, 因此 DP⊥平面 ABE,∠DAP 为 AD 和平面 ABE 所成 的角,
在 Rt△DPA 中,AD=
5,DP=1,sin∠DAP=
5 5.
因此
AD
和平面
ABE
所成角的正弦值为
5 5.
例 2 如图,在三棱锥 P-OCB 中,PO⊥平面 OCB, OB⊥OC,OB=OC= 2,PC=4,D 为 PC 中点,求 OD 与平面 PBC 所成的角.
15 3 OH
∵VP-OBC=VO-PBC,∴
315OH=
14 3
∴OH= 12510,
∴sin∠ODH=OOHD=
12510=
210 30
∴直线 OD 与平面 PBC 所成的角为 arcsin
210 30
方法二:取 BC 中点 E,连结 PE,作 OF⊥PE 于点 F,
连结 DF,则 OF⊥平面 PBC.
【解析】 如图,过点 P 作 PA⊥α 于 A,PB
⊥β于 B,设 PA、PB 确定的平面为 γ,设 a∩γ =O,则 γ∩α=OA,γ∩β=OB,连 OP.
∵PA⊥α,PB⊥β,∴PA⊥a,PB⊥a,PA ∩PB=P.∴a⊥γ.
又 AO⊂γ,BO⊂γ,∴AO⊥a,BO⊥a,
∴∠AOB=120°.
∴CM=MB=12PB=12
1+22=
5 2
在△BCM 中,BM·CM=BC· BM2-B2C2
∴BM=
2×
3 2=
5
6 5
2
∵AB=2,∴cos∠ANB=AN22×+ABNN×2-BANB2=-23
直线平面和简单几何体ppt

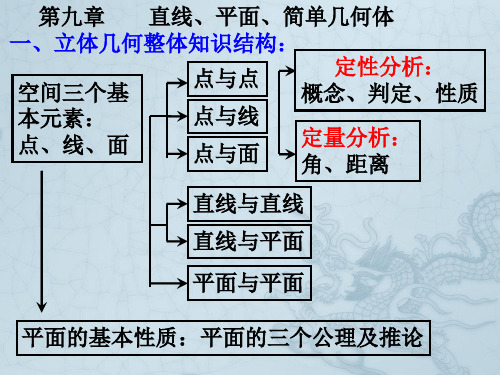
平 面 的 基 本 性 质
性 质
A l
B
公理2:
A B C
l
P
公理3:
A B C
推论2:
ap b
推论3:
b a
平行直线
公理4 等角定理 判 定
直线和直线
相交直线 异面直线
线在面内
判
定
如果一条直线和一个平面内 斜线和平面所成的角,是这条斜 如果两个平行平面同时和第 垂线段和斜线段中: 如果和这个平面的一条斜线 平行于同一直线的两条直 两角两边分别平行 过平面外一点和平面内一点的直 的两条相交直线都垂直,那 线和这个平面的直线所成角的一 三个平面相交,那么它们的 如果平面外一条直线和这个平面 如果一个平面经过另一个平 的射影垂直,那么它也和这 如果一条直线和一个平面平行,经 线互相平行。 且方向相同,两角 如果两条直线同垂直于一个平 么这条直线垂直于这个平面。 射影相等的两条斜线段相等,射 线,和平面内不经过该点的直线 如果一个平面内有两条相交直 如果两平面垂直,那么在 交线平行。 切角中最小的角。 条斜线垂直。 内的一条直线平行,那么这条直 面的一条垂线,那么这两个 相等。 过这条直线的平面和这个平面相交, 影较长的斜线段也较长。 面,那么这两条直线平行。 是异面直线。 线都平行于另一个平面,那么 一个平面内垂直于交线的 如果两条平行直线中的一条 线和这个平面平行。 平面互相垂直。 如果两个平面平行,那么其 那么这条直线和交线平行。 在平面内的一条直线,如果 单直三面角余弦公式: 这两个平面平行。 直线垂直于另一个平面。 相等的斜线段的射影相等,较长 垂直于一个平面,那么另一 异面直线的距离公式。 中一个平面的直线平行于另 和这个平面的一条斜线垂直, cosA=cosBcosC 的斜线段的射影也较长。 条也垂直于这个平面。
高三数学第一轮复习 第十章《直线、平面、简单几何体A》课件

思考题 2 (08·四川,文)如图,平面 ABEF⊥平面 ABCD,四边形 ABEF 与 ABCD 都是直角梯形,∠BAD= ∠FAB=90°,BC 綊21AD,BE 綊12FA,G、H 分别为 FA、
FD 的中点.
(Ⅰ)证明:四边形 BCHG 是平行四边形; (Ⅱ)C、D、F、E 四点是否共面?为什么?
• 探究3 所谓线共点问题就是证明三条或三条以上的直线交于 一点.
• (1)证明三线共点的依据是公理2.
• (2)证明三线共点的思路是:先证两条直线交于一点,再证明第 三条直线经过该点,把问题化归到证明点在直线上的问题.实 际上,点共线、线共点的问题都可以化归为点在直线上的问题 来处理.
• 思考题3 如图,在四面体ABCD中作截面PQR,若PQ、CB的延 长线交于M,RQ、DB的延长线交于N,RP、DC的延长线交于K.
四点共面,设为α
• 可证PS∥QN,∴P、Q、N、S四点共面,设为β • ∵α、β都经过P、N、S三点,∴α与β重合 • ∴P、Q、R、S四点共面.
• 探究2 (1)公理3及其推论是立体几何最基本、最重要的定理, 它的主要作用是确定平面
• (2)本题给出了判断四点是否共面的基本方法 • ①判断四点连结是否有平行直线或相交直线 • ②由部分元素确定平面,然后证明这些平面重合
• 7.①了解棱柱的概念,掌握棱柱的性质,会画直棱柱的直观 图.
• ②了解棱锥的概念,掌握正棱锥的性质,会画正棱锥的直观 图.
• 8.①了解多面体及正多面体的有关概念 • ②了解球的概念,掌握球的性质,掌握球的表面积和体积公式.
• 平面的基本性质
• ①公理1:如果一条直线上的两点在一个平面内,那么这条直
• 题型一 平面的性质 • 例1 下列命题: • ①空间不同三点确定一个平面; • ②有三个公共点的两个平面必重合; • ③空间两两相交的三条直线确定一个平面; • ④三角形是平面图形; • ⑤平行四边形、梯形、四边形都是平面图形; • ⑥垂直于同一直线的两直线平行; • ⑦一条直线和两平行线中的一条相交,也必和另一条相交; • ⑧两组对边相等的四边形是平行四边形. • 其中正确的命题是________.
高三数学第九章直线、平面、简单几何体知识点课件
a
命题
// , a a //
// , a , b a // b
l
// , l l
§9.5平面与平面垂直 一、垂直关系的转化(说出相关定理):
面面 垂直 判定
A
D
C B
AB ,AB
b a // b
二、面面平行的判定 图形 面 面 平 行 的 判 定
命题 a b l
A
a ,b ,a b=A, a// ,b// //
l, l //
*
// , // //
三、面面平行的性质 图形 面 面 平 行 的 性 质
(2) (3) (7)
线线垂直(12)(13)
(8) (12)三垂线定理 (9) (13)三垂线逆定理
线面平行 (4) (5)
线面垂直 (10) (11)
面面平行(6)
面面垂直
9.1平面的性质
公理1
作用
公理2
如果一条直线上的两点在一个平面内, 判断直线在平 那么这条直线上所有的点都在这个平面 面内的依据 内 如果两个平面有一个公共点,那么它们 两个平面相交 还有其他公共点,且所有这些公共点的 以及它们的交 点共线的依据 集合是一条过这个公共点的直线
PA
§9.4线面平行与面面平行
一,直线与平面平行的判定和性质
线 面 平 行 判 定 线 面 平 行 性 质
a
a a//
a , b , a // b a //
高考数学专题复习第9单元直线平面简单几何体(下)课件文大纲人教版

[解答] (1)p=a-b=(1,1,0)-(0,1,1)=(1,0,-1); q=a+2b-c=(1,1,0)+2(0,1,1)-(1,0,1)=(0,3,1); p·q=(1,0,-1)·(0,3,1) =1×0+0×3+(-1)×1=-1. (2)设 n=(x,y,z),则 n·a=-2x+2y=0,① n·b=-2x+2z=0.②
[证明] 设正方体的棱长为 1,以 D 点为原点,D→A、D→C、D→D1 为坐标向量,建立空间直角坐标系 D-xyz,如图所示.
(1)易知 A(1,0,0)、E1,1,12、F0,12,0、D1(0,0,1).∵A→E =0,1,12,D→1F=0,12,-1.
又A→E·D→1F=0,1,12·0,12,-1=0, ∴AE⊥D1F.
第57讲 │ 知识梳理
知识梳理
1.空间向量的加减和数乘的坐标表示 设 a=(a1,a2,a3),b=(b1,b2,b3),则 (1)a+b=_(_a_1_-__b_1, ___a_2-__b_2_,__a_3_-__b_3_) ___; (2)a-b=__(_a_1_+__b_1_,__a_2+__b_2_,__a_3_+__b_3_) ____; (3)λa=___(λ_a_1_,__λ_a_2_,__λ_a_3)_(_λ_∈__R_)_______; (4)a∥b(b≠0)⇔_a_1=__λ_b_1_,__a_2_=__λ_b_2,__a_3_=__λ_b_3_(λ. ∈R)
则 B(1,1,0),E11,34,1, D(0,0,0),F10,14,1, ∴B→E1=0,-41,1,D→F1=0,14,1,
第57讲 │ 要点探究
∴|B→E1|=|D→F1|= 417,B→E1·D→F1=0×0+-14×14+1×1=1156, 15cos〈B→EFra bibliotek,D→F1〉=
[证明] 设正方体的棱长为 1,以 D 点为原点,D→A、D→C、D→D1 为坐标向量,建立空间直角坐标系 D-xyz,如图所示.
(1)易知 A(1,0,0)、E1,1,12、F0,12,0、D1(0,0,1).∵A→E =0,1,12,D→1F=0,12,-1.
又A→E·D→1F=0,1,12·0,12,-1=0, ∴AE⊥D1F.
第57讲 │ 知识梳理
知识梳理
1.空间向量的加减和数乘的坐标表示 设 a=(a1,a2,a3),b=(b1,b2,b3),则 (1)a+b=_(_a_1_-__b_1, ___a_2-__b_2_,__a_3_-__b_3_) ___; (2)a-b=__(_a_1_+__b_1_,__a_2+__b_2_,__a_3_+__b_3_) ____; (3)λa=___(λ_a_1_,__λ_a_2_,__λ_a_3)_(_λ_∈__R_)_______; (4)a∥b(b≠0)⇔_a_1=__λ_b_1_,__a_2_=__λ_b_2,__a_3_=__λ_b_3_(λ. ∈R)
则 B(1,1,0),E11,34,1, D(0,0,0),F10,14,1, ∴B→E1=0,-41,1,D→F1=0,14,1,
第57讲 │ 要点探究
∴|B→E1|=|D→F1|= 417,B→E1·D→F1=0×0+-14×14+1×1=1156, 15cos〈B→EFra bibliotek,D→F1〉=
高三数学第一轮复习 第十章《直线、平面、简单几何体A》课件10A4

• (2)∵SA⊥平面AC,DC⊂平面AC,∴SA⊥DC. • 又AD⊥DC,SA∩AD=A,∴DC⊥平面SAD, • 又AG⊂平面SAD,∴DC⊥AG. • 又由(1)有SC⊥平面AEF,AG⊂平面AEF, • ∴SC⊥AG且SC∩CD=C,∴AG⊥平面SDC, • 又SD⊂平面SDC,∴AG⊥SD.
• 如果一个平面与另一个平面的一条垂线平行,那么这两 个平面垂直,这是一个真命题,故C对;
• 对D来讲若c∥α,α⊥β,则c与β的位置关系不定,故选C.
• 2.设α,β,γ是三个互不重合的平面,m,n是两条不重 合的直线,则下列命题中正确的是( )
• A.若α⊥β,β⊥γ,则α⊥γ
• B.若α∥β,m⊄β,m∥α,则m∥β
• ①若α∥β,α⊥γ,则β⊥γ; • ②若α⊥γ,β⊥γ,且α∩β=l,则l⊥γ; • ③若直线l与平面α内的无数条直线垂直,则直线l与平面 • α垂直; • ④若α内存在不共线的三点到β的距离相等,则平面α平行
于平面β. • 上面命题中,真命题的序号为________(写出所有真命题
的序号). • 答案 ①②
• 又∵侧面BB1C1C⊥底面A1B1C1,交线为B1C1, • ∴NC1⊥侧面BB1C1C. • 又∵NC1⊂面BNC1, • ∴截面C1NB⊥侧面BB1C1C, • 即截面MBC1⊥侧面BB1C1C.
• (3)结论是肯定的,充分性已由(2)证明.
• 下面仅证明必要性(即由截面BMC1⊥侧面BB1C1C推出AM= MA1,实质是证明M是AA1的中点),
A3演示文稿设计与制作 信息技术2.0 高三数学第一轮复习 第十章《直线、平面、简单几何体A》课件10A4
微能力认证作业
• 一、直线与平面垂直 • 1.判定定理 • (1)如果一条直线和一个平面内的 两条相交直线都垂
高中数学必修《简单几何体》ppt课件

棱柱用表示两底面多边形的顶点的字母表
示2024棱/1/9 柱;如:棱柱ABCDEA1B1C1D1E1
33
二 观察下列几何体;有什么相同点
2024/1/9
34
1 棱锥的概念
有一个面是多边形;其余各面是有一个公共 顶点的三角形; 由这些面所围成的几何体叫做 棱锥
这个多边形面叫做棱锥的底面
有公共顶点的各个三角形叫做棱锥 的侧面
3 棱台的表示法:棱台用表示上 下底面各顶
点的字母来表示;如图棱台ABCDA1B1C1D1
A1 D1
C B1 1
2024/1/9
41
❖ 思考题:1 用平行于圆柱;圆锥;圆台的底面的平
面去截它们;那么所得的截面是什么图形 性质1:平行于圆柱;圆锥;圆台底面的截面都是 圆 2 过圆柱;圆锥;圆台的旋转轴的截面是什么图形 性质2:过轴的截面轴截面分别是全等的矩形;等
2024/1/9
22
2 圆台的表示: 用表示它的轴的字母表示;如圆台OO′
O'
2024/1/9
O
底面
轴 侧面
母线 23
底面
总结:由于球体 圆柱 圆锥 圆台分别由平面图 形半圆 矩形 直角三角形 直角梯形通过绕着一 条轴旋转而生成的;所以把它们都叫旋转体
2024/1/9
24
§1 2:简单的多面体
❖ 大家知道:平静的桌面 黑板面 湖面都给我们一种平面的 局部感觉
❖ 请大家想一想;在空间中;平面给大家的感觉会是怎样的呢
❖ 在空间中;平面和直线一样;都是无限延展的;因此;我们不 能把一个无限延展的平面在一张纸上或书本上表示出来; 我们通常用平面的一部分表示整个平面
❖ 例如:
2024/1/9
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010届高考数学二轮 复习系列课件
23《直线平面简 单几何体》
二面角与距离
高考考纲透析: 熟练掌握求二面角的大小,空间距离的求法
高考热点: 求二面角每年必考,作为解答题可能性最大,空间距离则 主要是求点到面的距离
知识整合:1.转化思想:将异面直线所成的角,直线与平面所成的角转化为平面 角,然后解三角形;
C1
F
D A
EC B
热点题型2: 定义法作二面角的平面角
已知四棱锥P-ABCD的底面为直角梯形,
AB∥DC, D 1 A 9 B 0 ,P A 底面AB,C且D
PA=AD=DC = 2 AB=1,M是PB的中点 (Ⅰ)证明:面PAD⊥面PCD; (Ⅱ)求AC与PB所成的角; (Ⅲ)求面AMC与面BMC所成二面角的大小
高考热点: 异面直线所成角,直线与平面所成角
知识整合:1.转化思想:将异面直线所成的角,直线与平面所成的角转化为平面角, 然后解三角形;
知识整合: 1.转化思想:将异面直线所成的角,直线与平面所成 的角转化为平面角,然后解三角形;
线 线 平 行 线 面 平 行 面 面 平 行
线 线 线 面 面 面
(Ⅰ)求证OD∥平面PAB (Ⅱ) 求直线OD与平面
PBC所成角的大小;
P
D
C
A
O
B
热点题型3: 二面角及点到面的距离的求法
如图,直二面角D—AB—E中,四边形ABCD是边长为2的
正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
(Ⅰ)求证AE⊥平面BCE;
(Ⅱ)求二面角B—AC—E的大小;
如图,在四棱锥P—ABCD,底面ABCD为矩
形,侧棱PA⊥底面ABCD,AB= 3 ,BC=1,
PA=2,E为PD的中点
(Ⅰ)求直线AC与PB所成角的余弦值;
(内Ⅱ找一)点在N侧,面使PANBE⊥P
面PAC,并求出N
E
点到AB和AP的距离
D
C
A
B
热点题型4: 立体几何与转化的思想
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA, 点O、D分别1是AC、PC的中点,OP⊥底面ABC.
高考热点: 异面直线所成的角,直线和平面平行,垂直的 判定与性质,两个平面垂直的判定与性质,直 线和平面所成的角,二面角及其平面角,点到 平面的距离
知识整合: 用空间向量可以解决的立体几何问题有: ㈠利用两个向量共线的条件和共面向量定理,可以 证明有关线线平行,线面平行,面面平行问题
㈡利用两个向量垂直的充要条件可以证明有关线 线,线面,面面垂直问题
知识整合: 1.二面角的平面角的作法:
①定义 ②三垂线定义 ③ 垂面法 2. 点到平面的距离求法有: ①体积法 ②直接法,找出点在平面内的射影 3.转化思想: 例如求一个平面的一条平行线上一点到这个 平面的距离较难时,可转化为平行线上其他的点到这个平 面的距离
热点题型1: 异面直线所成角
如图所示的多面体是由底面为ABCD的长方体被截面 AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3, BE=1 (Ⅰ)求BF的长; (Ⅱ)求点C到平面AEC1F的距离
(Ⅲ)求点A到平面BDF的距离
A1
D1
F B1
A C1
D
E
B
C
THANKS
FOR WATCHING
演讲人: XXX
PPT文档·教学课件
如图,在长方体ABCD—A1B1C1D1,中,AD=AA1=1,AB=2 点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1—EC—D
的大小为
D1
C1
4
A1
B1
D
A
E
C B
线线角与线面角
高考考纲透析: 线线,线面,面面的平行与垂直,异面直线所成角,直 线与平面所成角
(Ⅲ)求点D到平面ACE的距离.
D
C
AF
B
E
样题4:
如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1, 直线BD与平面AA1BB1所成的角为300,AE垂直BD于E, F为A1B1的中点. (Ⅰ)求异面直线AE与BF所成的角;
(Ⅱ)求平面BDF与平面AA1B所成二面角(锐角)的大小;
P
M
A
B
D
C
热点题型3: 三垂线定理或逆定理作二面角的平面角
如左下图,已知ABCD是上,下底边长分别为2和6,
高为 3 的等腰梯形,将它沿对称轴OO1折成直二
面角,如右下图(Ⅰ)证明:AC⊥BO1;(Ⅱ) 求二面角O-AC-O1的大小.
D O1 C
O1 C
D
A
O
B
O
B
图1
图2
A
热点题型4: 二面角与探索问题
2.求角的三个步骤:一猜,二证,三算.猜是关 键,在作线面角时,利用空间图形的平行,垂 直,对称关系,猜斜线上一点或斜线本身的 射影一定落在平面的某个地方,然后再证
热点题型1: 异面直线所成角
C1
B1
A1
C
B
A
D
热点题型2: 直线与平面所成角
A1
F
C
A
C1 E B1
B
热点题型3: 立体几何中的探索问题
㈢利用两个向量的夹角公式可以求解有关角的问 题
㈣利用向量的模及向量在单位向量上的射影可以 求解有关的距离问题
热点题型1: 求异面直线所成的角角
D1 A1
D A
C1 B1
C B
热点题型2: 求直线与平面所成的角角
如=面图 A12 BP,CA在.,三点棱O、锥DP-分A别B是C中AC,、APBC⊥的B中C,点A,BO=PB⊥C底
(Ⅰ)当k= 2 时,求直线PA与平面PBC所成角的大小; (Ⅱ) 当k取何值时,O在平面PBC内的射影恰好为△PBC
的
B
空间向量及其应用
高考考纲透析: 线线,线面,面面的平行与垂直,空间角与距离,棱柱,棱 锥,球,空间向量
知识整合: 1.转化思想:将异面直线所成的角,直线与平面所成的角转化为平 面角,然后解三角形;
23《直线平面简 单几何体》
二面角与距离
高考考纲透析: 熟练掌握求二面角的大小,空间距离的求法
高考热点: 求二面角每年必考,作为解答题可能性最大,空间距离则 主要是求点到面的距离
知识整合:1.转化思想:将异面直线所成的角,直线与平面所成的角转化为平面 角,然后解三角形;
C1
F
D A
EC B
热点题型2: 定义法作二面角的平面角
已知四棱锥P-ABCD的底面为直角梯形,
AB∥DC, D 1 A 9 B 0 ,P A 底面AB,C且D
PA=AD=DC = 2 AB=1,M是PB的中点 (Ⅰ)证明:面PAD⊥面PCD; (Ⅱ)求AC与PB所成的角; (Ⅲ)求面AMC与面BMC所成二面角的大小
高考热点: 异面直线所成角,直线与平面所成角
知识整合:1.转化思想:将异面直线所成的角,直线与平面所成的角转化为平面角, 然后解三角形;
知识整合: 1.转化思想:将异面直线所成的角,直线与平面所成 的角转化为平面角,然后解三角形;
线 线 平 行 线 面 平 行 面 面 平 行
线 线 线 面 面 面
(Ⅰ)求证OD∥平面PAB (Ⅱ) 求直线OD与平面
PBC所成角的大小;
P
D
C
A
O
B
热点题型3: 二面角及点到面的距离的求法
如图,直二面角D—AB—E中,四边形ABCD是边长为2的
正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
(Ⅰ)求证AE⊥平面BCE;
(Ⅱ)求二面角B—AC—E的大小;
如图,在四棱锥P—ABCD,底面ABCD为矩
形,侧棱PA⊥底面ABCD,AB= 3 ,BC=1,
PA=2,E为PD的中点
(Ⅰ)求直线AC与PB所成角的余弦值;
(内Ⅱ找一)点在N侧,面使PANBE⊥P
面PAC,并求出N
E
点到AB和AP的距离
D
C
A
B
热点题型4: 立体几何与转化的思想
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA, 点O、D分别1是AC、PC的中点,OP⊥底面ABC.
高考热点: 异面直线所成的角,直线和平面平行,垂直的 判定与性质,两个平面垂直的判定与性质,直 线和平面所成的角,二面角及其平面角,点到 平面的距离
知识整合: 用空间向量可以解决的立体几何问题有: ㈠利用两个向量共线的条件和共面向量定理,可以 证明有关线线平行,线面平行,面面平行问题
㈡利用两个向量垂直的充要条件可以证明有关线 线,线面,面面垂直问题
知识整合: 1.二面角的平面角的作法:
①定义 ②三垂线定义 ③ 垂面法 2. 点到平面的距离求法有: ①体积法 ②直接法,找出点在平面内的射影 3.转化思想: 例如求一个平面的一条平行线上一点到这个 平面的距离较难时,可转化为平行线上其他的点到这个平 面的距离
热点题型1: 异面直线所成角
如图所示的多面体是由底面为ABCD的长方体被截面 AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3, BE=1 (Ⅰ)求BF的长; (Ⅱ)求点C到平面AEC1F的距离
(Ⅲ)求点A到平面BDF的距离
A1
D1
F B1
A C1
D
E
B
C
THANKS
FOR WATCHING
演讲人: XXX
PPT文档·教学课件
如图,在长方体ABCD—A1B1C1D1,中,AD=AA1=1,AB=2 点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1—EC—D
的大小为
D1
C1
4
A1
B1
D
A
E
C B
线线角与线面角
高考考纲透析: 线线,线面,面面的平行与垂直,异面直线所成角,直 线与平面所成角
(Ⅲ)求点D到平面ACE的距离.
D
C
AF
B
E
样题4:
如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1, 直线BD与平面AA1BB1所成的角为300,AE垂直BD于E, F为A1B1的中点. (Ⅰ)求异面直线AE与BF所成的角;
(Ⅱ)求平面BDF与平面AA1B所成二面角(锐角)的大小;
P
M
A
B
D
C
热点题型3: 三垂线定理或逆定理作二面角的平面角
如左下图,已知ABCD是上,下底边长分别为2和6,
高为 3 的等腰梯形,将它沿对称轴OO1折成直二
面角,如右下图(Ⅰ)证明:AC⊥BO1;(Ⅱ) 求二面角O-AC-O1的大小.
D O1 C
O1 C
D
A
O
B
O
B
图1
图2
A
热点题型4: 二面角与探索问题
2.求角的三个步骤:一猜,二证,三算.猜是关 键,在作线面角时,利用空间图形的平行,垂 直,对称关系,猜斜线上一点或斜线本身的 射影一定落在平面的某个地方,然后再证
热点题型1: 异面直线所成角
C1
B1
A1
C
B
A
D
热点题型2: 直线与平面所成角
A1
F
C
A
C1 E B1
B
热点题型3: 立体几何中的探索问题
㈢利用两个向量的夹角公式可以求解有关角的问 题
㈣利用向量的模及向量在单位向量上的射影可以 求解有关的距离问题
热点题型1: 求异面直线所成的角角
D1 A1
D A
C1 B1
C B
热点题型2: 求直线与平面所成的角角
如=面图 A12 BP,CA在.,三点棱O、锥DP-分A别B是C中AC,、APBC⊥的B中C,点A,BO=PB⊥C底
(Ⅰ)当k= 2 时,求直线PA与平面PBC所成角的大小; (Ⅱ) 当k取何值时,O在平面PBC内的射影恰好为△PBC
的
B
空间向量及其应用
高考考纲透析: 线线,线面,面面的平行与垂直,空间角与距离,棱柱,棱 锥,球,空间向量
知识整合: 1.转化思想:将异面直线所成的角,直线与平面所成的角转化为平 面角,然后解三角形;
