第二章复变函数的积分
复变函数及积分变换第二章

x
arg z在负实 轴上不连续.
若z0=x0+iy0不是原点也不是负实轴及虚轴上的点
arctan( y / x),
arg z arctan( y / x) π,
arctan( y / x), arctan( y / x),
x0 0
lim
z z0
arg
z
lim
( x, y)( x0
,
y0
)
arctan(
) ,则说函数 f(z) 在点 z0 处连 内每一点都连续,那么称函
数f(z)在区域D内连续.
定理2.3 若 f(z)、g(z) 在点z0连续,则其和、差、积、 商(要求分母不为零)在点z0处连续.
(1)多项式 w a0 zn a1zn1 an1z an 在整个复平
面上连续;
(2)任何一个有理分式函数
例2.2 判断下列函数在原点处的极限是否存在,若存
在,试求出极限值:
(1) f (z)
z Re(z) ; z
(2) f (z)
Re( z
z
2
2
)
.
解: (1)方法一
因为
f (z)
z
Re(z) z
z
所以 0,取 ,当0 z 时,总有
f (z) 0 f (z) z
根据极限定义 lim f (z) 0 z0
解:dw lim f (z Δz) f (z) lim (z Δz)n zn
dz Δz0
Δz
Δz 0
Δz
Δlizm0(Cn1 zn1 Cn2 zn2Δz
C n1 n
zΔz
n2
Cnn Δz n1 )
Cn1zn1 nzn1,
第二章 复变函数的积分

复积分的牛顿-莱布尼兹公式
记住
务必 记住
世界科技发展史 10万年前火的使用、石制工具 3万年前关于来世、生育等思想 1万年前栽种谷物、动物驯养、陶器出现 5000年前金字塔和庙宇、史前巨石阵 4000年前中国早期的天文学,金属加工,印度数学开 端 3000年前埃及历法 约2000年前后托勒密的天文学和地学 希腊数学家和哲学家毕达哥拉斯(公元前572--公元前 497年)、柏拉图(公元前427年--前347年)和亚里士多 德(公元前384 -- 公元前322)和希腊数学家如欧几里 得(公元前325--公元前265)
典型应用实例
例 3.2.1 计算积分
b
a
z sin z dz
2
【解】 函数 z sin z 2 在 z 平面上解析,
1 易知 cos z 2 为它的一个原函数,根 2
据复积分的牛顿-莱布尼兹公式有
b
a
1 1 2 2 z sin z dz cos z cos a 2 cos b 2 2 2 a
例
sinhz z
2
| z|1
dz
2 i ( n ) dz f (a) n 1 L n! ( z a) f ( z)
–例
• 问题:计算回路积分
2 i ( n ) dz f (a) n 1 L n! ( z a) f ( z)
sinhz z
2
| z|1
dz
• 分析:与推广的柯西公式比较, 可知f(z)=sinh(z),a = 0,n = 1 • 解:由推广的柯西公式
t 1 所以
1
i
z t t 1 zdz d( ) d( ) [1 (1)] 1 i 1 2 2 2 1 2
第二章复变函数的积分

f (z)dz lim f (k )(zk zk1)
l
积分n函 数k1
积分路径 一般来说,复变函数的积分值与积分路径有关.
2、复变函数积分计算方法
n
f (z)dz lim f (k )(zk zk1) n k 1
l
1)将复变函数的路积分化为两个实变函数的线积分
2)参数积分法
若积分曲线的参数方程z=z(t) ( ),dz z'(t)dt
则
f (z)dz f [z(t)]z'(t)dt
l
(极坐标法,通常用来计算积分路径为圆弧时的情况)
通常思路:
积分路径l为圆弧: 宗量用指数形式表示:
z z0
z z0 ei
n
n
f (z)dz f (z)dz;l lk
l
k 1 lk
k 1
f (z)dz f (z)dz
lAB
lBA
f (z)dz
l
f (z) dz ; dz
dx2 dy2 ds
l
Ms; M f (z) , s l的长度
用来求积分的估计值
r
1
z3 z
2
dz
z3 z r 1 z2
dz
(1)
z3
z r 1 z2
dz M
dz M
z r
ds Ms
z r
(2)
由(1)(2)式,得:
z3 dz Ms
z r 1 z2
M
1
r
3
r
2
s ds 2 r z r
数学物理方法第二章复变函数的积分
一般而言,复变函数的积分不仅与起点和终点有 关, 同时还与路径有关。
§2.2 柯西(Cauchy)定理
——研究积分与路径之间的关系 (一)单连通域情形 单连通域: 在其中作任何简单闭合围线,围 线内的点都是属于该区域内的点。 单连通区域的Cauchy 定理 :如果函数 f (z) 在闭 单连通区域 B 中单值且解析, 则沿 B 中任 何一个分段光滑的闭合曲线 l (也可以是 B 的 边界 l0 ), 函数的积分为零。
lim f( z z ) k)( k k 1
n
存在且与 k 的选取无关, 则这个和的极限称为 函数 f (z) 沿曲线 l 从 A 到 B 的路积分,记为
即
l
f (z) dz
n k k k 1
z ) d z lim f ( )( z z f(
l n k 1 max | z | 0 k
l 1 l 2
f (z)=Re (z)不是解析函数!
y i l2 o l1 1 l2
I1 Rez d z xd( x iy) 1 xd x i d y i 0 0 2 ( y = 0) (x=1)
1 1
1+i
l1 x
1 I 0 id y x d x 2 0 0 (x=0) ( y=i ) 2
l l l
v u u v d x d y i d x d y s s x y y x
又u、v 满足C-R条件 u v u v , x y y x
y
f ( z ) d z 0
l
B
l
o
第二章复变函数的积分

第二章 复变函数的积分在微积分学中,微分法与积分法是研究函数性质的重要方法。
同样,在复变函数中,积分法也跟微分法一样是研究复变函数性质十分重要的方法和解决实际问题的有力工具。
§2.1 复变函数积分的概念一、复变函数的积分设C 为平面上给定的一条光滑(或按段光滑)曲线。
若选定C 的两个可能方向中的一个作为正方向,那么就把C 理解为带有方向的曲线,称为有向曲线。
设曲线C 的两个端点为A 与B ,如果从A 到B 的方向作为C 的正方向,那么从B 到A 的方向就是C 的负方向,并把它记作-C 。
在今后的讨论中,常把两个端点中的一个作为起点,另一个作为终点。
除特殊声明外,正方向总是指从起点到终点的方向。
关于简单闭曲线的正方向是指当曲线上的点P 顺此方向沿该曲线前进时,临近P 点的曲线内部始终位于P 点的左方。
与之相反的方向就是曲线的负方向。
若光滑或逐段光滑的曲线C 的参数方程为)()()(t iy t x t z z +==,)(βα≤≤t (2.1) t 为实参数,则规定t 增加的方向为正方向,即由)(αz a =到)(βz b =的方向为正方向。
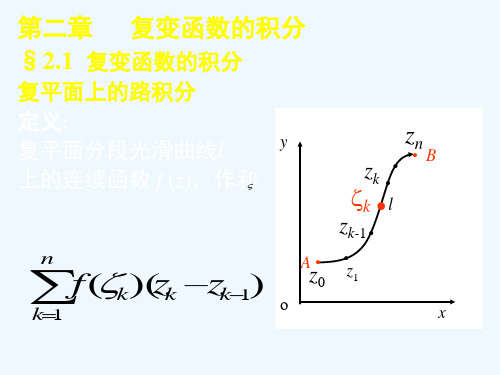
定义2.1 设函数)(z f w =定义在区域D 内,C 为区域D 内起点为A 终点为B 的一条光滑有向曲线,把曲线C 任意分成n 个弧段,设分点为:B z z z z z A n n ==-,...,,,1210 在每个小弧段上任取一点k ζ(图3.1),作和∑=∆=nk k k n z f S 1)(ζ其中1--=∆k k k z z z ,记=∆k s 的长度,}Δ{max 1k nk s δ≤≤=。
当n 无限增加,且δ趋于零时,如果不论对C 的分法及k ζ的取法如何,当n S 有唯一极限,那么称这个极限值为函数)(z f 沿曲线C 的积分,记作∑⎰=→=nk k kδCz ζf dz z f 1Δ)(lim )( (2.2)图2.1C 称为积分路径,⎰Cdz z f )(表示沿C 的正方向的积分,⎰-C dz z f )(表示沿C的负方向的积分。
数学物理方法第2章复变函数积分-2016方案

(2.1.3)
(2) 化为参数积分计算.设积分曲线L的参数方程为z(t),
将z(t)及dz(t)=z'(t)dt代入式(2.1.4),可得
3
【例2.1.1】计算积分I=
其中曲线L是
(1)沿1+ i 到2+4 i 的直线,见图2.2(a);
(2)沿1+ i 到2+i,再到2+4 i 的折线,见图2.2(b);
§2.2.1 单通区域的柯西定理
定理 若函数f(z)在单通区域D 内解析,则f(z)在D内沿任意 闭曲线的积分为零
∮l f(z)dz = 0 (2.2.1)
证明 这个定理的严格证明比较复 杂, 为简单起见, 我们在“f(z)在D 内连续” 附加条件下证明这个定 理.
先将复变积分化为两个实变积 分的线性叠加
29
这就是解析函数的定积分公式,它与实变 函数中的牛顿-莱布尼茨公式具有相同的形 式。
通常把f(z)的原函数的集合
称f(z)的不定积分,式中C为复常数。
30
(2.2.8)
31
§2.2.3 复通区域的柯西定理
定理 若f(z)在闭复通区域 解析,则f(z)沿所
有内、外边界线(L=L0+ 之和为零
37
【2.2.2】试计算 其中积分回路分别(图2.11) (1) |z-i|=2;(2) |z+i|=2;(3) |z|=3.
38
解 首先,将被积函数分解为部分分式(利用通 分可以凑出来)
≠0
=0
39
40
【例2.2.3】若f(z)=1/(z-a) 在z=a的无心邻域内 连续,积分回路是以a点为圆心的圆弧
由于a点在D内随意变动时,柯西公式依然成立, 有时分别用z和x代替式 (2.3.1)的a和z。将柯西公 式改写为
第二章 复变函数的积分chen

= ∫ [u( x , y )dx − v ( x , y )dy ] + i ∫ [u( x , y )dy + v ( x , y )dx ]
l l
结论: ※ 结论:复变函数的路积分可以归结为两个实变函数线 积分,它们分别构成路积分的实部和虚部。 积分,它们分别构成路积分的实部和虚部。
路积分的概念和性质
2
1
1 3 = 2 − + 2i = + 2i 2 2
路积分的计算例题
【例二】沿图所示的三条曲线分别计算复变函数 f ( z ) = Re z 从 O 到 B 的路积分。
∫
OAB
f ( z )dz = ∫
OAB
Re zdz = ∫ Re zdz + ∫ Re zdz
OA AB
OA段 z = iy , Re z = 0 dz = idy 段
C
C
f (z)dz
C
∫ [ f + g]dx = ∫
a
fdx + ∫ gdx
a
b
∫ [ f + g]dz = ∫
C
C
fdz + ∫ gdz
C
∫
b
a
f ( x)dx = −∫ f ( x)dx
b
a
∫
∫
C
f (z)dz = −∫ f (z)dz
f dz + ∫ f dz = ∫
C2 C1 ∪C2
∫
c
a
f dx + ∫ f dx = ∫ f dx
∫
l
f ( z )dz = ∫ [u( x , y )dx − v ( x , y )dy ] + i ∫ [v ( x , y )dx + u( x , y )dy ]
数学物理方法 第二章 复变函数的积分

证明: 1 dz 1 f (α )dz (1)已知f (α ) = f (α ) ⋅ ∫l z − α = 2πi ∫l z − α 2πi 1 f ( z )dz 1 f ( z ) − f (α ) 与f (α ) = 比较,只需证明 ∫l z − α ∫l z − α dz = 0即可. 2πi 2πi f ( z ) − f (α ) (2)因为z = α为 的奇点,因此,以α为圆心,取任意小 z −α f ( z ) − f (α ) ε为半径做小圆Cε , 这样在l及Cε 所围复通区域上 单值解析。 z −α f ( z ) − f (α ) 1 f ( z ) − f (α ) 1 根据柯西定理, ∫ dz = ∫Cε z − α dz l 2πi z −α 2πi 对于Cε 上的z有:z − α = εe iϕ , dz = iεeiϕ dϕ 于是, 有: 1 f ( z ) − f (α ) 1 2π f ( z ) − f (α ) iϕ 1 iεe dϕ = iϕ ∫l z − α dz = 2πi ∫0 εe 2πi 2π
wuxia@
∫
2π
0
[ f ( z ) − f (α )]dϕ
(3)现在需要对上式右端做估计 因为f ( z )连续,一定可以找到∆ > 0,当 | z − α |≤ ∆时, | f ( z ) − f (α ) |≤ ε ′ 因而有: 1 2π 1 2π 1 ∫0 [ f ( z ) − f (α )]dϕ ≤ 2π ∫0 | f ( z ) − f (α ) |⋅ | dϕ |< 2π 2π =ε 1 f ( z ) − f (α ) 1 f ( z) ∴ dz = 0, f (α ) = ∫l z − α ∫l z − α dz 2πi 2πi
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数值测试有盲人摸象的感
觉,其实这些结果可以很
好地用柯西定理来解释。
21
单通区域的柯西定理
如果函数f(z)在闭单通区域(区域加境界线) B 上解 析,则沿 B 上任一分段光滑闭合曲线l (可以是边 界),有:
条件可放宽为:
∫ f (z)dz = 0
l
在单通区域B上解析, 在闭单通区域B 上连续
无论沿顺时针还 是逆时针方向结 果均为0。由柯 西定理不难导出 解析函数路积分 的路径无关性。
1+i
1
∫ ∫ 积分值 = (x2 − y2 + 2xyi)dz = 2x2i(1+ i)dx
0
0
∫ =
2(i
1
−1)
x 2 dx
=
−
2
+
2
i
0
33
路径2结果和路径1积分结果相同。如果我们继续取 其他路径进行积分,仍然会得到相同结果。
11
3/17/2012
路积分与路径的关系
从上面的例子可以看到,某些路积分问题结 果与路径有关,而某些则与路径无关。
试计算以下路积分,积分路径如下图所示。积分 路径也是z=0至z=1+i。
I = ∫ z2dz l
这里被积函数z2是 一个解析函数。
3/17/2012
9
3/17/2012
路径1的情况
被积函数z2 = x2 − y2 + 2xyi
路径1的积分:
在0 → 1段,y = 0,我们有:
∫ ∫ 积分值 = 1 (x2 − y2 + 2xyi)dx = 1 x2dx = 1
∫
l
P(
x,
y)dx
+
Q(
x,
y)dy
=
∫∫
S
⎜⎜⎝⎛
∂Q ∂x
−
∂P ∂y
⎟⎟⎠⎞dxdy
其中线积分的积分方向为正方向。
24
单通区域柯西定理的证明
∫ f (z)dz = ∫ u(x, y)dx − v(x, y)dy + i∫ v(x, y)dx + u(x, y)dy
l
l
l
将格林公式∫ l
Pdx
I
=
∫
l
z
1 − (0.5 +
0.5i)
dz
本例直接解析计算较繁琐,我们 采用数值方法。
13
数值计算路积分
implicit none complex*16 s, z, dz, f complex*16 :: I=(0,1) integer :: n z=0 s=0 do n=0, 99
dz=0.01 f=1/(z-(0.5,0.5)) s=s+f*dz z=z+dz end do do n=0, 99 dz=0.01*I f=1/(z-(0.5,0.5)) s=s+f*dz z=z+dz end do print*, "z=",z, "s=",s e3n/1d7/2012
p.24 例 计算路积分I = ∫ Re zdz ,积分路径如下图所示。积
分路径为z=0至z=1+i。l
3/17/2012
关键问题:dz的形式,不同路径dz不同。
6
3/17/2012
路径1的情况
由于z = x + iy,有 :
被积函数 Re z = x,dz = dx + idy.
对于路径1的路积分:
再换一个路积分:
∫ I
=
l
[z
1 − (0.5 +
0.5i)]2
dz
公式2+路径1 s=(-2.000033, 2.000033)
公式2+路径2 s=(-2.000033, 2.000033)
这个积分函数也在围成区域内存在奇 点,但两路径的积分结果却相同。
3/17/2012
18
3/17/2012
其中,l为区域外境界线,li为区域内境界线,积分 沿各境界线的正方向进行。
代入上式,可得积分值 = 0。柯西定理得证。
3/17/2012
25
奇点对解析函 数的性质有非 常大的影响。
复通区域
单通区域内可能存在一些奇点,不解析甚至函数 值不存在。把这些点附近的区域挖去,剩下的区 域通常就变成了复通区域。
境界线的正方向 当观察者沿着这个方向前进 时,区域总是在观察者的左边。
分量形式
利用z=x+iy, f=u+iv,根据路积分的定义, 容易将其化为实函数u和v的线积分。
∫ f (z)dz = ∫ (u + iv)(dx + idy)
l
l
= ∫ u(dx + idy) + iv(dx + idy) l
= ∫ udx + iudy + ivdx − vdy l
= ∫ u(x, y)dx − v(x, y)dy + i∫ v(x, y)dx + u(x, y)dy
=
z2
b
之类的积分公式是否能用?
a
2 a
如果能用,为什么还会和路径有关?
19
3/17/2012
谜底在于多值函数
对于解析函数路积分,此类积分公式仍然可 用。但是,某些积分结果将是多值函数。此 时,虽然结果仍然是F(b)-F(a),但F的取值就 和具体路径有关,不同路径出现不同结果也 就不足为奇了。
0
0
3
在1 → 1+ i段,x = 1,我们有:
1
∫ 积分值 = (x2 − y2 + 2xyi)idy
0
∫ =
1
i
(1 −
y2
+
2 yi)dy
=
2
i
−1
0
3
所以,总的结果I = − 2 + 2 i 33
10
3/17/2012
路径2的情况
被积函数z2 = x2 − y2 + 2xyi
在路径2中,dz = (1+ i)dx,y = x,有:
多元积分中线积分的格林公式可做 到这一点。
23
3/17/2012
线积分的格林公式
数学上有好几个格林公式,这里需要用到的是线 积分的格林公式。
利用此格林公式可以实现回路线积分和二重面积 分之间的相互转换。线积分化为二重积分后,被 积函数的形式也会发生变化 (变为一阶偏导)
设l为逐段光滑的简单闭合曲线,围成单连通有界区域S, 若函数P(x, y)、Q(x, y)及它们一阶偏导在S + l上连续, 则有:
路积分实验结果小结
如果被积函数是非解析函数,积分结果一 般和路径有关。
如果被积函数是解析函数,且两条路径围 成区域内没有奇点,积分结果应相同。
如果被积函数是解析函数,且两条路径围 成区域内有奇点,积分结果可能不同,但 也可能相同。实际上,这与该函数在奇点 出的性质有关。
∫b
疑问:对于解析函数,zdz
对于一元实函数的积分,只 需给出积分上下限整个积分 路径就确定了。而复变函数 的情况就要复杂一些。
3/17/2012
以上过程可推广到复平面上,我们可以 沿着复平面上的AB之间的任意一条路径 进行积分。
这里Δz=zk-zk-1往往是各处不同的。 2
3/17/2012
路积分的定义
设在复平面的某分段光滑曲线l上定义了连续函数 f(z),在l上取一系列分点z0(起点A),z1,z2,..., zn(终点B),把l分成n段,在每一小段上任取一点 ζk,作和:
n
∑ f (ζ k )(zk − zk−1)
k =1
当n→∞且每一段都无限缩短时,如果这个和的极 限存在,且与各ζk选取无关,则这个和的极限称 作函数f(z)沿曲线l从A到B的路积分,记作:
n
∫ ∑ l
f (z)dz = lim n→∞ k =1
f (ζ k )(zk − zk−1)
3
3/17/2012
在i → 1+ i段,dz = dx,被积函数 Re z = x.
所以,
∫ ∫ I1
=
1 0
0 ⋅idy
+
1 0
xdx
=
1 2
沿着两条不同路径积分,得到结果并不相同。
可见一般的复变函数积分值不仅和起点终点有关,
还和积分路径有关。注意到本例中被积函数不是解
析函数,如果是解析函数结果又会如何?
8
解析函数的例子
沿路径1积分
我们采用如下数值积分公式:
n
∫ ∑ 1、 f (z)dz ~ f (zk )(zk − zk−1)
l
k =1
∫ ∑ 2、
l
n
f (z)dz ~
k =1
f
( zk
+ zk −1 2
)( zk
−
zk −1)
数值积分公式有很多不同的形式, 不同公式的精度差别很大。
14
公式2精度更高
3/17/2012
15
3/17/2012
奇点引起的问题?
前面的例子被积函数f(z)=z2不 存在奇点,而本例中的被积函 数f(z)=1/[z-(0.5+0.5i)]虽然在 两条积分路径上均解析,只是 在两条路径围成的区域中存在 一个奇点(0.5+0.5i)。难道是 它对积分结果有影响吗?
我们需要更多的实例来寻找规律
16
3/17/2012
继续实验
被积函数I
=
∫
l
z
