三角函数高考解答题常见题型6题
高考解答题专题:三角函数

高考解答题专题:三角函数1.已知()cos()sin 3f x x k x π=+-,且3()62f π=.(1)求实数k 的值;(2)求函数()f x 的最大值和最小值.2.已知ABC ∆的三个内角A 、B 、C 所对的边分别为a b c 、、,向量(4,1),m =-2(cos ,cos 2)2An A = ,且72m n ⋅= .(1)求角A 的大小;(2)若3a =,试判断b c ⋅取得最大值时ABC ∆形状.3.已知)2sin(3)2cos()(x x x f -+-=ππ∈x (R ).(1)求函数)(x f 的最小正周期;(2)求函数)(x f 的最大值,并指出此时x 的值4.在ABC ∆中,三个内角C B A ,,所对的边分别为cb a ,,(ac >),A C A C sin sin cos cos -= ,31sin =B(1)求A sin 的值,(2)若边长6=b ,求ABC ∆的面积5.记ABC ∆的内角ABC 的对边分别为abc ,函数()23=sin sin 122Bf x B ++(1)求函数()f B 值域(2)若()3,2,232f B b c ===,求a 的值6.已知函数()cos(2)2sin()sin()344f x x x x πππ=-+-+(Ⅰ)求函数()f x 的最小正周期;(Ⅱ)求函数()f x 在区间[,]122ππ-上的值域。
7.在ABC 中,C-A=, sinB=。
(I )求sinA 的值;(II)设AC=,求ABC 的面积。
8.设函数()sin cos 1 , 02f x x x x x π=-++<<,求函数()f x 的单调区间与极值9.在 ABC 中,a ,b ,c 分别为内角A ,B ,C 所对的边长,a=3,b=2,12cos()0B C ++=,求边BC 上的高.。
高一三角函数高考解答题常见题型6题

高一三角函数常见题型三角函数题是高考数学试卷的第一道解答题,试题难度一般不大,但其战略意义重大,所以稳拿该题12分对文理科学生都至关重要。
分析近年高考试卷,可以发现,三角解答题多数喜欢和平面向量综合在一起,且向量为辅,三角为主,主要有以下几类:一、运用同角三角函数关系、诱导公式、和、差、倍、半等公式进行化简求值类。
例1 已知向量33(cos ,sin ),(cos ,sin ),[,]22222x x x x x ππ==-∈且a b 。
(1)若||3+>a b ,求x 的取值范围;(2)函数()||f x =⋅++a b a b ,若对任意12,[,]2x x ππ∈,恒有12|()()|f x f x t -<,求t 的取值范围。
二、运用三角函数性质解题,通常考查正弦、余弦函数的单调性、周期性、最值、对称轴及对称中心。
例2 若(3sin ,0),(cos ,sin ),0x x x ωωωω==->m n ,在函数()()f x t =⋅++m m n 的图象中,对称中心到对称轴的最小距离为4π,且当[0,]3x π∈时,()f x 的最大值为1。
(1)求函数()f x 的解析式; (2)若13(),[0,]2f x x π+=-∈,求实数x 的值。
例3 已知向量α(sin =a , )21-,1(=b , )cos 2α,51=⋅b a ,)2,0(πα∈ (1)求ααsin 2sin 及的值;(2)设函数x x x f 2cos 2)22sin(5)(+++-=απ])2,24[(ππ∈x ,求x 为何值时,)(x f 取得最大值,最大值是多少,并求)(x f 的单调增区间。
例4 设向量]2,0[),23cos ,23(sin ),2sin ,2(cos π∈==x x x b x x a 向量.(Ⅰ)求||b a b a +⋅及; (Ⅱ)若函数||2)(b a b a x f ++⋅=,求)(x f 的最小值、最大值.三、解三角形问题,判断三角形形状,正余弦定理的应用。
高考数学解答题(新高考)三角函数的图象与性质(五点法作图)(典型例题+题型归类练)(解析版)
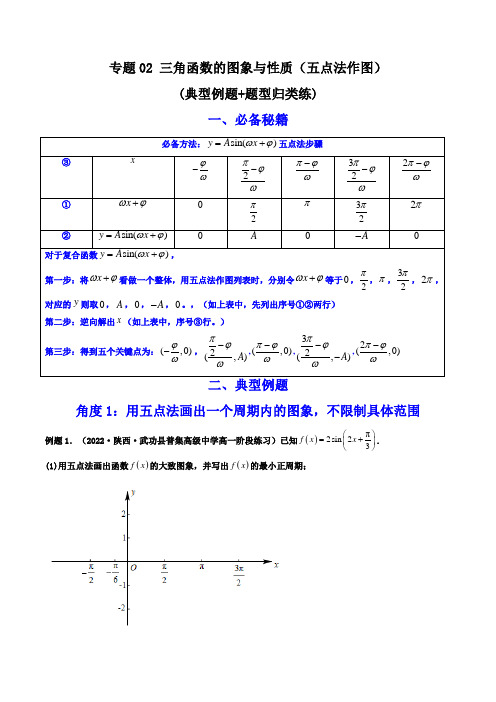
专题02 三角函数的图象与性质(五点法作图)(典型例题+题型归类练)一、必备秘籍角度1:用五点法画出一个周期内的图象,不限制具体范围例题1.(2022·陕西·武功县普集高级中学高一阶段练习)已知()π2sin23f x x⎛⎫=+⎪⎝⎭.(1)用五点法画出函数()f x的大致图象,并写出()f x的最小正周期;【答案】(1)图象见解析,T=π令ππ3π2=0π2π322x +,,,,,得到对应的,()x f x 值如下表所示: π23x +π2π3π2 2πxπ6-π12 π37π125π6 ()f x22-所以()f x 过πππ7π5π(,0),(,2),(,0),(,2),(,0)6123126--,图象如图所示思路点拨:由题意知,目标要求用五点法画出其一个周期的图象.采用列表法解答过程:先将看做一个整体,赋值如表中标记行(1);再求出的值,如表中标记行(2);再根据标记行(1)逆向求对于的,得到五个关键点的横坐标; (3) (1)(2)这样得到五个关键点为:,在坐标系中描点,画出图象周期为T=π例题2.(2022·宁夏吴忠区青铜峡市教育局高一开学考试)已知函数()sin 26f x x π⎛⎫=+ ⎪⎝⎭.请用“五点法”列表并画出函数()f x 在一个周期上的图象;思路点拨:由题意知,目标要求用五点法画出其一个周期的图象.采用列表法解答过程:先将看做一个整体,赋值如表中标记行(1);再求出的值,如表中标记行(2);再根据标记行(1)逆向求对于的,得到五个关键点的横坐标; (3)(1)(2)这样得到五个关键点为:,在坐标系中描点,画出图象【答案】(1)答案见解析列表如下:函数f x在一个周期上的图象如下:角度2:用五点法画出具体某个范围内的图象例题1.(2022·全国·高一课时练习)用五点法画出π2sin23y x⎛⎫=+⎪⎝⎭在π5π,66⎡⎤-⎢⎥⎣⎦内的图象时,应取的五个点为 ______;【答案】π,06⎛⎫- ⎪⎝⎭、π,212⎛⎫ ⎪⎝⎭、π,03⎛⎫ ⎪⎝⎭、7π,212⎛⎫- ⎪⎝⎭、5π,06⎛⎫ ⎪⎝⎭由题意可知,令π23X x =+,则123x X π⎛⎫=- ⎪⎝⎭,π5π,66x ⎡⎤∈-⎢⎥⎣⎦,列表,描点.xπ6-π12π3 7π12 5π6X0 π2π3π22π思路点拨:由题意知,目标要求写出五点法画在内的图象时对应的五个关键点解答过程:先将看做一个整体,赋值如表中标记行(1);再求出的值,如表中标记行(2);再根据标记行(1)逆向求对于的,得到五个关键点的横坐标;(3)(1)(2)这样得到五个关键点为:、、、、,在坐标系中描点,画出图象由于题目给定范围,故对于这个整体,需先求出其整体的范围,再进行判断是否能完整取到五点法画图的关键点;由,故对于这个整体,能完整取到由列表可得,应取的五个点为 π,06⎛⎫- ⎪⎝⎭、π,212⎛⎫ ⎪⎝⎭、π,03⎛⎫ ⎪⎝⎭、7π,212⎛⎫- ⎪⎝⎭、5π,06⎛⎫ ⎪⎝⎭,故答案为:π,06⎛⎫- ⎪⎝⎭、π,212⎛⎫ ⎪⎝⎭、π,03⎛⎫ ⎪⎝⎭、7π,212⎛⎫- ⎪⎝⎭、5π,06⎛⎫ ⎪⎝⎭.例题2.(2022·黑龙江·大庆外国语学校高一期末)已知函数()()3sin 2f x x πϕϕ=+∈-,(,2π)函数关于4x π=对称.(1)求()f x ϕ的值及的解析式;(2)用五点法在下列直角坐标系中画出()f x 在744ππ⎡⎤-⎢⎥⎣⎦,上的图象;【答案】(1)4πϕ=,()3sin 4f x x π⎛⎫=+ ⎪⎝⎭(2)详见解析(1)因为函数关于直线4x π=对称,所以,42k k Z ππϕπ+=+∈,,4k k Z πϕπ=+∈,因为,22ππϕ⎛⎫∈- ⎪⎝⎭,所以4πϕ=, 所以()3sin 4f x x π⎛⎫=+ ⎪⎝⎭(2)首先根据“五点法”,列表如下:第一问略;第(2)问思路点拨:由题意知,目标要求用五点法画在内的图象解答过程: 先将看做一个整体,赋值如表中标记行(1);再求出的值,如表中标记行(2);再根据标记行(1)逆向求对于的,得到五个关键点的横坐标;(3)(1)(2)这样得到五个关键点为:、、、、,在坐标系中描点,画出图象由于题目给定范围,故对于这个整体,需先求出其整体的范围,再进行判断是否能完整取到五点法画图的关键点;由,故对于这个整体,能完整取到三、题型归类练1.(2021·全国·高一专题练习)用“五点法”作y =2sin2x 的图象,首先描出的五个点的横坐标是( ) A .30,,,,222ππππ B . 30,,,,424ππππ C . 0,,2,3,4ππππ D .20,,,,6323ππππ【答案】B由“五点法”作图知:令2x =0,2π,π,32π,2π,解得x =0,4π,2π,34π,π,即为五个关键点的横坐标, 故选:B.2.(2022·北京东城·高一期末)某同学用“五点法”画函数()sin()(0,0)f x A x A ωϕω=+>>在一个周期内的简图时,列表如下:则()f x 的解析式为( )A .()2sin 12f x x π⎛⎫=- ⎪⎝⎭ B .()2sin 312⎛⎫=+ ⎪⎝⎭f x x πC .()sin 212f x x π⎛⎫=- ⎪⎝⎭D .n (4)2si 3x f x π⎛-=⎫ ⎪⎝⎭【答案】D由表中数据知:2A =且721243T πππ=-=,则23T π=, ∴223ππω=,即3ω=,又342ππϕ⨯+=,可得4πϕ=-. ∴n (4)2si 3x f x π⎛-=⎫ ⎪⎝⎭.故选:D.3.(2021·广东揭阳·高一期末)某同学用“五点法”画函数()()πsin 0,2f x A x ωϕωϕ⎛⎫=+>< ⎪⎝⎭在某一个周期内的图象时,列表并填入了部分数据,如下表:根据表格中的数据,函数f x 的解析式可以是( ) A .()π5sin 26f x x ⎛⎫=- ⎪⎝⎭B .()π5sin 26f x x ⎛⎫=+ ⎪⎝⎭C .()π5sin 23f x x ⎛⎫=- ⎪⎝⎭D .()π5sin 23f x x ⎛⎫=+ ⎪⎝⎭【答案】A由题意得最大值为5,最小值为-5,所以A =5,52632T πππ=-=,解得2T ππω==,解得2ω=,又232ππϕ⨯+=,解得6πϕ=-,所以()f x 的解析式可以是()π5sin 26f x x ⎛⎫=- ⎪⎝⎭故选:A4.(2022·北京·高一阶段练习)某同学用“五点法”画函数sin()(0,)2y A x ϖϕϖϕπ=+><在某一个周期内的图像时,列表并填入了部分数据,如下表.【答案】3sin(2)3y x π=+由表格知:3A =且12231227πϕπϕϖπϖπ⎧+=⎪⎪⎨⎪+=⎪⎩,可得23ϖπϕ=⎧⎪⎨=⎪⎩,所以3sin(2)3y xπ=+.故答案为:3sin(2)3y x π=+.5.(2022·河南省嵩县第一高级中学高一阶段练习)已知函数π()2sin 23f x x ⎛⎫=- ⎪⎝⎭.(1)利用“五点法”完成下面的表格,并画出()f x 在区间π7π,66⎡⎤⎢⎥⎣⎦上的图象;【答案】(1)答案见解析 完成表格如下:()f x 在区间π7π,66⎡⎤⎢⎥⎣⎦上的图象如图所示:6.(2022·辽宁省康平县高级中学高一阶段练习)已知函数()sin 23πf x x ⎛⎫=- ⎪⎝⎭.(1)请用“五点法”画出函数()f x 在一个周期7,66ππ⎡⎤⎢⎥⎣⎦上的简图;【答案】(1)答案见解析 因为()sin 23πf x x ⎛⎫=- ⎪⎝⎭取值列表:7.(2022·广西·钦州一中高一期中)已知函数()2sin 26f x x π⎛⎫=+ ⎪⎝⎭.(1)请用“五点法”画出函数()2sin 26f x x π⎛⎫=+ ⎪⎝⎭在一个周期上的图象;【答案】(1)作图见解析由图横坐标的范围,函数()f x 的周期为π,画出函数()f x 在11,1212ππ⎡⎤-⎢⎥⎣⎦上的图象.列表如下,8.(2022·江西·上饶中学高一阶段练习)已知函数()2sin 24f x x π⎛⎫=- ⎪⎝⎭.(1)利用“五点法”完成下面表格,并画出函数()f x 在区间9,88ππ⎡⎤⎢⎥⎣⎦上的图象.由正弦函数的性质,9,88ππ⎡⎤⎢⎥⎣⎦上的五点如下表:9.(2022·云南玉溪·高一期末)已知函数21()sin cos cos 22f x x x x x =+-.(2)填上面表格并用“五点法”画出()f x 在一个周期内的图象.【答案】(1)T π=,它的对称中心为,0212k ππ⎛⎫-⎪⎝⎭,k Z ∈(2)答案见解析.(1)21()sin cos cos 22f x x x x x =+-12cos 2sin 226x x x π⎛⎫+=+ ⎪⎝⎭ ∴函数()f x 的最小正周期22T ππ==;令26x k ππ+=,k Z ∈,解得212k x ππ=-,k Z ∈,可得它的对称中心为,0212k ππ⎛⎫-⎪⎝⎭,k Z ∈.。
三角函数解答题精选

教育资料免费下载 三角函数解答题精选1. 求函数y=sinx+cosx+1的最值及取得最值时相应x 的值.解:由y=sinx +cosx +1得y=2sin(x+4π)+1……………………2分 ∴y max =2+1………………4分y min =-2+1……………………………6分 由x+4π=2k π+2π得x=2k π+4π(k ∈Z) 即x=2k π+4π(k ∈Z)时,y 取最大值2+1 (9)分 由x+4π=2k π-2π即x=2k π-43π时y 取最小值1-2……………………12分2. 已知函数.2321)3(,2)0(,cos sin cos 2)(2+==+=πf f x x b x a x f 且(1)求f (x )的最大值与最小值; (2)若απα求),2,0(,0)(∈=a f 的值.解:(1)由f (0)=2a =2, 得a =1 ,2,4321)3(=+=b b a f 得π…………(3分)∴f (x )=2cos 2x +2sin x cos x =sin2x +cos2x +1=1)42sin(2++πx …………(5分)∴f (x )的最大值是12+,最小值是21-.………………(6分)(2)∵,22)42sin(01)42sin(2,0)(-=+⇒=++=παπαα得f .……(8分)).12(4743232),2,0()10(,24,452424242分或或或分或或 παπαπαπαπαππαππαπππαπππα====∴∈∈+=-=∴∈+=+-=+∴Z k k k Zk k k3. 已知函数)0.(23cos3cos sin )(2>++-⋅=a b a x a x x a x f(1)R x ∈,写出函数的单调递减区间;教育资料免费下载 (2)设)(],2,0[x f x π∈的最小值是-2,是大值是3,求实数b a ,的值.解:(1)b x x x a x f ++-⋅=)23cos3cos (sin )(2b xx a +++⨯-⨯=)2322c o s 132s i n 21(=b x a +-⋅)32sin(π…………4分)(,,0x f R x a ∈> 的递减区间是)](1211,125[Z k k k ∈++ππππ…………6分(2)]32,3[32],0[2]2,0[πππππ-∈-∴∈∴∈x x x ………………………7分]1,23[)32sin(-∈-∴πx ………………………………………………………9分∴函数)(x f 的最小值是223-=+-b a ……………………………………10分最大值3=+b a ………11分 解得23,2-==b a ……12分4. 求函数)6cos(sin sin2x x x y -+=π的周期和单调增区间.解 )s i n 6s i n c o s 6(c o s s i n s i n 2x x x x y ππ++=x x x cos sin 23sin 232+=xx 2sin 43)2cos 1(43+-=)2cos 432sin 43(43x x -+=)32sin(2343π++=x .…… 6分∴ 函数的周期 ππ==22T . ……………… 8分 当 22ππ-k ≤32π+x ≤22ππ+k ,即 125ππ-k ≤x ≤12ππ+k (k ∈Z ) 时函数单调增加,即函数的增区间是 [125ππ-k ,12ππ+k ] (k ∈Z ).…… 12分5. 已知函数235cos 35cos sin 5)(2+-=x x x x f(Ⅰ)求f(x)的最小正周期; (Ⅱ)求f(x)的递增区间.教育资料免费下载 解:(Ⅰ)235cos 35cos sin 5)(2+-=x x x x f)3sin2cos 3cos2(sin 52cos 352sin 2523522cos 1352sin 25ππx x x x xx -=-=++-=)32sin(5π-=x …………………………4分∴最小正周期T=ππ=22 ……………………………………6分(Ⅱ)由题意,解不等式πππππk x k 223222+≤-≤+-……………………8分得 )(12512Z k k x k ∈+≤≤+-ππππ)(x f ∴的递增区间是)](125,12[Z k k k ∈++-ππππ………………12分6. 已知函数)(,2cos sin 8cos 23)(42x f xxx x f 求--=的定义域,判断它的奇偶性,并求其值域. 解:xxx xxx x f 2cos sin8sin212cos sin8)sin1(23)(4242-+=---=)9.()(),()(,)()7}.(,42,|{,42,22,02cos )4(.1sin42cos )sin21)(sin 41(222分是偶函数且的定义域关于原点对称因为分且所以函数的定义域为解得得由分x f x f x f x f z k k x R x x z k k x k x x x xx x ∴=-∈+≠∈∈+≠+≠≠+=-+=ππππππ)12(}.3,51|{)(,42,1sin4)(2分且的值域为且又≠≤≤∴∈+≠+=y y y x f zk k x x x f ππ7. 已知函数.,12sin sin2)(2R x x x x f ∈-+=教育资料免费下载 (1)求)(x f 的最小正周期及)(x f 取得最大值时x 的集合; (2)在给定的坐标系中画出函数)(x f 在],0[π上的图象. 解:(I )x x x x x x x f 2cos 2sin )sin21(2sin 12sin sin2)(22-=--=-+==)42sin(2π-x ………………………………………………5分所以)(x f 的最小正周期是π……………………………………………………6分∈x R ,所以当∈+=+=-k k x k x (83,2242πππππ即Z )时,)(x f 的最大值为2. 即)(x f 取得最大值时x 的集合为∈+=k k x x ,83|{ππZ }……………………8分(II )图象如下图所示:(阅卷时注意以下3点)1.最小值2)83(=πf ,最小值2)87(-=πf .………………10分 2.增区间];,87[],83,0[πππ减区间]87,83[ππ……………………12分 3.图象上的特殊点:(0,-1),(1,4π),(1,2π),)1,(),1,43(--ππ………14分 [注:图象上的特殊点错两个扣1分,最多扣2分] 8. 已知函数.,2cos32sin R x x x y ∈+=(1)求y 取最大值时相应的x 的集合;(2)该函数的图象经过怎样的平移和伸变换可以得到)(sin R x x y ∈=的图象.解:).32sin(2π+=x y ……4分(1)当},34|{.2Z k k x x x y ∈+=∈=ππ最大……8分(2)把)32sin (2π+=x y 图象向右平移π32,再把每个点的纵坐村为原来的21,横坐标不变.然后再把每个点的横坐标变为原来的21,纵坐标不变,即可得到x y sin =的图象……12分教育资料免费下载 9. 已知函数.,22sin 2sin4)(2R x x x x f ∈-+=(1)求)(x f 的最小正周期及)(x f 取得最大值时x 的集合; (2)求证:函数)(x f 的图象关于直线8π-=x 对称(1)解:x x x x x x x f 2cos 22sin 2)sin 21(22sin 222sin 2sin2)(22-=--=-+==)42sin(22π-x ………………………………………………5分所以)(x f 的最小正周期是π……………………………………………………6分 ∈x R ,所以当∈+=+=-k k x k x (83,2242πππππ即Z )时,)(x f 的最大值为22.即)(x f 取得最大值时x 的集合为∈+=k k x x ,83|{ππZ }……………………8分(2)证明:欲证函数)(x f 的图象关于直线8π-=x 对称,只要证明对于任意R x ∈,有)8()8(x f x f +-=--ππ成立即可.).8()8(.2cos 22)22sin(22]4)8(2sin[22)8(;2cos 22)22sin(22]4)8(2sin[22)8(x f x f x x x x f x x x x f +-=--∴-=+-=-+-=+--=--=---=--ππππππππππ从而函数)(x f 的图象关于直线8π-=x 对称.……14分[注:如果学生用min ))((22)8(x f f =-=-π;或求出所有的对称轴方程,然后验证8π-=x 是其中一条,则(2)中扣去2分]10. 已知定义在区间]32,[ππ-上的函数)(x f y =的图象关于直线6π-=x 对称,当]32,6[ππ-∈x 时,函数)22,0,0()sin()(πϕπωϕω<<->>+=A x A x f ,其图象如图所示.教育资料免费下载 (1) 求函数)(x f y =在]32,[ππ-的表达式;(2) 求方程22)(=x f 的解.(1)当],[326ππ-∈x 时,函数),0,0()sin()(22ππϕωϕω<<->>+=A x A x f ,观察图象易得:3,1,1πϕω===A ,即],[326ππ-∈x 时,函数)sin()(3π+=x x f ,由函数)(x f y =的图象关于直线6π-=x 对称得,],[6ππ--∈x 时,函数xx f sin )(-=. ∴⎪⎩⎪⎨⎧--∈--∈+=),[sin ],[)sin()(63263πππππx x x x x f .(2)当],[326ππ-∈x 时,由223)s i n (=+πx 得,125124343πππππ=-=⇒=+x x x 或或;当],[6ππ--∈x 时,由22sin=-x 得,443ππ-=-=x x 或.∴方程22)(=x f 的解集为},,,{12512443ππππ---11. 已知函数()sin()cos()f x x x θθ=+++的定义域为R ,(1)当0θ=时,求()f x 的单调区间;(2)若(0,)θπ∈,且sin 0x ≠,当θ为何值时,()f x 为偶函数.解:(1)0θ=时,()sin cos )4f x x x x π=+=+当 322,2224244k x k k x k πππππππππ-<+<+-<<+即 (k Z ∈)时()f x 单调递增; 当3522,2224244k x k k x k πππππππππ+<+<++<<+即 (k Z ∈)时()f x 单调递减;(2)若()f x 偶函数,则sin()cos()sin()cos()x x x x θθθθ+++=-++-+即 sin()sin()cos()cos()x x x x θθθθ++-++--=02s i nc o s2s i n s i n x x θθ-=2s i n (c o s s i n )x θθ-=c o s ()04πθ+= (0,)θπ∈ 4πθ∴=,此时,()f x 是偶函数.教育资料免费下载 1求函数y=sinx+cosx+1的最值及取得最值时相应x 的值.2已知函数.2321)3(,2)0(,cos sin cos 2)(2+==+=πf f x x b x a x f 且(1)求f (x )的最大值与最小值; (2)若απα求),2,0(,0)(∈=a f 的值.3已知函数)0.(23cos3cos sin )(2>++-⋅=a b a x a x x a x f(1)R x ∈,写出函数的单调递减区间;(2)设)(],2,0[x f x π∈的最小值是-2,是大值是3,求实数b a ,的值.4求函数)6cos(sin sin 2x x x y -+=π的周期和单调增区间.5已知函数235cos 35cos sin 5)(2+-=x x x x f(Ⅰ)求f(x)的最小正周期; (Ⅱ)求f(x)的递增区间.教育资料免费下载 6 已知函数)(,2cos sin8cos23)(42x f xxx x f 求--=的定义域,判断它的奇偶性,并求其值域.7已知函数.,12sin sin2)(2R x x x x f ∈-+=(1)求)(x f 的最小正周期及)(x f 取得最大值时x 的集合;(2)在给定的坐标系中画出函数)(x f 在],0[π上的图象8已知函数.,2cos32sin R x x x y ∈+=(1)求y 取最大值时相应的x 的集合;(2)该函数的图象经过怎样的平移和伸变换可以得到)(sin R x x y ∈=的图象.9已知函数.,22sin 2sin4)(2R x x x x f ∈-+=(1)求)(x f 的最小正周期及)(x f 取得最大值时x 的集合; (2)求证:函数)(x f 的图象关于直线8π-=x 对称教育资料免费下载 10已知定义在区间]32,[ππ-上的函数)(x f y =的图象关于直线6π-=x 对称,当]32,6[ππ-∈x 时,函数)22,0,0()sin()(πϕπωϕω<<->>+=A x A x f ,其图象如图所示.(1) 求函数)(x f y =在]32,[ππ-的表达式;(2) 求方程22)(=x f 的解.11已知函数()sin()cos()f x x x θθ=+++的定义域为R ,(1)当0θ=时,求()f x 的单调区间;(2)若(0,)θπ∈,且sin 0x ≠,当θ为何值时,()f x 为偶函数.x。
高考三角函数经典解答题及答案

1在△ABC 中,角A 、B 、C 所对的边分别是a ,b ,c ,且.21222ac b c a =-+ (1)求B CA 2cos 2sin 2++的值; (2)若b=2,求△ABC 面积的最大值.解:(1) 由余弦定理:conB=14sin 22A B++cos2B= -14(2)由.415sin ,41cos ==B B 得 ∵b=2, a 2+c 2=12ac+4≥2ac,得ac ≤38,S △ABC =12acsinB ≤315(a=c 时取等号) 故S △ABC 的最大值为3152在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且.cos cos 3cos B c B a C b -= (I )求cosB 的值;(II )若2=⋅,且22=b ,求c a 和b 的值.解:(I )由正弦定理得C R c B R b A R a sin 2,sin 2,sin 2===,因此.31cos =B(II )解:由2cos ,2==⋅B a BC BA 可得,所以a =c = 63已知向量m =()B B cos 1,sin -, 向量n = (2,0),且m 与n 所成角为π3, 其中A 、B 、C 是ABC ∆的内角。
(1)求角B 的大小;(2)求 C A sin sin +的取值范围。
解:(1) m =()B B cos 1,sin -,且与向量n = (2,0)所成角为3π, 又 π<<B 0(2)由(1)知,32π=B ,∴A+C= 3π ∴C A sin sin +=)3sin(sin A A -+π=A A cos 23sin 21+=)3sin(A +π30π<<A ,∴)3sin(A +π⎥⎦⎤ ⎝⎛∈1,23,∴ C A sin sin +⎥⎦⎤⎝⎛∈1,23 4已知向量(1,2sin )m A =,(sin ,1cos ),//,3.n A A m n b c a =++=满足 (I )求A 的大小;(II )求)sin(6π+B 的值.解:(1)由m//n 得0cos 1sin 22=--A A ……2分 即01cos cos 22=-+A A 1cos 21cos -==∴A A 或1cos ,-=∆A ABC A 的内角是 舍去 3π=∴A(2)a c b 3=+由正弦定理,23sin 3sin sin ==+A C Bπ32=+C B23)32sin(sin =-+∴B B π5在△ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,C =2A ,43cos =A , (1)求BC cos ,cos 的值;(2)若227=⋅,求边AC 的长。
(浙江)高考三角函数解答题专项训练含答案

三角函数【1】1、 已知函数x x x f cos sin )(-=,R x ∈.(1)求函数)(x f 的最小正周期;(2)若函数)(x f 在0x x =处取得最大值,求)3()2()(000x f x f x f ++ 的值.解:(1))4sin(2cos sin )(π-=-=x x x x f ,()f x ∴的最小正周期为2π(2)依题意,4320ππ+=k x (Z k ∈),由周期性,)3()2()(000x f x f x f ++12)49cos 49(sin )23cos 23(sin )43cos 43(sin-=-+-+-=ππππππ 2、△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,a sin A +c sin C -2a sin C =b sin B .(1)求B ;(2)若A =75°,b =2,求a ,c .解:(1) 由正弦定理得a 2+c 2-2ac =b 2.由余弦定理得b 2=a 2+c 2-2ac cos B .故cos B =22,因此B =45°. (2)sin A =sin(30°+45°)=sin30°cos45°+cos30°sin45°=2+64. 故a =b ×sinA sinB =2+62=1+3,c =b ×sinC sinB =2×sin60°sin45°= 6.3、设ABC ∆的内角,,A B C 所对的边长分别为,,,a b c且()2cos cos b A C =(1) 求角A 的大小。
(2) 若角6B π=,BC 边上的中线AM ,求ABC ∆的面积。
解:1)6π=A (7)2)3=S (7)4、如图,在ABC ∆中,点D 在BC 边上,33AD =,5sin 13BAD ∠=,3cos 5ADC ∠=.(Ⅰ)求sin ABD ∠的值; (Ⅱ)求ABD ∆的面积.解:(I )由3cos 5ADC ∠=,得24sin 1cos 5ADC ADC ∠=-∠=……………2分又5sin 13BAD ∠=,则212cos 1sin 13BAD BAD ∠=-∠=…………4分故()sin sin ABD ADC BAD ∠=∠-∠sin cos cos sin ADC BAD ADC BAD =∠∠-∠∠412353351351365=⨯-⨯=……………………7分(Ⅱ)在△ABD 中,由正弦定理知,sin sin BD ADBAD ABD =∠∠,则533sin 132533sin 65AD BADBD ABD⨯⨯∠===∠……………………………………11分故ABD ∆的面积为1sin 3302S AD BD ADB =⋅∠=……………………14分5、设函数0)R,(x )4 x sin((x) f >∈+=ωπω的部分图象如右图所示。
(完整版)高考三角函数经典解答题及答案
(完整版)高考三角函数经典解答题及答案1. 在△ABC 中,角 A、B、C 所对的边分别是 a、b、c,且 a²+c²-b²=(1) 求 sin²(2A+C)+cos²B 的值;(2) 若 b=2,求△ABC 面积的最大值。
解:(1) 由余弦定理:cosB=(a²+ c²- b²)/(2ac)=4/√115,得sinB=√(1-cos²B)=3√(23)/23。
由正弦定理sin²(2A+C)+cos²B=4sin²B+cos²B=13/23。
2. 在△ABC 中,角 A、B、C 的对边分别为 a、b、c,且bcosC=3acosB-ccosB。
(I) 求 cosB 的值;(II) 若 BA·BC=2,且b=√2,求 a 和 c·b 的值。
解:(I) 由正弦定理得 a=2RsinA,b=2RsinB,c=2RsinC,则 2RsinBcosC=6RsinAcosB-2RsinCcosB,故sinBcosC=3sinAcosB-sinCcosB,可得sinBcosC+sinCcosB=3sinAcosB,即 sin(B+C)=3sinAcosB,可得 sinA=3sinAcosB/sinB。
又sinA≠0,因此 cosB=1/3。
3. 已知向量 m=(sinB,1-cosB),向量 n=(2,k),且 m 与 n 所成角为π/3,其中 A、B、C 是△ABC 的内角。
(1) 求角 B 的大小;(2) 求 sinA+sinC 的取值范围。
解:(1) ∠m与∠n所成角为π/3,且 m·n=2sinB+ k(1-cosB)=2√3/2cosB+k√(1-cos²B),又 m·n=2cosB+k(1-cosB),解得 k=4/3。
高中数学三角函数专题复习(内附类型题以及历年高考真题,含答案)
1.tan x =2,求sin x ,cos x 的值. 解:因为2cos sin tan ==xxx ,又sin 2x +cos 2x =1, 联立得⎩⎨⎧=+=,1cos sin cos 2sin 22x x xx 解这个方程组得.55cos 552sin ,55cos 552sin ⎪⎪⎩⎪⎪⎨⎧-=-=⎪⎪⎩⎪⎪⎨⎧==x x x x2.求)330cos()150sin()690tan()480sin()210cos()120tan(----的值.解:原式)30360cos()150sin()30720tan()120360sin()30180cos()180120tan(o--+---++-= .3330cos )150sin (30tan )120sin )(30cos (60tan -=---=3.假设,2cos sin cos sin =+-xx xx ,求sin x cos x 的值.解:法一:因为,2cos sin cos sin =+-xx xx所以sin x -cos x =2(sin x +cos x ),得到sin x =-3cos x ,又sin 2x +cos 2x =1,联立方程组,解得,,⎪⎪⎩⎪⎪⎨⎧=-=⎪⎪⎩⎪⎪⎨⎧-==1010cos 10103sin 1010cos 10103sin x x x x 所以⋅-=103cos sin x x 法二:因为,2cos sin cos sin =+-xx xx所以sin x -cos x =2(sin x +cos x ), 所以(sin x -cos x )2=4(sin x +cos x )2, 所以1-2sin x cos x =4+8sin x cos x , 所以有⋅-=103cos sin x x 4.求证:tan 2x ·sin 2x =tan 2x -sin 2x .证明:法一:右边=tan 2x -sin 2x =tan 2x -(tan 2x ·cos 2x )=tan 2x (1-cos 2x )=tan 2x ·sin 2x ,问题得证. 法二:左边=tan 2x ·sin 2x =tan 2x (1-cos 2x )=tan 2x -tan 2x ·cos 2x =tan 2x -sin 2x ,问题得证.5.求函数)6π2sin(2+=x y 在区间[0,2π ]上的值域. 解:因为0≤x ≤2π,所以,6π76π26π,π20≤+≤≤≤x x 由正弦函数的图象, 得到],1,21[)6π2sin(-∈+x所以y ∈[-1,2]. 6.求以下函数的值域.(1)y =sin 2x -cos x +2; (2)y =2sin x cos x -(sin x +cos x ). 解:(1)y =sin 2x -cos x +2=1-cos 2x -cos x +2=-(cos 2x +cos x )+3,令t =cos x ,那么,413)21(413)21(3)(],1,1[222++-=++-=++-=-∈t t t t y t利用二次函数的图象得到].413,1[∈y (2)y =2sin x cos x -(sin x +cos x )=(sin x +cos x )2-1-(sin x +cos x ),令t =sin x +cos x 2=,)4πsin(+x ,那么]2,2[-∈t 那么,,12--=t t y 利用二次函数的图象得到].21,45[+-∈y 7.假设函数y =A sin(ωx +φ)(ω>0,φ>0)的图象的一个最高点为)2,2(,它到其相邻的最低点之间的图象与x 轴交于(6,0),求这个函数的一个解析式.解:由最高点为)2,2(,得到2=A ,最高点和最低点间隔是半个周期,从而与x 轴交点的间隔是41个周期,这样求得44=T ,T =16,所以⋅=8πω又由)28πsin(22ϕ+⨯=,得到可以取).4π8πsin(2.4π+=∴=x y ϕ8.函数f (x )=cos 4x -2sin x cos x -sin 4x .(Ⅰ)求f (x )的最小正周期; (Ⅱ)假设],2π,0[∈x 求f (x )的最大值、最小值. 数xxy cos 3sin 1--=的值域.解:(Ⅰ)因为f (x )=cos 4x -2sin x cos x -sin4x =(cos 2x -sin 2x )(cos 2x +sin 2x )-sin2x )4π2sin(2)24πsin(22sin 2cos 2sin )sin (cos 22--=-=-=--=x x x x x x x所以最小正周期为π.(Ⅱ)假设]2π,0[∈x ,那么]4π3,4π[)4π2(-∈-x ,所以当x =0时,f (x )取最大值为;1)4πsin(2=--当8π3=x 时,f (x )取最小值为.2-1. 2tan =θ,求〔1〕θθθθsin cos sin cos -+;〔2〕θθθθ22cos 2cos .sin sin +-的值.解:〔1〕2232121tan 1tan 1cos sin 1cos sin 1sin cos sin cos --=-+=-+=-+=++θθθθθθθθθθ; (2) θ+θθ+θθ-θ=θ+θθ-θ222222cos sin cos 2cos sin sin cos 2cos sin sin324122221cos sin 2cos sin cos sin 2222-=++-=+θθ+θθ-θθ=.说明:利用齐次式的结构特点〔如果不具备,通过构造的方法得到〕,进行弦、切互化,就会使解题过程简化。
高考三角函数经典解答题及答案
31在△ ABC 中,角A 、B C 所对的边分别是 a, b, c,且a 2 + c 2 — b 2 =1ac. 2(1)求 sin 2——— + cos2 B 的值; 2 (2)若b=2,求△ ABC 面积的最大值.1解:(1)由余弦TE 理:conB=-41 +cos2B=- -4一, 1 1 (2)由 cosB = —,得 sin B48 ,S △AB =:acsinB & "15 (a=c 时取等号) 3 23故S AABC 的最大值为 ------32在^ABC 中,角 A, B, C 的对边分别为 a, b, c,且 bcosC = 3acosB -ccosB.(I)求cosB 的值;(II )若BA BC = 2 ,且b = 2/2 ,求a 和c b 的值.解:(I)由正弦定理得 a =2Rsin A,b =2Rsin B,c = 2RsinC , 贝U2Rsin BcosC = 6Rsin AcosB 一 2Rsin C cosB, 故sin B cosC = 3sin AcosB - sinC cosB, 可得 sin BcosC sinCcosB =3sin AcosB, 即sin(B C) =3sin AcosB,可得 sin A = 3sin AcosB.又 sin A = 0,…1因止匕cos B = —. 3(II )解:由 BA BC =2,可得acosB = 2,1 M 一又 cosB = 一,故 ac = 6,3由b 2=a 2c 2-2accosB, 可得 a 2c 2=12, 所以(a -c)2=0,即a =c,所以a= c= . 63已知向重m = (sin B, 1 - cosB ),向重n = ( 2, 0),且m 与n 所成角为—,sin2AB 21/口a 2 + c 2 =2ac+4 > 2ac,得4 已知向量 m=(1,2sinA), n =(sin A,1+cosA),满足 m//n,b+c = V3a. (I小;(II )求 sin( B +f)的值.解:(1)由 m//n 得 2 sin 2A -1 一 cos A = 0 ……2 分 即 2c os2A+8SA —1 =0, cos A 或 cos A = —12: A 是AABC 的内角,cosA=—1舍去. A 「3(2) : b +c =M 3a由正弦定理,sin B - sin C = 3sin A =32其中A 日C 是AABC 的内角。
解答题:三角函数、三角恒等变换与解三角形(6大题型)(解析版)
解答题:三角函数、三角恒等变换与解三角形目录题型一三角恒等变换与三角函数 1题型二正余弦定理解三角形的边与角 3题型三利用正弦定理求三角形外接圆 6题型四解三角形中边长或周长的最值范围 8题型五解三角形中面积的最值范围 10题型六三角形的角平分线、中线、垂线 13必刷大题 16三角恒等变换与三角函数大题典例1.(24-25高三上·河南·月考)已知向量m =(cos x +sin x ,3sin x ),n=(cos x -sin x ,2cos x ),函数g (x )=m ⋅n .(1)求g (x )的最小正周期;(2)若函数f (x )=g (x )-a 在区间0,π2上恰有两个零点,求实数a 的取值范围.【答案】(1)π;(2)[1,2).【解析】(1)g (x )=m ⋅n =cos 2x -sin 2x +23sin x cos x ,=cos2x +3sin2x =2sin 2x +π6∴g (x )的最小正周期T =2π2=π;(2)由题知g (x )=a 在区间0,π2上恰有两个不同的实数根,即函数g (x )在区间0,π2上的图象与直线y =a 恰有两个交点,令u =2x +π6,∵x ∈0,π2 ,∴u ∈π6,7π6 ,作出y =2sin u u ∈π6,7π6的图象与直线y =a ,如图.由图知,当1≤a <2时,y =2sin u u ∈π6,7π6的图象与直线y =a 有两个交点,∴实数a 的取值范围为[1,2).解法指导此类题型考察恒等变形和三角函数函数性质,涉及到三角恒等变形的公式比较多。
1、首先要通过降幂公式降幂,二倍角公式化角:(1)二倍角公式:sin 2α=2sin αcos α(S 2α);cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α(C 2α)(2)降幂公式:cos 2α=1+cos2α2,sin 2α=1-cos2α2,2、再通过辅助角公式“化一”,化为y =A sin (ωx +φ)+B3、辅助角公式:a sin α+b cos α=a 2+b 2sin (α+φ),其中tan φ=ba.4、最后利用三角函数图象和性质,求解计算:一般将ωx +ϕ看做一个整体,利用换元法和数形结合的思想解题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学-.三角函数高考常见题型
三角函数题是高考数学试卷的第一道解答题,试题难度一般不大,但其战略意义重大,所以稳拿该题12分对文理科学生都至关重要。
分析近年高考试卷,可以发现,三角解答题多数喜欢和平面向量综合在一起,且向量为辅,三角为主,主要有以下几类:
一、运用同角三角函数关系、诱导公式、和、差、倍、半等公式进行化简求值类。
例1 已知向量33(cos ,sin ),(cos ,sin ),[,]22222x x x x x ππ==-∈且a b 。
(1
)若||+>a b x 的取值范围;
(2)函数()||f x =⋅++a b a b ,若对任意12,[,]2x x π
π∈,恒有12|()()|f x f x t -<,求t 的取值范围。
二、运用三角函数性质解题,通常考查正弦、余弦函数的单调性、周期性、最值、对称轴及对称中心。
例2
若,0),(cos ,sin ),0x x x ωωωω==->m n ,在函数()()f x t =⋅++m m n 的图象中,对称中心到对称轴的最小距离为4π,且当
[0,]3x π∈时,()f x 的最大值为1。
(1)求函数()f x 的解析式; (2
)若
()[0,]f x x π=∈,求实数x 的值。
例3 已知向量α(sin =, )21-,1(=, )cos 2α,
51=⋅,)2,0(πα∈ (1)求ααsin 2sin 及的值;
(2)设函数x x x f 2cos 2)22sin(5)(+++-=απ])2,24[(ππ∈x ,求x 为何值时,)(x f 取得最大值,最大 值是多少,并求)(x f 的单调增区间。
例4 设向量
]2,0[),23cos ,23(sin ),2sin ,2(cos π∈==x x x x x 向量. (Ⅰ)求||+⋅及; (Ⅱ)若函数||2)(x f ++⋅=,求)(x f 的最小值、最大值.
三、解三角形问题,判断三角形形状,正余弦定理的应用。
例5
已知函数2()sin cos 333x x x
f x =+.
(I )将()f x 写成sin()A x B w j ++的形式,并求其图象对称中心的横坐标;
(II )如果△ABC 的三边a,b,c 满足b2= a c ,且边b 所对的角为x ,试求x 的范围及此时函数()f x 的
值域.
例6 在△ABC 中,角A,B ,C 的对边分别为a,b ,c .已知向量(,)a c b a =+-m ,(,)a c b =-n , 且⊥m n .
(1)求角C 的大小; (2
)若sin sin A B +=,求角A 的值。
三角函数高考常见题型
一、例1 解:(1)||||1,cos 2,||2cos x x ==⋅=∴
+==->Q a b a b a b ,
即5cos [,],26
x x x ππππ<∈∴<≤Q 。
(2)21
3()||cos 22cos 2(cos )22
f x x x x =⋅++=-=--a b a b 。
max min 1cos 0,()3,()1x f x f x -≤≤∴==-Q ,又12max min |()()|()()4,4f x f x f x f x t -≤-=∴>Q
二、例2 解:由题意得cos ,sin )x x x ωωω+=+-m n ,
()(),0)cos ,sin )f x t x x x x t ωωωω=⋅++=⋅+-+m m n
2cos )3sin cos x x x t x x x t ωωωωωω=++=⋅+
333
cos 2sin 2)22232
x x t x t πωωω=-++=-++ (1)∵对称中心到对称轴的最小距离为4
π,∴()f x 的最小正周期T π=, 23
,1,())232
f x x t πππωω∴==∴=-++。
当[0,]3x π
∈时,2[,],sin(2)[3333x x π
πππ-∈-∴-∈,()[,3]f x t t ∴∈+。
max 1()1,31,2,())32
f x t t f x x π=∴+==-∴=--Q 。
(2)由()f x =,得1sin(2)32x π-=-,由[0,]x π∈,得52333x πππ-≤-≤。
故732,366124
x x π
π
πππ-=-∴=或或。
例3 解:(1)51cos sin =
-=⋅αα,2512sin 1)cos (sin 2=-=-ααα,∴25242sin =α, 25
492sin 1)cos (sin 2=+=+ααα,∴57cos sin =+αα,∴53cos =α,54sin =α. (2)12cos )sin 2sin cos 2(cos 52cos 1)2cos(5)(+++=++-=x x x x x x f ααα
12sin 42cos 412cos )2sin 5
42cos 53(5++=+++=x x x x x 1)42sin(24++=πx ,∵224ππ≤≤x , ∴45423ππ
π
≤+≤x ,∴当24π=x 时,621)24
()(max +==πf x f ,要使)(x f y =单调递增, ∴ππ
π
ππ
k x k 224222+≤+≤+-,Z)(8
83∈+≤≤+-k k x k ππππ,又]2,24[ππ∈x ,∴)(x f y =的单调增区间为]8
,24[ππ.
例4 解:(I ),2sin )223sin(23cos 2sin 23sin
2cos x x x x x x x b a =+=+=⋅ ,2sin 222)(||2222x +=⋅++=+=+Θ
2)cos (sin 2)2sin 1(22sin 22||x x x x +=+=+=+∴]).2,0[).(cos (sin 2π∈+=x x x (II )由(I )得:).cos (sin 2cos sin 2)cos (sin 22sin )(x x x x x x x x f ++=++= 令,1cos sin 2],2,1[],2,0[,cos sin 2-=⋅∴∈∴∈=+t x x t x t x x π
Θ ]2,1[,2)1(2122∈-+=+-=∴t t t t y 。
2;2,1min ===∴t y t 当时当时,.221max +=y
三、例5 解:(I )f (x ) =12x sin 23(1+2cos 3x )=12x sin 232cos 3
x
=sin(23x +3p .由sin(2x 3+3p )= 0,即2x 3+3
p =kπ(k ∈Z),得x=3k-12p (k ∈Z),即对称中心的横坐标为3k-12
p ,(k ∈Z). (II )由已知
b 2=a
c ,得cosx=22222a c -b a c -ac 2ac 2ac ++=≥2ac-ac 12ac 2=.∴12≤cosx <1,0<x≤3p .
∴3p <23x +3p ≤59p .∵||32p p ->5||92p p -,∴sin 3p <sin(23x +3p )≤1. 23x +3
p ≤1,
即f (x ),1). 例6 解: (1)由⊥m n 得()()()0a c a c b a b +-+-=; 整理得2220a b c ab +--=.
即222
a b c ab +-=,又2221cos 222a b c ab C ab ab +-===.又因为0C π<<,所以3C π=. (2)因为3C π
=,所以23A B π+=, 故23
B A π=-.
由2sin sin sin sin()3A B A A π+=+-=得.即1sin sin 2A A A +=
cos A A +=sin()62
A π+=.因为203A π<<,所以5666A πππ<+<, 故64A ππ+
=或364A ππ+=,∴12
A π=或712A π=.。
