习题1.1参考答案
苑尚尊电工与电子技术基础第2版习题参考答案第1章
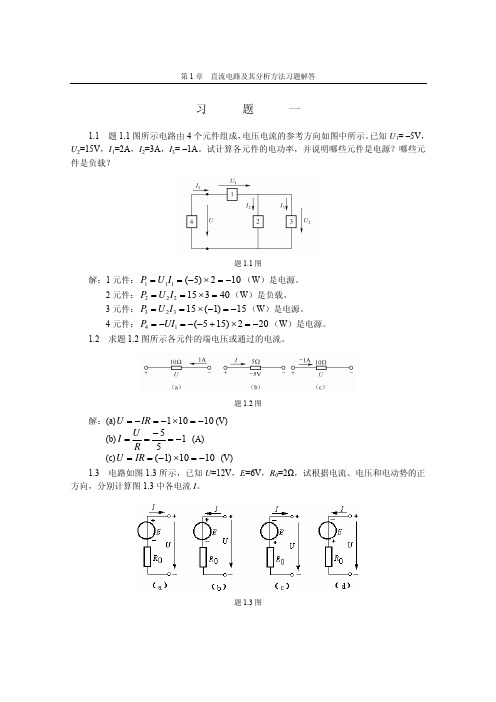
第1章 直流电路及其分析方法习题解答习 题 一1.1 题1.1图所示电路由4个元件组成，电压电流的参考方向如图中所示。
已知U 1= –5V ，U 2=15V ，I 1=2A ，I 2=3A ，I 3= –1A 。
试计算各元件的电功率，并说明哪些元件是电源？哪些元件是负载？题1.1图解：1元件：102)5(111−=×−==I U P （W ）是电源。
2元件：40315222=×==I U P （W ）是负载。
3元件：15)1(15323−=−×==I U P （W ）是电源。
4元件：202)155(14−=×+−−=−=UI P （W ）是电源。
1.2 求题1.2图所示各元件的端电压或通过的电流。
题1.2图解：(a)10101−=×−=−=IR U (V)(b)155−=−==R U I (A) (c)1010)1(−=×−==IR U (V)1.3 电路如图1.3所示，已知U =12V ，E =6V ，R 0=2Ω，试根据电流、电压和电动势的正方向，分别计算图1.3中各电流I 。
题1.3图第1章 直流电路及其分析方法习题解答2 解：(a) 0U E IR =− 03 (A)E UI R −==− (b) 0U E IR =+ 0 3 (A)U EI R −== ©0U E IR =−− 09 (A)E UI R −−==− (d) 0U E IR =−+ 09 (A)E UI R +==1.4 已知电路如题1.4图（a ）和（b ）所示，试计算a 、b 两端的电阻。
解：(a)由图可知，电阻的串并联关系可等效为下图所示：则710//10210//]6)12//6[(2=+=++=ab R （Ω） (b)由图可知，电阻的串并联关系可等效为下图所示：则4.54.236//46//6=+=+=ab R （Ω） 1.5 在题1.5图中，R 1=R 2=R 3=R 4=300Ω，R 5=600Ω，试求开关S 断开和闭合时a 、b 之间的等效电阻。
(完整版)结构化学习题参考答案-周公度-第5版
【1.1】将锂在火焰上燃烧，放出红光，波长λ=670.8nm ，这是Li 原子由电子组态 (1s)2(2p)1→(1s)2(2s)1跃迁时产生的，试计算该红光的频率、波数以及以k J ·mol -1为单位的能量。
解：811412.99810m s 4.46910s 670.8m cνλ--⨯⋅===⨯ 41711 1.49110cm670.810cm νλ--===⨯⨯3414123-1 -16.62610J s 4.46910 6.602310mol 178.4kJ mol A E h N sν--==⨯⋅⨯⨯⨯⨯=⋅【1.3】金属钾的临阈频率为5.464×10-14s -1，如用它作为光电极的阴极当用波长为300nm 的紫外光照射该电池时，发射光电子的最大速度是多少？解：2012hv hv mv =+()1201812341419312 2.998102 6.62610 5.46410300109.10910h v v m m s J s s m kgυ------⎡⎤=⎢⎥⎣⎦⎡⎤⎛⎫⨯⨯⨯-⨯⎢⎥ ⎪⨯⎝⎭⎢⎥=⎢⎥⨯⎢⎥⎣⎦134141231512 6.62610 4.529109.109108.1210J s s kg m s ----⎡⎤⨯⨯⨯⨯=⎢⎥⨯⎣⎦=⨯【1.4】计算下列粒子的德布罗意波的波长：（a ） 质量为10-10kg，运动速度为0.01m ·s -1的尘埃； （b ） 动能为0.1eV 的中子； （c ） 动能为300eV 的自由电子。
解：根据关系式：(1)34221016.62610J s 6.62610m 10kg 0.01m s h mv λ----⨯⋅===⨯⨯⋅ 34-11 (2) 9.40310mh p λ-====⨯3411(3) 7.0810mh p λ--====⨯【1.6】对一个运动速度c υ（光速）的自由粒子，有人进行了如下推导：1v vv v 2h h E m p m νλ=====①②③④⑤结果得出12m m υυ=的结论。
概率论与数理统计(茆诗松)第二版第一章课后习题1.1-1.3参考答案
（3）由定义条件 2，知 A1 ,A2 , L , An ∈ F ，根据（2）小题结论，可得 U Ai ∈ F ，
i =1
n
再由定义条件 2，知 U Ai ∈ F ，即 I Ai ∈ F ；
i =1 i =1
n
n
（4）由定义条件 2，知 A1 , A2 , L , An , L ∈ F ，根据定义条件 3，可得 U Ai ∈ F ，
n n −1 n （3）由二项式展开定理 ( x + y ) n = ⎜ ⎜0⎟ ⎟x + ⎜ ⎜1⎟ ⎟x y + L + ⎜ ⎜n⎟ ⎟ y ，令 x = y = 1，得 ⎝ ⎠ ⎝ ⎠ ⎝ ⎠
⎛n⎞ ⎛n⎞ ⎛n⎞ n ⎜ ⎜0⎟ ⎟+⎜ ⎜1⎟ ⎟ +L+ ⎜ ⎜n⎟ ⎟=2 ； ⎝ ⎠ ⎝ ⎠ ⎝ ⎠
⎛ n − 1⎞ ⎛ n − 1⎞ ⎛n⎞ (n − 1)! (n − 1)! (n − 1)! n! ⎟ ⎟ ⎟ [ r + (n − r )] = +⎜ = + = =⎜ ⎟ ⎜ ⎟ ⎟； r!(n − r )! ⎜ ⎝ r − 1⎠ ⎝ r ⎠ (r − 1)!(n − r )! r!(n − 1 − r )! r!( n − r )! ⎝r⎠ ⎛n⎞ ⎛ n⎞ ⎛n⎞
2
Ω A
B C (A − B )∪C
Ω
证： （1） AB U AB = A( B U B ) = AΩ = A ； （2） A U A B = ( A U A )( A U B ) = Ω( A U B ) = A U B ． 11．设 F 为一事件域，若 An ∈F ，n = 1, 2, …，试证： （1）∅ ∈F ； （2）有限并 U Ai ∈ F ，n ≥ 1；
《C语言程序设计教程》第三版课后习题参考答案
《C语言程序设计教程》第三版课后习题参考答案C语言程序设计教程第三版课后习题参考答案第一章：C语言概述1.1 C语言的特点答案：C语言是一种通用的、面向过程的程序设计语言，具有高效、简洁、灵活等特点。
它提供了丰富的程序设计元素和功能，适用于各种不同的应用领域。
1.2 C语言程序的基本结构答案：C语言程序由预处理指令、函数声明、函数定义、变量声明和语句组成。
其中，预处理指令用来引入头文件或定义宏，函数声明用来声明函数的名称和参数，函数定义用来实现函数的功能，变量声明用来声明变量的类型和名称，语句用来表达具体的计算过程。
1.3 C语言的数据类型答案：C语言提供了多种数据类型，包括基本类型（整型、浮点型、字符型等）和派生类型（数组、指针、结构体等）。
每种数据类型在内存中占据一定的存储空间，并具有特定的取值范围和操作规则。
1.4 C语言的运算符和表达式答案：C语言支持各种运算符和表达式，例如算术运算符（+、-、*、/等）、关系运算符（>、<、==等）、逻辑运算符（&&、||、!等）等。
通过运算符和表达式可以进行各种数值计算和逻辑判断。
第二章：基本数据类型与运算2.1 整型数据类型答案：C语言提供了不同长度的整型数据类型，包括有符号整型（int、long等）和无符号整型（unsigned int、unsigned long等）。
整型数据类型可以表示整数值，并具有不同的取值范围。
2.2 浮点型数据类型答案：C语言提供了浮点型数据类型（float、double等），用来表示带小数部分的实数值。
浮点型数据可以表示较大或较小的数值，并具有一定的精度。
2.3 字符型数据类型答案：C语言提供了字符型数据类型（char），用来表示单个字符。
字符型数据可以用于表示各种字符（包括字母、数字、符号等）。
2.4 布尔型数据类型答案：C语言不直接支持布尔型数据类型，但可以使用整型数据类型来表示布尔值（0表示假、非零表示真）。
概率论与数理统计课后习题参考问题详解高等教育出版社
概率论与数理统计课后习题参考答案高等教育习题1.1解答1. 将一枚均匀的硬币抛两次，事件C B A ,,分别表示“第一次出现正面”，“两次出现同一面”，“至少有一次出现正面”。
试写出样本空间及事件C B A ,,中的样本点。
解：{=Ω(正，正)，（正，反），（反，正），（反，反）}{=A (正，正)，（正，反）}；{=B （正，正），（反，反）} {=C (正，正)，（正，反），（反，正）}2. 在掷两颗骰子的试验中，事件D C B A ,,,分别表示“点数之和为偶数”，“点数之和小于5”，“点数相等”，“至少有一颗骰子的点数为3”。
试写出样本空间及事件D C B A BC C A B A AB ---+,,,,中的样本点。
解：{})6,6(,),2,6(),1,6(,),6,2(,),2,2(),1,2(),6,1(,),2,1(),1,1( =Ω；{})1,3(),2,2(),3,1(),1,1(=AB ；{})1,2(),2,1(),6,6(),4,6(),2,6(,),5,1(),3,1(),1,1( =+B A ；Φ=C A ；{})2,2(),1,1(=BC ；{})4,6(),2,6(),1,5(),6,4(),2,4(),6,2(),4,2(),5,1(=---D C B A3. 以C B A ,,分别表示某城市居民订阅日报、晚报和体育报。
试用C B A ,,表示以下事件：（1）只订阅日报； （2）只订日报和晚报； （3）只订一种报； （4）正好订两种报； （5）至少订阅一种报； （6）不订阅任何报； （7）至多订阅一种报； （8）三种报纸都订阅； （9）三种报纸不全订阅。
解：（1）C B A ； （2）C AB ； （3）C B A C B A C B A ++；（4）BC A C B A C AB ++; （5）C B A ++；（6）C B A ； （7）C B A C B A C B A C B A +++或C B C A B A ++（8）ABC ； （9）C B A ++4. 甲、乙、丙三人各射击一次，事件321,,A A A 分别表示甲、乙、丙射中。
12财政学习题参考答案
财政学习题武汉大学经济系赵伟习题1.1：市场失灵n1．你认为下列哪个市场会产生效率结果？为什么？（4）n（1）海滨住房的防潮险；n（2）医疗；n（3）股票市场；n（4）个人计算机。
n2．下列属于市场失灵现象的有（1、2、3、4）。
n（1）电信服务价格居高不下；n（2）传染性疾病流行；n（3）私人企业没有能力从事国防科技研究；n（4）政府提供医疗保险，但医疗费用飞速上升，无法控制。
n3．市场失灵是如何产生的，根源有哪些？习题1.1：公共产品基本概念私人产品竞争性排他性非排他性混合产品公共资源公共地的悲剧免费搭车问题准公共产品思考与练习1．你认为下列哪些属于公共产品，哪些属于私人产品？为什么？1、2、4属于公共产品，3属于私人产品(1)道路；(2)公共电视节目；(3)闭路电视节目；(4)提供航班时刻表的网站。
习题1.1：政府失灵n 1.假如有5 个选民：甲、乙、丙、丁、戊，他们对A、B、C、D 四个项目的排序如下。
（1）依照图3-2，画出各选民的效用曲线。
（2）按照简单多数规则，能否选出项目？如果能，是哪一个？如果不能，请说明为什么。
2．在世界各国广泛实行间接民主制和多数票规则下，公共决策的结果能否充分有效地反映纳税人的意愿？为什么？3．根据公共选择理论，说明政府失灵的主要原因及其矫正方法。
偏好形态图ABCD甲乙丙丁戊1234D wins in every pairwise vote?although multi-peaked preferences may lead to voting inconsistencies, this is not necessarily the case. 两两投票表决中D 方案胜出。
投票悖论出现一定是存在多峰偏好。
2．假如王某和李某对焰火的需求曲线分别为：P A=10-0.5Q，P B=20-Q；焰火的边际成本曲线为MC=2/3·Q （1）如果焰火是私人产品，请求出其均衡价格和数量以及王某和李某各自对焰火的需求量；（2）如果焰火具有非排他性，王某和李某的需求量以及他们的意愿支付价格分别是多少？（3）如果王某选择搭便车，焰火的均衡数量是多少？（4）请问如何解决搭便车问题？（详见后）3．公共产品的有效供给和私人产品的有效供给有何区别？为什么存在这样的区别？试分析之。
《装配式混凝土建筑概论》课后习题参考答案
第1章习题参考答案1.1 什么是建筑产业化?建筑产业化的主要特点有哪些?参考答案：（1）建筑产业化是指运用现代化管理模式,通过标准化的建筑设计以及模数化、工厂化的部品生产,实现建筑构部件的通用化和现场施工的装配化、机械化。
（2）建筑产业化的主要特点如下:1）主要构件在工厂或现场预制,采用机械化吊装,可以与现场各专业施工同步进行,具有施工速度快、有效缩短工程建设周期、有利于冬期施工的特点。
2）构件预制采用定型模板平面施工作业,代替现浇结构立体交叉作业,具有生产效率高、产品质量好、安全环保、有效降低成本的特点。
3）在预制构件生产环节可以采用反打一次成型工艺或立模工艺等将保温、装饰、门窗附件等特殊要求的功能高度集成,可以减少物料损耗和施工工序。
4）对从业人员的技术管理能力和工程实践经验要求较高,装配式建筑的设计、施工应做好前期策划,具体包括工期进度计划、构件标准化深化设计及资源优化配置方案等。
1.2 如何理解PC结构?PC结构的主要特点有哪些?参考答案：（1）PC结构是预制装配式混凝土结构的简称,PC是Prefabricated Concrete Structure 的缩写,是以预制混凝土构件为主要构件,经装配、连接部分现浇而形成的混凝土结构。
PC 构件是以构件加工单位工厂化制作而成的成品混凝土构件。
（2）PC结构的主要特点有：①产业化流水预制构件工业化程度高。
②成型模具和生产设备一次性投入后可重复使用,耗材少,节约资源和费用。
③现场装配、连接可避免或减轻施工对周边环境的影响。
④预制装配工艺的运用可使劳动力资源投入相对减少。
⑤机械化程度有明显提高,操作人员劳动强度得到有效降低。
⑥预制构件外装饰工厂化制作,直接浇捣于混凝土中,建筑物外墙无湿作业,不采用外脚手架,不产生落地灰,扬尘得到抑制。
⑦预制构件的装配化使得工程施工周期缩短。
⑧工厂化预制混凝土构件不采用湿作业和减少现浇混凝土浇捣,避免了垃圾源的产生,搅拌车、固定泵以及湿作业的操作工具洗清,大量废水和废浆污染源得到抑制。
算法设计与分析基础习题参考答案
5..证明等式gcd(m,n)=gcd(n,m mod n)对每一对正整数m,n都成立.Hint:根据除法的定义不难证明:●如果d整除u和v, 那么d一定能整除u±v;●如果d整除u,那么d也能够整除u的任何整数倍ku.对于任意一对正整数m,n,若d能整除m和n,那么d一定能整除n和r=m mod n=m-qn；显然，若d能整除n和r，也一定能整除m=r+qn和n。
数对(m,n)和(n,r)具有相同的公约数的有限非空集，其中也包括了最大公约数。
故gcd(m,n)=gcd(n,r)6.对于第一个数小于第二个数的一对数字,欧几里得算法将会如何处理?该算法在处理这种输入的过程中,上述情况最多会发生几次?Hint:对于任何形如0<=m<n的一对数字,Euclid算法在第一次叠代时交换m和n, 即gcd(m,n)=gcd(n,m)并且这种交换处理只发生一次.7.a.对于所有1≤m,n≤10的输入, Euclid算法最少要做几次除法?(1次)b. 对于所有1≤m,n≤10的输入, Euclid算法最多要做几次除法?(5次)gcd(5,8)习题1.21.(农夫过河)P—农夫W—狼G—山羊C—白菜2.(过桥问题)1,2,5,10---分别代表4个人, f—手电筒4. 对于任意实系数a,b,c, 某个算法能求方程ax^2+bx+c=0的实根,写出上述算法的伪代码(可以假设sqrt(x)是求平方根的函数)算法Quadratic(a,b,c)//求方程ax^2+bx+c=0的实根的算法//输入:实系数a,b,c//输出:实根或者无解信息D←b*b-4*a*cIf D>0temp←2*ax1←(-b+sqrt(D))/tempx2←(-b-sqrt(D))/tempreturn x1,x2else if D=0 return –b/(2*a)else return “no real roots”else //a=0if b≠0 return –c/belse //a=b=0if c=0 return “no real numbers”else return “no real roots”5.描述将十进制整数表达为二进制整数的标准算法a.用文字描述b.用伪代码描述解答：a.将十进制整数转换为二进制整数的算法输入：一个正整数n输出：正整数n相应的二进制数第一步：用n除以2，余数赋给Ki(i=0,1,2...)，商赋给n第二步：如果n=0，则到第三步，否则重复第一步第三步：将Ki按照i从高到低的顺序输出b.伪代码算法DectoBin(n)//将十进制整数n转换为二进制整数的算法//输入：正整数n//输出：该正整数相应的二进制数，该数存放于数组Bin[1...n]中i=1while n!=0 do {Bin[i]=n%2;n=(int)n/2;i++;}while i!=0 do{print Bin[i];i--;}9.考虑下面这个算法,它求的是数组中大小相差最小的两个元素的差.(算法略) 对这个算法做尽可能多的改进.算法MinDistance(A[0..n-1])//输入:数组A[0..n-1]//输出:the smallest distance d between two of its elements习题1.31.考虑这样一个排序算法,该算法对于待排序的数组中的每一个元素,计算比它小的元素个数,然后利用这个信息,将各个元素放到有序数组的相应位置上去.a.应用该算法对列表‖60,35,81,98,14,47‖排序b.该算法稳定吗?c.该算法在位吗?解:a. 该算法对列表‖60,35,81,98,14,47‖排序的过程如下所示:b.该算法不稳定.比如对列表‖2,2*‖排序c.该算法不在位.额外空间for S and Count[]4.(古老的七桥问题)习题1.41.请分别描述一下应该如何实现下列对数组的操作,使得操作时间不依赖数组的长度. a.删除数组的第i 个元素(1<=i<=n)b.删除有序数组的第i 个元素(依然有序) hints:a. Replace the i th element with the last element and decrease the array size of 1b. Replace the ith element with a special symbol that cannot be a value of the array ’s element(e.g., 0 for an array of positive numbers ) to mark the i th position is empty . (―lazy deletion ‖)第2章 习题2.17.对下列断言进行证明:(如果是错误的,请举例) a. 如果t(n )∈O(g(n),则g(n)∈Ω(t(n)) b.α>0时,Θ(αg(n))= Θ(g(n)) 解:a. 这个断言是正确的。
习题数电参考答案（终）
习题数电参考答案（终）第⼀章数字逻辑概论1.1 数字电路与数制信号1.1.1 试以表1.1.1所列的数字集成电路的分类为依据，指出下列IC器件属于何种集成度器件：（1）微处理器；（2）计数器；（3）加法器；（4）逻辑门；（5）4兆位存储器。
解：依照表1.1.1所⽰的分类，所列的五种器件：（1）、（5）属于⼤规模；（2）、（3）属于中规模；（4）属于⼩规模。
1.1.2⼀数字信号波形如图题1.1.2所⽰，试问该波形所代表的⼆进制数是什么？解：图题1.1.2所⽰的数字信号波形的左边为最⾼位（MSB），右边为最低位（LSB），低电平表⽰0，⾼电平表⽰1。
该波形所代表的⼆进制数为010110100。
1.1.3 试绘出下列⼆进制数的数字波形，设逻辑1的电压为5V，逻辑0的电压为0V。
（1）001100110011（2）0111010 （3）1111011101解：⽤低电平表⽰0，⾼电平表⽰1，左边为最⾼位，右边为最低位，题中所给的3个⼆进制数字的波形分别如图题1.1.3（a）、（b）、（c）所⽰，其中低电平为0V，⾼电平为5V。
1.1.4⼀周期性数字波形如图1.1.4所⽰，试计算：（1）周期；（2）频率；（3）占空⽐。
解：因为图题1.1.4所⽰为周期性数字波，所以两个相邻的上升沿之间持续的时间为周期，T=10ms。
频率为周期的倒数，f=1/T=1/0.01s=100Hz。
占空⽐为⾼电平脉冲宽度与周期的百分⽐，q=1ms/10ms×100%=10%。
1.2 数制1.2.1 ⼀数字波形如图1.2.1所⽰，时钟频率为4kHz，试确定：（1）它所表⽰的⼆进制数；（2）串⾏⽅式传送8位数据所需要的时间；（3）以8位并⾏⽅式传送的数据时需要的时间。
解：该波形所代表的⼆进制数为00101100。
时钟周期T=1/f=1/4kHz=0.25ms。
串⾏⽅式传送数据时，每个时钟周期传送1位数据，因此，传送8位数据所需要的时间t=0.25ms×8=2ms。
计量经济学精要习题参考答案(第四版)
计量经济学（第四版）习题参考答案第一章 绪论1.1 一般说来，计量经济分析按照以下步骤进行：（1）陈述理论（或假说） （2）建立计量经济模型 （3）收集数据 （4）估计参数 （5）假设检验 （6）预测和政策分析1.2 我们在计量经济模型中列出了影响因变量的解释变量，但它（它们）仅是影响因变量的主要因素，还有很多对因变量有影响的因素，它们相对而言不那么重要，因而未被包括在模型中。
为了使模型更现实，我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素，这些因素包括相对而言不重要因而未被引入模型的变量，以及纯粹的随机因素。
1.3时间序列数据是按时间周期（即按固定的时间间隔）收集的数据，如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体（如个人、公司、国家等）的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4 估计量是指一个公式或方法，它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中，依据估计量算出的一个具体的数值，称为估计值。
如Y 就是一个估计量，1nii YY n==∑。
现有一样本，共4个数，100，104，96，130，则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略，参考教材。
2.2 NS S x ==45=1.25 用α=0.05，N-1=15个自由度查表得005.0t =2.947，故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说，根据样本，我们有99%的把握说，北京男高中生的平均身高在170.316至177.684厘米之间。
2.3 原假设 120:0=μH备择假设 120:1≠μH2检验统计量()10/25XX μσ-Z ====查表96.1025.0=Z 因为Z= 5 >96.1025.0=Z ,故拒绝原假设, 即此样本不是取自一个均值为120元、标准差为10元的正态总体。
结构化学习题参考答案-周公度-第5版
【1.1】将锂在火焰上燃烧，放出红光，波长λ=670.8nm ，这是Li 原子由电子组态 (1s)2(2p)1→(1s)2(2s)1跃迁时产生的，试计算该红光的频率、波数以及以k J ·mol -1为单位的能量。
解：811412.99810m s 4.46910s 670.8m cνλ--⨯⋅===⨯ 41711 1.49110cm670.810cm νλ--===⨯⨯3414123-1 -16.62610J s 4.46910 6.602310mol 178.4kJ mol A E h N sν--==⨯⋅⨯⨯⨯⨯=⋅【1.3】金属钾的临阈频率为5.464×10-14s -1，如用它作为光电极的阴极当用波长为300nm 的紫外光照射该电池时，发射光电子的最大速度是多少？解：2012hv hv mv =+()1201812341419312 2.998102 6.62610 5.46410300109.10910h v v m m s J s s m kgυ------⎡⎤=⎢⎥⎣⎦⎡⎤⎛⎫⨯⨯⨯-⨯⎢⎥ ⎪⨯⎝⎭⎢⎥=⎢⎥⨯⎢⎥⎣⎦134141231512 6.62610 4.529109.109108.1210J s s kg m s ----⎡⎤⨯⨯⨯⨯=⎢⎥⨯⎣⎦=⨯【1.4】计算下列粒子的德布罗意波的波长：（a ） 质量为10-10kg，运动速度为0.01m ·s -1的尘埃； （b ） 动能为0.1eV 的中子； （c ） 动能为300eV 的自由电子。
解：根据关系式：(1)34221016.62610J s 6.62610m 10kg 0.01m s h mv λ----⨯⋅===⨯⨯⋅ 34-11 (2) 9.40310mh p λ-====⨯3411(3) 7.0810mh p λ--====⨯【1.6】对一个运动速度c υ（光速）的自由粒子，有人进行了如下推导：1v vv v 2h h E m p m νλ=====①②③④⑤结果得出12m m υυ=的结论。
微机原理及接口技术李干林—习题参考解答
习题参考解答1.1 什么是微处理器、微型计算机、微型计算机系统？参考答案：将运算器和控制器集成在一块大规模集成电路芯片上作为中央处理部件，简称为微处理器；以微处理器为核心，再配上存储器、接口电路等芯片，构成微型计算机；微型计算机系统由硬件和软件系统两大部分组成：(1)硬件系统由微型计算机和外设组成的计算机实体；(2)软件系统是指为微型计算机运行的全部技术资料和各种程序，由系统软件和应用软件构成。
1.2 什么是微型计算机的三种总线？参考答案：系统总线包含有三种不同功能的总线，即数据总线DB（Data Bus）、地址总线AB（Address Bus）和控制总线CB（Control Bus）。
“数据总线DB”用于传送数据信息。
数据总线是双向三态形式的总线，即他既可以把CPU的数据传送到存储器或I／O接口等其它部件，也可以将其它部件的数据传送到CPU。
“地址总线AB”是专门用来传送地址的，由于地址只能从CPU传向外部存储器或I／O端口，所以地址总线总是单向三态的。
“控制总线CB”用来传送控制信号和时序信号。
1.3 评估微型计算机的主要技术指标有哪些？参考答案：评估微型计算机的主要技术指标有：⑴CPU的字长，决定计算机内部一次可以处理的二进制代码的位数；⑵内存储器容量与速度，内存储器容量是衡量它存储二进制信息量大小的一个重要指标，内存储器的速度用存取周期来衡量；⑶CPU指令执行时间，反映CPU运算速度的快慢；⑷系统总线的传输速率等。
1.4 将下列十进制数分别转换为二进制、十六进制数。
⑴ 35 ⑵ 130 ⑶ 0.625 ⑷ 48.25参考答案：⑴ 100011B，23H ⑵⑶ 0.101B，0.AH ⑷ 110000.01B，30.4H1.5 将下列二进制数分别转换为十进制、八进制、十六进制数。
⑴ 101101B ⑵⑶ 110110.101B ⑷ 101011.011B参考答案：⑴ 45，55Q，2DH ⑵ 230，346Q，E6H⑶ 54.625，66.5Q，36.AH ⑷ 43.375，53.3Q，2B.6H1.6 写出下列十进制数的原码、反码、补码（分别采用8位二进制和16位二进制表示）。
有机化学课后习题参考答案
第一章 绪论1.1 扼要归纳典型的以离子键形成的化合物与以共价键形成的化合物的物理性质。
1.2是否相同？如将CH 4 及CCl 4各1mol 混在一起，与CHCl 3及CH 3Cl 各1mol 的混合物是否相同？为什么？答案： NaCl 与KBr 各1mol 与NaBr 及KCl 各1mol 溶于水中所得溶液相同。
因为两者溶液中均为Na + , K + , Br －, Cl －离子各1mol 。
由于CH 4 与CCl 4及CHCl 3与CH 3Cl 在水中是以分子状态存在，所以是两组不同的混合物。
1.3 碳原子核外及氢原子核外各有几个电子？它们是怎样分布的？画出它们的轨道形状。
当四个氢原子与一个碳原子结合成甲烷（CH 4）时，碳原子核外有几个电子是用来与氢成键的？画出它们的轨道形状及甲烷分子的形状。
答案：C+624HCCH 4中C 中有4个电子与氢成键为SP 3杂化轨道,正四面体结构CH 4SP 3杂化2p y2p z2p x2sH1.4 写出下列化合物的Lewis 电子式。
a. C 2H 4b. CH 3Clc. NH 3d. H 2Se. HNO 3f. HCHOg. H 3PO 4h. C 2H 6i. C 2H 2 j. H 2SO 4 答案：a.C C H H H HCC HH HH或 b.H C H H c.H N HHd.H S He.H O NO f.O C H Hg.O P O O H H Hh.H C C HHH H HO P O O H HH或i.H C C Hj.O S O HH OH H或1.5 下列各化合物哪个有偶极矩？画出其方向。
a. I 2b. CH 2Cl 2c. HBrd. CHCl 3e. CH 3OHf. CH 3OCH 3 答案：b.ClClc.HBrd.HCe.H 3COHH 3COCH 3f.1.6 根据S 与O 的电负性差别，H 2O 与H 2S 相比，哪个有较强的偶极-偶极作用力或氢键？答案：电负性 O > S , H 2O 与H 2S 相比，H 2O 有较强的偶极作用及氢键。
数据结构(C语言版)第三版习题答案
精神成就事业，态度决定一切。
附录习题参考答案习题1参考答案1.1.选择题(1). A. (2). A. (3). A. (4). B.C. (5). A. (6). A. (7). C. (8). A. (9). B. (10.) A.1.2.填空题(1). 数据关系(2). 逻辑结构物理结构(3). 线性数据结构树型结构图结构(4). 顺序存储链式存储索引存储散列表（Hash）存储(5). 变量的取值范围操作的类别(6). 数据元素间的逻辑关系数据元素存储方式或者数据元素的物理关系(7). 关系网状结构树结构(8). 空间复杂度和时间复杂度(9). 空间时间(10). Ο(n)1.3 名词解释如下：数据：数据是信息的载体是计算机程序加工和处理的对象包括数值数据和非数值数据数据项：数据项指不可分割的、具有独立意义的最小数据单位数据项有时也称为字段或域数据元素：数据元素是数据的基本单位在计算机程序中通常作为一个整体进行考虑和处理一个数据元素可由若干个数据项组成数据逻辑结构：数据的逻辑结构就是指数据元素间的关系数据存储结构：数据的物理结构表示数据元素的存储方式或者数据元素的物理关系数据类型：是指变量的取值范围和所能够进行的操作的总和算法：是对特定问题求解步骤的一种描述是指令的有限序列1.4 语句的时间复杂度为：(1) Ο(n2)(2) Ο(n2)(3) Ο(n2)(4) Ο(n-1)(5) Ο(n3)1.5 参考程序：main(){int XYZ；scanf("%d %d%d"&X&YZ)；if (X>=Y)if(X>=Z)if (Y>=Z) { printf("%d %d%d"XYZ);}else{ printf("%d %d%d"XZY);}else{ printf("%d %d%d"ZXY);}else if(Z>=X)if (Y>=Z) { printf("%d %d%d"YZX);}else{ printf("%d%d%d"ZYX);}else{ printf("%d%d%d"YXZ);}}1.6 参考程序：main(){int in;float xa[]p;printf("\nn=");scanf("%f"&n);printf("\nx=");scanf("%f"&x);for(i=0;i<=n;i++)scanf("%f "&a[i]);p=a[0];for(i=1;i<=n;i++){ p=p+a[i]*x;x=x*x;}printf("%f"p)'}习题2参考答案2.1选择题(1). C. (2). B. (3). B. (4). B. 5. D. 6. B. 7. B. 8. A. 9. A. 10. D.2.2.填空题(1). 有限序列(2). 顺序存储和链式存储(3). Ｏ(n) O(n)(4). n-i+1 n-i(5). 链式(6). 数据指针(7). 前驱后继(8). Ο(1) Ο(n)(9). s->next=p->next; p->next=s ;(10). s->next2.3. 解题思路：将顺序表A中的元素输入数组a若数组a中元素个数为n将下标为012...（n-1）/2的元素依次与下标为nn-1...（n-1）/2的元素交换输出数组a的元素参考程序如下：main(){int in;float ta[];printf("\nn=");scanf("%f"&n);for(i=0;i<=n-1;i++)scanf("%f "&a[i]);for(i=0;i<=(n-1)/2;i++){ t=a[i]; a[i] =a[n-1-i]; a[n-1-i]=t;} for(i=0;i<=n-1;i++)printf("%f"a[i]);}2.4 算法与程序：main(){int in;float ta[];printf("\nn=");scanf("%f"&n);for(i=0;i<n;i++)scanf("%f "&a[i]);for(i=1;i<n;i++)if(a[i]>a[0]{ t=a[i]; a[i] =a[0]; a[0]=t;}printf("%f"a[0]);for(i=2;i<n;i++)if(a[i]>a[1]{ t=a[i]; a[i] =a[1]; a[1]=t;}printf("%f"a[0]);}2.5 算法与程序：main(){int ijkn;float xta[];printf("\nx=");scanf("%f"&x);printf("\nn=");scanf("%f"&n);for(i=0;i<n;i++)scanf("%f "&a[i]); // 输入线性表中的元素for (i=0; i<n; i++) { // 对线性表中的元素递增排序k=i;for (j=i+1; j<n; j++) if (a[j]<a[k]) k=j; if (k<>j) {t=a[i];a[i]=a[k];a[k]=t;}}for(i=0;i<n;i++) // 在线性表中找到合适的位置if(a[i]>x) break;for(k=n-1;k>=i;i--) // 移动线性表中元素然后插入元素xa[k+1]=a[k];a[i]=x;for(i=0;i<=n;i++) // 依次输出线性表中的元素printf("%f"a[i]);}2.6 算法思路：依次扫描A和B的元素比较A、B当前的元素的值将较小值的元素赋给C如此直到一个线性表扫描完毕最后将未扫描完顺序表中的余下部分赋给C即可C的容量要能够容纳A、B两个线性表相加的长度有序表的合并算法：void merge (SeqList ASeqList BSeqList *C){ int ijk；i=0；j=0；k=0；while ( i<=st && j<=st )if (A.data[i]<=B.data[j])C->data[k++]=A.data[i++]；elseC->data[k++]=B.data[j++]；while (i<=st )C->data[k++]= A.data[i++]；while (j<=st )C->data[k++]=B.data[j++]；C->last=k-1；}2.7 算法思路：依次将A中的元素和B的元素比较将值相等的元素赋给C如此直到线性表扫描完毕线性表C就是所求递增有序线性表算法：void merge (SeqList ASeqList BSeqList *C){ int ijk；i=0；j=0；k=0；while ( i<=st)while（j<=st )if (A.data[i]=B.data[j])C->data[k++]=A.data[i++]；C->last=k-1；}习题3参考答案3.1.选择题(1). D (2). C (3). D (4). C (5). B (6). C (7). C (8). C (9). B (10).AB (11). D (12). B (13). D (14). C (15). C (16). D(17). D (18). C (19). C (20). C 3.2.填空题（1） FILOFIFO（2） -13 4 X * + 2 Y * 3 / -（3） stack.topstack.s[stack.top]=x（4） p>llink->rlink=p->rlinkp->rlink->llink=p->rlink（5） (R-F+M)%M（6） top1+1=top2（7） F==R（8） front==rear（9） front==(rear+1)%n（10） N-13.3 答：一般线性表使用数组来表示的线性表一般有插入、删除、读取等对于任意元素的操作而栈只是一种特殊的线性表栈只能在线性表的一端插入（称为入栈push）或者读取栈顶元素或者称为"弹出、出栈"(pop)3.4 答：相同点：栈和队列都是特殊的线性表只在端点处进行插入删除操作不同点：栈只在一端（栈顶）进行插入删除操作；队列在一端（top）删除一端(rear)插入3.5 答：可能序列有14种：ABCD; ACBD; ACDB; ABDC; ADCB; BACD; BADC; BCAD; BCDA; BDCA; CBAD; CBDA; CDBA; DCBA3.6 答：不能得到435612最先出栈的是4则按321的方式出不可能得到1在2前的序列可以得到135426按如下方式进行push(1)pop()push(2)push(3)pop()push(4)push(5)pop()pop()pop()push(6)pop()3.7 答：stack3.8 非递归:int vonvert (int noint a[]) //将十进制数转换为2进制存放在a[] 并返回位数{int r;SeStack s*p;P=&s;Init_stack(p);while(no){push(pno%2);no/=10;}r=0;while(!empty_stack(p)){pop(pa+r);r++;}return r;}递归算法:void convert(int no){if(no/2>0){Convert(no/2);Printf("%d"no%2);}elseprintf("%d"no);}3.9 参考程序：void view(SeStack s){SeStack *p; //假设栈元素为字符型char c;p=&s;while(!empty_stack(p)){c=pop(p);printf("%c"c);}printf("\n");}3.10 答：char3.11 参考程序：void out(linkqueue q){int e;while(q.rear !=q.front ){dequeue(qe);print(e); //打印}}习题4参考答案4.1 选择题：(1). A (2). D (3). C (4). C (5). B (6). B (7). D (8). A (9). B (10). D 4.2 填空题：（1）串长相等且对应位置字符相等（2）不含任何元素的串（3）所含字符均是空格所含空格数（4） 10（5） "hello boy"（6） 13（7） 1066（8）模式匹配（9）串中所含不同字符的个数（10） 364.3 StrLength (s)=14StrLength (t)=4SubStr( s87)=" STUDENT"SubStr(t21)="O"StrIndex(s"A")=3StrIndex (st)=0StrRep(s"STUDENT"q)=" I AM A WORKER"4.4 StrRep(s"Y""+");StrRep(s"+*""*Y");4.5 空串：不含任何字符；空格串：所含字符都是空格串变量和串常量:串常量在程序的执行过程中只能引用不能改变；串变量的值在程序执行过程中是可以改变和重新赋值的主串与子串：子串是主串的一个子集串变量的名字与串变量的值:串变量的名字表示串值的标识符4.6int EQUAl(ST){char *p*q;p=&S;q=&T;while(*p&&*q){if(*p!=*q)return *p-*q;p++;q++;}return *p-*q;}4.7(1)6*8*6=288(2)1000+47*6=1282(3)1000+(8+4)*8=1096(4)1000+(6*7+4)*8=13684.8习题5参考答案5.1 选择（1）C（2）B（3）C（4）B（5）C（6）D（7）C（8）C（9）B（10）C （11）B（12）C（13）C（14）C（15）C（16）B5.2 填空（1）1（2）1036；1040（3）2i（4） 1 ； n ; n-1 ; 2（5）2k-1；2k-1（6）ACDBGJKIHFE（7）p!=NULL（8）Huffman树（9）其第一个孩子; 下一个兄弟（10）先序遍历；中序遍历5.3叶子结点:C、F、G、L、I、M、K；非终端结点：A、B、D、E、J；各结点的度：结点： A B C D E F G L I J K M度： 4 3 0 1 2 0 0 0 0 1 0 0树深：4无序树形态如下：二叉树形态如下：5.5二叉链表如下:三叉链表如下:5.6先序遍历序列:ABDEHICFJG中序遍历序列:DBHEIAFJCG后序遍历序列:DHIEBJFGCA5.7(1) 先序序列和中序序列相同：空树或缺左子树的单支树；(2) 后序序列和中序序列相同：空树或缺右子树的单支树；(3) 先序序列和后序序列相同：空树或只有根结点的二叉树5.8这棵二叉树为:先根遍历序列:ABFGLCDIEJMK后根遍历序列:FGLBCIDMJKEA层次遍历序列:ABCDEFGLIJKM5.10证明：设树中结点总数为n叶子结点数为n0则n=n0 + n1 + ...... + nm （1）再设树中分支数目为B则B=n1 + 2n2 + 3n3 + ...... + m nm （2）因为除根结点外每个结点均对应一个进入它的分支所以有n= B + 1 （3）将（1）和（2）代入（3）得n0 + n1 + ...... + nm = n1 + 2n2 + 3n3 + ...... + m nm + 1 从而可得叶子结点数为：n0 = n2 + 2n3 + ...... + (m-1)nm + 15.11由5.10结论得n0 = (k-1)nk + 1又由 n=n0 + nk得nk= n-n0代入上式得n0 = (k-1)（n-n0）+ 1叶子结点数为：n0 = n (k-1) / k5.12int NodeCount(BiTree T){ //计算结点总数if(T)if (T-> lchild==NULL )&&( T --> rchild==NULL )return 1;elsereturn NodeCount(T-> lchild ) +Node ( T --> rchild )+1; elsereturn 0;}void ExchangeLR(Bitree bt){/* 将bt所指二叉树中所有结点的左、右子树相互交换 */ if (bt && (bt->lchild || bt->rchild)) {bt->lchild<->bt->rchild;Exchange-lr(bt->lchild);Exchange-lr(bt->rchild);}}/* ExchangeLR */5.14int IsFullBitree(Bitree T){/* 是则返回1否则返回0*/Init_Queue(Q); /* 初始化队列*/flag=0;In_Queue(QT); /* 根指针入队列按层次遍历*/while(!Empty_Queue (Q)){Out_Queue(Qp);if(!p) flag=1; /* 若本次出队列的是空指针时则修改flag值为1若以后出队列的指针存在非空则可断定不是完全二叉树 */else if (flag) return 0; /*断定不是完全二叉树 */ else{In_Queue(Qp->lchild);In_Queue(Qp->rchild); /* 不管孩子是否为空都入队列*/}}/* while */return 1; /* 只有从某个孩子指针开始之后所有孩子指针都为空才可断定为完全二叉树*/}/* IsFullBitree */转换的二叉树为：5.16对应的森林分别为：5.17typedef char elemtype;typedef struct{ elemtype data;int parent;} NodeType;(1) 求树中结点双亲的算法:int Parent(NodeType t[ ]elemtype x){/* x不存在时返回-2否则返回x双亲的下标(根的双亲为-1 */for(i=0;i<MAXNODE;i++)if(x==t[i].data) return t[i].parent; return -2;}/*Parent*/(2) 求树中结点孩子的算法:void Children(NodeType t[ ]elemtype x){for(i=0;i<MAXNODE;i++){if(x==t[i].data)break;/*找到x退出循环*/}/*for*/if(i>=MAXNODE) printf("x不存在\n"); else {flag=0;for(j=0;j<MAXNODE;j++)if(i==t[j].parent){ printf("x的孩子:%c\n"t[j].data);flag=1;}if(flag==0) printf("x无孩子\n");}/*Children*/5.18typedef char elemtype;typedef struct ChildNode{ int childcode;struct ChildNode *nextchild;}typedef struct{ elemtype data;struct ChildNode *firstchild;} NodeType;(1) 求树中结点双亲的算法:int ParentCL(NodeType t[ ]elemtype x){/* x不存在时返回-2否则返回x双亲的下标 */for(i=0;i<MAXNODE;i++)if(x==t[i].data) {loc=i;/*记下x的下标*/break;}if(i>=MAXNODE) return -2; /* x不存在 *//*搜索x的双亲*/for(i=0;i<MAXNODE;i++)for(p=t[i].firstchild;p!=NULL;p=p->nextchild) if(loc==p->childcode)return i; /*返回x结点的双亲下标*/}/* ParentL */(2) 求树中结点孩子的算法:void ChildrenCL(NodeType t[ ]elemtype x){for(i=0;i<MAXNODE;i++)if(x==t[i].data) /*依次打印x的孩子*/{flag=0; /* x存在 */for(p=t[i].firstchild;p;p=p->nextchild){ printf("x的孩子:%c\n"t[p-> childcode].data);flag=1;}if(flag==0) printf("x无孩子\n");return;}/*if*/printf("x不存在\n");return;}/* ChildrenL */5.19typedef char elemtype;typedef struct TreeNode{ elemtype data;struct TreeNode *firstchild; struct TreeNode *nextsibling; } NodeType;void ChildrenCSL(NodeType *telemtype x){ /* 层次遍历方法 */Init_Queue(Q); /* 初始化队列 */In_Queue(Qt);count=0;while(!Empty_Queue (Q)){Out_Queue(Qp);if(p->data==x){ /*输出x的孩子*/p=p->firstchild;if(!p) printf("无孩子\n");else{ printf("x的第%i个孩子:%c\n"++countp->data);/*输出第一个孩子*/p=p->nextsibling; /*沿右分支*/while(p){printf("x的第%i个孩子:%c\n"++countp->data);p=p-> nextsibling;}}return;}if(p-> firstchild) In_Queue(Qp-> firstchild);if(p-> nextsibling) In_Queue(Qp-> nextsibling);}}/* ChildrenCSL */5.20(1) 哈夫曼树为:(2) 在上述哈夫曼树的每个左分支上标以1右分支上标以0并设这7个字母分别为A、B、C、D、E、F和H如下图所示：则它们的哈夫曼树为分别为:A：1100B：1101C：10D：011E：00F：010H：111习题6参考答案6.1 选择题（1）C （2）A （3）B（4）C（5）B______条边（6）B（7）A（8）A（9）B（10）A（11）A（12）A（13）B（14）A（15）B（16）A（17）C 6.2 填空（1） 4（2） 1对多 ; 多对多（3） n-1 ; n（4） 0_（5）有向图（6） 1（7）一半（8）一半（9）___第i个链表中边表结点数___（10）___第i个链表中边表结点数___（11）深度优先遍历；广度优先遍历（12）O（n2）（13）___无回路6.3（1）邻接矩阵:（2）邻接链表：（3）每个顶点的度：顶点度V1 3V2 3V3 2V4 3V5 36.4（1）邻接链表：（2）逆邻接链表：（3）顶点入度出度V1 3 0V2 2 2V3 1 2V4 1 3V5 2 1V6 2 36.5（1）深度优先查找遍历序列：V1 V2 V3 V4 V5; V1 V3 V5 V4 V2; V1 V4 V3 V5 V2 （1）广度优先查找遍历序列：V1 V2 V3 V4 V5; V1 V3 V2 V4 V5; V1 V4 V3 V2 V56.6有两个连通分量：6.7顶点（1）（2）（3）（4）（5）Low Close Cost VexLow CloseCost VexLow CloseCost VexLow CloseCost VexLow CloseCost VexV10 00 00 00 00 0V21 00 00 00 00 0V31 01 00 00 00 0V43 02 12 10 10 1V5∞ 05 13 22 30 3U{v1} {v1v2} {v1v2v3} {v1 v2 v3 v4} {v1 v2 v3 v4 v5} T {} { (v1 v2) } {(v1 v2) (v1 v3) } {(v1 v2) (v1 v3) (v2 v4) } {(v1 v2) (v1v3)(v2v4)(v4v5) }最小生成树的示意图如下：6.8拓扑排序结果： V3--> V1 --> V4 --> V5 --> V2 --> V66.9（1）建立无向图邻接矩阵算法：提示：参见算法6.1因为无向图的邻接矩阵是对称的所以有for (k=0; k<G ->e; k++) /*输入e条边建立无向图邻接矩阵*/{ scanf("\n%d%d"&i&j);G ->edges[i][j]= G ->edges[j][i]=1;}(2)建立无向网邻接矩阵算法:提示：参见算法6.1初始化邻接矩阵：#define INFINITY 32768 /* 表示极大值*/for(i=0;i<G->n;i++)for(j=0;j<G->n;j++) G->edges[i][j]= INFINITY;输入边的信息：不仅要输入边邻接的两个顶点序号还要输入边上的权值for (k=0; k<G ->e; k++) /*输入e条边建立无向网邻接矩阵*/{ scanf("\n%d%d%d"&i&j&cost); /*设权值为int型*/G ->edges[i][j]= G ->edges[j][i]=cost;/*对称矩阵*/}(3)建立有向图邻接矩阵算法:提示：参见算法6.16.10(1)建立无向图邻接链表算法：typedef VertexType char;int Create_NgAdjList(ALGraph *G){ /* 输入无向图的顶点数、边数、顶点信息和边的信息建立邻接表 */scanf("%d"&n); if(n<0) return -1; /* 顶点数不能为负 */G->n=n;scanf("%d"&e); if(e<0) return =1; /*边数不能为负 */G->e=e;for(m=0;m< G->n ;m++)G-> adjlist [m].firstedge=NULL; /*置每个单链表为空表*/for(m=0;m< G->n;m++)G->adjlist[m].vertex=getchar(); /*输入各顶点的符号*/for(m=1;m<= G->e; m++){scanf("\n%d%d"&i&j); /* 输入一对邻接顶点序号*/if((i<0 || j<0) return -1;p=(EdgeNode*)malloc(sizeof(EdgeNode));/*在第i+1个链表中插入一个边表结点*/ p->adjvex=j;p->next= G-> adjlist [i].firstedge;G-> adjlist [i].firstedge=p;p=(EdgeNode*)malloc(sizeof(EdgeNode));/*在第j+1个链表中插入一个边表结点*/ p->adjvex=i;p->next= G-> adjlist [j].firstedge;G-> adjlist [j].firstedge=p;} /* for*/return 0; /*成功*/}//Create_NgAdjList(2)建立有向图逆邻接链表算法：typedef VertexType char;int Create_AdjList(ALGraph *G){ /* 输入有向图的顶点数、边数、顶点信息和边的信息建立逆邻接链表 */scanf("%d"&n); if(n<0) return -1; /* 顶点数不能为负 */G->n=n;scanf("%d"&e); if(e<0) return =1; /*弧数不能为负 */G->e=e;for(m=0;m< G->n; m++)G-> adjlist [m].firstedge=NULL; /*置每个单链表为空表*/for(m=0;m< G->n;m++)G->adjlist[m].vertex=getchar(); /*输入各顶点的符号*/for(m=1;m<= G->e ; m++){scanf("\n%d%d"&t&h); /* 输入弧尾和弧头序号*/if((t<0 || h<0) return -1;p=(EdgeNode*)malloc(sizeof(EdgeNode));/*在第h+1个链表中插入一个边表结点*/ p->adjvex=t;p->next= G-> adjlist [h].firstedge;G-> adjlist [h].firstedge=p;} /* for*/return 0; /*成功*/}//Create_AdjList6.11void Create_AdjM(ALGraph *G1MGraph *G2){ /*通过无向图的邻接链表G1生成无向图的邻接矩阵G2*/G2->n=G1->n; G2->e=G1->e;for(i=0;i<G2->n;i++) /* 置G2每个元素为0 */for(j=0;j<G2->n;j++) G2->edges[i][j]= 0;for(m=0;m< G1->n;m++)G2->vexs[m]=G1->adjlist[m].vertex; /*复制顶点信息*/num=（G1->n/2==0?G1->n/2:G1->n/2+1）; /*只要搜索前n/2个单链表即可*/for(m=0;m< num;m++){ p=G1->adjlist[m].firstedge;while(p){ /* 无向图的存储具有对称性*/G2->edges[m][ p->adjvex ]= G2->edges[p->adjvex ] [m] =1;p==p->next;}}/* for */}/*Create_AdjM */void Create_AdjL(ALGraph *G1MGraph *G2){ /*通过无向图的邻接矩阵G1生成无向图的邻接链表G2*/G2->n=G1->n; G2->e=G1->e;for(i=0;i<G1->n;i++) /* 建立每个单链表 */{ G2->vexs[i]=G1->adjlist[i].vertex;G2->adjlist[i].firstedge=NULL；for(j=i; j<G1->n; j++) /*对称矩阵只要搜索主对角以上的元素即可*/{ if(G1->edges[i][j]== 1){ p=(EdgeNode*)malloc(sizeof(EdgeNode));/*在第i+1个链表中插入一个边表结点*/p->adjvex=j;p->next= G-> adjlist [i].firstedge;G-> adjlist [i].firstedge=p;p=(EdgeNode*)malloc(sizeof(EdgeNode));/*在第j+1个链表中插入一个边表结点*/p->adjvex=i;p->next= G-> adjlist [j].firstedge;G-> adjlist [j].firstedge=p;}/*if*/}/* for*/}/* for*/}/* Create_AdjL */6.13(1) 邻接矩阵中1的个数的一半;(2) 若位于[i-1j-1]或[j-1i-1]位置的元素值等于1则有边相连否则没有(3) 顶点i的度等于第i-1行中或第i-1列中1的个数6.14(1) 邻接链表中边表结点的个数的一半;(2) 若第i-1（或j-1）个单链表中存在adjvex域值等于j-1（或i-1）的边表结点则有边相连否则没有(3) 顶点i的度等于第i-1个单链表中边表结点的个数提示：参见算法6.2 和6.3习题 7参考答案7.1 选择题（1）C (2)C (3) C (4)B (5) A (6)A (7) D (8)B (9)D (10) B(11)B (12)A (13)C (14)C (15)A (16)D (17)C (18)BC (19)B (20)A7.2 填空题（1） O(n)O(log2n)（2） 12485log2(n+1)-1（3）小于大于（4）增序序列（5）m-1（6） 70; 342055（7） n/m（8）开放地址法链地址法（9）产生冲突的可能性就越大产生冲突的可能性就越小（10）关键码直接（11）②①⑦（12） 1616821（13）直接定址法数字分析法平方取中法折叠法除留余数法随机数法（14）开放地址法再哈希法链地址法建立一个公共溢出区（15）装满程度（16）索引快（17）哈希函数装填因子（18）一个结点（19）中序（20）等于7.3 一棵二叉排序树(又称二叉查找树)或者是一棵空树或者是一棵同时满足下列条件的二叉树：(1)若它的左子树不空则左子树上所有结点的键值均小于它根结点键值(2)若它的右子树不空则右子树上所有结点的键值均大于它根结点键值(3)它的左、右子树也分别为二叉排序树7.4 对地址单元d=H(K)如发生冲突以d为中心在左右两边交替进行探测按照二次探测法键值K的散列地址序列为：do=H(K)d1=(d0+12)mod md2=(d0-12)mod md3=(d0+22)mod md4=(d0-12)mod m......7.5 衡量算法的标准有很多时间复杂度只是其中之一尽管有些算法时间性能很好但是其他方面可能就存在着不足比如散列查找的时间性能很优越但是需要关注如何合理地构造散列函数问题而且总存在着冲突等现象为了解决冲突还得采用其他方法二分查找也是有代价的因为事先必须对整个查找区间进行排序而排序也是费时的所以常应用于频繁查找的场合对于顺序查找尽管效率不高但却比较简单常用于查找范围较小或偶而进行查找的情况7.6此法要求设立多个散列函数Hii=1...k当给定值K与闭散列表中的某个键值是相对于某个散列函数Hi的同义词因而发生冲突时继续计算该给定值K在下一个散列函数Hi+1下的散列地址直到不再产生冲突为止7.7散列表由两个一维数组组成一个称为基本表另一个称为溢出表插入首先在基本表上进行；假如发生冲突则将同义词存人溢出表7.8 结点个数为n时高度最小的树的高度为1有两层它有n-1个叶结点1个分支结点；高度最大的树的高度为n-l有n层它有1个叶结点n-1个分支结点7.9 设顺序查找以h为表头指针的有序链表若查找成功则返回结点指针p查找失败则返回null值pointer sqesrearch(pointer hint xpointerp){p=null；while(h)if(x>h->key)h=h->link；else{if(x==h->key)p=h；return(p)；}}虽然链表中的结点是按从小到大的顺序排列的但是其存储结构为单链表查找结点时只能从头指针开始逐步进行搜索故不能用折半(二分)查找7.10 分析：对二叉排序树来讲其中根遍历序列为一个递增有序序列因此对给定的二叉树进行中根遍历如果始终能保证前一个值比后一个值小则说明该二叉树是二叉排序树int bsbtr (bitreptr T) ／*predt记录当前结点前趋值初值为-∞*／{ if (T==NULL) return(1)；else{b1=bsbtr(T->lchild)；／*判断左子树*／if (!b1|| (predt>=T->data)) return(0)；*当前结点和前趋比较*／ predt=T->data；／*修改当前结点的前趋值*／return(bsbtr(T->rchild))；／*判断右子树并返回最终结果*／}}7.11 (1)使用线性探查再散列法来构造散列表如表下所示散列表───────────────────────────────地址 0 1 2 3 4 5 6 7 8 9 10───────────────────────────────数据 33 1 13 12 34 38 27 22───────────────────────────────（2）使用链地址法来构造散列表如下图(3)装填因子a=8／11使用线性探查再散列法查找成功所需的平均查找次数为Snl=0．5(1+1／(1-a))=0．5*(1+1／(1-8／11))=7／3使用线性探查再散列法查找不成功所需的平均查找次数为：Unl=0．5(1+1／(1-a)2)=0．5*(1+1／(1-8／11)2)=65／9 使用链地址法查找成功所需的平均查找次数为：Snc=l+a／2=1+8／22=15／11使用链地址法查找不成功所需的平均查找次数为： 'Unl=a+e-a=8／1l+e-8／117.12 分析：在等查区间的上、下界处设两个指针由此计算出中间元素的序号当中间元素大于给定值X时接下来到其低端区间去查找；当中间元素小于给定值X时接下来到其高端区间去查找；当中间元素等于给定值X时表示查找成功输出其序号Int binlist(sqtable Aint stkeytype X) ／*t、s分别为查找区间的上、下界*／{ if(s<t) return(0)；／*查找失败*／else{ mid=(S+t)／2；switCh(mid){case x<A.item[midJ.key： return(binlist(Asmid-lX))；／*在低端区间上递归*／case x==A.item[mid].key： return(mid)；／+查找成功*／ case x>A.item[mid].key： return(amid+ltX))；／*在高端区间上递归*／}}}int sqsearch0 (sqtable Akeytype X) /*数组有元素n个*／{ i=l；A.item[n+1].key=X；／t设置哨兵*／while (A.item[n+1].key!=X) i++；return (i% (n／1))；／*找不到返回0找到返回其下标*／}查找成功平均查找长度为：(1+2+3+...+n)／n：(1+n)／2查找不成功平均查找长度为：n+17.14散列函数：H(key)=100+(key个位数+key十位数) mod l0；形成的散列表：100 101 102 103 104 105 106 107 108 10998 75 63 46 49 79 61 53 17查找成功时的平均长度为：(1+2+1+1+5+1+1+5+5+3)/10=2.5次由于长度为10的哈希表已满因此在插人第11个记录时所需作的比较次数的期望值为10查找不成功时的平均长度为10习题 8参考答案8．1 选择题（1）B (2)A (3)D (4)C (5)B (6)A (7)B (8)C (9)A (10)C(11)D (12)C (13) C （14）D （15）C (16)B (17) D （18）C （19）B （20）D8.2填空题（1）快速归并（2） O（log2n）O(nlog2n)（3）归并（4）向上根结点（5） 1918162030（6）（7）4913275076386597（8）88（9）插入选择（每次选择最大的）（10）快速归并(11)O(1)O(nlog2n)(12)稳定(13)3(14)(15205040)(15)O(log2n)(16)O(n2)(17)冒泡排序快速排序(18)完全二叉树n/2(19)稳定不稳定(20)24(2015)8.3. 假定给定含有n个记录的文件(r1f2...rn)其相应的关键字为(k1k2...kn)则排序就是确定文件的一个序列rrr2...rn使得k1'≤k2'≤...≤kn'从而使得文件中n个记录按其对应关键字有序排列如果整个排序过程在内存中进行则排序叫内部排序假设在待排序的文件中存在两个或两个以上的记录具有相同的关键字若采用某种排序方法后使得这些具有相同关键字的记录在排序前后相对次序依然保持不变则认为该排序方法是稳定的否则就认为排序方法是不稳定的8.4．稳定的有：直接插入排序、二分法插入排序、起泡排序、归并排序和直接选择排序8.5．初始记录序列按关键字有序或基本有序时比较次数为最多8.6．设5个元素分别用abcde表示取a与b、c与d进行比较若a>bc>d(也可能是a<bc<d此时情况类似)显然此时进行了两次比较取b与d再比较若b>d则a>b>d若b<d则有c>d>b此时已进行了3次比较要使排序比较最多7次可把另外两个元素按折半检索排序插入到上面所得的有序序列中此时共需要4次比较从而可得算法共只需7次比较8.7．题目中所说的几种排序方法中其排序速度都很快但快速排序、归并排序、基数排序和Shell排序都是在排序结束后才能确定数据元素的全部序列而排序过程中无法知道部分连续位置上的最终元素而堆排序则是每次输出一个堆顶元素(即最大或最少值的元素)然后对堆进行再调整保证堆顶元素总是当前剩下元素的最大或最小的从而可知欲在一个大量数据的文件中如含有15000个元素的记录文件中选取前10个最大的元素可采用堆排序进行8.8．二分法排序8.9．void insertsort(seqlist r)  ；{ ／／对顺序表中记录R[0一N-1)按递增序进行插入排序&NBSP；int ij；  ；for(i=n-2；i>=0; i--) ／／在有序区中依次插入r[n-2]．．r[0]  ；if(r[i].key>r[i+1].key) ／／若不是这样则r[i]原位不动 ；{  ；r[n]=r[i]；j=i+l；／／r[n]是哨兵 ；do{ ／／从左向右在有序区中查找插入位置 ；r[j-1]= r[j]；／／将关键字小于r[i]．key的记录向右移 ；j++；  ；}whle(r[j].key r[j-1]=r[n]；／／将引i)插入到正确位置上 ；}／／endif ；}／／insertsort．  ；8.10．建立初始堆：[937 694 863 265 438 751 742129075 3011]&NBSP；&NBSP；第一次排序重建堆：[863 694 751 765 438 301 742 129 075]9378.11．在排序过程中每次比较会有两种情况出现若整个排序过程至少需作t次比较则显然会有2^t个情况由于n个结点总共有n!种不同的排列因而必须有n!种不同的比较路径于是： 2t≥n!即t≥log2n!因为log2nl=nlog2n-n／ln2+log2n／2+O(1)故有log2n!≈nlog2n从而t≧nlog2n得证8.12．依据堆定义可知：序列(1)、(2)、(4)是堆(3)不是堆从而可对其调整使之为如下的大根堆(1009580604095821020)8.13．第一趟：[265 301] [129 751] [863 937] [694 742] [076 438]&NBSP； &NBSP；第二趟：[129 265 301 751] [694 742 863 937] [076 438]&NBSP；&NBSP；第三趟：[129 265 301 694 742 751 863 937] [076 438]&NBSP；&NBSP；第四趟：[076 129 265 301 438 694 742 751 863 937]&NBSP；8.14．(1)归并排序：(1829) (2547) (1258) (1051)(18252947) (10125158)(1012182529475158)(2)快速排序：(1018251229585147)(1018251229475158)(1012182529475158)(3)堆排序：初始堆(大顶堆)：(58 47512918122510)第一次调整：(51 472529181210)(58)第二次调整：(47 2925101812)(5158)第三次调整：(29 18251012)(475158)第四次调整：(25 181210)(29475158)第五次调整：(18 1012)(2529475158)第六次调整：(12 10) (182529475158)第七次调整：(10 12182529475158)8.15．(1)直接插入排序序号 1 2 3 4 5 6 7 8 9 10 11 12 关键字 83 40 63 13 84 35 96 57 39 79 61 151=2 40 83 [63 13 84 35 96 57 39 79 61 15] 1=3 40 63 83 [13 84 35 96 57 39 79 61 15] 1=4 13 40 63 83 [84 3 5 96 57 39 79 61 15] I=5 13 40 63 83 84 [35 96 57 39 79 61 15] I=6 13 35 40 63 83 84 [96 57 39 79 61 15] 1=7 13 35 40 63 83 84 96 [57 39 79 61 15] 1=8 13 35 40 57 63 83 84 96 [ 39 79 61 15] 1=9 13 35 39 40 57 63 83 84 96 [79 61 15] I=10 13 35 39 40 57 63 79 83 84 96 [61 15] I=11 13 35 39 40 57 61 63 79 83 84 96 [15] 1=12 13 15 35 39 40 57 61 63 79 83 84 96 (2)直接选择排序序号 1 2 3 4 5 6 7 8 9 10 11 12 关键字 83 40 63 13 84 35 96 57 39 79 61 15i=1 13 [ 40 63 83 84 35 96 57 39 79 61 15] i=2 13 15 [63 83 84 35 96 57 39 79 61 40] i=3 13 15 35 [83 84 63 96 57 39 79 61 40] i=4 13 15 35 39 [84 63 96 57 83 79 61 40] i=5 13 15 35 39 40 [63 96 57 83 79 61 84] i=6 13 15 35 39 40 57 [96 63 83 79 61 84] i=7 13 15 35 39 40 57 61 [63 83 79 96 84] i=8 13 15 35 39 40 57 61 63 [83 79 96 84] i=9 13 15 35 39 40 57 61 63 79 183 96 84] i=10 13 15 35 39 40 57 61 63 79 83 [96 84] i=11 13 15 35 39 40 57 61 63 79 83 84 [96] (3)快速排序关键字 83 40 63 13 84 35 96 57 39 79 61 15 第一趟排序后 [15 40 63 13 61 35 79 57 39] 83 [96 84] 第二趟排序后 [13] 15 [63 40 61 35 79 57 39] 83 84 [96] 第三趟排序后 13 15 [39 40 61 35 57] 63 [79] 83 84 96 第四趟排序后 13 15 [35] 39 [61 40 57] 63 79 83 84 96第五趟排序后 13 15 35 39 [57 40] 61 63 79 83 84 96 第六趟排序后 13 15 35 39 40 [57] 61 63 79 83 84 96 第七趟排序后 13 15 35 39 40 57 61 63 79 83 84 96 (4)堆排序关键字 83 40 63 13 84 35 96 57 39 79 61 15排序成功的序列 96 84 83 79 63 61 57 40 39 35 15 13(5)归并排序关键字 83 40 63 13 84 35 96 57 39 79 61 15 第一趟排序后 [40 83] [13 63] [3584] [57 96] [39 79] [15 61]第二趟排序后 [13 40 63 83] [35 57 84 96] [15 39 61 79] 第三趟排序后 [13 35 40 57 63 83 84 96]] [15 39 61 79] 第四趟排序后 13 15 35 39 40 57 61 63 79 83 84 96。
虚拟仪器应用习题答案
参考答案：
如温度监控项目一样，在程序设计中设置比较环节，结合条件结构，可以实现限速功能实现。
思考题
10.1是否有其他方法做自动门的仿真界面？ 比如可试试用3D控件。
参考答案：
可采用3D控件来实现。
参考答案：程序框图，保存路径可以自由选择，保存格式可以是二进制。
思考
5.3本节中介绍了10个最常用的DAQmx函数，在实际应用中，它们在数据流中所放置的先后顺序有没有一定的规律？本节中所介绍的实例大都是单一输入或者单一输出的情况，如果需要同时输入和输出，应该如何处理？
参考答案：
通常的规律是创建通道，设置采样时钟，配置触发等设置，（配置输出波形），开始任务，（获取采集波形），清除任务。
2）当连续8秒质量都为0g后，自动停止，可以在用条件结构来实现，见下图，在度数据的分支，把当前g与0比较，为真，执行真分支。该分支用来判断是否保持8s。由于该DAQ过程设置了没0.5s进行一次读写操作，这里计16个数就是8s。
8.2用状态机实容器液位监控。要求：初始水位100ms，水位上限200ms，下限50ms，越限要有报警指示。用一个进水阀和一个进水量调节控件来控制进水情况；一个出水阀和一个出水量调节控件来控制出水量。可以单独进水或出水，也可以同时进、出水。点击“结束”按钮，退出程序。
思考题1
1.1参考例题1创建一个VI，实现将华氏温度转换为摄氏温度的功能，并在前面板显示摄氏温度和华氏温度。
参考答案：
1.2创建一个VI实现两个输入数据的加、减、乘运算，并显示数据的和、差与乘积。
参考答案：
思考题2
2.1用0-100的随机数代替摄氏温度，将每500ms采集的温度的变化波形表示出来，并设定上限85，下限45，温度高于上限或者低于下限分别点亮对应的指示灯。并将其上下限也一并在波形中表示出来。
密码学答案
《密码学原理与实践(第三版)》课后习题参考答案(由华中科技大学信安09级提供)第一章1.1（李怡）(a)51 (b)30 (c)81 (d)74221.2（贾同彬）证明：令t1= (-a)mod m ,t2=m-(a mod m),则t1≡t2(mod m).又 0<t1<m,0<t2<m, （最小非负剩余系中每个剩余类只有一个代表元）所以t1=t2.1.3 （张天翼） 证明充分性：若(mod )a b m ≡，则可得a b km =+，设b jm r =+，0r m ≤<，j N ∈，则有()a k j m r =++，故有mod a m r =,由假设得mod b m r =，故mod mod a m b m =证明必要性：若mod mod a m b m =，则可设mod mod a m b m r ==，则有a km r =+，b jm r =+，其中,j k N ∈，因此()a b k j m -=-，即m a b -，故(mod )a b m ≡ 综上，问题得证1.4 （李怡）,0,mod ,.,-0,1,a km r r m r a ma r a km k m a r a a a k m r k k m m m m =+≤<=⎢⎥=-=⎢⎥⎣⎦-⎢⎥=-<≤-<≤=⎢⎥⎣⎦令则而所以只需证明因为所以即1.5 (李志远)穷举密钥法来破解移位密码即将这个字符串每个字母移位1，2，3…26次，然后判断这26个字符串哪个符合英语规则。
故我编写 如下的C++来实现如此功能 #include<iostream> using namespace std; char change(char word) {if(word=='Z')return 'A'; else return word+1; }int main(){cout<<"please input the string"<<endl;char string1[43];cin>>string1;int n;for(n=1;n<=26;n++){int num;for(num=0;num<43;num++){string1[num]=change(string1[num]);}cout<<string1<<endl<<"for turn "<<n<<endl;}}解释：1.代码专为本题编写，故输入字符数不能多于43个，且输入范围仅限大写英语字母2.将题中的42个字母BEEAKFYDJXUQYHYJIQRYHTYJIQFBQFBQDUYJIIKFUHC输入并回车3.得到的结果CFFBLGZEKYVRZIZKJRSZIUZKJRGCREVZKJJLGVIDREfor turn 1DGGCMHAFLZWSAJALKSTAJVALKSHDSFWALKKMHWJESFfor turn 2EHHDNIBGMAXTBKBMLTUBKWBMLTIETGXBMLLNIXKFTGfor turn 3FIIEOJCHNBYUCLCNMUVCLXCNMUJFUHYCNMMOJYLGUHfor turn 4GJJFPKDIOCZVDMDONVWDMYDONVKGVIZDONNPKZMHVIfor turn 5HKKGQLEJPDAWENEPOWXENZEPOWLHWJAEPOOQLANIWJfor turn 6ILLHRMFKQEBXFOFQPXYFOAFQPXMIXKBFQPPRMBOJXKfor turn 7JMMISNGLRFCYGPGRQYZGPBGRQYNJYLCGRQQSNCPKYLfor turn 8KNNJTOHMSGDZHQHSRZAHQCHSRZOKZMDHSRRTODQLZMfor turn 9LOOKUPINTHEAIRITSABIRDITSAPLANEITSSUPERMANfor turn 10MPPLVQJOUIFBJSJUTBCJSEJUTBQMBOFJUTTVQFSNBOfor turn 11NQQMWRKPVJGCKTKVUCDKTFKVUCRNCPGKVUUWRGTOCPfor turn 12ORRNXSLQWKHDLULWVDELUGLWVDSODQHLWVVXSHUPDQfor turn 13PSSOYTMRXLIEMVMXWEFMVHMXWETPERIMXWWYTIVQERfor turn 14 QTTPZUNSYMJFNWNYXFGNWINYXFUQFSJNYXXZUJWRFSfor turn 15 RUUQAVOTZNKGOXOZYGHOXJOZYGVRGTKOZYYAVKXSGTfor turn 16 SVVRBWPUAOLHPYPAZHIPYKPAZHWSHULPAZZBWLYTHUfor turn 17 TWWSCXQVBPMIQZQBAIJQZLQBAIXTIVMQBAACXMZUIVfor turn 18 UXXTDYRWCQNJRARCBJKRAMRCBJYUJWNRCBBDYNAVJWfor turn 19 VYYUEZSXDROKSBSDCKLSBNSDCKZVKXOSDCCEZOBWKXfor turn 20 WZZVFATYESPLTCTEDLMTCOTEDLAWLYPTEDDFAPCXLYfor turn 21 XAAWGBUZFTQMUDUFEMNUDPUFEMBXMZQUFEEGBQDYMZfor turn 22 YBBXHCVAGURNVEVGFNOVEQVGFNCYNARVGFFHCREZNAfor turn 23 ZCCYIDWBHVSOWFWHGOPWFRWHGODZOBSWHGGIDSFAOBfor turn 24 ADDZJEXCIWTPXGXIHPQXGSXIHPEAPCTXIHHJETGBPCfor turn 25 BEEAKFYDJXUQYHYJIQRYHTYJIQFBQDUYJIIKFUHCQDfor turn 26经过英语分析，发现当移位密码密钥为17时，字符串有英文含义LOOK UP IN THE AIR ITS A BIRD ITS A PLANE ITS SUPERMAN (看天上，是一只鸟，是一架飞机，是一位超人)故移位密码密钥为171.6（司仲峰）对合密钥为 0和131.7（陈诗洋）(a) m=30=2*3*5φ(30)=30*(1-1/2)*(1-1/3)*(1-1/5)=8故密钥量是 8*30=240(b)m=100=22*52φ(100)=100*(1-1/2)*(1-1/5)=40故密钥量是 40*100=4000(c)m=1225=52*72φ(1225)=1225*(1-1/5)*(1-1/7)=840故密钥量是 840*1225=10290001.8（周玉坤）解：在中若元素有逆，则必有gcd(a,m)=1;若元素a存在逆使得a=1,利用广义欧几里得除法，找到整数s和t，使得： sa+tm=1，则=s(modm)是a的逆。
信息传输原理 习题部分参考答案
第一章 习题题（1.1）英文字母中e 的出现概率为0.105，c 的出现概率为0.023，o 的出现概率为0.001，试分别计算它们的自信息量（以比特为单位）。
解：由题意可得Ie= -log0.105=3.25bit Io= -log0.001=9.97bit Ic= -log0.023=5.44bit∴字母e 的自信息量是3.25bit ，字母c 的自信息量是5.44bit ，字母o 的自信息量是9.97bit 。
题（1.2）某个消息由字符A,B,C,D 组成，已知它们的出现概率为83)(=A P ，41)(=B P ，41)(=C P ，81)(=D P ，试求由60个字符所构成的消息，其平均自信息量是多少比特。
解：由题意可得 H （x ）= -（38log 38+14*2*log 14+18log 18）=1.906bit ∴由60个字符构成的消息的平均自信息量是1.906*60=114.36bit题（1.3）在二进制信道中信源消息集为}1,0{=X ，且已知出现概率)1()0(P P =。
信宿消息集为}1,0{=Y ，信道传输概率为41)0|1(=P 和81)1|0(=P 。
试求该信道所能提供的平均互信息量),(Y X I 等于多少？解： ∵ P Y/X =13,4471,88⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦，P X =11,22⎡⎤⎢⎥⎣⎦∴P Y = P X *P Y/X =11,22⎡⎤⎢⎥⎣⎦*13,4471,88⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦=97,1616⎡⎤⎢⎥⎣⎦∴H （Y ）=-（916log 916+716log 716）=0.989bit H （Y/X ）=12H （14，34）+12H （78，18）=0.678bit∴I （X ，Y ）=H （Y ）-H （Y/X ）=0.989-0.678=0.311bit题（1.4）在二进制对称信道中传输消息}1,0{=X ，接收到的消息为}1,0{=Y 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一章 随机事件与概率
习题1.1
1． 写出下列随机试验的样本空间：
（1）抛三枚硬币；
（2）抛三颗骰子；
（3）连续抛一枚硬币，直至出现正面为止；
（4）在某十字路口，一小时内通过的机动车辆数；
（5）某市一天内的用电量．
解：（1）Ω = {(0, 0, 0)，(0, 0, 1)，(0, 1, 0)，(1, 0, 0)，(0, 1, 1)，(1, 0, 1)，(1, 1, 1)，(1, 1, 1)}，
其中出现正面记为1，出现反面记为0；
（2）Ω = {(x 1 , x 2 , x 3)：x 1 , x 2 , x 3 = 1, 2, 3, 4, 5, 6}；
（3）Ω = {(1)，(0, 1)，(0, 0, 1)，(0, 0, 0, 1)，…，(0, 0, …, 0, 1)，…}，
其中出现正面记为1，出现反面记为0；
（4）Ω = {0，1，2，3，…，n ，…}；
（5）Ω = {x ：x ≥ 0}．
2． 在抛三枚硬币的试验中写出下列事件的集合表示：
A = “至少出现一个正面”；
B = “最多出现一个正面”；
C = “恰好出现一个正面”；
D = “出现三面相同”．
解：设出现正面记为1，出现反面记为0，
则A = {(0, 0, 1)，(0, 1, 0)，(1, 0, 0)，(0, 1, 1)，(1, 0, 1)，(1, 1, 1)，(1, 1, 1)}；
B = {(0, 0, 0)，(0, 0, 1)，(0, 1, 0)，(1, 0, 0)}；
C = {(0, 0, 1)，(0, 1, 0)，(1, 0, 0)}；
D = {(0, 0, 0)，(1, 1, 1)}．
3． 设A , B , C 为三事件，试表示下列事件：
（1）A , B , C 都发生或都不发生；
（2）A , B , C 中不多于一个发生；
（3）A , B , C 中不多于两个发生；
（4）A , B , C 中至少有两个发生．
解：（1）C B A ABC U ；
（2）C B A C B A C B A C B A U U U ；
（3）ABC 或C B A C B A C B A C B A BC A C B A C AB U U U U U U ；
（4）ABC BC A C B A C AB U U U ．
4． 请指明以下事件A 与B 间的关系：
（1）检查两件产品，记事件A =“至少有一件不合格品”，B =“两次检查结果不同”；
（2）设T 表示轴承寿命，记事件A = {T > 5000 h}，B = {T > 8000 h}．
解：（1）因事件B 发生必有事件A 发生，故A ⊃ B ；
（2）因事件B 发生必有事件A 发生，故A ⊃ B ．
5． 设X 为随机变量，其样本空间为Ω = {0 ≤ X ≤ 2}，记事件A = {0.5 < X ≤ 1}，B = {0.25 ≤ X < 1.5}，写出
下列事件：
（1）B A ；
（2）B A U ；
（3）AB ；
（4）B A U ． 解：（1）}5.11{}5.025.0{<<≤≤=X X B A U ；
（2
）Ω=≤≤=}20{X B A U ；
（3）A X X AB =≤<≤≤=}21{}5.00{U ；
（4）B X X B A =≤≤<≤=}25.1{}25.00{U U ．
6． 对飞机进行两次射击，每次射一弹，设A = {恰有一弹击中飞机}，B = {至少有一弹击中飞机}，C = {两
弹都击中飞机}，D = {两弹都没击中飞机}．又设随机变量X 为击中飞机的次数，试用X 表示事件A , B , C , D ．进一步问中哪些是互不相容的事件？哪些是对立事件？
解：A = {X = 1}，B = {X ≥ 1}，C = {X = 2}，D = {X = 0}；
事件A 与C ，A 与D ，B 与D ，C 与D 分别是互不相容的事件；其中事件B 与D 是对立事件．
7． 试问下列命题是否成立？
（1）A − (B − C ) = (A − B )∪C ；
（2）若AB = ∅且C ⊂ A ，则BC = ∅；
（3）(A ∪B ) − B = A ；
（4）(A − B )∪B = A ．
解：（1）不成立，C B A AC B A AC B A C B A C B A C B A C B A U U U U )()()()(−≠−====−=−−；
（2）成立，因C ⊂ A ，有BC ⊂ AB = ∅，故BC = ∅；
（3）不成立，因A B A B A B B B A B B A B B A ≠−====−U U U )()(；
（4）不成立，因A B A B B B A B B A B B A ≠===−U U U U U ))(()(．
8． 试用维恩图说明，当事件A 与B 互不相容时，能否得出结论A 与B 相容．
解：不能得出此结论．事实上，此时若A 与B 互为对立事件，则A 与B 不相容，否则，A 与B 相容．
B A
Ω B A =A
B ==B A ∅
9． 请叙述下列事件的对立事件：
（1）A =“掷两枚硬币，皆为正面”；
（2）B =“射击三次，皆命中目标”；
（3）C =“加工四个零件，至少有一个合格品”．
解：（1）=A “掷两枚硬币，至少有一个反面”；
（2）=B “射击三次，至少有一次没有命中目标”；
（3）=C “加工四个零件，皆为不合格品”．
10．如果A 与B 互为对立事件，证明：A 与B 也互为对立事件．
证：如果A 与B 互为对立事件，有A B =且B A =，即==BA B A ∅且Ω==A B B A U U ， 故A 与B 也互为对立事件．
11．设F 为一事件域，若A n ∈F ，n = 1, 2, …，试证：
（1）∅ ∈F ；
（2）有限并∈=U n
i i A 1F ，n ≥ 1；
（3）有限交∈=I n
i i A 1F ，n ≥ 1；
（4）可列交∈+∞
=I 1i i A F ；
（5）差运算A 1 − A 2 ∈ F ．
证：（1）由事件域定义条件1，知 Ω ∈F ，再由定义条件2，可得∅∈Ω=F ；
（2）在定义条件3中，取A n + 1 = A n + 2 = … = ∅，可得∈=∞
==U U 11i i n i i A A F ；
（3）由定义条件2，知∈n A A A ,,,21L F ，根据（2）小题结论，可得∈=U n
i i A 1
F ，
再由定义条件2，知∈=U n i i A 1 F ，即∈=I n i i A 1
F ；
（4）由定义条件2，知∈L L ,,,,21n A A A F ，根据定义条件3，可得∈∞
=U 1
i i A F ，
再由定义条件2，知∈∞=U 1i i A F ，即∈∞=I 1
i i A F ；
（5）由定义条件2，知∈2A F ，根据（3）小题结论，可得∈21A A F ，即A 1 − A 2 ∈ F ．。