结构力学(一)第三版龙驭球第三章3.3静定刚架
龙驭球《结构力学Ⅰ》(第3版)配套题库【名校考研真题+课后习题+章节题库+模拟试题】(上册)

目 录第一部分 名校考研真题第1章 绪 论第2章 结构的几何构造分析第3章 静定结构的受力分析第4章 影响线第二部分 课后习题第1章 绪 论第2章 结构的几何构造分析第3章 静定结构的受力分析第4章 影响线第三部分 章节题库第1章 绪 论第2章 结构的几何构造分析第3章 静定结构的受力分析第4章 影响线第四部分 模拟试题龙驭球《结构力学Ⅰ》(第3版)配套模拟试题及详解第一部分 名校考研真题第1章 绪 论本章不是考研复习重点,暂未编选名校考研真题,若有最新真题会在下一版中及时更新。
第2章 结构的几何构造分析一、判断题图2-1所示体系的几何组成为几何不变体系,无多余约束。
( )[厦门大学2011研]图2-1二、选择题1.图2-2所示平面体系的几何组成是( )。
[浙江大学2010研]A .几何不变,无多余约束 B .几何不变,有多余约束C .几何常变D.几何瞬变图2-2图2-3错【答案】如图2-1(b ),分别视ABD 和基础为刚片Ⅰ和Ⅱ,两刚片通过链杆AC 、BE 和D 处的支座链杆相连,三根链杆相交于一点O ,故该体系为几何瞬变体系。
【解析】A【答案】如图2-3所示,把大地看成刚片3,刚片1和2形成瞬铰(1,2),刚片1和3形成瞬铰(1,3),刚片2和3形成无穷远处瞬铰(2,3),三个铰不共线,因此是无多余约束的几何不变体系。
【解析】2.图2-4(a )所示体系的几何组成是( )。
[武汉大学2012研、郑州大学2010研、华南理工大学2007研、河海大学2007研]A .无多余约束的几何不变体系B .几何可变体系C .有多余约束的几何不变体系D.瞬变体系图2-4三、填空题1.图2-5所示体系是几何________变体系,有________个多余约束。
[重庆大学2006研]图2-52.如图2-6(a )所示体系的几何组成为________体系。
[南京理工大学2011研]图2-6A【答案】鉴于刚片与构件可以等效互换,所以可将图2-4(a )所示体系替换为图2-4(b )所示体系,然后通过依次去除C 支座链杆与CE 杆、D 支座链杆与DE 杆所组成的二元体,以及二元体A-E-B 后,可知原体系为无多余约束的几何不变体系。
003★结构力学A上★第三章★静定结构的受力分析-刚架桁架组合结构及拱.ppt资料

5m 6 30m B1 A
43
5m
D 2C
100kN 100kN 100kN 100kN 100kN
FR左 250kN
FR右 250kN
37
38
39
1
FN 1
40
③ 联合应用——适于复杂桁架或截面上未知 多于3根时的内力计算问题
FP
FP
FP
FP
FP
FNEC 1.789kN
FNCD 1.86 sin 0.985 sin 1.789 cos 0
FNCD 0.839kN
18
§3-5 静定平面桁架的内力
31
由多根直杆组成
铰结点相联
荷载作用于结点上
钢筋混凝土组合屋架
19
武汉长江大桥采用的桁架形式
20
21
y
yx
MM0
0
x
HH
56
yx M0x
H
例:试求图示三铰拱的合理拱轴线。
q
y
C
A
x
0.5l
0.5l
q
H
M
0 C
ql 2
f 8f
f
B M 0 x 1 qlx 1 qx2
22
y x
4f l2
xl x
57
§3-7 组合结构
13
由桁架杆件和受弯杆件组成。
K
C FNK K
M xK , yK K FQK
FQK FNf K
FQ0K cosK H sinK FQ0K sinK H cosK
A
(精品)《结构力学》龙驭球第3章静定结构的受力分析

c、பைடு நூலகம்弯矩图及剪力图
1kN/m
1kN 3kN
A 1.39 4m
BC
D EF
5.05
0.23
1m 2m 1m 1m
M图
2.44
FQ图
1.39
2 2 1.33
2.89
2.44 1.44
2kN/m
G
H
5.33 3m 1m 1m
4
1
单位 kN·m
4
1.56
1.33
2.61
单位 kN
例3-2 试作图示静定多 跨梁的内力图。
C 4 26
E
G
30 8 8
8
第3章 静定结构受力分析
8kN 4kN/m
A C
17kN1m 1m 2m
2m
17
16kN∙m
E
G
1m 1m
7kN
9
FQ图 A
G
7
第3章 静定结构受力分析
注意: ①弯矩图叠加是竖标相加,不是图形的拼合; ②要熟练地掌握简支梁在跨中荷载作用下的弯矩图; ③利用叠加法可以少求或不求反力,就可绘制弯矩图; ④利用叠加法可以少求控制截面的弯矩; ⑤问题越复杂外力越多,叠加法的优越性越突出。
(1)基本部分与附属 部分间的支撑关系
(2) 先附属再基本
(3)画弯矩图和剪力图
M图
1.5FP
FP a
0.75FP
0.25FP 0.25FP
0.25FP a
FQ图
FP
0.5FP
0.5FP a
0.25FP
第3章 静定结构受力分析
第3章 静定结构受力分析
第3章 静定结构受力分析
《结构力学》龙驭球-静定结构的受力分析

3 ql() 8
FxB
ql 8
()
(b)
B ql/8
l /2
ql/8
注意:三铰刚架构造中,支座反力旳计算是内力计算旳关键所在。
(2) 作M 图
AD杆:
M DA
ql 2 16
(内侧受拉)
D ql2/16 ql2/16
C
ql2/16 E
AD杆中点弯矩为:
ql2/16
l /2
M中
1 ql2 2 16
④ 校核
16
14
D
1
-1
2 -30
24 D 28
4
1 C
D
E
1
30
2
A
B
FN 图(kN)
FBx=1kN
FAy=30kN
FBy=2kN
例3-3.3: 作图(a)示三铰刚架内力图。
解:⑴ 支座反力
C
三铰刚架有四个支座反力,
q
l /2
可利用三个整体平衡条件和中间
铰结点C 处弯矩等于零旳局部平 FxA
A
(a)
B
FxB
衡条件,共四个平衡方程就能够
l /2
l /2
求出这四个支座反力。
FyA
FyB
M A 0,
FyB
l
(
ql 2
l 4
)
0
FyB
ql 8
()
Fy 0,
FyA
ql 8
()
C
l /2
由CEB部分平衡 (图b) 示:
MC 0,
FxB
l 2
( ql 8
l) 2
0
由整体平衡:
Fx 0,
精选-一页纸简历模板-结构力学龙驭球第三版课后习题答案

思考: P.114 3-15
7 1
P.116 3-19 (a) 作组合结构的内力图
2m
q=1kN/m
A -4
-4 B
FC G
-4
-4
5.66 4
5.66
4D
E4
2m 支座2m反力和2轴m力 2m
(kN)
7 2
P.116 3-19 (a) 作组合结构的内力图
2
M图
FQ图
3 1
P.108 3-2 判断内力图正确与否,将错 误改正 ( d )
MM图图
FFQQ图图
3 2
P.108 3-2 判断内力图正确与否,将错 误改正 ( d )
MM图图
FFQQ图图
3 3
P.108 3-2 判断内力图正确与否,将错 误改正
(e )
M图
FQ图
M图
FQ图
FP1 FP2
M图
7
P.37 2-4(d)
O(II、III)
1
III
O(I、II)
2I
II
34
O(I、III) IIII
I 形成两无穷远瞬铰O(II、II)、 O(II、III)的4
根链杆1、2和3、4不全平行,体系几何不 变,无多余约束
8
P.37 2-4(e)
9
P.37 2-4(e)
三杆共线, 瞬变
1 0
P.38 2-6(b)
4
A
C
B4
Al C l B
2l
2l
2
2
C
A
C
B
A FP l
FBP l
F4P l
《结构力学》_龙驭球_第3章_静定结构的受力分析(3)

1、桁架的特点组成 、
桁架是由链杆组成的格构体系,当荷载仅作用在结点上时, 桁架是由链杆组成的格构体系,当荷载仅作用在结点上时,杆件仅承受 轴向力,截面上只有均匀分布的正应力,是最理想的一种结构形式。 轴向力,截面上只有均匀分布的正应力,是最理想的一种结构形式。
理想桁架: 桁架的结点都是光滑无摩擦的铰结点; 理想桁架:⑴ 桁架的结点都是光滑无摩擦的铰结点; 各杆的轴线都是直线,并通过铰的中心; ⑵ 各杆的轴线都是直线,并通过铰的中心; ⑶ 荷载和支座反力都作用在结点上 实际桁架:主应力、 实际桁架:主应力、次应力
A 30kN 60 2m 20kN D 0 E 60 2m F
20kN C 20 H 2m 2m 20kN G 0 B 30kN 1m
(3)求各杆轴力 求各杆轴力 取结点隔离体顺序为: 、 、 、 。 取结点隔离体顺序为:A、E、D、C。 结构对称,荷载对称,只需计算半边结构。 结构对称,荷载对称,只需计算半边结构。 结点A 结点 FyAD
1kN/m I C 3m FNDF 0.7 15kN I 3m G E 3m 6kN 0.5m B 0.7m
∑ MC = 0
3.0806 3
1.2 FNDE − 6 × 6 + (1× 6) × 3 = 0
FNDE = (6 × 6 − 1× 6 × 3) /1.2 = 15kN (拉)
结点D: 结点 :
5.5 FP a FN 4 = = 2.75 FP (拉) 2a
FP FP C FN1 FN2 a FN3 D 2.5FP FN4 0 0 A 0
Q Fx 2 = −0.5 FP , Fx 3 = −0.75 FP , FN 4 = 2.75FP
《结构力学》_龙驭球_第3章_静定结构的受力分析(2)
一、求支座反力
40 kN
在支座反力的计算过程中,应尽可能建立 独立方程。
B
D
C
20 kN/m
4m
MA 0 FY 0
FDY 4 40 2 (20 4) 2 0 FDY 60kN () FAY 40 60 0 FAY 20kN ()
FX 0 FAX 80kN ()
二、绘制内力图
⑴ 分段:根据荷载不连续点、结点;
解,本题剪力很容易用投影方程求得。
4kN/m
1kN
C
MDE D
E
8
14kN
4m
1kN B 4m
2kN
28 24
4
4D
8
E
F
A
B
M 图(kN·m)
14
D
E
2
2
16
1
F
A
B
FQ 图(kN)
③ 作FN 图 各杆轴力可以用投影方程求
解。也可根据剪力图, 取各结点 为隔离体,用投影方程求轴力。
④ 校核
16
14
40
载和B端外力偶作用的简支梁(图C)。
画M图时,将 B 端弯矩竖标画在受拉 80 A
侧,连以虚直线,再叠加上横向荷载产生
20
的简支梁的弯矩图,如图(d)示。
(b)
A
A
(c)
(d)
B 160
D
160
120
20 60
120
20
A M图 (kN·m)
80 F Q 图(kN)
F N 图(kN)
练习3-3.1:试计算图示简支刚架的支座反力,并绘制M、F Q 和 F N 图。
Fx 0, FBx 2 11kN()
结构力学龙驭球第三版课后习题答案

结构力学
2kN/m
5m
5m
6m
2.5 2.08
2.08 7.5
FQ图
(kN)
56
习题解答
P.112 3-8 (a) 作三铰刚架的内力图
结构力学
2kN/m
5m
5m
6m
2.08
2.5
7.5
FN图
(kN)
57
习题解答
P.112 3-8 (d) 作三铰刚架的内力图
67
习题解答
结构力学
P.115 3-17 (a) 用结点法或截面法求桁架各杆的轴力
4m
8kN 4kN 4kN
3m 3m
0 -4
-8.33 -1.67
0
0
53
-6.67 -6.67 6.67 -1.33
F Q图
F P2
F P1
M图
F Q图
FP1<FP2
34
习题解答
P.108 3-2 判断内力图正确与否,将错误改正
结构力学
(e)
M图
F Q图
M图
F Q图
M图
F Q图
F P2
F P1
M图
F Q图
FP1=FP2
35
习题解答
P.108 3-2 判断内力图正确与否,将错误改正
结构力学
(e)
M图
F Q图
M图
FP B
C
C
FP B
FP B
C
C
A
D
A
D
A
D
A
D
44
习题解答
P.110 3-4 (c) 判断M图的正误,并改正错误
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2m
1m
4.3 用截面法求静定刚架杆端截面内力 【例4.3 】计算图示刚架刚结点处各杆杆端截面的内力。
1kN/m
2kN
B C D
9
3kN 2kN
B
1kN/m
C
MCA
3kN
QCA D NCA
2qa2
4qa2
14qa
2
M图
QDC 0
QDB 0
QBD 6qa
N DC 0
3.2qa
QBE 3.2qa
QBA 0
6qa 8qa
Q图
N DB 0 N BD 0 N BE 2.4qa N BA 10qa
YA 10qa()
2.4qa
10qa
N图
X A 8qa()
1kN/m
C
2m
C D A 2kN 4kN B E
2
4 4 D A
2 4 E 4
2m
4m
4m
2kN 4kN
M图(kN· ) B m
4.5 三铰刚架及多层多跨静定刚架的内力图 【例4.8 】作出图示两跨静定刚架的弯矩图。
2kN/m
D
15
8 E
F
G
4m
1kN
A
B
C
1kN
D 4
4 E F
4
G 4
2m
2m
M CA 12 4 3 4 2 24kN m NCD 12 3 4 0
4kN
C
D
3kN/m
12kN 4kN
A
B
4m
4m
QCD 4kN
M CD 12 4 3 4 2 24kN m N DC 0 QCD 4kN M CD 0
Pl / 2
P
Pl / 4 3Pl / 4 Pl / 4
19
Pl / 2
l
3Pl / 4
l
l
0
练习: 作图示结构弯矩图
P
l
Pl
Pl
Pl / 2
2l
2l
P
l
Pl / 2
例2. 试计算下图所示悬臂刚架的支座反力,并绘制M、Q和N图。
20
解:(1)计算支座反力
2qa2 q E
x 0
3a
2q 4a X A 0
X 0, X
A
X C 0, X C 1kN
4.3 用截面法求静定刚架杆端截面内力
8
刚架的内力有M、Q、N 8kN A 弯矩不规定正负号,只规定弯矩图画在杆件受拉一侧; MDA、QDC C 剪力、轴力的正负号与梁相同。
D
弯矩M =截面一边所有外力对截面形心的外力矩之和。 外力矩和弯矩使杆同侧受拉时取正,反之取负。 ∑Y=0 B 剪力Q =截面一边所有外力沿杆轴法线方向投影代数和。 ∑Y=0 外力绕截面形心顺时针转动,投影取正,反之取负。 4m ∑MD=0 轴力N =截面一边所有外力沿杆轴切线方向投影的代数和。 外力指向截面投影取正,反之取负。
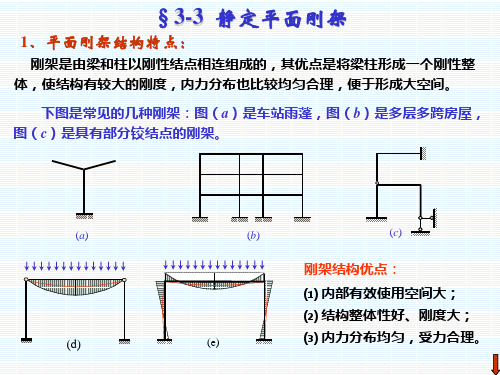
4.1 静定平面刚架的几何组成及特点
3
一、刚架 刚架是由若干直杆,部分或全部用刚结点连接而成的结构。
二、刚结点的特点 1.变形:刚结点处的各杆端不能发生相对移动和相对转 动,因而受力变形后,各杆杆断转动了同一角 度,即各杆之间的夹角保持不变。 2.受力:刚结点可承受和传递弯矩
(三)、基本形式
4
1. 悬臂刚架 2. 简支刚架 3. 三铰刚架 4. 组合刚架
4.4 静定刚架内力图的绘制
12
B D
1m
【例4.6 】作出图示刚架的内力图。 解: 4kN C 1)求支座反力 2)求各杆端内力
1kN/m
4m
7kN
并绘制内力图 M CD M AD M BD 0
M DC 4 1 4kN m (左边受拉)
M DB 7 4 28kN m (下边受拉)
刚架弯矩图做法:拆成单个杆,求出杆两端的弯矩, 按与单跨梁相同的叠加法画弯矩图.
例题1: 作图示结构弯矩图
Pl / 2 Pl / 2 l/2
P
练习: 作弯矩图
P P
17
l
l/2
l l
Pl / 2
l
2 Pl
Pl
Pl
P
l l
练习: 作图示结构弯矩图
P
l l l l
18
P
l
l
P
l
P
l/2 l/2
l
l
例题2: 作图示结构弯矩图
q 6qa E
(2)计算各杆端截面力,绘制各杆M图 1)杆CD 3a
21
2qa2
C D
2qa2
B
QDC 0 N DC 0
C D
QDC
M图
2q A
2a 2a 4a
4a
M DC 2qa 2 M DC
2)杆DB
N DC
6qa B
M BD
结点D
0ห้องสมุดไป่ตู้
2qa 2qa
2
2
0
D
QDB
M DB
N DB
N DB 0 QDB 0
沥青麻刀 1:2水泥砂浆
组 合 刚 架
细石混凝土
沥青麻刀 水泥砂浆
悬臂刚架
简支刚架
三铰刚架
5
刚架优点
(1)内部有效使用空间大;
(2)结构整体性好、刚度大;
(3)内力分布均匀,受力合理。
4、主从刚架
4.2 静定刚架支座反力的计算 【例4.1 】计算图示刚架的支座反力。 解:整体平衡
P A B
6
l/2
7kN
4m
3kN E
1kN 4kN F
A
B
C
2kN/m
1kN D E 4kN 1kN A
M图(kN· ) m
G
B
C
校核
3kN
7kN
速画下列刚架的弯矩图。
16
水平支座链杆的约束力可一眼看出。余下的两个支座约束力 不必求出,即可画出结构的弯矩图。
24kN m
2m 2m
25.5kN m 24kN m
6m
满足:∑X=0,∑Y=0,∑M=0
4.5 三铰刚架及多层多跨静定刚架的内力图
14
三铰刚架及多层多跨静定刚架内力图的绘制步骤仍然是:计 算支座反力;计算杆端截面的内力;绘制内力图。应注意的是: 计算支座反力时,对三铰刚架要利用中间铰M=0的条件;对多层 多跨静定刚架,一般应按照与几何组成相反的顺序。 【例4.7 】作出图示三铰门式刚架的弯矩图。
C B
13
N DC NCD N DB N BD 0
N DA N AD 7kN
D
7
A
N图(kN)
3)校核 a)微分关系的校核 b)平衡条件的校核
4kN D 7kN
4kN· m
D
28kN· m
4kN
24kN· m
7kN
在刚结点上,各杆端弯 矩和结点集中力偶应满足 结点的力矩平衡。尤其是 两杆相交的刚结点,无结 点集中力偶作用时,两杆 端弯矩应等值,同侧拉。
14qa2
2qa2 q
14qa
弯矩图
10
也可直接从悬臂端开始计算杆件 8 2qa2
8qa 2
B
10qa 2
6qa 2q
2
2qa 2
4qa2
14qa
2
M图
(4)绘制结构Q图和N图 2qa2 2qa2 C 6qa q E
24
10qa 2
D
2q A 2a 2a 4a B
3a
6qa
2
8qa
2
4a
2qa 2
l/2
l/2
l/2
C
l P M A 0, P YB l 0, YB 2 2 l P M B 0, P 2 YA l 0, YA 2
右半边平衡
l M C 0, X B l YB 2 0, 整体平衡
B
C
B QBA
N BA 10qa
QBA 0
4qa
2
2qa2
A 14qa2
8qa
M BA 2qa2
14qa2
M图
10qa
(3)绘制结构M图 2qa2
C
23
E
8qa 2
6qa
2
2qa2
10qa 2
B B B
6qa
2
8qa
2
10qa 2
D D
2qa 2
2qa
A
2
2qa 2
2qa2
4qa
2
2
4qa2
C
6qa
X A 8qa
y0 YA 6qa q 4a 0
D 2q B
4a
mA 0
YA 10qa
2qa2 q 4a 2a 6qa 2a 2q 4a 2 a M A 0
M A 14qa2
A
2a 2a
MA
XA
4a
YA
2qa2
M DB 2qa
2
D
N BD
10qa 2
N BD 0
QBD 6qa
QBD
6qa
2
M BD 10qa 2
2qa 2
M图
2qa2 C 6qa
