NPT型IGBT静态模型分析及仿真
IGBT开态的两种模型
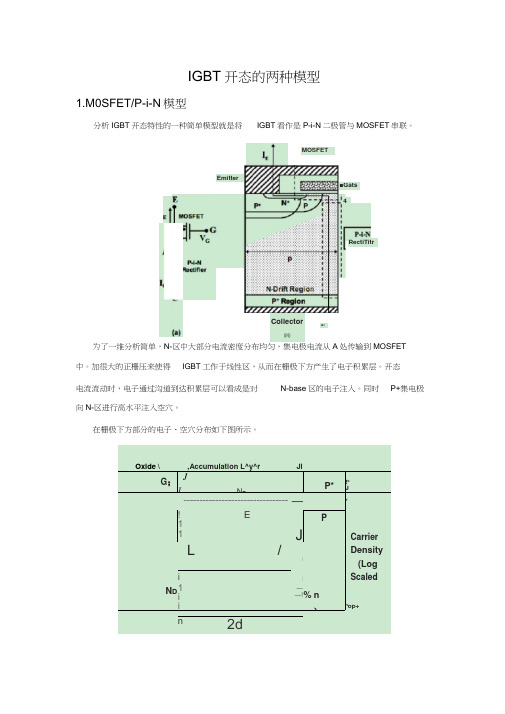
IGBT 开态的两种模型1.M0SFET/P-i-N 模型分析IGBT 开态特性的一种简单模型就是将IGBT 看作是P-i-N 二极管与MOSFET 串联。
为了一维分析简单，N-A 处传输到MOSFET中。
加很大的正栅压来使得 IGBT 工作于线性区，从而在栅极下方产生了电子积累层。
开态 电流流动时，电子通过沟道到达积累层可以看成是对 N-base 区的电子注入。
同时 P+集电极向N-区进行高水平注入空穴。
在栅极下方部分的电子、空穴分布如下图所示。
Oxide \ ,Accumulation L^y^r JiG ；JI N -P*!c J--------------------------------- ―►*! E1P1JCarrierL /Densityi(Logi i ScaledN D 1 i ——! % ni、 --n op+n2dMOSFET■cCollector㈣Emitter■Gats 4RectiTitr已知P-i-N 二极管的正向导通压降为:时，P-i-N 二极管对导通压降的大小约为1V ( J e =100 A/cm 2 )。
变换后写为J e工作在线性区时， MOSFET 沟道上的压降为:V F，MOSFET =I C R C H = J e PZR eHlicOXflv T因此IGBT 工作于线性区时的导通压降为:出现V Knee第一项占主导，此时IGBT 结构的集电极电流随集电极电压增加而指数增加；当较大的集电 极电流密度下时，第二项占主导，相当于一个电阻与P-i-N 二极管串联。
漂移区中你山)=蛙*-2C 寫胃，其中 d=l w N 。
2 NVF ,PiN斗__Iq ]2qD a mF(d/L a )J e d。
当L a = 1W N 时可以得到最小的导通压降。
开态4qD a 土 F,PiN /2kTV F T1ZJ e W NpJe L CH，其图像如下图。
U C VCollector BiM \ olligc Q J I %)N461J24 <」sHSJ 匕—■-HtMMe ■n(y)二 p(y)•HL J C cosh(y/l_a ) 2qL a _sinh(d/L a )sin h(y/L a ) 2cosh(d/L a )，其中 d=-W N 。
NPT型IGBT静态模型分析及仿真
函数 , 在静态时把 Imos = In ( W) 代入 MOSFET 伏2
安特性公式 (14) 中 , 则 Vds也为 Vgs和 P0 的函数 。
消去中间变量 P0 , 则得到伏安特性 。
当 把 MOSFET 中 饱 和 电 流 Imsaots = Kp ( Vgs -
Vds) 2/ 2 的关系式代入 In ( W) 的表达式 (9) 中时 ,
- μDnln
P0 + NB NB
(12)
式中
—5 —
© 1994-2007 China Academic Journal Electronic Publishing House. All rights reserved.
《电工技术杂志》2001 年第 11 期
0 Vgs < Vt
Imos =
Kp
( Vgs -
Vt) V ds -
1 2
V 2ds
0 < V ds < Vgs - V
(14)
Kp 2
( Vgs
-
Vt) 2
1-
1 ΔL mos/ L mos
V ds ≥ Vgs - Vt
313 静态 I2V 特性
程 , 计算微分 。这样添加的静态特性部分 , 才能用
射2基电压 。MOSFET 部分的简单模型和双极性传输
方程联立 , 来描述 IGBT 的通态电流电压特性 。双极
性传输方程的参考直角坐标系如图 1 右侧所示 。
(1) 过剩载流子浓度方程 在正偏工作条件下 ,
BJ T 的集电极2基极结是反偏的 , 它的耗尽层宽度为
Wbcj = 2εsi ( V bc + V bi) / qNB
IGBT的设计及仿真验证
在器件构造和仿真过程中，器件剖面结构、网格、掺杂 和正向阻断电压的数据文件分别被保存在名为PROFILE、 afterregrid、IGBT和bvds的这四个文件中。
medici程序运行后输出图形：
器件网格分布图 （A）正面 （B）背面
X=0 um处掺杂分布
X=10.25 um处掺杂分布
器件纵向掺杂（含N型和P型杂质）浓度分布图
使用穿通型结构 提高少子寿命 N-漂移区尽量薄 减小沟道电阻，降低栅氧厚度 减小JFET电阻，使用沟槽栅
提高开关速度采取的措施： 降低少子寿命 采用具有N+缓冲层的PT型结构 降低PNP晶体管电流增益 开关速度和导通压降这两个参数优化有时存在着矛盾， 因此必需根据设计者的需要进行折衷考虑。
N+
P+
N+
RCH
RAC RJFET
优化正向压降步骤：
（1）对于MOS通路相关的元胞参数 栅宽LG和P-阱宽Lwell进行优化，使得 MOS通路电流密度IMOS/ACELL最大； （2）对BJT通路的另一相关参数P+ 阱宽LDP进行合理选取，使得器件的 闩锁电流阈值尽量高。
RMOD
N-
N+ P+
C
减小正向压降采取的措施：
IGBT的设计 及仿真验证
本章内容
一、IGBT结构简介
二、IGBT元胞结构设计
三、高压终端结构的设计
四、IGBT工艺流程设计
本章内容
一、IGBT结构简介
二、IGBT元胞结构设计
三、高压终端结构的设计
四、IGBT工艺流程设计
IGBT基本结构及特点
与功率MOSFET只有一层之差，即背面P型层代替N 型层； 电压控制型器件； 具有MOS器件高输入阻抗，容易控制与双极型 （BJT）器件高电流密度，低导通电阻的双重优点； 广泛应用于各种功率转换、马达驱动等电力电子装 置中；
1700V／100A平面型NPT-IGBT静态特性研究
２ Ｏ １ ４年 ２月
固体 电 子学 研 究 与进 展
ＲＥ Ｓ Ｅ ＡＲＣ Ｈ＆Ｐ ＲＯＧＲ Ｅ Ｓ Ｓ ＯＦ Ｓ Ｓ Ｅ
Ｖｏ１ ．３ ４。 Ｎｏ ．１ Ｆｅ ｂ．。２Ｏｌ ４
＼
ｐ
硅 微 电 子 学
ｋ 、
１ ７ ０ ０ Ｖ ／ Ｉ Ｏ ０ Ａ 平 面 型 ＮＰ Ｔ － Ｉ ＧＢ Ｔ静 态 特 性 研 究
ＢＴ） ｂ ａ ｓ ｅ ｄ ｏ ｎ ｔ ｈｅ ｅ ｘｉ ｓ ｔ ｉ ｎ ｇ ｔ ｅ ｃ ｈ ｎｏ ｌ ｏｇ ｙ ｐ ｌ ａ ｔ ｆ ｏ ｒ ｍ ｗａ ｓ ｄ ｅ ｓ ｉ ｇ ｎｅ ｄ ｂｙ ｐｒ ｏ ｃ ｅ ｓ ｓ ｓ ｉ ｍｕ ｌ ａ ｔ ｉ ｏ ｎ，ｗｈ ｉ ｃ ｈ ｈ ａ ｄ ａ ｎ
Ｐｌ ａ ｎ ａ ｒ ＮＰＴ－ Ｉ ＧＢＴ
ＧＡＯ Ｍｉ ｎ ｇ ｃ ｈ ＡＯ Ｇｅ
Ｌ Ｉ Ｕ Ｊ ｉ ａ ｎ ｇ Ｊ Ｉ Ｎ Ｒｕ ｉ ＹＵ Ｋｕ ｎ ｓ ｈ ａ ｎ ＢＡＯ Ｈａ ｉ ｌ ｏ ｎ ｇ
（ Ｅ ｌ ｅ ｃ ｔ ｒ ｉ ｃ ａｌ Ｅｎｇｉ ｎｅ ｅ ｒ ｉ ｎ ｇ Ｎｅ ｗ Ｍａ ｔ ｅ ｒ ｉ ａｌ ａｎｄ Ｍｉ ｃ ｒ ｏ ｅ ｌ ｅ ｃ ｔ ｒ ｏ ｎｉ ｃ ｓ Ｄｅ ｐａｒ ｔ ｍｅ ｎｔ，Ｓｔ ａｔ ｅ Ｇｒ ｉ ｄ Ｓｍ ａｒ ｔ
Ａｂ ｓ ｔ ｒ ａ ｃ ｔ ： Ａ １ ７ ０ ０ Ｖ／ ｌ Ｏ Ｏ Ａ Ｎｏ ｎ Ｐｕ ｎ ｃ ｈ Ｔｈ ｒ ｏ ｕ ｇ ｈ Ｉ ｎ ｓ ｕ ｌ ａ ｔ ｏ ｒ Ｇａ ｔ ｅ Ｂｉ ｐ ｏ ｌ ａ ｒ Ｔｒ ａ ｎ ｓ ｉ ｓ ｔ ｏ ｒ（ ＮＰ Ｔ— Ｉ Ｇ—
高明 超 刘 隽 赵 哿 刘 江 金 锐 于坤山 包海龙 。
局域寿命控制NPT-IGBTs稳态模型
si n h
L2 W2
L2
Hale Waihona Puke (11)J p ( x(2) ) =
1
1 +
b
J
+
c os h W2 - x(2)
qD2 L2
p1
L2 sinh W2
L2
c os h x(2)
-
qD2 L2
p2
si n h
L2 W2
L2
(12)
在 Ⅲ区 ,电子和空穴电流密度分别为
J n ( x(3) ) =
(18) 这里基极电流 IB 等于基区的电子电流 In ( x = W ) , 即流过 MOS 结构的电流 IMOS0 . 集电极电流 IC 等于 基区的空穴电流 IP ( x = W ) , A 为 IGB T 器件面积. 这样可获得 np n 结构的电流增益
β=
IC IB
=
p
2 0
Isne
b
n
2 i
W1 L1
-
p1 D1 L1
×
1
sinh ( W1 / L 1 )
-
p2 D3 ×
1
L 3 si nh ( W3 / L3 )
(17)
IC
=
p
2 0
Isne
b n2i
+
qA
p0 D1 cot h bL 1
W1 L1
-
p1 D1 bL 1
×
1
sinh ( W1 / L 1 )
+
p2 D3 L3
×
1
sinh ( W3 / L3 )
I n0
=
Isne
(
p
现代电力电子技术之igbt建模与仿真
现代电力电子技术IGBT建模与仿真一、IGBT结构及工作原理自上世纪80年代绝缘栅双极型晶体管（IGBT）问世以来，逐渐取代了晶闸管和功率MOSFET等器件，在中频、中等功率变流领域获得了广泛的应用。
IGBT 克服了功率MOSFET高通态损耗的特性，同时保持了MOSFET门极电压驱动的优点。
IGBT是一种PNPN四层结构的器件，其结构剖面图和等效电路如图（1）所示。
(a) 剖面图(b) 达林顿等效结构图(1)IGBT结构剖面图及等效电路由图（1）（b）可知，IGBT相当于一个MOSFET和一个BJT的混合电路。
当在其栅极施加一个足够大的正向电压时，MOSFET内部将形成沟道，为晶体管提供基极电流，从而使IGBT导通。
此时由于P+区的空穴注入到N-区产生电导调制效应，能够减小N-区的电阻，从而使IGBT具有较小的通态压降。
二、IGBT工作特性IGBT的工作特性分为静态特性和动态特性两种。
(1)静态特性静态特性描述了稳态情况下IGBT的电流与电压关系，最常用的是其伏安特性和转移特性。
伏安特性指的是在不同的Vge下，Ice与Vce之间的关系，如图（2）左图所示。
转移特性是指集电极电流Ic与栅射电压Uge之间的关系，如图（2）右图所示。
图(2)IGBT的静态特性(2)动态特性动态特性描述了开关过程中IGBT的电压电流随时间变化的关系，分为开通特性和关断特性。
(a)开通过程 (b)关断过程图(3)IGBT的动态特性在开通过程中有两点值得关注：一是电流Ic上升率较快时，快恢复二极管的反向恢复电流将导致Ic出现尖峰，这一尖峰会引起电磁干扰等问题；二是寄生电容Cgc导致Miller效应，使Vge出现Miller平台，增加开通损耗。
在关断过程中，Cgc的分流作用使得在Vce下降过程中同样会出现Miller 平台，增加关断损耗。
此外电流下降过程中，二极管偏置导通将引起电压过冲，导致电磁干扰问题。
由于MOSFET快速关断，PNP双极管中存储的电荷不能及时释放，关断过程中还会有一个较长的拖尾电流，也增加了关断损耗。
IGBT参数建模与仿真分析
(
)
1.18 −1.77 T −31 2 T p + 400 + 3 × 10−3 N1 + × 1.83 10 300 300
2. IGBT 硅参数模型及仿真分析
IGBT 工作时不断承受功率循环与电热循环，过电压，过电流等；这些原因将诱发器件内部结构的变 化。而这些结构的变化与 IGBT 模块承受的温度密切相关。本章将详细分析温度变化对器件禁带宽度， 本征载流子，双核扩散系数等物理参数的影响，揭示 IGBT 开关速度减慢、通态压降、漏电流增大，阈 值电压突变，擎住效应等容易导致 IGBT 器件失效的电气现象的物理机理。
kT q
把上述式子(8)，(9)，(11)，(12)带入公式，可以得到高温时双极扩散系数表达式[9]
= D A
2k 11.2 × 107 T −0.94 × q 2.9 + 38.54T −0.73
(13)
式中： k 为硅玻尔兹曼常数= k 1.38 × 10−23 J K ， q 为电子电荷 = q 1.602 × 10−19 C 。
(Leabharlann )−1(3)
而在较高温度的情况下，载流子寿命模型只是温度的函数。 对于低掺杂基区 n = p < 1017 cm −3 ，对上式简化得到载流子寿命为：
(
)
τ (T ) = τ 0
T 300
1.7
(4)
其中， τ 0 为 300 K 时载流子寿命，载流子在 300 K 时的经验值为 2.5。 2.1.3. 本征载流子浓度 在本征半导体中，导电电子和空穴对仅能通过价键破裂而产生，电子和空穴成对生成，因此，电子 的浓度等于空穴浓度，这个浓度成为半导体的本征载流子浓度 ni ；其是晶格振动能量的函数，故而也是 温度的函数，它和温度、禁带宽度有关系，理论表达式为：
局域寿命控制NPT-IGBTs稳态模型
ＭＯＳ结 构 ． 用 Ｈｅｎ ｒ 采 ｆ ｅ 对普 通 Ｉ Ｔ描述 ： 件在 ＧＢ 器 导 通状 态下 ， 射结 的大 量 空穴注 入 ｎ基 区 ， 成大 发 形
密度 的空穴 电流 ； 与此 同时 ， 发射结 也存 在背 注 入 电
图 ２给 出分 析 局 域 寿 命 控 制 ＮＰ —ＧＢ 时所 ＴＩ Ｔ 采用 的坐标 系 ． 中 ， 其 发射 结 为 儿 ， 电结 为 Ｊ ， 集 ２ ｗ。 为集 电结 的冶 金 结 位 置 ， 为 中 性 基 区宽 度 ． 域 ｗ 局 寿命控 制 区将 整个 中性 基 区分 成 了 三个 部 分 ， 们 它 分别 为 Ｉ， Ⅲ区 ． 中 ， Ⅱ， 其 Ⅱ区 为 局 域 寿 命 控 制 区 （ 在 。 ～ 区域 内 ） 对 应 于 这 三 个 区 域 的 大 注 入 ． 寿命 和双 极 扩 散 系 数 分 别 为 ｒ ， ，。和 Ｄ－ Ｄｚ 。 ｚ ｒ ， ， Ｄ３ 宽 度分 别为 ｗ１ ｗ２ ｗ３ ， ， ， ．
方 蒋 平 明 张 李 健 华 乔 波 肇基
（ 子 科 技 大 学 微 电 子 与 固体 电 子学 院 ，成 都 ６ ０ ５ ） 电 １０ ４
摘要 ：提出 了局域寿命控制下 的值仿 真 比较 ， 明模 型结果 和仿 真结果 表 能较好地吻合 ． 基于该模 型， 详细地分析 了局域 寿命 区 的参数 对器 件正 向特性 的影 响 ． 通过 对 基 区空穴 浓度 的分 析， 澄清了长期 以来对 于最优局域低寿命区位置的不 同看法 ， 将各种结论统一起来 ．
＊国 家军 事 电 子 预研 基 金 （ 准 号 ：１ ０ ０ ０ ０ ） 武 器 装 备 预 研 基 金 （ 准 号 ：１０ ０ ０ ０ ＤＺ ２ ５ 资 助 项 目 批 ４３８２４５ 。 批 ５４８３４４ ０１） ｔ 通 信 作 者 ． ｍａｌｆ ｅｔ＠ ｕｓｃｅ ｕ ｃ Ｅ ｉ： ｕｓｃ ｅｔ，ｄ ＋ｎ ｊ ２ ０ ．４２ 到 。０ ５０ ．３定 稿 ０ ５０ ．８收 ２ ０ ．９２ ＠２０ ０ ６中 国 电 子 学 会
IGBT热仿真建模分析
IGBT热仿真建模分析IGBT(Insulated Gate Bipolar Transistor)是一种常用的功率半导体器件，其拥有低开通电压、高阻断电压和高电流能力的优点，因此在电力电子领域广泛应用。
热仿真建模分析是对IGBT进行电热特性模拟和分析的方法，本文将对IGBT热仿真建模分析进行探讨。
首先，IGBT的热仿真建模分析是基于热传导方程和瞬态热特性来进行的。
热传导方程描述了功率半导体器件内部的热传导过程，而瞬态热特性则描述了器件在瞬态工作条件下的温度变化过程。
在进行IGBT的热仿真建模分析时，首先需要确定模型的几何结构。
IGBT的结构包括导电层、绝缘层、衬底以及金属电极，这些结构在热仿真中需要被建立为相应的热传导模型。
其次，在建立热仿真模型时，需要确定IGBT的材料参数和边界条件。
材料参数包括导电层和绝缘层的热导率、热容以及密度等，而边界条件则包括器件的热界面温度和散热条件等。
然后，根据所选取的热传导模型和边界条件，利用热传导方程进行热仿真计算。
热传导方程是一个偏微分方程，其解可通过有限元方法或其他数值求解方法获得。
在进行瞬态热仿真时，需要考虑器件在工作过程中的瞬态功耗和瞬态散热等因素。
最后，根据热仿真分析的结果，可以得到IGBT的温度分布、温升和热耗散等信息。
这些结果可以用于评估器件的热稳定性、散热设计和寿命预测等方面。
总结起来，IGBT热仿真建模分析是一种对该功率半导体器件进行电热特性模拟和分析的方法，主要涉及到几何结构建模、材料参数确定、热传导方程求解以及结果分析等步骤。
通过热仿真建模分析，可以更好地了解IGBT的热特性，为器件的设计和应用提供参考依据。
局域寿命控制NPT-IGBT瞬态模型
中 图分 类 号 ：ＴＮ ８ ３６
文 献 标 识 码 ：Ａ
文 章 编 号 ：０ ５ －１７ ２
１ 引言
对 于绝 缘 栅 双 极 晶体 管 （ｎｕａｅ ｇ ｔ ｉｏａ ｉｓ ｌｔ ａｅｂｐ ｌｒ
ｊ ｐ． ｃ
Ｊ ｃ＝ ，ｐ＝ ａｐ ３０ ｃ ０ ｂ ／
ｔａ ｓ ｔｒ Ｉ Ｔ） 局 域 寿 命 控 制 是 有 效 提 高 器 件 ｒｎ ｉ ｏ ，ＧＢ ， ｓ 关 断速 度 ， 且 改善 其 正 向导 通 电压 和 关 断 时 间折 并 中关 系 的一种 有 效方 法［ ． １ 目前 ， 许多 文献 对 Ｐ Ｎ ］ 有 Ｉ 和 Ｉ Ｔ等 器件 的局 域 寿命控 制 技术进 行 了试 验和 ＧＢ 数值 分 析 研 究 口 ． 于 普 通 的 Ｉ Ｔ， ａｉｇ引， 叫］ 对 ＧＢ Ｂ ｌ Ｅ ａ Ｈｅ ｎ ｒ Ｊ Ｆ ｓｕ 等 人［ 分 别 提 出 了不 同 的 Ｉ ｆｅ ［ 和 ｏｓ ｍ ６ ７ ］ Ｇ．
程 的物理 图像 ， 同时 也 可 以 用 于 指 导该 类 器 件 的设 计 和 优化 ．
为分 析局 域寿 命 控 制 Ｉ Ｔ的 瞬 态 过 程 ， 建 ＧＢ 可 立 如 图 １ 示 的坐标 系 ． 中 ， 射 结 为 儿 ， 电结 所 其 发 集 为 Ｊ ， 为局 域 寿命 区宽度 ． 中虚线 为 稳 态下 的 ２ ｗｚ 图 空穴 分 布 ， 在发 射 结 处 浓 度 为 Ｐ ． 快 速 下 降 阶段 。在 结 束 后空 穴浓 度 出现 再 分 布 ， 耗 尽 区 的 边 界可 能 且 有两 种情况 ： 中点划 线 Ａ 对 应 耗 尽 区厚 度 小 图 于 ｗ。 况下 的耗 尽 区边 界 ， 时 空 穴 分 布对 应 实 情 此 线 Ａ， 射结处 空穴 浓度 为 Ｐ 。 图 中点 划线 Ｂ对 应 发 ， 耗尽 区厚 度 ｘ 岫大 于 Ｗｚ ｗ。 况 下 的 耗 尽‘ ＋ 情 区边 界 ， 时空 穴分 布对 应实 线 Ｂ， 射结处 空 穴 浓度 为 此 发
IGBT电路工作演示稿解析
工作原理 电路分析
工作原理
IGBT(Insulated Gate Bipolar Transistor)，绝 缘栅双极型晶体管，是由GTR(双极型三极管) 和MOS(绝缘栅型场效应管)组成的复合全控 型电压驱动式功率半导体器件, 兼有MOSFET 的高输入阻抗和GTR的低导通压降两方面的 优点。GTR饱和压降低，载流密度大，但驱 动电流较大;MOSFET驱动功率很小，开关速 度快，但导通压降大，载流密度小。IGBT综 合了以上两种器件的优点，驱动功率小而饱 和压降低。非常适合应用于直流电压为600V 及以上的变流系统如交流电机、变频器、开 关电源、照明电路、牵引传动等领域。
安全工作区
❖ 安全工作区SOA反映了一个晶体管同时能承受一定电压和电流的能力。 IGBT开通时为正向偏置，其安全工作区称为正向偏置安全工作区简称 FBSOA。 FBSOA于IGBT的导通时间密切关切相关。 FBSOA为矩形方 块。随着导通时间的增加，安全工作区逐渐减小，直流工作时安全工作 最小。这是因为导通时间越长，发热越严重；因而安全工作区越小。
输出 报警
驱动电路 1≦
过电流保护 R 短路保护 控制电源 控制信号 低压保护 检测信号
控制电源
输出 报警
驱动电路 1≦
过电流保护 短路保护 R
控制电源 控制信号 低压保护 检测信号
热敏元件 过热保护 检测温度信号
A B C
M
IPM优势
❖ IPM设有过流和短路保护、欠电压保护、当工作不 正常时，通过驱动电路封锁IGBT的栅极信号同时发 出警报信号；过热保护是通过设置在IPM基板上的 热敏器件检测IGBT芯片温度，当温度超过额定值时， 通过驱动电路栅极信号并报警。
GTR电路分析
IGBT的设计与仿真(张斌)PPT课件
18.05.2020
.
16
thank you！
18.05.2020
.
17
IGBT的设计与仿真
18.05.2020
学生:张斌 指导教师:韩雁教授
2009.1.14
.
1
主要内容
1.研究内容简介 2.设计指标 3.研究设计方案 4.工艺流程设计 5.主要工艺指标 6.器件仿真 7.主要器件指标仿真结果 8.结论及说明
18.05.2020
.
2
1.研究内容简介
• IGBT的全称是Insulated Gate Bipolar Transistor，即绝 缘栅双极晶体管，它是适应了功率半导体器件的发展而产 生的,是一种新型的电力电子器件。
P+阳极 1E17 N+缓冲层 1E16
0.
P-阱
5E16 6.4um
P+阱
5E18 2.2um
N+源区 2E19 1.1um
栅氧
800A
Poly
1E20 5000A
18.05.2020
.
8
表2 主要工艺步骤与工艺条件列表：
主要工艺步骤 衬底 P+阱注入 P-阱注入 P-扩散 Gate Oxide Poly N+源区注入 N+扩散
• 它具有输入阻抗高，通态压降低，速度快，热稳定性好， 驱动电路简单，安全工作区宽，电流处理能力强等优点。
• 三重扩散晶体管的制作方法是指晶体管的集电区、基区、 发射区皆由扩散方法获得，便称为三重扩散。现也指使用 高温长时间扩散工艺获得结深很深的PN结的过程。
• 本课题从IGBT的工作原理出发，研究使用三重扩散技术进 行高压IGBT生产的可行性,设计工艺流程，借助ISE-TCAD 仿真工具进行IGBT器件结构和工艺研究。
完整word版,IGBT模型总结,推荐文档
I. IGBT器件模型的研究背景：实时仿真已经在汽车，航天，电子和机械制造中得到了广泛的应用，其中一个应用最广泛的就是硬件在回路。
在电压型变流器的仿真中，IGBT的建模是一个很关键的问题。
特别是模型要考虑到非线性的开关特性，电感损耗和反并联二极管的回复特性。
IGBT的离线仿真模型可以划归为两类：系统级和器件级。
系统级的仿真模型主要包含的是电力电子期间的一些如关断电压，电流谐波等电气特性，如在MATLAB/SIMULINK等软件使用的模型。
这些工具利用有限元数值计算如梯形积分公式，建立器件常用的离散模型。
通常可以分为以下几个开关模型：1.理想模型；2.开关函数模型；3.平均模型。
所有三种模型在实时仿真中都有使用，并且通过一些算法在DSP和PC机上实现，如通过自动预测下变流器下一状态来减小仿真时间。
虽然，系统级的模型仿真速度比较快，但是反应器件的非线性不够准确。
器件级的模型中，主要内容包括开关的暂态特性，功率损耗，和器件的发热特性。
SABER和SPICE系列软件都是通过有限元数值计算如Newton--Raphson 或者Katzenelson方法来实现器件的非线性特性。
器件级的模型十分全面，但是仿真时间较长。
通常可以划分为一下三个模型：1.分析模型；2.经验模型；3.有限元数值模型。
这三种模型由于计算复杂，没有一种运用到实时仿真中。
其中，分析模型是基于器件描述载流子动态的半导体物理特性。
在这种模型中，最具代表的是Hefner模型和Kraus模型，并且已经在SABER和SPICE中所使用。
在动作模型中，IGBT的相关开关特性通过不同的方法表示出来，并且这种方法已经在离线的仿真工具EMTP中比较准确的使用。
但是，为了能够在传统的DSP 上使用，这种模型仍然需要更小的仿真步长。
II. 系统级的仿真模型2.1理想模型引用来自论文：Behavior-Mode Simulation of Power Electronic Circuits图1. IGBT的伏安特性曲线图2. IGBT 的理想开关状态比如，对于三相逆变器来说 +-V dci a135图3. 三相逆变器电路拓扑三相电压型逆变器结构如图3中所示，由6支IGBT 及其反并联二极管构成，引入A ，B ，C 桥臂的开关变量a S 、b S 、c S （1i S =表示上桥臂导通，0i S =表示该下桥臂导通，i=a,b,c ）。
IGBT究竟是什么？看完这篇你就明白了（附：IGBT的设计及仿真验证PPT）
IGBT究竟是什么？看完这篇你就明白了（附：IGBT的设计及仿真验证PPT）2017-04-09近日CCTV2《经济半小时》做了中国芯生存状态系列报道，其中一期谈到了中国IGBT的进展，我们姑且不谈我国IGBT目前究竟是否超过了美欧日，我们只谈谈技术，为大家普及一下究竟什么是IGBT，对于已经熟悉或从事IGBT设计的同学可以直接看后半部分 IGBT的设计及仿真验证PPT 。
(本文由EETOP在2015年12月17日首发，作者：芯苑网小桂，现在再次发给大家）大功率器件-《从PowerMOS到IGBT》电的发现是人类历史的革命，由它产生的动能每天都在源源不断的释放，人对电的需求不亚于人类世界的氧气，如果没有电，人类的文明还会在黑暗中探索。
然而在电力电子里面，最重要的一个元件就是IGBT。
没有IGBT就不会有高铁的便捷生活。
一说起IGBT，半导体制造的人都以为不就是一个分立器件(Power Disceret)嘛，都很瞧不上眼。
然而他和28nm/16nm集成电路制造一样，是国家“02专项”的重点扶持项目，这玩意是现在目前功率电子器件里技术最先进的产品，已经全面取代了传统的Power MOSFET，其应用非常广泛，小到家电、大到飞机、舰船、交通、电网等战略性产业，被称为电力电子行业里的“CPU”，长期以来，该产品（包括芯片）还是被垄断在少数IDM手上(FairChild、Infineon、TOSHIBA)，位居“十二五”期间国家16个重大技术突破专项中的第二位（简称“02专项”）。
究竟IGBT是何方神圣？让我们一起来学习它的理论吧。
1、何为IGBT？IGBT全称为绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor)，所以它是一个有MOS Gate的BJT晶体管。
奇怪吧，它到底是MOSFET还是BJT？其实都不是又都是。
不绕圈子了，他就是MOSFET和BJT的组合体。
我在前面讲MOSFET和BJT的时候提到过他们的优缺点，MOSFET主要是单一载流子(多子)导电，而BJT是两种载流子导电，所以BJT的驱动电流会比MOSFET大，但是MOSFET的控制级栅极是靠场效应反型来控制的，没有额外的控制端功率损耗。
基于Simplorer的IGBT模块建模与仿真
基于Simplorer的IGBT模块建模与仿真一、IGBT模块建模过程,以英飞凌IGBT模块FF400R06KE3为例1、选取高级模型，如图1.图12、根据IGBT数据手册查找相对应的参数,具体参数如图2所示。
该模块包含两个单管，所以单个IGBT正常工作电压为300V.图2 3、同样查找、填写参数，如图3.图34、提取文档中Ic=f（Vge）的图片,分别提取25℃、150℃的对应关系。
图4图5 Ic=f（Vge)拟合曲线与文档曲线对比图5、提取文档中Ic=f(Vce)的图片，分别取Vge为13V、15V。
图6图7 Ic=f（Vce）拟合曲线与文档曲线对比图6、提取文档中If=f（Vf)的图片，分别提取25℃、150℃的对应关系图8图9 If=f(Vf)拟合曲线与文档曲线对比图7、隔热设置图108、在文档中找到对应参数填入，执行后生成测试电路,如图11—13。
图11图12图13二、 IGBT模块 FF400R06KE3模型的电路测试与应用仿真1、自动生成的测试电路如图14所示，仿真时间设置如图15.图14图15图16 栅级驱动波形图17 Vce电压图18 开通过程IGBT过电流波形测试波形证明设计的IGBT符合使用要求，并且工作良好，满足快速性的动态要求，而且可以突出管子内部寄生电感电容参数对开关过程的影响。
可以从二次开通的过电流看出。
同时,在12us的时刻IGBT关断过程中的电流拖尾现象可以很早地被仿真出来。
2、IGBT双脉冲测试电路如图18所示。
其中电源电压设置为100V。
t0时，门极电压拉高，VT2饱和导通，电源电压加到电感上，电感电流线形上升,如图21所示。
T1时刻，VT2关断电感电流通过上管二极管续流。
T2时刻，第二个脉冲到达，VT2开通，VT2续流二极管出现反向恢复,如图22所示，t2时出现了一个大约为1A的电流尖峰即为反向恢复电流。
其中t0与t2时刻，观察IGBT的关断过程，由于杂散电感的存在，电流急剧变化会在管子产生电压尖峰。
IGBT的设计及仿真验证
场限环与主结以及其它电极并没有电接触，因此又称为浮 空场限环。 浮空环能抑制最外侧主结边缘曲率效应引起的电场集中， 将高压以分压的方式逐渐环降低，从而维持整个IGBT器件的 击穿电压在较高水平。
E P+ J2 P+ P+ P+
N-
场限环结构示意图
当主结加反向电压时，主结与环结的电场与电位分布可用半 导体表面的二维泊松方程求解：
Ex x
x ys
q
S
(N
S E
q y
x yS
)
求解以上方程得到的环分压比及环间距：
环分压比： Ui Ui 1 (1 i
Ui 1 ) g
1 (1 )/2
环间距：
Li (Ui Ui 1 )
g ri / WPP 称为归一化结深；
间距(um)
环n
间距(um)
18个场限环结构的击穿电压仿真结果：1875V
本章内容
一、IGBT结构简介
二、IGBT元胞结构设计
三、高压终端结构的设计
四、IGBT工艺流程设计
（1）使用材料的选择
硅外延片（适用于≤ 1200V 产品 ）
硅单晶 两种硅单晶比较 Method
直径（mm） 电阻率
由于元胞的对称性，仿真时只需建立半个元胞即可 采用穿通型结构 元胞长度为20.5 um（半元胞长度10.5 um），其中多晶硅 长度14 um 背面P+集电极掺杂浓度1E18 cm-3，结深0.4 um N+缓冲层厚度30 um，表面浓度1E16 cm-3 N-漂移区厚度190 um，电阻率75 Ω-cm P-阱表面浓度3E17 cm-3，结深2.6 um P+阱表面浓度1E19 cm-3，结深3.2 um N+源区表面浓度2E20 cm-3，结深0.3 um，宽度1 um
NPT型IGBT电热仿真模型参数提取方法综述_徐铭伟
电力自动化设备Electric Power Automation Equipment Vol．33No．1 Jan.2013第33卷第1期2013年1月0引言近年来，绝缘栅双极型晶体管IGBT（Insulated Gate Bipolar Transistor）因其不断改善的电压、电流承受能力和工作频率、功率损耗等性能指标而被广泛应用到机车牵引、开关电源、新能源发电等电能变换和处理领域中［1］，因此IGBT的可靠性受到国内外科研工作者的广泛关注。
研究表明，与IGBT器件结温（T j）相关的热循环过程和器件封装材料热膨胀系数不一致是致其故障的主要诱因［2-3］，IGBT的电热仿真模型可以估计结温的变化情况，从而可用于IGBT可靠性的评估。
国内外对IGBT的电热仿真模型开展了大量研究工作［4-6］，其中基于半导体物理并考虑自热效应（Self-heating）的IGBT A.R.Hefner器件模型［6］和反映其封装传热过程的Cauer网络［7-9］联合组成的IGBT 电热模型准确度较高，并已在Saber、Pspice等电路仿真软件中得到应用［10-11］，但是，仿真软件有限的器件模型库无法满足仿真需要，同时出于技术保密的缘故，半导体制造商并不会提供建立电热模型需要的模型参数，因此如何建立一种有效并准确的参数提取方法就显得十分必要。
IGBT电热仿真模型参数同半导体物理、器件以及封装结构直接相关，无法直接测量，只能通过一定的技术方法和手段获取。
一个有效的参数提取过程是获得有效的电热模型的前提条件；此外，实现模型参数的准确提取对于分析IGBT的性能、优化驱动电路的设计、指导其应用以及选型都具有重要意义。
在参数提取之后，有效性验证也至关重要，可以让使用者合理选择器件的工作范围。
由于非穿通（NPT）型IGBT目前在工业领域中已获得了广泛而成熟的应用［12］，本文将以其作为参数提取的研究对象。
本文从NPT型IGBT电热仿真模型的工作原理出发，首先将模型参数分为电参数和热参数两大类。
IGBT的设计及仿真验证
IGBT的设计及仿真验证IGBT(Insulated Gate Bipolar Transistor)是一种高性能功率开关器件，广泛应用于工业和交通领域。
其设计和仿真验证过程如下：设计：1.确定需求：首先确定使用IGBT的具体应用场景和要求，包括额定电压、额定电流、开关频率和耐受能力等。
2. 选择器件参数：根据需求，选择合适的IGBT，考虑参数如最大允许电压（Vce(max)），最大允许电流（Ic(max)），漏极导通电压（Vf(on)）等。
3.确定散热设计：根据选定的IGBT参数，计算散热要求，确定合适的散热器材和散热方式，保证IGBT的温度在安全范围内工作。
4.控制电路设计：设计IGBT的驱动电路，通常使用光耦隔离和电平变换电路，确保IGBT能够正确地开关。
5.确定保护措施：为了保护IGBT免受电压过高、电流过大和温度过高等因素的影响，设计合适的保护电路，如过压保护、过流保护和温度保护等。
仿真验证：1. 建立电路模型：使用电路仿真软件（如LTSpice、PSIM等），建立包含IGBT、驱动电路和保护电路的电路模型。
2.输入参数：设置IGBT的参数，包括电压、电流和开关频率等。
3.进行仿真：运行仿真，观察IGBT的工作状态，包括开关特性、导通损耗和开关损耗等。
4.分析结果：通过仿真结果，评估IGBT的性能是否符合设计要求，分析其开关速度、损耗和温度等方面的性能，并进行必要的调整。
5.优化设计：根据仿真结果，优化IGBT的驱动电路、保护电路和散热设计等，以提高IGBT的性能和可靠性。
6.重复验证：根据优化后的设计，再次进行仿真验证，直至满足设计要求。
需要注意的是，在设计和仿真过程中，还需要考虑IGBT的可靠性和寿命问题。
因此，除了基本的IGBT选型和电路设计外，还需要进行可靠性评估和寿命预测，以确保设计的可靠性和稳定性。
综上所述，IGBT的设计和仿真验证是一个复杂的过程，需要全面考虑各种因素，包括电路设计、热分析、驱动电路和保护电路等。
(参考资料)IGBT热仿真建模分析
IGBT功率管热仿真工作总结一、【问题描述】：大功率IGBT是我司产品中的常用器件，尤其是在功率模块中，例如风能功率模块，光伏逆变器等。
在这些产品中，IGBT有一个共同特点：功率密度大，工作温度高。
如果不能建立有效的散热途径，将热量散出，IGBT工作温度超过允许值，就会损毁。
在产品设计的初始阶段，如何利用仿真手段准确评估IGBT的结温，建立有效的散热途径就成为热设计工程师急需解决的问题。
二、【原因分析】：IGBT芯片Diode芯片图1 IGBT内部结构图硅凝胶DBC图 2 IGBT内部芯片焊接结构简图IGBT内部结构如图1所示，发热器件由多组芯片组成，每一组芯片由一个IGBT芯片和一个Diode（二极管）芯片组成（视具体情况而定，有些IGBT中，一组芯片中IGBT 芯片数和Diode芯片数不同）。
图1中绿色方框中的为IGBT芯片，黄色方框中的为Diode 芯片。
如图2所示，IGBT芯片和Diode芯片正上方是一层厚度约5mm ，导热系数为0.15W/m.K的透明硅凝胶；芯片直接焊接在DBC层上，DBC层再焊接在铜基板表面。
DBC层由0.38mm厚氧化铝陶瓷片上下紧密贴附0.3mm厚铜皮组成（DBC的具体结构和制造厂家有关，另外相同厂家不同型号的产品具体结构也不相同，本文只介绍一种典型的结构）。
由于芯片上部的硅凝胶导热系数很小，芯片产生的热量主要通过下方的铜基板传到散热器上。
芯片和散热器之间的热阻分布如图3所示，归纳起来可分为两部分：①结壳热阻（芯片到铜基板的热阻）；②壳到散热器的热阻（铜基板和散热器之间的热阻）。
热流方向图3 IGBT热阻网络图IGBT的最高使用温度和热阻数据可以从厂家提供的器件资料中查到。
通常产品中使用的IGBT管子（一个桥臂）实际是将两个IGBT封装在一起，如图4所示。
厂家给定的热阻值可能是其中一个IGBT的值，也可能是整个IGBT管子（一个桥臂）的热阻，根据具体资料确定。
以英飞凌FF1000R17IE4为例，FF1000R17IE4管子内部共有12组芯片（一组芯片包含一个IGBT芯片和一个Diode芯片；一个IGBT有6组芯片）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
311 IGBT 中 BJT 的模型分析 从结 构 图 来 看 , IGBT 相 当 于 一 个 由 MOSFET
驱 动 的 BJ T , 其 等 效 电 路 如 图 2 所 示 。在 模 型
图 2 NPT2IGBT 等效电路图
中性基区的靠发射极和集电极边缘处的多数载流子 浓度不同引起的 。在高增益 、窄基区的晶体管中 , 式 (12) 的欧姆电压降被忽略 , 认为电压全部降落 在 PN 结上 。 312 IGBT 中 MOSFET 的模型分析
沟道电流采用对饱和特性进行改进的模型 [ 6 ]
P0/ ln [ ( P0/ NB) csch ( W/ L ) ] 。式中第二项是由在
1 引言
电力电子电路的仿真的关键是电力电子器件的 仿真 , 电力电子器件的模型直接影响仿真的范围 、 效果和精确程度 。自 80 年代绝缘栅双极型晶体管 ( IGBT) 问世以来 , 它的仿真模型的建立一直受到人 们的广泛关注 。国外的一些文献已经讨论了构造 IGBT 模型的方法 。Hefner[1]和 Kraus[2]是其中对模型 特性描述比较全面 、具有代表性的两类模型 。在这 两类模型的理论基础上 , Kuang Shen[3]等发展了模型 的某些特性 , 建立了改进模型 。这些模型最终添加 到 Saber 仿真软件包中 , 以实现模型的动态仿真 。 但 Saber 仿真环境价格较昂贵 , 国内应用并不十分 广泛 。本文将利用 MATLAB , 实现非穿通型绝缘栅 双极晶体管的静态特性 , 为实现 MATLAB 中动态仿 真提供前提条件 。
—6 —
图 3 600V/ 20A IGBT伏安特性
图 4 600V/ 20A IGBT饱和特性
5 结论
与传统的双极性晶体管模型相比较 , 此模型考
© 1994-2007 China Academic Journal Electronic Publishing House. All rights reserved.
0 Vgs < Vt
Imos =
Kp
( Vgs -
Vt) V ds -
1 2
V 2ds
0 < V ds < Vgs - V
(14)
Kp 2
( Vgs
-
Vt) 2
1-
1 ΔL mos/ L mos
V ds ≥ Vgs - Vt
313 静态 I2V 特性
程 , 计算微分 。这样添加的静态特性部分 , 才能用
- μDnln
P0 + NB NB
(12)
式中
—5 —
© 1994-2007 China Academic Journal Electronic Publishing House. All rights reserved.
《电工技术杂志》2001 年第 11 期
得到 Imsaots与 P0 的关系 。
4 静态特性的 S2function 描述
对于 IGBT 的静态特性 , 可以直接编程实现 , 但 为了在 MATLAB 仿真环境 simulink 中最终实现 IGBT 模型的动态仿真 , 采用 simulink 中提供的 S2function 模型构造语言完成模型的静态特性的描述 。因为 MATLAB 描述状态方程形式的模型较为方便 , 所以 把 IGBT 模型看作一个连续系统 。
射2基电压 。MOSFET 部分的简单模型和双极性传输
方程联立 , 来描述 IGBT 的通态电流电压特性 。双极
性传输方程的参考直角坐标系如图 1 右侧所示 。
(1) 过剩载流子浓度方程 在正偏工作条件下 ,
BJ T 的集电极2基极结是反偏的 , 它的耗尽层宽度为
Wbcj = 2εsi ( V bc + V bi) / qNB
又由于基区载流子总电荷 Q = qA δp ( x) d x 得 0
到 ,对上式积分得
Q
=
qP0 ALtanh
W 2L
(7)
第一个边界条件是设发射结处的载流子浓度 P0 为
模型参数 , 作为模型中间变量 ; 而第二个边界条件
规定在耗尽区边缘 x = W 处 , 过剩载流子浓度为零 ,
这是因为集电结反偏 , 到达这里的任何少数载流子
(4)
准中性基区的宽度为
W = WB - Wbcj
(5)
则在稳态时 9δp/ 9 t = 0 , 并且利用边界条件
9 p/ 9 x| x = 0 = P0 , 9 p/ 9 x| x = W = 0 求解方程 (3)
δp ( x)
=
P0
sinh[ ( W sinh ( W/
x) / L)
L
]
(6)
∫W
因为 IGBT 的集电极和发射极之间的电压降 V 于 simulink 的动态仿真 。
为 MOSFET 的源极2漏极压降和 BJ T 的集电极2发射极
以下给出 MATLAB 中得到的静态特性如图 3 、
压降的总和
图 4 所示 。
V = V ds + Veb
(15)
IGBT 总电流 I 为 P0 的二次函数 , 而 Ved为 I 和 P0 的
是一个轻掺杂 、宽基区 、低增益 ( In～ Ip ) 的双极 性晶体管 , 这与传统的高增益 、低注入的 BJ T 不同 。 使得传统 BJ T 模型不能应用在这里 , 很多行为模型 简单地用模型库中的 MOS 和 BJ T 模型复合为 IGBT 模型是很不准确的 。
图 1 NPT2IGBT 元胞结构图及模型坐标
《电工技术杂志》2001 年第 11 期
·研究与开发 ·
NPT 型 IGBT 静态模型分析及仿真
廖家平 刘劲楠 (湖北工学院 430064)
摘 要 对非穿通型绝缘栅双极晶体管 (NPT2IGBT) 的静态工作特性进行了理论分析 。从 IGBT 结构入手 , 把它看作 MOSFET 驱动的 BJ T , 从其包含的 BJ T 和 MOSFET 分别讨论 。并且对比 了传统 BJ T 模型和 IGBT 中包含的 BJ T 模型的分析方法 , 详细讨论了用双极传输方程分析 BJ T 模 型 。在 MATLAB 的仿真环境中添加相应的模型描述语言 S2function , 实现静态特性 , 为实现动态 仿真提供前提条件 。 关键词 非穿通型绝缘栅双极晶体管静态模型 双极传输方程 模型描述语言
Veb = (φpej - φnej) + (φnej - φnb)
(11)
式中 φpej - φnej ———电子在发射极中准费密级电压 降 , 由式 (8) 给出
φnej - φnb ———电子在准中性基区中准费密级
电压降
∫ φnej - φnb = -
W 0
dφn ( x) dx
dx
=
(1
I ·W + 1/ b) μn Aqneff
点的总电流相等 , 即 9 I/ 9 x = 0 , 代入空穴连续方程
得双极扩散方程
92δp 9 x2
=
δp
L2
+
1 D
9δp 9t
(3)
式中 L = DτHL为双极扩散长度
Hefner IGBT 模 型 中 用 一 系 列 参 数 方 程 来 表 示
IGBT 中的 BJ T 的发射极和基极电流 、载流子浓度 、
(8)
则基极和发射极的电流可从式 (1) 、(2) 、(6) 、(8) 得
到
IB
=
In ( W)
=
P20 Isne n2i
+
qP0 AD ·
L
cosh
W L
-
1 sinh ( W/ L )
(9)
IC =
Ip ( W)
=
P20 Isne bn2i
+
qP0 AD ·
L
cosh ( W/ L )
b
+
会立刻被电场扫到集电极去 。等式 (7) 只在静态
时 , Q 和 P0 的关系才满足 。
(2) 集电极和基极电流方程 在大注入条件下 ,
利用准平衡近似 , 可推出从发射极注入的电子电流
为
In (0) I sne
=
exp
q kT
(φpej
-
φnej)
=
P0 ( NB + n2i
P0)
≈
P20 n2i
由于在实际工作范围内 , IGBT 中的这个双极性 晶体管 (BJ T) 处于低增益 、大注入状态 , 电子和空 穴电流相互耦合 , 因此不能分开处理电子和空穴 , 必须用双极传输方程来描述 。这里利用了 IGBT 的总 电流 I 与位置无关 , 即 I = In + Ip , 消去双极传输方 程中的电场得到 。
函数 , 在静态时把 Imos = In ( W) 代入 MOSFET 伏2
安特性公式 (14) 中 , 则 Vds也为 Vgs和 P0 的函数 。
消去中间变量 P0 , 则得到伏安特性 。
当 把 MOSFET 中 饱 和 电 流 Imsaots = Kp ( Vgs -
Vds) 2/ 2 的关系式代入 In ( W) 的表达式 (9) 中时 ,
电子和空穴的电流的传输方程 [ 1 ]
In
=
1
b +
bI
+
qAD
9n 9x
(1)
Ip
=
1
b +
bI
-
qAD
9p 9x
(2)
式中 b = μn/ μp
D = 2 Dn Dp/ ( Dn + Dp) 以上的两个表达式都与总电流 I 有关 , 且不能