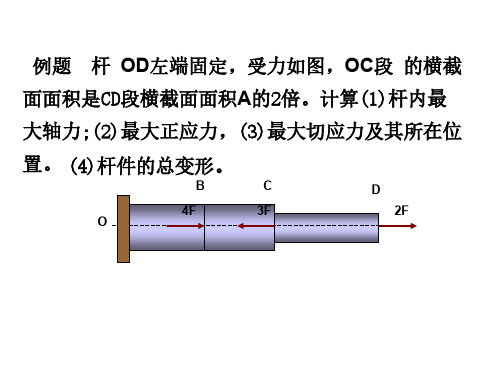
材料力学例题
材料力学例题
0.75m 1m
A
D 1.5m
B
F
横梁BC为刚杆，自重Q＝2KN，力P＝10KN可在横 梁BC上自由移动。AB杆的许用应力为[σ]=100MP ａ，设计AB杆的横截面面积。如果AB杆采用直径 为10毫米的细丝，需要几根？
P C
30°
Ｂ
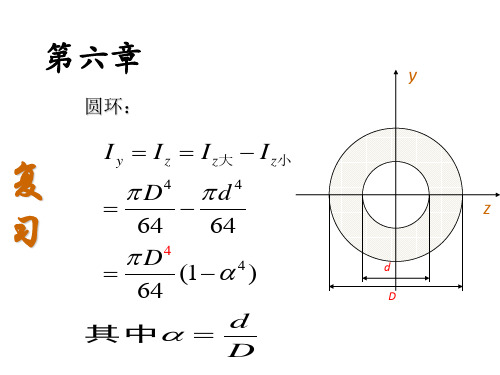
• [例] 长为 L=2m 的圆杆受均布力偶 m=20Nm/m 的作用，如图，若杆的内外径之比为 =0.8 ，
例题 空心圆杆AB和CD杆焊接成整体结构，受力如图.AB杆的外径 D=140mm，内外 径之比α= d/D=0.8，材料的许用应力[] = 160MPa。试用第三强度理论校核AB杆的 强度。 解:（1）外力分析 将力向AB杆的B截面形心简化得
10kN
0.8m A
B D
F 25kN
M e 15 1 . 4 10 0 . 6 15 kN m
G=80GPa ，许用剪应力 []=30MPa，试设计杆
的外径；若[]=2º /m ，试校核此杆的刚度，并
求右端面转角。
[例题] 某传动轴设计要求转速n = 500 r / min，输入功率P1 = 500 马力， 输出功率分别 P2 = 200马力及 P3 = 300马力，已 知：G=80GPa ，[ ]=70M Pa，[ ]=1º /m ，试确定： ①AB 段直径 d1和 BC 段直径 d2 ？ ②若全轴选同一直径，应为多少？ ③主动轮与从动轮如何安排,轴的受力合理？ P2 A 500 B 400 P3 C
y Me A x B l/2 F1
F2
D F2 D M e C ( F1 F 2 ) 2 2 20 F2 kN 3 F 20kN
轴产生扭转和垂直纵向对称面内的平 面弯曲
材料力学典型例题及解析 12.冲击问题典型习题解析
击构件瞬间的速度为 υ
，只须将前面（a）式右端改为
1 2
⋅
Pυ2 g
= Vε
，即可导出 kd
=
υ2 。 g∆st
（4）、前面推导过程中，冲击物的势能取为 Ep = P(h + ∆d ) ，一般情况下 ∆d << h ，可将其忽
略，取 Ep = Ph ，读者可仿照上面推导一下，并讨论忽略后对 kd 有什么影响。
所以本问题的动载荷因数为： kd
=
∆d ∆st
=1+
1+ 2h = 1+ ∆st
1+
2
× 440 ×10 −3 2 ×10 −3 m
m
= 22
讨论：（1）、在线弹性范围内，载荷、变形、应变、应力之间都是线性关系，也就是说，当
外载荷被放大 kd 倍，则变形、应力、应变也同样被放大 kd 倍。所以有σ d = kdσ st 。有了 kd 很
动能完全转化为橡皮筋的应变能。即 Ek = Vε 。
解：设小球离开木拍瞬间速度为υ ，则其动能 Ek
=
1 2பைடு நூலகம்
W g
υ 2 ；而橡皮筋被拉至最长时应变能
Vε
=
1 2
F ⋅ ∆L ，其中
F
为小球速度为零时橡皮筋所受拉力。由于假设橡皮筋为线弹性变形，
3
所以 F
=σ
A
=
Eε
A=
∆L L0
EA ，于是Vε
=
∆d
=
∆d ∆st
P 。定义
∆d ∆st
= kd 为动载荷因数，则有
Fd P
=
∆d ∆st
= σd σ st
材料力学求形心位置例题
材料力学求形心位置例题对于一个物体，定位其形心位置是物体力学中的基本问题之一。
形心位置是一个物体整体平衡的位置，也可以被认为是物体质量的重心。
通过求解形心位置，可以帮助我们更好地理解物体的平衡状态和运动性质。
下面我们来看一个求解形心位置的例题。
例题：一个均匀的长方形板有边长为a和b，其质量密度为ρ。
求解板的形心位置。
解答：为了求解板的形心位置，我们需要用到物体的质量和质量元的概念。
质量(m)可以通过物体的质量密度(ρ)和物体体积(V)相乘得到，即m = ρV。
对于一个均匀的长方形板，可以将其看作无数个宽度微小但高度为b的质量元叠加而成。
首先，我们将长方形板沿着宽度(b)方向进行切割，得到宽度为Δx的无数个矩形质量元。
然后，对于每个质量元，我们需要确定其质量(dm)和距离形心位置的距离(x)。
由于板的质量密度为ρ，那么每个矩形质量元的质量(dm)可以表示为dm = ρΔx。
而每个质量元距离形心位置的距离(x)可以表示为x = Δx/2。
然后，我们可以将质量元质量(dm)和距离形心位置的距离(x)相乘，然后将所有的质量元的乘积累加起来得到形心位置的坐标。
形心位置的x坐标可以表示为x_cm = Σ(dm*x) / Σ(dm)。
而形心位置的y坐标则与矩形板的宽度(b)无关，即y_cm = 0。
接下来，我们将上面的表达式代入求解。
解得，形心位置的x坐标为x_cm = (b/2) * (a/3) = ab/6。
因此，长方形板的形心位置为(ab/6, 0)。
通过求解形心位置，我们可以得到长方形板的形心位置坐标。
这个结果说明，在一个均匀的长方形板上，形心位置位于长方形的重心位置，且形心位置的x坐标与长方形的长和宽有关，y坐标为0。
在实际问题中，求解形心位置对于分析物体的平衡和运动至关重要。
对于复杂的物体形状，求解形心位置可能需要更加复杂的数学方法，但其基本原理是相同的。
形心位置的求解是物体力学中的一个基础知识点，对于学习物理学的人来说具有重要意义。
材料力学考试典型题目
2
(4)
Fx 2 EIw Flx C1 (3) 2 2 3 Flx Fx EIw C 1x C 2 2 6 边界条件 x 0, w 0
x 0, w 0
(4)
将边界条件代入（3）（4）两式中,可得 C1 0 梁的转角方程和挠曲线方程分别为
C2 0
ql 2 q 3 EIw x x C 4 6
ql 3 q 4 EIw x x Cx D 12 24
边界条件x=0 和 x=l时, w
0
x
q
wmax B
梁的转角方程和挠曲线方程 A 分别为
A
l
B
q 2 3 3 (6lx 4 x l ) 24 EI qx w (2lx 2 x 3 l 3 ) 24 EI
FN 3 l3 -4 1.58 10 m uB ΔlCD Δl BC -0.3mm EA3
-4
Δl AD Δl AB Δl BC ΔlCD -0.47 10 mm
例题5 图示等直杆,已知直径d=40mm,a=400mm,材料的剪切弹性
模量G=80GPa，DB=1°. 试求：
x= l , M = 0
M 0
+
Mb l
梁上集中力偶作用处左、右两侧
FRA
A a
M
FRB
C b l B
横截面上的弯矩值(图)发生突变，其
突变值等于集中力偶矩的数值.此处 剪力图没有变化.
M /l
+ +
Mb l
Ma l
例题1 图示一抗弯刚度为 EI 的悬臂梁, 在自由端受一集中力 F 作用.试求梁的挠曲线方程和转角方程, 并确定其最大挠度 wmax 和最大转角 max w
《材料力学》弯曲计算-习题
②无均布载荷段弯矩图均为直线。有均布载荷段，弯矩图为
抛物线，其开口与均布载荷方向相同。
(3)弯矩、剪力、载荷集度的关系
①
M '(x) F S (x) F S'(x) q(x)
② FS=0的点是M图的取极值的点，FS=0的段M图是平行
于轴线的直线。
注意: 内力图上要注明控制面值、特殊点纵坐标值。
利用微分关系绘内力图
y
B截面 30.3 +
z
C截面 15.1 z
-
+
69
34.5
(d) 单位:MPa
Engineering Mechanics
四、弯曲 弯曲强度计算
例3 之二
解：（1）求截面形心轴，即中性轴z轴。
yC
( yi Ai ) Ai
170 30 170 30 200 (170 30)
2
2
17030 30 200
解：（1）外力分析，判变形。
10kN
50kN
(a) A
CD
B
z
4m
2m
4m
求得支坐反力
FA 26kN ,FB 34kN
荷载与梁轴垂直，梁将发
26kN 26 16
34kN
生平面弯曲。中性轴z过形心
+ (b)
与载荷垂直，沿水平方向。
FQ(kN)
104 136
34
（2）内力分析，判危险面。剪力
+
(c)
⑤解题步骤：
1）外力分析，判变形、中性轴，求截面的几何性质、支反力。 2）内力分析，判危险面，画剪力图、弯矩图（可只画弯矩图）
3）应力分析，判危险点。 4）强度计算。
工程力学---材料力学(第七章- 梁弯曲时位移计算与刚度设计)经典例题及详解
得： D 0
Pl 2 得： C 16
AC段梁的转角方程和挠曲线方程分别为：
P 2 2 (4 x l ) 16 EI Px y (4 x 2 3 l 2 ) 48 EI
y
P
B
A
x
l 2
C
l 2
x
最大转角和最大挠度分别为：
max A B
ymax y
q 7qa 8k 384 EI
3
q/2
B C
q/2
A B C
顺时针
q/2
例16：图示梁Ｂ处为弹性支座，弹簧刚 度
EI k 求C端挠度fC。 2a 3
q
A
EI k
B
C
2a
a
解：(1)梁不变形，仅弹簧变形引起的C点挠度为 4 3 qa 3qa B处反力=qa fC 1 2 k EI
q
B
x
l
由边界条件： x 0时，y 0
x l时，y 0
得：
ql 3 C , D0 24
梁的转角方程和挠曲线方程分别为：
y
q 2 3 3 (6lx 4 x l ) 24 EI
q
x
A qx y (2lx 2 x 3 l 3 ) 24 EI
ql 3 24 EI
A a a
q
B C
a
qa 12 EI
顺时针
3 3
P=qa
A B
P=qa
m=qɑ²/2
qa qa C B 6 EI 4 EI
4
顺时针
B
q
C
qa 5qa fC B a 8EI 24 EI
工程力学--材料力学(第五、六章)经典例题及讲解
P
A
0.5 m
C D
0.4 m 1m
B
20
40
解：C点的应力 σ C = E ε = 200 × 10 3 × 6 × 10 − 4
= 120M Pa
C截面的弯矩
M C = σ C W z = 640 N ⋅ m
由 M C = 0.5 R A = 0.5 × 0.4 P = 0.2 P = 640 N ⋅ m 得 P = 3.2kN
度减小一半时，从正应力强度条件考虑， 该梁的承载能力将是原来的多少倍？ 解： 由公式
σ max
M max M max = = 2 Wz bh 6
可以看出：该梁的承载能力将是原来的2 可以看出：该梁的承载能力将是原来的2倍。
例4：主梁AB，跨度为l，采用加副梁CD AB，跨度为l 采用加副梁CD
的方法提高承载能力， 的方法提高承载能力，若主梁和副梁材料 相同，截面尺寸相同， 相同，截面尺寸相同，则副梁的最佳长度 a为多少？ 为多少？
2 2
2
bh b( d − b ) Wz = = 6 6
2 2 2
∂ Wz d 2 b 2 = − =0 ∂b 6 2
d 由此得 b = 3
d
2 2
h
h = d −b =
h = 2 ≈3:2 b
2 d 3
b
例12:跨长l =2m的铸铁梁受力如图示,已知材料许用拉、 12:跨长l =2m的铸铁梁受力如图示 已知材料许用拉、 的铸铁梁受力如图示,
10 kN / m
200 2m 4m 100
10 kN / m
200
2m
Fs( kN ) 25 Fs(
45 kN
4m
100
材料力学例题
B
DC
1
3
2
A
B
DC
1
3
2
A
1 32
A
Δl1
Δl3
F
A'
A'
变形几何方程为 Δl1 Δl3 cos
物理方程为
Δl1
FN1l1 EA1
Δl3
FN3l cos
E3 A3
（3）补充方程
FN1
FN 3
EA E3 A3
cos2
（4）联立平衡方程与补充方程求解 B
DC
FN1 FN2
FN1 cos FN2 cos FN3 F 0
d
[] = 60MPa ,许用挤压应力为 [bs]= 200MPa .试校核销钉的
强度.
F
B
A
d1
d d1
F
解: （1）销钉受力如图b所示
F
剪切面
F
d
F
F
2
2
挤压面
d
B
A
d1
d d1
F
（2）校核剪切强度
剪切面
F
由截面法得两个面上的剪力
FS
F 2
d
剪切面积为 A d 2
4
FS 51MPa
3
2
1
l
a
a
B
C
A
F
解：（1） 平衡方程
Fx 0 Fx 0 l
3 a
2 a
1
Fy 0
B
C
A
FN1 FN2 FN3 F 0
MB 0
F FN3
FN2
FN1
3 a
2 a
1
工程力学材料力学-知识点-及典型例题
作出图中AB杆的受力图。
A处固定铰支座B处可动铰支座作出图中AB、AC杆及整体的受力图。
B、C光滑面约束A处铰链约束DE柔性约束作图示物系中各物体及整体的受力图。
AB杆：二力杆E处固定端C处铰链约束（1）运动效应：力使物体的机械运动状态发生变化的效应。
（2）变形效应：力使物体的形状发生和尺寸改变的效应。
3、力的三要素：力的大小、方向、作用点。
4、力的表示方法：（1）力是矢量，在图示力时，常用一带箭头的线段来表示力；（注意表明力的方向和力的作用点！）（2）在书写力时，力矢量用加黑的字母或大写字母上打一横线表示，如F、G、F1等等。
5、约束的概念：对物体的运动起限制作用的装置。
6、约束力（约束反力）：约束作用于被约束物体上的力。
约束力的方向总是与约束所能限制的运动方向相反。
约束力的作用点，在约束与被约束物体的接处7、主动力：使物体产生运动或运动趋势的力。
作用于被约束物体上的除约束力以外的其它力。
8、柔性约束：如绳索、链条、胶带等。
(1)约束的特点：只能限制物体原柔索伸长方向的运动。
(2)约束反力的特点：约束反力沿柔索的中心线作用，离开被约束物体。
（）9、光滑接触面：物体放置在光滑的地面或搁置在光滑的槽体内。
（1）约束的特点：两物体的接触表面上的摩擦力忽略不计，视为光滑接触面约束。
被约束的物体可以沿接触面滑动，但不能沿接触面的公法线方向压入接触面。
（2）约束反力的特点：光滑接触面的约束反力沿接触面的公法线，通过接触点，指向被约束物体。
（）10、铰链约束：两个带有圆孔的物体，用光滑的圆柱型销钉相连接。
约束反力的特点:是方向未定的一个力；一般用一对正交的力来表示，指向假定。
（）11、固定铰支座（1）约束的构造特点：把中间铰约束中的某一个构件换成支座，并与基础固定在一起，则构成了固定铰支座约束。
（2）约束反力的特点：固定铰支座的约束反力同中间铰的一样，也是方向未定的一个力；用一对正交的力来表示，指向假定。
()12、可动铰支座（1）约束的构造特点把固定铰支座的底部安放若干滚子，并与支撑连接则构成活动铰链支座约束，又称锟轴支座。
材料力学典型例题与详解(经典题目)
所以石柱体积为
V3
=
G ρ
=
[σ ]A(l) − ρ
F
= 1×106 Pa ×1.45 m 2 −1000 ×103 N = 18 m3 25 ×103 N/m3
三种情况下所需石料的体积比值为 24∶19.7∶18，或 1.33∶1.09∶1。 讨论：计算结果表明，采用等强度石柱时最节省材料，这是因为这种设计使得各截面的正应 力均达到许用应力，使材料得到充分利用。 3 滑轮结构如图，AB 杆为钢材，截面为圆形，直径 d = 20 mm ，许用应力 [σ ] = 160 MPa ，BC 杆为木材，截面为方形，边长 a = 60 mm ，许用应力 [σ c ] = 12 MPa 。试计算此结构的许用载
= 1.14 m 2
A
2=
F+ρ [σ ] −
A1 l1 ρ l2
=
1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m 1×106 N/m 2 − 25×103 N/m3 × 5 m
= 1.31 m 2
A
3=
F
+ ρA1l1 + ρA2l2 [σ ] − ρ l3
= 1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m + 25×103 N/m3 ×1.31 m 2 × 5 m = 1.49m 2 1×106 N/m 2 − 25 ×103 N/m3 × 5 m
解：1、计算 1-1 截面轴力：从 1-1 截面将杆截成两段，研究上半段。设截面上轴力为 FN1 ，
为压力（见图 b），则 FN1 应与该杆段所受外力平衡。杆段所受外力为杆段的自重，大
材料力学例题 workbench静力学
材料力学例题 workbench静力学下载温馨提示：该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。
文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, suchas educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!材料力学是研究材料在外力作用下的力学性能和变形规律的学科。
材料力学典型例题及解析 3.扭转典型习题解析
的切向内力所形成的力偶矩将由哪个力偶矩来平衡？
A M
B
A
M
B
C
z
D
A
(a)
C
dρ
ρ
R
(c)
D
题2图
BC Dx
(b)
θ dθ
(d)
解题分析：由切应力互等定理可知截面ABCD上的切向内力分布及其大小。该截面上切向内
力形成一个垂直向上的力偶矩。在图b中，左右两个横截面上的水平切向内力分量形成垂直
于截面ABCD的竖直向下的力偶矩，正好与截面ABCD上切向内力的合力偶矩平衡。
应力相等的条件下，试确定空心轴的外径，并比较实心轴和空心轴的重量。
解题分析：用空心轴代替实心轴，须保证二者强度相同。根据强度条件可求出D值，再用面
积比得出重量比。
解：1、根据两轴切应力相等的条件，确定空心轴外径
Tmax = Tmax = [τ ] WP实 WP空
πd 3 = πD3 (1 − α 4 ) 16 16
解得 D = 107.7 ×10−3 m = 107.7 mm
δ = D − d = 107.7mm −100mm = 3.85 mm
2
2
比较可知，两种设计的结果非常接近。
讨论: 当 δ ≤ R0 /10 时，即认为是薄壁圆管，可以直接使用薄壁管扭转公式。
2 图示受扭圆杆，沿平面ABCD截取下半部分为研究对象，如图b所示。试问截面ABCD上
4
即在强度相同条件下，空心轴可以节约近30％的材料。
讨论：在实际工程中常用空心圆轴代替实心圆轴，在保障安全运行的前提下，可以节约材料。
5 已知钻探机杆的外径D = 60 mm，内径d = 50 mm，功率P = 7.46 kW，转速n =180 r/min， 钻杆入土深度l = 40 m，G = 80 GPa，[τ]= 40 MPa。设土壤对钻杆的阻力是沿长度均匀分布 的，试求：(1) 单位长度上土壤对钻杆的阻力矩M；(2) 作钻杆的扭矩图，并进行强度校核； (3) 求A、B两截面相对扭转角。 解题分析：根据题意，为圆轴扭转问题。土壤对钻杆的阻力形成扭力矩作用在钻杆上，并沿
材料力学强校核例题
360
r3
M
2 D
T
2
W
804
32
M
2 D
T
2
d 3
d 49.3(mm)
[北科大题8-9] 一轴上装有两个圆轮，P、Q两力分别作用在
(P287)
两轮上并处于平衡状态。圆轴直径 d=110mm，
[]=60MPa，试按第四强度理论确定许可载荷。
1m 2m
A
C
1.5m
2m
Q
T
(N·m) 2.55P
Fz
A
B
A
C
D
x
B
z
38
Fz’
5
My
(N·m)
[北科大题8-10] (P287)
铁道路标的圆信号板，空心圆柱的外径D=60mm，板上作
用的最大风载的压强p=2kPa， []=60MPa，试按第三强度理
论确定空心柱的壁厚。
解：板上的压力
F 392.7(N)
危险截面在A截面
600
MF800 0.314(kNm)
Fy'
Mx
Mx
x
z
Fz'
y
Fy
Fy’
A
C
D
x
B
152
113
Mz
(N·m)
y
Fy Fz
Fy'
Mx
Mx
x
z
Fz'
Fz
A
B
A
C
D
x
B
z
38
Fz’
5
My
(N·m)
[北科大题8-1] AB梁，截面为100mm×100mm的正方形， (P285) P=3kN，试求最大拉应力和最大压应力。
材料力学力法典型例题解
l
q
RB
B
l q
X1
B Δ1F
B δ11
1
Example 2 .画图示钢架旳弯矩图，EI=const .
P
a
B
A
CP B
A
a
CP
a
B
C
B
C
X1
M
1
M
A
A
Pa
a
解 : 1）选图示相当系统（：一次超静定）
2）力法方程：
X 0
11 1
1P
3）利用图乘法求系数:
a
P
a
B
A
a
C
P
a
B
C
B
C
M
1
M
A
A
PPal
X1
2）力法方程
F
X 0
11 1
1P
3）图乘法求系数
11
2 EI
(1 2
aa
2 3
a)
2a3 3EI
1P
2 EI
(1 2
a
Fa
2 3
a)
a a
2Fa3
M
3EI
4）解得:
1
C
X1
1P
11
F
1
C
Fa
X1=1 Fa
F
1
M
F
F1 C
F
Example 1 . 求RB (EI=const.).
解: 1）选图示相当系统 （一次超静定）
B
CP
P
P
a
a
X1
a a
X1 1
A
Pa
解：1）选图示静定基及相当系统
工程力学材料力学_知识点_及典型例题
说明：一、二强度理论适用于脆断破坏，三、四强度理论适用于塑性破坏。上述四个强度理论的强度条件中，不等式右面部分就是相应的强度理论所对应的相当应力。
5、应力状态分类
（１）、只有一个主应力不为零的应力状态，称为单向应力状态。也称为简单应力状态。
（２）、两个主应力不为零的应力状态，称为二向应力状态。
（３）、三个主应力全不为零的应力状态，称为三向应力状态。
单向应力状态和二向应力状态又称为平面应力状态。
二向应力状态和三向应力状态又称为复杂应力状态。
6、平面应力状态任一斜截面上正应力和切应力公式为：
11、轴向拉压杆横截面上正应力的计算公式：
12、极限应力（σu）：材料失效时的应力。
塑性材料的极限应力是屈服极限（σs）；脆性材料的极限应力是强度极限（σb）。
13、许用应力[σ]：保证构件安全工作，材料许可承担的最大应力。
其中：n---安全系数
14、安全系数：为保证构件具有一定安全贮备而选取的一个大于1的系数。安全系数越大构件越安全，但越不经济。
知识点：
1、剪切的受力特点：构件受到一对大小相等、方向相反、作用线相隔很近的平行力作用。
2、剪切的变形特点：沿平行两力作用线之间的面发生相对错动。发生相对错动的面称为剪切面。
剪切变形是工程实际中常见的一种基本变形。常出现于联接件中，如：铆钉联接、螺栓联接、销钉联接、键联接、榫头联接等等。
材料力学典型例题及解析 7.应力应变状态典型习题解析
应力、应变状态分析典型习题解析1 已知矩形截面梁，某截面上的剪力F S =120 kN 及弯矩m kN 10⋅=M 。
绘出表示1、2、3及4点应力状态的微体，并求出各点的主应力。
b = 60 mm ，h = 100 mm 。
解题分析： 从图中可分析1、4点是单向应力状态，2点在中性轴上为纯剪切应力状态，31取平行和垂直与梁横截面的六个平面，构成微体。
则各点处的应力状态如图示。
2、 梁截面惯性矩为 点微体上既有正应力又有切应力。
解：、画各点处微体的应力状态图计算各点处主应力4843333m 1050012m 10100(106012−−−×=×××==）bh I z1点处弯曲正应力（压应力）MPa 100Pa 10100m 10500m1050m N 101064833−=×=×××⋅×==−−zI My σ 1点为单向压缩受力状态，所以 021==σσ，MPa 1003−=σ 2点为纯剪切应力状态， MPa 30Pa 1030m10100602N 1012036263=×=×××××=−τ（向下）容易得到，MPa 301=σ，02=σ，MPa 303−=σ 3点为一般平面应力状态弯曲正应力MPa 50Pa 1050m 10500m 1025m N 101064833=×=×××⋅×==−−zI My σ 弯曲切应力F S =120 kN题图1MPa 5.22Pa 1050.22m10500m 1060m 105.372560N 101206483393*S =×=××××××××==−−−z z bI S F τ MPa 6.8MPa 6.58Pa)105.22()2Pa 1050(2Pa 1050)2(22626622min max −=×+×±×=+−±+=xy x y x τσσσσσσ所以 MPa 6.581=σ，02=σ，MPa 6.83−=σ4点为单向拉伸应力状态，拉伸正应力的大小与1点相等。
材料力学经典例题
Ip R
称为抗扭截面 系数(模量 模量)， 系数 模量 ， 单位： 单位：mm3。
Nm mm
3
MT = W p
=10 MPa
3
五、Ip和Wp公式
π D4
32
工程上采用空心截面构件：提高强度， 工程上采用空心截面构件：提高强度，节约 材料， 材料，重量轻 结构轻便，应用广泛。 结构轻便，应用广泛。
Ip =
例题2.4 例题2.4 油缸盖与缸体采用6个螺栓连接。已知油缸内径 油缸盖与缸体采用6个螺栓连接。 D=350mm，油压p=1MPa 螺栓许用应力[σ]=40MPa p=1MPa。 [σ]=40MPa， D=350mm，油压p=1MPa。螺栓许用应力[σ]=40MPa， 求螺栓的内径。 求螺栓的内径。 解： 油缸盖受到的力 F = D 2 p
目录
FN 1 = 2 F1 ≤ [σ ] A1
失效、 §2.7 失效、安全因数和强度计算
3、根据水平杆的强度，求许可载荷 根据水平杆的强度， 查表得水平杆AB的面积为A2=2×12.74cm2 =2×
FN 2 = − FN 1 cos α = − 3F
FN 2 = 3F2 ≤ [σ ] A2
FN 1
（kN·m） ）
MT
2. 校核强度
MT1 10×103 ×16 ×103 = 50.9MPa＜ [τ] (τmax )1 = W = π×1003 p1
MT2 3×103 ×16 τmax ) 2 = = ×103 = 70.7 MPa ＞ [τ] ( Wp2 π×603
MT1 180 10×103 ×32 180 ⋅ = ⋅ = 0.7 o m ＜[θ] θ1 = GIp1 π 80×109 ×π×1004 ×10−12 π MT2 180 3×103 ×32 3 180 ⋅ = ×10 ⋅ = 1.7 o m ＞[θ] θ2 = GIp2 π 80×π×604 π
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Ⅲ
FRD
Ⅱ
F3
DⅢ l3
C
Ⅱ
B
l2
（2） 杆的最大正应力max
AB段 AB
FN1 176.8MPa A1
()
BC段 BC
FN2 A2
74.6MPa
()
DC段 DC
FN3 A3
110.5MPa
()
Ⅰ
F2
F1
ⅠA
l1
FN1 =20kN （+） FN2 =-15kN ( - ) FN3 =- 50kN ( - )
max = 176.8MPa
发生在AB段.
Ⅲ
FRD
DⅢ l3
Ⅱ
F3
C
Ⅱ
l2
Ⅰ
F2
F1
B
A Ⅰ
l1
（3） B截面的位移及AD杆的变形
Δl AB
FN1l1 EA1
2.53 10-4m
ΔlBC
FN2l2 EA2
1.42 10-4m
ΔlCD
FN 3 l3 EA3
1.58 10-4m
uB ΔlCD ΔlBC -0.3mm
FN1
FN 3
EA E3 A3
cos2
F
FN3 1 2
EA
cos3
E3 A3
FN1
FN 2
2 cos
F E
E3 A3
A cos2
Δl3
1
3
2
A
1 3F 2
A
Δl1
A'
例题10 图示平行杆系1、2、3 悬吊着刚性横梁AB，在 横梁上作用着荷载F。各杆的截面积、长度、弹性模量 均相同，分别为A，l，E.试求三杆的轴力 FN1, FN2, FN3.
B
DC
1
3
2
A
B
DC
1
3
2
A
1 32
A
Δl1
Δl3
F
A'
A'
变形几何方程为 Δl1 Δl3 cos
物理方程为
Δl1
FN1l1 EA1
Δl3
FN3l cos
E3 A3
（3）补充方程
FN1
FN 3
EA E3 A3
cos2
（4）联立平衡方程与补充方程求解 B
DC
FN1 FN2
FN1 cos FN2 cos FN3 F 0
F
Abs
π(D2 4
d2)
挤压面
例15 冲床的最大冲压力F=400kN,冲头材料的许用压
应力[]=440MPa,钢板的剪切强度极限u=360MPa,试 求冲头能冲剪的最小孔径d和最大的钢板厚度 d .
F
钢板
冲头
d
冲模
F
钢板
F
冲模
F
冲头
d
剪切面
x
（4）平衡方程 FN1 FN2
FN3 FN1 FN2 0 联立平衡方程与补充方程求解,即可得装配内力， 进而求出装配应力.
例题12 图示等直杆 AB 的两端分别与刚性支 承连结.设两支承的距离（即杆长）为 l,杆的 横截面面积为 A,材料的弹性模量为 E,线膨
胀系数为 .试求温度升高 T 时杆内的温
AA
Δl1
cos
Fl
2EAcos2
1.293mm()
例题7 图示三角形架AB和AC 杆的弹性模量 E=200GPa A1=2172mm2，A2=2548mm2. 求:F=130kN时节点A的位移.
解：(1)由平衡方程得两杆的 轴力
FN1 2F
FN2 1.732F
1 杆受拉,2 杆受压
（2）两杆的变形
例题4 刚性杆ACB有圆杆CD悬挂在C点,B端作用集中力
F=25kN,已知CD杆的直径d=20mm,许用应力
[]=160MPa，试校核CD杆的强度,并求：
（1）结构的许可荷载[F];
D
（2）若F=50kN,设计CD杆的直径.
F
A
C B
2a
a
解：
（1） 求CD杆的内力
MA 0
FNCD
3F 2
A
FNCD A
B
2m
1
30°
C2
A2 l2
Al1 A1
A2 A
F
A'
l 2
30°
l1 A1
A A3 ( AA2 )2 ( A2 A3 )2 3.797mm 30°
A3
例题8 设横梁ABCD为刚梁，钢索的横截面面积为
76.36mm²的钢索绕过无摩擦的滑轮。设 P=20kN， E=177GPa，试求钢索的应力和 C点的垂直位移。
B1
1
C1
A1
2
l
C1 3
B
C
a
A
a
e C'
B1
1
C1
A1
2
l1 = l2
B C
A
l C1
3
l3 e
C''
（1）变形几何方程为 Δl1 Δl3 Δe
（2）物理方程
Δl1
FN1l1 EA
Δl3
FN3l E3 A3
FN1
B'
（3）补充方程
FN3l Δe FN1l
E3 A3
EA
FN3 C' FN2 A'
[ ] [ ]
d 2 3F / 2
4 [ ]
FRAy FRAx
d=24.4mm 取d=25mm A
D
F
C B
2a
a
FNCD
F
C
B
例题5 图示为一变截面圆杆ABCD.已知F1=20kN，
F2=35kN，F3=35kN. l1=l3=300mm，l2=400mm.d1=12mm，
d2=16mm，d3=24mm. 弹性模量为 E=210GPa. 试求： （1） Ⅰ-Ⅰ、Ⅱ-Ⅱ、III-III截面的轴力并作轴力图
d
[] = 60MPa ,许用挤压应力为 [bs]= 200MPa .试校核销钉的
强度.
F
B
A
d1
d d1
F
解: （1）销钉受力如图b所示
F
剪切面
F
d
F
F
2
2
挤压面
d
B
A
d1
d d1
F
（2）校核剪切强度
剪切面
F
由截面法得两个面上的剪力
FS
F 2
d
剪切面积为 A d 2
4
FS 51MPa
3F / 2 d 2 / 4
119MPa
[ ]
（2）结构的许可荷载[F]
由
CD
FNCD A
[ ]
FRAy FRAx
A
D
F
C B
2a
a
FNCD
F
C
B
得
FNCD
[
]A
3F 2
[F]=33.5kN
（3） 若F=50kN，设计CD杆的直径
由
CD
FNCD A
[ ]
A
得 A FNCD 3F / 2
Ⅲ
FRD
DⅢ l3
Ⅱ
F3
C
Ⅱ
l2
FRD
FN3 FN2
Ⅰ
F2
F1
B
ⅠA
l1
F1 F2
FN3 FRD 0 FN3 50kN ()
F1 F2 FN2 0 FN2 15kN ()
Ⅲ
FRD
DⅢ l3
-
50
Ⅱ
F3
C
Ⅱ
l2
15
Ⅰ
F2
F1
B
ⅠA
l1
20
+
FN1 =20kN （+） FN2 =-15kN （-） FN3 =- 50kN （-）
钢索
A
B 60° 60° D
800 400C 400
P
TT
A
BC D
P
解：能量法：（外力功等于变形能 1）求钢索内力：以ABD为对象：
mA T sin 60 0.8 1.2P 1.6T sin 60 0
T P / 3 11.55KN
2) 钢索的应力为：
T 11.55 109 151MPa
A 76.36 3) C点的位移为：
1
T2L
W 2 Pc
U 2EA
W U
T 2L 11.552 1.6 c PEA 20177 76.36 0.79mm
三、一般超静定问题举例 (Examples for general statically
indeterminate problem)
例题9 设 1，2，3 三杆用铰链连结如图所 示，l1 = l2 = l，A1 = A2 = A， E1 = E2 = E，3杆 的长度 l3 ,横截面积 A3 ,弹性模量E3 。试求 在沿铅垂方向的外力F作用下各杆的轴力.
28.5MPa
（3）校核挤压强度
bs
F Abs
F lh 2
57 103 100 6106
95MPa
bs
综上，键满足强度要求.
例题14 一销钉连接如图所示， 已知外力 F=18kN,被连接的构件
A 和 B 的厚度分别为 d=8mm 和 d1=5mm ,销钉直径 d=15mm ,
销钉材料的许用切应力为
3
2
1
l
a
a
B
C
A
F
解：（1） 平衡方程