高考数学答题模板总结
【高考宝典】高考数学解答题常考公式及答题模板
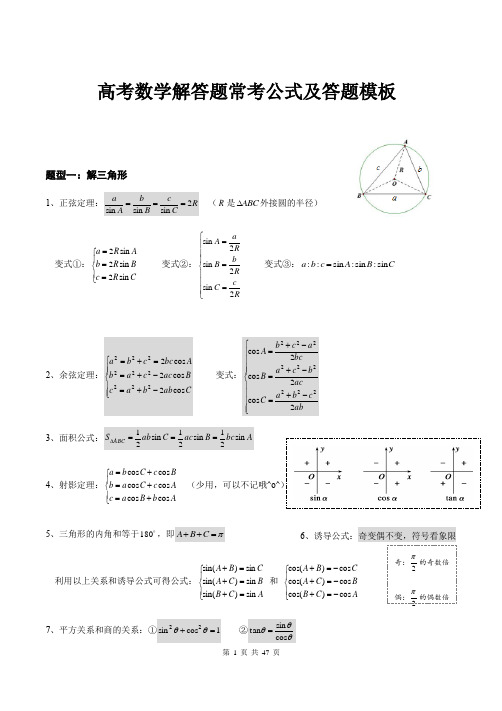
高考数学解答题常考公式及答题模板题型一:解三角形1、正弦定理:R CcB b A a 2sin sin sin === (R 是ABC ∆外接圆的半径) 变式①:⎪⎩⎪⎨⎧===C R c B R b A R a sin 2sin 2sin 2 变式②:⎪⎪⎪⎩⎪⎪⎪⎨⎧===Rc C R bB R a A 2sin 2sin 2sin 变式③:C B A c b a sin :sin :sin ::=2、余弦定理:⎪⎪⎩⎪⎪⎨⎧-+=-+==+=C ab b a c B ac c a b A bc c b a cos 2cos 2cos 2222222222 变式:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-+=-+=-+=ab c b a C ac b c a B bc a c b A 2cos 2cos 2cos 2222222223、面积公式:A bc B ac C ab S ABC sin 21sin 21sin 21===∆ 4、射影定理:⎪⎩⎪⎨⎧+=+=+=A b B a c A c C a b Bc C b a cos cos cos cos cos cos (少用,可以不记哦^o^)5、三角形的内角和等于 180,即π=++C B A6、诱导公式:奇变偶不变,符号看象限利用以上关系和诱导公式可得公式:⎪⎩⎪⎨⎧=+=+=+A C B B C A C B A sin )sin(sin )sin(sin )sin( 和⎪⎩⎪⎨⎧-=+-=+-=+A C B B C A CB A cos )cos(cos )cos(cos )cos(7、平方关系和商的关系:①1cos sin 22=+θθ ②θθθcos sin tan = 奇:2π的奇数倍 偶:2π的偶数倍8、二倍角公式:①θθθcos sin 22sin =②θθθθθ2222sin 211cos 2sin cos 2cos -=-=-= ⇒降幂公式:22cos 1cos 2θθ+=,22cos 1sin 2θθ-= ③θθθ2tan 1tan 22tan -=8、和、差角公式:①⎩⎨⎧-=-+=+βαβαβαβαβαβαsin cos cos sin )sin(sin cos cos sin )sin(②⎩⎨⎧+=--=+βαβαβαβαβαβαsin sin cos cos cos(sin sin cos cos cos())③⎪⎪⎩⎪⎪⎨⎧+-=--+=+βαβαβαβαβαβαtan tan 1tan tan )tan(tan tan 1tan tan )tan( 9、基本不等式:①2ba ab +≤),(+∈R b a ②22⎪⎭⎫ ⎝⎛+≤b a ab ),(+∈R b a ③222b a ab +≤ ),(R b a ∈注意:基本不等式一般在求取值范围或最值问题中用到,比如求ABC ∆面积的最大值时。
高考数学各科答题格式范文推荐11篇

高考数学各科答题格式范文推荐11篇(经典版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的经典范文,如工作总结、工作计划、合同协议、条据文书、策划方案、句子大全、作文大全、诗词歌赋、教案资料、其他范文等等,想了解不同范文格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample essays for everyone, such as work summaries, work plans, contract agreements, doctrinal documents, planning plans, complete sentences, complete compositions, poems, songs, teaching materials, and other sample essays. If you want to learn about different sample formats and writing methods, please stay tuned!高考数学各科答题格式范文推荐11篇高考数学各科答题格式范文第一篇进入考试先审题考试开始后,很多学生喜欢奋笔疾书;但切记:审题一定要仔细,一定要慢。
高考数学答题万能模板

高考数学答题万能模板一、问题分析在高考数学答题过程中,我们常常遇到各种类型的题目,而每个题目又有不同的解题思路和方法。
为了提高答题效率和准确性,我们可以使用以下的万能模板来辅助解答。
二、万能模板1. 解决方案模板当遇到复杂的数学问题时,我们可以使用以下的解决方案模板来有条理地解答问题:- 问题陈述:清晰地陈述题目所给的条件和要求。
问题陈述:清晰地陈述题目所给的条件和要求。
- 思路分析:分析问题的关键点和难点,明确解题思路。
思路分析:分析问题的关键点和难点,明确解题思路。
- 公式运用:根据问题所涉及的数学知识,选择适当的公式或定理进行运用。
公式运用:根据问题所涉及的数学知识,选择适当的公式或定理进行运用。
- 计算过程:按照步骤进行计算,注意每一步的细节和注意事项。
计算过程:按照步骤进行计算,注意每一步的细节和注意事项。
- 最终结果:得出最终的答案,并且注意核对答案的有效性和合理性。
最终结果:得出最终的答案,并且注意核对答案的有效性和合理性。
2. 图形解析模板当遇到涉及图形的题目时,我们可以使用以下的图形解析模板来进行问题分析和解答:- 给定图形的特点描述。
- 根据特点分析,确定所需解题的步骤和方法。
- 运用几何相关定理和公式,进行计算和推理。
- 最后给出答案及解答的过程。
3. 数据分析模板当遇到涉及数据分析的题目时,我们可以使用以下的数据分析模板来进行问题分析和解答:- 给定数据的描述和要求。
- 理清问题的思路和逻辑,确定解题的步骤。
- 运用统计学知识和相关公式,进行数据分析和计算。
- 最后给出答案及解答的过程。
三、总结高考数学答题万能模板可以提供一个结构化的解题方法和思路,帮助我们更有效地解答各种类型的数学题目。
在使用模板时,我们要根据实际题目的要求和题型,灵活运用模板的内容,以达到解题的目的。
希望这份高考数学答题万能模板能对您有所帮助!。
高考数学高考数学题型(推荐5篇)

高考数学高考数学题型(推荐5篇)1.高考数学高考数学题型第1篇直接法、特殊化法、数形结合法、等价转化法。
【解答题答题模板】专题一、三角变换与三角函数的性质问题1、解题路线图①不同角化同角②降幂扩角③化f(x)=Asin(ωx+φ)+h④结合性质求解。
2、构建答题模板①化简:三角函数式的化简,一般化成y=Asin(ωx+φ)+h的形式,即化为“一角、一次、一函数”的形式。
②整体代换:将ωx+φ看作一个整体,利用y=sin x,y=cos x的性质确定条件。
③求解:利用ωx+φ的范围求条件解得函数y=Asin(ωx+φ)+h的性质,写出结果。
④反思:反思回顾,查看关键点,易错点,对结果进行估算,检查规范性。
专题二、解三角形问题1、解题路线图(1) ①化简变形;②用余弦定理转化为边的关系;③变形证明。
(2) ①用余弦定理表示角;②用基本不等式求范围;③确定角的取值范围。
2、构建答题模板①定条件:即确定三角形中的已知和所求,在图形中标注出来,然后确定转化的方向。
②定工具:即根据条件和所求,合理选择转化的工具,实施边角之间的互化。
③求结果。
④再反思:在实施边角互化的时候应注意转化的方向,一般有两种思路:一是全部转化为边之间的关系;二是全部转化为角之间的关系,然后进行恒等变形。
专题三、数列的通项、求和问题1、解题路线图①先求某一项,或者找到数列的关系式。
②求通项公式。
③求数列和通式。
2、构建答题模板①找递推:根据已知条件确定数列相邻两项之间的关系,即找数列的递推公式。
②求通项:根据数列递推公式转化为等差或等比数列求通项公式,或利用累加法或累乘法求通项公式。
③定方法:根据数列表达式的结构特征确定求和方法(如公式法、裂项相消法、错位相减法、分组法等)。
④写步骤:规范写出求和步骤。
⑤再反思:反思回顾,查看关键点、易错点及解题规范。
专题四、利用空间向量求角问题1、解题路线图①建立坐标系,并用坐标来表示向量。
②空间向量的坐标运算。
关于高考数学答题模板及技巧有哪些.doc

关于高考数学答题模板及技巧有哪些高中数学答题模板整理1、高考数学选择填空题答题方法高考数学选择题十大速解方法:排除法、增加条件法、以小见大法、极限法、关键点法、对称法、小结论法、归纳法、感觉法、分析选项法。
填空题四大速解方法:直接法、特殊化法、数形结合法、等价转化法。
2、高中数学解答题答题技巧与模板1)三角变换与三角函数的性质问题一、解题路线图①不同角化同角②降幂扩角③化f(x)=Asin(ωx+φ)+h④结合性质求解。
二、构建答题模板①化简:三角函数式的化简,一般化成y=Asin(ωx+φ)+h的形式,即化为“一角、一次、一函数”的形式。
②整体代换:将ωx+φ看作一个整体,利用y=sinx,y=cosx的性质确定条件。
③求解:利用ωx+φ的范围求条件解得函数y=Asin(ωx+φ)+h的性质,写出结果。
④反思:反思回顾,查看关键点,易错点,对结果进行估算,检查规范性。
2)高中数学解三角形问题一、解题路线图①化简变形;②用余弦定理转化为边的关系;③变形证明。
①用余弦定理表示角;②用基本不等式求范围;③确定角的取值范围。
二、构建答题模板①定条件:即确定三角形中的已知和所求,在图形中标注出来,然后确定转化的方向。
②定工具:即根据条件和所求,合理选择转化的工具,实施边角之间的互化。
③求结果。
④再反思:在实施边角互化的时候应注意转化的方向,一般有两种思路:一是全部转化为边之间的关系;二是全部转化为角之间的关系,然后进行恒等变形。
3)数列的通项、求和问题一、数学解题路线图①先求某一项,或者找到数列的关系式。
②求通项公式。
③求数列和通式。
二、构建答题模板①找递推:根据已知条件确定数列相邻两项之间的关系,即找数列的递推公式。
②求通项:根据数列递推公式转化为等差或等比数列求通项公式,或利用累加法或累乘法求通项公式。
③定方法:根据数列表达式的结构特征确定求和方法(如公式法、裂项相消法、错位相减法、分组法等)。
④写步骤:规范写出求和步骤。
高考数学高分答题模板

高考数学高分答题模板高考数学答题黄金模板1选择填空题易错点归纳:九大模块易混淆难经历考点分析,如概率和频率概念混淆、数列求和公式经历错误等,强化基础知识点经历,躲开因为知识点失误造成的客观性解题错误。
针对审题、解题思路不严谨如集合题型未考虑空集情形、函数问题未考虑定义域等主观性因素造成的失误进行专项训练。
答题方法:选择题十大速解方法:排除法、增加条件法、以小见大法、极限法、关键点法、对称法、小结论法、归纳法、感受法、分析选项法;填空题四大速解方法:直截了当法、专门化法、数形结合法、等价转化法。
2突破解答题三角函数:考点题型归纳:通常考察正弦、余弦公式、三角形差不多性质、三种差不多三角函数之间的转化与角度的化简。
通常题型:Q1:带入求值,化简等;Q2:利用正弦、余弦公式转化,依照角度取值范畴确定正负号,求某角某边等。
答题方法:七大解题思想:如巧用数形结合、化归转化等方法解题。
概率统计:考点题型归纳:通常考察排列、组合运用分布列排列、期望运算等知识点。
通常题型:Q1:求某条件的概率;Q2:利用Q1所求的概率,求分布列以及期望。
答题方法:如互斥时刻和对立事件的巧妙运用等数列:考点题型归纳:通常考察通项公式和求和公式的运用。
通常题型:Q1:求某一项,求通项公式,求数列和通式;Q2:证明,求新数列第N项和,绝对值比较等。
答题方法:如通项公式三大解法:和作差,积作商,找规律叠加化简等;求和公式三大解法:直截了当公式,错位相减,分组求和等。
立体几何:通常题型:Q1:证明线面,线线,面面垂直等;Q2:求距离,求二面角等。
答题方法:如直截了当逻辑法:面面,线面,线面垂直平行等性质的运用;空间向量法:线面垂直,平行时用向量如何表达,公式;等面积、体积法:找到最方便运算的图形。
解析几何:考点题型归纳:椭圆,双曲线,抛物线方程的长短轴性质,离心率等,直线与圆锥曲线联立,求解某点,证明某直线与圆锥曲线的关系等。
通常题型:Q1:求圆锥曲线方程式;Q2:证明某点在某线某面上,求位置关系,求直线方程等。
高考数学阅读理解常见题型及答题模板

高考数学阅读理解常见题型及答题模板
一、选择题型
1. 单选题
在阅读理解模块中,单选题是十分常见的题型。
在解答单选题时,要注意分析用户提供的问题和提取关键信息,再利用数学知识
结合选项进行判断。
同时查看其他选项和题干,以免被选项误导。
答题模板:根据题目中要求,提取关键信息和条件,代入公式
求解即可。
2. 多选题
多选题要求解答者根据题目提供的条件判断每个选项是否正确,是一种比较有难度的题型。
解答多选题,需要较高的数理思维和定
量分析能力,要仔细查看每个选项,对于条件的掌握和理解要更加
深入,因为每一项都可能是正确或者错误的。
答题模板:阅读题目同时查看各选项条件是否满足,若条件全
部满足,则该选项可勾选。
二、常见问题
1. 理解问题
在阅读理解中,提供的信息和条件往往具有一定的复杂性,考
生需要全面理解题目及各项条件,以正确解答问题。
在此过程中需
要广泛应用数学知识和技能进行综合分析、解决问题。
同时要注意
题目中的限制条件和变量、方程等数学运算的表达方式。
答题模板:全面理解题目及各项条件,运用数学知识进行分析、解题。
2. 计算方法
在阅读理解题目中经常需要进行计算,需要熟悉各种计算方法
及速算技巧,并能快速准确地进行计算。
答题模板:熟悉各种计算方法并掌握快速计算技巧。
三、总结
阅读理解作为数学高考的重要组成部分,考生需要熟练掌握各
种题型和答题技巧,建立正确的数学思维方式和适应高考的解题风格,最终提高数学分数,顺利考取理想的(大学)录取分数线。
高考数学解答题常考公式及答题模板(Word版,28页,免费下载)

第 1 页 共 24 页高考数学解答题常考公式及答题模板题型一:解三角形1、正弦定理:R CcB b A a 2sin sin sin === (R 是ABC ∆外接圆的半径) 变式①:⎪⎩⎪⎨⎧===C R c B R b A R a sin 2sin 2sin 2 变式②:⎪⎪⎪⎩⎪⎪⎪⎨⎧===Rc C R bB R a A 2sin 2sin 2sin 变式③:C B A c b a sin :sin :sin ::=2、余弦定理:⎪⎪⎩⎪⎪⎨⎧-+=-+==+=C ab b a c B ac c a b A bc c b a cos 2cos 2cos 2222222222 变式:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-+=-+=-+=ab c b a C ac b c a B bc a c b A 2cos 2cos 2cos 2222222223、面积公式:A bc B ac C ab S ABC sin 21sin 21sin 21===∆ 4、射影定理:⎪⎩⎪⎨⎧+=+=+=A b B a c A c C a b Bc C b a cos cos cos cos cos cos (少用,可以不记哦^o^)5、三角形的内角和等于 180,即π=++C B A6、诱导公式:奇变偶不变,符号看象限利用以上关系和诱导公式可得公式:⎪⎩⎪⎨⎧=+=+=+A C B B C A C B A sin )sin(sin )sin(sin )sin( 和⎪⎩⎪⎨⎧-=+-=+-=+A C B B C A CB A cos )cos(cos )cos(cos )cos(7、平方关系和商的关系:①1cos sin 22=+θθ ②θθθcos sin tan = 8、二倍角公式:①θθθcos sin 22sin =②θθθθθ2222sin 211cos 2sin cos 2cos -=-=-= ⇒降幂公式:22cos 1cos 2θθ+=,22cos 1sin 2θθ-= ③θθθ2tan 1tan 22tan -=8、和、差角公式:①⎩⎨⎧-=-+=+βαβαβαβαβαβαsin cos cos sin )sin(sin cos cos sin )sin(②⎩⎨⎧+=--=+βαβαβαβαβαβαsin sin cos cos cos(sin sin cos cos cos())③⎪⎪⎩⎪⎪⎨⎧+-=--+=+βαβαβαβαβαβαtan tan 1tan tan )tan(tan tan 1tan tan )tan( 9、基本不等式:①2ba ab +≤),(+∈R b a ②22⎪⎭⎫ ⎝⎛+≤b a ab ),(+∈R b a ③222b a ab +≤ ),(R b a ∈奇:2π的奇数倍 偶:2π的偶数倍第 2 页 共 24 页注意:基本不等式一般在求取值范围或最值问题中用到,比如求ABC ∆面积的最大值时。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学答题模板总结
1易错点归纳:
九大模块易混淆难记忆考点分析,如概率和频率概念混淆、数列求和公式记忆错误等,强化基础知识点记忆,避开因为知识点失误造成的客观性解题错误。
针对审题、解题思路不严谨如集合题型未考虑空集情况、函数问题未考虑定义域等主
观性因素造成的失误进行专项训练。
答题方法设计:
选择题十大速解方法:排除法、增加条件法、以小见大法、极限法、关键点法、对称法、小结论法、归纳法、感觉法、分析选项法;
填空题四大速解方法:直接法、特殊化法、数形结合法、等价转化法。
⑵三角函数
考点题型归纳:
通常考察正弦、余弦公式、三角形基本性质、三种基本三角函数之间的转化与角度的
化简。
通常题型:
Q1:带入求值,化简等;
Q2:利用正弦、余弦公式转化,根据角度取值范围确定正负号,求某角某边等。
答题方法设计:
七大解题思想:如巧用数形结合、化归转化等方法解题。
⑶概率统计
考点题型归纳:
通常考察排列、组合运用分布列罗列、期望计算等知识点。
通常题型
Q1:求某条件的概率;
Q2:利用Q1所求的概率,求分布列以及期望。
答题方法设计:
如互斥时间和对立事件的巧妙运用等
⑷数列
考点提醒归纳:
通常考察通项公式和求和公式的运用。
通常题型
Q1:求某一项,求通项公式,求数列和通式;
Q2:证明,求新数列第N项和,绝对值比较等。
答题方法设计:
如通项公式三大解法:和作差,积作商,找规律叠加化简等;
求和公式三大解法:直接公式,错位相减,分组求和等。
⑸立体几何
考点题型归纳:
通常题型
Q1:证明线面,线线,面面垂直等;
Q2:求距离,求二面角等。
答题方法设计:
如直接逻辑法:面面,线面,线面垂直平行等性质的运用;
空间向量法:线面垂直,平行时用向量如何表达,公式;
等面积、体积法:找到最方便计算的图形。
⑹解析几何
考点题型归纳:
椭圆,双曲线,抛物线方程的长短轴性质,离心率等,直线与圆锥曲线联立,求解某点,证明某直线与圆锥曲线的关系等。
通常题型
Q1:求圆锥曲线方程式;
Q2:证明某点在某线某面上,求位置关系,求直线方程等。
答题模板设计:
四步理清解题思路。
⑺导数函数
考点提醒归纳:
题型通常为求函数表达式,求某函数值,求某常数值,求单调区间,最大最小值,证明等。
答题模板设计:
七步理清解题思路。
考点提醒归纳:
压轴题通常为解析几何和函数导数的题型,难度较大。
答题方法设计:
课程主要讲解解答压轴题的解题思路,如复杂问题简单化、运动问题静止化、一般问题特殊化等思维方法,以求突破。
感谢您的阅读,祝您生活愉快。
