导线测量对贯通影响的误差预计新公式(精)
5.1隧道贯通误差(精)

mh M L
式中,M为每千米水准测量的偶然中误差,以mm计 ;L为洞外或洞内两开挖洞口间高程路线长度的公里数。
八、案例 1.平面控制测量案例
某铁路隧道为直线隧道,设计长度为L = 1136. 29m,洞外平
面控制设计为单导线,其布设如图。试确定测量等级并判定该设计 方案能否满足贯通的精度要求。
为四等水准测量,布设六个临时水准点。各测段水准路线长度、往
返测高差观测值及高程计算列于表中,试计算每千米水准测量高差 中数的偶然中误差mΔ,并估算mΔh。
往返测高差观测值及高程计算
点 号 实 测 高 往 测 -2.345 -6.299 P1 -19.326 P2 23.632 P3 17.423 P4 -27.576 P5 -9.048 P6 21.072 BM24-1 BM24 ∑ -1.288 -3.755 1.287 3.756 -1.2875 -3.7555 -21.074 21.073 567.292 566.0045 定测为 66.003m 断高为 0.0015m 9.045 -9.0465 546.219 27.580 -27.578 555.2655 -17.427 17.425 582.8435 -23.626 23.629 565.4185 19.322 -19.324 541.7895 差( m) 返 测 2.347 6.302 平 均 高 差 ( m) -2.346 -6.3005 561.1135 高 程 ( m) 569.760 567.414 备 注 BM23 BM23-1 起算高程
D' E' B C A Y F' X
贯通面
D E B' C' F
(1)估算数据图解 ①A、F为导线的始、终点,亦为隧道洞口控制点。 ②以洞外导线的始点A做为坐标系原点,以隧道中线按里程 增加方向为X 轴正向,建立测量坐标系。在地形图上,各导线点
贯通误差预计例子

10.2 5号井与新建立井间巷道贯通偏差预计1.贯通相遇点k 横向(预计图中kx '方向)偏差预计 [1]GPS E 级网测量误差引起的贯通相遇点k 在kx '方向上的偏差GPS 测量误差对k 点横向偏差的影响由两部分误差引起,一是新建立井近井点ZG1点与5号井近井点澡堂点在kx '方向上的相对点位误差,二是ZG1-ZG2边、澡堂-队部楼边方位角相对中误差。
(1)新建立井近井点ZG1点与5号井近井点澡堂点的相对点位误差计算取GPS 网两端近井点ZG1点-澡堂点基线长度中误差的余弦项(kx '方向)分量做两点的点位相对误差: mmD b a M ZG 7.15081cos )110.101(5cos )(22221--±='*⨯+='*⨯+= α澡堂本次观测使用的GPS 接收机标称精度:=+bD a 5mm+1×10-6²D其中:ZG1点-澡堂点基线长(设计值)D=10.110km ZG1点-澡堂点基线在预计坐标系中的方位角81º05´ (2)两近井点后视方向ZG1点—ZG2点、澡堂点—队部楼点方位角相对中误差计算1)计算澡堂点—队部楼方位角中误差澡堂点—队部楼点基线长度中误差:mm D b a 00.5)156.01(5)(22221±=⨯+=⨯+=σ引起澡堂点—队部楼点方位误差的分量:mm d 1.177cos 0.5cos 111±=⨯='⨯= ασ 澡堂点—队部楼点方位误差4.11560001.101''±=+=+''=ρρD d c m 其中:c ''接收机方位固定误差(忽略)澡堂点—队部楼点基线长D=0.156km=156000mm 澡堂点—队部楼点在预计坐标系中的方位角 771='α 2)计算ZG1点—ZG2点方位角中误差 计算ZG1点—ZG2点基线长度中误差:mm D b a 0.5)814.01(5)(22222±=⨯+=⨯+=σ引起ZG1点—ZG2点方位误差的分量:mm d 6.083cos 0.5cos 222±=⨯='⨯= ασ ZG1点—ZG2点方位误差2.08140006.00222''±=''+=+''=ρρD d c m 其中:c ''接收机方位固定误差(忽略)ZG1点—ZG2点基线长D=0.814km=814000mm ZG1点—ZG2点在预计坐标系中的方位角 831='α 3)考虑最不利情况时两边的方位角相对误差为6.121''±=+=∆m m M α(3)地面GPS 网测量误差引起的K 点横向误差m R R M M M ZG ZG G 051.0)2()2(2122221-±=++±=∆澡堂澡堂ρα式中:9235m =澡堂R ;740m 1=ZG R ,分别为两近井点与贯通相遇点K 的连线在贯通预计坐标系Y 方向上的分量。
(贯通误差预计用)

225.104 621.2324
693.303 309.7826
945.954 225.7104
704.695 804.3179
161.63 843.6319
547.916 102.4951
5.998 459.7529
174.263 761.4508
815.728 513.3588
0.0
0.0
图6 加测两条陀螺定向边
图8 加测一条陀螺定向边
1 11 7 4 0.000000 0.000000 70.000000 3.000000 140.000000 7.000000 149.000000 45.000000 164.000000 114.000000 179.000000 182.000000 194.000000 250.000000 209.000000 319.000000 223.000000 387.000000 238.000000 456.000000 253.000000 524.000000 268.000000 592.000000 0.000000 0.000000 -70.000000 -4.000000 -140.000000 -7.000000 -209.000000 -11.000000 -279.000000 -14.000000 -349.000000 -18.000000 -419.000000 -21.000000 -489.000000 -25.000000
225.104 621.2324
693.303 309.7826
945.954 225.7104
704.695 804.3179
736.725 964.2209
563.173 895.3012
贯通误差预计计算表

点号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 X 4370205.954 4370205.956 4370205.959 4370205.961 4370205.964 4370205.966 4370205.969 4370205.971 4370205.974 4370205.976 4370205.979 4370205.981 4370205.984 4370205.987 4370205.989 4370205.992 4370205.994 4370205.997 4370205.999 4370206.002 4370206.004 4370206.007 4370206.009 4370285.849 4370382.458 4370443.010 4370443.008 4370443.005 4370443.003 4370443.004 4370442.998 4370442.995 4370442.993 4370442.990 4370442.988 4370442.985 4370442.982 4370442.980 4370442.977 4370442.975 4370442.972 4370442.970 4370442.965 Y 37411567.265 37411817.265 37412067.265 37412317.265 37412567.265 37412817.265 37413067.265 37413317.295 37413567.265 37413817.265 37414067.265 37414317.265 37414567.265 37414817.265 37415067.265 37415317.265 37415567.266 37415817.265 37416067.265 37416317.144 37416567.265 37416817.265 37417067.265 37417100.198 37417140.048 37417165.025 37416915.025 37416665.025 37416415.025 37416164.967 37415915.025 37415665.024 37415415.025 37415165.024 37414915.025 37414665.025 37414415.025 37414165.025 37413915.025 37413665.025 37413415.025 37413164.893 37412915.025 0 预 计 方 位 : 7 测 角 中 误 差 : 3 量边固定误差: 2 量边比例误差: 起 始 定 向 边 : 24 25 陀 螺 边 :5 6 3 陀螺定向中误差: ° " mm mm/km 14 " 15 34
导线测量对贯通影响的误差预计新公式(精)
2 公式推导
2.1 导线在贯通点K处的误差计算式
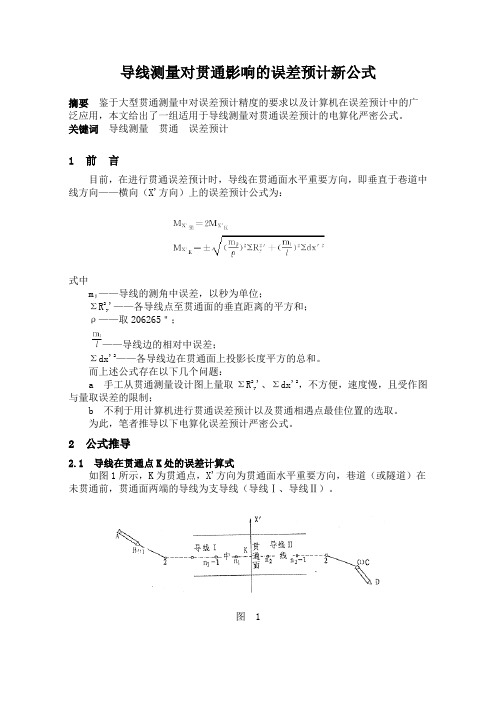
如图1所示,K为贯通点,X'方向为贯通面水平重要方向,巷道(或隧道)在未贯通前,贯通面两端的导线为支导线(导线Ⅰ、导线Ⅱ)。
图 1
a 支导线I在贯通点K处的方差及协方差计算式
把K点看作为支导线I的终点,则有:
(1)
而导线任意边i的方位角是所测角度的函数,即
(2)
上列两式中
XB——支导线I起算点B的已知X坐标;
YB——支导线I起算点B的已知Y坐标;
αAB——支导线I起算边AB的已知坐标方位角;
βj——支导线I各转折角;
li——支导线I各边的边长,如ln1表示导线点n1至贯通点K的边长;
(5)
c 导线在贯通点K处的方差及协方差计算式
因,由支导线Ⅰ、Ⅱ分别推算到K点时,在X与Y方向上的偏差为:
将上式写成矩阵形式,为:
F=AX
式中
而,
所以,运用协方差传播定律,得支导线Ⅰ、Ⅱ对K点综合影响的方差及协方差为:
(6)
上式中
n——导线Ⅰ、Ⅱ的导线点数之总和,即n=n1+n2。
d 导线在贯通点K处的误差计算式
式中
mβ——导线的测角中误差,以秒为单位;
ΣR2y'——各导线点至贯通面的垂直距离的平方和;
ρ——取206265";
——导线边的相对中误差;
Σdx'2——各导线边在贯通面上投影长度平方的总和。
而上述公式存在以下几个问题:
a 手工从贯通测量设计图上量取ΣR2y'、Σdx'2,不方便,速度慢,且受作图与量取误差的限制;
αi——支导线I各边的坐标方位角,如αn1表示导线点n1至贯通点K的坐标方位角;
xxx贯通测量设计及误差预计

xxx贯通测量设计及误差预计xxx综采工作面贯通测量设计及误差预计一、前言0541-1综采工作面是一矿1512综采工作面的接续采面,为了保证此项施工巷道快速、准确地完成,特进行贯通测量设计及误差预计。
二、施工巷道概况由于0541-1综采工作面的延长,测点增加,导线加长,导线由原来的2559米增加到现在的3739米,所以对原来的误差预计进行补充说明。
方位均为175°03′11″回风巷断面宽3.8m、高3.740m。
机巷断面宽4.7m、高3.3m,施工长度(1488.6米)2668.6m。
贯通精度:中线误差小于0.3m,腰线误差小于0.2m。
三、矿井测量概况预计2010年3月中旬实现贯通。
导线等级为7s级,共设测41站,导线全长3739米。
相对闭合差达到1/9000,测角中误差Mβ=6.71s,三角高程任意两点往返高差小于10+0.3L,闭合差不小于25√L,平差值为:导线量边偶然误差系数a平=0.0004865,b斜=0.000046;系统误差系数a平=0.000091,b斜=0.00065。
四、贯通测量方案设计1.布置方式此贯通属一井贯通,均由导线边A45-△起始,故布设为闭合导线,闭合导线自检能力强,受其它因素影响小。
2、布设精度(1)测角精度根据现状有两种方案:方案1——7s级经纬仪导线,方案2——15s级经纬仪导线。
首先考虑测角中误差导致最终贯通点重要方向误差: 7s级导线Mxβ=7/206265×3739=0.126m15s级导线Mxβ=15/206265×3739=0.272 m精度评定选择方案1——施测7s级导线。
(2)量边精度根据现状有两种方案:方案1——使用全站仪测距量边,方案2——使用钢尺量边。
精度预测:钢尺量边:ML=22a=0.000091, b=0.000486, L=90(平均)ML=0.0040全站仪测距:Δd=D往?D返≤2√2 mDmD为仪器的标称精度mD=(1+1ppm)可见前面两种方案均满足精度要求,但第1方案工作强度低,效率高,因此选择方案1——使用全站仪量边。
导线精度估算
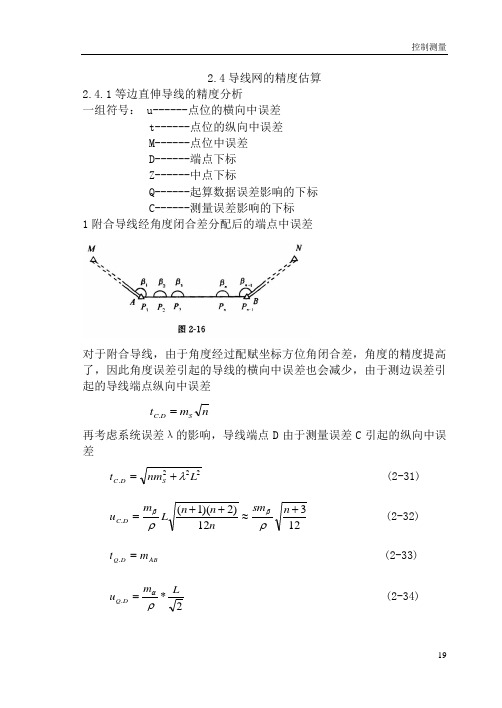
2.4导线网的精度估算2.4.1等边直伸导线的精度分析一组符号: u------点位的横向中误差 t------点位的纵向中误差 M------点位中误差 D------端点下标 Z------中点下标Q------起算数据误差影响的下标 C------测量误差影响的下标1附合导线经角度闭合差分配后的端点中误差对于附合导线,由于角度经过配赋坐标方位角闭合差,角度的精度提高了,因此角度误差引起的导线的横向中误差也会减少,由于测边误差引起的导线端点纵向中误差n m t SD C =.再考虑系统误差λ的影响,导线端点D 由于测量误差C 引起的纵向中误差222.Lnmt SD C λ+=(2-31)12312)2)(1(.+≈++=n sm nn n Lm u D C ρρββ(2-32)ABD Q m t =.(2-33)2*.L m u D Q ρα=(2-34)2.2.2.2.D Q D Q D C D C Du t u t M+++=(2-35)式中:n —边数,L —导线全长,S —平均边长,S m —测边中误差,λ—测边系统误差,βm —测角中误差,AB m —AB 边长的中误差,αm —起始方位角的中误差。
推导(2-32)式设转折角的观测值为i β,真误差为i d β,改正数为i v ,经过坐标方位角配赋后为)(i i i v +='ββ,其真误差为i d β'。
坐标方位角条件180)1(11=-+-'+∑+BN n iMA n αβα或11=+∑+βf vn i(1)式中0180)1(11=-+-+=∑+BN n iMA n f αβαβ当观测角是等精度,只考虑坐标方位角条件时,角度改正数1121+-====+n f v v v n β{}BNn iMAi i i i i n n n f v αβαβββββ-+-++-=+-=+='∑+180)1(11111微分∑++-='1111n ii i d n d d βββ (2) 当第一个转折角1β'有误差1β'd ,其它转折角没有误差时,将使导线终点产生横向位移1u ∆,ρβ'''=∆11d nsu同样 ρβ'''-=∆22)1(d sn u (3)……ρβ'''=∆nn d su由于n βββ''',,,21 有真误差n d d d βββ''',,,21 将使导线终点产生横向位真误差n u u u u ∆++∆+∆=∆ 21(4)将(2-)代入(3)再代入(4)并将真误差换写成中误差,得横向中误差D C u .⎭⎬⎫⎩⎨⎧+++-+''=2222.12)12()2(2 n n sm u D C ρβ12324)2)(1(2+''≈++''=n sm n n n sm ρρββ(2-32)2附合导线平差后的各边方位角中误差任意一条附合导线应满足三个条件,即坐标方位角条件、纵横坐标条件。
论述隧道贯通测量中导线设计与误差预计

论述隧道贯通测量中导线设计与误差预计作者:李树波来源:《科技视界》2016年第11期【摘要】随着经济和科学技术的发展,对道路的建设的要求也越来越高。
长大隧道作为道路建设的控制性工程之一,其贯通的水平在很大程度上代表了我国隧道的技术发展水平,而且贯通测量是测量学科内一项最综合性的测量工作,非常值得探讨、研究,也是对测量理论和知识方面的一次全面性的训练和培养。
【关键词】控制测量;贯通测量;导线测量1 隧道贯通当前现状测绘技术的发展,使得越来越多的先进仪器和方法应用于隧道贯通测量。
国家1:10000基本地形图为隧道选址提供了基础图件;遥感技术提供了多光谱影像,可对隐患地质构造和水文地质条件进行推断;光电测距仪,电子全站仪以及全球定位系统技术的应用,使隧道施工平面控制图的建立得到革命性的改变;电子计算机的普遍应用,使隧道控制网的优化设计和贯通误差变的十分简单。
目前世界最长的隧道为日本本州和北海道全长53.9公里的青函隧道。
迄今为止,我国最长的隧道为太行山隧道,其全长27.839公里。
随着时间的推移,一定会出现更长的隧道,且其更新的速度也会越来越快。
误差在测量过程中是不可避免的,隧道贯通中的主要误差为隧道贯通测量重要方向上的误差。
在实际施工中,通常因为提高工程进度、缩短工程期限以及改善隧道中的工作环境等,我们一般采用隧道两端的开切口为施工点,从隧道的两端同时进行开工。
为了保证隧道在贯通的方向和贯通点的的误差满足《工程测量规范》中的精度要求,所以在工程施工前,隧道贯通过程中测量设计方案及预计误差都是相当重要的。
此次举例来说明一下隧道贯通测量的导线设计和误差预计本次的贯通测量地面控制网为四等GPS控制网,采用边连式的方法进行,最长边长2360米,最短边长1300米,平均边长约1805.83m,隧道高6m,宽13m。
仪器的标称精度为±(1+lppm×D)mm。
(1)基线条件精度指标各等级GPS相邻点间弦长精度用下式表示:(2)最弱边相对中误差为:2 隧道导线测量方案的设计2.1 隧道内平面测量隧道平面测量包括井下施工导线测量、施工控制导线测量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图2所示,K点为贯通点,X—O—Y坐标系为测量坐标系,X'—K—Y'坐标系为K点处假定坐标系,X'轴垂直于巷道中线方向,Y'轴为巷道中线方向。
图 2
因在给定方位角φ方向上的位差计算式为:
m2φ=m2o(Qxxcos2φ+Qyysin2φ+Qxysin2φ)
图 3
a 原设计采用老公式进行误差预计,得MX'预=±0.130m。
b 现采用本文公式,运用Quick BASIC语言编程计算,得
MX'预=±0.134m。
该巷道贯通后,在水平重要方向上的实际偏差值为0.095m。更进一步证明了本文所提出公式的正确性与适用性。
4 结束语
本公式推导严密,可用于井上、下导线对贯通测量的误差预计,特别是适用于运用计算机进行贯通误差预计与最佳贯通点位置的选取。由计算机编程进行预计时,公式中所需的各导线边的坐标方位角与坐标增量、各导线点的坐标,可考虑由计算机根据巷道的设计数据以及布设导线的位置、边长等有关信息,自动算出。
mli——导线各边的测边中误差;
mβi——导线各转折角的测角中误差;
ρ——取206265"。
如测边采用相对中误差,并顾及m2β1=…=m2βn=m2β,则由上式可得:
(8)
式中
dxi——导线各边在X方向上的坐标增量;
dyi——导线各边在Y方向上的坐标增量;
——导线边的边长相对中误差;
其它同式(7)。
所以,由导线引起的K点在X 方向上的位差计算式如下:
(9)
式中
γ——X'轴在测量坐标系X—O—Y中的坐标方位角,γ=α中线±90°。
2.3 误差预计公式
取2倍中误差作为极限误差。
a 导线测量一次时,误差预计公式为:
(10)
b 导线复测n次时,误差预计公式为:
(11)
3 实 例
图3所示为某矿一已贯通巷道,贯通导线总长约5.0km(其中地面布设为长约1.7km的二级导线,井下为长约3.3km的15"基本控制导线),平均边长200m。水平角观测采用T2经纬仪,测距采用REDmini(5+5ppm)型测距仪,导线进行复测。取mβ地面=±10"、mβ井下=±15"、
(5)
c 导线在贯通点K处的方差及协方差计算式
因,由支导线Ⅰ、Ⅱ分别推算到K点时,在X与Y方向上的偏差为:
将上式写成矩阵形式,为:
F=AX
式中
而,
所以,运用协方差传播定律,得支导线Ⅰ、Ⅱ对K点综合影响的方差及协方差为:
(6)
上式中
n——导线Ⅰ、Ⅱ的导线点数之总和,即n=n1+n2。
d 导线在贯通点K处的误差计算式
把K点看作为支导线I的终点,则有:
(1)
而导线任意边i的方位角是所测角度的函数,即
(2)
上列两式中
XB——支导线I起算点B的已知X坐标;
YB——支导线I起算点B的已知Y坐标;
αAB——支导线I起算边AB的已知坐标方位角;
βj——支导线I各转折角;
li——支导线I各边的边长,如ln1表示导线点n1至贯通点K的边长;
以σ2xK、σ2yK、σxyK、σ2l1、…、σ2ln、σ2β1、…、σ2βn的估值m2xK、m2yK、mxyK、m2l1、…、m2ln、m2β1、…、m2βn代入式(6),得:
(7)
式中
n——导线的总点数,n=n1+n2;
αi——导线各边的坐标方位角;
xK、yK——贯通点K的X、Y坐标;
xi、yi——导线各点的X、Y坐标大型贯通测量中对误差预计精度的要求以及计算机在误差预计中的广泛应用,本文给出了一组适用于导线测量对贯通误差预计的电算化严密公式。
关键词导线测量 贯通 误差预计
1 前 言
目前,在进行贯通误差预计时,导线在贯通面水平重要方向,即垂直于巷道中线方向——横向(X'方向)上的误差预计公式为:
αi——支导线I各边的坐标方位角,如αn1表示导线点n1至贯通点K的坐标方位角;
n1——支导线I的总点数,起算点B编为1号,贯通点K前最后一个导线点编为n1号。
考虑到式(2),对式(1)进行全微分,得:
(3)
运用协方差传播定律,并顾及到观测量之间相互独立,方差阵为如下一对角阵:
得:
(4)
b 同理,得支导线Ⅱ在贯通点K处的方差及协方差计算式
b 不利于用计算机进行贯通误差预计以及贯通相遇点最佳位置的选取。
为此,笔者推导以下电算化误差预计严密公式。
2 公式推导
2.1 导线在贯通点K处的误差计算式
如图1所示,K为贯通点,X'方向为贯通面水平重要方向,巷道(或隧道)在未贯通前,贯通面两端的导线为支导线(导线Ⅰ、导线Ⅱ)。
图 1
a 支导线I在贯通点K处的方差及协方差计算式
式中
mβ——导线的测角中误差,以秒为单位;
ΣR2y'——各导线点至贯通面的垂直距离的平方和;
ρ——取206265";
——导线边的相对中误差;
Σdx'2——各导线边在贯通面上投影长度平方的总和。
而上述公式存在以下几个问题:
a 手工从贯通测量设计图上量取ΣR2y'、Σdx'2,不方便,速度慢,且受作图与量取误差的限制;
