应用多元统计分析习题解答_朱建平_第五章
SPSS-朱建平版应用多元统计答案

5#703Spss实习作业上机操作余聪0701020223数学二班数据变换是正式分析前的重要一步,通过数据变换,一个优秀的统计分析员可以将原始记录整理成所需的任何形式,从而为后面的精确分析打下坚实的基础——这正是他和普通分析员的区别所在。
-------张文彤3.61992年美国总统选举的三位候选人为布什、佩罗特和克林顿。
支持三位候选人的选民中抽取了20人,假定三组都服从多元正态分布,检验这三组的总体均值是否都显著性差异( )。
解:我们知道One-Way ANOVA 过程用于两组及多组间样本均值的比较,即成组设计的方差分析。
具体操作步骤:1.先对数据进行预处理,1代表布什,2代表佩罗特,3代表华盛顿。
2.Analyze---Compare Mean---One-Way ANOVADependent List框:总统分组Options: Homogeneity-of-varianceContinuePost Hoc:S-N-K:ContinueOK3.运行结果1:结果解释:上图给出单因子方差分析的结果,可见F=3.095,P=0.034<0.05,所以证明假设不成立,选民年龄程度存在差异。
运行结果2:结果解释:上图给出单因子方差分析的结果,可见F=2.354,P=0.065>0.05,所以证明假设成立,选民受教育程度不存在差异。
4.10从胃癌者、萎缩性胃炎患者和非胃炎患者中分别抽取五个病人进行四项生化指标的化验:血清铜蛋白(X1)、蓝色反应(X2)、尿吲哚乙酸(X3)和中性硫化物(X4),数据见下表。
试用距离判别法建解:1.费希尔判别法的主要思想:从k各总体中具有P个样品观测数据,借助发差分析的思想构造现行判别函数U(x)=u1*X1+ u2*X2+ u2*X2+ u3*X3++ up*Xp= u’X其中,系数u =(u1, u2, u3,…,u p)’确定的原则是使总体之间区别最大,而使每个总体之间的离差最小。
应用多元统计分析课后答案

第二章2.1.试叙述多元联合分布和边际分布之间的关系。
解:多元联合分布讨论多个随机变量联合到一起的概率分布状况,12(,,)p X X X X '=的联合分布密度函数是一个p 维的函数,而边际分布讨论是12(,,)p X X X X '=的子向量的概率分布,其概率密度函数的维数小于p 。
2.2设二维随机向量12()X X '服从二元正态分布,写出其联合分布。
解:设12()X X '的均值向量为()12μμ'=μ,协方差矩阵为21122212σσσσ⎛⎫ ⎪⎝⎭,则其联合分布密度函数为1/21222112112222122121()exp ()()2f σσσσσσσσ--⎧⎫⎛⎫⎛⎫⎪⎪'=---⎨⎬ ⎪⎪⎝⎭⎝⎭⎪⎪⎩⎭x x μx μ。
2.3已知随机向量12()X X '的联合密度函数为121212222[()()()()2()()](,)()()d c x a b a x c x a x c f x x b a d c --+-----=--其中1a x b ≤≤,2c x d ≤≤。
求(1)随机变量1X 和2X 的边缘密度函数、均值和方差; (2)随机变量1X 和2X 的协方差和相关系数; (3)判断1X 和2X 是否相互独立。
(1)解:随机变量1X 和2X 的边缘密度函数、均值和方差;112121222[()()()()2()()]()()()dx cd c x a b a x c x a x c f x dx b a d c --+-----=--⎰12212222222()()2[()()2()()]()()()()dd cc d c x a x b a x c x a x c dx b a d c b a d c -------=+----⎰ 12122222()()2[()2()]()()()()dd cc d c x a x b a t x a t dt b a d c b a d c ------=+----⎰2212122222()()[()2()]1()()()()d cdcd c x a x b a t x a t b a d c b a d c b a------=+=----- 所以由于1X 服从均匀分布,则均值为2b a +,方差为()212b a -。
应用多元统计分析习题解答_朱建平_第五章

Abbo无私奉献,只收1个金币,BS收5个金币的…何老师考简单点啊……第五章 聚类分析5.1 判别分析和聚类分析有何区别?答:即根据一定的判别准则,判定一个样本归属于哪一类。
具体而言,设有n 个样本,对每个样本测得p 项指标(变量)的数据,已知每个样本属于k 个类别(或总体)中的某一类,通过找出一个最优的划分,使得不同类别的样本尽可能地区别开,并判别该样本属于哪个总体。
聚类分析是分析如何对样品(或变量)进行量化分类的问题。
在聚类之前,我们并不知道总体,而是通过一次次的聚类,使相近的样品(或变量)聚合形成总体。
通俗来讲,判别分析是在已知有多少类及是什么类的情况下进行分类,而聚类分析是在不知道类的情况下进行分类。
5.2 试述系统聚类的基本思想。
答:系统聚类的基本思想是:距离相近的样品(或变量)先聚成类,距离相远的后聚成类,过程一直进行下去,每个样品(或变量)总能聚到合适的类中。
5.3 对样品和变量进行聚类分析时, 所构造的统计量分别是什么?简要说明为什么这样构造?答:对样品进行聚类分析时,用距离来测定样品之间的相似程度。
因为我们把n 个样本看作p 维空间的n 个点。
点之间的距离即可代表样品间的相似度。
常用的距离为 (一)闵可夫斯基距离:1/1()()pq qij ik jk k d q X X ==-∑q 取不同值,分为 (1)绝对距离(1q =)1(1)pij ik jk k d X X ==-∑(2)欧氏距离(2q =)21/21(2)()pij ik jk k d X X ==-∑(3)切比雪夫距离(q =∞)1()max ij ik jkk pd X X ≤≤∞=-(二)马氏距离(三)兰氏距离对变量的相似性,我们更多地要了解变量的变化趋势或变化方向,因此用相关性进行衡量。
21()()()ij i j i j d M -'=--X X ΣX X 11()p ik jkij k ik jk X X d L p X X =-=+∑将变量看作p 维空间的向量,一般用(一)夹角余弦(二)相关系数5.4 在进行系统聚类时,不同类间距离计算方法有何区别?选择距离公式应遵循哪些原则?答: 设d ij 表示样品X i 与X j 之间距离,用D ij 表示类G i 与G j 之间的距离。
应用多元统计分析课后的答案解析_朱建平版

2.1.试叙述多元联合分布和边际分布之间的关系。
解:多元联合分布讨论多个随机变量联合到一起的概率分布状况,12(,,)p X X X X '=的联合分布密度函数是一个p 维的函数,而边际分布讨论是12(,,)p X X X X '=的子向量的概率分布,其概率密度函数的维数小于p 。
2.2设二维随机向量12()X X '服从二元正态分布,写出其联合分布。
解:设12()X X '的均值向量为()12μμ'=μ,协方差矩阵为21122212σσσσ⎛⎫ ⎪⎝⎭,则其联合分布密度函数为1/21222112112222122121()exp ()()2f σσσσσσσσ--⎧⎫⎛⎫⎛⎫⎪⎪'=---⎨⎬ ⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭x x μx μ。
2.3已知随机向量12()X X '的联合密度函数为121212222[()()()()2()()](,)()()d c x a b a x c x a x c f x x b a d c --+-----=--其中1ax b ≤≤,2c x d ≤≤。
求(1)随机变量1X 和2X 的边缘密度函数、均值和方差; (2)随机变量1X 和2X 的协方差和相关系数;(3)判断1X 和2X 是否相互独立。
(1)解:随机变量1X 和2X 的边缘密度函数、均值和方差;112121222[()()()()2()()]()()()dx cd c x a b a x c x a x c f x dx b a d c --+-----=--⎰12212222222()()2[()()2()()]()()()()dd c c d c x a x b a x c x a x c dx b a d c b a d c -------=+----⎰ 121222202()()2[()2()]()()()()dd c c d c x a x b a t x a t dt b a d c b a d c ------=+----⎰ 2212122222()()[()2()]1()()()()d cdc d c x a x b a t x a t b a d c b a d c b a------=+=----- 所以 由于1X 服从均匀分布,则均值为2b a+,方差为()212b a -。
多元统计课后题精选全文完整版
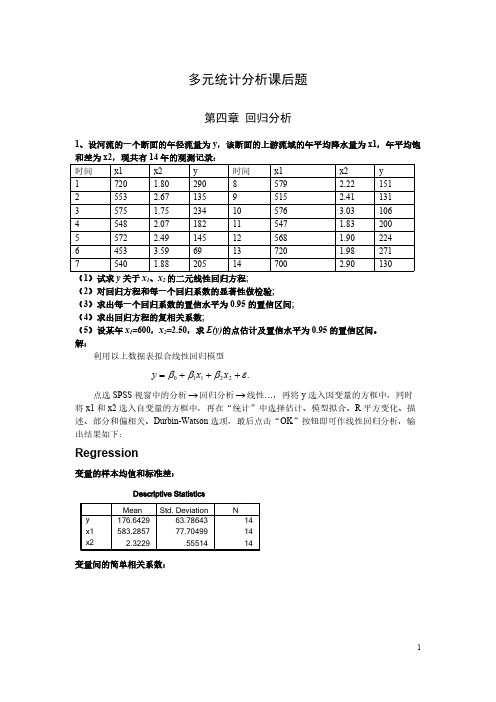
多元统计分析课后题第四章 回归分析1、设河流的一个断面的年径流量为y ,该断面的上游流域的年平均降水量为x1,年平均饱和差为x2,现共有14年的观测记录:时间x1x2y 时间x1x2y17201.8029085792.221512553 2.6713595152.411313575 1.75234105763.031064548 2.07182115471.832005572 2.49145125681.902246453 3.5969137201.982717540 1.88205147002.90130(1)试求y 关于x 1、x 2的二元线性回归方程;(2)对回归方程和每一个回归系数的显著性做检验;(3)求出每一个回归系数的置信水平为0.95的置信区间;(4)求出回归方程的复相关系数;(5)设某年x 1=600,x 2=2.50,求E(y)的点估计及置信水平为0.95的置信区间。
解:利用以上数据表拟合线性回归模型.22110εβββ+++=x x y 点选SPSS 视窗中的分析回归分析线性…,再将y 选入因变量的方框中,同时→→将x1和x2选入自变量的方框中,再在“统计”中选择估计、模型拟合、R 平方变化、描述、部分和偏相关、Durbin-Watson 选项,最后点击“OK ”按钮即可作线性回归分析,输出结果如下:Regression变量的样本均值和标准差:变量间的简单相关系数:这里给出了回归方程的样本决定系数和P值以及DW值:下面的框图是方差分析表,从中可以看出,y关于x1和x2的线性回归方程通过了显著性检验,均方残差为554.963,F统计量值为42.155,P值为0.000,回归方程在0.000的统计意义上是显著的。
上面的框图给出了非标准化和标准化的回归方程,以及回归系数的t 统计量检验结果。
从中我们可以看出,非标准化的回归方程为:(1)21x 647.87292.0875.209-+=x y(2)回归系数、均通过了显著性检验。
应用多元统计分析讲稿(朱建平)

第一章多元分析概述第一节引言多元统计分析是运用数理统计方法来研究解决多指标问题的理论和方法。
近30年来,随着计算机应用技术的发展和科研生产的迫切需要,多元统计分析技术被广泛地应用于地质、气象、水文、医学、工业、农业和经济等许多领域,已经成为解决实际问题的有效方法。
然而,随着Internet的日益普及,各行各业都开始采用计算机及相应的信息技术进行管理和决策,这使得各企事业单位生成、收集、存储和处理数据的能力大大提高,数据量与日俱增,大量复杂信息层出不穷。
在信息爆炸的今天,人们已经意识到数据最值钱的时代已经到来。
显然,大量信息在给人们带来方便的同时也带来一系列问题。
比如:信息量过大,超过了人们掌握、消化的能力;一些信息真伪难辩,从而给信息的正确应用带来困难;信息组织形式的不一致性导致难以对信息进行有效统一处理等等,这种变化使传统的数据库技术和数据处理手段已经不能满足要求.Internet 的迅猛发展也使得网络上的各种资源信息异常丰富,在其中进行信息的查找真如大海捞针。
这样又给多元统计分析理论的发展和方法的应用提出了新的挑战。
多元统计分析起源于上世纪初,1928年Wishart发表论文《多元正态总体样本协差阵的精确分布》,可以说是多元分析的开端。
20世纪30年代R.A. Fisher 、H.Hotelling、S.N.Roy、许宝騄等人作了一系列得奠基性工作,使多元分析在理论上得到了迅速得发展。
20世纪40年代在心理、教育、生物等方面有不少得应用,但由于计算量大,使其发展受到影响,甚至停滞了相当长得时间。
20世纪50年代中期,随着电子计算机得出现和发展,使多元分析方法在地质、气象、医学、社会学等方面得到广泛得应用。
20世纪60年代通过应用和实践又完善和发展了理论,由于新的理论、新的方法不断涌现又促使它的应用范围更加扩大。
20世纪70年代初期在我国才受到各个领域的极大关注,并在多元统计分析的理论研究和应用上也取得了很多显著成绩,有些研究工作已达到国际水平,并已形成一支科技队伍,活跃在各条战线上。
第五章习题答案

第五章习题答案本章主要涉及多元统计基础,包括散点图、相关分析、回归分析以及方差分析等内容。
下面是本章部分习题的答案与解析。
1. 对于以下散点图,请判断变量之间的线性关系及相关系数大小。
答案:变量之间的线性关系:(1) 正相关(2) 弱负相关(3) 强正相关(4) 强负相关相关系数大小:(1) 0.82(2) -0.28(3) 0.96(4) -0.89解析:散点图是一种直观表示两个变量之间关系的图形,可以通过观察散点图的形状和位置来判断其相关性。
相关系数则是一种量化变量之间关系的方法,取值范围为-1到1,数值越接近 ±1,则相关性越强。
2. 请计算以下数据的相关系数,并判断相关性的方向和强度。
答案:相关系数:0.68相关性方向:正相关相关性强度:较强解析:相关系数为0.68,属于正相关,说明两个变量之间的关系呈现出一种正向趋势。
相关系数越接近1,则表明相关性越强,并且两个变量之间的关系越容易被预测和解释。
3. 请根据以下数据进行线性回归,并计算拟合优度和截距。
答案:回归分析结果:y = 2.5x + 5.5拟合优度:0.74截距:5.5解析:线性回归分析是一种用于探究变量之间关系的方法,通过拟合一条直线来表达变量之间的线性关系。
本题中,得到的回归方程为y = 2.5x + 5.5,即y的变化量与x成正比,斜率为2.5,截距为5.5。
同时,拟合优度为0.74,说明回归直线与数据点之间的拟合程度中等。
4. 在方差分析中,请简述组内变异与组间变异的概念以及作用。
答案:组内变异是指同一组内不同观测值之间的差异,反映了个体间的异质性和误差。
组间变异是指不同组之间观测值的差异,被用来衡量处理之间的区别和实验效应。
组内变异和组间变异在方差分析中具有不同的作用。
组内变异越小,则说明样本内部的方差较小,也就意味着各组之间的差异更大。
而组间变异越大,则意味着不同组之间的方差更大,也就是说各组之间的区分度更高,效应也越大。
应用多元统计分析课后习题答案详解北大高惠璇部分习题解答省名师优质课赛课获奖课件市赛课一等奖课件

4.7067
取a 1 A1( (1) (2) )
d
1 65 1381
3323 ,
则aAa
1,
且a满足 : Ba Aa ( d 2 ).
12
第五章 鉴别分析
判别效率(a) aBa 4.7067.
aAa
Fisher线性判别函数为u( X ) aX
1 89765
(32
X1
33X
2 判别准则为 判X G1 , 当W ( X ) 0,
判X G2 , 当W ( X ) 0, 试求错判概率P(2 |1)和P(1| 2).
解 : 记a 1 ( (1) (2) ),W ( X ) ( X )a是X的
线性函数,当X
G1时,W
(
X
)
~
N1
(1,
2 1
), 且
20
第五章 鉴别分析
20 20
时,
u
(
X
(1)
)
1 89765
(32,33)
20 20
4.3390
因u( X (1) ) 4.3390 u* , 判X (1) G2.
当X (1)
15 20
时,
u
(
X
(2)
)
1 89765
(32,33)1250
3.8050
因u( X (2) ) 3.8050 u* 判X (2) G1.
其中W ( X ) a( X *)
( X * )1( (1) (2) ) ,
* 1 ( (1) (2) ).
2 10
第五章 鉴别分析
5-4 设有两个正态总体G1和G2,已知(m=2)
(1)
1105, (2)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Abbo无私奉献,只收1个金币,BS收5个金币的…何老师考简单点啊……第五章 聚类分析5.1 判别分析和聚类分析有何区别?答:即根据一定的判别准则,判定一个样本归属于哪一类。
具体而言,设有n 个样本,对每个样本测得p 项指标(变量)的数据,已知每个样本属于k 个类别(或总体)中的某一类,通过找出一个最优的划分,使得不同类别的样本尽可能地区别开,并判别该样本属于哪个总体。
聚类分析是分析如何对样品(或变量)进行量化分类的问题。
在聚类之前,我们并不知道总体,而是通过一次次的聚类,使相近的样品(或变量)聚合形成总体。
通俗来讲,判别分析是在已知有多少类及是什么类的情况下进行分类,而聚类分析是在不知道类的情况下进行分类。
5.2 试述系统聚类的基本思想。
答:系统聚类的基本思想是:距离相近的样品(或变量)先聚成类,距离相远的后聚成类,过程一直进行下去,每个样品(或变量)总能聚到合适的类中。
5.3 对样品和变量进行聚类分析时, 所构造的统计量分别是什么?简要说明为什么这样构造?答:对样品进行聚类分析时,用距离来测定样品之间的相似程度。
因为我们把n 个样本看作p 维空间的n 个点。
点之间的距离即可代表样品间的相似度。
常用的距离为 (一)闵可夫斯基距离:1/1()()pq qij ik jk k d q X X ==-∑q 取不同值,分为 (1)绝对距离(1q =)1(1)pij ik jk k d X X ==-∑(2)欧氏距离(2q =)21/21(2)()pij ik jk k d X X ==-∑(3)切比雪夫距离(q =∞)1()max ij ik jkk pd X X ≤≤∞=-(二)马氏距离(三)兰氏距离对变量的相似性,我们更多地要了解变量的变化趋势或变化方向,因此用相关性进行衡量。
21()()()ij i j i j d M -'=--X X ΣX X 11()p ik jkij k ik jk X X d L p X X =-=+∑将变量看作p 维空间的向量,一般用(一)夹角余弦(二)相关系数5.4 在进行系统聚类时,不同类间距离计算方法有何区别?选择距离公式应遵循哪些原则?答: 设d ij 表示样品X i 与X j 之间距离,用D ij 表示类G i 与G j 之间的距离。
(1). 最短距离法,mini k j rkr ij X G X G D d ∈∈=min{,}kp kq D D =(2)最长距离法,maxi p j qpq ij X G X G D d ∈∈=,maxi k j rkr ij X G X G D d ∈∈=max{,}kp kq D D =(3)中间距离法其中(4)重心法2()()pq p q p q D X X X X '=-- )(1q q p p rrX n X n n X +=12211cos ()()pik jkk ij p pik jk k k X X X X θ====∑∑∑12211()()()()pik i jk j k ij p pik i jk j k k X X X X r X X X X ===--=--∑∑∑ij G X G X ij d D jj i i ∈∈=,min22222121pq kq kp kr D D D D β++=22222p q p q krkpkqpq rrr n n n n D D D D n n n =+-(5)类平均法221i p j jpq ij X G X G p qD d n n ∈∈=∑∑221i k j rkr ijX G X G k rD d n n ∈∈=∑∑22p q kp kqrrn n D D n n =+(6)可变类平均法其中β是可变的且β <1(7)可变法22221()2kr kp kq pq D D D D ββ-=++ 其中β是可变的且β <1 (8)离差平方和法1()()tn t it t it t t S X X X X ='=--∑2222k p k q k krkpkq pq r kr kr kn n n n n D D D D n n n n n n ++=+-+++通常选择距离公式应注意遵循以下的基本原则:(1)要考虑所选择的距离公式在实际应用中有明确的意义。
如欧氏距离就有非常明确的空间距离概念。
马氏距离有消除量纲影响的作用。
(2)要综合考虑对样本观测数据的预处理和将要采用的聚类分析方法。
如在进行聚类分析之前已经对变量作了标准化处理,则通常就可采用欧氏距离。
(3)要考虑研究对象的特点和计算量的大小。
样品间距离公式的选择是一个比较复杂且带有一定主观性的问题,我们应根据研究对象的特点不同做出具体分折。
实际中,聚类分析前不妨试探性地多选择几个距离公式分别进行聚类,然后对聚类分析的结果进行对比分析,以确定最合适的距离测度方法。
5.5试述K 均值法与系统聚类法的异同。
2222(1)()pq kr kpkq pqrrn n D D D D n n ββ=-++答:相同:K —均值法和系统聚类法一样,都是以距离的远近亲疏为标准进行聚类的。
不同:系统聚类对不同的类数产生一系列的聚类结果,而K —均值法只能产生指定类数的聚类结果。
具体类数的确定,离不开实践经验的积累;有时也可以借助系统聚类法以一部分样品为对象进行聚类,其结果作为K —均值法确定类数的参考。
5.6 试述K 均值法与系统聚类有何区别?试述有序聚类法的基本思想。
答:K 均值法的基本思想是将每一个样品分配给最近中心(均值)的类中。
系统聚类对不同的类数产生一系列的聚类结果,而K —均值法只能产生指定类数的聚类结果。
具体类数的确定,有时也可以借助系统聚类法以一部分样品为对象进行聚类,其结果作为K 均值法确定类数的参考。
有序聚类就是解决样品的次序不能变动时的聚类分析问题。
如果用)()2()1(,,,n X X X Λ表示n 个有序的样品,则每一类必须是这样的形式,即)()1()(,,,j i i X X X Λ+,其中,1n i ≤≤且n j ≤,简记为},,1,{j i i G i Λ+=。
在同一类中的样品是次序相邻的。
一般的步骤是(1)计算直径{D (i,j )}。
(2)计算最小分类损失函数{L[p(l,k)]}。
(3)确定分类个数k 。
(4)最优分类。
5.7 检测某类产品的重量, 抽了六个样品, 每个样品只测了一个指标,分别为1,2,3,6,9,11.试用最短距离法,重心法进行聚类分析。
(1)用最短距离法进行聚类分析。
采用绝对值距离,计算样品间距离阵0 1 0 2 1 0 5 4 3 0 8 7 6 3 0 10 9 8 5 2 0由上表易知 中最小元素是 于是将,,聚为一类,记为计算距离阵3 06 3 08 5 2 0中最小元素是=2 于是将,聚为一类,记为计算样本距离阵3 06 3 0中最小元素是于是将,聚为一类,记为因此,(2)用重心法进行聚类分析计算样品间平方距离阵1 04 1 025 16 9 064 49 36 9 0100 81 64 25 4 0易知中最小元素是于是将,,聚为一类,记为计算距离阵16 049 9 081 25 4 0注:计算方法,其他以此类推。
中最小元素是=4 于是将,聚为一类,记为计算样本距离阵16 064 16 0中最小元素是于是将,聚为一类,记为因此,5.8 下表是15个上市公司2001年的一些主要财务指标,使用系统聚类法和K-均值法分别对这些公司进行聚类,并对结果进行比较分析。
公司编号净资产收益率每股净利润总资产周转率资产负债率流动负债比率每股净资产净利润增长率总资产增长率111.090.210.0596.9870.53 1.86-44.0481.99211.960.590.7451.7890.73 4.957.0216.11300.030.03181.99100-2.98103.3321.18411.580.130.1746.0792.18 1.14 6.55-56.325-6.19-0.090.0343.382.24 1.52-1713.5-3.366100.470.4868.486 4.7-11.560.85710.490.110.3582.9899.87 1.02100.2330.32811.12-1.690.12132.14100-0.66-4454.39-62.759 3.410.040.267.8698.51 1.25-11.25-11.4310 1.160.010.5443.7100 1.03-87.18-7.411130.220.160.487.3694.880.53729.41-9.97128.190.220.3830.31100 2.73-12.31-2.771395.79-5.20.5252.3499.34-5.42-9816.52-46.821416.550.350.9372.3184.05 2.14115.95123.4115-24.18-1.160.7956.2697.8 4.81-533.89-27.74解:令净资产收益率为X1,每股净利润X2,总资产周转率为X3,资产负债率为X4,流动负债比率为X5,每股净资产为X6,净利润增长率为X7,总资产增长率为X8,用spss对公司聚类分析的步骤如下:a)系统聚类法:1.在SPSS窗口中选择Analyze→Classify→Hierachical Cluster,调出系统聚类分析主界面,并将变量X8-X1移入Variables框中。
在Cluster 栏中选择Cases单选按钮,即对样品进行聚类(若选择Variables,则对变量进行聚类)。
在Display栏中选择Statistics和Plots复选框,这样在结果输出窗口中可以同时得到聚类结果统计量和统计图。
图5.1 系统分析法主界面2.点击Statistics按钮,设置在结果输出窗口中给出的聚类分析统计量。
我们选择Agglomeration schedule与Cluster Membership中的Range of solution 2-4,如图5.2所示,点击Continue按钮,返回主界面。
(其中,Agglomeration schedule表示在结果中给出聚类过程表,显示系统聚类的详细步骤;Proximity matrix 表示输出各个体之间的距离矩阵;Cluster Membership 表示在结果中输出一个表,表中显示每个个体被分配到的类别,Range of solution 2-4即将所有个体分为2至4类。
)3.点击Plots按钮,设置结果输出窗口中给出的聚类分析统计图。
