矩形件排样程序的实现王晨浩-试题b
2014下半年程序员考试真题及答案-下午卷

2014下半年程序员考试真题及答案-下午卷试题一(共15分)阅读以下说明和流程图,填补流程图中的空缺(1)〜(5),将解答填入答题纸的对应栏内。
【说明】本流程图旨在统计一本电子书中各个关键词出现的次数。
假设已经对该书从头到尾依次分离出各个关键词{A(i)|i=1,…,n}(n>1) },其中包含了很多重复项,经下面的流程处理后,从中挑选出所有不同的关键词共m个{K(j)lj=l,…,m},而每个关键词K(j)出现的次数为K(j),j=1,…,m。
【流程图】【参考答案】(1) 1 (2) K(j)(3)NK(j)+1->NK(j) 或NK(j)++ 或等价表示(4)m+1->m 或m++ 或等价表示(5)A(i)【试题解析】流程图中的第1框显然是初始化。
A (1) ->K(1)意味着将本书的第1个关键词作为选出的第1个关键词。
1->NK (1)意味着此时该关键词的个数置为1。
m是动态选出的关键词数目,此时应该为1,因此(1)处应填1。
本题的算法是对每个关键词与已选出的关键词进行逐个比较。
凡是遇到相同的,相应的计数就增加1;如果始终没有遇到相同关键词的,则作为新选出的关键词。
流程图第2框开始对i=2,n循环,就是对书中其他关键词逐个进行处理。
流程图第3 框开始j=l,m循环,就是按已选出的关键词依次进行处理。
接着就是将关键词A(I)与选出的关键词K(j)进行比较。
因此(2)处应填K(j)。
如果A(i)=K(j),则需要对计数器NK(j)增1,即执行NK(j)+1->NK(j)。
因此(3)处应填NK(j)+1->NK(j)。
执行后,需要跳出j循环,继续进行i循环,即根据书中的下一个关键词进行处理。
如果A(i)不等于NK(j),则需要继续与下个NK(j)进行比较,即继续执行j循环。
如果直到j循环结束仍没有找到匹配的关键词,则要将该A(i)作为新的已选出的关键词。
高中通用技术必修2苏教版第二单元流程与设计练习题-普通用卷

高中通用技术必修2苏教版第二单元流程与设计练习题一、选择题1.生活中使用高压锅烹饪食物,出锅前要先释放锅内蒸汽再开锅盖,否则会发生危险。
以上事例说明()A. 流程的时序都是不可颠倒的B. 时序具有相对性,可以自由安排C. 合理的时序可以为我们的安全提供保障D. 环节划分反映了事物的内在规律2.如图所示是一新产品的设计流程图,关于该流程,以下说法中正确的是()A. 若方案不可行,则重新进行市场调查B. 样品制造和修改是并行环节C. 草拟方案和方案论证是串行环节D. 评价不满意,则重新草拟方案3.如图所示是某垃圾处理厂有机生活垃圾生化处理流程图.下列对该流程的分析中正确的是()A. 油水分离环节与粉碎环节是串行环节B. 废水收集环节与生物发酵环节的时序可以颠倒C. 固液分离出来的固体经过加工处理后产出生物柴油D. 废水经过生物处理后产出生物菌肥4.如图所示是某制药厂的废水处理流程图.下列对该流程的分析中正确的是()A. 废水经过过滤处理后,全部排放B. 注入空气与回流是并行工序C. 接触氧化环节所处理的废水均来自于水解吸附环节D. 该流程完成实现了废水的环保处理5.小明学习通用必修课程后,发现很多章节贯穿了流程思想,下列描述不正确是A. 控制方框图是一种流程图B. 系统分析的一般步骤可以用流程表达C. 工艺中的零件加工需要经历一定的流程D. 设计的一般步骤和设计原则都属于流程6.下列流程中哪一个是正确的()A. 专利申请流程:提交申请→受理→发明专利申请公布→初审→发明专利申请实质审查→授权B. 制定设计方案流程:收集信息→设计分析→方案构思→方案筛选→方案呈现C. 轴承零件淬火工艺流程:落料→加热→淬火→清洗→回火→出料D. 自行车前轮装圈上轴流程:上钢丝→编花→装前轴→装内胎→装外胎→装气门7.用大小合适的钢板制作如图所示的开瓶器,以下工艺流程中合理的是()A. 划线→钻孔→锯割→锉削→抛光B. 划线→钻孔→锉削→锯割→抛光C. 划线→锉削→锯割→钻孔→抛光D. 划线→锯割→锉削→钻孔→抛光8.某物流公司要将一车商品送往甲、乙、丙、丁四个超市,每个超市接收四分之一商品,各超市距离如图(单位:千米),物流公司的地点在起点O处,合理的送货流程为()A. OCBADOB. ODCBAOC. ODABCOD. OCDABO9.小李准备设计制作一个木马(如图所示),画好草图和视图后,在设计制作流程时,不必考虑的是()A. 加工工具B. 加工精度C. 木料质地D. 原料成本10.如图所示,手工制造菜刀一般有以下几个环节:加热锻打成形、安装木手柄、热处理(提高硬度)、制刃。
软件工程期末复习应用题

1.建立窗口系统旳对象模型。
问题陈说如下.窗口分为对话窗、图形窗、流动窗三种;对话窗中有若干对话项, 由唯一旳项名字来确定, 对.项分为按钮、选择项、正文项三种, 选择项中有若干选项入口;图形窗口有若干形状元素, 形.元素分为一维形状和二维形状, 一维形状又分为直线、圆弧、折线;二维形状分为圆、椭圆、.形、多边形, 其中多边形和折线由若干有序顶点构成, 正文窗是滚动窗旳一种, 而图形滚动窗.是一种图形窗又是一种滚动窗。
答案:2.假设某航空企业规定, 乘客可以免费托运行李旳重量不超过30公斤。
当行李旳重量超过30公斤时, 对一般舱旳国内乘客超重部分每公斤收费4元, 对头等舱旳国内乘客超重部分每公斤收费6元。
对国外乘客超重部分每公斤收费比国内乘客多一倍, 对残疾乘客超重部分每公斤收费比正常乘客少二分之一。
试画出对应鉴定表。
答案:请用鉴定表画出如下问题旳行为逻辑。
人们往往根据天气状况决定出门时旳行装;天气也许下雨, 也也许不下雨;天气也许变冷, 也也许不变冷。
假如天气要下雨, 出门时带上雨伞;假如天气变冷, 出门时要穿上大衣。
建立鉴定表旳环节:2.用SA措施画出下列问题旳顶层和0层数据流图。
某运动会管理系统接受来自运动员旳报名单、裁判旳比赛项目及项目成绩, 产生运动员号码单发送给运动员, 项目参与者发送给裁判, 单项名次、团体名次发送给公布台。
该系统有两部分功能:(1)登记报名单: 接受报名单、比赛项目, 产生运动员号码单、项目参与者, 形成运动员名单及团体成绩表两种数据存储。
(2)记录成绩:接受项目成绩, 查询运动员名单, 产生单项名次, 填写团体成绩, 最终产生团体名次。
3.某图书馆借阅系统有如下功能:(1)借书: 根据读者旳借书证查询读者档案, 若借书数目未超过规定数量, 则办理借阅手续(修改库存记录及读者档案), 超过规定数量者不予借阅。
对于第一次借阅者则直接办理借阅手续。
(2)还书:根据读者书中旳条形码, 修改库存记录及读者档案, 若借阅时间超过规定期限则罚款。
(典型题)高中数学选修1-2第二章《框图》测试卷(含答案解析)
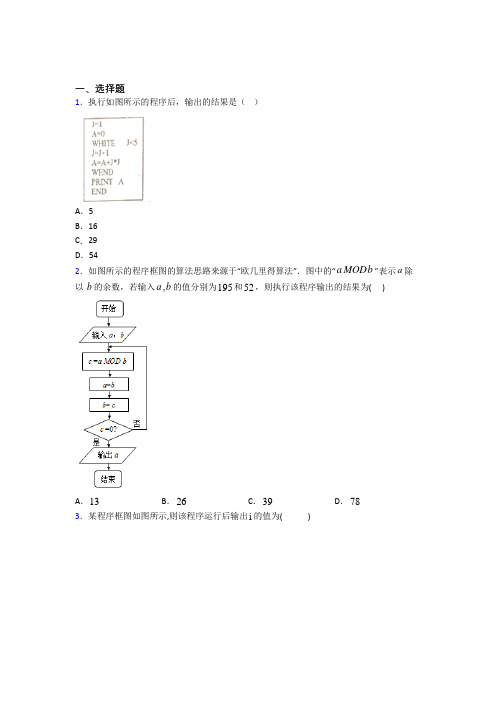
一、选择题1.执行如图所示的程序后,输出的结果是()A.5B.16C.29D.542.如图所示的程序框图的算法思路来源于“欧几里得算法”.图中的“a MODb”表示a除以b的余数,若输入,a b的值分别为195和52,则执行该程序输出的结果为( )A.13B.26C.39D.783.某程序框图如图所示,则该程序运行后输出i的值为()A .6B .7C .8D .94.执行如下程序框图,如果输入的[,]4x ππ∈-,则输出y 的取值范围是( )A .[1,0]-B .[1,2]-C .[1,2]D .[1,1]- 5.某算法的程序框如图所示,若输出结果为12,则输入的实数x 的值是 ( )A 2B .32-C .52D .46.执行如图所示的算法流程图,则输出的结果的值为A .2B .1C .0D .-1 7.一程序框图如图所示,如果输出的函数值在区间[]1,2上,那么输入的实数x 的取值范围是( )A .(),0-∞B .[]1,0-C .[)1,+∞ D .[]0,1 8.执行如图1所示的程序框图,若输出b 的值为16,则图中判断框内①处应填( )A .0B .1C .2D .39.执行如图所示的程序框图,若输入的40N =,则输出的S =( )A .115B .116C .357D .35810.阅读如图所示的程序,若执行循环体的次数为5,则程序中a 的取值范围为()A .56a ≤≤B .56a <<C .56a ≤<D .56a <≤ 11.执行如图所示的程序框图,若输入2x =,则输出的S 值为( )A .8B .19C .42D .8912.执行如图所示的程序语句,则输出的s 的值为( )A .22 B .1 C .212+ D 21二、填空题13.下面程序运行后输出的结果为________.520033"";""x y IF x THENy x ELSE y x END IFPRINT x y y x END=-=-<=-=+-=-=14.如图的算法,最后输出的k =_______.15.执行如图所示的流程图,若输入n的值为8,则输出s的值为_________.16.如图程序是求一个函数的函数值的程序,若执行此程序的结果为3,则输入的x值为.17.如图所示的茎叶图为高二某班54名学生的政治考试成绩,程序框图中输入的1254,,a a a 为茎叶图中的学生成绩,则输出的S 和n 的值之和是___.18.程序框图如图所示,若输出的y =0,那么输入的x 为________.19.如图是计算1111232010232010+++++⋅⋅⋅++的值的程序框图.(I)图中空白的判断框应填,执行框应填;(II)写出与程序框图相对应的程序.20.执行如图所示的流程图,则输出的n为________.三、解答题21.银行办理房屋抵押贷款手续如下:先按顺序进行房屋评估、银行审查、签订合同、办理保险产权过户.然后有三种选择:(1)若直接办理抵押贷款,则只进行抵押登记,然后发放贷款;(2)若采用全程担保方式,则直接发放贷款;(3)若采用阶段性担保方式,则先发放贷款,然后再办理抵押登记.试画出办理房屋抵押贷款手续的流程图.22.把下列程序用程序框图表示出来.A=20B=15A=A+BB=A-B A=A BPRINT A+BEND23.[2019·朝鲜中学]在如图所示的程序框图中,有这样一个执行框1()i i x f x -=,其中的函数关系式为42()1x f x x -=+,程序框图中的D 为函数()f x 的定义域.(1)若输入04965x =,请写出输出的所有x 的值; (2)若输出的所有i x 都相等,试求输入的初始值0x .24.我们在人教A 版选修1-2教材的第一章中学习了《统计案例》,请你画出《统计案例》这一章的章节结构图.25.回忆人教A 版必修3《算法初步》这一章,试画出《算法初步》这一章的知识结构图.26.已知函数y=2x+3,设计一个算法,给出函数图象上任一点的横坐标x,求该点到坐标原点的距离,并画出程序框图.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【解析】【分析】结合所给的程序语句确定输出值即可.【详解】程序运行过程如下:首先初始化数据:1,0J A ==,此时满足5J <;执行12,*4J J A A J J =+==+=,此时满足5J <;执行13,*13J J A A J J =+==+=,此时满足5J <;执行14,*29J J A A J J =+==+=,此时满足5J <;执行15,*54J J A A J J =+==+=,此时不满足5J <;跳出循环,输出54A =. 本题选择D 选项. 【点睛】本题主要考查循环语句的理解及其计算等知识,意在考查学生的转化能力和计算求解能力.2.A解析:A 【解析】 【分析】模拟执行程序框图,只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可得到输出的a 的值. . 【详解】若输入,a b 的值分别为195,52,则39,52,39c a b ===,不满足条件,循环;5239÷,余数为13 ,即13,39,31c a b ===,不满足条件,循环; 3913÷,余数为0 ,即0,13,1c a b ===,满足条件,输出13a =,故选A.【点睛】本题主要考查程序框图的循环结构流程图,属于中档题. 解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支结构还是循环结构;(3) 注意区分当型循环结构和直到型循环结构;(4) 处理循环结构的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,(6)在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可.3.B解析:B 【解析】 【分析】模拟执行程序框图,只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可得到输出的i 的值. 【详解】执行程序框图,输入1,1,1m n i ===, 第一次循环2,4,2m n i ===; 第二次循环4,9,3m n i ===; 第三次循环8,16,4m n i ===; 第四次循环16,25,5m n i ===; 第五次循环32,36,6m n i ===; 第六次循环64,49,7m n i ===, 退出循环,输出7i =,故选B. 【点睛】本题主要考查程序框图的循环结构流程图,属于中档题. 解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支结构还是循环结构;(3) 注意区分当型循环结构和直到型循环结构;(4) 处理循环结构的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,(6)在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可.4.B解析:B 【解析】分析:讲原问题转化为分段函数的问题,然后求解函数的值域即可. 详解:流程图计算的输出值为分段函数:()222cos sin 21,2cos 2sin 1,2x x x f x x x x ππ⎧+-<⎪⎪=⎨⎪+-≥⎪⎩,原问题即求解函数()f x 在区间,4ππ⎡⎤-⎢⎥⎣⎦上的值域. 当42x ππ-≤<时:()22cos sin 21cos 21sin 2124f x x x x x x π⎛⎫=+-=++-=+ ⎪⎝⎭,42x ππ-≤<,则152444x πππ-≤+<,此时函数的值域为1,2;当2x ππ≤≤时:()22cos 2sin 1sin 2sin f x x x x x =+-=-+,2x ππ≤≤,则0sin 1x ≤≤,此时函数的值域为[]0,1;综上可得,函数的值域为[]0,1⎡⎡-⋃=-⎣⎣. 即输出y的取值范围是⎡-⎣.本题选择B 选项.点睛:识别、运行程序框图和完善程序框图的思路: (1)要明确程序框图的顺序结构、条件结构和循环结构. (2)要识别、运行程序框图,理解框图所解决的实际问题. (3)按照题目的要求完成解答并验证.5.A解析:A 【解析】分析:先根据循环得函数解析式,再解方程得实数x 的值.详解:因为2log ,12,1x x y x x >⎧=⎨-≤⎩,所以211log 2x x >⎧⎪⎨=⎪⎩或1122x x ≤⎧⎪⎨-=⎪⎩所以x = 选A.点睛:本题考查算法与流程图,考查识别流程图的含义,利用分段函数解决问题能力.6.C解析:C 【解析】分析:由程序框图可知,该程序的功能是利用循环结构计算并输出变量S 的值,模拟程序的运行过程,可得结果.详解:因为cos2n y π=的周期为4, 且一个周期内函数值的和为0,而满足进行循环的n 的最大值为2017,201745041÷=+,故32017cos cos cos ...cos 222S ππππ=++++cos 02π==,故选C.点睛:本题主要考查程序框图,分组求和法求和,余弦函数的周期性,属于中档题. 算法是新课标高考的一大热点,其中算法的交汇性问题已成为高考的一大亮,这类问题常常与函数、数列、不等式等交汇自然,很好地考查考生的信息处理能力及综合运用知识解决问題的能力,解决算法的交汇性问题的方:(1)读懂程序框图、明确交汇知识,(2)根据给出问题与程序框图处理问题即可.7.D解析:D 【解析】分析:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算分段函数的函数值.根据函数的解析式,结合输出的函数值在区间[]1,2,即可得到答案.详解::根据题意,得 当x ∈[﹣2,2]时,f (x )=2x , ∴1≤2x ≤2, ∴0≤x≤1;当x ∉[﹣2,2]时,f (x )=3,不符合, ∴x 的取值范围是[0,1].故选:D .点睛:本题考查了程序框图的应用问题,也考查了分段函数的应用问题,解题时应模拟程序框图的运行过程,以便正确解答问题,属于基础题.8.C解析:C 【解析】分析:模拟执行程序框图,只要按照程序框图规定的运算方法逐次计算,直到达到到输出b 的值为16,即可得输出条件.详解:执行程序框图,输入0,1a b ==,第一次循环,2,1b a ==; 第二次循环,4,2b a ==;第三次循环,16,3b a ==时,应退出循环, 故图中判断框内①处应填2,故选C.点睛:本题主要考查程序框图的循环结构流程图,属于中档题. 解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支结构还是循环结构;(3) 注意区分当型循环结构和直到型循环结构;(4) 处理循环结构的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,(6)在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可.9.D解析:D 【解析】结合题意,程序运行如下: 首先初始化40,1,0N n S ===,第一次循环,22S S n =+=,此时不满足n N >,执行314n n =+=; 第二次循环,210S S n =+=,此时不满足n N >,执行3113n n =+=; 第三次循环,236S S n =+=,此时不满足n N >,执行3140n n =+=; 第四次循环,2116S S n =+=,此时不满足n N >,执行31121n n =+=; 第五次循环,2358S S n =+=,此时满足n N >,跳出循环,输出358S =. 本题选择D 选项.点睛:此类问题的一般解法是严格按照程序框图设计的计算步骤逐步计算,逐次判断是否满足判断框内的条件,决定循环是否结束.要注意初始值的变化,分清计数变量与累加(乘)变量,掌握循环体等关键环节.10.C解析:C 【解析】 输入0,1S i ==执行循环体1,12S S i i i =+==+=,不满足i a > 继续执行循环体3,13S S i i i =+==+=,不满足i a > 继续执行循环体6,14S S i i i =+==+=,不满足i a >继续执行循环体10,15S S i i i =+==+=,不满足i a >继续执行循环体15,16S S i i i =+==+=,由题可知满足6i a =>,输出15S = 故[)5,6a ∈ 故选C11.C解析:C 【解析】执行程序框图,输入,2,0,1,x k S === 第一次循环1,3,k S ==第二次循环2,8,k S ==第三次循环3,19,k S ==第四次循环4,42,k S ==第五次循环5k =,退出循环,输出42S = ,故选C.【方法点睛】本题主要考查程序框图的循环结构流程图,属于中档题. 解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支结构还是循环结构;(3) 注意区分当型循环结构和直到型循环结构;(4) 处理循环结构的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,(6)在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可.12.C解析:C 【解析】模拟程序框图的运行过程,如下:1i =,0s =,0sin 42S π=+=;2i =,50i ≥?,否,2sin 222S π=+=;3i =,50i ≥?,否,3sin 14S π=+==;4i =,50i ≥?,否,101S =+=;5i =,50i ≥?,否,521sin 42S π=+=;6i =,50i ≥?,否,2122S =-=;7i =,50i ≥?,否,7sin 024S π=+=;8i =,50i ≥?,否,0sin 20S π=+=;9i =,50i ≥?,否,90sin42S π=+=;…;s 的值是随i 的变化而改变的,且周期为8,又50682=⨯+,此时终止循环,∴输出的s 值与2i =时相同,为12S =+,故选C. 二、填空题13.3-3【解析】∵输入x =-5<0∴y =x -3=-5-3=-8∴输出x -y =-5-(-8)=3y -x =-8-(-5)=-3点睛:(1)条件结构中条件的判断关键是明确条件结构的功能然后根据是的分支成立的解析:3,-3 【解析】 ∵输入x =-5<0, ∴y =x -3=-5-3=-8,∴输出x -y =-5-(-8)=3,y -x =-8-(-5)=-3.点睛: (1)条件结构中条件的判断关键是明确条件结构的功能,然后根据“是”的分支成立的条件进行判断. (2)对条件结构,无论判断框中的条件是否成立,都只能执行两个分支中的一个,不能同时执行两个分支.14.11【解析】阅读流程图首先初始化数据:进入循环体:满足进行第一次循环:;满足进行第二次循环:;满足进行第三次循环:;满足进行第四次循环:;满足进行第五次循环:;不满足此时跳出循环输出点睛:利用循环结解析:11 【解析】阅读流程图,首先初始化数据:1,0kS,进入循环体:满足20s <,进行第一次循环:1,23S S k k k =+==+=; 满足20s <,进行第二次循环:4,25S S k k k =+==+=; 满足20s <,进行第三次循环:9,27S S k k k =+==+=; 满足20s <,进行第四次循环:16,29S S k k k =+==+=; 满足20s <,进行第五次循环:25,211S S k k k =+==+=; 不满足20s <,此时跳出循环,输出11k =.点睛:利用循环结构表示算法,一定要先确定是用当型循环结构,还是用直到型循环结构;当型循环结构的特点是先判断再循环,直到型循环结构的特点是先执行一次循环体,再判断.15.【解析】试题分析:通过第一次循环得到通过第二次循环得到通过第三次循环得到此时不满足判断框中的条件执行输出故答案应填:考点:程序框图 解析:8【解析】试题分析:通过第一次循环得到1,4,22s i k ←←←,通过第二次循环得到1(24)4,6,32s i k ←⨯=←←,通过第三次循环得到1(46)8,8,43s i k ←⨯=←←,此时不满足判断框中的条件,执行输出8s ←.故答案应填:8. 考点:程序框图.16.4或﹣3【解析】试题分析:根据程序语言的运行过程得程序运行后输出的函数y=;令y=3求出对应x 的值解:根据程序语言的运行过程得该程序运行后输出的是函数y=;又输出y=3所以当x≤0时y=﹣x=3解得解析:4或﹣3【解析】试题分析:根据程序语言的运行过程,得程序运行后输出的函数y=;令y=3,求出对应x的值.解:根据程序语言的运行过程,得该程序运行后输出的是函数y=;又输出y=3,所以,当x≤0时,y=﹣x=3,解得x=﹣3,满足题意;当0<≤1时,y=0,不满足题意;当x>1时,y=x﹣1=3,解得x=4,满足题意;综上,x的值是4或﹣3.故答案为4或﹣3考点:程序框图.17.8613【解析】S为大于等于80分的学生的平均成绩计算得S=86;n表示60分以下的学生人数由茎叶图可知n=13解析:86,13【解析】S为大于等于80分的学生的平均成绩,计算得S=86;n表示60分以下的学生人数,由茎叶图可知n=13.18.-3或0【解析】分析程序中各变量各语句的作用再根据流程图所示的顺序可知:该程序的作用是计算分段函数的函数值当x<0时y=x+3=0∴x=-3满足要求当x=0时y=0∴x=0满足要求当x>0时y=x+解析:-3或0【解析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算分段函数3,00,05,0x xy xx x+<⎧⎪==⎨⎪+>⎩的函数值,当x<0时,y=x+3=0,∴x=-3满足要求,当x=0时,y=0,∴x=0满足要求,当x>0时,y=x+5,∴x=-5,不满足要求,故输入的x的值为:-3或0.19.(I);(II)见解析【解析】试题分析:(I)由已知得本程序的作用是计算由于第一次执行循环时的循环变量初值为2步长为1最后一次执行循环进循环变量值为2010我们根据利用循环结构进行累加的方法不难给出解析:(I )2010?i ≤,1S S i i=++;(II )见解析. 【解析】试题分析:(I )由已知得本程序的作用是计算111123 (2010232010)+++++++,由于第一次执行循环时的循环变量初值为2,步长为1,最后一次执行循环进循环变量值为2010,我们根据利用循环结构进行累加的方法,不难给出结论;(II )先判定循环的结构,然后选择对应的循环语句,对照流程图进行逐句写成语句即可.试题解:(I )判断框:i≤2010或i <2011 执行框:S=S+i+1/i… (II )程序: 程序语言不对扣分 1.运算符号不对扣一分 2.程序结构翻译错误扣2分 (当型用直到型) 3.没有输出语句扣一分 4.没有END 扣一分 考点:循环结构;伪代码.20.【解析】试题分析:第一次循环:第二次循环:第三次循环:结束循环输出考点:循环结构流程图 解析:4【解析】试题分析:第一次循环:255,2S n ==,第二次循环:127,3S n ==,第三次循环:6363,4S n =≤=,结束循环输出4n =考点:循环结构流程图三、解答题21.见解析【解析】【分析】根据顺序确定流程图.【详解】解:【点睛】本题考查流程图画法,考查基本设计能力.22.见解析;【解析】试题分析:首尾加开始与结束圆角矩形框图,赋值语句改为矩形框图,输出语句改为平行四边形框图试题程序框图如下:点睛:23.(1)111,195(2)01x =或02x = 【分析】 ⑴当04965x =时,可以求出11119x =,满足条件i x D ∈,执行循环体,依此类推,而1D -∉,不满足于条件,终止循环,解出i x 的所有项即可⑵要使输出的所有i x 都相等,根据程序框图可得000421x x x -=+,解方程求出初始值0x 的值即可 【详解】(1)当x 0=时,x 1=f(x 0)=f =,x 2=f(x 1)=f=,x 3=f(x 2)=f=-1,终止循环.∴输出的数为,.(2)要使输出的所有x i 都相等,则x i =f(x i -1)=x i -1,此时有x 1=f(x 0)=x 0,即=x 0,解得x 0=1或x 0=2,∴当输入的初始值x 0=1或x 0=2时,输出的所有x i 都相等. 【点睛】本题是一道关于程序框图和函数的综合题,需要理清题中程序框图的逻辑关系,属于中档题.24.【解析】【分析】根据结构图的定义,结合第一章《统计案例》的知识体系可完成其知识结构图.【详解】人教A版选修1-2教材的第一章《统计案例》中,一共有两节:1 回归分析的基本思想及其初步应用,2 独立性检验的基本思想及其初步应用.章节结构图如下图所示:【点睛】本题考查流程图的画法,考查利用数学知识解决实际问题的能力,比较基础.25.见解析.【分析】根据要表达的先后关系,画出环形结构图即可.【详解】知识结构图如下图所示:【点睛】(1)表达逻辑先后关系时,通常使用“环”形结构图.在绘制“环”形结构图时,可以先根据逻辑先后关系按照从左到右或从上到下的顺序画出各要素的图框,再用连线或方向箭头适当连接.(2)“环”形结构图经常用来表示知识的网络关系,即复杂的知识结构图一般都呈“环”形结构,这种图能从多种不同联系的角度来理解知识各版块之间的关系.(3)画“环”形结构图时,必须从整体上理清层次,并抓住系统的主要要素进行分解至基本单元,通过把握各要素之间的相互关系,确定各基本单元之间的逻辑先后顺序,然后按照一定的顺序连接基本单元.26.见解析【解析】试题分析:根据到原点的距离公式22d x y =+,先求出y 值,再求出距离。
粤教版 高中信息技术 修 1第一、二、三、四章 综合 训练(含答案)

第一、二、三、四章综合训练-粤教版(2019)高中信息技术修1一、选择题1.列表q=[1,2,3,4,5,6],删除列表数值1,下列代码不能实现此功能的代码是()A.del q[1]B.del q[0]C.q.pop(0)D.ABC都不可以。
2.下列哪种结构,可是实现计算机自动完成重复性的工作()。
A.顺序结构B.选择结构C.循环结构D.组合结构3.表达式14 % 6 和14 % -6的结果分别是()A.2和-2B.2和2C.2和-4D.2和44.复合数据类型则由简单数据类型组成。
如()()()()。
A.元组、字典、范围、列表B.元素、范围、集合、列表C.元组、字典、集合、列表D.元素、字典、数据、范围5.下列变量名不合法的是()A.2a B.c0C.c_8D.E6a6.将长度为奇数的字符串s从首位字符开始依次存入a(1),a(n - 1),a(3),a(n - 3)...。
如:字符串“xuankao”分存后得到a(1)=“x”,a(6)=“u”,a(3)=“a”,a(4)=“n”,a(5)=“k”,a(2)= “a”,a(7)= “o”,下列能实现该功能的程序段是()A.For i = 1 To Len(s)If I Mod 2= 0 Thena(i) = Mid(s, i, 1)Elsea(Len(s) - i + 1) = Mid(s, i, 1)End IfNext iB.For i = 1 To Len(s)If i Mod 2= 0 Thena(Len(s) - i+1) = Mid(s, i, 1)Elsea(i) = Mid(s, Len(s) - i+1, 1)End IfNext iC.For i = 1 To Len(s)If i Mod 2 = 1 Thena(i) = Mid(s, i, 1)Elsea(Len(s) - i+1) = Mid(s, i, 1)End IfNext iD.For i= 1 To Len(s)If i Mod 2 = 1 Thena(i) = Mid(s, i, 1)Elsea(Len(s) - i+1) =Mid(s, Len(s) - i+1, 1)End IfNext i7.计算机能够直接识别和执行的程序设计语言是()。
(好题)高中数学选修1-2第二章《框图》检测题(包含答案解析)

一、选择题1.商家生产一种产品,需要先进行市场调研,计划对北京、上海、广州三地进行市场调研,待调研结束后决定生产的产品数量,下列四种方案中最可取的是()A.B.C.D.2.执行如图所示的程序框图,则输出n的值是()A.3 B.5 C.7 D.93.执行如图所示的程序框图,当输出S的值为6-时,则输入的0S=()A.7B.8C.9D.10 4.执行如图所示的程序框图,则输出的a=A.1B.1-C.4-D.5 2 -5.执行如图1所示的程序框图,若输出b的值为16,则图中判断框内①处应填()A.0B.1C.2D.36.执行如图所示的程序框图,运行相应的程序,则输出的a的值为()A .32B .23C .13D .2-7.执行下面的程序框图,若1516p =,则输出n 的值为( )A .3B .4C .5D .68.某程序的框图如图所示,执行该程序,若输入的p 为12,则输出的,n s 的值分别为A .3,18n s ==B .4,9n s ==C .3,9n s ==D .4,18n s ==9.执行如图的框图,则输出的s 是( )A .9B .10C .132D .132010.下边程序框图的算法思路是来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图时,若输入的a b 、分别为16、18,输出的结果为a ,则二项式6a x x ⎛- ⎪⎝⎭的展开式中常数项是( )A .-20B .52C .-192D .-16011.某程序框图如图,该程序运行后输出的S 值是( )A.8 B.9 C.10 D.11 12.下列程序框能表示赋值、计算功能的是()A.B.C.D.二、填空题13.执行如图所示的程序框图,则输出的i __________.14.如图是一个算法流程图,则输出的S的值为______________.15.如图所示的流程图是将一系列指令和问题用框图的形式排列而成.箭头说明下一步是到哪一个框图,阅读这个流程图,回答下列问题:如果,那么输出的数是______.(用a,b,c 填空) 16.执行如图所示的程序框图,输出的S 值为__________.17.执行如图所示的程序框图,若输入1S =,1k =,则输出的S =_____________.18.设某程序框图如图所示,该程序运行后输出的k的值是_____.19.如图的程序框图,若任意输入区间[1,18]中的整数x,则输出的x大于39的概率是_______.20.下图是一个算法流程图,则输出k的值是_____三、解答题21.已知数列{}n a 的各项均为正数,观察程序框图,若5k =,10k =时,分别有511S =和1021S =,求数列{}n a 的通项;22.某大学远程教育学院网上学习流程如下:(1)学生凭录取通知书到当地远程教育中心报到,交费注册,领取网上学习注册码;(2)网上选课,课程学习,完成网上平时作业,获得平时作业成绩;(3)预约考试,参加期末考试获得期末考试成绩,获得综合成绩,成绩合格获得学分,否则重修.试画出该远程教育学院网上学习的流程图.23.某班的行政结构如下:班主任下设班委会和团支部,班委会设班长一名,管理学习委员、生活委员、劳动卫生委员、文娱委员和体育委员,团支部设团支书一名,管理组织委员和宣传委员.试画出该班的组织结构图.24.已知函数f(x)=x 2+3x+1,编写一个程序来计算f(4)的值.25.已知数列{}n a 中,1=2a ,下列伪代码的功能是求数列{}n a 的第m 项m a 的值(2)m ≥,现给出此算法流程图的一部分.(1)直接写出流程图中的空格①、②处应填上的内容,并写出n a 与1n a +之间的关系;(2)若输入的m 值为2015,求输出的a 值(写明过程).26.阅读下列乌龙茶的制作工序步骤,并绘制其工序流程图.通过萎调散发部分水分,提高叶片韧性,便于后续工序进行.做青是乌龙茶制作的重要工序,经过做青,叶片边缘细胞受到破坏,发生轻度氧化,呈现红色,叶片中央部分,叶色由暗绿转变为黄绿,即所谓的“绿叶红镶边”.炒青是承上启下的转折工序,主要是抑制鲜叶中的酶的活性,控制氧化进程,防止叶子继续变红,固定做青形成的品质.揉捻是塑造外形的一道工序,通过外力作用使叶片揉破变轻,卷转成条,体积缩小,且便于冲泡.干燥可抑制酶性氧化,蒸发水分和软化叶片,并起热化作用,消除苦涩味,使滋味醇厚.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【解析】试题分析:四种方案中最可取的是,分别派出调研人员齐头并进赴三地搞调研,以便提早结束调研,尽早投产,由此可得结论.解:方案A .立顶→派出调研人员先后赴深圳、天津、成都调研,待调研人员回来后决定生产数量.方案B .立顶→派出调研人员先齐头并进赴深圳、天津调研,结束再赴成都调研,待调研人员回来后决定生产数量.方案C .立顶→派出调研人员先赴成都调研,结束后再齐头并进赴深圳、天津调研,待调研人员回来后决定生产数量.方案D .分别派出调研人员齐头并进赴三地搞调研,以便提早结束调研,尽早投产. 通过四种方案的比较,方案D 更为可取.故选D .点评:本题考查结构图,考查学生分析解决问题的能力,属于基础题.2.D解析:D【分析】由已知的框图可知,该程序的功能是利用循环结构计算输出变量n 的值,模拟程序运行的过程,分析循环中各变量的变化情况,可得答案,本题中在计算S 时,还需要结合数列中的裂项求和法解决问题,即:1111111111114113355779233557799S ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+++=-+-+-+-= ⎪ ⎪ ⎪ ⎪⎢⎥⨯⨯⨯⨯⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦. 【详解】解:由程序框图知:第一次循环:S 初始值为0,不满足49S ≥,故11133S ==⨯,3n =; 第二次循环:当13S =,不满足49S ≥,故11111121133523355S ⎛⎫=+=-+-= ⎪⨯⨯⎝⎭,5n =; 第三次循环:当25S =,不满足49S ≥,故11131335577S =++=⨯⨯⨯,7n =; 第四次循环:当37S =,不满足49S ≥,故11114133557799S =+++=⨯⨯⨯⨯,9n =; 此时,49S =,满足49S ≥,退出循环,输出9n =,故选D. 【点睛】本题考查了程序框图的应用问题,解题时模拟程序框图的运行过程,便可得出正确的结论,这类题型往往会和其他知识综合,解题需结合其他知识加以解决.3.B解析:B 【解析】 【详解】分析:根据循环结构的特征,依次算出每个循环单元的值,同时判定是否要继续返回循环体,即可求得S 的值. 详解:01,i S S ==02,2S S i =-=024,3S S i =--= 0248,4S S i =---=因为当4i < 不成立时,输出S ,且输出-6S = 所以06248S -=--- 所以08S = 所以选B点睛:本题考查了循环结构在程序框图中的应用,按照要求逐步运算即可,属于简单题.4.C解析:C 【解析】分析:模拟执行程序框图,只要按照程序框图规定的运算方法逐次计算,直到达到输出条件,即可得到输出的a 的值. 详解:输入1,4i a ==-;第一次循环,得1,1,2b a i =-=-=;第二次循环,得55,,322b a i =-=-=; 第三次循环,得4,4,4b a i =-=-=,…,以此类推,知该程序框图的周期3,又知当40i =退出循环,此时共循环了39次, 所以输出的4a =-,故选C.点睛:本题主要考查程序框图的循环结构流程图,属于中档题. 解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支结构还是循环结构;(3) 注意区分当型循环结构和直到型循环结构;(4) 处理循环结构的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,(6)在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可.5.C解析:C 【解析】分析:模拟执行程序框图,只要按照程序框图规定的运算方法逐次计算,直到达到到输出b 的值为16,即可得输出条件.详解:执行程序框图,输入0,1a b ==,第一次循环,2,1b a ==; 第二次循环,4,2b a ==;第三次循环,16,3b a ==时,应退出循环, 故图中判断框内①处应填2,故选C.点睛:本题主要考查程序框图的循环结构流程图,属于中档题. 解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支结构还是循环结构;(3) 注意区分当型循环结构和直到型循环结构;(4) 处理循环结构的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,(6)在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可.6.C解析:C 【解析】执行程序框图,输入2,1a n =-=时,32a =;2n =时,13a =;3n =时,2a =-;4n =时,32a =,a 的值呈周期性出现,周期为3,201867232=⨯+,所以2018=n 时,1,20193a n ==,退出循环,输出13a =,故选C.【方法点睛】本题主要考查程序框图的循环结构流程图,属于中档题. 解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支结构还是循环结构;(3) 注意区分当型循环结构和直到型循环结构;(4) 处理循环结构的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,(6)在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可.7.C解析:C 【解析】 循环依次为21111331771150,2;,3;,4;,5;2222448881616S n S n S n S n =+===+===+===+== 结束循环,输出5n = ,选C. 8.D解析:D 【解析】输入参数12,0,1p s n ===012s =<,执行第一次循环,33,12s s n n n =+==+= 312s =<,执行第二次循环,39,13s s n n n =+==+=912s =<,执行第三次循环,318,14s s n n n =+==+= 1812s =>退出循环,输出18,4s n ==故选D点睛:算法与流程图的考查,侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环起点条件、循环次数、循环终止条件,更要通过循环规律,明确流程图研究的数学问题,是求和还是求项.9.C解析:C 【解析】循环依次为11212,11;1112132,10S i S i =⨯===⨯==,结束循环,输出132S = ,选C.10.D解析:D 【解析】由题意知,框图的功能是求两数a b 、的最大公约数,故输入16、18后输出的结果为2a =,所以二项式为6⎛ ⎝,其展开式的通项为616(r rr r T C -+= 666(1)2,0,1,2,,6r r r rC x r --=-=,令3r =可得展开式中的常数项为33346(1)2160T C =-=-.选D .11.B解析:B 【解析】由题设中提供的算法流程图可知程序执行的是求和运算:由于()cos12if i π=+的周期是24,104222T ππ===⨯+,所以101cos1011092i iS π==+=-+=∑,应选答案B .12.C解析:C 【解析】根据算法语言特征及算法流程图的要求与规定,表示赋值、计算的处理的图框应是矩形,应选答案C 。
基于两阶段排放算法的矩形件排样优化方法

基于两阶段排放算法的矩形件排样优化方法摘要:矩形件排样优化是在工业生产中普遍存在的问题,有效的排样方法可以节约原材料、提高生产效率。
本文提出了一种基于两阶段排放算法的矩形件排样优化方法,通过两阶段的排放算法对矩形件进行排样,同时结合优化算法,得到了较好的排样效果。
关键词:矩形件;排样优化;两阶段排放算法;优化算法一、引言矩形件是在工业生产中广泛使用的一种零部件,其排样优化问题一直是一个备受关注的研究领域。
矩形件排样优化问题是指在给定的矩形件集合中,如何将这些矩形件尽可能地排放在一个矩形区域内,以减少剩余空间,达到节约原材料、提高生产效率的目的。
目前,关于矩形件排样优化的研究有很多,其中基于排放算法的方法是一种比较常见的方法。
排放算法是指将一组或多组物体放置到一个给定的区域中,并且使得它们之间不发生碰撞,从而尽可能地减少剩余空间。
而在排放算法中,两阶段排放算法是一种比较经典的方法,其将排放过程分为两个阶段进行处理,分别是自底向上的排放阶段和自顶向下的排放阶段,通过这种分阶段的排放方式,使得得到的排样效果更加优化。
本文将提出一种基于两阶段排放算法的矩形件排样优化方法,通过两阶段的排放过程,结合优化算法,使得排样结果更加紧凑,达到了一定的优化效果。
1. 基本思路基于两阶段排放算法的矩形件排样方法主要分为两个阶段进行处理,即自底向上的排放阶段和自顶向下的排放阶段。
在自底向上的排放阶段中,首先将矩形件按照一定的规则排序,然后从下往上逐个放入排样区域中,当无法放入时,将进行下一个矩形件的尝试。
在自顶向下的排放阶段中,使用优化算法对排样进行优化,使得得到的排样更加紧凑。
2. 自底向上的排放阶段自底向上的排放阶段是基于经典的排放算法,其主要思路是将矩形件从下往上逐个放入排样区域中,直到无法再放入为止。
在这个过程中,要保证矩形件的位置能够使得整体排样效果更加紧凑。
在自底向上的排放过程中,可以采用一些启发式算法来确定矩形件的放置位置,例如先放置矩形件底部距离排样区域底部最近的位置,再逐步向上尝试放入,直到找到合适位置或无法放入为止。
初级程序员2006上半年下午试题 原版文件

第2章程序员下午试题分析与解答试题一阅读以下说明和流程图,回答问题1至问题3。
[说明]信息处理过程中经常需要将图片或汉字点阵做旋转处理。
一个矩阵以顺时针方向旋转90°后可以形成另一个矩阵,如下图所示:流程图2-1描述了对n*n矩阵的某种处理。
流程图2-2是将矩阵A顺时针旋转90°形成矩阵B的具体算法。
[问题1]请写出以下3*3单位矩阵沿顺时针方向旋转90°后所形成的矩阵。
[问题2]如果以下3*3矩阵沿顺时针方向旋转90°后所形成的矩阵就是原来的矩阵:其中,位于*处的元素需要考生填写请完整地写出该矩阵。
[问题3]在上述流程图2-1和图2-2的算法中,(1)矩阵A第i行第j列的元素A(i,j)被复制到矩阵B中的哪个位置?(2)A(i,j)后来又被复制到矩阵C中的哪个位置?(3)填补流程图2-2中的空缺。
试题一[分析]信息处理过程中经常需要将图片点阵或汉字点阵做旋转处理。
这种方法可以简化为对n*n矩阵的旋转处理。
其中,n应该是一个变量,运行时由该程序模块外部导入具体的值。
编程技术的一个基本要点就是对通用的情况找出规律,再按规律进行处理。
试题中给出了“按顺时针方向旋转90°”的例子。
在这种场合,用案例说明比叙述定义更为简单。
人们也不难在案例的基础上推广理解。
对于问题1,人们不难获得另一个案例:对于问题2,根据按顺时针方向旋转90°保持矩阵不变,可以逐步推断出一些元素的值:对于问题3,矩阵A按顺时针方向旋转90°得到矩阵B,矩阵B按顺时针方向旋转90°得到矩阵C。
矩阵A的第1行复制到矩阵B的第n列。
矩阵A的第2行复制到矩阵B的第n-1列。
矩阵A的第3行复制到矩阵B的第n-2列。
按照上述规律,矩阵A的第i行应复制到矩阵B的第n-i+1列。
A(i,j)是矩阵A的第i行第j列的元素,它应复制到矩阵B的第n-i+1列中,第j行元素。
即A(i,j)→B(j,n-i+1)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矩形件排样程序的实现王晨浩摘要针对样板矩形排样程序的实现问题,本人通过实施FORTRAN90编程,采用直接明了的数字排列的方式,直观清晰的展现了一个矩形样板中矩形件排样的最优方案。
而程序语言本身,结构明朗,层次清晰,适合懂本语言的人斟酌损益和修缮完美;程序运行系统,清晰明朗的输入输出步骤,将程序层序化和普遍化展现淋漓;程序表述方式,人性化的中文语言提示,将程序的可接受度和观赏度大大提高。
本程序采取了通过对板面和具体矩形的数字化展现,通过对整体的数字比较描摹和判定板面的整体矩形排列方式,最终以一个具体的数字排列,实现对矩形排列的宏观显现。
关键词:FORTRAN90程序,矩形排列方案,板面矩形设计一、问题重述(一)问题简介工业上经常需要在一块大板材上下料得到若干个小的矩形件,使得板材的利用率最高,即所剩余的边角料最少。
例如在一块宽15、高无限制的矩形板材上,排列25块尺寸已知的小矩形,25块小矩形的尺寸如表1,板材的利用率达100%,如图1所示。
图1 一种排样方案表1 小矩形的尺寸序号宽 高 112 6 24 7 36 7 410 2 52 5 66 4 74 2 84 6 97 9 104 5 116 4 124 6 136 3 144 5 152 4 168 4 178 6 188 3 196 3 202 6 218 2 223 5 232 5 243 4 252 4如果上述排样方案未知,即不知道图1的排法,那么如何将这25块小矩形按照某种次序排在一个大的板材上呢?目前这仍是一个世界难题。
通常要求在一个排样图中,任何一个矩形件在不超出板材边界的情况下,按照一个排样方案(给定的次序)采用下列一些方法来安排实际矩形件的排列,对于一个排样方案(解)},{R P D =,其中),,,(21n p p p P =,),,,(21n r r r R =,p i 为矩形件的序号,r i 为排样方式,r i =1表示将矩形件旋转90°, r i =0表示矩形件不旋转。
将第i 个矩形件安排在板材上的过程中,均不能再往下、往左移动,则称其满足BL 条件(bottom-left-condition ,BL-condition )。
(二) 剩余矩形排样法简介剩余矩形排样法是目前所提出的一种有效的排样算法,该方法记录了所有可利用的空间,更能合理地分配给待排样的矩形件,提高了每个排样方案的板材利用率,更接近最优排样方案。
例如对于同一个矩形件序列)4,3,2,1(进行排样,图3(a)中下方的空洞以往的排样算法都无法利用,矩形4只能被排到上方。
而利用剩余矩形排样法可以很好的解决这个问题,它可以使矩形4充分利用下方的空间,如图3(b)。
图3 剩余矩形排样法的优越性剩余矩形排样算法用一个矩形数据集合来表示板材目前的剩余位置情况,任何未被排样的空间(包括孤立的缝隙),都在剩余矩形集合中表示,不会遗漏任何一个。
而在每一个矩形件被排入前,都需根据这个剩余矩形集合中的数据来选择最为合理的位置进行排放。
下面给出剩余矩形的具体形成方法(这里用矩形的左下角坐标和右上角坐标来确定这个矩形的的位置):(1) 板材的左下角和右上角坐标分别为),()0,0(H W 和,于是开始时剩余矩形数据集中只有一个矩形为)],(),0,0[(1H W R =。
(2) 当排入一个矩形件i (宽i w 高i h )后,需将剩余矩形数据集合中的每一个矩形都减掉此矩形件所占的位置。
若此矩形件的左下角坐标为),(11i i y x ,且为横排(即矩形件不旋转90°),则每个剩余矩形都减掉与矩形件)],(),,[(11111i i i i i i h y w x y x ++相交的部分。
例如矩形)],(),0,0[(1H W R =减掉与矩形件i 相交的部分后,形成了四个新的剩余矩形为:)],(),,[()],(),0,0[(1111i i i i i i h y w x y x H W ++- )]},(),0,[()],,(),,0[()],,(),0,0[()],,(),0,0{[(1111H W w x H W h y H x y W i i i i i i ++= 按顺时针方向记录矩形。
如图4所示。
若为竖排(即矩形件旋转90°),计算方法类似。
图4 剩余矩形表示法依此类推,将矩形数据集中的所有剩余矩形都作如此操作,减去所排入矩形件i 所占位置,形成新的剩余矩形。
(3) 由于新的剩余矩形的产生,又将引起原矩形数据集的改变,因此对其进行整理:去掉面积为零的或已无法排下所剩的任何一个矩形件的剩余矩形;把具有完全包含关系的剩余矩形中面积小的矩形去除、有相交关系的矩形全部保留。
得到新的剩余矩形集,为下一次排放使用。
用剩余矩形表示法可记录每个可形成最大矩形的空间,用于排样。
将这种表示法与BL 排样算法结合,就形成了剩余矩形排样算法,对于给定的一个排样方案},{R P D =,其中),,,(21n p p p P =,),,,(21n r r r R =,具体排样过程如下:(1) 开始时剩余矩形集S 中仅有一个矩形,即板材本身)],(),0,0[(1H W R =。
(2) 从排列P 中取出第一个需排的矩形件1p (宽1p w ,高1p h ),将1p 根据相应排放方式 1r 排放在板材的左下角,用上面所述的剩余矩形表示法计算新的板材剩余矩形集},{21R R S =:若01=r (横排),则)],(),0,[(11H W w R p =,)],(),,0[(12H W h R p =,如图5;若11=r (竖排),则)],(),0,[(11H W h R p =,)],(),,0[(12H W w R p =。
图5 剩余矩形排样过程(3) 依此类推,按顺序逐一排放),,2(n i p i =,直至所有矩形排放完毕。
每放入一矩形件,都需根据剩余矩形集确定其排放位置,即在剩余矩形集中选择宽高均大于等于此矩形件的底部最低的最靠左的剩余矩形(先靠下后靠左),让矩形件与剩余矩形的左下角重叠。
同时放入矩形后要对剩余矩形集进行整理更新。
同样,剩余矩形排样算法也满足BL 条件。
二、 问题分析随着科学技术的日益发展,计算机科学的进步往往使我们叹为观止,在工业等领域的一些现实生活的难题,往往为我们所关注并且深深的影响着我们。
对于本题,现有的一些方法往往比较复杂和难算,那么计算机能不能帮助我们较简便的解决这个问题呢?面对着本题中的算法,我想采用了学过的FORTRAN90来编程实现。
而此计算机语言最大的特点就是用于计算,那么能不能把实际问题和计算交织在一起呢?所以我选择了用数组中的数字宏观显现此实际的分配方案,并采用数字的整改来体现排列矩形的过程,采用对数字的比较和相应的算法来实现判别和判定。
而此方法的难点在于判定算法的确定,回顾此计算机语言,我们采用最多的是数组定义、循环语句和条件选择等程序的设计。
反观本算法,我们可以得到以下结论:1,在判定之前,我们要对本题所已知的已知量进行分析和总结,即板面特点(宽15米,长度不限),25个矩形的规格(宽和高),矩形在此期间的变化(顺序和旋转)。
并将其合理载入。
2,在判定时,我们首先从板面的最底行判定,并且以最底行的宽为判定首要问题,而后以由底行到高层的顺序依次进行判定,其次在判定行后,我们需要对整个矩形的版面数字进行综合判定,即对该矩形的确定行进行展开,综合判定此矩形的位置。
3,在判定后,我们需要在判定合格的基础上进行整改,及将所要求的矩形进行摆放。
三、模型假设模型假设分别对判定前、中、后期进行假设。
1、前期:记板面整体为一个大数组,由于本题可假设为高50,宽15的数组,数组元素全为0,其他矩形可依次按序号和规格确定该矩形,即用1—25的序号表示。
并可用三维数组综合表示此几个矩形。
在排列矩形顺序和旋转方式上可分别定义为一个含25个元素的一维数组。
2、中期:可分别建立3个循环:1,25个矩形顺序循环,即一个一个的写入板面。
2,判定最底行的宽是否符合矩形宽的要求,即判断一共有几个连续的0。
3,判定整个矩形边框是否都符合要求,即判断以上述边为底边,向上判断该矩形的面积的元素是否都是0。
4、后期:可以建立一个循环,即整改数组的元素,如果以上条件均符合,那么将该矩形的代号均写入该板面的数组。
并按照要求输出。
四、模型建立(一)模型准备设一个三维数组(s),分别以矩形的长(chang)、宽(kuan)、矩形序数(i)为三维坐标。
定义一个四个一维数组,分别把各矩形的长(chang)、宽(kuan)、顺序(shunxu)、旋转方式(xuanzhuan)记为一个数组。
用三维数组s(chang,kuan,i)分别综合表示1个样板面和25个矩形,chang(i)、kuan(i)分别依次表示25个矩形的长和宽,shunxu(i)代表本次排列的顺序,xuanzhuan(i)代表本次矩形旋转的角度(1—代表旋转90度,0—代表不旋转)。
运行时,当xuanzhuan(shunxu(i))=1时,该矩形chang(shunxu (i))和kuan(shunxu(i))互换。
(二)模型实施模型按矩形顺序shunxu(i)输入,循环25次,分别写入juxing(chang(shunxu (i)),kuan(shunxu(i)),shunxu(i)),并从下至上依次对连续0个数(即未被剩余的空间长)进行检验count,以寻找chang(i)=count的矩形的底层线段末端在某点(横坐标j,纵坐标k)上,在意这条线为底做矩形,划定区域{j-chang(shunxu(i))——j,k-kuan(shunxu(i))——k},一次检验此区域的0个数(未被剩余空间区域),如果0的个数(c)=chang(shunxu(i))*kuan (shunxu(i)),则进行依次写入给矩形的顺序号(shunxu(i)),一旦写入成功,则轮到下一个矩形juxing(chang(shunxu(i+1)),kuan(shunxu(i+1)),shunxu (i+1))的写入程序。
(三)模型求解按照实施阶段具体实施后,结果将以一个长为15,高为50的矩阵输出,1—25的数字将以一个横纵方块的形式在样板面上出现。
除此之外,还可以将各个板面进程和相关数据进行写入和输出。
五、模型分析本程序采取了通过对板面和具体矩形的数字化展现,通过对整体的数字比较描摹和判定板面的整体矩形排列方式,最终以一个具体的数字排列,实现对矩形排列的宏观显现。
本程序优点在于综合运用了循环、条件、数组等多方面的FORTRAN90知识,拟合剩余矩形排列算法,综合成一个实用模型。
