1.1.1正弦定理2解的个数
(完整)1.1.1正弦定理(用)

解三角形.
C 30o, a c 4 3
(2)已知两边和其中一边的对角,求其他边和角.
例2:在ABC中,a= 3,b 2, B 450,求A,C,c
解:
sin A a sin B
3 2 2
3
b
2
2
Q a b, A B,且00 A 1800 A 600 或A 1200
sin A sin B sin B sin C sin C sin A
2sin A : sin B : sin C a : b : c
(3) a b c sin A sin B sin C
abc
k(k 0)
sin A sin B sinC
或a k sin A,b k sin B,c k sinC (k 0).
(1)当A 600,C 1800 ( A B) 75(0 三角形中大边对大角)
c bsin C 2 6 2 6 2
sin B 2 4
2
2 (2)当A 1200,C 1800 ( A B) 150
c bsin C 2 6 2 6 2
k,由
正
弦
定理,
得
a ksinA,b ksinB,c ksinC
代入已知条件,得:
sinA
sinB
sinC
cosA cosB cosC
即 tanA tanB tanC
又A,B,C (0,π),A B C, 从而ΔABC为正三角形。
3.在△ABC中,A、B、C的对边分别为a、b、c, 若b=acos C,试判断△ABC的形状.
1.1.1 正弦定理

已知两角和任意一边, 已知两角和任意一边, 求其他两边和一角 。 。 【例 1】 在△ABC 中,已知A = 45 , C = 30 , C c = 10,解三角形. 解: B =180° (A + C) =105° a b
定理的应用
c sin A 10×sin 45° ∴a = =10 2 = sinC sin30° b c = ∵ sin B sin C c sin B 10×sin 105° ∴ b= = = 5( 6 + 2 ) sin 30° sin C
a c = ∵ sin A sinC
A
c
B
【巩固练习】
6+ 2 sin 75 = 4
1.在△ABC中,已知 A=75°,B= 45°, c= 3 2 ,解三角形.
答案:C = 60°, a = 3 + 3 , b = 2 3
2.在△ABC中,已知 A=30°,B=120°, b=12 ,解三角形.
答案:C = 30°, a = 4 3 , c = 4 3
回应情境 △ABC中,已知 =75,C=60,AC=100,求 中 已知A= , = , = , B AB. . c 解: = 180° (A + C) = 45° B
b c a ∵ = sin B sinC 60 b sinC 100× sin60° ∴c = = C sin B sin45° = 50 6
b
A
c
D
B
C
a
c
B
D
a b c b 同理可得 = = sin A sin B sinC sin B
在一个三角形中,各边和它所对角的正弦的比相等, 在一个三角形中,各边和它所对角的正弦的比相等, 即
§1.1.1-2 正弦定理(二)

§1.1.1-2 正弦定理(二)
课堂练习 <<教材>> P.4
练习1.2
书面作业
<<教材>> P.10 习题1.1 A组1(1).2(1.3) B组2
2013-1-16
重庆市万州高级中学 曾国荣 wzzxzgr@
12
(3)正弦定理的变形:
①
a 2R sin A, b 2R sin B, c 2R sin C
边角 互化
③ a : b : c sin A : sin B : sin C
2013-1-16
a b c , sin B , sin C wzzxzgr@ 11
①
a 2R sin A, b 2R sin B, c 2R sin C
边角 互化
a b c , sin B , sin C ② sin A 2R 2R 2R
③ a : b : c sin A : sin B : sin C
2013-1-16
重庆市万州高级中学 曾国荣 wzzxzgr@
解法二:由正弦定理 a b c 2 R 得:
sin A sin B sin C
sin A
a b c , sin B , sin C 2R 2R 2R
b c a 2 b2 c2 所以 b c , 2 2 2 2R 2R 4R 4R 4R 即 b2 c2 , a 2 b2 c2,则 b c, a2 b2 c2 ,
4
§1.1.1-2 正弦定理(二)
已知边a,b和角A,求其他边和角.
A为锐角
C b A a<bsinA 无解 C b a A C b a b C a C
§1.1.1正弦定理(2)
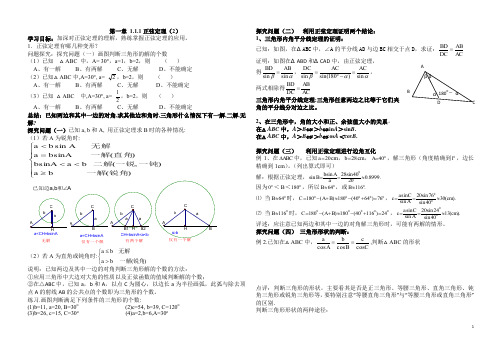
第一章 1.1.1正弦定理(2)学习目标:加深对正弦定理的理解,熟练掌握正弦定理的应用。
1.正弦定理有哪几种变形?问题探究:探究问题(一)画图判断三角形的解的个数 (1)已知 △ABC 中,A= 30°,a=1,b=2,则 ( ) A 、有一解 B 、有两解 C 、无解 D 、不能确定 (2)已知△ABC 中,A=30°, a= 2,b=2,则 ( )A 、有一解B 、有两解C 、无解D 、不能确定(3)已知 △ABC 中,A=30°, a= 21,b=2,则 ( )A 、有一解B 、有两解C 、无解D 、不能确定总结:已知两边和其中一边的对角,求其他边和角时,三角形什么情况下有一解,二解,无解?探究问题(一)已知a, b 和A, 用正弦定理求B 时的各种情况: (1)若A 为锐角时:⎪⎪⎩⎪⎪⎨⎧≥<<=<)( b a ) ,(b a bsinA )( bsinAasin 锐角一解一钝一锐二解直角一解无解A b a已知边a,b 和∠A有两个解仅有一个解无解CH=bsinA<a<b a=CH=bsinA a<CH=bsinA(2)若A 为直角或钝角时:⎩⎨⎧>≤)( b a 锐角一解无解b a说明:已知两边及其中一边的对角判断三角形解的个数的方法:①应用三角形中大边对大角的性质以及正弦函数的值域判断解的个数;②在△ABC 中,已知a ,b 和A ,以点C 为圆心,以边长a 为半径画弧,此弧与除去顶点A 的射线AB 的公共点的个数即为三角形的个数。
练习.画图判断满足下列条件的三角形的个数:(1)b=11, a=20, B=30o (2)c=54, b=39, C=120o (3)b=26, c=15, C=30o (4)a=2,b=6,A=30o探究问题(二) 利用正弦定理证明两个结论: 1、三角形内角平分线定理的证明:已知:如图,在ΔABC 中,∠A 的平分线AD 与边BC 相交于点D ,求证:BD ABDC AC=证明:如图在ΔABD 和ΔCAD 中,由正弦定理,得sin sin BD AB βα=,0sin sin(180)sin DC AC ACβαα==-,两式相除得BD ABDC AC = 三角形内角平分线定理:三角形任意两边之比等于它们夹角的平分线分对边之比。
正弦定理2

等腰三角形或直角三角形
D
)
例2.在∆ABC中,a + b = 6 + 6 3, A = 30°, B = 60° 求边长c
C=12
变式2.在∆ABC中,下列结论正确的是: a b−c (1) = sin A sin B − sin C 2 2 2 2 a +b b+c sin A + sin B sin B + sin C (2) = ⇔ = c a sin C sin A (3)a=b ⇔ sin2A=sin2B (4) sin B > sin C ⇔ b > c ⇔ B > C
C a b h 60° B
A
2.在△ABC中,a=m, b=2, B=30°, 若这个三角形 中 °
有两个解, 的取值范围是_______. 有两个解,则m的取值范围是 的取值范围是
m 30°
m
m 2
m <2<m 2
B
30
°
2<m<4
探究新知( 探究新知(一)
正弦定理的常见变形公式有哪些? 正弦定理的常见变形公式有哪些?
a+b a+b+c (4) = = 2 R(比例的性质) sin A + sin B sin A + sin B + sin C
注意:根据( ),(2 注意:根据(1),(2)可以实现三 角形中的边和角之间的相互转化。 角形中的边和角之间的相互转化。
典例分析
a b 例1.(1)∆ABC中, , ∆ABC 为( C ) = cos A cos B
小结 1.正弦定理的常见变形公式: 正弦定理的常见变形公式: 正弦定理的常见变形公式 ()a = 2R sin A, b = 2R sin B, c = 2R sin C 1
1.1.1正弦定理2

a b a sin B 1 sin A 解:由 sin A sin B 得 b 2
∵ 在 ABC 中 a b ∴ A 为锐角
A 30
变式:在例 2 中,将已知条件改为以下 几种情况,角B的结果有几种?
1 2
b 20, A 60 , a 20 3 ;
S ABC
∴
S ABC
1 ab sin C bc sin A ac sin B 2 2 2
1 1 S ABC ac sin B ab sin C 2 2 1 bc sin A 2 1 1
正弦定理
在一个三角形中,各边和它所对角的 正弦的比相等.
即
变式:
a b c sin A sin B sin C
j AB j AC j CB
B A
j
csin A asinC
同理,过点C作 j BC
a c sin A sin C
则
j AB j (AC CB )
变式训练:
(1) 在△ABC中,已知b= , 3 A=
45 , B=
,求 60 a。
b sin A a b 3 sin 45 = = 2 解: ∵ ∴ a sin B sin A sin B sin 60
(2) 在△ABC中,已知c= , 3A=
, 75B =
60b。 ,求
a b c 3 2 R(R为△ABC外接圆半径) sin A sin B sin C
a b b c c a 1 ; ; sin A sin B sin B sin C sin C sin A 2sin A : sin B : sin C a : b : c
天津市塘沽区紫云中学2014年高中数学 1.1.1 正弦定理课件(二)新人教A版必修5

研一研·问题探究、课堂更高效
1.1.1(二)
问题探究一 问题 1
已知两边及其中一边的对角, 判断三角形解的个数
本 课 栏 目 开 关
在△ABC 中,已知 a,b 和 A,若 A 为直角,讨论三
角形解的情况.(请完成下表) 关系 式 a≤ b a>b
图形
解的 个数
无
解
一
解
研一研·问题探究、课堂更高效
1.1.1(二)
问题2 在△ABC中,已知a,b和A,若A为钝角,讨论三角 形解的情况.(请完成下表) 关系 式 a≤b a>b
本 课 栏 目 开 关
图形
解的 个数
无解
一解
研一研·问题探究、课堂更高效
1.1.1(二)
本 课 栏 目 开 关
问题3 在△ABC中,已知a,b和A,若A为锐角,讨论三角 形解的情况.(请完成下表) 关 a=bsin A bsin A<a<b a≥ b 系 a<bsin A 式
本 课 栏 目 开 关
角,一钝角) (锐角) a>b 一解(锐角)
1.1.1(二)
本 课 栏 目 开 关
2.判断三角形的形状,最终目的是判断三角形是否是特殊三 角形,当所给条件含有边和角时,应利用正弦定理将条件统 一为“边”之间的关系式或“角”之间的关系式.
1.1.1(二)
1.1.1 正弦定理(二)
【读一读学习要求,目标更明确】 1.熟记正弦定理的有关变形公式. 2. 探究三角形面积公式的表现形式, 能结合正弦定理解与面 积有关的斜三角形问题. 3.能根据条件,判断三角形解的个数. 【看一看学法指导,学习更灵活】 1.已知两边及其中一边对角解三角形,其解不一定唯一,应 注意运用大边对大角的理论判断解的情况. 2. 判断三角形形状时, 不要在等式两边轻易地除以含有边角 的因式,造成漏解.
黑龙江省哈尔滨市高中数学 第一章 解三角形 1.1.1 正

1.1.1 正弦定理(二)【学习目标】1.能应用正弦定理解三角形;2.掌握三角形面积公式;3.能利用条件判断三角形解的个数【重点难点】正弦定理及其应用;解三角形中知两边一对角型中解的判断.【知识梳理】1.正弦定理:a sin A =b sin B =c sin C=2R 的常见变形: (1)sin A ∶sin B ∶sin C =a ∶b ∶c ;(2)a sin A =b sin B =c sin C =a +b +c sin A +sin B +sin C=2R ; (3)a =2R sin A ,b =2R sin B ,c =2R sin C ;(4)sin A =a 2R ,sin B =b 2R ,sin C =c2R. 2.正弦定理的应用 从理论上正弦定理可解决两类问题:(1)两角和任意一边,求其它两边和一角;(2)两边和其中一边对角,求另一边的对角,进而可求其它的边和角 3.三角形面积公式:S =12ab sin C =12bc sin A =12acsin B . 4.ABC ∆中,已知,a b 及锐角A ,则a 、b 、sin A 满足什么关系时,三角形无解,有一解,有两解?⑴若A 为锐角时:⎪⎪⎩⎪⎪⎨⎧≥<<=<)( b a ),( b a bsinA )( bsinA a sin 锐角一解一钝一锐二解直角一解无解A b a ⑵若A 为直角或钝角时:⎩⎨⎧>≤)( b a 锐角一解无解b a【课内练习】1、已知△ABC 的面积为23,且3,2==c b ,则∠A 等于 ( ) A .30° B .30°或150° C .60°D .60°或120° 2.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知A =60°,a =3, b =1,则c =________.3.(1)在C A a c B b ABC ,,1,60,30和求中,===∆;(2)在C B b a A c ABC ,,2,45,60和求中,===∆.4.在△ABC 中,a ,b ,c 分别是三个内角A ,B ,C 的对边,若a =2,C =π4, cos B 2=255,求△ABC 的面积S .【课外练习】1.△ABC 中,∠A、∠B 的对边分别为a ,b ,且∠A=60°,4,6==b a ,那么满足条件的△ABC( )A .有一个解B .有两个解C .无解D .不能确定2.已知三角形面积为14,外接圆面积为π,则这个三角形的三边之积为( ) A .1 B .2C. 12D .4 3.在△ABC 中,已知a =32,cos C =13,S △ABC =43,则b =________. 4.(1)在ABC △中,3,6,30a c A ===o ,求ABC △的面积S .(2)在ABC △中,4,30,45a B C ===o o,求ABC △的外接圆半径R 和面积S .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a b sin A 无解
a bsinA 一解(直角) bsinA a b 二解(一锐,一钝)
a ≥ b
一解(锐角)
已知边a,b和A
C b
a
A H
a<CH=bsinA 无解
C
C
b a
A B
b
a
a
A
B1 H B2
a=CH=bsinA 仅有一个解
CH=bsinA<a<b 有两个解
C
b
a
A
H
B
ab
仅有一个解
⑵若A为直角或钝角时:
a ≤ b 无解 a b 一解(锐角)
C a
b
A
C
b
a
A
已知两边和其中一边的对角”的三角形的解
的个数的表格
A 90o
A 90o
a b 一解
一解
a b 无解
一解
a bsin A 二解
a b 无解 a bsin A 一解
C
∵
2√3
3
> 1,
20
∴ 无解.
60° A
思考: 当b=20,A=60°,a=?时,
有1解、2解、无解.
练习
ABC中,
(1)已知c=√3,A=45°,B=75°, 则a=√_2___,
(2)已知c=2,A=120°,a=2√3,
则B=_3_0_°_,
(3)已知c=2,A=45°,a= 2√6 ,则
B=_7_5_°__或__1_5_°____.
3
小结
1. 正弦定理 解三角形时,注意大边对大角
a= b =c sinA sinB sinC
=2R
是解斜三角形的工具之一.
2. 正弦定理可解以下两种类型的三角形: (1)已知两角及一边;(只有一解) (2)已知两边及其中一边的对角→↓.
⑴若A为锐角时:
无解!
C
a
b
B
c
A
为啥呢?
在△ABC中,将已知条件改为以下几 种情况,结果如何?
(1) b=20,A=60°,a=20√3 ;
(2) b=20,A=60°,a=10√3 ;
(3) b=20,A=60°,a=15.
C
b
A 60°
B
(1) b=20,A=60°,a=20√3
sinB=
b
sinA a
=
1 2
,
B=30°或150°,
C
2060° 20√3
A
B
∵ 150°+60°> 180°,
∴ B=150°应舍去.
(2) b=20,A=60°,a=10√3 C
sinB=
b sinA a
=1 ,
20
B=90°.
60°
A
B
(3) b=20,A=60°,a=15.
sinB=
b
sinA a
=
2√3
3
,
1.1.1正弦定理 ----解的个数
复习回顾:1. Βιβλιοθήκη 弦定理abc
sin A sin B sinC
是解斜三角形的工具之一.
注:每个等式可视为一 个方程:知三求一
2. 正弦定理可解以下两种类型的三角形: (1)已知两角及一边; (2)已知两边及其中一边的对角.
上一节课后探究结果展示
在△ABC中,已知 a=4,b=10 , A=30°, 三角形的解的情况又怎样呢? 你能画三角形吗?
a bsin A 无解
作业:
1、已知在 ABC中,c 10, A 450 ,C 300 ,求a,b和B
2、在 ABC中,b 3, B 60 0 , c 1,求a和A,C
3、 ABC中,c 6, A 450 , a 2,求b和B,C
