RLS算法实现自适应均衡器的Matlab仿真
RLS算法及其仿真

RLS算法及其仿真RLS(Recursive Least Square)算法是一种用于递归估计的算法,主要用于实现自适应滤波器和系统的参数估计。
本文将对RLS算法以及其仿真进行阐述。
首先,我们来介绍一下RLS算法的基本原理。
RLS算法是一种在线递归最小二乘算法,主要用于估计线性滤波器的权值。
该算法通过不断地更新权值来最小化滤波器的误差平方和。
RLS算法的基本原理如下:1.初始化滤波器权值为一些初始值,并初始化协方差矩阵P和增益向量K。
2.递归更新增益向量K和协方差矩阵P:K=P*H'/(H*P*H'+λ)P=(I-K*H)*P/λ其中,H是输入信号的延迟版本,λ是正则化参数,I是单位矩阵。
3.更新滤波器权值:w=w+K*(d-H*w)其中,w是滤波器的权值向量,d是期望输出信号。
4.重复步骤2和3,不断地更新滤波器的权值,直到收敛或达到一些停止条件。
接下来,我们将通过仿真来展示RLS算法的性能。
我们将使用MATLAB软件来进行仿真。
首先,我们定义一个输入信号x,并假设期望输出信号d是x的加权和加上一些噪声。
我们可以通过下面的代码来生成输入信号和期望输出信号:```MATLABn=1000;%生成1000个采样点x = randn(1, n); % 生成正态分布的随机数作为输入信号w_true = [0.5, -0.3, 0.2]'; % 真实的权值向量d = conv(w_true, x); % 计算期望输出信号d = d + 0.1 * randn(size(d)); % 加入噪声```接下来,我们使用RLS算法来估计滤波器的权值。
我们可以通过下面的代码来实现RLS算法的仿真:```MATLABlambda = 0.99; % 正则化参数w = zeros(length(w_true), 1); % 初始化权值向量P = eye(length(w_true)); % 初始化协方差矩阵for i = 1:nH = [x(i), x(max(i-1, 1)), x(max(i-2, 1))]'; % 构造输入信号的延迟版本K = P * H / (H' * P * H + lambda); % 更新增益向量P = (eye(length(w_true)) - K * H') * P / lambda; % 更新协方差矩阵e(i)=d(i)-H'*w;%计算误差信号w=w+K*e(i);%更新权值向量end```最后,我们可以绘制出估计的权值和真实的权值之间的比较图,以及估计的输出信号和期望输出信号之间的比较图。
基于LMS和RLS算法的自适应滤波器仿真

基于LMS和RLS算法的自适应滤波器仿真自适应滤波器是一种可以自动调整其权重参数来适应不断变化的信号环境的滤波器。
常用的自适应滤波算法包括最小均方(LMS)和最小二乘(RLS)算法。
本文将对基于LMS和RLS算法的自适应滤波器进行仿真,并分析其性能和特点。
首先,介绍LMS算法。
LMS算法是一种基于梯度下降的自适应滤波算法。
其权重更新规则为:w(n+1)=w(n)+μ*e(n)*x(n),其中w(n)为当前时刻的权重,μ为步长(学习速率),e(n)为当前时刻的误差,x(n)为输入信号。
通过不断迭代和更新权重,LMS算法可以使滤波器的输出误差逐渐减小,从而逼近期望的输出。
接下来,进行LMS自适应滤波器的仿真实验。
考虑一个声纳系统的自适应滤波器,输入信号x(n)为声波信号,输出信号y(n)为接收到的声纳信号,期望输出信号d(n)为理想的声纳信号。
根据LMS算法,可以通过以下步骤进行仿真实验:1.初始化权重w(n)为零向量;2.读取输入信号x(n)和期望输出信号d(n);3.计算当前时刻的滤波器输出y(n)=w^T(n)*x(n),其中^T表示矩阵的转置;4.计算当前时刻的误差e(n)=d(n)-y(n);5.更新权重w(n+1)=w(n)+μ*e(n)*x(n);6.重复步骤2-5,直到滤波器的输出误差满足预设条件或达到最大迭代次数。
然后,介绍RLS算法。
RLS算法是一种递推最小二乘的自适应滤波算法。
其基本思想是通过不断迭代更新滤波器的权重,使得滤波器的输出误差的二范数最小化。
RLS算法具有较好的收敛性和稳定性。
接下来,进行RLS自适应滤波器的仿真实验。
基于声纳系统的例子,RLS算法的步骤如下:1.初始化滤波器权重w(n)为一个较小的正数矩阵,初始化误差协方差矩阵P(n)为一个较大的正数矩阵;2.读取输入信号x(n)和期望输出信号d(n);3.计算增益矩阵K(n)=P(n-1)*x(n)/(λ+x^T(n)*P(n-1)*x(n)),其中λ为一个正则化参数;4.计算当前时刻的滤波器输出y(n)=w^T(n)*x(n);5.计算当前时刻的误差e(n)=d(n)-y(n);6.更新滤波器权重w(n+1)=w(n)+K(n)*e(n);7.更新误差协方差矩阵P(n)=(1/λ)*(P(n-1)-K(n)*x^T(n)*P(n-1));8.重复步骤2-7,直到滤波器的输出误差满足预设条件或达到最大迭代次数。
RLS自适应算法分析及仿真

RLS 自适应算法分析及仿真RLS 自适应算法是为了设计自适应的横向滤波器把最小二乘法推广为一种自适应算法。
使得在已知n-1时刻横向滤波器抽头系数的情况吓,能够通过简单的更新,求出n 时刻的滤波器抽头权系数。
这样一种自适应的最小二乘法称为递推最小二乘法,简称RLS 算法。
RLS 自适应算法使用的确定性线性回归模型Kalman 滤波算法的一种特殊的无激励的状态空间模型。
一、RLS 算法步骤:步骤一:初始化:(0)0w =,1(0)P I δ-=,其中δ是一个很小的值。
步骤二:更新: n=1,2,……()()(1)()H e n d n w n u n =--(1)()()()(1)()H P n u n k n u n P n u n λ-=+- 1()[(1)()()(1)]H P n P n k n u n P n λ=---*()(1)()()w n w n k n e n =-+其中,11(0)(0)P R I δ--==,δ是一个很小的正数。
二、仿真结果:从上图可以看出RLS滤波的跟踪性能是比较好的,滤波器的输入与输出在初始值之后几乎重合。
由于RLS存在自适应更新过程,因此其效果比LMS更好。
由下图可以看出,其RLS算法误差是具有收敛性的,收敛结果与δ密切相关,δ在取值为1的时候严重影响RLS算法的收敛速度及结果。
三、仿真程序:clear allclcM=5;%权系数个数N=100;%数据点数n=1:N;wn=0.36*randn(1,N);vn=randn(1,N);d(1)=0;for n=2:Nd(n)=0.8*d(n-1)+wn(n); %期望响应enduu=d+vn;w=zeros(M,1);P=0.05*eye(M,M);q=0.1; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%for n=M:N;u=uu(n:-1:n-M+1)' ;e(n)=d(n)-w'*u;k=P*u*inv(q+u'*P*u);P=(1/q)*(P-k*u'*P);w=w+k*e(n);out(n)=w'*u;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%subplot(211)t=1:N;hold on;plot(d(t));hold on;plot(out(t),'r');grid onlegend('滤波器输入','滤波器输出')subplot(212)semilogy(abs(out-d));title('误差值')。
LMS和RLS算法应用及仿真分析

LMS 和RLS 算法应用及仿真分析摘要:本文采用MATLAB 软件对LMS 和RLS 两种自适应均衡算法在回波抵消器中的应用进行仿真,分析收敛步长μ、抽头w 、遗忘因子λ 等参数对回波抵消器性能的影响,并对两种算法下的性能做出比较。
关键词:LMS ;RLS ;自适应;回波抵消1 引言进入90 年代后期,通过网络拨打长途电话即IP 电话开始盛行,由于发话端到受话端的延迟达100ms 以上,而人耳对大于50ms 的回声就能辨别出来,因此IP 电话的回声严重影响通话效果。
如何消除回声成为非常重要的问题,回波抵消器就是一个自适应辨识系统,它通过特定的算法辨识未知的目标系统,即回声路径。
本文采用LMS 和RLS 算法实现回波抵消,并对收敛步长μ、抽头w 、遗忘因子λ 等相关参数对回波抵消性能的影响进行了仿真分析,从而为一种通用的回波抵消技术的实际应用提供理论参考。
回波抵消算法原理图如图1 所示。
图1 回波抵消算法原理图 2 LMS 和RLS 算法概述最陡下降法(LMS )和递归最小二乘算法(RLS )是自适应滤波最常用,也是最基本的两种算法。
下面分别对LMS 和RLS 两种算法原理做简单介绍。
2.1 LMS 算法设J(n)是n 时刻均方误差,J(n+1)是n+1 时刻的均方误差,W(n)、W(n+1)分别是n 、n+1时刻M 维抽头权向量011()[()()...()]T M W n w n w n w n -= (1)为使J(n+1)<J(n) (2)W(n)必须按J(n)的负方向变化即(1)()W n W n J μ→→→+=-∇ (μ>0) (3)最后以U (n )*e (n )瞬时值代替统计平均,得到抽头权向量迭代式 *(1)()()()W n W n U n e n μ→→+=- (4)式中U(n)式n 时刻的输入向量[u(n) u(n-1) u(n-2)···u(n-M+1)]。
RLS算法的自适应滤波器MATLAB仿真作业

RLS 自适应滤波器仿真作业工程1班220150820 王子豪1. 步骤1)令h M(-1)=0,计算滤波器的输出d(n)=X M T=h M(n-1);2)计算误差值e M(n)=d(n)-d(n,n-1);3)计算Kalman增益向量K M(n);4)更新矩阵的逆R M-1(N)=P M(N);5)计算h M(n)=h M(n-1)+K M(n)e M(n);2. 仿真RLS 中取T (-1)=10,λ=1及λ= 0.98;信号源x(n)与之前LMS算法仿真不变,对自适应滤波器采用RLS算法。
通过对比不同遗忘因子λ的情况下RLS的误差收敛情况。
取λ=0.98和λ=1两种情况下的性能曲线如图1所示。
其系数收敛情况如图2所示。
图1 不同λ值下的RLS算法性能曲线(100次实验平均)图2 不同λ值下的RLS算法系数收敛情况(100次实验平均)3. 结果分析RLS算法在算法的稳态阶段、即算法的后期收敛阶段其性能和LMS算法相差不明显。
但在算法的前期收敛段,RLS算法的收敛速度要明显高于LMS算法。
但是RLS算法复杂度高,计算量比较大。
遗忘因子λ越小,系统的跟踪能力越强,同时对噪声越敏感;其值越大,系统跟踪能力减弱,但对噪声不敏感,收敛时估计误差也越小。
4. Matlab程序clear;clc;N=2048; %信号的取样点数M=2;%滤波器抽头的个数iter=500;%迭代次数%初始化X_A=zeros(M,1); %X数据向量y=zeros(1,N); %预测输出err=zeros(1,iter); %误差向量errp=zeros(1,iter); %平均误差wR=zeros(M,iter); %每一行代表一次迭代滤波器的M个抽头参数T=eye(M,M)*10; %RLS算法下T参数的初始化,T初始值为10X=zeros(1,M);lamuta=0.98 ; %遗忘因子for j=1:100ex=randn(1,N); %噪声信号e(n)x=filter(1,[1,-1.6,0.8],ex);%经过系统H(Z)之后输出xd=x; %参考信号for k=(M+1):iter-1X=x(k-1:-1:k-M)';K=(T*X)/(lamuta+X'*T*X); %k时刻增益值e1=x(k)-wR(:,k-1)'*X;wR(:,k)=wR(:,k-1)+K*e1; %k时刻权值y(k)=wR(:,k)'*X;err(k)=x(k)-y(k);T=(T-K*X'*T)/lamuta; %k时刻的维纳解enderrp=errp+err.^2;enderrp=errp/100;figure(1);subplot(2,1,i);plot(errp) ;title(['100次平均得到的性能曲线,λ=',num2str(lamuta_v(i))]) ;learn1=wR(1,1:iter-1);learn2=wR(2,1:iter-1);figure(2);subplot(1,2,1;plot(learn1);title('λ=0.98'时a1的学习曲线');subplot(1,2,2);plot(learn2);title('λ=0.98时a2的学习曲线');THANKS !!! 致力为企业和个人提供合同协议,策划案计划书,学习课件等等打造全网一站式需求欢迎您的下载,资料仅供参考。
rls算法及matlab实现

RLS(Recursive Least Squares)算法是一种自适应滤波算法,用于在线估计线性系统的参数。
与最小二乘法类似,RLS算法通过最小化误差平方和来计算参数估计值。
不同的是,RLS算法采用递归方式,可以逐步更新参数估计值,适应系统变化。
RLS算法的基本思想是利用前一时刻的参数估计值和当前时刻的观测数据,计算当前时刻的参数估计值。
具体实现过程如下:1.初始化参数:选定一个合适的初始参数向量,并设置初始协方差矩阵和遗忘因子。
2.计算增益向量:利用前一时刻的参数估计值、协方差矩阵和当前时刻的观测数据,计算增益向量。
3.更新参数估计值:利用增益向量和前一时刻的参数估计值,计算当前时刻的参数估计值。
4.更新协方差矩阵:利用前一时刻的协方差矩阵、增益向量和当前时刻的观测数据,更新协方差矩阵。
5.返回参数估计值:输出当前时刻的参数估计值。
下面是一个简单的MATLAB实现:matlab复制代码function[theta, P] = rls(theta, P, x, y, lambda)% theta: 参数向量% P: 协方差矩阵% x: 输入向量% y: 输出标量% lambda: 遗忘因子K = P * x / (lambda + x' * P * x); % 计算增益向量theta = theta + K * (y - x' * theta); % 更新参数估计值P = (P - K * x' * P) / lambda; % 更新协方差矩阵end上述代码中,输入参数包括前一时刻的参数向量theta、协方差矩阵P、当前时刻的输入向量x和输出标量y,以及遗忘因子lambda。
输出参数为当前时刻的参数估计值theta和协方差矩阵P。
在实际应用中,可以将该函数嵌入到主程序中,通过循环调用实现递归计算。
自适应均衡rls算法仿真流程

自适应均衡rls算法仿真流程Reinforcement learning is a type of machine learning algorithm that allows an agent to learn how to make decisions by trial and error. It is particularly useful in situations where a clear set of rules cannot be defined, and the agent must learn from its interactions with the environment. 自适应均衡rls算法是一种基于强化学习的算法。
它允许代理通过不断尝试来学习如何做出决策。
在无法定义明确规则的情况下,强化学习尤其有用,代理必须从与环境的互动中学习。
One of the key challenges in using reinforcement learning algorithms is finding the right balance between exploration and exploitation. Exploration refers to the agent's willingness to try out new actions in order to discover more about the environment and potentially find better strategies. Exploitation, on the other hand, involves choosing actions that the agent already knows to be effective based on its past experiences. 在使用强化学习算法时面临的一个关键挑战是在探索和开发之间找到合适的平衡。
RLS算法实现自适应均衡器的Matlab仿真
基于RLS算法实现自适应均衡器的MATLAB仿真1. 实验目的用RLS算法实现自适应均衡器,画出一次实验的误差平方的收敛曲线,给出最后设计滤波器系数。
一次实验的训练序列长度为500。
进行20次独立实验,画出误差平方的收敛曲线。
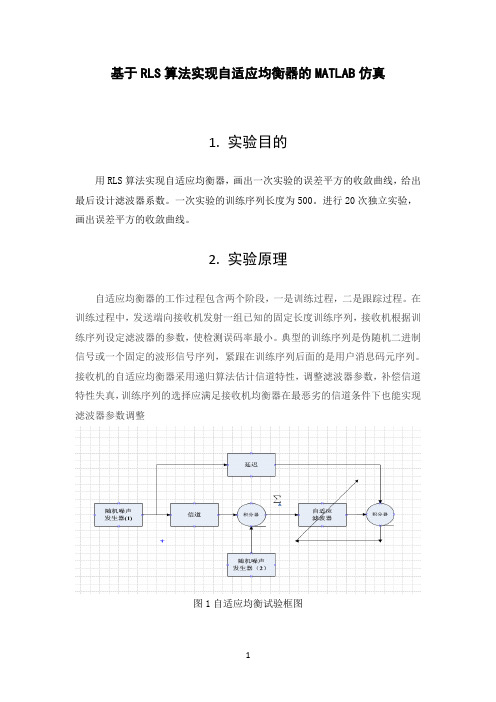
2. 实验原理自适应均衡器的工作过程包含两个阶段,一是训练过程,二是跟踪过程。
在训练过程中,发送端向接收机发射一组已知的固定长度训练序列,接收机根据训练序列设定滤波器的参数,使检测误码率最小。
典型的训练序列是伪随机二进制信号或一个固定的波形信号序列,紧跟在训练序列后面的是用户消息码元序列。
接收机的自适应均衡器采用递归算法估计信道特性,调整滤波器参数,补偿信道特性失真,训练序列的选择应满足接收机均衡器在最恶劣的信道条件下也能实现滤波器参数调整图1自适应均衡试验框图如图1所示,系统中使用两个独立的随机数发生器,一个用xn来表示,用来测试信道。
另一个用v(n)来表示,用来模拟接收器中加性白噪声的影响。
序列xn是xn=1的Bernoulli2序列,随变量xn具有零均值和单位方差。
第二个序列v(n)具有零均值,其方差v由实验中需要的信噪比决定。
均衡器有11个抽头。
3. MATLAB仿真1. RLS法1次实验clear;N=500;db=25;sh1=sqrt(10^(-db/10));u=;m=*sh1^2;error_s=0;for loop=1:1w=zeros(1,11)';p=1/m*eye(11,11);V=sh1*randn(1,N );Z=randn(1,N);x=sign(Z);for n=3:N;M(n)=*x(n)+*x(n-1)+*x(n-2);endz=M+V;for n=8:N;d(n)=x(n-7);endfor n=11:N;z1=[z(n) z(n-1) z(n-2) z(n-3) z(n-4) z(n-5) z(n-6) z(n-7) z(n-8) z(n-9) z(n-10)]';k=u^(-1).*p*z1./(1+u^(-1).*z1'*p*z1);e(n)=d(n)-w'*z1;w=w+k.*conj(e(n));p=u^(-1).*p-u^(-1).*k*z1'*p;y(n)=w'*z1;e1(n)=d(n)-w'*z1;enderror_s=error_s+e.^2;endwerror_s=error_s./1;n=1:N;plot(n,error_s);xlabel('n (忘却因子u=1;DB=25时)');ylabel('误差');title('RLS法1次实验误差平方的均值曲线 ');2. RLS法20次实验clear;N=500;db=25;sh1=sqrt(10^(-db/10));u=;m=*sh1^2;error_s=0;for loop=1:20w=zeros(1,11)';p=1/m*eye(11,11);V=sh1*randn(1,N );Z=randn(1,N);x=sign(Z);for n=3:N;M(n)=*x(n)+*x(n-1)+*x(n-2);endz=M+V;for n=8:N;d(n)=x(n-7);endfor n=11:N;z1=[z(n) z(n-1) z(n-2) z(n-3) z(n-4) z(n-5) z(n-6) z(n-7) z(n-8) z(n-9) z(n-10)]';k=u^(-1).*p*z1./(1+u^(-1).*z1'*p*z1);e(n)=d(n)-w'*z1;w=w+k.*conj(e(n));p=u^(-1).*p-u^(-1).*k*z1'*p;y(n)=w'*z1;e1(n)=d(n)-w'*z1;enderror_s=error_s+e.^2;endwerror_s=error_s./20;n=1:N;plot(n,error_s);xlabel('n (忘却因子u=1;DB=25时)');ylabel('误差');title('RLS法20次实验误差平方的均值曲线 ');4. 实验结果图2图3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于RLS算法实现自适应均衡器的MATLAB仿真
1. 实验目的
用RLS算法实现自适应均衡器,画出一次实验的误差平方的收敛曲线,给出最后设计滤波器系数。
一次实验的训练序列长度为500。
进行20次独立实验,画出误差平方的收敛曲线。
2. 实验原理
自适应均衡器的工作过程包含两个阶段,一是训练过程,二是跟踪过程。
在训练过程中,发送端向接收机发射一组已知的固定长度训练序列,接收机根据训练序列设定滤波器的参数,使检测误码率最小。
典型的训练序列是伪随机二进制信号或一个固定的波形信号序列,紧跟在训练序列后面的是用户消息码元序列。
接收机的自适应均衡器采用递归算法估计信道特性,调整滤波器参数,补偿信道特性失真,训练序列的选择应满足接收机均衡器在最恶劣的信道条件下也能实现滤波器参数调整
图1自适应均衡试验框图
如图1所示,系统中使用两个独立的随机数发生器,一个用xn来表示,用来测试信道。
另一个用v(n)来表示,用来模拟接收器中加性白噪声的影响。
序列xn是xn=1的Bernoulli2序列,随变量xn具有零均值和单位方差。
第二个序列v(n)具有零均值,其方差v由实验中需要的信噪比决定。
均衡器有11个抽头。
3. MATLAB仿真
1. RLS法1次实验
clear;
N=500;
db=25;
sh1=sqrt(10^(-db/10));
u=0.8;
m=0.0001*sh1^2;
error_s=0;
for loop=1:1
w=zeros(1,11)';
p=1/m*eye(11,11);
V=sh1*randn(1,N );
Z=randn(1,N)-0.5;
x=sign(Z);
for n=3:N;
M(n)=0.3*x(n)+0.9*x(n-1)+0.3*x(n-2);
end
z=M+V;
for n=8:N;
d(n)=x(n-7);
end
for n=11:N;
z1=[z(n) z(n-1) z(n-2) z(n-3) z(n-4) z(n-5) z(n-6) z(n-7) z(n-8) z(n-9) z(n-10)]';
k=u^(-1).*p*z1./(1+u^(-1).*z1'*p*z1);
e(n)=d(n)-w'*z1;
w=w+k.*conj(e(n));
p=u^(-1).*p-u^(-1).*k*z1'*p;
y(n)=w'*z1;
e1(n)=d(n)-w'*z1;
end
error_s=error_s+e.^2;
end
w
error_s=error_s./1;
n=1:N;
plot(n,error_s);
xlabel('n (忘却因子u=1;DB=25时)');
ylabel('误差');
title('RLS法1次实验误差平方的均值曲线');
2. RLS法20次实验
clear;
N=500;
db=25;
sh1=sqrt(10^(-db/10));
u=0.8;
m=0.0001*sh1^2;
error_s=0;
for loop=1:20
w=zeros(1,11)';
p=1/m*eye(11,11);
V=sh1*randn(1,N );
Z=randn(1,N)-0.5;
x=sign(Z);
for n=3:N;
M(n)=0.3*x(n)+0.9*x(n-1)+0.3*x(n-2);
end
z=M+V;
for n=8:N;
d(n)=x(n-7);
end
for n=11:N;
z1=[z(n) z(n-1) z(n-2) z(n-3) z(n-4) z(n-5) z(n-6) z(n-7) z(n-8) z(n-9) z(n-10)]';
k=u^(-1).*p*z1./(1+u^(-1).*z1'*p*z1);
e(n)=d(n)-w'*z1;
w=w+k.*conj(e(n));
p=u^(-1).*p-u^(-1).*k*z1'*p;
y(n)=w'*z1;
e1(n)=d(n)-w'*z1;
end
error_s=error_s+e.^2;
end
w
error_s=error_s./20;
n=1:N;
plot(n,error_s);
xlabel('n (忘却因子u=1;DB=25时)');
ylabel('误差');
title('RLS法20次实验误差平方的均值曲线');
4. 实验结果
图2
图3。
