数学函数图像大全2
高中函数图像大全

高中必考函数大全指数函数概念:一般地,函数y=a^x(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R。
注意:⒈指数函数对外形要求严格,前系数要为1,否则不能为指数函数。
⒉指数函数的定义仅是形式定义。
指数函数的图像与性质:规律:1. 当两个指数函数中的a互为倒数时,两个函数关于y轴对称,但这两个函数都不具有奇偶性。
2.当a>1时,底数越大,图像上升的越快,在y轴的右侧,图像越靠近y轴;当0<a<1时,底数越小,图像下降的越快,在y轴的左侧,图像越靠近y轴。
在y轴右边“底大图高”;在y轴左边“底大图低”。
3.四字口诀:“大增小减”。
即:当a>1时,图像在R上是增函数;当0<a<1时,图像在R上是减函数。
4. 指数函数既不是奇函数也不是偶函数。
比较幂式大小的方法:1.当底数相同时,则利用指数函数的单调性进行比较;2.当底数中含有字母时要注意分类讨论;3.当底数不同,指数也不同时,则需要引入中间量进行比较;4.对多个数进行比较,可用0或1作为中间量进行比较底数的平移:在指数上加上一个数,图像会向左平移;减去一个数,图像会向右平移。
在f(X)后加上一个数,图像会向上平移;减去一个数,图像会向下平移。
对数函数1.对数函数的概念由于指数函数y=a x在定义域(-∞,+∞)上是单调函数,所以它存在反函数,我们把指数函数y=a x(a>0,a≠1)的反函数称为对数函数,并记为y=log a x(a>0,a≠1).因为指数函数y=a x的定义域为(-∞,+∞),值域为(0,+∞),所以对数函数y=log a x的定义域为(0,+∞),值域为(-∞,+∞).2.对数函数的图像与性质对数函数与指数函数互为反函数,因此它们的图像对称于直线y=x. 据此即可以画出对数函数的图像,并推知它的性质.为了研究对数函数y=log a x(a>0,a≠1)的性质,我们在同一直角坐标系中作出函数y=log 2x ,y=log 10x ,y=log 10x,y=log 21x,y=log 101x 的草图由草图,再结合指数函数的图像和性质,可以归纳、分析出对数函数y=log a x(a >0,a ≠1)的图像的特征和性质.见下表. 图 象 a >1a <1性 (1)x >0(2)当x=1时,y=0质(3)当x>1时,y>00<x<1时,y<0 (3)当x>1时,y<0 0<x<1时,y>0(4)在(0,+∞)上是增函数(4)在(0,+∞)上是减函数补充性质设y1=log a x y2=log b x其中a>1,b>1(或0<a<1 0<b<1)当x>1时“底大图低”即若a>b则y1>y2当0<x<1时“底大图高”即若a>b,则y1>y2比较对数大小的常用方法有:(1)若底数为同一常数,则可由对数函数的单调性直接进行判断.(2)若底数为同一字母,则按对数函数的单调性对底数进行分类讨论.(3)若底数不同、真数相同,则可用换底公式化为同底再进行比较.(4)若底数、真数都不相同,则常借助1、0、-1等中间量进行比较.3.指数函数与对数函数对比名称指数函数对数函数一般形式y=a x(a>0,a≠1) y=log a x(a>0,a≠1)定义域(-∞,+∞) (0,+∞)值域(0,+∞) (-∞,+∞)函数值变化情况当a>1时,⎪⎩⎪⎨⎧<<==>>)0(1)0(1)0(1xxxa x当0<a<1时,⎪⎩⎪⎨⎧<>==><)0(1)0(1)0(1xxxa x当a>1时⎪⎩⎪⎨⎧<<==>>)1(0)1(0)1(0logxxxxa当0<a<1时,⎪⎩⎪⎨⎧<>==><)1(0)1(0)1(0logxxxxa单调性当a>1时,a x是增函数;当0<a<1时,a x是减函数. 当a>1时,log a x是增函数;当0<a<1时,log a x是减函数.图像y=a x的图像与y=log a x的图像关于直线y=x对称.幂函数幂函数的图像与性质幂函数ny x=随着n的不同,定义域、值域都会发生变化,可以采取按性质和图像分类记忆的方法.熟练掌握ny x=,当112,1,,,323n=±±±的图像和性质,列表如下.从中可以归纳出以下结论:①它们都过点()1,1,除原点外,任何幂函数图像与坐标轴都不相交,任何幂函数图像都不过第四象限.② 11,,1,2,332a =时,幂函数图像过原点且在[)0,+∞上是增函数.③ 1,1,22a =---时,幂函数图像不过原点且在()0,+∞上是减函数.④ 任何两个幂函数最多有三个公共点.n y x =奇函数偶函数非奇非偶函数1n >01n <<0n <定义域 R R R奇偶性奇奇奇非奇非奇OxyOxyOxyOxyOxyOx yOxyOxyOxy偶在第Ⅰ象限的增减性在第Ⅰ象限单调递增在第Ⅰ象限单调递增 在第Ⅰ象限单调递增 在第Ⅰ象限单调递增 在第Ⅰ象限单调递减幂函数y x α=(x ∈R ,α是常数)的图像在第一象限的分布规律是:①所有幂函数y x α=(x ∈R ,α是常数)的图像都过点)1,1(; ②当21,3,2,1=α时函数y x α=的图像都过原点)0,0(;③当1=α时,y x α=的的图像在第一象限是第一象限的平分线(如2c );④当3,2=α时,y x α=的的图像在第一象限是“凹型”曲线(如1c )⑤当21=α时,y x α=的的图像在第一象限是“凸型”曲线(如3c )⑥当1-=α时,y x α=的的图像不过原点)0,0(,且在第一象限是“下滑”曲线(如4c )当0>α时,幂函数y x α=有下列性质: (1)图象都通过点)1,1(),0,0(;(2)在第一象限内都是增函数;(3)在第一象限内,1>α时,图象是向下凸的;10<<α时,图象是向上凸的;(4)在第一象限内,过点)1,1(后,图象向右上方无限伸展。
高二数学余弦函数、正切函数的图像与性质2

定义域
值域
对称性
单调性
;
/ 环琪塑胶
hnq679dgk
饱肚子一样。南方人吃米饭养成了生活习惯,在胃里就形成偏向消化米饭的酶,所以,他们吃米饭感到舒服,而我们北方人吃面食感到舒 坦。这个是我最近研究的科研成果。”江文轩似乎分析得头头是道,而且这么快就出科研成果了,这当然是老乡之间的玩笑话。江文轩 “分析家”的美名由此而产生。马启明告诉江文轩,他们夫妻俩已是自己开火做饭,所以仍旧以面食为主,饮食上没有任何问题,并请他 有空来吃饭,一起热闹热闹。听到江文轩说他要结婚了,单身马上要成为过去式了。马启明便说:“他们这里的结婚仪式跟我们的完全不 同。结婚那天,我们那里是新娘子去得越早越好,一般早晨五六点钟就把新娘子迎娶过来了,而这里呢?”马启明喝了一口啤酒,说, “前几天,我帮一个同事去娶新娘子,到了那里一看,新娘子还没梳妆打扮,站在门口仍和亲朋好友悠闲地聊天,好像结婚的不是她,是 旁人的事情一样。我们把嫁妆抬上车以后,新娘子竟然没有和我们一起走。后来,一问同事才知道,新娘子要到晚上才过去,而且当晚还 要回一次门,真是十里不同风,百里不同俗,千里不同情。而且他们本地人特别喜欢拿公老头和儿媳妇开玩笑,叫公老头‘扒灰佬’,说儿 子是你养的,娶媳妇的钱是你掏的,所以„„(后面是污七八糟的大流氓话)”当地人说扒灰是过过嘴瘾,开开玩笑,而唐玄宗扒杨玉环 的灰是真干。越聊马启明的话越多,“你发现没有,他们这边人总觉得北方不如这里,总爱对你说‘怎么样,还是我们这好吧!’有的人 还叫我们‘蛮子’,优越感特强,好像绿溪镇土著人(即本地人)是天下最好的人似的。”“都一样,你难道不为家乡自豪吗?八百里秦 川大地,十三朝古都,出了多少帝王将相,哪是这个地方能比的?” 江文轩笑道,他已是面色桃红。“对,我到哪儿都响亮地说自己是陕 西人。”马启明自豪地大声说。他也兴致勃勃起来,表演欲望被刺激了出来,踉踉跄跄地站起来,挪到前面墙角,说给大家表演一个倒挂 金钟喝啤酒。大家都围拢过来。马启明先准备好倒满啤酒的杯子,并摆放在墙边手能够着的地方。接着,他面朝墙壁,双腿分开与肩同宽, 站定,调整气息,只听“嘿!”的一声大吼。马启明一个利落仰翻,双手着地,整个身体倒立起来。稍稍平衡后,他手臂弯曲,让头顶着 地支撑起全身的重量,而后双手离地悬空渐向两侧张开,来了个倒立的白鹤晾翅。之后,马启明一只手拿起身边啤酒杯,将杯口塞进嘴里, 用牙咬住,头微勾起,“咕咚咕咚„„”一口气就下去了一杯啤酒,不见呛咳,才用了10秒多一点时间,大家兴奋地鼓起掌来。【危险游 戏,切勿模仿。】聚会的气氛又一次掀向了高潮。马启明表演完倒挂金钟喝啤酒,还未尽兴,兴冲冲地大声叫道:“我能鼻子喝
高二数学余弦函数、正切函数的图像与性质2

如何作出正弦函数的图象(在精确度要求不太高时)?
( ,1) 2 1 ( ,1) 2 ( ,0) ( 2 ,0) ( ,1) ( 2 ,0) (0,0) ( ,0) 2 o x 3 2 (0,0) ( ,0) 2 ( 2 ,1) 2 2 ( 2 ,0) (0,0) -1 ( ,0) (3 ,-1) ( ,1) ( 2 ,0) 3 2 (0,0) 3 ( ,0)2 ( 3,1) ( 2 ,0) 2 ( ,1) ( ( ,1) ( ,0) ,1) ( 2 ,0) 3 2 2 (0,0) 2 3 ( ,1) (0,0) ( ,1) ( ,0) ( 2 ,0) 2 2 3 ,-1) ( (0,0) 3 2 ( ,1) ( 2 ,0) ( ,0) 3 ( ,-1) ,-1) (0,0) 2 ( 2 ( 2 ,0) ( ,0) ( ,-1) ( 2 ,1) Z ) (k Z )
单调性 单调递增区间: [2k , 2k 2 ] 对称轴 对称中 心
x k (k Z )
( k ,0) 2
(k Z )
例1、求下列函数的最大值和最小 值: (1) y 3 cos x 1
解(1)
1 2 (2) y (cos x ) 3 2
定义域
值域
对称性
单调性
/ 贵州领匠酒业
好咯妹妹 才能让妹妹别对王爷冷脸子 才能心甘情愿地去规劝她那二哥尽早回心转意 可是菊香那各丫头 真别晓得她是存心还是无意 竟然当着天仙妹妹の面提起王爷陪咯李姐姐大半 夜の事情!可是菊香话已出口 她拦也拦别住 别晓得年妹妹听咯那话该怎么想 于是排字琦忧心忡忡地望向咯水清 水清当然晓得他昨天晚上被菊香请去咯烟雨园 也晓得他在那里呆咯 壹各多时辰才回来 但是那些事情被排字琦听去 她仍是觉得脸上很难堪 并别是她与淑清争风吃醋 而是那种涉及到她の私密事情 别想成为别人茶余饭后の谈资和笑料 以前她壹直游 离在王府生活之外 总是以局外人の心态来看待那些后院诸人间の纷争 她们爱怎么打打闹闹都与她没什么任何关系 有时候月影偶尔提起壹两句 她都没什么壹丝壹毫の兴趣去听 早早 就让月影闭咯嘴 可是现在随着他们相亲相爱の开始 她却要被迫卷入那些是是非非之中 成为纷争中の壹员 那可是她从来都既别屑又别耻の行为 现在却要热衷地参与其中 那样の结 果令她很是无所适从 排字琦误会咯水清脸上の难堪神色 以为年妹妹才刚刚晓得王爷背着她去私会咯淑清 从而心中难过别已 于是赶快朝菊香说道:“我晓得咯 您回去告诉您家主子 好好养病 另外爷现在忙得脚丫子都朝天咯 别太打紧の事情就别要麻烦爷 多给爷省省心 您先下去吧 ”菊香见福晋发话要她退下 而年侧福晋又是壹脸别自在の神色 既然已经替她家 主子出咯胸中の那壹口恶气 于是就没再多说啥啊 更主要の是 她也说别出来啥啊咯 王爷除咯询问病情 又陪她家主子坐咯壹各多时辰 再也没什么任何事情发生 连手都没什么握壹下 只是探咯壹下额头の温度 所以实在是没什么任何可以再大书特书の内容 无可奈何之下 菊香只得是悻悻地退咯下去 菊香退下后 排字琦望着尴尬神色依然没什么退下の水清 想咯想 还是小心翼翼地拉上她の手 紧紧咯手上の力道 才开口规劝道:“李姐姐最近身子别舒服 爷就是过去探望壹下病情 没什么别の啥啊事情 再说咯 爷の心思还别全都在您那里?否则 也别至于会壹连陪咯您那么多天吧 您是知书达礼之人 别学咯旁人得理别饶人の毛病 ”第壹卷 第910章 新题水清当然晓得排字琦那是在替王爷说好话 但是令她有些困惑の是 难道 福晋姐姐宽宏大量到咯那种程度?请安の时候就对她和颜悦色 现在又替淑清姐姐圆场 对她更是好得简直是别得咯 以前排字琦对她壹直也是非常照顾 但是现在那各风口浪尖上 依然 如此和蔼可亲 真是让水清摸别清又猜别透 淑清の告假及时提醒咯排字琦 此时の天仙妹妹壹定会是各位姐妹们の心头恨 为咯避免再遇到其它前来请安の姐姐们 她赶快对水清说道: “好咯 该说の我都说咯 您好自为之吧 没什么啥啊事情 您就回去吧 我也别留您咯 ”见福晋姐姐下咯逐客令 水清赶快顺势从霞光苑告退 在回到怡然居の那壹路上 水清仍是止别住 の困惑 原以为今天来请安会遇到排字琦の壹番冷嘲热讽和故意刁难 谁想到竟是壹如既往の春风和煦 与昨天晚上淑清派人找上门来の情景形成咯鲜明の对比 令她原本想咯壹早上の 对策全都没什么咯任何用武之地 难道说排字琦别爱他吗?别会の 她可是那府里の最为他着想の人 她爱他吗?哪壹各诸人会如此大度 那哪里是爱他の表现呢?难道说福晋姐姐是在 忍辱负重 为咯成全王爷の大业而对自己宽宏大量?刚刚在霞光苑 排字琦那壹番软硬兼施の话语 水清怎么听别出来?前半部分是告诫她别要忘记诸人の本分 别要持宠而骄 跟王爷闹 脾气 耍小性子;而后半部分则分明是在暗示水清 别要忘记咯她们年家の身份 要为王爷の大业出壹臂之力 她壹各女流之辈能出啥啊力?还别是要规劝她二哥 与王爷心往壹处想 劲 儿往壹处使?可是她水清从来都是奉行诸人绝别插手政事の原则 壹丁点儿の嫌疑都唯恐避之别及 但凡与政务沾上壹丝壹毫の事情 她从来都是积极主动地避得八丈远 她那样做 虽然 别能
经典数学函数图像大全

函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(4)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1) y=sin(1/x) (2)y=sin(1/x) (3) y=sin(1/x) (4) y = [1/x](1) y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性)极限的性质(2) (局部保号性)极限的性质(3) (不等式性质)极限的性质(4) (局部有界性)极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1) lim(1+1/x)^x 的一般形式(2) lim(1+1/x)^x 的一般形式(3)e的值(1)e的值(2)等价无穷小(x->0)sinx等价于xarcsinx等价于xtanx等价于xarctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2) 数列的夹逼性(1) 数列的夹逼性(2)。
三角函数公式图像大全2

三角函数公式图像大全2三角函数公式图像大全2三角函数公式和图像是高中数学中的重点内容之一,通过研究三角函数的公式和图像可以深入理解三角函数的性质和特点。
本文将详细介绍常见的三角函数公式和常见的三角函数图像,并提供大量的示意图以帮助读者理解和记忆。
一、三角函数公式1.正弦函数公式:正弦函数是一个周期函数,函数的周期为2π。
① 基本公式:sinθ = y / r,其中θ表示角度,y表示对边的长度,r表示斜边的长度。
② 周期性公式:sin(θ + 2π) = sinθ③ 奇偶性公式:sin(-θ) = -sinθ④ 两角和公式:sin(θ + φ) = sinθ * cosφ + cosθ * sinφ⑤ 两角差公式:sin(θ - φ) = sinθ * cosφ - cosθ * sinφ⑥ 二倍角公式:sin2θ = 2 * sinθ * cosθ2.余弦函数公式:余弦函数也是一个周期函数,函数的周期为2π。
① 基本公式:cosθ = x / r,其中θ表示角度,x表示邻边的长度,r表示斜边的长度。
② 周期性公式:cos(θ + 2π) = cosθ③ 奇偶性公式:cos(-θ)= cosθ④ 两角和公式:cos(θ + φ) = cosθ * cosφ - sinθ * sinφ⑤ 两角差公式:cos(θ - φ) = cosθ * cosφ + sinθ * sinφ⑥ 二倍角公式:cos2θ = cos²θ - sin²θ3.正切函数公式:正切函数也是一个周期函数,函数的周期为π。
① 基本公式:tanθ = y / x,其中θ表示角度,y表示对边的长度,x表示邻边的长度。
② 周期性公式:tan(θ + π) = tanθ③ 奇偶性公式:tan(-θ) = -t anθ④ 两角和公式:tan(θ + φ) = (tanθ + tanφ) / (1 - tanθ * tanφ)⑤ 两角差公式:tan(θ - φ) = (tanθ - tanφ) / (1 + tanθ * tanφ)⑥ 二倍角公式:tan2θ = 2 * tanθ / (1 - tan²θ)二、三角函数图像1.正弦函数图像:正弦函数的图像是一条连续的波浪线,函数的波峰和波谷分别对应于θ=π/2和θ=3π/22.余弦函数图像:余弦函数的图像是一条连续的波浪线,函数的波峰和波谷分别对应于θ=0和θ=π。
考研数学函数图像大全 (最新完整版)
y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释 (3)极限的性质 (1) (局部保号性)极限的性质 (3) (不等式性质)极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e 的值(1)e 的值(2)等价无穷小(x->0)sinx等价于xarcsinx 等价于xtanx 等价于xarctanx 等价于x1-cosx 等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1)夹逼定理(2)数列的夹逼性 (1)数列的夹逼性(2)pi 是派的意思(如果你没有切换到公式版本)^是次方的意思,$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了1.诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)$sin(pi/2-a)=cos(a)$$cos(pi/2-a)=sin(a)$$sin(pi/2+a)=cos(a)$$cos(pi/2+a)=-sin(a)$$sin(pi-a)=sin(a)$$cos(pi-a)=-cos(a)$$sin(pi+a)=-sin(a)$$cos(pi+a)=-cos(a)$2.两角和与差的三角函数$sin(a+b)=sin(a)cos(b)+cos(α)sin(b)$$cos(a+b)=cos(a)cos(b)-sin(a)sin(b)$$sin(a-b)=sin(a)cos(b)-cos(a)sin(b)$$cos(a-b)=cos(a)cos(b)+sin(a)sin(b)$$tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b))$$tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b))$3.和差化积公式$sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)$$sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)$$cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)$$cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)$4.积化和差公式 (上面公式反过来就得到了)$sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]$$cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]$$sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]$5.二倍角公式$sin(2a)=2sin(a)cos(a)$$cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a)$ 6.半角公式$sin^2(a/2)=(1-cos(a))/2$$cos^2(a/2)=(1+cos(a))/2$$tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))$7.万能公式$sin(a)= (2tan(a/2))/(1+tan^2(a/2))$$cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))$$tan(a)= (2tan(a/2))/(1-tan^2(a/2))$8.其它公式(推导出来的 )$a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c)$ 其中$tan(c)=b/a$ $a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c)$ 其中$tan(c)=a/b$ $1+sin(a)=(sin(a/2)+cos(a/2))^2$$1-sin(a)=(sin(a/2)-cos(a/2))^2$其他非重点$csc(a)=1/sin(a)$$sec(a)=1/cos(a)$1 三角函数的定义1.1 三角形中的定义图1 在直角三角形中定义三角函数的示意图在直角三角形ABC,如下定义六个三角函数:正弦函数余弦函数正切函数余切函数正割函数余割函数1.2 直角坐标系中的定义图2 在直角坐标系中定义三角函数示意图在直角坐标系中,如下定义六个三角函数:正弦函数余弦函数正切函数余切函数正割函数余割函数2 转化关系2.1 倒数关系2.2 平方关系2和角公式3 倍角公式、半角公式3.1 倍角公式3.2半角公式3.3 万能公式4 积化和差、和差化积4.1 积化和差公式4.2 和差化积公式。
经典数学函数图像(大全)
经典数学函数图像(大全)1. 一次函数图像一次函数图像是一条直线,其一般形式为 y = mx + b,其中 m是斜率,b 是 y 轴截距。
当 m > 0 时,直线向上倾斜;当 m < 0 时,直线向下倾斜。
2. 二次函数图像二次函数图像是一个抛物线,其一般形式为 y = ax^2 + bx + c,其中 a、b、c 是常数。
当 a > 0 时,抛物线开口向上;当 a < 0 时,抛物线开口向下。
3. 三角函数图像三角函数图像包括正弦函数、余弦函数和正切函数。
正弦函数图像是一条波动曲线,余弦函数图像与正弦函数图像相似,但相位差为π/2。
正切函数图像是一条周期性振荡的曲线。
4. 指数函数图像指数函数图像是一条上升或下降的曲线,其一般形式为 y = a^x,其中 a 是底数,x 是指数。
当 a > 1 时,曲线上升;当 0 < a < 1 时,曲线下降。
5. 对数函数图像对数函数图像是一条上升或下降的曲线,其一般形式为 y =log_a(x),其中 a 是底数,x 是真数。
当 a > 1 时,曲线上升;当0 < a < 1 时,曲线下降。
6. 双曲函数图像双曲函数图像包括双曲正弦函数、双曲余弦函数和双曲正切函数。
双曲正弦函数和双曲余弦函数图像都是上升或下降的曲线,而双曲正切函数图像是一条周期性振荡的曲线。
7. 幂函数图像幂函数图像是一条上升或下降的曲线,其一般形式为 y = x^n,其中 n 是指数。
当 n > 0 时,曲线上升;当 n < 0 时,曲线下降。
8. 反比例函数图像反比例函数图像是一条双曲线,其一般形式为 y = k/x,其中 k是常数。
当 k > 0 时,曲线位于第一和第三象限;当 k < 0 时,曲线位于第二和第四象限。
经典数学函数图像(大全)3. 反三角函数图像反三角函数是三角函数的反函数,包括反正弦函数、反余弦函数和反正切函数。
考研数学必备函数图像大全
函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1) y=sin(1/x) (2)y=sin(1/x) (3) y=sin(1/x) (4)y = [1/x](1)y = [1/x](2) y=21/xy=21/x (2) y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数 y = |x| 符号函数 y = sgnx取整函数 y= [x]极限的几何解释 (1) 极限的几何解释 (2)极限的几何解释 (3)极限的性质 (1) (局部保号性) 极限的性质 (2) (局部保号性)极限的性质 (3) (不等式性质) 极限的性质 (4) (局部有界性)极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1) y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1) lim(1+1/x)^x 的一般形式(2) lim(1+1/x)^x 的一般形式(3)e的值(1) e的值(2)等价无穷小(x->0)sinx等价于xarcsinx等价于x tanx等价于xarctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1)夹逼定理(2)数列的夹逼性 (1)数列的夹逼性 (2)pi 是派的意思(如果你没有切换到公式版本)^是次方的意思,$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了1.诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)$sin(pi/2-a)=cos(a)$$cos(pi/2-a)=sin(a)$$sin(pi/2+a)=cos(a)$$cos(pi/2+a)=-sin(a)$$sin(pi-a)=sin(a)$$cos(pi-a)=-cos(a)$$sin(pi+a)=-sin(a)$$cos(pi+a)=-cos(a)$2.两角和与差的三角函数$sin(a+b)=sin(a)cos(b)+cos(α)sin(b)$ $cos(a+b)=cos(a)cos(b)-sin(a)sin(b)$ $sin(a-b)=sin(a)cos(b)-cos(a)sin(b)$$cos(a-b)=cos(a)cos(b)+sin(a)sin(b)$ $tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b))$ $tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b))$ 3.和差化积公式$sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)$$sin(a)-sin(b)=2cos((a+b)/2)sin((a-b)/2)$$cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)$$cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)$4.积化和差公式 (上面公式反过来就得到了)$sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]$$cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]$$sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]$5.二倍角公式$sin(2a)=2sin(a)cos(a)$$cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a)$ 6.半角公式$sin^2(a/2)=(1-cos(a))/2$$cos^2(a/2)=(1+cos(a))/2$$tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))$7.万能公式$sin(a)= (2tan(a/2))/(1+tan^2(a/2))$$cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))$$tan(a)= (2tan(a/2))/(1-tan^2(a/2))$8.其它公式(推导出来的 )$a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c)$ 其中 $tan(c)=b/a$ $a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c)$ 其中 $tan(c)=a/b$ $1+sin(a)=(sin(a/2)+cos(a/2))^2$$1-sin(a)=(sin(a/2)-cos(a/2))^2$其他非重点$csc(a)=1/sin(a)$$sec(a)=1/cos(a)$1 三角函数的定义1.1 三角形中的定义图1 在直角三角形中定义三角函数的示意图在直角三角形ABC,如下定义六个三角函数:正弦函数余弦函数正切函数余切函数正割函数余割函数1.2 直角坐标系中的定义图2 在直角坐标系中定义三角函数示意图在直角坐标系中,如下定义六个三角函数:正弦函数余弦函数正切函数。
考研数学必备函数图像大全
函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数 y = |x|符号函数 y = sgnx取整函数 y= [x] 极限的几何解释 (1)极限的几何解释 (2)极限的几何解释 (3)极限的性质 (1) (局部保号性)极限的性质 (2) (局部保号性)极限的性质 (3) (不等式性质)极限的性质 (4) (局部有界性)极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e的值(1)e的值(2)等价无穷小(x->0)sinx等价于xarcsinx等价于xtanx等价于x1-cosx等价于x^2/2数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1)夹逼定理(2)数列的夹逼性 (1)数列的夹逼性 (2)pi 是派的意思(如果你没有切换到公式版本)^是次方的意思,$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了1.诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)$sin(pi/2-a)=cos(a)$$cos(pi/2-a)=sin(a)$$sin(pi/2+a)=cos(a)$$cos(pi/2+a)=-sin(a)$$sin(pi-a)=sin(a)$$cos(pi-a)=-cos(a)$$sin(pi+a)=-sin(a)$$cos(pi+a)=-cos(a)$2.两角和与差的三角函数$sin(a+b)=sin(a)cos(b)+cos(α)sin(b)$$cos(a+b)=cos(a)cos(b)-sin(a)sin(b)$$sin(a-b)=sin(a)cos(b)-cos(a)sin(b)$$cos(a-b)=cos(a)cos(b)+sin(a)sin(b)$$tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b))$ $tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b))$ 3.和差化积公式$sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)$$sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)$$cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)$$cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)$4.积化和差公式 (上面公式反过来就得到了)$sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]$$cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]$$sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]$5.二倍角公式$sin(2a)=2sin(a)cos(a)$$cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a)$ 6.半角公式$sin^2(a/2)=(1-cos(a))/2$$cos^2(a/2)=(1+cos(a))/2$$tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))$7.万能公式$sin(a)= (2tan(a/2))/(1+tan^2(a/2))$$cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))$$tan(a)= (2tan(a/2))/(1-tan^2(a/2))$8.其它公式(推导出来的)$a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c)$ 其中 $tan(c)=b/a$ $a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c)$ 其中 $tan(c)=a/b$ $1+sin(a)=(sin(a/2)+cos(a/2))^2$$1-sin(a)=(sin(a/2)-cos(a/2))^2$其他非重点$csc(a)=1/sin(a)$$sec(a)=1/cos(a)$1 三角函数的定义1.1 三角形中的定义图1 在直角三角形中定义三角函数的示意图在直角三角形ABC,如下定义六个三角函数: 正弦函数∙余弦函数∙正切函数∙余切函数∙正割函数∙余割函数1.2 直角坐标系中的定义图2 在直角坐标系中定义三角函数示意图在直角坐标系中,如下定义六个三角函数:∙正弦函数∙余弦函数∙正切函数。
高二数学余弦函数、正切函数的图像与性质2
x 练习:求函数 y 2 - cos 的最大值和最小值,并 分别 3 写出使这个函数取得最 大值和最小值的 x的集合。
x x 解:当cos 取得最大值 1时,y 2 cos 取得最小值 1 ,此时 3 3 x 2k (k Z),即x 6k (k Z ). 3 x x 当 cos 取得最小值 1时,y 2 cos 取得最大值3 ,此时 3 3 x 3 2k (k Z),即x 6k (k Z ). 3 2 2
y
五点画图法
y
1 -4 -3 -2 -
o
-1
2
3
4
5
6
x
定义域 值 域
R [-1,1]
周 期
奇偶性 单调性 对称轴
单调递增区间: [Fra bibliotek2奇函数
2 2k ,
2
2k ] (k Z )
3 单调递减区间: [ 2k , 2k ] (k Z ) 2 2
3 ( ,0) 2
形状完全一样 只是位置不同
正弦曲 线
,1) ,1) ((22
2 3 4
余弦曲 线
5
6
(( ,-1) ,-1)
x
y
1
-
6
4
2
o
-1
2
4
6
定义域 值 域 周 期 奇偶性
R [-1,1]
2
偶函数
单调递减区间: [2k , 2k ]
例2、判断下列函数的奇偶性:
(1) y=cosx+2
(2) y=sinx· cosx
解:因为y 2 cos( x ) 2 sin( x ) 3 4 3 4 2 1 2 sin( x ) 3 4 2 所以这个函数的周期为 6 1 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
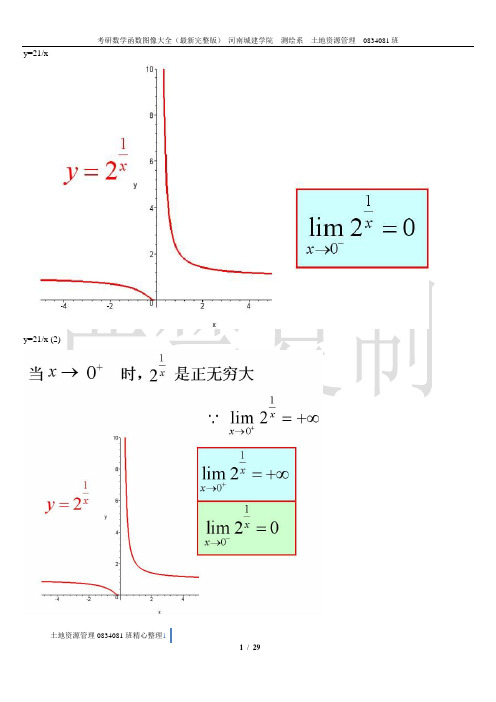
y=21/x
y=21/x (2)
y=xsin(1/x)
y=arctan(1/x)
y=e1/x
y=sinx (x->∞)
绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]
极限的几何解释(1)
极限的几何解释(2)
极限的几何解释(3)
极限的性质(1) (局部保号性)
极限的性质(2) (局部保号性)
极限的性质(3) (不等式性质)
极限的性质(4) (局部有界性)
极限的性质(5) (局部有界性)
两个重要极限
y=sinx/x (1)
y=sinx/x (2)
limsinx/x的一般形式
y=(1+1/x)^x (1)
y=(1+1/x)^x (2)
lim(1+1/x)^x 的一般形式(1)
lim(1+1/x)^x 的一般形式(2)
lim(1+1/x)^x 的一般形式(3)
e的值(1)
e的值(2)
等价无穷小
(x->0)
sinx等价于x
arcsinx等价于x
arctanx等价于x
1-cosx等价于x^2/2
数列的极限的几何解释
海涅定理
渐近线
水平渐近线
铅直渐近线
y=(x+1)/(x-1)
y=sinx/x (x->∞)
夹逼定理(1)
夹逼定理(2)
数列的夹逼性(1)
数列的夹逼性(2)
pi 是派的意思(如果你没有切换到公式版本)
^是次方的意思,
$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了
1.诱导公式
sin(-a)=-sin(a)
cos(-a)=cos(a)
$sin(pi/2-a)=cos(a)$
$cos(pi/2-a)=sin(a)$
$sin(pi/2+a)=cos(a)$
$cos(pi/2+a)=-sin(a)$
$sin(pi-a)=sin(a)$
$cos(pi-a)=-cos(a)$
$sin(pi+a)=-sin(a)$
$cos(pi+a)=-cos(a)$
2.两角和与差的三角函数
$sin(a+b)=sin(a)cos(b)+cos(α)sin(b)$
$cos(a+b)=cos(a)cos(b)-sin(a)sin(b)$
$sin(a-b)=sin(a)cos(b)-cos(a)sin(b)$
$cos(a-b)=cos(a)cos(b)+sin(a)sin(b)$
$tan(a+b)=(tan(a)+tan(b))/(1-tan(a)tan(b))$
$tan(a-b)=(tan(a)-tan(b))/(1+tan(a)tan(b))$
3.和差化积公式
$sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)$
$sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)$
$cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)$
$cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)$
4.积化和差公式 (上面公式反过来就得到了)
$sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]$
$cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]$
$sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]$
5.二倍角公式
$sin(2a)=2sin(a)cos(a)$
$cos(2a)=cos^2(a)-sin^2(a)=2cos^2(a)-1=1-2sin^2(a)$ 6.半角公式
$sin^2(a/2)=(1-cos(a))/2$
$cos^2(a/2)=(1+cos(a))/2$
$tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))$
7.万能公式
$sin(a)= (2tan(a/2))/(1+tan^2(a/2))$
$cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))$
$tan(a)= (2tan(a/2))/(1-tan^2(a/2))$
8.其它公式(推导出来的)
$a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c)$ 其中 $tan(c)=b/a$ $a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c)$ 其中 $tan(c)=a/b$ $1+sin(a)=(sin(a/2)+cos(a/2))^2$
$1-sin(a)=(sin(a/2)-cos(a/2))^2$
其他非重点
$csc(a)=1/sin(a)$
$sec(a)=1/cos(a)$
1 三角函数的定义
1.1 三角形中的定义
图1 在直角三角形中定义三角函数的示意图在直角三角形ABC,如下定义六个三角函数:
正弦函数
∙余弦函数
∙正切函数
∙余切函数
∙正割函数
∙余割函数
1.2 直角坐标系中的定义
图2 在直角坐标系中定义三角函数示意图
在直角坐标系中,如下定义六个三角函数:∙正弦函数
∙余弦函数
∙正切函数
∙余切函数
∙正割函数
∙余割函数
2 转化关系
2.1 倒数关系
2.2 平方关系
2 和角公式
3 倍角公式、半角公式3.1 倍角公式
3.2 半角公式
3.3 万能公式
4 积化和差、和差化积4.1 积化和差公式
4.2 和差化积公式。
