四波混频
关于四波混频的理论探讨

收稿日期 : 2008 - 05 - 07 作者简介 : : 黄湘宁 ( 1964 —) ,男 ,湖南洞口人 ,副教授 。研究方向 : 计算机应用。
第 6期
黄湘宁 :关于四波混频的理论探讨
71
→
→
→
→
kc
(ω 1
+
ω 2
-
ω p
)
=
k1
(ω ) 1
+
k2
(ω 2
)
-
kp
(ω p
)
若三列入射波频率均为 ω,则相位共轭波的频率也为 ω,此过程为简并四波混频 (DFWM ) 。
光学相位共轭是指光波行进到特殊介质或环境时 ,产生与该光波波形完全吻合 (相位共轭 ) 的反向 光波 (即共轭光波 ) 。光学相位共轭发现于 20世纪 70年代 ,目前已在实时自适应光学校正 、光学信息处 理 、光计算 、信息存储 、图像处理 、超低噪音检测 、干涉测量技术及非线性激光光谱等领域中广泛应用。本 文通过对四波混频的探讨 ,为如何选取克尔介质的最佳尺寸提供一定的理论指导意义 。
第 26卷 第 6期 2008年 12月
青海 大学学 报 (自然科 学版 ) Journal of Q inghai Unive rsity (N ature Sc ience)
Vol126 No16 D e c 12008
关于 四波混频的理论探讨
黄湘宁
(青海师范大学实验教学管理中心 , 青海 西宁 810008)
→
在 k1
→
= k2 的情况下为前向四波混频 ,产生的相位共轭波矢
→
→
→
kc
(ω c
= ω)
= 2 k1 (ω)
第四章三次谐波与四波混频

分类: 分类:
2、非参量过程---非参量过程---介质在与光场相互作用后的终态与初态不同了, 介质在与光场相互作用后的终态与初态不同了,发生 质间的能量转移。 了光场与介 质间的能量转移。
受激拉曼散射(SRS)、受激布里渊散射(SBS)。 受激拉曼散射(SRS)、受激布里渊散射(SBS)。 双光子吸收(TPA)。 双光子吸收(TPA)。 饱和吸收(SA)。 饱和吸收(SA)。
实现三次谐波的困难
(1)晶体中的激光损伤强度阈值较低,无法使用高强度的入射激光。 晶体中的激光损伤强度阈值较低,无法使用高强度的入射激光。 (2)晶体中的双折射特性难以实现三次谐波所要求的位相匹配。 晶体中的双折射特性难以实现三次谐波所要求的位相匹配。 所以,一般难以在晶体中直接实现三次谐波(THG), 所以,一般难以在晶体中直接实现三次谐波(THG),方解石直接实现 THG相位匹配的晶体 THG相位匹配的晶体。 相位匹配的晶体。 −6 目前实验结果: 4mm长方解石晶体中以 目前实验结果:在4mm长方解石晶体中以 3 × 10 的转换效率得到了 三次谐波输出。 三次谐波输出。 (3) 对紫外光吸收较强
三次谐波
实现三次谐波的介质 I. 晶体: 晶体:
χ (3) ~ 10− 20 − 10− 23 ( SI制) χ (3) ( SI ) = χ ( 2) ~ 10 −11 − 10−13 ( SI制)
4π ×10 −8 χ ( 3) (esu ) 9 4π χ ( 2) ( SI ) = ×10 − 4 χ ( 2 ) (esu ) 3
三阶非线性光学效应概述
主要特点: 及耦合波方程描述。 主要特点:1、基于 χ (3) 及耦合波方程描述。 2、无论介质有何种对称性,总存在一些非零的 无论介质有何种对称性, χ ( 3) 张量元,原则上三阶非线性光学效应可 张量元, 所有介质中观察到 中观察到。 在所有介质中观察到。 3、比二阶效应弱几个数量级( χ (3) << χ ( 2) ),更难 比二阶效应弱几个数量级( ), 于观察。 于观察。 4、三阶效应中参与相互作用的有四个光电场, 三阶效应中参与相互作用的有四个光电场, 现象更加丰富。 现象更加丰富。
四波混频
E ( w1 ) χ(3) E ( w2 )
E ( w3 )
E ( w4 )
四个不同频率的波失在介质中混频.在四波混频过程中 光子的能量与动量守恒
w4 = w1 + w2 + w3 ∆k = k1 − k2 − k3
在四个波得频率相等的情况下,四波混频称为 简并四波混频
虽然简并四波混件下,必须保证 。
改变信道间距
用适当不等间距的波长信道配置设计来实现 ,通常选择通 道频率,使产生的新频率分量大部分落在通道滤波器通带 之外,这种技术用于10个信道,每个信道速率为10G/s 以下 的系统可大大减小四波混频的影响 加大信道间距也可抑 制四波混频的效率,却是以牺牲系统带宽为代价的 实际上 , 采用部分等间距信道更为有意义,其核心在于使通道间隔 相对远的信道之间的四波混频所产生的频率分量落在信道 滤波器通带内,由于四波混频的效率随着波长间隔加大而 降低,引入的恶化并不严重,这样可使系统容纳更多的波长。
∆k = k4 − (k1 − k2 − k3 ) = 0
考虑一种特殊情况,如下图,存在两对波矢方向相反的光,输 出为-k‘,它们满足如下相位匹配条件 k ' + (−k ' ) = k + (−k ) 。
简并四波混频的相位匹配
四波混频效应
这种简并四波混频非线性过程与典型的全息照过程很 相似。可以将k‘当做物光,k当做参考光,两者在介质 中互相干涉,形成全息图,如果全息图被记录下来了, 在参考光k的照射下,沿物光k’相反的方向-k‘可见物得 虚像。若挡住物光k’,在另一参考光-k的照射下,会 产生-k‘方向的赝像,该赝像就是原物光的相位共轭光。 虽然全照息过程和四波混频过程都产生相位共轭光, 但两者根本不同之处:全息照相的记录和重现过程在 时间上式分段进行的,而四波混频的相位共轭光与原 入射光几乎是同时产生。
四波混频

非线性光学中,四波混频是介质中四个光波相互作用所引起的非线性光学效应,它起因于介质的三阶非线性极化。 四波混频相互作用的方式一般可分为以下三类:
一,三个泵浦场的作用情况;二,输出光与一个光具有相同模式的情况;三,后向参量放大和振荡
由于四波混频在所有介质中都能很容易的观察到,而且变换形式很多,所以它已经得到了很多有意义的应用。例如,利用四波混频可以把可调谐相干光源的频率范围扩展到红外和紫外;在简笔的情况下,四波混频可用于自适应光学的波前再现;在材料应用中共振四波混频技术又非常有效的光谱和分析工具等待
发生四波混频的原因是入射光中的某一个波长上的变化,从而产生了新的波长的光波。
在DWDM系统中,当信道间距与光纤色散足够小且满足相位匹配时,四波混频将成为非线性串扰的主要因素。当信道间隔达到10GHZ 以下时,FWM 对系统的影响将最严重。
通信中,四波混频(Four-Wave Mixing,FWM) 亦称四声子混合,是光纤介质三阶极化实部作用产生的一种光波间耦合效应,是因不同波长的两三个光波相互作用而导致在其它波长上产生所谓混频产物,或边带的新光波,这种互作用可能发生于多信道系统的信号之间,可以产生三倍频、和频、差频等多种参量效应。
目前的DWDM系统的信道间隔一般在100GHZ ,零色散导致四波混频成为主要原因,所以,采用G.653 光纤传输DWDM系统时,容易产生四波混频效应,而采用G.652 或G.655 光纤时,不易产生四波混频效应。但G.652 光纤在1550nm 窗口存口存在一定的色散,传输10G信号时,应加色散补偿,G.655 光纤在1550nm 窗口的色散很小,适合10G DWDM 系统的传输。
四波混频对DWDM系统的影响主要表现在:(1)产生新的波长,使原有信号的光能量受到损失,影响系统的信噪比等性能;(2)如果产生的新波长与原有某波长相同或交叠,从而产生严重的串扰。四波混频的产生要求要求各信号光的相位匹配,当各信号光在光纤的零色散附近传输时,材料色散对相位失配的影响很小,因而较容易满足相位匹配条件,容易产生四波混频效应。
光子晶体光纤中四波混频效应与色散测量的研究的开题报告

光子晶体光纤中四波混频效应与色散测量的研究的开题报告标题:光子晶体光纤中四波混频效应与色散测量的研究一、研究背景光纤通信技术已经成为现代通信领域的支柱,而在光纤通信中,光纤中的色散是一个非常重要的问题。
因此,对光纤中的色散进行研究一直是光纤通信技术中的热点问题。
同时,四波混频效应也是一种应用广泛的非线性光学效应,具有很大的实用价值。
光子晶体光纤是一种新型的光纤,由于其具有高质量因子、小尺寸和良好的非线性特性等优点,已经成为研究的热点。
因此,研究光子晶体光纤中四波混频效应与色散的关系具有很大的研究价值。
二、研究内容本文将研究光子晶体光纤中四波混频效应与色散之间的关系,并将通过实验方法进行验证。
具体研究内容包括:1.通过对光子晶体光纤中的模式进行计算和模拟,研究光子晶体光纤中的色散机制。
2.探究光子晶体光纤中四波混频所需的功率和光场波长的变化规律,并进行数值模拟和实验验证。
3.通过实验方法分析光子晶体光纤中四波混频效应与色散的关系,在此基础上搭建一套完整的色散测量系统。
三、研究意义通过本文的研究,可以更深层次地了解光子晶体光纤中的非线性特性,探究其色散机制和四波混频效应与色散之间的关系。
同时,也可以为光纤通信技术的发展带来重要的参考和指导。
四、研究方法本文将采用理论计算、数值模拟和实验验证相结合的方法进行研究。
其中理论计算和数值模拟主要用于预测和分析光子晶体光纤中的非线性特性,而实验验证则是为了验证理论计算和数值模拟的正确性,并从实验数据中提取有用的信息。
五、研究进程计划(1)第1-2个月:对光子晶体光纤中的模式进行计算和模拟,研究光子晶体光纤中的色散机制。
(2)第3-4个月:探究光子晶体光纤中四波混频所需的功率和光场波长的变化规律,并进行数值模拟和实验验证。
(3)第5-6个月:通过实验方法分析光子晶体光纤中四波混频效应与色散的关系,并搭建一套完整的色散测量系统。
(4)第7-8个月:根据实验数据,分析光子晶体光纤中四波混频效应与色散的关系,并撰写论文。
四波混频
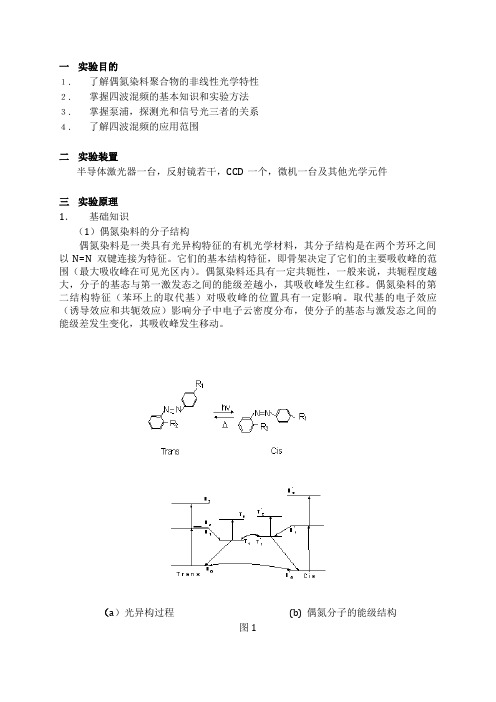
一实验目的1.了解偶氮染料聚合物的非线性光学特性2.掌握四波混频的基本知识和实验方法3.掌握泵浦,探测光和信号光三者的关系4.了解四波混频的应用范围二实验装置半导体激光器一台,反射镜若干,CCD一个,微机一台及其他光学元件三实验原理1.基础知识(1)偶氮染料的分子结构偶氮染料是一类具有光异构特征的有机光学材料,其分子结构是在两个芳环之间以N=N双键连接为特征。
它们的基本结构特征,即骨架决定了它们的主要吸收峰的范围(最大吸收峰在可见光区内)。
偶氮染料还具有一定共轭性,一般来说,共轭程度越大,分子的基态与第一激发态之间的能级差越小,其吸收峰发生红移。
偶氮染料的第二结构特征(苯环上的取代基)对吸收峰的位置具有一定影响。
取代基的电子效应(诱导效应和共轭效应)影响分子中电子云密度分布,使分子的基态与激发态之间的能级差发生变化,其吸收峰发生移动。
(a)光异构过程(b) 偶氮分子的能级结构图1(2)偶氮染料的光异构特性偶氮染料是一种偏振敏感的有机染料,它具有反式(trans)和顺式(cis)两种分子结构,如图1(a)所示(其中R1和R2表示不同的取代基,本实验所用甲基橙的取代基R1为NaO3S , R2 为N(CH3)2 )。
它们的分子主轴均为氮氮双键。
两者对应能态的能量是反式结构能量低,结构稳定;顺式结构能量高,结构不稳定,所以一般情况下偶氮分子多以稳定的反式结构存在。
图 1 (b) 是偶氮分子的能级结构图,由图可见,当用激光激发时,反式偶氮分子的基态粒子So吸收一个光子后,跃迁到第一激发态的某一振动能级Sv上,并迅速驰豫到第一激发态的最低能级S1上。
处于S1能级上的粒子可以进一步吸收一个光子并跃迁到第二重激发态S2上,也可经过系间跃迁无辐射驰豫到三重激发态T1上,这种跃迁由S1与T1间能级差决定。
差距越小,跃迁越容易。
T1态的粒子可以吸收光子跃迁到T2态上,也可通过无辐射跃迁回到So态上。
同时当激光强度达到一定值后,S2、T2等能级上的粒子还可以进一步吸收光子跃迁到更高一级激发态上去。
非线性光学-四波混频课件

四波混频(Four-wave mixing) 现象产生的条件理论应用和危害定义:在量子力学术语中,一个或几个光波的光子被湮灭,同时产生了几个不同频率的新光子,且在此过程中,净能量和动量是守恒的。
起源:光纤中的三阶电极化率1、四波混频现象——理论描述22222*1111121112341234222222*2221222212342134222233313233122(2)22(2)22(222i kzi kzA A A i A i A CD A C A A A iC A A A e z t tA A A i A i CD A A A C A A iC A A A e z t tA A A i A i C A A A z t tαββγγαββγγαββγ−Δ−Δ∂∂∂++=−+++++∂∂∂∂∂∂++=−+++++∂∂∂∂∂∂++=−+++∂∂∂22*34312422222*44414244123441232)(2)22i kzi kzC A A iC A A A eA A A i A i A C A C A A A iC A A A e z t tγαββγγΔΔ++∂∂∂++=−+++++∂∂∂2、四波混频产生的条件1、非线性光纤2、输入一个或以上不同频率的光波(简并条件下两个光波)3、输入光波的强度较强4、能量守恒:ω1+ω2=ω3+ω45、动量守恒:即满足相位匹配条件3、四波混频的理论方程•For FWM in DSF with not very long, we neglect the walk-offbetween the four waves and dispersion-induced pulse broaden, thus in Eq. (2) we have β11≈β12≈β13≈β14≡1/v g and β2j =0, where v g is the group velocity. Introducing a retarded frame in which T =t -z /v g , and decomposing the complex amplitude A j into their abosolute amplitudes and phases (j =1,2,3,4), eight equations with realvariables are obtained22222*1111121112341234222222*2221222212342134222233313233122(2)22(2)22(222i kzi kzA A A i A i A CD A C A A A iC A A A e z t t A A A i A i CD A A A C A A iC A A A e z t tA A A i A i C A A A z t tαββγγαββγγαββγ−Δ−Δ∂∂∂++=−+++++∂∂∂∂∂∂++=−+++++∂∂∂∂∂∂++=−+++∂∂∂22*34312422222*44414244123441232)(2)22i kzi kzC A A iC A A A e A A A i A i A C A C A A A iC A A A e z t tγαββγγΔΔ++∂∂∂++=−+++++∂∂∂FWMSelf phase modulation/ Cross phase modulation Fiber absorptionWalk-offGroup-velocity dispersion22222*1111121112341234222222*2221222212342134222233313233122(2)22(2)22(222i kzi kzA A A i A i A CD A C A A A iC A A A ez t tA A A i A i CD A A A C A A iC A A A e z t tA A A i A i C A A A z t tαββγγαββγγαββγ−Δ−Δ∂∂∂++=−+++++∂∂∂∂∂∂++=−+++++∂∂∂∂∂∂++=−+++∂∂∂22*34312422222*44414244123441232)(2)22i kzi kzC A A iC A A A e A A A i A i A C A C A A A iC A A A e z t tγαββγγΔΔ++∂∂∂++=−+++++∂∂∂Neglecting fiber absorption, walk-off between pulses, group-velocity dispersion (GVD)-induced pulse broadening:(,)exp()j j j A z T P i φ=2222*1123412342222*2123421342222*3123431242222*412344123(2)(2)(2)(2)i kz z i kzz i kzz i kz z A i A CD A C A A A iC A A A eA i CD A A A C A A iC A A A e A i C A A A Cd A A iC A A A eA i A C A Cd A A A iC A A A e γγγγγγγγ−Δ−ΔΔΔ∂=++++∂=++++∂=++++∂=++++相对相位1/2112341/211234123411/2212341/221234123421/2312342()sin (2)()cos /2()sin (2)()cos /2()sin z z zzz zzP C PP P P e z P CDP CP P e C PP P P e P z P C PP P P e z CDP P P CP e C PP P P e P z P C PP P P e z αααααααγθφγγθγθφγγθγ−−−−−−−∂=∂∂=++++∂∂=∂∂=++++∂∂=−∂1/231234123431/2412341/24123412344(2)()cos /2()sin (2)()cos /z zzz zCP P P CP e C PP P P e P z P C PP P P e z P CP CP P e C PP P P e P zαααααθφγγθγθφγγθ−−−−−∂=++++∂∂=−∂∂=++++∂1234(,)(,)(,)(,)(,)T z kz T z T z T z T z θφφφφ=Δ++−−Then from the 2nd , 4th , 6th , and 8th equations wecan obtain12341/2111112341234[(1)(1)] ()cos ()zzk CD C P CD C P P P e zC PP P P e P P P P ααθγγθ−−−−−−∂=Δ+−−+−−++∂++−−4、四波混频的应用及害处四波混频的应用四波混频的害处1.四波混频应用分类1PIA based on FWMP hase-inputSignal IdlerPump 1Pump 2PSA based on FWM 3P hase-s ensitive a mplification (PSA ): FWM with idler inputPump 1Pump 2Signal Idler1/21123412341(2)()cos /z z zP CDP CP P e C PP P P e P zααφγγθ−−∂∂=++++∂应用优势及挑战快速全光纤化……挑战?5(1) Wavelength conversion6(2) All-optical amplifier: PIA8(2) All-optical amplifier: PSAAmplifier with low noise-figure; Suppression of phase noise; Phase regeneration2. Applications of FWM(3) Optical phase conjugationEs ( z, t ) = As exp(−iωt )PumpEc ( z, t ) = As* exp(−iωt )Signal PumpPC signal9相位共轭系统又称频谱反转相位共轭器(OPC)Es ( z , t ) = As exp(−iωt )泵浦 共轭光 信号Ec ( z , t ) = As* exp(−iωt )泵浦5/18/20111利用相位共轭器的优点 仅利用一个器件就可以极大抑制多种非线性; 同时补偿偶数阶色散; 对调制格式、光纤种类透明; 已铺设好的系统易于升级.25/18/2011相位共轭 (OPC)的抑制原理相位共轭器(OPC)Es ( z , t ) = As exp(−iωt )Ec ( z , t ) = As* exp(−iωt )功率5/18/2011OPC功率对称系统:α(-z)= -α(z)3相位共轭技术抑制各种非线性损伤 1983年,脉冲自相位调制(SPM); 1994年,信道间四波混频; 2004年,信道间交叉相位调制 信道内非线性作用…5/18/20114相位共轭实验的原理泵浦 信号ωω0 ω0+Ωω新生成的共轭光A = Ap + As exp(−iΩt )k输入:∂Ai* = −2iγ Pp As e iΔkz ∂z四波 混频+∞ k −1 i βk ( z) ⎛ ∂ ⎞ ∂A α 2 + A+∑ ⎜ ⎟ A = iγ A A k ! ⎝ ∂t ⎠ ∂z 2 k =2非线性克尔效应5/18/201152. Applications of FWM(4) All-optical regeneration102. Applications of FWM(5) Slow light112. Applications of FWM(5) Slow light4000 3000 延迟量 /ps 2000 1000 0 -1000 1540 SMF3.4ns15451550 波长 λ /nm15551560122. Applications of FWM(6) RZ pulse generationO-TDM switchAll-optical samplingAll-optical logic gateAll-optical switching 142. Applications of FWM Others。
光纤通信实验4光纤中的四波混频效应
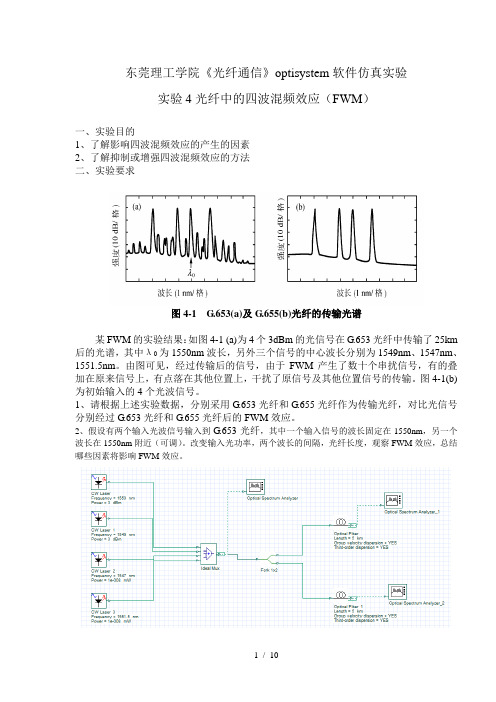
东莞理工学院《光纤通信》optisystem软件仿真实验实验4光纤中的四波混频效应(FWM)一、实验目的1、了解影响四波混频效应的产生的因素2、了解抑制或增强四波混频效应的方法二、实验要求图4-1 G.653(a)及G.655(b)光纤的传输光谱某FWM的实验结果:如图4-1 (a)为4个3dBm的光信号在G.653光纤中传输了25km 后的光谱,其中λ0为1550nm波长,另外三个信号的中心波长分别为1549nm、1547nm、1551.5nm。
由图可见,经过传输后的信号,由于FWM产生了数十个串扰信号,有的叠加在原来信号上,有点落在其他位置上,干扰了原信号及其他位置信号的传输。
图4-1(b) 为初始输入的4个光波信号。
1、请根据上述实验数据,分别采用G.653光纤和G.655光纤作为传输光纤,对比光信号分别经过G.653光纤和G.655光纤后的FWM效应。
2、假设有两个输入光波信号输入到G.653光纤,其中一个输入信号的波长固定在1550nm,另一个波长在1550nm附近(可调)。
改变输入光功率,两个波长的间隔,光纤长度,观察FWM效应,总结哪些因素将影响FWM效应。
图4-2 仿真实验系统搭建三、思考题:1、G.653光纤有什么缺点?为什么要研制G.655光纤?G.655光纤有什么优点?2、如何抑制光纤中的FWM效应?附录:计算并输出G.653或G.655光纤的色散文件clear all;close all;WL=linspace(1450,1630,1801);S0=0.06;WL0=1550;D=S0*(WL-WL0);%G.653%S0=0.0467;WL0=1480;D=S0*(WL-WL0);%G.655figure(1)plot(WL,D,'k');hold on;plot(WL,D*0,'k');hold on;axis([1450,1630,-20,20]);WL=WL';D=D';da=[WL D]save E:\G652.txt-ascii da1:G.653:G.655:2:(1)改变波长间隔:1545:1542:1520:1515:(2)改变光功率:10dbm:5dbm:-10dbm:-20dbm:-50dbm:(3)改变光纤长度:50km:10km:5km:1km:0.2km:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三次谐波与四波混频
(2013年12月31)
摘要:讨论了各向同性介质中的三阶非线性过程,以及四波混频和它的特殊情况。
关键词:三阶非线性过程,四波混频。
一、 各向同性介质中的三阶非线性过程
只有不具有中心对称性的介质或者各向异性介质才具有二阶非线性,但是所有介质都存在着三阶非线性。
一般(3)χ比(2)χ小得多,故三阶效应要比二阶效应弱得多。
在三阶非线性现象中,也存在着光与介质不发生能量交换,而参与作用的光波之间发生能量交换的非线性效应,这被称为波动非线性效应。
设输入光场()E t 是由沿z 方向传播的三个不同频率的单色光场组成
312123().i t i t i t E t E e E e E e c c ωωω---=+++ (1.1) 相应的各向同性介质中的三阶非线性极化强度为
(3)(3)30()()P t E t
εχ= (1.2) 将式(1.1)代入式(1.2),可见(3)()P t 是具有不同频率的(包括零频)的各项极化强度之和,可以写成
(3)()()n i t n n
P t P e ωω-=∑ (1.3)
式中n 取±,负号表示复数共轭量,包括极化强度的各种频率成分:
11211231231200,0,3,,,2ωωωωωωωωωωωω+++-+等。
这些频率项分别表示三次谐
波、四波混频、相位共轭、光克尔效应、自聚焦、饱和吸收、双光子吸收、受激散射等三阶非线性光学效应。
三倍频效应是频率为ω的光场入射介质产生频率为3ω光场的过程,其极化强度为
(3)(3)30(3)(3;,,)(
)P E ωεχωωωωω= (1.4) 这里D=1. 很少有晶体能实现三倍频的相位匹配,而且输入激光的强度往往受到光损伤的限制。
气体激光损伤极限强度比固体要高几个数量级,研究表明碱金属蒸汽在可见光区极化率
(3)χ有很强的共振增强,因此具有较强的三倍频效应。
以功率比表示的三倍频的转换效率为
222(3)223243039()sin ()2P P L kL c P c n n S ωωω
ωωωηχε∆== (1.5) 定义相干长度c c /,L=L kL /2/2c L k ππ=∆∆=当时,,三倍频效率很快下降;当0k ∆=,相位匹配,有最大的转换效率。
二、 四波混频
四个不同频率的波在介质中混频,如图2.1所示。
入射波为
1234(),(),(),E E E E ωωωω合成波为()。
在四波混频过程中,光子的能量守恒与动量守恒关系如下
图2.1 四波混频示意图
4123=++ωωωω
4123k k k k k ∆=---
频率为4ω的光波的三阶非线性极化强度为
(3)(3)404123123()6(;,,)()()()P E E E ωεχωωωωωωω=
(2.1)
假设各平面波皆沿z 方向传播,则对频率为4ω的四波混频波方程为
344404
()()2i kz dE i P e dz cn ωωωε-∆= (2.2)
此外,其他组合方式,如四波的差频与和频:4123ωωωω=+-和413122()ωωωωω=+=
等过程也可能存在。
四个波频率相等情况下的四波混频过程
称为简并四波混频,即满足条件
1234ωωωωω==== (2.3) 考虑能量守恒,ωωωω=-+,三阶极化率为(3)(;,,)χωωωω-,则极化强度表达为
(3)(3)2*0()3(;,,)()P E E ωεχωωωωω
=- (2.4) 这里D=3。
虽然简并四波混频的4个光子的频率相同,但是它们的波失方向可以不相同,在相位匹配条件下,必然保证
41230k k k k k ∆=---= (2.5)
考虑一种特殊情况,如图2.2.即存在着两对波失方向相反的光:'',,k k k k --和。
若入射光为',k k k -与,输出光为'k -,它们必然满足如下相位匹配条件
''()k k k k -=+-- ()
图2.2
这里k 和k -为泵浦光;''
k k -波是波的相位共轭波。
这种简并四波混频非线性过程与典型的全息照相过程很相似。
可以把 'k 看作物光,k 为参考光,两者在
介质中相互干涉,形成全息。
如果全息图被记录下来了,在参考光k的照射下,在沿物光'k相反的'k-方向可见物的虚像;若挡住物光'k,在另一参考光k-的照射下,会产生'k-方向的赝像,该赝像就是原物光的相位共轭光。
虽然全息照相个四波混频过程都能产生相位共轭,但两者有根本不同之处:全息照相的记录和重现过程在时间上是分段产生的,而四波混频的相位共轭光与原入射光几乎同时产生。
三、参考文献
1.《非线性光学》李淳飞著
2.《非线性光学物理》叶佩弦著。
