电路分析基础第四版课后习题答案
电路分析基础第四版课后答案 (2)

电路分析基础第四版课后答案第一章电路基本概念和定律1.1 电路基本概念1.什么是电路?2.什么是电流?3.什么是电压?4.什么是电阻?5.什么是电导?1.2 电路定律1.请简述欧姆定律的表达式及其在电路分析中的应用。
2.请简述基尔霍夫电流定律的表达式及其在电路分析中的应用。
3.请简述基尔霍夫电压定律的表达式及其在电路分析中的应用。
第二章电路分析方法2.1 参考方向和参考极性1.请简述参考方向在电路分析中的作用。
2.请说明电流方向和电压极性的确定方法。
2.2 串联与并联电路1.什么是串联电路?2.什么是并联电路?3.串联和并联电路的特点有哪些?2.3 电压分流和电流合并定律1.请简述电压分流定律的表达式及其在电路分析中的应用。
2.请简述电流合并定律的表达式及其在电路分析中的应用。
2.4 电阻网络简化1.什么是电阻网络简化?2.列举电阻网络简化的方法。
第三章基本电路3.1 电压源与电流源1.请简述理想电压源的特性及其在电路分析中的应用。
2.请简述理想电流源的特性及其在电路分析中的应用。
3.2 集总元件与非集总元件1.什么是集总元件?2.什么是非集总元件?3.请举例说明集总元件和非集总元件的特点。
3.3 电阻的平均功率和瞬时功率1.请简述电阻的平均功率和瞬时功率的计算方法。
3.4 等效电路和戴维南定理1.什么是等效电路?2.请简述戴维南定理及其在电路分析中的应用。
第四章变流电路4.1 正弦波电压和正弦波电流1.什么是正弦波电压?2.什么是正弦波电流?3.请简述正弦波电压和正弦波电流的特点。
4.2 交流电路中的电阻、电感和电容1.请简述交流电路中电阻、电感和电容的特性及其在电路分析中的应用。
4.3 相量法和复数法分析交流电路1.请简述相量法分析交流电路的基本原理。
2.请简述复数法分析交流电路的基本原理。
4.4 等效电路和史密斯图分析交流电路1.什么是等效电路?2.请简述史密斯图分析交流电路的基本原理。
第五章电流电压分析基础5.1 直流稳态分析1.什么是直流稳态?2.请简述直流稳态分析的基本步骤。
电路分析基础(第四版)课后答案第1章

目录 Contents
• 电路分析的基本概念 • 电路分析的基本定律 • 电路分析的基本方法 • 电路分析的应用
01
电路分析的基本概念
电路的定义和组成
总结词
电路是由若干个元件按照一定的方式连接起来,用于实现电能或信号传输的闭 合部分组成。电源是提供电能的设备,负载是消 耗电能的设备,中间环节则包括导线和开关等用于连接电源和负载的元件。
详细描述
电流是指单位时间内通过导体横截面的电荷量,电压是指电场力将单位正电荷从一点移动到另一点所做的功,功 率是指单位时间内完成的电功或电能消耗,能量则是指电荷在电场中由于电场力作用而具有的势能。这些物理量 在电路分析中具有重要的作用。
02
电路分析的基本定律
欧姆定律
总结词
欧姆定律是电路分析中最基本的定律之一,它描述了电路中 电压、电流和电阻之间的关系。
电路元件的分类
总结词
电路元件可以分为线性元件和非线性元件两大类。
详细描述
线性元件的电压和电流关系可以用线性方程表示,而非线性元件的电压和电流关 系则不能用线性方程表示。常见的线性元件包括电阻、电容和电感,而非线性元 件有二极管、晶体管等。
电路的基本物理量
总结词
电路的基本物理量包括电流、电压、功率和能量等。
详细描述
网孔电流法是以网孔电流为未知量,根据基尔霍夫定律列出节点电流方程和回路电压方程,求解各网 孔电流的方法。该方法适用于具有多个网孔的电路,特别是网孔较多的复杂电路。
04
电路分析的应用
电阻电路的分析
总结词
电阻电路是最基本的电路类型,其分析方法 主要包括欧姆定律、基尔霍夫定律等。
详细描述
电路分析基础(第四版)张永瑞答案第6章

42
第6 章
电路频率响应
(2) 当发生串联谐振时回路中电流有效值
U s 100 I0 10 A r 10
UC0=QUs=100×100×10-6=10 mV
43
第6 章
电路频率响应
6.9 一个rLC串联谐振电路如题6.9图所示, 已知该电 路的谐振角频率ω0=10 000 rad/s, 通频带BW=100 rad/s, r=10
第6 章
电路频率响应
第6章 电路频率响应
6.1 题6.1图所示的简单RC并联电路在电子线路中常 用来产生晶体管放大器的自给偏压。 图中电流 I 看成是
激励, 电压 U 看成是响应。 试求该一阶网络的网络函数
H(jω)、截止角频率ωc,并画出它的幅频特性和相频特性。
1
第6 章
电路频率响应
题6.1图
2
最高调谐频率为
f0max 1 1 1692 kHz 6 12 2 LCmin 2 3.14 295 10 30 10
f=(1692~530)kHz
38
第6 章
电路频率响应
6.8 在图示的rLC串联谐振电路中, 已知r=10 Ω, 回路
的品质因数Q=100, 谐振频率f0=1000 kHz。
UC 8 Q 80 U s 0.1
1 r r 25 12 Q2 f 0 10
r′=25-r=25-20=5 Ω
33
第6 章
电路频率响应 Gx=1.25×10-6 S
将r′与C的串联化为并联,
所以并接Yx前、 后电路的通频带分别为
f 0 106 BW 104 Hz Q 100
G1G2 jC (G1 G2 g m )
电路分析基础第四版课后习题第四章第五章第六章答案
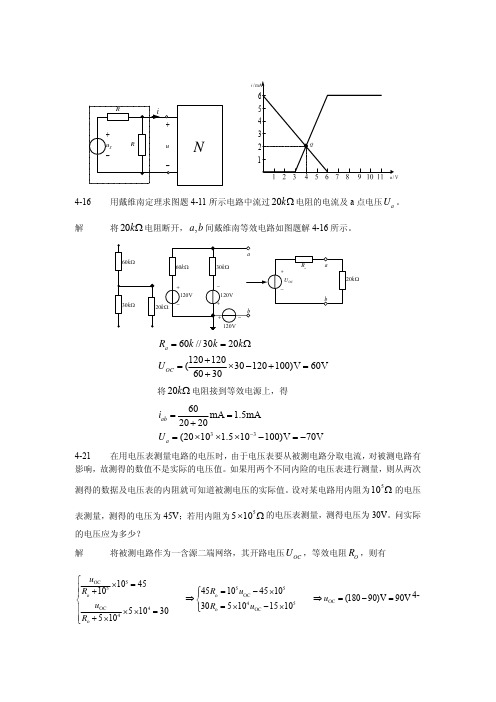
/i4-16 用戴维南定理求图题4-11所示电路中流过20k Ω电阻的电流及a 点电压。
a U 解将电阻断开,间戴维南等效电路如图题解4-16所示。
20k Ω,a bk Ω60//3020120120(30120100)V 60V6030a OCR k k k U ==Ω+=×−+=+ 将电阻接到等效电源上,得20k Ω3360mA 1.5mA2020(2010 1.510100)V 70V ab a i U −==+=×××−=− 4-21 在用电压表测量电路的电压时,由于电压表要从被测电路分取电流,对被测电路有影响,故测得的数值不是实际的电压值。
如果用两个不同内险的电压表进行测量,则从两次测得的数据及电压表的内阻就可知道被测电压的实际值。
设对某电路用内阻为的电压表测量,测得的电压为45V ;若用内阻为510Ω5510×Ω的电压表测量,测得电压为30V 。
问实际的电压应为多少? 解将被测电路作为一含源二端网络,其开路电压,等效电阻OC U O R ,则有5OC 555o o OC OC 454OCo OC 4o 10451045104510(18090)V 90V 30510151051030510u R R u u u R u R ⎧×=⎪⎧+=−×⎪⎪⇒⇒=⎨⎨=×−×⎪⎪⎩××=⎪+×⎩−=4-28 求图题4-20所示电路的诺顿等效电路。
已知:12315,5,10,R R R =Ω=Ω=Ω。
10V,1A S S u i ==解对图题4-20所示电路,画出求短路电流和等效内阻的电路,如下图所示SC i对左图,因ab 间短路,故0,0i i α==,10A 0.5A 155SC i ==+ 对右图,由外加电源法,106ab R α=Ω− 4-30 电路如图题4-22所示。
电路分析基础(第四版)张永瑞答案第5章
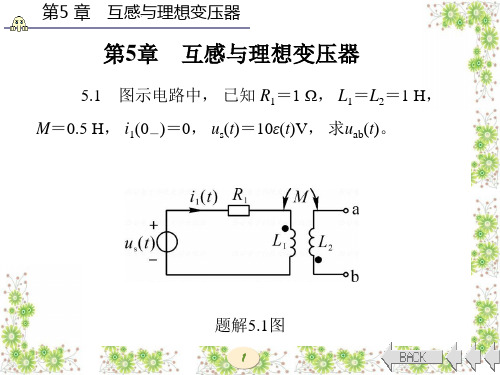
第5 章 互感与理想变压器
题5.4图
17
第5 章 互感与理想变压器 解 在画耦合电感T形去耦等效电路时, 若互感线圈两个
异名端子作为T形等效电路的公共端子, 则与公共端相连的就 是-M(M>0)的一个等效负电感。
18
第5 章 互感与理想变压器 据以上分析, 使所设计的互感电路以a点作为异名端公共
I2
U2 2
2000 2
1000 A
I1
N2 N1
I2
1 1000 1.1
90.90
A
42
第5 章 互感与理想变压器 返回题5.9图所示电路, 由KCL, 得
I3 I1 I2 90.90 1000 9.1 9.1180 A
I1=90.9 A, I3=9.1 A
6
第5 章 互感与理想变压器
题5.2图
7
第5 章 互感与理想变压器
解 由题5.2图(a)互感线圈所示同名端位置及电压、 电 流参考方向可得
u1(t)
L1
d i1 dt
M
d i2 dt
4 d i1 dt
0.5 d i2 dt
(1)
u2 (t)
L2
d i2 dt
M
d i1 dt
2
d i2 dt
0.96
阻抗Z′中的感抗
X L Z sinjz 25 1 0.962 7
等效电感
L X L 7 22.3mH
2 f 100
27
第5 章 互感与理想变压器 由于反接的等效电感
L L1 L2 2M 22.3mH
电路分析基础(四版)课后答案

I1 3 / /6 12 / /6 1 3A
再应用电阻并联分流公式, 得
I2
6 3
6
I1
2 3
3
2A
24
第1章 电路基本概念
I3
6 12
6
I1
13 3
1A
对节点a应用KCL, I=I2-I3=2-1=1 A
解答 题解1.7(c)图所示电路时, 不要设很多支路电流 建立很多的KCL、 KVL方程组, 然后联立求解。 这样求解 的思路能求解正确, 但费时费力, 不如应用串并联等效求 解简便。
所以
I 6 2 4A 2
20
第1章 电路基本概念
题解1.7图
21
第1章 电路基本概念 图(b)电路中, 设电流I1节点a及回路A, 如题解1.7图
(b)所示。 对节点a列写KCL方程, I1=1+I
对回路A列写KVL方程, -1+1×I+1×(I+1)=0
I=0
22
第1章 电路基本概念 当然, 本问亦可先将1 Ω电阻与1 V电压源的串联互换等
24
24 10 A
[8 / /8 2] / /[4 / /4 2] 2.4
再应用电阻并联分流公式, 得电流
因I与Us参考方向非关联, 所以电压源Us Ps=UsI=15×3=45 W
32
第1章 电路基本概念 1.10 求图示各电路中的电流I。
题解1.10图
33
第1章 电路基本概念 解 图(a):
I
100
2A
[50 / /50 6 / /30] / /60 / /20 40
电路分析基础第四版课后习题第六章第七章答案

uOC
=1 1.2 − 0.4α
, iSC
= 10mA , Rab
=
uOC iSC
=
250 3−α
Ω
微分方程为
duC dt
+ (12 − 4α ) ×103uC
= 104
6-6 电路如图题 6-6 所示。(1)t = 0 时 S1 闭合( S2 不闭合),求 i, t ≥ 0 ;(2)t = 0 时 S2 闭
,τ
=
L R
=
2s
iL (t)
=
4.5 1.5
(1 −
e−0.5t
)A
=
3(1 −
e−0.5t
)A
,t
≥0
(2)
S2
闭合(
S1 不闭合),断开电感,得戴维南等效电路,其中 uOC
=
6 6+
2
×12
=
8V
,
Ro
=
2Ω // 6Ω
= 1.5Ω
,τ
=
L R
= 1.5s
iL (t)
=
8 2
(1 −
−1t
e 1.5 )A
电感分别视为短路和开路,冲激电流全部流过电容,故电容电压为
∫ uc
(0+
)
=
1 C
0+δ (t)dt = 1
0−
C
由于它是有限值,所以电感的电流不会发生跃变, iL (0+ ) = iL (0− ) = 0 。
综上所述,冲激电压作用于 RLC 串联电路时,仅在换路瞬间电感的电流才会发生跃变, 而电容的电压不会发生跃变;冲激电流作用于 RLC 并联电路,仅在换路瞬间电容的电压发生 跃变,而电感电流不发生跃变。
电路分析基础第四版课后习题第一章第二章第三章第四章答案
+ 42V
−
i1
18Ω
i2 3Ω
i3
gu
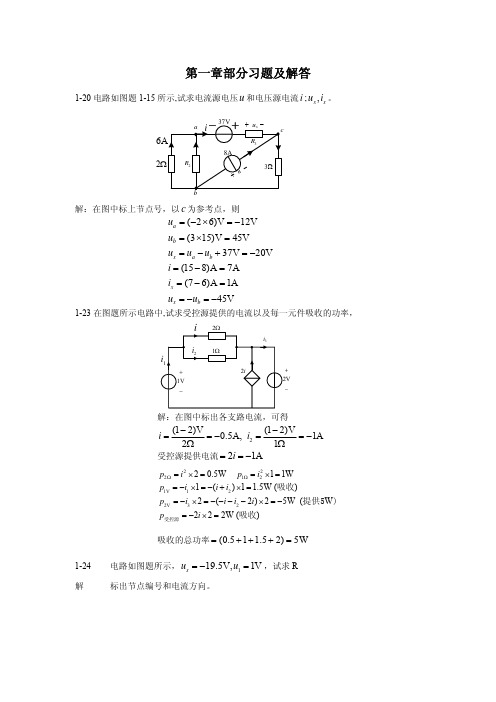
2−5
解
设网孔电流为 i1, i2 , i3 ,则 i3 = −guA = −0.1uA ,所以只要列出两个网孔方程
27i1 −18i2 = 42 −18i1 + 21i2 − 3(−0.1uA ) = 20
因 uA = 9i1 ,代入上式整理得
−15.3i1 + 21i2 = 20
⎪⎩i3 = 4A
第二章部分习题及解答
2-1 试用网孔电流法求图题所示电路中的电流 i 和电压 uab 。
4Ω
1Ω
i2
+
7V
−
i1
2Ω
i3 i
+ 3V
−
解
设网孔电流为 i1, i2 ,i3 ,列网孔方程
⎪⎨⎧3−ii11
− i2 − 2i3 = 7 + 8i2 − 3i3 = 9
⎪⎩−2i1 − 3i2 + 5i3 = −12
解得
i1 = 4.26A uA = (9× 4.26)V = 38.34V i3 = −0.1uA = −3.83A
2-8 含 CCVS 电路如图题 2-6 所示,试求受控源功率。
1Ω i3
5Ω
+
i 4Ω
+
50V i1 −
20Ω i2
15i −
2−6
解
标出网孔电流及方向,
⎧⎪⎨2−52i01i−1 +202i42i−2 −5i43 i=3
50 = −15i
⎪⎩−5i1 − 4i2 +10i3 = 0
又受控源控制量 i 与网孔电流的关系为 i = i1 − i2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i = = 0.5A, i 2 = =1A 第一章部分习题及解答1-20 电路如图题 1-15 所示,试求电流源电压 u 和电压源电流 i ; u x , i x 。
i+ u2Rb解:在图中标上节点号,以 c 为参考点,则u a = ( 2 ⋅ 6)V = 12V u b = (3⋅15)V = 45V u x = u a u b + 37V = 20V i = (15 8)A = 7A i x = (7 6)A = 1A x b 1-23+解:在图中标出各支路电流,可得(1 2)V (1 2)V 2∧ 1∧受控源提供电流 = 2i = 1Ap 2∧ = i 2 ⋅ 2 = 0.5Wp 1∧ = i 22 ⋅1 = 1Wp 1V = i 1 ⋅1 = (i + i 2 ) ⋅1 = 1.5W (吸收)p 2V = i 3 ⋅ 2 = ( i i 2 2i ) ⋅ 2 = 5W (提供5W ) p 受控源 = 2i ⋅ 2 = 2W (吸收)吸收的总功率 = (0.5 + 1 + 1.5 + 2) = 5W1-24 解电路如图题所示,u s = 19.5V, u 1 = 1V ,试求R标出节点编号和电流方向。
ai +3∧u∧b+ui2∧4∧i+10ucRiiei1 =u11= 1A, u bc = u1 10u1 = 9Vu bc2u ab = i s ⋅ 3 = 10.5Vu ce = u cb + u ba + u s = (9 + 10.5 19.5) = 0V为确定R,需计算i4,u ce = u cd + u de = 0 ® u de = u cd = 10u1 = 10V故1-33 试用支路电流法求解图题所示电路中的支路电流i1, i2 , i3。
a 1∧ci+6Vb解求解三个未知量需要三个独立方程。
由KCL可得其中之一,即i1 + i2 + i3 = 5对不含电流源的两个网孔,列写KVL方程,得网孔badb网孔bdacb2i1 3i2 + 8 = 08 + 3i2 i3 + 6 = 0i 2 = = 4.5A, i s = i 1 + i 2 = 3.5Ai 3 = = 2.5A, i 4 = i s i 3 = ( 3.5 + 2.5)A = 1A整理得: ♦ 2i 1 2 = 8+ 3i ® ♦i 2 = 2A♥♥♣i 1 + i 2 + i 3 = 5 ♣i 1 = 1A ♠ ♠♠3i 2 i 3 = 2 ♠i 3 = 4A♦ i1 + 8i2 3i3 = 9 ® ♦i2 = 1A♥i3 = 1A® ♦♠(R +R)i M2 R1i M 1 R2i M 3 =u ♠♠♠==0♣i M 1 = 24 u® ♦(3 + 4)i M 3 = u ® ♦ ♥i M 3 i M 1 = 8♥ 第二章部分习题及解答2-1试用网孔电流法求图题所示电路中的电流i和电压u ab。
3V 解设网孔电流为i1, i2 , i3,列网孔方程♣3i1 i2 2i3 = 7♠♠ 2i1 3i2 + 5i3 = 12 ♣i1 = 2A♠♠♣i = i1 i3 = 3A♥u ab = 3(i2 i3 ) 9 = 3V2-2电路中若R1 = 1∧, R2 = 3∧, R3 = 4∧, i s1 = 0, i s 2 = 8A, u s = 24V,试求各网孔电流。
解设网孔电流为i M 1, i M 2 , i M 3,列网孔方程♣R1i M 1 R1i M 2 R1i M 3 = u S u1 2♦(R2 + R3 )i M 3 R2i M 3 = u♠ M 2♠♥i M 3 i M 1 = i S 2♠ ♣i M 3 = 4A♠ ♥i M 1 = 4A2-5 电路如图题所示,其中g = 0.1S,用网孔分析法求流过8∧电阻的电流。
9∧♦ 20i 1 2 3i = 15i + 24i 4 代入并整理得: ♦ 5i 1 2 3 = 0 + 9i 4i ♥i 2 = 28A♥♥解设网孔电流为i 1, i 2 , i 3 ,则 i 3 = gu A = 0.1u A ,所以只要列出两个网孔方程27i 1 18i 2 = 4218i 1 + 21i 2 3( 0.1u A ) = 20因u A = 9i 1 ,代入上式整理得15.3i 1 + 21i 2 = 20解得i 1 = 4.26Au A = (9 ⋅ 4.26)V = 38.34V i 3 = 0.1u A = 3.83A2-8 含 CCVS 电路如图题 2-6 所示,试求受控源功率。
i2 6解标出网孔电流及方向,♣25i 120i 2 5i 3 =50 ♠♠ 5i 1 4i 2 + 10i 3 = 0又受控源控制量 i 与网孔电流的关系为i = i 1 i 2♣25i 1 20i 2 5i 3 = 50 ♠ ♠ 5i 1 4i 2 + 10i 3 = 0解得 ♣i 1 =29.6A ♦受控源电压受控源功率15i = 15(i 1 i 2 ) = 24V 24V ⋅ 28A=672W♠ 2 u 1 = 4 i 1 ♠ 1 ♠(1 1 1 (u 1 + 24) = 2 + )u 3 ® ♦3u 1 3 1i + 72 2u = 2 ® ♦u 1 = 14V ♥i 1 = 11A故得 ( 1 + 1 )U 1 ⋅12 ⋅ ( 4) = 0 ®♦ 1♠2-13 电路如图题所示,试用节点分析求i 1, i 2i2 13解 设节点电压为u 1, u 2 , u 3 。
由于 u 1, u 2 之间是 24V 电压源,所以有 u 2 = u 1 + 24 ,并增设24V 电压源支路电流 i 1 为变量,可列出方程♣♠♦( + 1)(u + 24) u = i ♠ 2♠ 1 1 1 ♥♣u = 8 2i ♠ ♥2u u = 22♣u = 4V ♠♠2-14U 1, IUk ∧3kΩI12V+ 4V 4V解由图题解 2-14 可知,该电路有 3 个独立节点,计有 3 个节点电压U 1,U 2 ,U 3 ,但U 2 = 12V U 3 = 4V1 15000 3000 5000 3000♣U = 2V ♥I = 2mA♠♠( 9 18)u = i 1+♠ 1 ⋅ (u 4) = 1 u i ♠♥ 4 3® ♦® ♦ 1= 2 ,2-18电路如图题 2-15 所示,其中 g =ui 11 3 S 。
试求电压 u 和电流 i 。
uu 4 ,列出节点方程♣ 1 1 ♦1♣u = 6i 1 ♥u = 12i 1 12♣i = 2A♥u = 12V由 i + i 1 = gu = 4 ,得i = 2A第三章部分习题及解答3-2 电路如图题 3-2 所示,(1)若u 2 = 10V ,求 i 1, u S ;(2)若 u S = 10V ,求 u 2 。
i10∧132u4解(1)应从输出端向输入端计算,标出节点编号,应用分压、分流关系可得i 24 =u 220 =0.5Au 32 = (10 ⋅ 0.5)V = 5V, u 34 = (10 + 5)V = 15V i 34 =15 30A = 0.5A,i 13 = (0.5 + 0.5)A = 1A u 13 = (10 ⋅1)V = 10V,u 14 = (10 + 15)V = 25V i 14 = 2525 A = 1A, i 1 = (1 + 1)A = 2A(2)应用线性电路的比例性10 u 45 10® u 2 =100 45 V =2.2V♥ 8a + 4b = 0® ♦ ' ''''3-7 电路如图题 3-7 所示,欲使u ab = 0, u s 应为多少?10V4∧解应用叠加原理,改画成图题解 3-7。
由图(a ),应用分压公式,u ab ' = (23 + 2⋅10)V = 4V为使 u ab = u ab + u ab = 0 ,应使 u ab = 4V 。
应用分压公式( u Sau+4∧(a )b4∧4∧(b )b4∧3-10(1)图题 3-10 所示线性网络 N 只含电阻。
若 i S 1 = 8A,i S 2 = 12A, 则 u x = 80V ;若i S 1 = 8A,i S 2 = 4A, 则 u x = 0 。
求:当 i S 1 = i S 2 = 20A 时, u x 是多少?(2)若所示网络N 含有一个电源,当i S 1 = i S 2i S 1 = i S 2 = 20A 时, u x iN解方程,(1)设 i S 1 = 1A 能产生 u x 为 a ,而 i S 2 = 1A 能产生 u x 为 b ,则根据叠加定理列出♣9a +12b = 80 ♦♣a = 2.5♥b = 5® u x =(20 ⋅ 5 + 20 ⋅ 2.5)V = 150V♦ 8a + 4b + i S c = 0 ® ♦ ® ♦ + )u = i♥i = 2mA ♠♠i 1 = 2000 A = 4mA ♦ ♠i = A = 2mA ♠2000♥(2)当 N 内含电源i S = 1A 能产生 u x 为 c ,则根据叠加定理列出方程,♣8a + 12b + i c = 80 ♠♠i c = 40♣8a + 12b = 120♥ 8a + 4b = 40♣a = 0 ♥b = 10® u =(20 ⋅ 0 + 20 ⋅10 40)V = 160V第四章部分习题及解答4-3 试求图题 4-3 所示电路的 VCR 。
解 施加电压源u S 于 a , b 两端,则 KVL 和 KCL ,可得u S = (i 1 + 〈 i 1 ) R L = (1 + 〈 )R L i 1即本电路的 VCR 为:u = (1 + 〈 )R L ia+ui〈 iRRb4-6 电路如图题 4 6(a ) 所示, u S = 12V,R = 2k ∧ ,网络 N 的 VCR 如图题 4 6(b ) 所示,求u , i ,并求流过两线性电阻的电流。
+RR+uN 65 4 3 21解求解虚线框内电路的 VCR ,可列出节点方程: (1 1 u S R R R得u =u S R 2 2i = 61000i♣u = 4V可在右边图中作出其特性曲线,与 N 的特性曲线相交于 Q 点,解得: ♦以 4V 电压源置换 N ,可得U OC = (♠ R + 105 ⋅10 = 45⋅ 5 ⋅104 = 30 ♠♣45R o = 10 u OC 45 ⋅10 ♥i / mA6R i 5+ +43u RuN 21Qu /V4-16 解用戴维南定理求图题4-11所示电路中流过20k∧电阻的电流及a点电压U a。
