三角形的四心&欧拉线的证明
三角形的外心内心垂心重心

三角形的外心内心垂心重心三角形的“四心所谓三角形的“四心”是指三角形的重心、垂心、外心及内心•当三角形是正三角形时,四心重合为一点,统称为三角形的中心.一、外心【定义】三角形三条中垂线的交点叫外心,即外接圆圆心.\ABC的重心一般用字母0表示.【性质】1・外心到三顶点等距,即OA = OB = 0C・2 •外心与三角形边的中点的连线垂直于三角形的这一边,即OD 丄BC,OEA.4C,OF丄/〃・3.ZJ = -ZBOC,ZB = L"OC,ZC = -ZAOB ・2 2 2二、内心【定义】三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心.MBC的内心一般用字母/表示.C【性质】1 •内心到三角形三边等距,且顶点与内心的连线平分顶角.2•三角形的面积=三角形的周长x内切圆的半径.23. AE = AF. BF = BD, CD = CE ;AE + BF±CD =三角形的周长的一半.44一90。
+存,8“90。
+护,W9O +"C・三、垂心【定义】三角形三条高的交点叫重心.\ABC的重心一般用字母H表示.1 •顶点与垂心连线必垂直对边,即AH丄BC、BH丄AC,CH丄AB.2.A ABH的垂心为C, NBHC的A 垂心为/\ACH的垂心为3 •【定义】三角形三条中线的交点叫重心・AJBC 的重心一般用字母G 表示. 【性质】1 •顶点与重心G 的连线必平分对边.2•重心定理:三角形重心与顶点的距离等于它与对边中点的距离的2倍.即 GA = 2GD, GB = 2GE, GC = 2GF3 .重心的坐标是三顶点坐标的平均值. 即总二邑逬竺,儿=2^匕严4•向量性质:(1) GA + GB + GC = O ;三角形“四心”的向量形式:结论1:若点O 为\ABC 所在的平面内一点,满足OAOB = OBOC = OCOA t则点。
为MBC 的垂心.结论2:若点O 为AABC 所在的平面内一点,满足OA +~BC 2 =OB -}-CA =OC\7B~ f 则点 O 为\ABC 的垂心.结论3:若点G 满足GA + GB^GC = O f 则点G 为\ABC 的重心.结论4:若点G 为\ABC 所在的平面内一点,满足~OG = -(OA^OB + OC)t则点G 为\ABC 的重心.结论5:若点/为AJBC 所在的平面内一点,并且满足a H + b •用+ c •丘=6(其中a,b,c 为三角形的三边),则点/为AABC 的内心.结论6:若点O 为MBC 所在的平面内一点,满足(^ + OB) BA = (dB + OC) CB = (dc + OA) AC ,则点 O 为 \ABC 的夕卜心.结论7:设/lw(0,+oo),则向量仲=久(«+ <£■),则动点P 的轨迹过的 \AB\ \AC\■ •I ■ • I •I •(2) PG = -(PA + PB + PC),5・ S^GC = S^CG/l =S“GBMB内心.向量和“心”一、重心”的向量风采【命题1】 已知G 是厶ABC 所在平面上的一点,若"G B -GG0,则G 是△ ABC 的重心.如图⑴.定通过△ ABC 的重心.边上的中线所在直线的向量,所以动点 ⑵. P 的轨迹一定通过 △ ABC 的重心,如图二、垂心”的向量风采【命题3】 P 是厶ABC 所在平面上一点,若 PA P^PB P^ PC PA ,则P 是 △ ABC 的垂心. 【解析】由 况,韋「P "B ,P ^得(祚 L F ) C0即卩P"B ,UfO ,所以【命题4】 已知O 是平面上一定点,A, B C 是平面上不共线的三个点,动点【解析】由题意 AP 「(AB AC),当’(0::时,由于■ (AB AC)表示 BC图⑵(是平面上不共线的三个点,动点CA 同理可证P C ± A ,PALB C 二P 是厶ABC 的垂心.如图⑶.图⑶A BP 满足 OP =0A ■ (AB AC) , ■ ( 0 BBP 满足O?=OA+扎 1 A ----- +------ |,九匸(0,+°°),贝U 动点 P 的轨迹 疋AB cosB AC cosC |通过△ ABC 的垂心.的轨迹一定通过△ ABC 的垂心,如图⑷. 三、内心”的向量风采 【命题5】 已知IABC 所在平面上的一点,且AB 二cAC 二bBC 二a .若T i TaIA bIB cIC =0,贝U I 是厶ABC 的内心.【解析】 AB c o BAC c Cs,由于= 'BC'—'CB|=0,所以AP 表示垂直于BC 的向量,即P 点在过点A 且垂直于BC 的直线上,所以动点P二 AI由题意AC cosCAB BC AC ■ BC即岡盂+冋盂AC ••• bAB cACbc a b c分别为AB 和AC 方向上的单位向量,••• AI与/ BAC平分线共线,即AI平分.BAC .同理可证:BI 平分.ABC , CI 平分.ACB .从而I 是△ ABC 的内心,如图⑸.【命题6】 已知0是平面上一定点,A , B (是平面上不共线的三个点,动点的内心.则O 是厶ABC 的外心,如图⑺.【命题7】 已知O 是平面上的一定点,A B C 是平面上不共线的三个点,动轨迹一定通过△ ABC 的外心.A C——C 表示垂直于BC 的向量,所以P 在BC 垂直平分线上, o sC,川(0 +叱),则动点P 的轨迹一定通过 △ ABC,二当儿三(0 ■二时,AP 表示一 BAC 的平分线所在直线方向的向量,故动点 P 的轨迹一定通过△ ABC 的内心,如图⑹. 四、外心”的向量风采 【命题7】 已知0是△ ABC 所在平面上一点,若0V "0B =—0,则 o 是△ ABC 的外心.^^2 2 2【解析】 若O A = O B = 0,则 图⑻龙=用6=|二「. 0^=RB~0,C点P 满足OP 二(TT 3 IT :AB +ACACCOBc CsJ【解析】由于°-B —°过C BC 的中点,2P 满足【解析】由题意得APAC■OB OC .2人乏(0 + °°),则动点P 的A C动点P 的轨迹一定通过△ ABC 的外心,如图⑻练习:数.满足:AB • AC 二‘ AP ,则.的值为() 3A . 2B .C . 3D . 622.若.ABC 的外接圆的圆心为 0,半径为1,OA ,OB ・OC=0,贝U OA OB =()A . 1B . 0C . 12OA 2OB 2OC = 0,贝U ABC 面积与凹四边形 ABOC 面积之比是( )3 5A . 0B .C .— 2 40,若OH -OA OB OC ,贝U H 是 ABC 的(——2 ——2 ——■ 2 5.0是平面上一定点,A 、B 、C 是平面上不共线的三个点,若OA BC = 0B■ - 2 j 2 ■ 2CA =OC AB ,则 O 是 ABC 的( )A .外心B .内心C .重心 6^ ABC 的外接圆的圆心为0,两条边上的高的交点为H, OH = m (OA OB OC ),则实数m = ______ 7. (06陕西)已知非零向量AB 与AC 满足+AC ) BC=0且•— =2 ,|Afe| |AC| |Afe| |AC| 2A .外心B .内心C .重心D .垂心 1■已知 ABC 三个顶点A 、B 、C 及平面内一点P ,满足 PA PB PC3 .点O 在ABC 内部且满足 4. =ABC 的外接圆的圆心为 D .垂心则厶ABC为()A.三边均不相等的三角形C.等腰非等边三角形B.直角三角形D .等边三角形——2 ——————■ 一■ ——一■8.已知ABC 三个顶点A、B、C,若AB -AB AC AB CB BC CA,则ABC 为()A .等腰三角形C .直角三角形练习答案:C、D、C、D、D、B.等腰直角三角形D .既非等腰又非直角三角形1、D、C。
真奇妙的三角形的四心

三角形的四心编辑同义词三角形三心一般指三角形的四心本词条缺少信息栏,补充相关内容使词条更完整,还能快速升级,赶紧来编辑吧!三角形的四心是指三角形的重心(center of gravity)、外心、内心、垂心。
当且仅当三角形是正三角形的时候,重心、垂心、内心、外心四心合一心,称做正三角形的中心。
目录1 三角形的四心▪来源▪三角形的五心2 三角形的外心▪三角形的三条垂直平分线必交于一点▪三角形的外心的性质3 三角形的内心▪证明▪性质4 三角形的垂心▪三角形的三条高必交于一点▪三角形的垂心的性质5 三角形的重心▪三角形的三条中线必交于一点▪三角形的重心的性质6 三角形的旁心▪介绍▪三角形旁心的性质7 欧拉线▪欧拉线的证法1▪欧拉线的证法2▪欧拉线的证法3三角形的四心编辑来源事实上,三角形有五心,但旁心并不常用。
因此常被称为四心。
三角形的五心旁心不与其他四心重合。
三角形的外心编辑三角形的外心是三角形三条垂直平分线的交点(或三角形外接圆的圆心) 。
三角形的三条垂直平分线必交于一点三角形的三条垂直平分线必交于一点已知:△ABC中,AB,AC的垂直平分线DO,EO相交于点O求证:O点在BC的垂直平分线上证明:连结AO,BO,CO,∵DO垂直平分AB,∴AO=BO∵EO垂直平分AC,∴AO=CO∴BO=CO即O点在BC的垂直平分线上三角形的外心的性质1.三角形三条边的垂直平分线的交于一点,该点即为三角形外接圆的圆心.2三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合。
3.锐角三角形的外心在三角形内;钝角三角形的外心在三角形外;直角三角形的外心与斜边的中点重合4.OA=OB=OC=R5.∠BOC=2∠BAC,∠AOB=2∠ACB,∠COA=2∠CBA6.S△ABC=abc/4R三角形的内心编辑三角形的内心是三角形三条内角平分线的交点(或内切圆的圆心)。
初中数学八年级三角形的四心及特点

三角形的内心、外心、中心、重心三角形的四心定义:1、内心:三角形三条内角平分线的交点,即内切圆的圆心。
内心是三角形角平分线交点的原理:经圆外一点作圆的两条切线,这一点与圆心的连线平分两条切线的夹角(原理:角平分线上点到角两边距离相等)。
2、外心:是三角形三条边的垂直平分线的交点,即外接圆的圆心。
外心定理:三角形的三边的垂直平分线交于一点。
该点叫做三角形的外心。
3、中心:三角形只有五种心重心、垂心、内心、外心、旁心,当且仅当三角形是正三角形的时候,四心合一心,称做正三角形的中心。
4、重心:重心是三角形三边中线的交点。
三角形的重心:三角形的重心是三角形三条中线的交点。
三角形的三条中线必交于一点已知:△ABC的两条中线AD、CF相交于点O,连结并延长BO,交AC于点E。
求证:AE=CE证明:延长OE到点G,使OG=OB∵OG=OB,∴点O是BG的中点又∵点D是BC的中点∴OD是△BGC的一条中位线∴AD∥CG∵点O是BG的中点,点F是AB的中点∴OF是△BGA的一条中位线∴CF∥AG∵AD∥CG,CF∥AG,∴四边形AOCG是平行四边形∴AC、OG互相平分,∴AE=CE三角形的重心的性质1.重心到顶点的距离与重心到对边中点的距离之比为2:1。
2.重心和三角形3个顶点组成的3个三角形面积相等。
3.重心到三角形3个顶点距离的平方和最小。
4.在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3);空间直角坐标系——横坐标:(X1+X2+X3)/3 纵坐标:(Y1+Y2+Y3)/3 竖坐标:(Z1+Z2+Z3)/35.重心和三角形3个顶点的连线的任意一条连线将三角形面积平分。
6.重心是三角形内到三边距离之积最大的点。
三角形的重心坐标:数学中,重心坐标是由单形(如三角形或四面体等)顶点定义的坐标。
重心坐标是齐次坐标的一种。
设v1, ..., vn 是向量空间V 中一个单形的顶点,如果V 中某点p 满足,(\lambda_{1}+\cdots +\lambda _{n})\,p=\lambda_{1}\,v_{1}+\cdots +\lambda _{n}\,v_{n}, 那么我们称系数(λ1, ..., λn) 是p 关于v1, ..., vn 的重心坐标。
三角形“四心”定义与性质

三角形“四心”定义与性质-CAL-FENGHAI.-(YICAI)-Company One1三角形“四心”定义与性质所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。
当三角形是正三角形时,四心重合为一点,统称为三角形的中心。
一、三角形的外心定 义:三角形三条中垂线的交点叫外心,即外接圆圆心。
ABC ∆的重心一般用字母O 表示。
性 质:1.外心到三顶点等距,即OC OB OA ==。
2.外心与三角形边的中点的连线垂直于三角形的这一边,即AB OF AC OE BC OD ⊥⊥⊥,,. 3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21。
二、三角形的内心 定 义:三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心。
ABC ∆的内心一般用字母I 表示,它具有如下性质:性 质:1.内心到三角形三边等距,且顶点与内心的连线平分顶角。
2.三角形的面积=⨯21三角形的周长⨯内切圆的半径. 3.CE CD BD BF AF AE ===,,;=++CD BF AE 三角形的周长的一半。
4.,2190A BIC ∠+=∠ B CIA ∠+=∠2190 ,C AIB ∠+=∠2190 。
三、三角形的垂心定 义:三角形三条高的交点叫重心。
ABC ∆的重心一般用字母H 表示。
性 质:1.顶点与垂心连线必垂直对边,即AB CH AC BH BC AH ⊥⊥⊥,,。
2.△ABH 的垂心为C ,△BHC 的垂心为A ,△ACH 的垂心为B 。
四、三角形的“重心”:定 义:三角形三条中线的交点叫重心。
ABC ∆的重心一般用字母G 表示。
性 质:1.顶点与重心G 的连线必平分对边。
2.重心定理:三角形重心与顶点的距离等于它与对边中点的距离的2倍。
即GF GC GE GB GD GA 2,2,2===3.重心的坐标是三顶点坐标的平均值. 即3,3C B AG C B A G y y y y x x x x ++=++=. 4.向量性质:(1)0=++GC GB GA ;(2))(31++=,5.ABC AGB CGA BGC S S S S ∆∆∆∆===31。
有关三角形“四心”的坐标公式的推导及应用

我们知道,三角形有“四心”:重心、内心、外心、垂心.其中重心是三角形三边中线的交点;内心是三角形三条内角平分线的交点,即内切圆的圆心;外心是三角形三条边的垂直平分线的交点,即外接圆的圆心;垂心是三角形三条边的垂线的交点.而这“四心”均有其对应的坐标公式,可运用向量法来推导三角形“四心”的坐标公式.若ΔABC三个顶点坐标分别为A(x1,y1),B(x2,y2),C(x3,y3),三个角A、B、C的对边||BC=a,||AC=b,||AB=c.1.ΔABC的重心坐标(x1+x2+x33,y1+y2+y33).证明:当P为ΔABC的重心时,PA+PB+PC=0 ,则OP=13( OA+ OB+ OC)=(x1+x2+x33,y1+y2+y33),其中O为坐标原点,所以点P的坐标为(x1+x2+x33,y1+y2+y33).2.ΔABC的内心坐标为(ax1+bx2+cx3a+b+c,ay1+by2+cy3a+b+c).证明:当P为ΔABC的内心时,a⋅PA+b⋅PB+c⋅PC=0 ,可得OP=aa+b+cOA+ba+b+cOB+ca+b+cOC=(ax1+bx2+cx3a+b+c,ay1+by2+cy3a+b+c),即为P点的坐标.3.ΔABC的外心坐标为(sin2A⋅x1+sin2B⋅x2+sin2C⋅x3sin2A+sin2B+sin2C,sin2A⋅y1+sin2B⋅y2+sin2C⋅y3sin2A+sin2B+sin2C).证明:当P为ΔABC的外心时,sin2A⋅PA+sin2B⋅PB+sin2C⋅PC=0 ,所以OP=1sin2A+sin2B+sin2C(sin2A⋅ OA+sin2B⋅ OB+sin2C⋅ OC)=(sin2A⋅x1+sin2B⋅x2+sin2C⋅x3sin2A+sin2B+sin2C,sin2A⋅y1+sin2B⋅y2+sin2C⋅y3sin2A+sin2B+sin2C),即为P点的坐标.4.ΔABC的垂心坐标为(tan A⋅x1+tan B⋅x2+tan C⋅x3tan A+tan B+tan C,tan A⋅y1+tan B⋅y2+tan C⋅y3tan A+tan B+tan C).证明:当P为ΔABC(非直角三角形)的垂心时,tan A⋅PA+tan B⋅PC+tan C⋅PC=0 ,所以OP=1tan A+tan B+tan C(tan A⋅ OA+tan B⋅OB+tan C⋅OC)=(tan A⋅x1+tan B⋅x2+tan C⋅x3tan A+tan B+tan C,tan A⋅y1+tan B⋅y2+tan C⋅y3tan A+tan B+tan C),即为P点的坐标.运用三角形“四心”公式,可以快速求得三角形的重心、内心、外心、垂心.例题:已知A(0,0),B(4,2),C(1,1),(1)求ΔABC的垂心H的坐标;(2)求ΔABC外接圆的方程.解:∵AB=(4,2) ,AC=(1,1), BC=(-3,-1) ,∴cos A=cosAB,AC=AB⋅AC|| AB|| AC=31010,∴sin A=1-cos2A 10∴cos B= BA⋅BC|| BA|| BC=7210 ,sin B∴cos C=-cos(A+B)=-255,sin C(1) a=||BC=10,b=2,c=25,tan A=sin A cos A=3,tan B=7,tan C=-12,tan A⋅x1+tan B⋅x2+tan C⋅x3tan A+tan B+tan C=5519,tan A⋅y1+tan B⋅y2+tan C⋅y3tan A+tan B+tan C=1319,所以ΔABC垂心H的坐标为(5519,1319).(2)sin2A=2sin A cos A=35,sin2B=725,sin2C=-45, sin2A⋅x1+sin2B⋅x2+sin2C⋅x3sin2A+sin2B+sin2C=4, sin2A⋅y1+sin2B⋅y2+sin2C⋅y3sin2A+sin2B+sin2C=-3,则ΔABC外接圆的圆心为 M(4,-3),r=||MA=5,所以ΔABC外接圆的方程为(x -4)2+(y+3)2=25.解答本题的常规方法是利用直线的方程之间的关系建立关系式,但利用三角形“四心”的坐标公式,解题更加方便快速.三角形“四心”的坐标公式是解答向量、平面几何、解三角形问题、圆锥曲线问题的重要工具.同学们可以熟记该公式并将其灵活地应用于解题当中.(作者单位:安徽省马鞍山市和县第二中学)考点透视41Copyright©博看网. All Rights Reserved.。
(完整版)三角形“四心”定义与性质(可编辑修改word版)
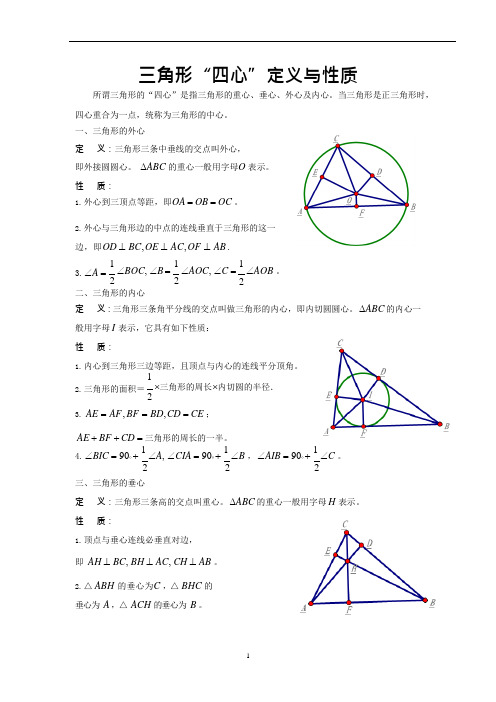
三角形“四心”定义与性质所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。
当三角形是正三角形时,四心重合为一点,统称为三角形的中心。
一、三角形的外心定义:三角形三条中垂线的交点叫外心,即外接圆圆心。
∆ABC 的重心一般用字母O 表示。
性质:1.外心到三顶点等距,即OA =OB =OC 。
2.外心与三角形边的中点的连线垂直于三角形的这一边,即OD ⊥BC, OE ⊥AC, OF ⊥AB .3. ∠A = 1∠BOC, ∠B =21∠AOC, ∠C =21∠AOB 。
2二、三角形的内心定义:三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心。
∆ABC 的内心一般用字母I 表示,它具有如下性质:性质:1.内心到三角形三边等距,且顶点与内心的连线平分顶角。
12.三角形的面积=⨯三角形的周长⨯内切圆的半径.23.AE =AF ,BF =BD, C D =CE ;AE +BF +CD =三角形的周长的一半。
4. ∠BIC = 90 +1∠A, ∠CIA = 90 +1∠B ,∠AIB = 90 +1∠C 。
2 2 2三、三角形的垂心定义:三角形三条高的交点叫重心。
∆ABC 的重心一般用字母H 表示。
性质:1.顶点与垂心连线必垂直对边,即AH ⊥BC, BH ⊥AC, CH ⊥AB 。
2.△ABH 的垂心为C ,△ BHC 的垂心为A ,△ ACH 的垂心为B 。
+ = + = + 四、三角形的“重心”:定义:三角形三条中线的交点叫重心。
∆ABC 的重心一般用字母G 表示。
性 质:1. 顶点与重心G 的连线必平分对边。
2. 重心定理:三角形重心与顶点的距离等于它与对边中点的距离的2 倍。
即GA = 2GD , GB = 2GE , GC = 2GF3. 重心的坐标是三顶点坐标的平均值. 即 x G =x A + x B + x C , y 3 G = y A + y B + y C . 34. 向量性质:(1) GA + GB + GC = 0 ;1 (2) = (PA + PB + PC ) ,5. 3 S ∆BGC = S ∆CGA = S ∆AGB = 1 S 3∆ABC 。
三角形“四心”定义与性质

三角形“四心”界说与性质之南宫帮珍创作 创作时间:二零二一年六月三十日所谓三角形的“四心”是指三角形的重心、垂心、外心及内心.当三角形是正三角形时, 四心重合为一点, 统称为三角形的中心.一、三角形的外心定 义:三角形三条中垂线的交点叫外心,即外接圆圆心.ABC ∆的重心一般用字母O 暗示.性 质:1.外心到三极点等距, 即OC OB OA ==.2.外心与三角形边的中点的连线垂直于三角形的这一边, 即AB OF AC OE BC OD ⊥⊥⊥,,.3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21.二、三角形的内心定 义:三角形三条角平分线的交点叫做三角形的内心, 即内切圆圆心.ABC ∆的内心一般用字母I 暗示, 它具有如下性质: 性 质:1.内心到三角形三边等距, 且极点与内心的连线平分顶角.2.三角形的面积=⨯21三角形的周长⨯内切圆的半径.3.CE CD BD BF AF AE ===,,;=++CD BF AE 三角形的周长的一半. 4.,2190A BIC ∠+=∠ B CIA ∠+=∠2190 , C AIB ∠+=∠2190 .三、三角形的垂心定 义:三角形三条高的交点叫重心.ABC ∆的重心一般用字母H 暗示.性 质:1.极点与垂心连线必垂直对边,即AB CH AC BH BC AH ⊥⊥⊥,,.2.△ABH 的垂心为C , △BHC 的垂心为A , △ACH 的垂心为B .四、三角形的“重心”:定 义:三角形三条中线的交点叫重心.ABC ∆的重心一般用字母G 暗示.性 质:G 的连线必平分对边.2.重心定理:三角形重心与极点的距离即是它与对边中点的距离的2倍.即GF GC GE GB GD GA 2,2,2===3.重心的坐标是三极点坐标的平均值.即3,3C B AG C B A G y y y y x x x x ++=++=.4.向量性质:(1)0=++GC GB GA ;(2))(31PC PB PA PG ++=, 5.ABC AGB CGA BGC S S S S ∆∆∆∆===31. 五、三角形“四心”的向量形式:结论1:若点O 为ABC ∆所在的平面内一点, 满足OA OC OC OB OB OA ⋅=⋅=⋅,则点O 为ABC ∆的垂心.结论2:若点O 为△ABC 所在的平面内一点, 满足222222AB OC CA OB BC OA +=+=+,则点O 为ABC ∆的垂心.结论3:若点G 满足0=++GC GB GA , 则点G 为ABC ∆的重心. 结论4:若点G 为ABC ∆所在的平面内一点, 满足)(31OC OB OA OG ++=,则点G 为ABC ∆的重心.结论5:若点I 为ABC ∆所在的平面内一点, 而且满足0=⋅+⋅+⋅IC c IB b IA a(其中c b a ,,为三角形的三边), 则点I 为△ABC 的内心.结论6:若点O 为ABC ∆所在的平面内一点, 满足AC OA OC CB OC OB BA OB OA ⋅+=⋅+=⋅+)()()(, 则点O 为ABC ∆的外心.结论7:设()+∞∈,0λ, 则向量||||(AC AC AB AB AP =λ, 则动点P 的轨迹过ABC ∆的内心.。
三角形的四心定义及其性质总结

三角形的四心定义及其性质总结
三角形是几何图形中最常见的形状,许多几何中的问题都与它有关。
三角形的形态也极其复杂,可以根据它的内部特征和外部特征来分类。
其中,四心定义及其性质决定了三角形的结构特征,在几何图形学中非常重要,下面就四心定义及其性质进行总结。
四心定义是指重心、内心、外心和垂心四种中心,它们对三角形的特征有着重要的影响,如重心是三角形内任何两点连线的重点,内心是三角形内角平分线交点;外心是三角形外接圆的圆心;垂心是三角形内角垂线的交点。
四心定义的性质也极其复杂,其中最重要的性质有:
1、重心的性质:重心是三角形内任何两点连线的重点,同时也
是三角形三条边的重点,所有三角形的重心都在三角形内部,而且重心到三角形内角的距离都相等,构成了三角形的等腰三角形。
2、内心的性质:内心是三角形内角平分线的交点,由内心和三
角形的三个顶点构成的三条线段相等,所以又称之为等边三角形;内心到三角形三个顶点的距离都相等,也构成了三角形的等腰三角形。
3、外心的性质:外心是三角形外接圆的圆心,同时也是三角形
三条外边中点的重点,所有三角形的外心都在三角形外部。
4、垂心的性质:垂心是三角形内角垂线的交点, three medians of a triangle are concurrent at the orthocenter,以又称之为
正切点,垂心到三角形三个顶点的距离都不相等。
总之,四心定义及其性质是了解三角形结构特征不可或缺的知识,
在几何图形学中发挥着重要作用。
例如它可以帮助我们判断一个三角形是等腰三角形还是等边三角形,也可以用来求取一个三角形的边长、面积等其他参数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形的四心三角形的四心是指三角形的重心、外心、内心、垂心。
等边三角形的四心重合。
一、三角形的重心三角形的重心是三角形三条中线的交点。
三角形的三条中线必交于一点已知:△ABC的两条中线AD、CF相交于点O,连结并延长BO,交AC于点E。
三角形的三条中线必交于一点求证:AE=CE证明:延长OE到点G,使OG=OB∵OG=OB,∴点O是BG的中点又∵点D是BC的中点∴OD是△BGC的一条中位线∴AD∥CG∵点O是BG的中点,点F是AB的中点∴OF是△BGA的一条中位线∴CF∥AG∵AD∥CG,CF∥AG,∴四边形AOCG是平行四边形∴AC、OG互相平分,∴AE=CE三角形的重心的性质1.重心到顶点的距离与重心到对边中点的距离之比为2:1。
2.重心和三角形3个顶点组成的3个三角形面积相等。
3.重心到三角形3个顶点距离的平方和最小。
4.在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3);空间直角坐标系——横坐标:(X1+X2+X3)/3 纵坐标:(Y1+Y2+Y3)/3 竖坐标:(Z1+Z2+Z3)/35.重心和三角形3个顶点的连线的任意一条连线将三角形面积平分。
6.重心是三角形内到三边距离之积最大的点。
二、三角形的外心三角形的外心是三角形三条垂直平分线的交点(或三角形外接圆的圆心) 。
三角形的三条垂直平分线必交于一点三角形的三条垂直平分线必交于一点已知:△ABC中,AB,AC的垂直平分线DO,EO相交于点O求证:O点在BC的垂直平分线上证明:连结AO,BO,CO,∵DO垂直平分AB,∴AO=BO∵EO垂直平分AC,∴AO=CO∴BO=CO即O点在BC的垂直平分线上三角形的外心的性质1.三角形三条边的垂直平分线的交于一点,该点即为三角形外接圆的圆心.2三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合。
3.锐角三角形的外心在三角形内;钝角三角形的外心在三角形外;直角三角形的外心与斜边的中点重合4.OA=OB=OC=R5.∠BOC=2∠BAC,∠AOB=2∠ACB,∠COA=2∠CBA 5.S△ABC=abc/4R三、三角形的内心三角形的内心是三角形三条角平分线的交点(或内切圆的圆心)。
三角形的三条角平分线必交于一点己知:在△ABC中,∠A与∠B的角平分线交于点O,连接OC求证:OC平分∠ACB证明:过O点作OD,OE,OF分别垂直于AC,BC,AB,垂足分别为D,E,F ∵AO平分∠BAC,∴OD=OE;∵BO平分∠ABC,∴OD=OF ;∴OE=OF∴O在∠ACB角平分线上∴CO平分∠ACB三角形的内心的性质1.三角形的三条角平分线交于一点,该点即为三角形的内心2.三角形的内心到三边的距离相等,都等于内切圆半径r3.r=2S/(a+b+c)4.在Rt△ABC中,∠C=90°,r=(a+b-c)/2.5.∠BOC = 90 °+∠A/2 ,∠BOA = 90 °+∠C/2 ,∠AOC = 90 °+∠B/2 6.S△ABC=abc/4R四、三角形的垂心三角形的垂心是三角形三边上的高的交点(通常用H表示)。
三角形的三条高必交于一点已知:△ABC中,AD、BE是两条高,AD、BE交于点O,连接CO并延长交AB于点F三角形的三条高必交于一点求证:CF⊥AB证明:连接DE ∵∠ADB=∠AEB=90°,且在AB同旁,∴A、B、D、E四点共圆∴∠ADE=∠ABE (同弧上的圆周角相等)∵∠EAO=∠DAC ∠AEO=∠ADC =90°∴△AEO∽△ADC ∴AE/AD=AO/AC 即AE/AO=AD/AC∴ΔEAD∽ΔOAC ∴∠ACF=∠ADE=∠ABE又∵∠ABE+∠BAC=90° ∴∠ACF+∠BAC=90° ∴CF⊥AB三角形的垂心的性质1.锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外2.三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心3. 垂心O关于三边的对称点,均在△ABC的外接圆上4.△ABC中,有六组四点共圆,有三组(每组四个)相似的直角三角形,且AO·OD=BO·OE=CO·OF5. H、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为一—垂心组)。
6.△ABC,△ABO,△BCO,△ACO的外接圆是等圆。
7.在非直角三角形中,过O的直线交AB、AC所在直线分别于P、Q,则AB/AP·tanB+ AC/AQ·tanC=tanA+tanB+tanC8.三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍。
9.设O,H分别为△ABC的外心和垂心,则∠BAO=∠HAC,∠ABH=∠OBC,∠BCO=∠HCA。
10.锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍。
11.锐角三角形的垂心是垂足三角形的内心;锐角三角形的内接三角形(顶点在原三角形的边上)中,以垂足三角形的周长最短。
12.西姆松(Simson)定理(西姆松线)从一点向三角形的三边所引垂线的垂足共线的重要条件是该点落在三角形的外接圆上五、欧拉线非等边三角形的外心、重心、垂心,依次位于同一直线上,这条直线就叫三角形的欧拉线。
其中,重心到外心的距离是重心到垂心距离的一半。
欧拉线的证法1作△ABC的外接圆,连结并延长BO,交外接圆于点D。
连结AD、CD、AH、CH、OH。
作中线AM,设AM交OH于点G’∵ BD是直径∴ ∠BAD、∠BCD是直角∴ AD⊥AB,DC⊥BC∵ CH⊥AB,AH⊥BC∴ DA‖CH,DC‖AH∴ 四边形ADCH是平行四边形∴ AH=DC∵ M是BC的中点,O是BD的中点∴ OM= 1/2DC∴ OM= 1/2AH∵ OM‖AH∴ △OMG’ ∽△HAG’∴AG/GM=2/1∴ G’是△ABC的重心∴ G与G’重合∴ O、G、H三点在同一条直线上如果使用向量,证明过程可以极大的简化,运用向量中的坐标法,分别求出O G H三点的坐标即可.欧拉线的证法2设H,G,O,分别为△ABC的垂心、重心、外心。
连接AG并延长交BC于D, 则可知D为BC中点。
连接OD ,又因为O为外心,所以OD⊥BC。
连接AH并延长交BC于E,因H 为垂心,所以AE⊥BC。
所以OD//AE,有∠ODA=∠EAD。
由于G为重心,则GA:GD=2:1。
连接CG并延长交BA于F,则可知F为AB中点。
同理,OF//CM.所以有∠OFC=∠MCF连接FD,有FD平行AC,且有DF:AC=1:2。
FD平行AC,所以∠DFC=∠FCA,∠FDA=∠CAD,又∠OFC=∠MCF,∠ODA=∠EAD,相减可得∠OFD=∠HCA,∠ODF=∠EAC,所以有△OFD∽△HC A,所以OD:HA=DF:AC=1:2;又GA:GD=2:1所以OD:HA=GA:GD=2:1又∠ODA=∠EAD,所以△OGD∽△HGA。
所以∠OGD=∠AGH,又连接AG并延长,所以∠AGH+∠DGH=180°,所以∠OGD+∠DGH=180°。
即O、G、H三点共线。
欧拉线的证法3设H,G,O,分别为△ABC的垂心、重心、外心.则向量OH=向量OA+向量+OB+向量OC向量OG=(向量OA+向量OB+向量OC)/3,向量OG*3=向量OH所以O、G、H三点共线(2010•内江)下面的方格图案中的正方形顶点叫做格点,图1中以格点为顶点的等腰直角三角形共有4个,图2中以格点为顶点的等腰直角三角形共有10个,图3中以格点为顶点的等腰直角三角形共有28个,图4中以格点为顶点的等腰直角三角形共有50个.考点:等腰直角三角形.专题:规律型.分析:根据正方形的性质,知图1中,连接2条对角线,可以有4个以格点为顶点的等腰直角三角形;图2中,连接每个正方形的2条对角线,在图1的基础上,则共有4×2+2=10(个)以格点为顶点的等腰直角三角形;图3中,在图1和图2的基础上,则共有10×2+8=28(个)以格点为顶点的等腰直角三角形;图4中,在图2和图3的基础上,分解为几个(2)(3)的图形,然后观察形状不是(2)(3)的四边形中是否存在满足条件的三角形,利用勾股定理的逆定理即可作出判断.解答:解:第一空 4 (设正方形边长为1,直角边长为1的等腰三角形有4个);第二空4×2+2=10 (每个正方形都有4个边长为1的等腰直角三角形,还有2个直角边长为的就是以2为斜边)第三空4×4+2×4+4=28 (4个小正方形就是4×4而相邻的两个小正方形都有2个直角边为的等腰直角三角形,这样相邻的有4对所以是2×4,然后再加上4个直角边长为2的)第四空4×6+2×7+4×2+4=50(6个小正方形,7对相邻的两个小正方形,2对直角边为2的大正方形,4个直角边长为的斜边为.工人师傅粉刷墙壁,现用4米长的木梯,如图(1)其安全使用范围是木梯于墙面夹角在30°与60°之间(当然包括30°和60°),当木梯顶端上下移动时,求木梯底端移动的最大距离是多少?(2)如果AO=3米,D在AO之间移动(不与A重合),当OD为多少米时,△AOB≌△COD?匿名回答:1 人气:17 解决时间:2010-08-22 18:15满意答案好评率:26%解:(1)木梯底端移动到最大距离时,即木梯于墙面夹角为60°所以d=4xsin60°=2√3米即OCmax=2√3米(2)△AOB≌△COD,所以OC=AO=3,又AB=4,即DC=4所以DO=√(4^2-3^2)=√7提问人的追问 2010-08-22 17:50什么意思?团队的补充 2010-08-22 18:10解:木梯在平面OC是能移动的,则OC能移动的最大值为木梯于墙面夹角为60°时OC的长,即为4xsin60°=2√3米,max是数学中常用的英文单词缩写,意为“最大值”已知如图所示,甲乙丙三个人做传球游戏,游戏规则如下:甲将球传给乙,乙将球传给丙,然后丙又立刻将球传给甲,若甲站在∠AOB的P点,乙站在OA 上,丙站在OB上并且甲乙丙三人的传球速度相同,乙和丙必须站在何处,才能使球从甲到乙,乙到丙,最后丙到甲这一轮所用的时间最少?最佳答案分别作点P关于OA和OB的对称点M和N,连接MN,分别交OA和OB于点P和Q。
