中考数学复习试卷
2024年中考数学专题复习:一次函数的图像与性质-试卷

2024年中考数学专题复习:一次函数的图像与性质一、选择题(本大题共10道小题)1. (2023•沈阳)一次函数y =-3x+1的图象不经过( )A.第一象限B.第二象限C.第三象限D.第四象限2. (2023八上·太原期中)课堂上,同学们研究正比例函数y=-x 的图象时,得到如下四个结论,其中错误的是( )A.当x=0时,y=0,所以函数y=-x 的图象经过原点B.点P(t,-t)一定在函数y=-x 的图象上C.当x>0时,y<0,当x<0时,y>0,所以函数y=-x 的图象经过二、四象限D.将函数的图象向左平移2个单位,即可得到函数y=-x+2的图象3. (2023·太原模拟)已知y 是x 的正比例函数,当x =3时,y =-6,则y 与x 的函数关系式为( )A.y =2xB.y =-2xC.y =12 xD.y =-12x 4. (2023•柳州)若一次函数y =kx+b 的图象如图所示,则下列说法正确的是( )A.k >0B.b =2C.y 随x 的增大而增大D.x =3时,y =0 5. (2023·贵州毕节·二模)已知正比例函数y=kx(k ≠0)的图象过点(2,3),把正比例函数y=kx(k ≠0)的图象平移,使它过点(1,-1),则平移后的函数图象大致是( )A. B. C.D. 6. (2023秋•会宁县)已知关于x 的一次函数y =(k 2+1)x-2图象经过点A(3,m)、B(-1,n),则m,n 的大小关系为( )A.m ≥nB.m >nC.m ≤nD.m <n7. (2023·随州模拟)如图,在平面直角坐标系中,动点A,B 分别在x 轴上和函数y =x 的图象上,AB =4,CB ⊥AB,BC =2,则OC 的最大值为( )A.222B.224C.2 5D.2528. (2023·鄂州中考)数形结合是解决数学问题常用的思想方法.如图,直线y =2x -1与直线y =kx +b(k ≠0)相交于点P(2,3).根据图象可知,关于x 的不等式2x -1>kx +b 的解集是( )A.x <2B.x <3C.x >2D.x >39. (2023•贵阳)小星在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线y =k n x+b n (n =1,2,3,4,5,6,7),其中k 1=k 2,b 3=b 4=b 5,则他探究这7条直线的交点个数最多是( )A.17个B.18个C.19个D.21个10. (2023·湖南永州·中考真题)已知点P(x 0,y 0)和直线y=kx+b,求点P 到直线y=kx+b 的距离d 可用公式0021kx y b d k -+=+计算.根据以上材料解决下面问题:如图,⊙C 的圆心C 的坐标为(1,1),半径为1,直线l 的表达式为y=-2x+6,P 是直线l 上的动点,Q 是⊙C 上的动点,则PQ 的最小值是( )A.355B.3515-C.6515-D.2二、填空题(本大题共8道小题)11. (2023•毕节市)将直线y =-3x 向下平移2个单位长度,平移后直线的解析式为 .12. (2023·四川成都市)在正比例函数y=kx 中,y 的值随着x 值的增大而增大,则点P(3,k)在第_____象限.13. (2023·贵州黔西·二模)如图,平面直角坐标系中,经过点B(-4,0)的直线y =kx+b 与直线y =mx+2相交于点3(,1)2A --,则关于x 的方程mx+2=kx+b 的解为________.14. (2023秋•宁化县)若函数y =4x ﹣1与y =﹣x+a 的图象交于x 轴上一点,则a 的值为( )A.4B.﹣4C.D.±415. (2023黔西南州)如图,正比例函数的图象与一次函数y =-x +1的图象相交于点P,点P 到x 轴的距离是2,则这个正比例函数的解析式是 .16. (2023·湖南湘西·中考真题)在平面直角坐标系中,O 为原点,点A(6,0),点B 在y 轴的正半轴上,∠ABO=30o .矩形CODE 的顶点D,E,C 分别在OA,AB,OB 上,OD=2.将矩形CODE 沿x 轴向右平移,当矩形CODE 与△ABO 重叠部分的面积为63时,则矩形CODE 向右平移的距离为___________.17. (2023•毕节市)如图,在平面直角坐标系中,点N 1(1,1)在直线l:y =x 上,过点N 1作N 1M 1⊥l,交x 轴于点M 1;过点M 1作M 1N 2⊥x 轴,交直线于N 2;过点N 2作N 2M 2⊥l,交x 轴于点M 2;过点M 2作M 2N 3⊥x 轴,交直线l 于点N 3;…,按此作法进行下去,则点M 2023的坐标为 .18. (2023•泰安)如图,点B 1在直线l:y =21x 上,点B 1的横坐标为2,过点B 1作B 1A 1⊥l,交x 轴于点A 1,以A 1B 1为边,向右作正方形A 1B 1B 2C 1,延长B 2C 1交x 轴于点A 2;以A 2B 2为边,向右作正方形A 2B 2B 3C 2,延长B 3C 2交x 轴于点A 3;以A 3B 3为边,向右作正方形A 3B 3B 4C 3,延长B 4C 3交x 轴于点A 4;…;照这个规律进行下去,则第n 个正方形A n B n B n+1∁n 的边长为 (结果用含正整数n 的代数式表示).三、解答题(本大题共6道小题)19. (2023秋•安徽月考)已知经过点A(4,-1)的直线y =kx+b 与直线y =-x 相交于点B(2,a),求两直线与x 轴所围成的三角形的面积.20. (2023春•西丰县)如图,一次函数y=kx+b的图象经过A(2,4),B(﹣2,﹣2)两点,与y轴交于点C.(1)求k,b的值,并写出一次函数的解析式;(2)求点C的坐标.21. (2023秋•兰州)如图,直线l1:y=-x+4分别与x轴,y轴交于点D,点A,直线l2:y x+1与x轴交于点C,两直线l1,l2相交于点B,连AC.(1)求点B的坐标和直线AC的解析式;(2)求△ABC的面积.22. (2023•滨州)如图,在平面直角坐标系中,直线y x﹣1与直线y=﹣2x+2相交于点P,并分别与x轴相交于点A、B.(1)求交点P的坐标;(2)求△PAB的面积;(3)请把图象中直线y=﹣2x+2在直线y x﹣1上方的部分描黑加粗,并写出此时自变量x的取值范围.23. (2023·河北中考真题)表格中的两组对应值满足一次函数y=kx+b,现画出了它的图象为直线l ,如图.而某同学为观察k,b 对图象的影响,将上面函数中的k 与b 交换位置后得另一个一次函数,设其图象为直线l '.(1)求直线l 的解析式; (2)请在图上画出..直线l '(不要求列表计算),并求直线l '被直线l 和y 轴所截线段的长; (3)设直线y=a 与直线l ,l '及y 轴有三个不同的交点,且其中两点关于第三点对称,直接..写出a 的值.24. (2023•黑龙江)如图,矩形ABOC 在平面直角坐标系中,点A 在第二象限内,点C 在y 轴正半轴上,OA 2-9x+20=0的两个根.解答下列问题:(1)求点A 的坐标;(2)若直线MN 分别与x 轴,AB,AO,y 轴交于点D,M,F,N,E,S △AMN =2,tan ∠AMN =1,求直线MN 的解析式;(3)在(2)的条件下,点P 在第二象限内,使以E,F,P,Q 为顶点的四边形是正方形?若存在;若不存在,请说明理由.。
初三中考必考的数学试卷

一、选择题(每题3分,共30分)1. 下列各数中,有理数是()A. √9B. πC. √-1D. √42. 若a > b,那么下列不等式中正确的是()A. a + 2 > b + 2B. a - 2 < b - 2C. 2a > 2bD. 2a < 2b3. 下列函数中,定义域为实数集R的是()A. y = √xB. y = x^2C. y = 1/xD. y = |x|4. 在直角坐标系中,点A(-2,3)关于原点的对称点是()A. (2,-3)B. (-2,-3)C. (-2,3)D. (2,3)5. 若一个等腰三角形的底边长为6cm,腰长为8cm,则该三角形的周长是()A. 22cmB. 24cmC. 26cmD. 28cm6. 已知一次函数y = kx + b的图象经过点(2,3)和(-1,1),则该函数的解析式为()A. y = 2x - 1B. y = -2x + 1C. y = 2x + 1D. y = -2x - 17. 下列图形中,不是轴对称图形的是()A. 矩形B. 正方形C. 菱形D. 梯形8. 在三角形ABC中,若∠A = 60°,∠B = 45°,则∠C的度数是()A. 45°B. 60°C. 75°D. 90°9. 若一个数x满足不等式x - 3 < 2x + 1,则x的取值范围是()A. x > -4B. x < -4C. x ≥ -4D. x ≤ -410. 下列等式中,正确的是()A. (a + b)^2 = a^2 + 2ab + b^2B. (a - b)^2 = a^2 - 2ab + b^2C. (a + b)^2 = a^2 - 2ab + b^2D. (a - b)^2 = a^2 + 2ab - b^2二、填空题(每题3分,共30分)11. 若m = 2,则方程2m - 3 = 0的解是______。
初中数学中考必考题试卷

1. 已知三角形ABC中,∠A=60°,∠B=45°,则∠C的度数是()A. 75°B. 90°C. 105°D. 120°2. 下列各数中,有理数是()A. √2B. πC. √-1D. 0.1010010001…3. 下列运算正确的是()A. (-2)^3 = -8B. (-2)^3 = 8C. (-2)^2 = -4D. (-2)^2 = 44. 已知等腰三角形ABC中,AB=AC,AD是底边BC上的高,则∠BAD的度数是()A. 45°B. 60°C. 90°D. 120°5. 下列函数中,一次函数是()A. y = x^2B. y = 2x + 3C. y = √xD. y = 1/x6. 已知一元二次方程ax^2 + bx + c = 0(a≠0)的解为x1、x2,则下列结论正确的是()A. x1 + x2 = aB. x1 x2 = bC. x1 + x2 = -bD. x1 x2 = c7. 下列图形中,中心对称图形是()A. 等腰三角形B. 等边三角形C. 正方形D. 等腰梯形8. 已知函数y = kx + b(k≠0)的图象经过点A(2,3),则下列结论正确的是()A. k > 0,b > 0B. k < 0,b < 0C. k > 0,b < 0D. k < 0,b > 09. 下列各数中,无理数是()A. √2B. πC. √-1D. 0.1010010001…10. 已知一元一次方程3x - 2 = 5的解是x = 3,则下列方程的解也是x = 3的是()A. 2x + 1 = 7B. 2x - 1 = 7C. 3x + 2 = 9D. 3x - 2 = 711. 若a > b,则a - b > 0,a + b > 0。
2024年深圳市中考数学复习与检测试卷(解析版)

2024年深圳市中考数学复习与检测试卷(解析版)一、选择题(本大题共有10个小题,每小题3分,共30分)1. 2024的倒数是()A.12024B.2024 C.2024−D.12024−【答案】A【分析】本题主要考查了倒数,解题的关键是熟练掌握倒数的定义,“乘积为1的两个数互为倒数”.【详解】解:2024的倒数1 2024.故选:A.2. 下列图形中,既是轴对称又是中心对称图形的是()A.B.C.D.【答案】A【分析】根据轴对称图形与中心对称图形的概念结合各图形的特点求解.【详解】A、是轴对称图形,也是中心对称图形,故本选项符合题意,B、是轴对称图形,不是中心对称图形,故本选项不合题意,C、不是轴对称图形,是中心对称图形,故本选项不合题意,D、是轴对称图形,不是中心对称图形,故本选项不合题意,故选:A.3.随着2024年2月第十四届全国冬季运动会临近,吉祥物成为焦点,某日通过搜索得出相关结果约为16000000个.将“16000000”用科学记数法表示为()A .61610×B .71.610×C .81.610×D .80.1610×【答案】B 【分析】本题考查了科学记数法;根据科学记数法计算方法计算即可;解题的关键是掌握科学记数法的计算方法.【详解】解:716000000 1.610=×4 . 某校10名篮球队员进行投篮命中率测试,每人投篮10次,实际测得成绩记录如下表: 命中次数(次)5678 9人数(人) 1 4 3 1 1由上表知,这次投篮测试成绩的中位数与众数分别是( )A .6,6B .6.5,6C .6,6.5D .7,6【答案】B【分析】根据中位数及众数可直接进行求解.【详解】解:由题意得:中位数为67 6.52+=,众数为6; 故选B .5.实数,a b 在数轴上的对应点的位置如图所示,下列关系式不成立的是( )A .55a b −>−B .66a b >C .a b −>−D .0a b −>【答案】C【分析】根据数轴判断出,a b 的正负情况以及绝对值的大小,然后解答即可.【详解】由图可知,0b a <<,且b a <,∴55a b −>−,66a b >,a b −<−,0a b −>,∴关系式不成立的是选项C .故选C .6 . 某学校将国家非物质文化遗产——“抖空竹”引入阳光特色大课间,某同学“抖空竹”的一个瞬间如图所示,若将左图抽象成右图的数学问题:在平面内,AB CD ,DC 的延长线交AE 于点F ;若7535BAE AEC ∠=°∠=°,,则DCE ∠的度数为( )A .120°B .115°C .110°D .75°【答案】C 【分析】根据平行线的性质得到75EFC BAE ∠=∠=°,根据三角形外角性质求解即可. 【详解】解:∵AB CD ,75BAE ∠=°, ∴75EFC BAE ∠=∠=°, ∵35DCE AEC EFC AEC ∠=∠+∠∠=°,,∴110DCE ∠=°, 故选:C .7 . 《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根木头的长,绳子还剩余4.5尺;将绳子对折再量木头,则木头还剩余1尺,问木头长多少尺?可设木头长为x 尺,绳子长为y 尺,则所列方程组正确的是( )A . 4.521y x x y −= −=B . 4.521x y x y −= −=C . 4.512x y y x −= −= D . 4.512y x y x −= −= 【答案】D【分析】设木头长为x 尺,绳子长为y 尺,根据“用一根绳子去量一根木头的长,绳子还剩余4.5尺;将绳子对折再量木头,则木头还剩余1尺”,即可得出关于x ,y 的二元一次方程组,此题得解.【详解】解:设木头长为x 尺,绳子长为y 尺, 由题意可得 4.512y x y x −= −=. 故选:D .8. 赵州桥是当今世界上建造最早,保存最完整的中国古代单孔敞肩石拱桥.如图,主桥拱呈圆弧形,跨度约为37m ,拱高约为7m ,则赵州桥主桥拱半径R 约为( )A. 20mB. 28mC. 35mD. 40m【答案】B【解析】 【分析】由题意可知,37m AB =,7m =CD ,主桥拱半径R ,根据垂径定理,得到37m 2AD =,再利用勾股定理列方程求解,即可得到答案.【详解】解:如图,由题意可知,37m AB =,7m =CD ,主桥拱半径R ,()7m OD OC CD R ∴=−=−,OC 是半径,且OC AB ⊥,137m 22AD BD AB ∴===, 在Rt △ADO 中,222AD OD OA +=,()2223772R R ∴+−= , 解得:156528m 56R =≈, 故选B9 . 如图,DE 是ABC 的中位线,点F 在DB 上,2DF BF =.连接EF 并延长,与CB 的延长线相交于点M .若6BC =,则线段CM 的长为( )A. 132B. 7C. 152D. 8【答案】C【解析】【分析】根据三角形中中位线定理证得DE BC ∥,求出DE ,进而证得DEF BMF ∽,根据相似三角形的性质求出BM ,即可求出结论.【详解】解:DE 是ABC 的中位线,DE BC ∴∥,116322DE BC ==×=, DEF BMF ∴ ∽, ∴22DEDF BF BM BF BF===, 32BM ∴=, ∴152CM BC BM =+=. 故选:C .10.如图,已知开口向上的抛物线2y ax bx c ++与x 轴交于点()1,0−,对称轴为直线1x =.下列结论: ①0abc >;②20a b +=;③若关于x 的方程210ax bx c +++=一定有两个不相等的实数根;④13a >. 其中正确的个数有( )A .1个B .2个C .3个D .4个【答案】D 【分析】利用二次函数图象与性质逐项判断即可.【详解】解:∵抛物线开口向上,∴0a >,∵抛物线与y 轴交点在负半轴,∴0c <,∵对称轴为12b x a=−=, ∴20b a −=<,∴0abc >,故①正确;∵抛物线的对称轴为=1x , ∴12b a−=, ∴2=0a b +,故②正确;∵函数2y ax bx c ++与直线1y =−有两个交点.∴关于x 的方程210ax bx c +++=一定有两个不相等的实数根,故③正确;∵=1x −时,0y =即0a b c −+=, ∵=2b a ,∴20a a c ++=,即3a c −=, ∵1c <−,∴31a −<−, ∴13a >, 故④正确,故选:D二、填空题(本大题共有5个小题,每小题4分,共20分)11.分解因式:2441a a −+= .【答案】()221a −【分析】根据完全平方公式的特点:两项平方项的符号相同,另一项是两底数积的两倍, 本题可以用完全平方公式.【详解】原式()()2222221121a a a =−××+=−. 故答案为:()221a −.12. 一只不透明的袋中装有2个白球和n 个黑球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到白球的概率为14,那么黑球的个数是 . 【答案】6【分析】根据概率公式建立分式方程求解即可【详解】∵袋子中装有2个白球和n 个黑球,摸出白球的概率为14, ∴22n +=14, 解得n =6,经检验n =6是原方程的根,故答案为:613. 已知关于x 的一元二次方程()2230x m x −++=的一个根为1,则m = . 【答案】2【分析】把1x =代入方程计算即可求出m 的值.【详解】解:把1x =代入方程得:1(2)30m −++=, 去括号得:1230m −−+=, 解得:2m =,故答案为:214. 如图,正六边形ABCDEF 的边长为2,以顶点A 为圆心,AB 的长为半径画圆,则图中阴影部分的面积为 .【答案】43π 【分析】延长FA 交⊙A 于G ,如图所示:根据六边形ABCDEF 是正六边形,AB =2,利用外角和求得∠GAB =360606°=°,再求出正六边形内角∠FAB =180°-∠GAB =180°-60°=120°, 利用扇形面积公式代入数值计算即可.【详解】解:延长FA 交⊙A 于G ,如图所示:∵六边形ABCDEF 是正六边形,AB =2,∴∠GAB =360606°=°, ∠FAB =180°-∠GAB =180°-60°=120°, ∴2120443603603FAB n r S πππ××===扇形, 故答案为43π. 15 . 如图,图1是一盏台灯,图2是其侧面示意图(台灯底座高度忽略不计),其中灯臂40cm AC =,灯罩30cm CD =,灯臂与底座构成的60CAB ∠=°. CD 可以绕点C 上下调节一定的角度.使用发现:当CD 与水平线所成的角为30°时,台灯光线最佳,则此时点D 与桌面的距离是________.(结果精确到1cm 1.732)【答案】50cm【分析】过点D 作DH AB ⊥,交AB 延长线于点H ,过点C 作CF AH ⊥于F ,过点C 作CE DH ⊥于E , 分别在Rt ACF 和Rt CDE △中,利用锐角三角函数的知识求出CF 和DE 的长,再由矩形的判定和性质得到CF EH =,最后根据线段的和差计算出DH 的长,问题得解.【详解】过点D 作DH AB ⊥,交AB 延长线于点H ,过点C 作CF AH ⊥于F ,过点C 作CE DH ⊥于E ,在Rt ACF 中,60A ∠=°,40cm AC =, ∵sin CF A AC=∴sin 60CF AC =°=,在Rt CDE △中,30DCE ∠=°,30cm CD =, ∵sin DE DCE CD∠=, ∴sin 3015DE CD=°=(cm), ∵DH AB ⊥,CF AH ⊥,CE DH ⊥, ∴四边形CFHE 是矩形, ∴CF EH =,∵DH DE EH =+,∴1550DH DE EH +≈(cm).答:点D 与桌面的距离约为50cm .三、解答题(本大题共有6个小题,共50分)16. 计算:101()2cos 451)4π−°−+−−−. 【答案】2【详解】分析:代入45°角的余弦函数值,结合“负整数指数幂和零指数幂的意义及绝对值的意义”进行计算即可.详解:原式=)4211−++=411−+,=2−.17. 先化简,再求值:(1﹣31x +)÷2441x x x −++,其中x =3. 【答案】1,12x −. 【分析】先将括号里的分式通分,然后按照分式减法法则计算,再根据分式除法法则进行运算即可将分式化简,最后代入字母取值进行计算即可求解. 【详解】解:原式=()2213111x x x x x −+ −÷ +++, =()22112x x x x −+⋅+−, =12x −, 当x =3时,原式=11 32=−.18.“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).请根据以上信息回答:(1)本次参加抽样调查的居民有多少人?(2)将两幅不完整的图补充完整;(3)若居民区有8000人,请估计爱吃D粽的人数;(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.【答案】(1)600;(2)见解析;(3)3200;(4)1 4【详解】(1)60÷10%=600(人).答:本次参加抽样调查的居民有600人.(2)如图,(3)8000×40%=3200(人).答:该居民区有8000人,估计爱吃D粽的人有3200人.(4)如图;共有12种等可能的情况,其中他第二个吃到的恰好是C粽的有3种,∴P(C粽)=312=14.答:他第二个吃到的恰好是C粽的概率是14.19.某厂家生产一批遮阳伞,每个遮阳伞的成本价是20元,试销售时发现:遮阳伞每天的销售量y(个)与销售单价x(元)之间是一次函数关系,当销售单价为28元时,每天的销售量为260个;当销售单价为30元时,每天的销售量为240个.(1)求遮阳伞每天的销出量y(个)与销售单价x(元)之间的函数关系式;(2)设遮阳伞每天的销售利润为w(元),当销售单价定为多少元时,才能使每天的销售利润最大?最大利润是多少元?【答案】(1)y=﹣10x+540;(2)当销售单价定为37元时,才能使每天的销售利润最大,最大利润是2890元【分析】(1)设函数关系式为y =kx +b ,由销售单价为28元时,每天的销售量为260个; 销售单价为30元时,每天的销量为240个;列方程组求解即可;(2)由每天销售利润=每个遮阳伞的利润×销售量,列出函数关系式,再由二次函数的性质求解即可;【详解】(1)解:设一次函数关系式为y =kx +b ,由题意可得:2602824030k b k b =+ =+, 解得:10540k b =− =, ∴函数关系式为y =﹣10x +540;(2)解:由题意可得:w =(x ﹣20)y =(x ﹣20)(﹣10x +540)=﹣10(x ﹣37)2+2890,∵﹣10<0,二次函数开口向下,∴当x =37时,w 有最大值为2890,答:当销售单价定为37元时,才能使每天的销售利润最大,最大利润是2890元.20. 已知:如图,在ABC 中,AB BC =,D 是AC 中点,BE 平分ABD ∠交AC 于点E ,点O 是AB 上一点,O 过B 、E 两点,交BD 于点G ,交AB 于点F .(1)试说明直线AC 与O 的位置关系,并说明理由;(2)当2BD=,1sin2C=时,求⊙O的半径.解:(1)证明:如图,连接OE,∵AB=BC且D是BC中点,∴BD⊥AC,∵BE平分∠ABD,∴∠ABE=∠DBE,∵OB=OE,∴∠OBE=∠OEB,∴∠OEB=∠DBE,∴OE∥BD,∴OE⊥AC,∴AC与⊙O相切.(2)∵BD=2,sinC=12,BD⊥AC,∴BC=4,∴AB=4,设⊙O的半径为r,则AO=4-r,∵AB =BC ,∴∠C =∠A ,∴sinA =sinC =12,∵AC 与⊙O 相切于点E ,∴OE ⊥AC∴sinA =142r r =−, ∴r =43, 经检验:r =43是原方程的解. 21. 如图,抛物线2y x bx c =−++交x 轴于A ,B 两点,交y 轴于点C ,直线BC 的表达式为3y x =−+.(1) 求抛物线的表达式;(2) 动点D 在直线BC 上方的二次函数图像上,连接DC ,DB ,设四边形ABDC 的面积为S ,求S 的最大值;(3) 当点E 为抛物线的顶点时,在x 轴上是否存在一点Q ,使得以A ,C ,Q 为顶点的三角形与BCE 相似?若存在,请求出点Q 的坐标.【答案】(1)223y x x =−++ (2)758(3)存在,Q 的坐标为()0,0或()9,0 【分析】(1)用待定系数法即可求解;(2)由DFB AOC COFD SS S S =++△△梯形,即可求解;(3)分AQC ECB ∽、QAC ECB △∽△、ACQ ECB △∽△三种情况,分别求解即可.【详解】(1)解:∵直线BC 的表达式为3y x =−+, 当0x =时,得:3y =,∴()0,3C ,3OC =,当0y =时,得:03x =−+,解得:3x =, ∴()3,0B ,3OB =,∵抛物线2y x bx c =−++交x 轴于A ,B 两点,交y 轴于点C , ∴9303b c c −++= =, 解得:23b c = = , ∴抛物线的表达式为223y x x =−++; (2)过点D 作DF x ⊥轴于点F ,设()2,23D x x x −++,∴(),0F x ,OF x =,3BF x ,∴223DF x x =−++,∵抛物线223y x x =−++交x 轴于A ,B 两点, 当0y =时,得:2230x x −++=,解得:11x =−,23x =,∴()1,0A −,1OA =,∵DFB AOC COFD SS S S =++△△梯形()()()2211132332313222x x x x x x =−+++−−+++×× 23375228x =−−+ , 又∵302−<,即抛物线的图像开口向下, ∴当32x =时,S 有最大值,最大值为758.(3)存在,理由:∵()222314y x x x =−++=−−+, ∴()1,4E ,又∵()0,3C ,()3,0B ,∴CEBC =BE =∴((22222220CE BC BE ++===,∴90ECB ∠=°, 如图所示,连接AC ,①()1,0A −,()0,3C ,∴1OA =,3OC =,AC === ∴13AO EC CO BC ==, 又∵90AOC ECB ∠=∠=°, ∴AOC ECB ∽,∴当点Q 的坐标为()0,0时,AQC ECB ∽; ②过点C 作CQ AC ′⊥,交x 轴与点'Q , ∵Q AC ′ 为直角三角形,CO AQ ⊥′,∴90ACQ AOC ′∠=∠=°,90AQ C CAQ ACO ′′∠=°−∠=∠, ∴ACQ AOC ′ ∽,又∵AOC ECB ∽,∴ACQ ECB ′ ∽,∴AQ EB AC EC ′== 解得:10AQ ′=,∴()9,0Q ′;③过点A 作AQ AC ⊥,交y 轴与点Q ,∵ACQ 为直角三角形,CA AQ ⊥,∴90QAC AOC ∠=∠=°,90ACQ CQA OAQ ∠=°−∠=∠, ∴QAC AOC △∽△,又∵AOC ECB ∽,∴QAC ECB △∽△,∴QC AC EB CB ==, 解得:103QC =, ∴103Q −,, 此时点Q 在y 轴上,不符合题意,舍去. 综上所述:当在x 轴上的点Q 的坐标为()0,0或()9,0时,以A ,C ,Q 为顶点的三角形与BCE 相似.22. 综合与探究在矩形ABCD 的CD 边上取一点E ,将BCE 沿BE 翻折,使点C 恰好落在AD 边上的点F 处.(1) 如图①,若2BC BA =,求CBE ∠的度数;(2) 如图②,当5AB =,且10AF FD ⋅=时,求EF 的长; (3) 如图③,延长EF ,与ABF ∠的角平分线交于点M ,BM 交AD 于点N ,当NFAN FD =+时,请直接写出AB BC的值. 【答案】(1)15° (2)3 (3)35 【分析】(1)由折叠的性质得出BC BF =,FBE CBE ∠=∠,根据直角三角形的性质得出30AFB ∠=°,可求出答案;(2)证明FAB EDF △∽△,由相似三角形的性质得出AF AB DE DF=,可求出2DE =,得出3EF =,由勾股定理求出DF =AF ,即可求出BC 的长; (3)过点N 作NG BF ⊥于点G ,证明NFG BFA △∽△,12NG FG NF BA FA BF ===,设AN x =,FG y =,则2AF y =,由勾股定理得出()()()222222x y x y +=+,解出43y x =,则可求出答案. 【详解】(1)解:∵四边形ABCD 是矩形, ∴90C ∠=°,∵将BCE 沿BE 翻折,使点C 恰好落在AD 边上点F 处,∴BC BF =,FBE CBE ∠=∠,90C BFE ∠=∠=°, ∵2BC AB =,∴2BF AB =,∴30AFB ∠=°, ∵四边形ABCD 是矩形,∴AD BC ∥,∴30CBF AFB ∠=∠=°, ∴1152CBE FBC ∠=∠=°,∴CBE ∠的度数为15°;(2)∵将BCE 沿BE 翻折,使点C 恰好落在AD 边上点F 处,∴90BFE C ∠=∠=°,FE CE =, 又∵矩形ABCD 中,90A D ∠=∠=°, ∴90AFB DFE∠+∠=°,90DEF DFE ∠+∠=°, ∴AFB DEF ∠=∠, ∴FAB EDF △∽△, ∴AF AB DE DF=, ∴AF DF AB DE ⋅=⋅,∵10AF DF ⋅=,5AB =, ∴2DE =,∴523CE DC DE =−=−=,∴3EFEC ==, ∴EF 的长为3;(3)过点N 作NG BF ⊥于点G ,∵NFAN FD =+, ∴1122NF AD BC ==, ∵BC BF =,∴12NF BF =, ∵NFG BFA ∠=∠,90NGF BAF ∠=∠=°, ∴NFG BFA △∽△, ∴12NG FG NF BA FA BF ===, 设AN x =,∵BN 平分ABF ∠,AN AB ⊥,NG BF ⊥,∴NGAN x ==,2AB x =, 在Rt BNG △和Rt BNA 中, NG NA BN BN= = , ∴()Rt Rt HL BNG BNA △≌△∴2BGAB x ==, 设FG y =,则2AF y =, 在Rt BAF △中,222AB AF BF +=, ∴()()()222222x y x y +=+, 解得:43y x =, ∴410233BF BG GF x x x =+=+=, ∴231053AB AB x BC BF x ===, ∴AB BC 的值为35.。
益阳市2024年中考数学试卷

选择题在益阳市的某次数学调研考试中,若一个多项式的次数是3,且它包含x²y这一项,那么下列哪个多项式可能符合这一条件?( )A. x³ + y³B. xy² + x²C. x²y + xy²(正确答案)D. x³y - y³小明在益阳市的中考数学复习中,遇到了一个关于函数图像平移的问题。
若将函数y = 2x的图像向左平移1个单位,得到的函数解析式是?( )A. y = 2(x + 1)(正确答案)B. y = 2(x - 1)C. y = 2x + 1D. y = 2x - 1在益阳市的中考数学试卷中,有一道题目是关于圆的性质。
若一个圆的半径为r,那么它的面积S等于?( )A. πrB. 2πrC. πr²(正确答案)D. 2πr²小华在益阳市的某次数学测验中,遇到了一个关于方程组的问题。
若方程组{x + y = 5, x - y = 1}的解是?( )A. {x = 2, y = 3}B. {x = 3, y = 2}(正确答案)C. {x = 4, y = 1}D. {x = 1, y = 4}在益阳市的中考数学复习中,学生们正在讨论一个关于概率的问题。
若一个不透明的袋子中装有3个红球和2个白球,从中随机摸出一个球是红球的概率是?( )A. 1/5B. 2/5C. 3/5(正确答案)D. 4/5小丽在益阳市的中考数学模拟考试中,遇到了一个关于三角形的问题。
若一个等腰三角形的底角为45°,那么它的顶角是?( )A. 45°B. 60°C. 90°(正确答案)D. 120°在益阳市的某次数学竞赛中,有一道题目是关于不等式的。
若不等式2x - 1 > 5的解集是?( )A. x > 2B. x > 3(正确答案)C. x < 2D. x < 3小明在益阳市的中考数学复习中,遇到了一个关于比例的问题。
中考数学试题试卷及答案

中考数学试题试卷及答案一、选择题(每题3分,共30分)1. 下列哪个选项是不等式2x-3>0的解集?A. x>1B. x<1C. x>3/2D. x<3/2答案:C2. 一个圆的半径为3cm,其面积是多少平方厘米?A. 28.26B. 18.84C. 9.42D. 15.7答案:B3. 如果一个数的立方根等于它本身,那么这个数可能是?A. 0B. 1C. -1D. A和B答案:D4. 计算下列哪个表达式的结果为-1?A. (-2)^3B. (-2)^2C. (-1)^3D. (-1)^2答案:C5. 以下哪个函数的图像是一条直线?A. y = 2x + 3B. y = x^2C. y = √xD. y = 3/x答案:A6. 一个等腰三角形的两边长分别为5cm和10cm,那么它的周长是多少?A. 20cmB. 15cmC. 25cmD. 不能构成三角形答案:D7. 计算下列哪个表达式的结果是正数?A. (-3) × (-2)B. (-3) × 2C. 3 × (-2)D. (-3) × (-2) + 1答案:A8. 一个数的相反数是-5,那么这个数是?A. 5B. -5C. 0D. 10答案:A9. 下列哪个分数是最简分数?A. 6/8B. 9/12C. 5/10D. 7/14答案:A10. 一个等差数列的首项是3,公差是2,那么第5项是多少?A. 13B. 11C. 9D. 7答案:A二、填空题(每题3分,共30分)11. 一个直角三角形的两个直角边长分别是3cm和4cm,那么斜边的长度是_________。
答案:5cm12. 一个数的绝对值是5,那么这个数可能是_________或_________。
答案:5或-513. 一个正数的平方根是2,那么这个数是_________。
答案:414. 一个数除以-1/2等于乘以_________。
中考数学《平行线分线段成比例》专题复习检测试卷
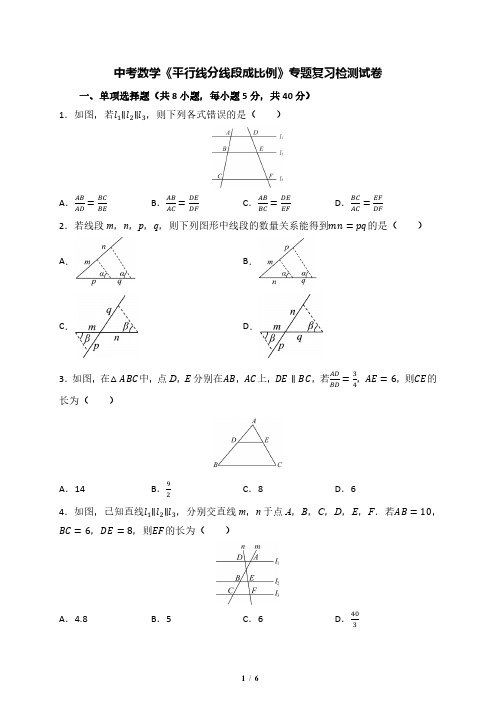
中考数学《平行线分线段成比例》专题复习检测试卷一、单项选择题(共8小题,每小题5分,共40分)1.如图,若l 1∥l 2∥l 3,则下列各式错误的是( )A .AB AD =BC BE B .AB AC =DE DF C .AB BC =DE EFD .BC AC =EF DF 2.若线段m ,n ,p ,q ,则下列图形中线段的数量关系能得到mn =pq 的是( ) A . B .C .D .3.如图,在△ABC 中,点D ,E 分别在AB ,AC 上,DE ∥BC ,若AD BD =34,AE =6,则CE 的长为( )A .14B .92C .8D .64.如图,已知直线l 1∥l 2∥l 3,分别交直线m ,n 于点A ,B ,C ,D ,E ,F .若AB =10,BC =6,DE =8,则EF 的长为( )A .4.8B .5C .6D .4035.如图,矩形ABCD 的四个顶点分别在直线l 1,l 3,l 4,l 2上,若直线l 1∥l 2∥l 3且相邻两直线间距离相等.若AB =6,BC =4,则l 2,l 3之间的距离为( )A .5B .65C .125D .245 6.如图,在△ABC 中,AD 平分∠BAC ,按如下步骤作图:第一步,分别以点A 、D 为圆心,以大于12AD 的长为半径作弧, 两弧交于点M 、N ;第二步,过 M 、 N 两点作直线,分别交AB 、AC 于点E 、F ;第三步,连接DE 、DF .若BD =8,AF =6,CD =4,则BE 的长是( )A .12B .11C .13D .10 7.AD 是△ABC 的中线,E 是AD 上一点,AE =14AD ,BE 的延长线交AC 于F ,则AF FC 的值为( )A .14B .15C .16D .17 8.如图,点D ,E ,F 分别在△ABC 的边上,AD BD =13,DE∥BC ,EF ∥AB ,点M 是DF 的中点,连接CM并延长交AB于点N,MNCM的值是()A.15B.14C.16D.17二、填空题(共8小题,每小题5分,共40分)9.在△ABC所在平面内,DE∥BC,且分别交直线AB,AC于D,E,AD:AB=1:3,EC=12,则AE=________.10.如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,AB=2cm.则线段BC=________cm.11.已知,如图,点D、F和E G分别在△ABC的边AB、AC上,且DE∥FG∥BC,若AD:DF:FB=1:2:3,则DE:FG:BC=________.12.如图,已知四边形DGFE是△ABC的内接正方形,AH⊥BC于H,AH=7 cm且BD:AD=4:3,则GF=________.13.如图,在△ABC中,F为AC的中点,过点F作EF⊥AB于点E,交BC的延长线于点D ,若EF =3,AB =14,BC CD =32,则BC 的长为________.第13题图 第14题图 14.如图,AD 、BC 相交于点O ,点E 、F 分别在BC 、AD 上,AB∥CD∥EF .若CE =6,EO =4,BO =5,AF =6,则AD =________.15.如图,在△ABC 中,点D 、E 分别为AB 、AC 的中点,点F 为DE 中点,连接BF 并延长交AC 于点G ,则AG:GE =________.16.如图,在△ABC 中,∠A =90°,D 是AB 的中点,过点D 作BC 的平行线,交AC 于点E ,作BC 的垂线,交BC 于点F .若AB =CE ,且△DEF 的面积为12,则BC 的长是_____.三、解答题(共6小题,共70分)17.如图,DE∥BC ,且DB =AE ,若AB =6,AC =10,求AE 的长.第17题图 第18题图 18.如图,已知D 为△ABC 的边AC 上的一点,E 为CB 的延长线上的一点,且EF FD =AC BC .求证:AD=EB.19.如图,在△ABC中,D,E,F分别是AB,BC上的点,且DE∥AC,DF∥AE,BDAD =32,BF=9cm,求EF和EC的长.20.如图,已知AD∥BE∥CF,它们依次交直线l1、l2、l3于点A、B、C和点D、E、F和点Q、H、P,l2与l3相交于DE的中点G,若ABAC =27.(1)如果EF=10,求DE、DF的长.(2)在(1)的条件下,如果QG=3,求PH的长.第20题图第21题图21.如图,已知四边形ABCD是菱形,点E是对角线AC上的一点,连接BE并延长交AD于点F,交CD的延长线于点G,连接DE.(1)求证:∠G=∠ADE.(2)求证:EB2=EF·EG.22.阅读与计算:请阅读以下材料,并完成相应的问题.角平分线分线段成比例定理:三角形内角平分线定理:三角形任意两边之比等于它们夹角的平分线分对边之比.如图①,在△ABC中,AD平分∠BAC,则ABAC =BDCD.下面是这个定理的部分证明过程.证明:如图②,过点C作CE∥DA,交BA的延长线于点E.∴∠BAD=∠E,∠CAD=∠ACE,……(1)请按照上面的证明思路,写出该证明过程的剩余部分.(2)如图①,在△ABC中,AD是角平分线,AB=5cm,AC=4cm,BC=7cm.求BD 的长.(3)如图③,在△ABC中,E是BC中点,AD是∠BAC的平分线,EF∥AD交AB于F,若AB=11,AC=9,直接写出线段FB的长.。
初三数学中考必考题试卷

一、选择题(每题3分,共30分)1. 下列各数中,有理数是()A. √-1B. πC. 0.1010010001…(循环小数)D. √162. 已知二次函数y=ax^2+bx+c(a≠0)的图像与x轴有两个交点,且这两个交点的横坐标分别为-1和2,则a、b、c的关系是()A. a+b+c=0B. a-b+c=0C. a+b-c=0D. a-b-c=03. 在等边三角形ABC中,角A的度数是()A. 60°B. 75°C. 80°D. 90°4. 下列函数中,自变量x的取值范围是全体实数的是()A. y=√(x-1)B. y=1/xC. y=x^2-4x+4D. y=2x-15. 在直角坐标系中,点P(-2,3)关于y轴的对称点坐标是()A.(-2,-3)B.(2,-3)C.(2,3)D.(-2,3)6. 下列命题中,正确的是()A. 等腰三角形的底角相等B. 所有平行四边形都是矩形C. 相似三角形的对应边成比例D. 直线与平面垂直的充分必要条件是直线与平面上的任意直线垂直7. 已知一元二次方程x^2-4x+3=0的两个根分别为x1和x2,则x1+x2的值是()A. 1B. 3C. 4D. 78. 在梯形ABCD中,AD∥BC,AB=CD,若AD=4cm,BC=6cm,则梯形ABCD的面积是()A. 10cm^2B. 12cm^2C. 14cm^2D. 16cm^29. 下列图形中,是轴对称图形的是()A. 正方形B. 等边三角形C. 正五边形D. 正六边形10. 若等比数列{an}的首项a1=2,公比q=3,则第5项a5的值是()A. 18B. 54C. 162D. 486二、填空题(每题3分,共30分)11. 若x^2-5x+6=0,则x的值是________。
12. 已知等边三角形ABC的边长为a,则其周长是________。
13. 在直角三角形中,若∠A=30°,∠B=60°,则∠C的度数是________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.按要求画出旋转后的图形。
(1)把梯形绕A点顺时针旋转90°。
(2)把三角形绕点O逆时针旋转90°。
3.(1)把三角形绕点A顺时针旋转90°,再向右平移3格。
(2)在方格纸上设计一个轴对称图形,并画出它的一条对称轴。
4.(1)将梯形先向下平移2格,再绕A点顺时针旋转90°。
(2)将小旗先绕B点逆时针旋转90°,再向上平移5格。
5.(1)将图形A向右平移3格得到图形B;以直线a为对称轴,作图形B的轴对称图形,得到图形C。
(2)将图形D绕点O顺时针旋转90°得到图形E;将图形E向右平移
4格,再向下平移2格,得到图形F。
6.画出下面图形的对称轴。
二.认识多位数
1.数的组成。
69050400里有()个千万,()个百万,()
个万和()个百。
它也是可以由()个万,()个一组成。
200600000000是()位数,它是由()个千亿和()个亿组成,240000000是由()个亿和()个万组成的。
2.由35个亿和35个万组成的数是()。
3.10个一千万是(),10个()是十亿,()个十亿是一百亿,()是10个一百亿。
4.一个八位数,它的个位上的数字是4,十位上的数字是个位上的数字的2倍,任意三个相邻数位上的数字之和都是15。
这个八位数是()
5.用万做单位,写出它们的近似数。
8994900≈6021500≈
6.用亿做单位,写出它们的近似数
999010000≈60970050000≈
7.在7080后面添上()个0是七百零八万。
8.249005024省略万后面的尾数约是()万,省略亿后面的尾数是()亿。
9.省略最高位后面的尾数,写出近似数。
705≈385≈1994≈3208≈
10.一个整数省略亿位后面的尾数约是20亿,这个整数最大是(),最小是()。
11.45万,4502700,450000,50万,45042中,最大的数是(),最小的数是(),()和()相等。
12.一枚1元的硬币重6克,1000枚1元硬币大约重()千克,100万枚1元硬币大约重()吨,1亿枚1元硬币大约重()吨。
13.用3004678这7个数字,组成最大的七位数是(),最小的七位数是(),只读出一个零的七位数是(),一个零也不读的七位数()
三.1.450的15倍是(),12个600的和是()。
2.每台电视机3200元,可以写成()。
自行车的速度是每
分钟210米,可以写成()。
3.已知总价和单价可以求(),关系式是(),
已知单价和数量可以求(),关系式是(),已知总价和数量可以求(),关系式是()。
已知路程和速度可以求出(),关系式是(),已知速度和时间可以求(),关系式是(),已知路程和时间可以求(),关系式是()。
位数乘最大的两位数,积是()位数。
由此可知,三位数乘两位数的积,最少是()位数,最多是()位数。
6.超市的某种糖果进行优惠促销活动,下面是超市的宣传广告。
7.四年级三个班要开联欢会,分别购买糖果的数量如下表:
(1)三个班分开购买,分别需要多少元?
(2)三个班合起来购买,一共需要多少元?
8.()×()=1600 ()×()=2400
9.两个不为0的数相乘,第一个数乘8,第二个数乘6,积扩大到
原来的()倍。
一个乘数乘8,另一个乘数÷8,积()。
10.找规律填空。
333667×3=1001001
333667×6= 333667×12=
333667×9= 333667×18=
11.小明在用计算器计算58×9时,计算器的数字5键坏了,你有什么方法能算出来?
12.开机键:(),关机键(),消除键(),
改错键()。
四。
1.张宁和王晓星一共有画片86张。
王晓星给张宁8张后,两人画片的张数同样多。
两人原来各有画片多少张?(画线段图并解答)
2.甲,乙两地相距495千米,一辆汽车从甲地开往乙地,已经
行了3小时,剩下的路程比已经行的多45千米。
这辆汽车的平
均速度是多少千米/小时?(画线段图并解答)
3.有一个长60米,宽40米的长方形鱼塘,如果要把它扩建成
正方形鱼塘,面积至少增加多少平方米?(画示意图并解答)4.王晓芳有一张宽30厘米的长方形彩纸,她从这张彩纸上裁下一
个最大的正方形做小旗,剩下彩纸的面积是360平方厘米。
原来彩纸的面积是多少平方厘米?(画示意图并解答)
5.一个长方形菜园,种黄瓜的面积比菜园的一半还多8平方米其
余的14平方米种番茄。
这个菜园有多少平方米?(画示意图并解答)
6.一个长方形,如果它的长减少4米,面积就减少80平方米;如果它的宽增加2米,面积就增加48平方米。
原来长方形的面积是多少平方米?(画示意图并解答)
7.一个长方形花圃长10米,宽7米。
张师傅想用只改变它的长或宽的办法,将它变成一个正方形花圃。
改变后它的面积最大是多少平方
9.利民商店上星期共售出矿泉水196箱,照这样计算,六月份能售
出矿泉水多少箱?
10.小华的爸爸是花匠,他的菊花成本是12元/盆,卖出的价格是23
元/盆,这个星期一共卖出125盆,共可以挣多少钱?
五.竖式计算
89×276= 802×60= 40×650=
508×60= 76×125= 540×70=
36×250= 408×23= 72×105=
124×43= 506×35= 183×47=
309×15= 598×24= 860×35=
10米
7米。
