2019年中考数学总复习【特殊的平行四边形】专项精练题及解析

合集下载

2019届中考数学专题复习演练：特殊的平行四边形(含答案)

2019届中考数学专题复习演练：特殊的平行四边形（含答案）特殊的平行四边形一、选择题1.如果要证明平行四边形ABCD为正方形，那么我们需要在四边形ABCD是平行四边形的基础上，进一步证明（）.A. AB＝AD且AC⊥BDB. AB＝AD且AC＝BDC. ∠A＝∠B且AC＝BDD. AC和BD互相垂直平分2.如图，在平行四边形ABCD中，E是CD的中点，AD、BE的延长线交于点F，DF=3，DE=2，则平行四边形ABCD的周长为（）A. 5B. 12C. 14D. 163.如图，菱形ABCD的两条对角线相交于O，若AC=8，BD=6，则菱形ABCD的周长是（）A. 32B. 24C. 40D. 204.在正方形ABCD中，AB＝12cm，对角线AC、BD相交于O，则△ABO的周长是（）A. B. C. D.5.正方形具有而菱形不一定具有的性质是（）A. 对角线相等B. 对角线互相垂直C. 对角线互相平分D. 对角线平分一组对角6.如图，P是边长为1的正方形ABCD的对角线BD上的一点，点E是AB的中点，则PA+PE的最小值是（）A. B. C. D.7.如图，P是▱ABCD上一点．已知S△ABP=3，S△PDC=2，那么平行四边形ABCD的面积是（）A. 6B. 8C. 10D. 无法确定8.如图，在▱ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD，交AD于点E，AB=6，EF=2，则BC长为（）A. 8B. 10C. 12D. 149.关于四边形ABCD：①两组对边分别平行；②两组对边分别相等；③有一组对边平行且相等；④对角线AC和BD相等；以上四个条件中可以判定四边形ABCD是平行四边形的有（）A. 1个B. 2个C. 3个D. 4个10.如图，在□ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中一定成立的是( ) ．①∠DCF=∠BCD；②EF=CF；③S△BEC＝2S△CEF；④∠DFE=3∠AEF．A. ①②③B. ①③C. ①②④D. ①②③④11.如图，菱形ABCD中，AB=5，∠BCD=120°，则对角线AC的长是( )A. 20B. 15C. 10D. 512.如图，在▱ABCD中，AB=4，AD=2，E，F分别为边AB，CD上的点，若四边形AECF为正方形，则∠D的度数为（）A. 30°B. 45°C. 60°D. 75°二、填空题13.如图，平行四边形ABCD的周长为40，△BOC的周长比△AOB的周长多10，则AB为________．14.请你写出一个正方形具有而平行四边形不一定具有的特征：________．15.如图，在▱ABCD中，AB＝5，AD＝3，AE平分∠DAB交BC的延长线于点F，则CF＝________.16.如图，如果要使平行四边形ABCD成为一个菱形，需要添加一个条件，那么你添加的条件是________．17.如图，在正方形ABCD中，AB=，点P为边AB上一动点（不与A、B重合），过A、P在正方形内部作正方形APEF，交边AD于F点，连接DE、EC，当△CDE为等腰三角形时，AP=________ ．18. 如图，已知菱形ABCD的两条对角线长分别为AC=8和BD=6，那么，菱形ABCD的面积为________．19.如图，在平行四边形ABCD中，点E，F分别在边BC，AD上，请添加一个条件________，使四边形AECF是平行四边形（只填一个即可）．20.如图，矩形ABCD中，BE平分∠ABC交AD于点E，F为BE上一点，连接DF，过F作FG⊥DF交BC于点G，连接BD交FG于点H，若FD=FG，BF=3 ，BG=4，则GH的长为________．21.如图，在矩形ABCD中，BC=2AB．以点B为圆心，BC长为半径作弧交AD于点E，连结BE．若AB=1，则DE的长为________．22.如图，矩形ABCD中，BC=3，AB=4，点E在AB上，点F在CD上，点G、H在对角线AC上，若四边形EGFH是菱形，则AE=________三、解答题23.如图在平行四边形ABCD中，AC交BD于点O，AE⊥BD，CF⊥BD，垂足分别为E、F，求证：四边形AECF为平行四边形．24.如图，已知E、F是平行四边形ABCD对角线AC上的两点，且BE⊥AC，DF⊥AC．求证：△ABE≌△CDF．25.如图，▱ABCD中，对角线AC与BD相交于O，EF是过点O的任一直线交AD于点E，交BC于点F，猜想OE和OF的数量关系，并说明理由．26.如图，在□ 中，、分别为边、的中点，是对角线，求证：= .27.如图：在矩形ABCD中，AD=60cm，CD=120cm，E、F为AB边的三等分点，以EF为边在矩形内作等边三角形MEF，N为AB边上一点，EN=10cm；请在矩形内找一点P，使△PMN为等边三角形（画出图形，并直接写出△PMF的面积）．28.已知，如图1，D是△ABC的边上一点，CN∥AB，DN交AC于点M，MA=MC．（1）求证：四边形ADCN是平行四边形．（2）如图2，若∠AMD=2∠MCD，∠ACB=90°，AC=BC．请写出图中所有与线段AN相等的线段（线段AN除外）29.如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连接BF．（1）BD与CD有什么数量关系，并说明理由；（2）①当△ABC满足什么条件时，四边形AFBD是矩形？并说明理由．②当△ABC满足什么条件时，四边形AFBD是菱形？并说明理由．参考答案一、选择题1. B2.C3.D4. A5. A6.A7. C8. B9.C 10.C 11. D 12. B二、填空题13.5 14.一组邻边相．（答案不唯一）15.216.AB=AD或AC⊥BD 17.﹣1或18.24 19.AF=CE 20.21.2﹣22.三、解答题23.证明：∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD，∴∠ABE=∠CDF，∵AE⊥BD，CF⊥BD，∴AE∥CF，∠AEB=∠CFD=90°，在△AEB和△CFD中，∵，∴△AEB≌△CFD（AAS），∴AE=CF，∴四边形AECF是平行四边形．24.证明：∵四边形ABCD是平行四边形，∴AB=CD，∠BAE=∠DCF，在△ABE和△CDF中，∴△ABE≌△CDF（AAS）．25.解：结论：OE=OF．理由∵四边形ABCD是平行四边形，∴OA=OC，AD∥BC，∴∠OAE=∠OCF，在△AOE和△COF中，，∴△AOE≌△COF，∴OE=OF．.26.证明：∵四边形是平行四边形，∴∥，DC=AB，又∵、分别为边、的中点，∴∥，= ，即∥，DF=BE，∴四边形是平行四边形，∴= ．27.解：如图，以MN为边，可作等边三角形PMN；△PMF的面积为400．（求解过程如下）．连接PE，∵△MEF和△PMN为等边三角形，∴∠PMN=∠NMF=∠MFE=60°，MN=MP，NE=NF，∴∠PME=∠NMF，在△MPE和△MNF中，，∴△MPE≌△MNF（SAS），∴∠MEP=∠MFE=60°，∴∠PEN=60°，∴PE∥MF，∴S△PMF=S△MEF=EF2=400．四、综合题28.（1）证明：∵CN∥AB，∴∠DAM=∠NCM，在△ADM和△CNM中，，∴△AMD≌△CMN（ASA），∴MD=MN，∴四边形ADCN是平行四边形（2）解：∵∠AMD=2∠MCD，∠AMD=∠MCD+∠MDC，∴∠MCD=∠MDC，∴MC=MD，∴AC=DN，∴▱ADCN是矩形，∵AC=BC，∴AD=BD，∵∠ACB=90°，∴CD=AD=BD= AB，∴▱ADCN是正方形，∴AN=AD=BD=CD=CN．29.（1）证明：∵E是AD的中点，∴AE=ED，∵AF∥BC，∴∠AFE=∠ECD，在△AEF和△DEC中，，∴△AEF≌△DEC，∴AF=DC，∵AF=BD，∴BD=DC．（2）①当AB=AC时，四边形AFBD是矩形．证明：∵AF=BD，AF∥BD，∴四边形AFBD是平行四边形，∵AB=AC，BD=DC，∴AD⊥BC，∴∠ADB=90°，∴四边形AFBD是矩形．②当∠BAC=90°时，四边形AFBD是菱形．证明：：∵AF=BD，AF∥BD，∴四边形AFBD是平行四边形，∵∠BAC=90°，BD=DC，∴AD=BD=DC，∴四边形AFBD是菱形．。

中考题汇编---特殊的平行四边形含答案

特殊的平行四边形1.(2019·海南中考)如图,在▱ABCD 中,将△ADC沿AC折叠后,点D恰好落在DC的延长线上的点E处,若∠B=60°,AB=3,则△ADE的周长为( C )A.12B.15C.18D.21【解析】选C.方法一:在▱ABCD 中,由将△ADC沿AC折叠后,点D恰好落在DC的延长线上的点E处,得∠ACD=∠ACE=90°,DC=CE=AB=3,AE=AD,∴DE=6,∵∠B=60°,∴∠D=60°,∠CAD=30°,∴AD=AE=2CD=6,∴△ADE的周长为6+6+6=18.方法二:在▱ABCD 中,由将△ADC沿AC折叠后,点D恰好落在DC的延长线上的点E处,得AE=AD, DC=CE=AB=3,∴DE=6,∵∠B=60°,∴∠B=∠D=∠E=60°,∴△ADE是等边三角形,∴AD=AE=ED=6,∴△ADE的周长为6+6+6=18.2.(2019·河池中考)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是( B )A.∠B=∠FB.∠B=∠BCFC.AC=CFD.AD=CF【解析】选B.∵在△ABC中,D,E分别是AB,BC的中点,∴DE是△ABC的中位线,∴DE=AC.A、根据∠B=∠F不能判定AB∥CF,即不能判定四边形ADFC为平行四边形,故本选项错误.B、根据∠B=∠BCF可以判定CF∥AB,即CF∥AD,由“两组对边分别平行的四边形是平行四边形”得到四边形ADFC为平行四边形,故本选项正确.C、根据AC=CF,AC∥DF,不能判定四边形ADFC为平行四边形,故本选项错误.D、根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项错误.3.(2019·天津中考)如图,四边形ABCD为菱形,A,B两点的坐标分别是(2,0),(0,1),点C,D在坐标轴上,则菱形ABCD的周长等于( C )A. B.4 C.4 D.20【解析】选C.∵A,B两点的坐标分别是(2,0),(0,1),∴AB==,∵四边形ABCD是菱形,∴菱形的周长为4.4.(2019·临沂中考)如图,在平行四边形ABCD中,M,N是BD上两点,BM=DN,连接AM,MC,CN,NA,添加一个条件,使四边形AMCN是矩形,这个条件是( A )A.OM=ACB.MB=MOC.BD⊥ACD.∠AMB=∠CND【解析】选A.∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵对角线BD上的两点M,N满足BM=DN,∴OB-BM=OD-DN,即OM=ON,∴四边形AMCN是平行四边形,∵OM=AC,∴MN=AC,∴四边形AMCN是矩形.5.(2019·绍兴中考)正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FG过点D.在点E从点A移动到点B的过程中,矩形ECFG的面积 ( D )A.先变大后变小B.先变小后变大C.一直变大D.保持不变【解析】选D.∵在正方形ABCD和矩形ECFG中,∠DCB=∠FCE=90°,∠F=∠B=90°,∴∠DCF=∠ECB,∴△BCE∽△FCD,∴=,∴CF·CE=CB·CD,∴矩形ECFG与正方形ABCD的面积相等.6.(2019·广州中考)如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为 ( A )A.4B.4C.10D.8【解析】选A.连接AE,设AC交EF于O,依题意,有AO=OC,∠AOF=∠COE,∠OAF=∠OCE,所以△OAF≌△OCE,所以EC=AF=5,因为EF为线段AC的中垂线,所以EA=EC=5,又BE=3,由勾股定理,得:AB=4,所以AC===4.7.(2019·达州中考)如图,▱ABCD的对角线AC,BD相交于点O,点E是AB的中点,△BEO的周长是8,则△BCD的周长为16 .【解析】∵▱ABCD的对角线AC,BD相交于点O,∴BO=DO=BD,BD=2OB,∴O为BD中点.∵点E是AB的中点,∴AB=2BE,BC=2OE.∵四边形ABCD是平行四边形,∴AB=CD,∴CD=2BE.∵△BEO的周长为8,∴OB+OE+BE=8,∴BD+BC+CD=2OB+2OE+2BE=2(OB+OE+BE)=16,∴△BCD的周长是16.答案:168.(2019·株洲中考)如图所示,在Rt△ABC中,∠ACB=90°,CM是斜边AB上的中线,E,F分别为MB,BC的中点,若EF=1,则AB= 4 .【解析】∵E,F分别为MB,BC的中点,∴EF是△BCM的中位线,∴CM=2EF=2,∵∠ACB=90°,CM 是斜边AB上的中线,∴AB=2CM=4.答案:49.(2019·武汉中考)如图,在▱ABCD中,E,F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为21°.【解析】设∠ADE=x,∵AE=EF,∠ADF=90°,∴DE=AF=AE=EF,∠DAE=∠ADE=x,∵AE=EF=CD,∴DE=CD,∴∠DCE=∠DEC=2x.∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAE=∠BCA=x,∴∠DCE=∠BCD-∠BCA=63°-x,∴2x=63°-x,解得:x=21°,即∠ADE=21°. 答案:21°10.(2019·北部湾中考)如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AH⊥BC于点H,已知BO=4,S=24,则AH= .菱形ABCD【解析】∵四边形ABCD是菱形,∴BO=DO=4,AO=CO,AC⊥BD,∴BD=8,=AC×BD=24,∴AC=6,∵S菱形ABCD∴OC=AC=3,∴BC==5,=BC×AH=24,∴AH=.∵S菱形ABCD答案:11.(2019·菏泽中考)如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是8.【解析】如图,连接BD交AC于点O,∵四边形ABCD为正方形,∴BD⊥AC,OD=OB=OA=OC,∵AE=CF=2,∴OA-AE=OC-CF,即OE=OF,∴四边形BEDF为平行四边形,又BD⊥EF,∴四边形BEDF为菱形,∴DE=DF=BE=BF,∵AC=BD=8,OE=OF==2,由勾股定理得:DE===2,∴四边形BEDF的周长=4DE=4×2=8.答案:812.(2019·广安中考)如图,点E是▱ABCD的CD边的中点,AE,BC的延长线交于点F,CF=3,CE=2,求▱ABCD的周长.【解析】∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAE=∠F,∠D=∠ECF.又ED=EC,∴△ADE≌△FCE(AAS).∴AD=CF=3,DE=CE=2.∴DC=4.∴平行四边形ABCD的周长为2(AD+DC)=14.13.(2019·扬州中考)如图,在平行四边形ABCD中,AE平分∠DAB,已知CE=6,BE=8,DE=10.(1)求证:∠BEC=90°.(2)求cos∠DAE.【解析】(1)∵四边形ABCD是平行四边形,∴DC=AB,AD=BC,DC∥AB,∴∠DEA=∠EAB,∵AE平分∠DAB,∴∠DAE=∠EAB,∴∠DAE=∠DEA,∴AD=DE=10,∴BC=10.∵CE2+BE2=62+82=100=BC2,∴△BCE是直角三角形,∠BEC=90°.(2)由(1)知,AB=DC=DE+CE=16,∵AB∥CD,∴∠ABE=∠BEC=90°,∴AE===8,∴cos∠DAE=cos∠EAB===.14.(2019·荆门中考)如图,已知平行四边形ABCD中,AB=5,BC=3,AC=2.(1)求平行四边形ABCD的面积.(2)求证:BD⊥BC.【解析】(1)作CE⊥AB,交AB的延长线于E,设BE=x,CE=h,在Rt△CEB中:x2+h2=9 ①在Rt△CEA中:(5+x)2+h2=52 ②联立①②解得:x=,h=,∴平行四边形ABCD的面积为AB·h=12.(2)如图,作DF⊥AB,垂足为F,∵△ADF≌△BCE,∴AF=BE=,BF=,DF=,在Rt△DFB中:BD2=DF2+BF2=+=16,∴BD=4,又∵BC=3,DC=5,DC2=BD2+BC2,∴BD⊥BC.15.(2019·长沙中考)如图,正方形ABCD,点E,F分别在AD,CD上,且DE=CF,AF与BE相交于点G.(1)求证:BE=AF.(2)若AB=4,DE=1,求AG的长.【解析】(1)∵四边形ABCD是正方形,∴∠BAE=∠ADF=90°,AB=AD=CD,∵DE=CF,∴AE=DF,在△BAE和△ADF中,∴△BAE≌△ADF(SAS),∴BE=AF.(2)由(1)得:△BAE≌△ADF,∴∠EBA=∠FAD,∴∠GAE+∠AEG=90°,∴∠AGE=90°,∵AB=4,DE=1,∴AE=3,∴BE===5,在Rt△ABE中,AB×AE=BE×AG,∴AG==.16.(2019·海南中考)如图,在边长为1的正方形ABCD中,E是边CD的中点,点P是边AD上一点(与点A,D不重合),射线PE与BC的延长线交于点Q.(1)求证:△PDE≌△QCE.(2)过点E作EF∥BC交PB于点F,连接AF,当PB=PQ时,①求证:四边形AFEP是平行四边形;②请判断四边形AFEP是否为菱形,并说明理由.【解析】(1)∵四边形ABCD是正方形,∴∠D=∠BCD=90°,∴∠ECQ=90°=∠D, ∵E是CD的中点,∴DE=CE.又∵∠DEP=∠CEQ,∴△PDE≌△QCE.(2)①如图,由(1)可知△PDE≌△QCE,∴PE=QE=PQ.又∵EF∥BC,∴PF=FB=PB.∵PB=PQ,∴PF=PE,∴∠1=∠2.∵四边形ABCD是正方形,∴∠BAD=90°,∴在Rt△ABP中,F是PB的中点,∴AF=BP=FP,∴∠3=∠4.又∵AD∥BC,EF∥BC,∴∠1=∠4. ∴∠2=∠3.又∵PF=FP,∴△APF≌△EFP. ∴AP=EF,又∵AP∥EF,∴四边形AFEP是平行四边形.②四边形AFEP不一定为菱形,∵AP不一定等于AF,只有当AP=BP时,才有四边形AFEP为菱形.。

初三数学中考总复习特殊的平行四边形专题复习练习含答案

2019 初三数学中考总复习特殊的平行四边形专题复习练习1．下列命题中，真命题是( C )A ．对角线相等的四边形是矩形B ．对角线互相垂直的四边形是菱形C ．对角线互相平分的四边形是平行四边形D ．对角线互相垂直平分的四边形是正方形2．如图，四边形ABCD 是菱形，AC ＝8，DB ＝6，DH ⊥AB 于点H ，则DH 等于( A )A.245B.125C ．5D ．4 3．如图，四边形ABCD 为平行四边形，延长AD 到E ，使DE ＝AD ，连接EB ，EC ，DB ，添加一个条件，不能使四边形DBCE 成为矩形的是( B )A ．AB ＝BE B ．BE ⊥DC C ．∠ADB ＝90°D ．CE ⊥DE4．如图，四边形ABCD 和四边形BEFD 都是矩形，且点C 恰好在EF 上．若AB ＝1，AD ＝2，则S △BCE 为( D )A ．1 B.255 C.23 D.455．如图，在矩形ABCD 中(AD ＞AB)，点E 是BC 上一点，且DE ＝DA ，AF ⊥DE ，垂足为点F ，在下列结论中，不一定正确的是( B )A ．△AFD ≌△DCEB ．AF ＝12AD C ．AB ＝AF D ．BE ＝AD －DF 6．如图，E 是边长为1的正方形ABCD 的对角线BD 上一点，且BE ＝BC ，P 为CE 上任意一点，PQ ⊥BC 于点Q ，PR ⊥BE 于点R ，则PQ ＋PR 的值是( D )A.23B.12C.32D.227．如图，菱形ABCD 的边长为2，∠ABC ＝45°，则点D 的坐标为．8．如图，在正方形ABCD 外作等腰直角△CDE，DE ＝CE ，连接BE ，则tan ∠EBC＝__13__． 9．将矩形纸片ABCD 按如图所示的方式折叠，得到菱形AECF.若AB ＝3，则BC的长为．10．如图，在矩形ABCD 中，点E 、F 分别在边CD ，BC 上，且DC ＝3DE ＝3a.将矩形沿直线EF 折叠，使点C 恰好落在AD 边上的点P 处，则FP ＝．11．如图，A ，B ，C 三点在同一条直线上，AB ＝2BC ，分别以AB ，BC 为边做正方形ABEF 和正方形BCMN ，连接FN ，EC.求证：FN ＝EC.证明：在正方形ABEF 和正方形BCMN 中，AB ＝BE ＝EF ，BC ＝BN ，∠FEN ＝∠EBC＝90°，∵AB ＝2BC ，即BC ＝BN ＝12AB ，∴BN ＝12BE ，即N 为BE 的中点，∴EN ＝NB ＝BC ，∴△FEN ≌△EBC(SAS)，∴FN ＝EC12．如图，在菱形ABCD 中，对角线AC 与BD 相交于点O ，MN 过点O 且与边AD ，BC 分别交于点M 和点N.(1)请你判断OM 和ON 的数量关系，并说明理由；(2)过点D 作DE∥AC 交BC 的延长线于点E ，当AB ＝6，AC ＝8时，求△BDE 的周长．解：(1)∵四边形ABCD 是菱形，∴AD ∥BC ，AO ＝OC ，∴OM ON ＝AO OC＝1，∴OM ＝ON (2)∵四边形ABCD 是菱形，∴AC ⊥BD ，AD ＝BC ＝AB ＝6，∴BO ＝AB 2－AO 2＝62－（8÷2）2＝25，∴BD ＝2BO ＝2×25＝45，∵DE ∥AC ，AD ∥CE ，∴四边形ACED 是平行四边形，∴DE ＝AC ＝8，∴△BDE 的周长是：BD ＋DE ＋BE ＝BD ＋AC ＋(BC ＋CE)＝45＋8＋(6＋6)＝20＋45，即△BDE 的周长是20＋4 513．如图1，四边形ABCD 是正方形，M 是BC 边上的一点，E 是CD 边的中点，AE 平分∠DAM.(1)证明：AM ＝AD ＋MC ；(2)AM ＝DE ＋BM 是否成立？若成立，请给出证明；若不成立，请说明理由；(3)若四边形ABCD 是长与宽不相等的矩形，其他条件不变，如图2，探究展示(1)、(2)中的结论是否成立？请分别作出判断，不需要证明．解：(1)过点E 作EF⊥AM 交AM 于F 点，连接EM ，由角平分线性质易得AD ＝AF ，EF ＝DE ＝EC ，由HL 易证△EFM≌△ECM，所以FM ＝MC ，AM ＝AF ＋FM ＝AD ＋MC(2)AM ＝DE ＋BM 成立，证明：将△ADE 绕点A 顺时针旋转90°，得到新△ABF，∴BF ＝DE ，∠F ＝∠AED.∵AB∥DC，∴∠AED ＝∠BAE.∵∠FAB＝∠EAD＝∠EAM，∴∠AED ＝∠BAE＝∠BAM＋∠EAM＝∠BAM＋∠FAB＝∠FAM.∴∠F＝∠FAM.∴AM ＝FM.∴AM＝FB ＋BM ＝DE ＋BM(3)①结论AM ＝AD ＋MC 仍然成立．②结论AM ＝DE ＋BM 不成立14. 如图，正方形ABCD 的对角线AC ，BD 相交于点O ，延长CB 至点F ，使CF ＝CA ，连接AF ，∠ACF 的平分线分别交AF ，AB ，BD 于点E ，N ，M ，连接EO.(1)已知EO ＝2，求正方形ABCD 的边长；(2)猜想线段EM 与CN 的数量关系并加以证明．解：(1) ∵四边形ABCD 是正方形，∴CA ＝2BC 2＝2BC ，∵CF ＝CA ，CE 是∠ACF 的角平分线，∴E 是AF 的中点，∵E ，O 分别是AF ，AC 的中点，∴EO ∥BC ，且EO ＝12CF ，∴△EOM ∽△CBM ，∴EO CB ＝EM CM，∵CF ＝CA ＝2CB ， ∴EO CB ＝12×2CB CB ＝22，∵EO ＝2，∴BC ＝2，∴正方形ABCD 的边长为2(2) EM ＝12CN.证明：∵CF ＝CA ，CE 是∠ACF 的平分线，∴CE ⊥AF ， ∴∠AEN ＝∠CBN ＝90°，∵∠ANE ＝∠CNB ，∴∠BAF ＝∠BCN ，在△ABF 和△CBN 中，⎩⎪⎨⎪⎧∠BAF ＝∠BCN ，∠ABF ＝∠CBN ＝90°，AB ＝BC ，∴△ABF ≌△CBN(AAS )，∴AF ＝CN ，∵∠BAF ＝∠BCN ，∠ACN ＝∠BCN ，∴∠BAF ＝∠OCM ， ∵四边形ABCD 是正方形，∴AC ⊥BD ，∴∠ABF ＝∠COM ＝90°，∴△ABF ∽△COM ，∴CM AF ＝OC AB ，∴CM CN ＝OC AB ＝22，即CM ＝22CN ，由(1)知EO CB ＝EM CM ＝22，∴EM ＝22CM ＝22×22CN ＝12CN。

中考数学专题21 特殊的平行四边形试题(含解析)-2019word版可打印

2．矩形的判定
会用判定定理判定平行四边形是否是矩形及一般四边形是否是矩形
菱形
1．菱形性质
能应用这些性质计算线段的长度
2．菱形的判别
能利用定理解决一些简单的问题
正方形
1．正方形的性质
了解平行四边形、矩形、菱形、正方形及梯形之间的相互关系，能够熟练运用正方形的性质解决具பைடு நூலகம்问题
2．正方形判定
掌握正方形的判定定理，并能综合运用特殊四边形的性质和判定解决问题，发现决定中点四边形形状的因素，熟练运用特殊四边形的判定及性质对中点四边形进行判断，并能对自己的猜想进行证明
【答案】（1）证明见试题解析；（2）．
【解析】
考点：1．正方形的性质；2．全等三角形的判定与性质；3．勾股定理；4．综合题．
19．（20xx恩施州）如图，四边形ABCD、BEFG均为正方形，连接AG、CE．
（1）求证：AG=CE；
（2）求证：AG⊥CE．
【答案】（1）证明见试题解析；（2）证明见试题解析．
2．（20xx连云港）已知四边形ABCD，下列说法正确的是（）
A．当AD=BC，AB∥DC时，四边形ABCD是平行四边形
B．当AD=BC，AB=DC时，四边形ABCD是平行四边形
C．当AC=BD，AC平分BD时，四边形ABCD是矩形
D．当AC=BD，AC⊥BD时，四边形ABCD是正方形
【答案】B．
A． B． C． D．
【答案】A．
考点：1．全等三角形的判定与性质；2．勾股定理；3．正方形的性质；4．综合题；5．压轴题．
9．（20xx鄂州）在平面直角坐标系中，正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置，其中点B1在y轴上，点C1、E1、E2、C2、E3、E4、C3…在x轴上，已知正方形A1B1C1D1的边长为1，∠B1C1O=60°，B1C1∥B2C2∥B3C3…则正方形A20xxB20xxC20xxD20xx的边长是（）

2019学年度九年级数学二次函数综合题题型归类之特殊四边形问题(附答案详解)

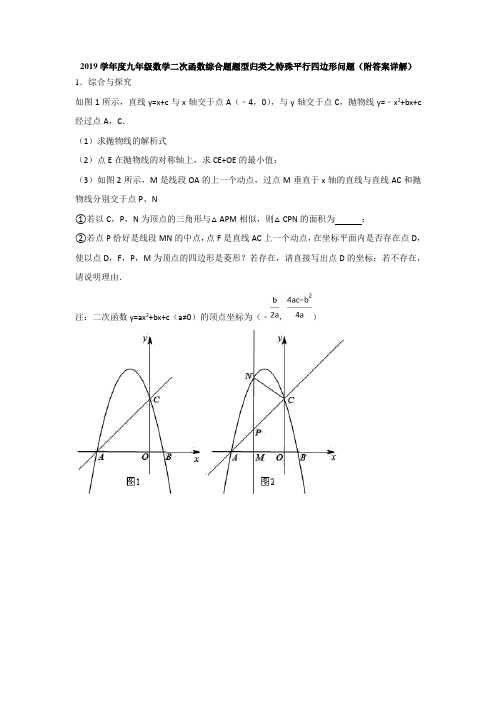
2019学年度九年级数学二次函数综合题题型归类之特殊平行四边形问题（附答案详解）1．综合与探究如图1所示，直线y=x+c与x轴交于点A（﹣4，0），与y轴交于点C，抛物线y=﹣x2+bx+c 经过点A，C．（1）求抛物线的解析式（2）点E在抛物线的对称轴上，求CE+OE的最小值；（3）如图2所示，M是线段OA的上一个动点，过点M垂直于x轴的直线与直线AC和抛物线分别交于点P、N①若以C，P，N为顶点的三角形与△APM相似，则△CPN的面积为；②若点P恰好是线段MN的中点，点F是直线AC上一个动点，在坐标平面内是否存在点D，使以点D，F，P，M为顶点的四边形是菱形？若存在，请直接写出点D的坐标；若不存在，请说明理由．注：二次函数y=ax2+bx+c（a≠0）的顶点坐标为（﹣，）2．如图，在平面直角坐标系中，已知矩形的三个顶点，，，以为顶点的抛物线过点，动点从点出发，以每秒个单位的速度沿线段向点运动，运动时间为秒，过点作轴交抛物线于点，交于点．直接写出点的坐标，并求出抛物线的解析式；当为何值时，的面积最大？最大值为多少？点从点出发，以每秒个单位的速度沿线段向点运动，当为何值时，在线段上存在点，使以，，，为顶点的四边形为菱形？3．如图，已知抛物线y=x2+bx+c与直线AB：y=x+相交于点A（1，0）和B（t，），直线AB交y轴于点C．（1）求抛物线的解析式及其对称轴；（2）点D是x轴上的一个动点，连接BD、CD，请问△BCD的周长是否存在最小值？若存在，请求出点D的坐标，并求出周长最小值；若不存在，请说明理由．（3）设点M是抛物线对称轴上一点，点N在抛物线上，以点A、B、M、N为顶点的四边形是否可能为矩形？若能，请求出点M的坐标，若不能，请说明理由．4．如图，已知二次函数y=ax2+2x+c的图象经过点C（0，3），与x轴分别交于点A，点B（3，0）．点P是直线BC上方的抛物线上一动点．（1）求二次函数y=ax2+2x+c的表达式；（2）连接PO，PC，并把△POC沿y轴翻折，得到四边形POP′C．若四边形POP′C为菱形，请求出此时点P的坐标；（3）当点P运动到什么位置时，四边形ACPB的面积最大？求出此时P点的坐标和四边形ACPB的最大面积．5．如图①，若直线交轴于点、交轴于点，将绕点逆时针旋转得到．过点，，的抛物线．求抛物线的表达式；若与轴平行的直线以秒钟一个单位长的速度从轴向左平移，交线段于点、交抛物线于点，求线段的最大值；如图②，点为抛物线的顶点，点是抛物线在第二象限的上一动点（不与点、重合），连接，以为边作图示一侧的正方形．随着点的运动，正方形的大小、位置也随之改变，当顶点或恰好落在轴上时，直接写出对应的点的坐标．6.如图，抛物线与x轴交于A、B两点，与y轴交于点C，其对称轴交抛物线于点D，交x轴于点E，已知OB=OC=6.（1）求抛物线的解析式及点D的坐标；（2）连接BD，F为抛物线上一动点，当∠FAB=∠EDB时，求点F的坐标；（3）平行于x轴的直线交抛物线于M、N两点，以线段MN为对角线作菱形MPNQ，当点P在x轴上，且PQ=MN时，求菱形对角线MN的长.答案详解：1．（1）y=﹣x2﹣3x+4；（2）CE+OE的最小值为5；（3）或4；存在，当PF=FM时，点D在MN垂直平分线上，则D（）；当PM=PF时，由菱形性质点D坐标为（﹣1+，）（﹣1﹣，﹣）；当MP=MF时，M、D关于直线y=﹣x+4对称，点D坐标为（﹣4，3）.（1）把已知点坐标代入解析式；（2）取点C关于抛物线的对称轴直线l的对称点C′，由两点之间线段最短，最小值可得；（3）①由已知，注意相似三角形的分类讨论．②设出M坐标，求点P坐标．注意菱形是由等腰三角形以底边所在直线为对称轴对称得到的．本题即为研究△CPN为等腰三角形的情况．解：（1）将A（﹣4，0）代入y=x+c∴c=4将A（﹣4，0）和c=4代入y=﹣x2+bx+c∴b=﹣3∴抛物线解析式为y=﹣x2﹣3x+4（2）做点C关于抛物线的对称轴直线l的对称点C′，连OC′，交直线l于点E．连CE，此时CE+OE的值最小．∵抛物线对称轴位置线x=﹣∴CC′=3由勾股定理OC′=5∴CE+OE的最小值为5（3）①当△CNP∽△AMP时，∠CNP=90°，则NC关于抛物线对称轴对称∴NC=NP=3∴△CPN的面积为当△CNP∽△MAP时由已知△NCP为等腰直角三角形，∠NCP=90°过点C作CE⊥MN于点E，设点M坐标为（a，0）∴EP=EC=﹣a，则N为（a，﹣a2﹣3a+4），MP=﹣a2﹣3a+4﹣（﹣2a）=﹣a2﹣a+4∴P（a，﹣a2﹣a+4）代入y=x+4解得a=﹣2∴△CPN的面积为4故答案为：或4②存在设M坐标为（a，0）则N为（a，﹣a2﹣3a+4）则P点坐标为（a，）把点P坐标代入y=﹣x+4解得a1=﹣4（舍去），a2=﹣1当PF=FM时，点D在MN垂直平分线上，则D（，）当PM=PF时，由菱形性质点D坐标为（﹣1+，）（﹣1﹣，﹣）当MP=MF时，M、D关于直线y=﹣x+4对称，点D坐标为（﹣4，3）2．；时，的最大值为．以，，，为顶点的四边形为菱形时，或．(1)A点的横坐标同B点，纵坐标同D点，然后设顶点式求解抛物线即可；(2)求解直线的解析式为，设从而表示出M和N的坐标；将的面积拆分为和两部分进行计算即可；(3)本问题分在上方和下方两种情况讨论，利用四边形是菱形的四边相等条件，将相关线段用t表示；当在上方时，运用三角形相似进行求解，当在下方时，运用勾股定理进行求解.解：，由题意知，可设抛物线解析式为∵抛物线过点，∴，解得．∴抛物线的解析式为，即；如图，∵，，∴可求直线的解析式为．∵点．∴将代入中，解得点的纵坐标为，∴把，代入抛物线的解析式中，可求点的纵坐标为，∴，又点到的距离为，到的距离为，即．当时，的最大值为．由题意和知，，，，，，，可求，当在上方时，如图，过点作，由四边形是菱形，可知：，此时，，，∴，，解得：，当点在下方时，如图，由四边形是菱形，可知：，∴，，在直角三角形中，，∴，解得或（舍去），所以，以，，，为顶点的四边形为菱形时，或3．（1）y=x2+x﹣，x=﹣1；（2）5+2；（3）能为矩形，M（﹣1，4）（1）利用待定系数法求函数解析式；（2）的周长，其中为定值，当该三角形的周长最小时，需要的值最小，即点、、共线时，它们的值最小，所以利用轴对称的性质找到点的坐标；结合一次函数图象上点坐标求得点的坐标；（3）需要分类讨论：①为四边形的边长；②为四边形的对角线.①若为四边形的边长，作，交轴于点，又，构造，可得，根据直线与抛物线的交点的求法得到：直线与抛物线只有一个交点为；②若为四边形的对角线，当四边形是平行四边形时，对角线互相平分，据此求得.解：（1）对于y=x+，令y=得x=﹣4，∴B（﹣4，）．分别把A（1，0）和B（﹣4，）代入y=x2+bx+c，得.解得，则该抛物线解析式为：y=x2+x﹣，∵﹣=﹣1，∴对称轴为直线x=﹣1；（2）直线AB：y=x+相交于点C（0，），作点C关于x轴的对称点C′，则C′（0，﹣），连接BC′交x轴于点D，根据“两点之间线段最短”可得BD+CD的和最小，从而△BCD的周长也最小，∵B（﹣4，），C′（0，﹣），∴直线BC′的解析式为y=﹣x﹣．令y=0，可得x=﹣，∴D（﹣，0），∴当△BCD的周长最小时，点D的坐标为（﹣，0），最小周长=BC+BC′=+=5+2；（3）①若AB为四边形的边长，作AE⊥AB，交y轴于点E，又OA⊥CE，∴△AOC∽△EOA，∴OE=2OA=2，∴E（0，﹣2）.∴直线AE为y=2x﹣2，令2x﹣2=x2+x﹣，解得x1=x2=1，∴直线AE与抛物线只有一个交点为A，∴不存在满足题意的矩形；②若AB为四边形的对角线，当四边形是平行四边形时，对角线互相平分，有x A+x B=x M+x N，即：1+（﹣4）=﹣1+x N，解得x N=﹣2．把x N=﹣2代入y=x2+x﹣，得y N=﹣，由y A+y B=y M+y N得：y M=4，∴M（﹣1，4），N（﹣2，﹣），此时MN==，AB==，∴MN=AB，∴平行四边形AMBN为矩形，综上，能为矩形，M（﹣1，4）．4．（1）y=﹣x2+2x+3；（2）（，）；（3）当点P的坐标为（，）时，四边形ACPB的最大面积值为.（1）已知二次函数上两点的坐标，利用待定系数法求解二次函数的解析式。

特殊四边形问题2019中考数学高端精品(解析版)

专题15 特殊四边形问题【考点综述评价】平行四边形、矩形、菱形、正方形等特殊四边形，是近年中考的热点问题之一，掌握它们的概念，了解它们之间的关系，掌握有关的性质和判定．通常是通过添加适当的辅助线转化为三角形来解决数学问题和现实问题，注重考查同学们的观察、猜想、推理、探究等活动的能力以及对知识的理解能力．突显出要把平行四边形转化为三角形来解决，把复杂的图形分解为线段相等或平行等基本图形，运用函数、列方程求解．【考点分类总结】考点1：特殊四边形与函数的联系【典型例题】（2017四川省乐山市）如图，平面直角坐标系xOy 中，矩形OABC 的边OA 、OC 分别落在x 、y 轴上，点B 坐标为（6，4），反比例函数x y 6=的图象与AB 边交于点D ，与BC 边交于点E ，连结DE ，将△BDE 沿DE 翻折至△B 'DE 处，点B '恰好落在正比例函数y =kx 图象上，则k 的值是（）A ．52- B ．211- C ．51- D ．241- 【答案】B ．【分析】根据矩形的性质得到，CB ∥x 轴，AB ∥y 轴，于是得到D （6，1），E （32，4），根据勾股定理得到ED 的长，连接BB ′，交ED 于F ，过B ′作B ′G ⊥BC 于G ，根据轴对称的性质得到BF =B ′F ，BB ′⊥ED 求得BB ′的长，设EG =x ，则BG =92﹣x 根据勾股定理即可得到结论．∴BF =B ′F ，BB ′⊥ED ，∴BF •ED =BE •BD ，即3132BF =3×92，∴BF =13，∴BB ′=13，设EG =x ，则BG =92﹣x ，∵BB ′2﹣BG 2=B ′G 2=EB ′2﹣GE 2，∴222299()()()2213x x --=-，∴x =4526，∴EG =4526，∴CG =4213，∴B ′G =5413，∴B ′（4213，﹣213），∴k =211-．故选B ．【方法归纳】结合特殊四边形的性质，列出关系式，结合选项进行判断．【变式训练】（2017湖北省襄阳市）如图，矩形OABC 的两边在坐标轴上，点A 的坐标为（10，0），抛物线24y ax bx =++过点B ，C 两点，且与x 轴的一个交点为D （﹣2，0），点P 是线段CB 上的动点，设CP =t （0＜t ＜10）．（1）请直接写出B 、C 两点的坐标及抛物线的解析式；学科/网（2）过点P 作PE ⊥BC ，交抛物线于点E ，连接BE ，当t 为何值时，∠PBE =∠OCD ？（3）点Q 是x 轴上的动点，过点P 作PM ∥BQ ，交CQ 于点M ，作PN ∥CQ ，交BQ 于点N ，当四边形PMQN 为正方形时，请求出t 的值．【答案】（1）B （10，4），C （0，4），215463y x x =-++；（2）3；（3）t 的值为103或203．【分析】（1）由抛物线的解析式可求得C 点坐标，由矩形的性质可求得B 点坐标，由B 、D 的坐标，利用待定系数法可求得抛物线解析式；（2）可设P （t ，4），则可表示出E 点坐标，从而可表示出PB 、PE 的长，由条件可证得△PBE ∽△OCD ，利用相似三角形的性质可得到关于t 的方程，可求得t 的值；（3）当四边形PMQN 为正方形时，则可证得△COQ ∽△QAB ，利用相似三角形的性质可求得CQ 的长，在Rt △BCQ 中可求得BQ 、CQ ，则可用t 分别表示出PM 和PN ，可得到关于t 的方程，可求得t 的值．【解答】（1）在24y ax bx =++中，令x =0可得y =4，∴C （0，4），∵四边形OABC 为矩形，且A （10，0），∴B （10，4），把B 、D 坐标代入抛物线解析式可得：10010444240a b a b ++=⎧⎨-+=⎩，解得：1653a b ⎧=-⎪⎪⎨⎪=⎪⎩，∴抛物线解析∠CQO +∠OCQ =90°，∴∠OCQ =∠AQB ，∴Rt △COQ ∽Rt △QAB ，∴CO OQ AQ AB =，即OQ •AQ =CO •AB ，设OQ =m ，则AQ =10﹣m ，∴m （10﹣m ）=4×4，解得m =2或m =8；①当m =2时，CQ =22OC OQ +25BQ 22AQ AB +5sin ∠BCQ =BQ BC =55，sin ∠CBQ =CQ CB =55，∴PM =PC •sin ∠PCQ =55t ，PN =PB •sin ∠CBQ =55（10﹣t ），∴55t =55（10﹣t ），解得t =103； ②当m =8时，同理可求得t =203，∴当四边形PMQN 为正方形时，t 的值为103或203．考点2：平行四边形探究【典型例题】（2017山东省泰安市）如图，四边形ABCD 是平行四边形，AD =AC ，AD ⊥AC ，E 是AB 的中点，F 是AC 延长线上一点．（1）若ED ⊥EF ，求证：ED =EF ；（2）在（1）的条件下，若DC的延长线与FB交于点P，试判定四边形ACPE是否为平行四边形？并证明你的结论（请先补全图形，再解答）；（3）若ED=EF，ED与EF垂直吗？若垂直给出证明．【答案】（1）证明见解析；（2）四边形ACPE为平行四边形；（3）垂直．【分析】（1）根据平行四边形的想知道的AD=AC，AD⊥AC，连接CE，根据全等三角形的判定和性质即可得到结论；（2）根据全等三角形的性质得到CF=AD，等量代换得到AC=CF，于是得到CP=12AB=AE，根据平行四边形的判定定理即可得到四边形ACPE为平行四边形；（3）过E作EM⊥DA交DA的延长线于M，过E作EN⊥FC交FC的延长线于N，证得△AME≌△CNE，△ADE≌△CFE，根据全等三角形的性质即可得到结论．（3）解：垂直，理由：过E作EM⊥DA交DA的延长线于M，过E作EN⊥FC交FC的延长线于N．∵∠NAE=∠EAM=45°，∴EM=EN．在Rt△DME与Rt△FNE中， EM＝EN DE＝EF，∴Rt△DME≌Rt△FNE，∴∠ADE=∠CFE，在△ADE与△CFE中，∵∠ADE=∠CFE，∠DAE=∠FCE=135°，DE=EF，∴△ADE≌△CFE，∴∠DEA=∠FEC，∵∠DEA+∠DEC=90°，∴∠CEF+∠DEC=90°，∴∠DEF=90°，∴ED⊥EF．【方法归纳】利用平行四边形对边平行且相等这一特征，一般作平行线找到平行四边形的顶点位置，再根据线段相等转化为方程解决．【变式训练】（2017青海省西宁市）如图，在平面直角坐标系中，矩形OABC 的顶点A ，C 分别在x 轴，y 轴的正半轴上，且OA =4，OC =3，若抛物线经过O ，A 两点，且顶点在BC 边上，对称轴交BE 于点F ，点D ，E 的坐标分别为（3，0），（0，1）．（1）求抛物线的解析式；（2）猜想△EDB 的形状并加以证明；（3）点M 在对称轴右侧的抛物线上，点N 在x 轴上，请问是否存在以点A ，F ，M ，N 为顶点的四边形是平行四边形？若存在，请求出所有符合条件的点M 的坐标；若不存在，请说明理由．【答案】（1）2334y x x =-+；（2）△EDB 为等腰直角三角形；（3）存在，M 623+，2）或6215+，﹣2）．【分析】（1）由条件可求得抛物线的顶点坐标及A 点坐标，利用待定系数法可求得抛物线解析式；（2）由B 、D 、E 的坐标可分别求得DE 、BD 和BE 的长，再利用勾股定理的逆定理可进行判断；（3）由B 、E 的坐标可先求得直线BE 的解析式，则可求得F 点的坐标，当AF 为边时，则有FM ∥AN 且FM =AN ，则可求得M 点的纵坐标，代入抛物线解析式可求得M 点坐标；当AF 为对角线时，由A 、F 的坐标可求得平行四边形的对称中心，可设出M 点坐标，则可表示出N 点坐标，再由N 点在x 轴上可得到关于M 点坐标的方程，可求得M 点坐标．学+-科/网（3）存在．理由如下：设直线BE 解析式为y =kx +b ，把B 、E 坐标代入可得：341k b b =+⎧⎨=⎩，解得：121k b ⎧=⎪⎨⎪=⎩，∴直线BE 解析式为112y x =+，当x =2时，y =2，∴F （2，2），①当AF 为平行四边形的一边时，则M 到x 轴的距离与F 到x 轴的距离相等，即M 到x 轴的距离为2，∴点M 的纵坐标为2或﹣2，在2334y x x =-+中，令y =2可得23234x x =-+，解得x 623±，∵点M 在抛物线对称轴右侧，∴x ＞2，∴x 623+，∴M 点坐标为623+，2）；在2334y x x =-+中，令y =﹣2可得23234x x -=-+，解得x =6153±，∵点M 在抛物线对称轴右侧，∴x ＞2，∴x =62153+，∴M 点坐标为（6153+，﹣2）； ②当AF 为平行四边形的对角线时，∵A （4，0），F （2，2），∴线段AF 的中点为（3，1），即平行四边形的对称中心为（3，1），设M （t ，2334t t -+），N （x ，0），则23324t t -+=，解得t 623±，∵点M 在抛物线对称轴右侧，∴x ＞2，∵t ＞2，∴t 623+M 623+2）；综上可知存在满足条件的点M，其坐标为（6233+，2）或（62153+，﹣2）．考点3：菱形探究【典型例题】（2017山东省潍坊市）边长为6的等边△ABC中，点D、E分别在AC、BC边上，DE∥AB，EC=23．（1）如图1，将△DEC沿射线方向平移，得到△D′E′C′，边D′E′与AC的交点为M，边C′D′与∠ACC′的角平分线交于点N，当CC′多大时，四边形MCND′为菱形？并说明理由．（2）如图2，将△DEC绕点C旋转∠α（0°＜α＜360°），得到△D′E′C，连接AD′、BE′．边D′E′的中点为P．①在旋转过程中，AD′和BE′有怎样的数量关系？并说明理由；②连接AP，当AP最大时，求AD′的值．（结果保留根号）【答案】（1）当CC'=3时，四边形MCND'是菱形；（2）①AD'=BE'；②221．【分析】（1）先判断出四边形MCND'为平行四边形，再由菱形的性质得出CN=CM，即可求出CC'；（2）①分两种情况，利用旋转的性质，即可判断出△ACD≌△BCE'即可得出结论；②先判断出点A，C，P三点共线，先求出CP，AP，最后用勾股定理即可得出结论．是菱形，∴CN=CM，∴CC'=12E'C3；（2）①AD '=BE '，理由：当α≠180°时，由旋转的性质得，∠ACD '=∠BCE '，由（1）知，AC =BC ，CD '=CE '，∴△ACD '≌△BCE '，∴AD '=BE '，当α=180°时，AD '=AC +CD '，BE '=BC +CE '，即：AD '=BE '，综上可知：AD '=BE '．②如图连接CP ，在△ACP 中，由三角形三边关系得，AP ＜AC +CP ，∴当点A ，C ，P 三点共线时，AP 最大，如图1，在△D 'CE '中，由P 为D 'E 的中点，得AP ⊥D 'E '，PD '=3，∴CP =3，∴AP =6+3=9，在Rt △APD '中，由勾股定理得，AD '=22'AP PD =221．【方法归纳】利用菱形的四边相等关系转化为方程解决，也可以转化为等腰三角形问题解决，或者先作出平行四边形，再利用两邻边相等转化为方程解决．【变式训练】（2017辽宁省阜新市）在菱形ABCD 中，点E 为对角线BD 上一点，点F ，G 在直线BC 上，且BE =EG ，∠AEF =∠BEG ．（1）如图1，求证：△ABE ≌△FGE ；（2）如图2，当∠ABC =120°时，求证：AB =BE +BF ；（3）如图3，当∠ABC =90°，点F 在线段BC 上时，线段AB ，BE ，BF 的数量关系如何？（请直接写出你猜想的结论）【答案】（1）证明见解析；（2）证明见解析；（3）BF +AB 2BE ．【分析】由等腰三角形性质得到∠EBG =∠EGB ．再由菱形性质得到∠ABE =∠EBG ，从而有∠ABE =∠EGB ．由等量代换得到∠AEB =∠FEG ，从而可证△ABE ≌△FGE ；（2）由△ABE≌△FGE，得到AB=FG．由∠ABC=120°，得到∠ABE=∠EBG=60°，从而得到△BEG为等边三角形，得到BE=BG，从而可证结论；（3）BF+AB=2BE．由△ABE≌△FGE，得到AB=FG．由∠ABC=90°，得到∠EBG=45°，进而得到△BEG为等腰直角三角形，从而得到结论．考点4：矩形探究【典型例题】（2017山西省）综合与实践背景阅读早在三千多年前，我国周朝数学家商高就提出：将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三，股四，弦五”．它被记载于我国古代著名数学著作《周髀算经》中．为了方便，在本题中，我们把三边的比为3：4：5的三角形称为（3，4，5）型三角形．例如：三边长分别为9，12，15或32,42,523，4，5）型三角形．用矩形纸片按下面的操作方法可以折出这种类型的三角形．实践操作如图1，在矩形纸片ABCD中，AD=8cm，AB=12cm．第一步：如图2，将图1中的矩形纸片ABCD沿过点A的直线折叠，使点D落在AB上的点E处，折痕为AF，再沿EF折叠，然后把纸片展平．第二步：如图3，将图2中的矩形纸片再次折叠，使点D与点F重合，折痕为GH，然后展平，隐去AF．第三步：如图4，将图3中的矩形纸片沿AH折叠，得到△AD′H，再沿AD′折叠，折痕为AM，AM与折痕EF交于点N，然后展平．问题解决（1）请在图2中证明四边形AEFD 是正方形．（2）请在图4中判断NF 与ND ′的数量关系，并加以证明．（3）请在图4中证明△AEN 是（3，4，5）型三角形．探索发现（4）在不添加字母的情况下，图4中还有哪些三角形是（3，4，5）型三角形？请找出并直接写出它们的名称．【答案】（1）证明见解析；（2）NF =ND ′，证明见解析；（3）证明见解析；（4）△MFN ，△MD ′H ，△MDA ．【分析】（1）根据题中所给（3，4，5）型三角形的定义证明即可；（2）NF =ND ′，证明Rt △HNF ≌Rt △HND ′即可；（3）根据题中所给（3，4，5）型三角形的定义证明即可；（4）由△AEN 是（3，4，5）型三角形，凡是与△AEN 相似的△都是（3，4，5）型三角形．∵四边形AEFD 是正方形，∴∠EFD =90°．∵∠AD ′H =90°，∴∠HD ′N =90°．在Rt △HNF 和Rt △HND ′中，∵HN =HN ，HF =HD ′，∴Rt △HNF ≌Rt △HND ′，∴NF =ND ′．（3）∵四边形AEFD 是正方形，∴AE =EF =AD =8cm ，由折叠知：AD ′=AD =8cm ，EN =EF -NF =（8-x ）㎝．在Rt △AEN 中，由勾股定理得：222AN AE EN =+ ，即222(8)8(8)x x +=+-，解得：x =2，∴AN =8+x =10（㎝），EN =6（㎝），∴AN =6：8：10=3：4：5，∴△AEN 是（3，4，5）型三角形．（4）图4中还有△MFN ，△MD ′H ，△MDA 是（3，4，5）型三角形．∵CF ∥AE ，∴△MFN ∽△AEN ．∵EN ：AE ：AN =3：4：5，∴FN ：MF ：CN =3：4：5，∴△MFN 是（3，4，5）型三角形；同理，△MD ′H ，△MDA 是（3，4，5）型三角形．【方法归纳】一是转化为直角三角形问题，二是利用对角线相等转化为方程解决．【变式训练】（2017甘肃省兰州市）如图，抛物线2y x bx c =-++与直线AB 交于A （﹣4，﹣4），B （0，4）两点，直线162y x =--交y 轴于点C ．点E 是直线AB 上的动点，过点E 作EF ⊥x 轴交AC 于点F ，交抛物线于点G ．（1）求抛物线2y x bx c =-++的表达式；（2）连接GB ，EO ，当四边形GEOB 是平行四边形时，求点G 的坐标；（3）①在y 轴上存在一点H ，连接EH ，HF ，当点E 运动到什么位置时，以A ，E ，F ，H 为顶点的四边形是矩形？求出此时点E ，H 的坐标；学*科+网②在①的前提下，以点E 为圆心，EH 长为半径作圆，点M 为⊙E 上一动点，求12AM +CM 它的最小值．【答案】（1）224y x x =--+；（2）G （﹣2，4）；（3）①E （﹣2，0）．H （0，﹣1）55．【分析】（1）利用待定系数法求出抛物线解析式；（2）先利用待定系数法求出直线AB 的解析式，进而利用平行四边形的对边相等建立方程求解即可；（3）①先判断出要以点A ，E ，F ，H 为顶点的四边形是矩形，只有EF 为对角线，利用中点坐标公式建立方程即可；②先取EG 的中点P 进而判断出△PEM ∽△MEA 即可得出PM=12AM ，连接CP 交圆E 于M ，再求出点P 的坐标即可得出结论．【解答】（1）∵点A （﹣4，﹣4），B （0，4）在抛物线2y x bx c =-++上，∴16444b c c --+=-⎧⎨=⎩，∴24b c =-⎧⎨=⎩，∴抛物线的解析式为224y x x =--+；（2）设直线AB 的解析式为y =kx +n 过点A ，B ，∴444n k n =⎧⎨-+=-⎩，∴24k n =⎧⎨=⎩，∴直线AB 的解析式为y =2x +4，取EG 的中点P ，∴PE =52．连接PC 交⊙E 于M ，连接EM ，∴EM =EH 5525PE ME = =12，∵525ME AE ==12，∴PE ME ME AE ==12，∵∠PEM =∠MEA ，∴△PEM ∽△MEA ，∴PM ME AM AE ==12，∴PM =12AM ，∴12AM +CM 的最小值=PC ，设点P （p ，2p +4），∵E （﹣2，0），∴PE 2=（p +2）2+（2p +4）2=5（p +2）2，∵PE 55（p +2）2=54，∴p =﹣52或p =﹣32（由于E （﹣2，0），所以舍去），∴P （﹣52，﹣1），∵C （0，﹣6），∴PC 225()(16)2-+-+552，即：12AM +CM =552．考点5：正方形探究【典型例题】（2017贵州省遵义市）边长为22的正方形ABCD 中，P 是对角线AC 上的一个动点（点P 与A 、C 不重合），连接BP ，将BP 绕点B 顺时针旋转90°到BQ ，连接QP ，QP 与BC 交于点E ，QP 延长线与AD （或AD 延长线）交于点F ．（1）连接CQ ，证明：CQ =AP ；（2）设AP =x ，CE =y ，试写出y 关于x 的函数关系式，并求当x 为何值时，CE =38BC ；（3）猜想PF 与EQ 的数量关系，并证明你的结论．【答案】（1）证明见解析；（2）2224y x x =-+ （0＜x ＜4），当x =3或1时，CE =38BC ；（3）PF =EQ ．【分析】（1）证出∠ABP =∠CBQ ，由SAS 证明△BAP ≌△BCQ 可得结论；（2）如图1证明△APB ∽△CEP ，列比例式可得y 与x 的关系式，根据CE =38BC 计算CE 的长，即y 的长，代入关系式解方程可得x 的值；（3）如图3，作辅助线，构建全等三角形，证明△PGB ≌△QEB ，得EQ =PG ，由F 、A 、G 、P 四点共圆，得∠FGP =∠F AP =45°，所以△FPG 是等腰直角三角形，可得结论．如图4，当F 在AD 的延长线上时，同理可得结论．∠ABP ，∵∠BAC =∠ACB =45°，∴△APB ∽△CEP ，∴AP AB CE CP =，∴224x y x =-，∴y =22x （4﹣x ），即2224y x x =-+ （0＜x ＜4），由CE =38BC =38×22=324，∴2224y x x =-+=324，x 2﹣4x +3=0，（x ﹣3）（x ﹣1）=0，x =3或1，∴当x =3或1时，CE =38BC ；（3）解：结论：PF =EQ ，理由是：如图2，当F 在边AD 上时，过P 作PG ⊥FQ ，交AB 于G ，则∠GPF =90°，∵∠BPQ =45°，∴∠GPB =45°，∴∠GPB =∠PQB =45°，∵PB =BQ ，∠ABP =∠CBQ ，∴△PGB ≌△QEB ，∴EQ =PG ，∵∠BAD =90°，∴F 、A 、G 、P 四点共圆，连接FG ，∴∠FGP =∠F AP =45°，∴△FPG 是等腰直角三角形，∴PF =PG ，∴PF =EQ ．当F 在AD 的延长线上时，如图3，同理可得：PF =PG =EQ ．【方法归纳】画出图形，转化为等腰三角形问题解决法归纳总结．【变式训练】（2017黑龙江省龙东地区）在四边形ABCD中，对角线AC、BD交于点O．若四边形ABCD是正方形如图1：则有AC=BD，AC⊥BD．旋转图1中的Rt△COD到图2所示的位置，AC′与BD′有什么关系？（直接写出）若四边形ABCD是菱形，∠ABC=60°，旋转Rt△COD至图3所示的位置，AC′与BD′又有什么关系？写出结论并证明．【答案】图2结论：AC′=BD′，AC′⊥BD′；图3结论：BD′=3AC′，AC′⊥BD’．【分析】图2：根据四边形ABCD是正方形，得到AO=OC，BO=OD，AC⊥BD，根据旋转的性质得到OD′=OD，OC′=OC，∠D′OD=∠C′OC，等量代换得到AO=BO，OC′=OD′，∠AOC′=∠BOD′，根据全等三角形的性质得到AC′=BD′，∠OAC′=∠OBD′，于是得到结论；图3：根据四边形ABCD是菱形，得到AC⊥BD，AO=CO，BO=DO，求得OB=3OA，OD=3OC，根据旋转的性质得到OD′=OD，OC′=OC，∠D′OD=∠C′OC，求得OD′=3OC′，∠AOC′=∠BOD′，根据相似三角形的性质得到BD′=3AC′，于是得到结论．理由：∵四边形ABCD是菱形，∴AC⊥BD，AO=CO，BO=DO，∵∠ABC=60°，∴∠ABO=30°，∴OB3，OD=3OC，∵将Rt△COD旋转得到Rt△C′OD′，∴OD′=OD，OC′=OC，∠D′OD=∠C′OC，∴OD′=3OC′，∠AOC′=∠BOD′，∴''OB ODOA OC==3，∴△AOC′∽△BOD′，∴''BD OBAC OA= =3，∠OAC′=∠OBD′，∴BD′=3AC′，∵∠AO′D′=∠BO′O，∠O′BO+∠BO′O=90°，∴∠O′AC′+∠AO′D′=90°，∴AC′⊥BD′．学/-科+网【新题好题训练】1．（2017贵州省贵阳市）如图，在矩形纸片ABCD中，AB=2，AD=3，点E是AB的中点，点F是AD边上的一个动点，将△AEF沿EF所在直线翻折，得到△A′EF，则A′C的长的最小值是．101．【分析】连接CE，根据折叠的性质可知A′E=1，在Rt△BCE中利用勾股定理可求出CE的长度，再利用三角形的三边关系可得出点A′在CE上时，A′C取最小值，最小值为CE﹣A′E101，此题得解．【解答】连接CE，如图所示．根据折叠可知：A′E=AE=12AB=1．在Rt△BCE中，BE=12AB=1，BC=3，∠B=90°，∴CE22BE BC+10CE10A′E=1，∴点A′在CE上时，A′C取最小值，最小值为CE﹣A′E101-．101．2．（2017江苏省盐城市）如图，矩形ABCD中，∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F．（1）求证：四边形BEDF是平行四边形；（2）当∠ABE为多少度时，四边形BEDF是菱形？请说明理由．【答案】（1）证明见解析；（2）∠ABE=30°．【分析】（1）由矩形可得∠ABD=∠CDB，结合BE平分∠ABD、DF平分∠BDC得∠EBD=∠FDB，即可知BE∥DF，根据AD∥BC即可得证；（2）当∠ABE=30°时，四边形BEDF是菱形，由角平分线知∠ABD=2∠ABE=60°、∠EBD=∠ABE=30°，结合∠A=90°可得∠EDB=∠EBD=30°，即EB=ED，即可得证．ABE=30°，∵四边形ABCD是矩形，∴∠A=90°，∴∠EDB=90°﹣∠ABD=30°，∴∠EDB=∠EBD=30°，∴EB=ED，又∵四边形BEDF是平行四边形，∴四边形BEDF是菱形．3．（2017江苏省盐城市）【探索发现】如图①，是一张直角三角形纸片，∠B=90°，小明想从中剪出一个以∠B为内角且面积最大的矩形，经过多次操作发现，当沿着中位线DE、EF剪下时，所得的矩形的面积最大，随后，他通过证明验证了其正确性，并得出：矩形的最大面积与原三角形面积的比值为．【拓展应用】如图②，在△ABC 中，BC =a ，BC 边上的高AD =h ，矩形PQMN 的顶点P 、N 分别在边AB 、AC 上，顶点Q 、M 在边BC 上，则矩形PQMN 面积的最大值为．（用含a ，h 的代数式表示）【灵活应用】如图③，有一块“缺角矩形”ABCDE ，AB =32，BC =40，AE =20，CD =16，小明从中剪出了一个面积最大的矩形（∠B 为所剪出矩形的内角），求该矩形的面积．【实际应用】如图④，现有一块四边形的木板余料ABCD ，经测量AB =50cm ，BC =108cm ，CD =60cm ，且tan B =tan C =43，木匠徐师傅从这块余料中裁出了顶点M 、N 在边BC 上且面积最大的矩形PQMN ，求该矩形的面积．【答案】【探索发现】12；【拓展应用】4ab ；【灵活应用】720；【实际应用】1944．【分析】【探索发现】由中位线知EF =12BC 、ED =12AB 、由ABC S S ∆矩形FEDB =12EF DE AB BC ⋅⋅可得；【拓展应用】由△APN ∽△ABC 知PN AE BC AD =，可得PN =a ﹣a h PQ ，设PQ =x ，由S 矩形PQMN =PQ •PN ═2()24a h ah x h --+，据此可得；【灵活应用】添加如图1辅助线，取BF 中点I ，FG 的中点K ，由矩形性质知AE =EH =20、CD =DH =16，分别证△AEF ≌△HED 、△CDG ≌△HDE 得AF =DH =16、CG =HE =20，从而判断出中位线IK 的两端点在线段AB 和DE 上，利用【探索发现】结论解答即可；【实际应用】延长BA 、CD 交于点E ，过点E 作EH ⊥BC 于点H ，由tan B =tan C 知EB =EC 、BH =CH =54，EH =43BH =72，继而求得BE =CE =90，可判断中位线PQ 的两端点在线段AB 、CD 上，利用【拓展应用】结论解答可得．【拓展应用】∵PN ∥BC ，∴△APN ∽△ABC ，∴PN AE BC AD =，即=PN h PQ a h -，∴PN =a ﹣a hPQ ，设PQ =x ，则S 矩形PQMN =PQ •PN =x （a ﹣a h x ）=2a x ax h -+ =2()24a h ah x h --+，∴当PQ =2h 时，S 矩形PQMN 最大值为4ab ，故答案为：4ab ；【灵活应用】如图1，延长BA 、DE 交于点F ，延长BC 、ED 交于点G ，延长AE 、CD 交于点H ，取BF 中点I ，FG 的中点K ．由题意知四边形ABCH 是矩形，∵AB =32，BC =40，AE =20，CD =16，∴EH =20、DH =16，∴AE =EH 、CD =DH ，在△AEF 和△HED 中，∵∠F AE =∠DHE ，AE =AH ，∠AEF =∠HED ，∴△AEF ≌△HED （ASA ），∴AF =DH =16，同理△CDG ≌△HDE ，∴CG =HE =20，∴BI =12（AB +AF ）=24，∵BI =24＜32，∴中位线IK 的两端点在线段AB 和DE 上，过点K 作KL ⊥BC 于点L ，由【探索发现】知矩形的最大面积为12BG •12BF =12×（40+20）×12×（32+16）=720．答：该矩形的面积为720；【实际应用】答：该矩形的面积为1944cm2．学/科.+网4．（2017山东省威海市）如图，四边形ABCD为一个矩形纸片，AB=3，BC=2，动点P自D点出发沿DC 方向运动至C点后停止，△ADP以直线AP为轴翻折，点D落在点D1的位置，设DP=x，△AD1P与原纸片重叠部分的面积为y．（1）当x为何值时，直线AD1过点C？（2）当x为何值时，直线AD1过BC的中点E？（3）求出y与x的函数表达式．【答案】（1）1343；（2）1023；（3）2(02)4(23)2x xy xxx<≤⎧⎪=⎨+<≤⎪⎩．【分析】（1）根据折叠得出AD=AD1=2，PD=PD1=x，∠D=∠AD1P=90°，在Rt△ABC中，根据勾股定理求出AC，在Rt△PCD1中，根据勾股定理得出方程，求出即可；（2）连接PE ，求出BE =CE =1，在Rt △ABE 中，根据勾股定理求出AE ，求出AD 1=AD =2，PD =PD 1=x ，D 1E =10﹣2，PC =3﹣x ，在Rt △PD 1E 和Rt △PCE 中，根据勾股定理得出方程，求出即可；（3）分为两种情况：当0＜x ≤2时，y =x ；当2＜x ≤3时，点D 1在矩形ABCD 的外部，PD 1交AB 于F ，求出AF =PF ，作PG ⊥AB 于G ，设PF =AF =a ，在Rt △PFG 中，由勾股定理得出方程（x ﹣a ）2+22=a 2，求出a 即可．（2）如图2，连接PE ，∵E 为BC 的中点，∴BE =CE =1，在Rt △ABE 中，AE =22AB BE +=10，∵AD 1=AD =2，PD =PD 1=x ，∴D 1E =10﹣2，PC =3﹣x ，在Rt △PD 1E 和Rt △PCE 中，x 2+（10﹣2）2=（3﹣x ）2+12，解得：x =2102-，∴当x =2102-时，直线AD 1过BC 的中点E ；（3）①如图3，当0＜x ≤2时，y =x ；5．（2017德州）如图1，在矩形纸片ABCD中，AB=3cm，AD=5cm，折叠纸片使B点落在边AD上的E处，折痕为PQ，过点E作EF∥AB交PQ于F，连接BF．（1）求证：四边形BFEP为菱形；（2）当点E在AD边上移动时，折痕的端点P、Q也随之移动；①当点Q与点C重合时（如图2），求菱形BFEP的边长；②若限定P、Q分别在边BA、BC上移动，求出点E在边AD上移动的最大距离．【答案】（1）证明见解析；（2）①53；②2．【分析】（1）由折叠的性质得出PB=PE，BF=EF，∠BPF=∠EPF，由平行线的性质得出∠BPF=∠EFP，证出∠EPF=∠EFP，得出EP=EF，因此BP=BF=EF=EP，即可得出结论；（2）①由矩形的性质得出BC=AD=5cm，CD=AB=3cm，∠A=∠D=90°，由对称的性质得出CE=BC=5cm，在Rt△CDE中，由勾股定理求出DE=4cm，得出AE=AD﹣DE=1cm；在Rt△APE中，由勾股定理得出方程，解方程得出EP=53cm即可；②当点Q与点C重合时，点E离点A最近，由①知，此时AE=1cm；当点P与点A重合时，点E离点A最远，此时四边形ABQE为正方形，AE=AB=3cm，即可得出答案．②当点Q与点C重合时，如图2：点E离点A最近，由①知，此时AE=1cm；当点P与点A重合时，如图3所示：点E离点A最远，此时四边形ABQE为正方形，AE=AB=3cm，∴点E在边AD上移动的最大距离为2cm．6．（2017湖南省永州市）已知点O是正方形ABCD对角线BD的中点．（1）如图1，若点E是OD的中点，点F是AB上一点，且使得∠CEF=90°，过点E作ME∥AD，交AB 于点M，交CD于点N．①∠AEM=∠FEM；②点F是AB的中点；（2）如图2，若点E是OD上一点，点F是AB上一点，且使13DE AFDO AB==，请判断△EFC的形状，并说明理由；学科+-网（3）如图3，若E是OD上的动点（不与O，D重合），连接CE，过E点作EF⊥CE，交AB于点F，当DE m DB n=时，请猜想AFAB的值（请直接写出结论）．【答案】（1）①证明见解析；②证明见解析；（2）△EFC是等腰直角三角形；（3）2mn．【分析】（1）①由正方形的性质得出∠ABD=45°，∠BAD=∠ABC=∠BCD=∠ADC=90°，AE=CE，由HL 证明Rt△AME≌Rt△ENC，得出∠AEM=∠ECN，再由角的互余关系即可得出结论；②由三角形内角和定理得出∠EAF=∠EF A，证出AE=FE，由等腰三角形的性质得出AM=FM，AF=2AM，求出14DEDB=，由平行线分线段成比例定理得出AMAB=14DEDB=，得出AFAB=12，即可得出结论；（2）过点E作ME∥AD，交AB于点M，交CD于点N．同（1）得：AE=CE，Rt△AME≌Rt△ENC，得出∠AEM=∠ECN，由13DEDO=，O是DB的中点，证出16AM DEAB DB==，得出AF=2AM，即M是AF的中点，由线段垂直平分线的性质得出AE=FE，证出∠AEM=∠FEM，FE=CE，由角的互余关系证出∠CEF=90°，即可得出结论；（3）同（1）即可得出答案．∴AFAB=12，∴点F是AB的中点；（2）解：△EFC 是等腰直角三角形；理由如下：过点E 作ME ∥AD ，交AB 于点M ，交CD 于点N ．如图所示：同（1）得：AE =CE ，Rt △AME ≌Rt △ENC ，∴∠AEM =∠ECN ，∵13DE DO =，O 是DB 的中点，∴16DE DB =，∵ME ∥AD ，∴16AM DE AB DB ==，∵13AF AB =，∴AF =2AM ，即M 是AF 的中点，∵ME ⊥AB ，∴AE =FE ，∴∠AEM =∠FEM ，FE =CE ，∵∠ECN +∠CEN =90°，∴∠FEM +∠CEN =90°，∴∠CEF =90°，∴△EFC 是等腰直角三角形；（3）解：当DE m DB n =时，AF AB =2m n；理由同（1）．7．（2017四川省南充市）如图，在正方形ABCD 中，点E 、G 分别是边AD 、BC 的中点，AF =14AB ．（1）求证：EF ⊥AG ；（2）若点F 、G 分别在射线AB 、BC 上同时向右、向上运动，点G 运动速度是点F 运动速度的2倍，EF ⊥AG 是否成立（只写结果，不需说明理由）？（3）正方形ABCD 的边长为4，P 是正方形ABCD 内一点，当PAB OAB S S ∆∆=，求△P AB 周长的最小值．【答案】（1）证明见解析；（2）成立；（34264．【分析】（1）由正方形的性质得出AD =AB ，∠EAF =∠ABG =90°，证出AF BG AE BA=，得出△AEF ∽△BAG ，由相似三角形的性质得出∠AEF =∠BAG ，再由角的互余关系和三角形内角和定理证出∠AOE =90°即可；（2）证明△AEF ∽△BAG ，得出∠AEF =∠BAG ，再由角的互余关系和三角形内角和定理即可得出结论；（3）过O 作MN ∥AB ，交AD 于M ，BC 于N ，则MN ⊥AD ，MN =AB =4，由三角形面积关系得出点P 在线段MN 上，当P 为MN 的中点时，△P AB 的周长最小，此时P A =PB ，PM =12MN =2，连接EG ，则EG ∥AB ，EG =AB =4，证明△AOF ∽△GOE ，得出OF AF OE EG = =14，证出AM OF EM OE = =14，得出AM =15AE =25，由勾股定理求出P A ，即可得出答案．学科.网则MN ⊥AD ，MN =AB =4，∵P 是正方形ABCD 内一点，当S △P AB =S △OAB ，∴点P 在线段MN 上，当P 为MN的中点时，△P AB 的周长最小，此时P A =PB ，PM =12MN =2，连接EG 、P A 、PB ，则EG ∥AB ，EG =AB =4，∴△AOF ∽△GOE ，∴OF AF OE EG ==14，∵MN ∥AB ，∴AM OF EM OE = =14，∴AM =15AE =15×2=25，由勾股定理得：P A =22PM AM + =2265，∴△P AB 周长的最小值=2P A +AB =42645+．8．（2017枣庄）如图，抛物线212y x bx c =-++ 与x 轴交于点A 和点B ，与y 轴交于点C ，点B 坐标为（6，0），点C 坐标为（0，6），点D 是抛物线的顶点，过点D 作x 轴的垂线，垂足为E ，连接BD ．（1）求抛物线的解析式及点D 的坐标；（2）点F 是抛物线上的动点，当∠FBA =∠BDE 时，求点F 的坐标；（3）若点M 是抛物线上的动点，过点M 作MN ∥x 轴与抛物线交于点N ，点P 在x 轴上，点Q 在坐标平面内，以线段MN 为对角线作正方形MPNQ ，请写出点Q 的坐标．【答案】（1）21262y x x =-++，D （2，8）；（2）（﹣1，72）或（﹣3，﹣92）；（3）（2，2217-+）或（2，2217--）．【分析】（1）由B 、C 的坐标，利用待定系数法可求得抛物线解析式，再求其顶点D 即可；（2）过F 作FG ⊥x 轴于点G ，可设出F 点坐标，利用△FBG ∽△BDE ，由相似三角形的性质可得到关于F 点坐标的方程，可求得F 点的坐标；（3）由于M 、N 两点关于对称轴对称，可知点P 为对称轴与x 轴的交点，点Q 在对称轴上，可设出Q 点的坐标，则可表示出M 的坐标，代入抛物线解析式可求得Q 点的坐标．【解答】（1）把B 、C 两点坐标代入抛物线解析式可得：18606b c c -++=⎧⎨=⎩，解得：26b c =⎧⎨=⎩，∴抛物线解析式为21262y x x =-++ ，∵21262y x x =-++=21(2)82x --+，∴D （2，8）；当点F在x轴下方时，有21261 262 x xx-++=--，解得x=﹣3或x=6（舍去），此时F点的坐标为（﹣3，﹣92）；综上可知F点的坐标为（﹣1，72）或（﹣3，﹣92）；（3）如图2，设对角线MN、PQ交于点O′，∵点M、N关于抛物线对称轴对称，且四边形MPNQ为正方形，∴点P为抛物线对称轴与x轴的交点，点Q在抛物线的对称轴上，设Q（2，2n），则M坐标为（2﹣n，n），∵点M在抛物线21262y x x=-++的图象上，∴n=﹣12（2﹣n）2+2（2﹣n）+6，解得n=117-+或n=117--，∴满足条件的点Q有两个，其坐标分别为（2，2217-+）或（2，2217--）．9．（2017山东省烟台市）如图，菱形ABCD中，对角线AC，BD相交于点O，AC=12cm，BD=16cm，动点N从点D出发，沿线段DB以2c m/s的速度向点B运动，同时动点M从点B出发，沿线段BA以1c m/s的速度向点A运动，当其中一个动点停止运动时另一个动点也随之停止，设运动时间为t（s）（t＞0），以点M 为圆心，MB长为半径的⊙M与射线BA，线段BD分别交于点E，F，连接EN．（1）求BF的长（用含有t的代数式表示），并求出t的取值范围；（2）当t为何值时，线段EN与⊙M相切？（3）若⊙M与线段EN只有一个公共点，求t的取值范围．【答案】（1）BF=85t（0＜t≤8）；（2）t=329；（3）0＜t≤327或409＜t＜8．【分析】（1）连接MF ．只要证明MF ∥AD ，可得BM BF BA BD =，即1016t BF =，解方程即可；（2）当线段EN 与⊙M 相切时，易知△BEN ∽△BOA ，可得BE BN OB AB =，即2162810t t -=，解方程即可；（3）①由题意可知：当0＜t ≤329时，⊙M 与线段EN 只有一个公共点．②当F 与N 重合时，则有85t +2t =16，解得t =409，观察图象即可解决问题；②当F 与N 重合时，则有85t +2t =16，解得t =409，关系图象可知，409＜t ＜8时，⊙M 与线段EN 只有一个公共点．综上所述，当0＜t ≤327或409＜t ＜8时，⊙M 与线段EN 只有一个公共点．10．（2017山东省烟台市）如图1，抛物线22y ax bx =++与x 轴交于A ，B 两点，与y 轴交于点C ，AB =4，矩形OBDC 的边CD =1，延长DC 交抛物线于点E ．学-/科+网（1）求抛物线的解析式；（2）如图2，点P 是直线EO 上方抛物线上的一个动点，过点P 作y 轴的平行线交直线EO 于点G ，作PH ⊥EO ，垂足为H ．设PH 的长为l ，点P 的横坐标为m ，求l 与m 的函数关系式（不必写出m 的取值范围），并求出l 的最大值；（3）如果点N 是抛物线对称轴上的一点，抛物线上是否存在点M ，使得以M ，A ，C ，N 为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的点M 的坐标；若不存在，请说明理由．【答案】（1）224233y x x =--+；（2）l =221492()3448m -++，l 的最大值为49248；（3）M 的坐标为（2，﹣103）或（﹣4，﹣103）或（﹣2，2）．【分析】（1）由条件可求得A 、B 的坐标，利用待定系数法可求得抛物线解析式；（2）可先求得E 点坐标，从而可求得直线OE 解析式，可知∠PGH =45°，用m 可表示出PG 的长，从而可表示出l 的长，再利用二次函数的性质可求得其最大值；（3）分AC 为边和AC 为对角线，当AC 为边时，过M 作对称轴的垂线，垂足为F ，则可证得△MFN ≌△AOC ，可求得M 到对称轴的距离，从而可求得M 点的横坐标，可求得M 点的坐标；当AC 为对角线时，设AC 的中点为K ，可求得K 的横坐标，从而可求得M 的横坐标，代入抛物线解析式可求得M 点坐标．【解答】（1）∵矩形OBDC 的边CD =1，∴OB =1，∵AB =4，∴OA =3，∴A （﹣3，0），B （1，0），把A 、B两点坐标代入抛物线解析式可得：209320a b a b ++=⎧⎨-+=⎩，解得：2343a b ⎧=-⎪⎪⎨⎪=-⎪⎩，∴抛物线解析式为224233y x x =--+；（2）在224233y x x =--+中，令y =2可得2=224233x x --+，解得x =0或x =﹣2，∴E （﹣2，2），∴直线OE 解析式为y =﹣x ，由题意可得P （m ，224233m m --+），∵PG ∥y 轴，∴G （m ，﹣m ），∵P 在直线OE 的上方，∴PG =224233m m --+﹣（﹣m ）=221233m m --+=22149()3424m -++，∵直线OE 解析式为y =﹣x ，∴∠PGH =∠COE =45°，∴l 2PG 2 [22149()3424m -++]=221492)4m ++，∴当m =14-时，l 有最大值，最大值为248；。

2019年全国各地中考数学解析汇编22 特殊的平行四边形

2019年全国各地中考数学解析汇编22 特殊的平行四边形（2018湖南益阳，7，4分）如图，点A 是直线l 外一点，在l 上取两点B 、C ，分别以A 、C 为圆心，BC 、AB 长为半径画弧，两弧交于点D ，分别连结AB 、AD 、CD ，则四边形ABCD 一定是（） A ．平行四边形 B ．矩形C ．菱形D ．梯形【解析】从题目中（BC 、AB 长为半径画弧，两弧交于点D ，）可以得到四边形ABCD 的两组对边分别相等，所以得到四边形ABCD 是平行四边形。

【答案】A【点评】根据尺规作图得到对边相等，只要考生记住两组对边分别相等的四边形是平行四边形这一定义，就可以得到答案，难度不大。

23.1 矩形（2018湖北襄阳，9，3分）如图4，ABCD 是正方形，G 是BC 上（除端点外）的任意一点，DE ⊥AG 于点E ，BF ∥DE ，交AG 于点F ．下列结论不一定成立的是A ．△AED ≌△BFAB ．DE －BF ＝EFC ．△BGF ∽△DAED ．DE －BG ＝FG【解析】由ABCD 是正方形，得AD ＝BA ，∠BAD ＝∠ABG ＝90°，∴∠DAE ＋∠BAF ＝90°．又∵DE ⊥AG ，BF ∥DE ，∴BF ⊥AG ，∠BAF ＋∠ABF ＝90°．∴∠DAE ＝∠ABF ．而∠AED ＝∠BFA ＝90°，∴△AED ≌△BFA ．∴DE ＝AF ，AE ＝BF ．∴DE －BF ＝AF －AE ＝EF ．由AD ∥BC 得∠DAE ＝∠BGF 及∠AED ＝∠GFB ＝90°，可知△BGF ∽△DAE ．可见A ，B ，C 三选项均正确，只有D 选项不能确定．【答案】D【点评】此题是由人教课标版数学教材八年级下册第104页的第15题改编而成，并将九年级下册第48页练习2融合进来，源于教材而又高于教材，综合考查了正方形的性质、全等三角形、相似三角形知识，是一道不可多得的基础好题．（2018山东泰安，9，3分）如图，在矩形ABCD 中，AB=2，BC=4，对角线AC 的垂直平分线分别交AD 、AC 于点E 、O ，连接CE ，则CE 的长为（） A. 3 B.3.5 C.2.5 D.2.8图4【解析】设CE 的长为x,因为EO 垂直平分AC ，所以AE=CE=x,所以ED=4-x, 在Rt △CED 中，由勾股定理得CD 2+ED 2=CE 2，22+（4-x ）2=x 2,解得x=2.5. 【答案】C.【点评】本题在矩形中综合考查了线段垂直平分线的性质、勾股定理等知识，用方程的思想解几何问题是一种行之有效的思想方法。

2019年北师大版九年级数学上册第一章特殊的平行四边形培优专题(中考真题)(含答案)

2019年北师大版九年级上册第一章特殊的平行四边形培优专题（中考真题）（含答案）一、单选题1．（2019·广西中考真题）如图，E 是正方形ABCD 的边AB 的中点，点H 与B 关于CE 对称，EH 的延长线与AD 交于点F ，与CD 的延长线交于点N ，点P 在AD 的延长线上，作正方形DPMN ，连接CP ，记正方形ABCD ，DPMN 的面积分别为1S ，2S ，则下列结论错误的是（）A ．212S S CP +=B ．2AF FD =C ．4CD PD = D ．3cos 5HCD ∠=2．（2019·江苏中考真题）如图，菱形ABCD 的顶点B 、C 在x 轴上（B 在C 的左侧），顶点A 、D 在x 轴上方，对角线BD 的长是103，点()2,0E -为BC 的中点，点P 在菱形ABCD 的边上运动．当点()0,6F 到EP 所在直线的距离取得最大值时，点P 恰好落在AB 的中点处，则菱形ABCD 的边长等于（）A ．103BC ．163D ．33．（2018·四川中考真题）如图，在 ABCD 中，CD=2AD ，BE ⊥AD 于点E ，F 为DC 的中点，连结EF 、BF ，下列结论：①∠ABC=2∠ABF ；②EF=BF ；③S 四边形DEBC =2S △EFB ；④∠CFE=3∠DEF,其中正确结论的个数共有（）.A ．1个B ．2个C ．3个D ．4个4．（2019·天津中考模拟）如图，在菱形ABCD 中，60ABC ∠=︒，E 为BC 边的中点，M 为对角线BD 上的一个动点。

则下列线段的长等于12AM BM +最小值的是（）A ．ADB ．AEC ．BD D ．BE5．（2019·河南省实验中学中考模拟）如图①，在菱形ABCD 中，动点P 从点B 出发，沿折线B→C→D→B 运动．设点P 经过的路程为x ，△ABP 的面积为y ．把y 看作x 的函数，函数的图象如图②所示，则图②中的b 等于（）A ．B ．37C ．5D ．46．（2019·河南省实验中学中考模拟）如图，四边形OABC 为矩形，点A ，C 分别在x 轴和y 轴上，连接AC ，点B 的坐标为（8，6），以A 为圆心，任意长为半径画弧，分别交AC 、AO 于点M 、N ，再分别以M 、N 为圆心，大于12MN 长为半径画弧两弧交于点Q ，作射线AQ 交y 轴于点D ，则点D 的坐标为（）A ．()0,1B ．80,3⎛⎫ ⎪⎝⎭C ．50,3⎛⎫ ⎪⎝⎭D ．()0,27．（2019·辽宁中考模拟）如图，菱形ABCD 的边长为2，∠A=60°，点P 和点Q 分别从点B 和点C 出发，沿射线BC 向右运动并且始终保持BP=CQ ，过点Q 作QH ⊥BD ，垂足为H ，连接PH ，设点P 运动的距离为x （0＜x≤2），△BPH 的面积为s ，则能反映s 与x 之间的函数关系的图象大致为（）A ．B ．C ．D ．8．（2019·湖南中考真题）我国古代数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的三角形，如图所示，已知90A ︒∠=，4BD =，6CF =，则正方形ADOF 的边长是（）A B ．2C D ．49．（2019·内蒙古中考真题）如图，矩形ABCD 与菱形EFGH 的对角线均交于点O ，且//EG BC ，将矩形折叠，使点C 与点O 重合，折痕MN 过点G ．若AB 6=，2EF =，120H ∠=，则DN 的长为（）A -B C D ．10．（2015·四川中考真题）如图，在菱形ABCD 中，AB=BD ，点E 、F 分别是AB 、AD 上任意的点（不与端点重合），且AE=DF ，连接BF 与DE 相交于点G ，连接CG 与BD 相交于点H ．给出如下几个结论：①△AED ≌△DFB ；②S 四边形BCDG =；③若AF=2DF ，则BG=6GF ；④CG 与BD 一定不垂直；⑤∠BGE 的大小为定值．其中正确的结论个数为（）A ．4B ．3C ．2D ．111．（2019·江西中考真题）如图，由10根完全相同的小棒拼接而成，请你再添2根与前面完全相同的小棒，拼接后的图形恰好有3个菱形的方法共有（）A ．3种B ．4种C ．5种D ．6种12．（2019·内蒙古中考真题）如图，在正方形ABCD 中，1AB =，点,E F 分别在边BC 和CD 上，AE AF =，60EAF ∠=，则CF 的长是（）A B C 1D ．2313．（2019·贵州中考真题）如图，四边形ABCD 为菱形，AB ＝2，∠DAB ＝60°，点E 、F 分别在边DC 、BC 上，且CE ＝13CD ，CF ＝13CB ，则S △CEF ＝( )A ．2B ．3C ．4D ．914．（2019·浙江中考真题）正方形ABCD 的边AB 上有一动点E ，以EC 为边作矩形ECFG ，且边FG 过点D ，在点E 从点A 移动到点B 的过程中，矩形ECFG 的面积（）A．先变大后变小B．先变小后变大C．一直变大D．保持不变15．（2018·海南中考真题）如图1，分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC，EG剪开，拼成如图2所示的▱ALMN，若中间空白部分四边形OPQR恰好是正方形，且▱ALMN的面积为50，则正方形EFGH的面积为（）A．24 B．25 C．26 D．2716．（2018·贵州中考真题）如图，点P是矩形ABCD的对角线AC上一点，过点P作EF∥BC，分别交AB，CD于E、F，连接PB、PD．若AE=2，PF=8．则图中阴影部分的面积为（）A．10 B．12 C．16 D．1817．（2014·黑龙江中考真题）如图，在矩形ABCD中，AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：①∠AED=∠CED；②OE=OD；③BH=HF；④BC﹣CF=2HE；⑤AB=HF，其中正确的有（）A．2个B．3个C．4个D．5个18．（2018·广西中考真题）如图，在正方形ABCD中，AB=3，点M在CD的边上，且DM=1，ΔAEM与ΔA DM 关于AM所在的直线对称，将ΔADM按顺时针方向绕点A旋转90°得到ΔABF，连接EF，则线段EF的长为（）A．3 B．C．D．19．（2015·湖北中考真题）如图，正方形ABCD的边长为6，点E、F分别在AB，AD上，若CE=3，且∠ECF=45°，则CF长为（）A．2B．3C．D．二、填空题20．（2019·贵州中考真题）如图，平行四边形纸片ABCD 的边AB ，BC 的长分别是10cm 和7.5cm ，将其四个角向内对折后，点B 与点C 重合于点C '，点A 与点D 重合于点A ′．四条折痕围成一个“信封四边形”EHFG ，其顶点分别在平行四边形ABCD 的四条边上，则EF ＝__cm ．21．（2019·四川中考真题）如图，在边长为1的菱形ABCD 中，60ABC ∠=︒，将ABD ∆沿射线BD 的方向平移得到A B D '''∆，分别连接A C '，A D '，B C '则A C B C ''+的最小值为____.22．（2019·四川中考真题）如图，在菱形ABCD 中，4sin 5B =，点,E F 分别在边,AD BC 上，将四边形AEFB 沿EF 翻折，使AB的对应线段MN 经过顶点C ，当MN BC ⊥时，AEAD的值是_____．23．（2019·湖北中考真题）如图，先有一张矩形纸片48ABCD AB BC ，＝，＝，点M N ，分别在矩形的边AD BC ，上，将矩形纸片沿直线MN 折叠，使点C 落在矩形的边AD 上，记为点P ，点D 落在G 处，连接PC ，交MN 于点Q ，连接CM ．下列结论：CQ CD ①＝；②四边形CMPN 是菱形；③P A ，重合时，MN =；④PQM 的面积S 的取值范围是35S ≤≤．其中正确的是_____（把正确结论的序号都填上）．24．（2019·黑龙江中考真题）如图，四边形11OAA B 是边长为1的正方形，以对角线1OA 为边作第二个正方形122OA A B ，连接2AA ，得到12AA A ∆；再以对角线2OA 为边作第三个正方形233OA A B ，连接13A A ，得到123A A A ∆；再以对角线3OA 为边作第四个正方形，连接24A A ，得到234A A A ∆……记12AA A ∆、123A A A ∆、231A A A ∆的面积分别为1S 、2S 、3S ，如此下去，则2019S =_____．25．（2019·四川中考真题）如图，在ABC ∆中，已知3AC =，4BC =，点D 为边AB 的中点，连结CD ，过点A 作AE CD ⊥于点E ，将ACE ∆沿直线AC 翻折到ACE '∆的位置．若//CE AB '，则CE '=_______．26．（2019·江苏中考真题）如图，正方形ABCD 的边长为4，E 为BC 上一点，且1BE =，F 为AB 边上的一个动点，连接EF ，以EF 为边向右侧作等边EFG ∆，连接CG ，则CG 的最小值为_____．27．（2019·江苏中考真题）“七巧板”是我们祖先的一项卓越创造，可以拼出许多有趣的图形，被誉为“东方魔板”，图①是由边长10cm 的正方形薄板分成7块制作成的“七巧板”图②是用该“七巧板”拼成的一个“家”的图形，该“七巧板”中7块图形之一的正方形边长为_______cm (结果保留根号).28．（2019·山东中考真题）如图，在正方形纸片ABCD 中，E 是CD 的中点，将正方形纸片折叠，点B 落在线段AE 上的点G 处，折痕为AF ．若AD＝4 cm，则CF 的长为___________cm ．29．（2018·贵州中考真题）如图，在菱形ABCD中，∠ABC=120°，将菱形折叠，使点A恰好落在对角线BD上的点G处（不与B、D重合），折痕为EF，若DG=2，BG=6，则BE的长为______．30．（2018·浙江中考真题）如图，在正方形ABCD中，AB=3，点E，F分别在CD，AD上，CE=DF，BE，CF相交于点G．若图中阴影部分的面积与正方形ABCD的面积之比为2：3，则△BCG的周长为_____．31．（2018·四川中考真题）如图，在菱形中，，分别在边上，将四边形沿翻折，使的对应线段经过顶点，当时，的值为__________.参考答案1．D 【解析】【分析】根据勾股定理可判断A ；连接CF ，作FG EC ⊥，易证得FGC ∆是等腰直角三角形，设EG x =，则2FG x =，利用三角形相似的性质以及勾股定理得到2CG x =，CF =，3EC x =，5BC x =，5FD x =，即可证得3FD AD =，可判断B ；根据平行线分线段成比例定理可判断C ；求得cos HCD ∠可判断D. 【详解】解：∵正方形ABCD ，DPMN 的面积分别为1S ，2S ，∴21S CD =，22S PD =，在Rt PCD ∆中，222PC CD PD =+，∴212S S CP +=，故A 结论正确；连接CF ，∵点H 与B 关于CE 对称， ∴CH CB =，BCE ECH ∠=∠，在BCE ∆和HCE ∆中，CH CB ECH BCE CE CE =⎧⎪∠=∠⎨⎪=⎩∴()BCE HCE SAS ∆≅∆，∴BE EH =，90EHC B ∠=∠=︒，BEC HEC ∠=∠， ∴CH CD =，在Rt FCH ∆和Rt FCD ∆中CH CDCF CF =⎧⎨=⎩∴()Rt FCH Rt FCD HL ∆≅∆， ∴FCH FCD ∠=∠，FH FD =， ∴1452ECH ECH BCD ∠+∠=∠=︒，即45ECF ∠=︒，作FG EC ⊥于G ，∴CFG ∆是等腰直角三角形， ∴FG CG =，∵BEC HEC ∠=∠，90B FGE ∠=∠=︒， ∴FEG CEB ∆∆，∴12EG EB FG BC ==， ∴2FG EG =，设EG x =，则2FG x =，∴2CG x =，CF =， ∴3EC x =，∵222EB BC EC +=， ∴22594BC x =， ∴22365BC x =，∴BC x =，在Rt FDC ∆中，FD x ===， ∴3FD AD =，∴2AF FD =，故B 结论正确； ∵//AB CN ， ∴12ND FD AE AF ==，∵PD ND =，12AE CD =， ∴4CD PD =，故C 结论正确； ∵EG x =，2FG x =，∴EF =，∵5FH FD x ==，∵BC x =，∴5AE x =，作HQ AD ⊥于Q ， ∴//HQ AB ，∴HQ HF AE EF =，即355x=，∴25HQ x =，∴CD HQ x x -=-=，∴cos CD HQ HCD CF -∠===，故结论D 错误，故选：D ．【点睛】本题考查了正方形的性质，三角形全等的判定和性质三角形相似的判定和性质，勾股定理的应用以及平行线分线段成比例定理，作出辅助线构建等腰直角三角形是解题的关键. 2．A 【解析】【分析】如图1中，当点P 是AB 的中点时，作FG ⊥PE 于G ，连接EF ．首先说明点G 与点F 重合时，FG 的值最大，如图2中，当点G与点E重合时，连接AC交BD于H，PE交BD于J．设BC=2a．利用相似三角形的性质构建方程求解即可．【详解】如图1中，当点P是AB的中点时，作FG⊥PE于G，连接EF．∵E（-2，0），F（0，6），∴OE=2，OF=6，∴0，4=21∵∠FGE=90°，∴FG≤EF，∴当点G与E重合时，FG的值最大．如图2中，当点G与点E重合时，连接AC交BD于H，PE交BD于J．设BC=2a．∵PA=PB，BE=EC=a，∴PE∥AC，BJ=JH，∵四边形ABCD是菱形，∴AC⊥BD，BH=DH=3，BJ=6，∴PE⊥BD，∵∠BJE=∠EOF=∠PEF=90°，∴∠EBJ=∠FEO，∴△BJE∽△EOF，∴BE BJ EF EO=，∴62=，∴a=53，∴BC=2a=103，故选A．【点睛】本题考查菱形的性质，坐标与图形的性质，相似三角形的判定和性质，垂线段最短等知识，解题的关键是理解题意，学会添加常用辅助线，构造相似三角形解决问题，属于中考选择题中的压轴题．3．D【解析】分析：如图延长EF交BC的延长线于G，取AB的中点H连接FH．证明△DFE≌△FCG 得EF=FG，BE⊥BG，四边形BCFH是菱形即可解决问题；详解：如图延长EF交BC的延长线于G，取AB的中点H连接FH．∵CD=2AD，DF=FC，∴CF=CB，∴∠CFB=∠CBF，∵CD∥AB，∴∠CFB=∠FBH，∴∠CBF=∠FBH，∴∠ABC=2∠ABF．故①正确，∵DE∥CG，∴∠D=∠FCG，∵DF=FC，∠DFE=∠CFG，∴△DFE≌△FCG，∴FE=FG，∵BE⊥AD，∴∠AEB=90°，∵AD∥BC，∴∠AEB=∠EBG=90°，∴BF=EF=FG，故②正确，∵S△DFE=S△CFG，=S△EBG=2S△BEF，故③正确，∴S四边形DEBC∵AH=HB，DF=CF，AB=CD，∴CF=BH，∵CF∥BH，∴四边形BCFH是平行四边形，∵CF=BC，∴四边形BCFH是菱形，∴∠BFC=∠BFH，∵FE=FB，FH∥AD，BE⊥AD，∴FH⊥BE，∴∠BFH=∠EFH=∠DEF，∴∠EFC=3∠DEF，故④正确，故选：D．点睛：本题考查平行四边形的性质和判定、菱形的判定和性质、直角三角形斜边中线的性质、全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考选择题中的压轴题．4．B【解析】【分析】过点M作PM⊥CB于P，根据菱形和直角三角形的性质可得PM=1BM2，从而可得1AM BM2+=AM+PM，根据垂线段最短可知，AM+PM的最小值为AE的长；【详解】过点M作PM⊥CB于P，∵四边形ABCD是菱形，∴∠PBM=12∠ABC=30°，AB=BC∴PM=12 BM，∴1AM BM2+=AM+PM，∵AB=BC,ABC60∠=︒∴ABC是等边三角形∵E为BC边的中点，∴AE⊥BC；根据垂线段最短可知，AM+PM的最小值为AE的长，故选：B．【点睛】本题考查轴对称-最短问题，菱形的性质等知识，解题的关键是学会用转化的思想思考问题，属于中考常考题型．5．B【解析】【分析】连接AC交BD于O，根据图②求出菱形的边长为4，对角线BD为6，根据菱形的对角线互相垂直平分求出BO，再利用勾股定理列式求出CO，然后求出AC的长，再根据菱形的面积等于对角线乘积的一半求出菱形的面积，b为点P在CD上时△ABP的面积，等于菱形的面积的一半，从而得解．【详解】解：如图，连接AC交BD于O，由图②可知，BC=CD=4，BD=14-8=6， ∴BO=12BD=12×6=3，在Rt △BOC 中，，，所以，菱形的面积=12AC•BD=12×，当点P 在CD 上运动时，△ABP 的面积不变，为b ，所以，b=12×．故选：B ．【点睛】本题考查了动点问题的函数图象，主要利用了菱形的对角线互相垂直平分的性质，菱形的面积等于对角线乘积的一半，根据图形得到菱形的边长与对角线BD 的长是解题的关键． 6．B 【解析】【分析】过点D 作DE ⊥AC 于点E ，由勾股定理可求AC=10，由“AAS”可证△ADO ≌△ADE ，可证AE=AO=8，OD=DE ，可得CE=2，由勾股定理可求OD 的长，即可求点D 坐标．【详解】解：如图，过点D 作DE ⊥AC 于点E ，∵四边形OABC 为矩形，点B 的坐标为（8，6），∴OA=8，OC=6∴由题意可得AD 平分∠OAC∴∠DAE=∠DAO ，AD=AD ，∠AOD=∠AED=90° ∴△ADO ≌△ADE （AAS ） ∴AE=AO=8，OD=DE ∴CE=2， ∵CD 2=DE 2+CE 2， ∴（6-OD ）2=4+OD 2， ∴OD=83∴点D （0，83）故选：B ．【点睛】本题考查了矩形的性质，坐标与图形的性质，勾股定理，全等三角形的判定和性质，证明△ADO ≌△ADE 是本题的关键． 7．C 【解析】【分析】根据菱形的性质得到∠DBC=60°，根据直角三角形的性质得到BH=12 BQ=1+12x ，过H 作HG ⊥BC ，得到BH=2+4x ，根据三角形的面积公式即可得到结论．【详解】∵菱形ABCD 的边长为2,∠A=60°，∴∠DBC=60°，∵BQ=2+x ，QH ⊥BD ， ∴BH=12BQ=1+12x ，过H 作HG ⊥BC ，∴，∴s=12PB ⋅2x ⩽2)，故选C 【点睛】此题考查动点问题的函数图象，解题关键在于作辅助线 8．B 【解析】【分析】设正方形ADOF 的边长为x ，在直角三角形ACB 中，利用勾股定理可建立关于x 的方程，解方程即可．【详解】设正方形ADOF 的边长为x ，由题意得：BE BD 4==，CE CF 6==，BC BE CE BD CF 10∴=+=+=，在Rt △ABC 中，222AC AB BC +=，即()()2226x x 410+++=，整理得，2x 10x 240+-=，解得：x=2或x=-12(舍去)，x 2∴=，即正方形ADOF 的边长是2，故选B ．【点睛】本题考查了正方形的性质、全等三角形的性质、一元二次方程的解法、勾股定理等知识；熟练掌握正方形的性质，由勾股定理得出方程是解题的关键． 9．A【解析】【分析】延长EG 交DC 于P 点，连接GC 、FH ；由四边形EFGH 是菱形，120EHG ∠=，得2GH EF ==，60OHG ︒∠=，EG FH ⊥，sin 6022OG GH ︒=⋅=⨯=，根据根据折叠性质，再证四边形OGCM 为菱形，得PG 是梯形MCDN 的中位线，根据中位线性质求解. 【详解】延长EG 交DC 于P 点，连接GC 、FH ；如图所示：则12CP DP CD ===，GCP ∆为直角三角形， ∵四边形EFGH 是菱形，120EHG ∠=， ∴2GH EF ==，60OHG ︒∠=，EG FH ⊥，∴sin 602OG GH ︒=⋅==，由折叠的性质得：CG OG ==OM CM =，MOG MCG ∠=∠，∴6PG ==∵//OG CM ，∴180MOG OMC ︒∠+∠=， ∴180MCG OMC ︒∠+∠=， ∴//OM CG ，∴四边形OGCM 为平行四边形， ∵OM CM =，∴四边形OGCM 为菱形，∴CM OG ==根据题意得：PG 是梯形MCDN 的中位线，∴2DN CM PG +==∴DN =故选：A ．【点睛】考核知识点：矩形折叠，菱形判定和性质，三角函数.理解折叠的性质是关键.10．B【解析】试题分析：①∵ABCD为菱形，∴AB=AD，∵AB=BD，∴△ABD为等边三角形，∴∠A=∠BDF=60°，又∵AE=DF，AD=BD，∴△AED≌△DFB，故本选项正确；②∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD，即∠BGD+∠BCD=180°，∴点B、C、D、G四点共圆，∴∠BGC=∠BDC=60°，∠DGC=∠DBC=60°，∴∠BGC=∠DGC=60°，过点C作CM⊥GB于M，CN⊥GD于N（如图1），则△CBM≌△CDN（AAS），∴S四边形BCDG=S四边形CMGN，S四边形CMGN=2S△CMG，∵∠CGM=60°，∴GM=CG，CM=CG，∴S四边形CMGN=2S△CMG=2××CG×CG=，故本选项错误；③过点F作FP∥AE于P点（如图2），∵AF=2FD，∴FP：AE=DF：DA=1：3，∵AE=DF，AB=AD，∴BE=2AE，∴FP：BE=FP：AE=1：6，∵FP∥AE，∴PF∥BE，∴FG：BG=FP：BE=1：6，即BG=6GF，故本选项正确；④当点E，F分别是AB，AD中点时（如图3），由（1）知，△ABD，△BDC为等边三角形，∵点E，F分别是AB，AD中点，∴∠BDE=∠DBG=30°，∴DG=BG，在△GDC与△BGC中，∵DG=BG，CG=CG，CD=CB，∴△GDC≌△BGC，∴∠DCG=∠BCG，∴CH⊥BD，即CG⊥BD，故本选项错误；⑤∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°，为定值，故本选项正确；综上所述，正确的结论有①③⑤，共3个，故选B．考点：四边形综合题．11．D【解析】【分析】根据菱形的性质，找出各种拼接法，此题得解．【详解】解：共有6种拼接法，如图所示．故选：D ．【点睛】本题考查了图形的剪拼以及菱形的判定，依照题意，画出图形是解题的关键． 12．C 【解析】【分析】由正方形的性质得出∠B=∠D=∠BAD=90°，AB=BC=CD=AD=1，证明Rt △ABE ≌Rt △ADF 得出∠BAE=∠DAF ，求出∠DAF=15°，在AD 上取一点G ，使∠GFA=∠DAF=15°，则AG=FG ，∠DGF=30°，由直角三角形的性质得出DF=12FG=12AG ，，设DF=x ，则，AG=FG=2x ，则，解得：，得出DF=2-【详解】解：四边形ABCD 是正方形，90,B D BAD ︒∴∠=∠=∠=1AB BC CD AD ====，在Rt ABE ∆和Rt ADF ∆中， AE AFAB AD=⎧⎨=⎩，()Rt ABE Rt ADF HL ∴∆≅∆，BAE DAF ∴∠=∠，60EAF ︒∠=，30BAE DAF ︒∴∠=+∠， 15DAF ︒∴∠=，在AD 上取一点G ，使15GFA DAF ︒∠=∠=，如图所示：,30AG FG DGF ︒∴=∠=，11,22DF FG AG DG ∴===，设DF x =，则,2DG AG FG x ===，AG DG AD +=，21x ∴=，解得：2x =-2DF ∴=1(21CF CD DF ∴=-=-=；故选：C ．【点睛】本题考查了正方形的性质、全等三角形的判定与性质、等腰三角形的判定、直角三角形的性质等知识；熟练掌握正方形的性质，证明三角形全等是解题的关键． 13．D 【解析】【分析】根据菱形的性质得出△CEF 为等边三角形，即可解答【详解】∵四边形ABCD 为菱形，AB ＝2，∠DAB ＝60° ∴AB ＝BC ＝CD ＝2，∠DCB ＝60°∵CE ＝13CD ，CF ＝13CB ∴CE ＝CF ＝23∴△CEF 为等边三角形∴S △CEF 22()3=故选：D . 【点睛】此题考查菱形的性质和等边三角形的性质，解题关键在于得出△CEF 为等边三角形 14．D 【解析】【分析】连接DE ，△CDE 的面积是矩形CFGE 的一半，也是正方形ABCD 的一半，则矩形与正方形面积相等．【详解】连接DE ，∵S △CDE ＝12S 四边形CEGF ， S △CDE ＝12S 正方形ABCD ， ∴矩形ECFG 与正方形ABCD 的面积相等．故选D ．【点睛】此题考查了正方形的性质、矩形的性质，连接DE 由面积关系进行转化是解题的关键． 15．B【解析】【分析】此题涉及的知识点是正方形、长方形的性质，先根据正方形和长方形的性质求出各边长的关系，再根据▱ALMN 的面积，求出各边长的关系，最后得出面积. 【详解】设EF=a ，BC=b ，AB=c ，则PQ=a-c ，RQ=b-a ，PQ=RQ ∴a=2b c+， ∵▱ALMN 的面积为50，∴bc+a 2+(a-c)2=50, 把a=2b c+代入化简求值得b+c=10, ∴a=5, ∴正方形EFGH 的边长为5， ∴正方形EFGH 的面积为25，故选B. 【点睛】此题重点考查学生对于正方形和长方形的性质的理解，熟练掌握这两个性质是解题的关键. 16．C 【解析】【分析】首先根据矩形的特点，可以得到S △ADC =S △ABC ，S △AMP =S △AEP ，S △PFC =S △PCN ，最终得到S 矩形EBNP = S 矩形MPFD ,即可得S △PEB =S △PFD ，从而得到阴影的面积．【详解】作PM ⊥AD 于M ，交BC 于N ．则有四边形AEPM ，四边形DFPM ，四边形CFPN ，四边形BEPN 都是矩形， ∴S △ADC =S △ABC ，S △AMP =S △AEP ，S △PFC =S △PCN ∴S 矩形EBNP = S 矩形MPFD , 又∵S △PBE =12S 矩形EBNP ，S △PFD =12S 矩形MPFD ，∴S△DFP=S△PBE=12×2×8=8，∴S阴=8+8=16，故选C．【点睛】本题考查矩形的性质、三角形的面积等知识，解题的关键是证明S△PEB=S△PFD．17．D【解析】试题分析：∵在矩形ABCD中，AE平分∠BAD，∴∠BAE=∠DAE=45°，∴△ABE是等腰直角三角形，∴AE=AB，∵AD=AB，∴AE=AD，又∠ABE=∠AHD=90°∴△ABE≌△AHD（AAS），∴BE=DH，∴AB=BE=AH=HD，∴∠ADE=∠AED=（180°﹣45°）=67.5°，∴∠CED=180°﹣45°﹣67.5°=67.5°，∴∠AED=∠CED，故①正确；∵∠AHB=（180°﹣45°）=67.5°，∠OHE=∠AHB（对顶角相等），∴∠OHE=∠AED，∴OE=OH，∵∠DOH=90°﹣67.5°=22.5°，∠ODH=67.5°﹣45°=22.5°，∴∠DOH=∠ODH，∴OH=OD，∴OE=OD=OH，故②正确；∵∠EBH=90°﹣67.5°=22.5°，∴∠EBH=∠OHD，又BE=DH，∠AEB=∠HDF=45°∴△BEH≌△HDF（ASA），∴BH=HF，HE=DF，故③正确；由上述①、②、③可得CD=BE、DF=EH=CE，CF=CD-DF，∴BC-CF=（CD+HE）-（CD-HE）=2HE，所以④正确；∵AB=AH，∠BAE=45°，∴△ABH不是等边三角形，∴AB≠BH，∴即AB≠HF，故⑤错误；综上所述，结论正确的是①②③④共4个．故选C．考点：1、矩形的性质；2、全等三角形的判定与性质；3、角平分线的性质；4、等腰三角形的判定与性质18．C【解析】分析：连接BM.证明△AFE≌△AMB得FE=MB，再运用勾股定理求出BM的长即可.详解：连接BM，如图，由旋转的性质得：AM=AF.∵四边形ABCD是正方形，∴AD=AB=BC=CD，∠BAD=∠C=90°,∵ΔAEM与ΔADM关于AM所在的直线对称，∴∠DAM=∠EAM.∵∠DAM+∠BAM=∠FAE+∠EAM=90°,∴∠BAM=∠EAF,∴△AFE≌△AMB∴FE=BM.在Rt△BCM中，BC=3，CM=CD-DM=3-1=2,∴BM=∴FE=.故选C.点睛：本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了正方形的性质．19．B【解析】试题分析：如图，延长FD到G，使DG=BE，连接CG、EF；∵四边形ABCD为正方形，在△BCE与△DCG中，∵CB=CD，∠CBE=∠CDG，BE=DG，∴△BCE≌△DCG（SAS），∴CG=CE，∠DCG=∠BCE，∴∠GCF=45°，在△GCF与△ECF中，∵GC=EC，∠GCF=∠ECF，CF=CF，∴△GCF≌△ECF（SAS），∴GF=EF，∵CE=，CB=6，∴BE===3，∴AE=3，设AF=x，则DF=6﹣x，GF=3+（6﹣x）=9﹣x，∴EF==，∴，∴x=4，即AF=4，∴GF=5，∴DF=2，∴CF===，故选A．考点：1．全等三角形的判定与性质；2．勾股定理；3．正方形的性质；4．综合题；5．压轴题．20．10．【解析】【分析】先根据有三个角是直角的四边形是矩形证明四边形EHFG是矩形，再证明△FCH≌△EAG，可得CF=AE=FC'，可知EF=AB，即可得结论．【详解】如图中，由翻折可知：∠CHF ＝∠FHC'，∠BHE ＝∠EHC'， ∴∠FHE ＝∠FHC'+∠EHC'12=（∠CHC'+∠BHC'）＝90°，同法可证：∠HFG ＝∠GEH ＝90°， ∴四边形EHFG 是矩形． ∴FH ＝EG ，FH ∥EG ， ∴∠HFC'＝∠FEG ，∵∠CFH ＝∠HFC'，∠AEG ＝∠GEA'， ∴∠CFH ＝∠AEG ，∵四边形ABCD 是平行四边形， ∴∠C ＝∠A ，BC ＝AD ，由翻折得：CH ＝C'H ＝BH 12=BC ，AG ＝A'G ＝DG 12=AD ， ∴CH ＝AG ，∴△HCF ≌△GAE （AAS ）， ∴CF ＝AE ，∴EF ＝FC'+EC'＝AE+BE ＝AB ＝10cm ，故答案为：10．【点睛】本题考查了平行四边形的性质，翻折变换，矩形的判定和性质，三角形全等的性质和判定等知识，解题的关键是理解题意，灵活运用所学知识解决问题．21【解析】【分析】过C 点作BD 的平行线l ，以l 为对称轴作B 点的对称点1B ，连接1AB 交直线l 于点1C ，当11,,A B C 三点共线时11AC BC +取最小值，再根据勾股定理即可求解.【详解】如图，过C 点作BD 的平行线l ，以l 为对称轴作B 点的对称点1B ，连接1AB 交直线l 于点1C根据平移和对称可知11A C B C AC BC +=+''，当11,,A B C 三点共线时11AC BC +取最小值，即1AB ，又1AB 1BB ==，根据勾股定理得，1AB【点睛】此题主要考查菱形的性质，解题的关键是熟知平移的性质及勾股定理的应用. 22．29. 【解析】【分析】延长CM 交AD 于点G ，进而利用翻折变换的性质得出AE ME =，A EMC ∠=∠，BF FN =，B N ∠=∠，AB MN =，再利用菱形的性质得出AB BC CD AD ===，B D ∠=∠，180A B ︒∠+∠=，设4C F x =，5FN x =，利用勾股定理得出9BC x AB CD AD ====，再根据三角函数进行计算即可解答【详解】延长CM 交AD 于点G ，∵将四边形AEFB 沿EF 翻折，∴AE ME =，A EMC ∠=∠，BF FN =，B N ∠=∠，AB MN = ∵四边形ABCD 是菱形∴AB BC CD AD ===，B D ∠=∠，180A B ︒∠+∠=∵4sin sin 5CF B N FN===， ∴设4CF x =，5FN x =，∴3CN x ==，∴9BC x AB CD AD ====， ∵4sin sin 5GCB D CD===∴365x GC =∴()36x 6655GM GC MN CN x x =--=-= ∵180A B ︒∠+∠=，180EMC EMG ︒∠+∠= ∴B EMG ∠=∠ ∴4sin sin 5EG B EMG EM=∠==∴3cos 5GMEMG EM∠==∴=2EM x ， ∴2AE x =， ∴2299AE x AD x == 故答案为：29. 【点睛】此题考查翻折变换，菱形的性质，三角函数，解题关键在于利用折叠的性质进行解答 23．②③ 【解析】【分析】先判断出四边形CNPM 是平行四边形，再根据翻折的性质可得CN NP ＝，然后根据邻边相等的平行四边形是菱形证明，判断出②正确；假设CQ CD ＝，得Rt CMQ CMD ≌，进而得30DCM QCM BCP ∠∠∠︒＝＝＝，这个不一定成立，判断①错误；点P 与点A 重合时，设BN x ＝，表示出8AN NC x -＝＝，利用勾股定理列出方程求解得x 的值，进而用勾股定理求得MN ，判断出③正确；当MN 过D 点时，求得四边形CMPN 的最小面积，进而得S 的最小值，当P 与A 重合时，S 的值最大，求得最大值便可．【详解】如图1，//PM CN ， PMN MNC ∴∠∠＝， MNC PNM ∠∠＝， PMN PNM ∴∠∠＝， PM PN ∴＝， NC NP ＝， PM CN ∴＝， //MP CN ，∴四边形CNPM 是平行四边形，CN NP ＝，∴四边形CNPM 是菱形，故②正确；CP MN BCP MCP ∴⊥∠∠，＝，90MQC D ∴∠∠︒＝＝，CP CP ＝，若CQ CD ＝，则Rt CMQ CMD ≌，30DCM QCM BCP ∴∠∠∠︒＝＝＝，这个不一定成立，故①错误；点P 与点A 重合时，如图2，设BN x ＝，则8AN NC x -＝＝，在222Rt ABN AB BN AN +中，＝，即22248x x +-＝（），解得3x ＝，835CN AC ∴=＝﹣＝，12CQ AC ∴==5QN CN CQ ∴=-=2MN QN ∴＝＝,故③正确；当MN 过点D 时，如图3，此时，CN 最短，四边形CMPN 的面积最小，则S 最小为1144444CMPN S S ==⨯⨯=菱形，当P 点与A 点重合时，CN 最长，四边形CMPN 的面积最大，则S 最大为15454S =⨯⨯=， 45S ∴≤≤，故④错误．故答案为：②③．【点睛】此题是四边形综合题，主要考查了折叠问题与菱形的判定与性质、勾股定理的综合应用，熟练掌握菱形的判定定理和性质定理、勾股定理是解本题的关键． 24．20172 【解析】【分析】首先求出S1、S2、S3，然后猜测命题中隐含的数学规律，即可解决问题．【详解】四边形11OAA B 是正方形，1111OA AA A B ∴===，1111122S ∴=⨯⨯=，190OAA ∠=，211111AO ∴=+=∴，2232OA A A ∴==，212112S ∴=⨯⨯=，同理可求：312222S =⨯⨯=，44S =…， 22n n S -∴=，201720192S ∴=，故答案为：20172．【点睛】此题考查正方形的性质，规律型：图形变换，解题关键在于找到规律25．95．【解析】【分析】如图，作CH AB ⊥于H ．首先证明90ACB ︒∠=，解直角三角形求出AH ，再证明CE AH '=即可．【详解】解：如图，作CH AB ⊥于H ．由翻折可知：90AE C AEC ︒'∠=∠=，ACE ACE '∠=∠， ∵//CE AB '， ∴ACE CAD '∠=∠， ∴ACD CAD ∠=∠， ∴DC DA =， ∵AD DB =， ∴DC DA DB ==， ∴90ACB ︒∠=，∴5AB ==，∵1122AB CH AC BC =， ∴125CH =，∴95AH ==， ∵//CE AB ，∴180E CH AHC ︒'∠+∠=， ∵90AHC ︒∠=， ∴90E CH ︒'∠=，∴四边形AHCE '是矩形， ∴95CE AH '==，【点睛】本题考查翻折变换，平行线的性质等知识，解题的关键是学会添加常用辅助线，构造特殊四边形解决问题，属于中考常考题型． 26．52【解析】【分析】由题意分析可知，点F 为主动点，G 为从动点，所以以点E 为旋转中心构造全等关系，得到点G 的运动轨迹，之后通过垂线段最短构造直角三角形获得CG 最小值．【详解】由题意可知，点F 是主动点，点G 是从动点，点F 在线段上运动，点G 也一定在直线轨迹上运动将EFB ∆绕点E 旋转60︒，使EF 与EG 重合，得到EFB EHG ∆≅∆，从而可知EBH ∆为等边三角形，点G 在垂直于HE 的直线HN 上，作CM HN ⊥，则CM 即为CG 的最小值，作EP CM ⊥，可知四边形HEPM 为矩形，则1351222CM MP CP HE EC =+=+=+=. 故答案为52．【点睛】本题考查了线段极值问题，分清主动点和从动点，通过旋转构造全等，从而判断出点G 的运动轨迹，是本题的关键．27．2【解析】【分析】由题目中第一个图可到小正方形的边长与小等腰三角形的直角边相等，与平行四边形的短边相等，所以大正方形的对角线长度为4倍小正方形边长，设出小正方形边长，利用大正方形面积列出方程，解出方程即可【详解】设小正方形边长为a ，由题目中第一个图可到小正方形的边长与小等腰三角形的直角边相等，与平行四边形的短边相等，所以大正方形对角线长4a ，S 大正方形=442a a ⨯=10×10，解得2a =±，舍去负值，得到2a =，故填2 【点睛】本题主要考查正方形的面积公式，能够用a 表示出正方形对角线的长度是本题关键28．6- 【解析】【分析】设BF=x ，则FG=x ，CF=4-x ，在Rt △GEF 中，利用勾股定理可得EF 2=（）2+x 2，在Rt △FCE 中，利用勾股定理可得EF 2=（4-x ）2+22，从而得到关于x 方程，求解x ，最后用4-x 即可．【详解】设BF=x ，则FG=x ，CF=4-x ．在Rt △ADE 中，利用勾股定理可得根据折叠的性质可知AG=AB=4，所以．在Rt △GEF 中，利用勾股定理可得EF 2=（）2+x 2，在Rt △FCE 中，利用勾股定理可得EF 2=（4-x ）2+22，所以（）2+x 2=（4-x ）2+22，解得．则故答案为：【点睛】本题主要考查了折叠的性质、勾股定理．折叠问题主要是抓住折叠的不变量，在直角三角形中利用勾股定理求解是解题的关键． 29．2.8 【解析】【分析】作EH ⊥BD 于H ，根据折叠的性质得到EG=EA ，根据菱形的性质、等边三角形的判定定理得到△ABD 为等边三角形，得到AB=BD ，根据勾股定理列出方程，解方程即可．【详解】解：作EH ⊥BD 于H ，由折叠的性质可知，EG=EA ，由题意得，BD=DG+BG=8，四边形ABCD 是菱形， ∴AB=BD ，∠ABD=∠CBD=12∠ABC=60° ∴△ABD 为等边三角形， ∴AB=BD=8，设BE=x ，则EG=AE=8-x ，在Rt △EHB 中，BH=12x ，，在Rt △EHG 中，EG 2=EH 2+GH 2，即(8-x)22+(6-12x)2，解得，x=2.8，即BE=2.8，故答案为：2.8．【点睛】本题考查的是翻转变换的性质、菱形的性质、勾股定理、解直角三角形，掌握翻转变换是一种对称变换，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等是解题的关键．30．【解析】分析：根据面积之比得出△BGC的面积等于正方形面积的16，进而依据△BCG的面积以及勾股定理，得出BG+CG的长，进而得出其周长．详解：∵阴影部分的面积与正方形ABCD的面积之比为2：3，∴阴影部分的面积为23×9=6，∴空白部分的面积为9-6=3，由CE=DF，BC=CD，∠BCE=∠CDF=90°，可得△BCE≌△CDF，∴△BCG的面积与四边形DEGF的面积相等，均为12×3=32，设BG=a，CG=b，则12ab=32，又∵a2+b2=32，∴a2+2ab+b2=9+6=15，即（a+b）2=15，∴∴△BCG的周长15，．点睛：此题考查了全等三角形的判定与性质、正方形的性质以及三角形面积问题．解题时注意数形结合思想与方程思想的应用．31．【解析】分析：首先延长NF与DC交于点H，进而利用翻折变换的性质得出NH⊥DC，再利用边角关系得出BN，CN的长进而得出答案．详解：延长NF与DC交于点H，∵∠ADF=90°，∴∠A+∠FDH=90°，∵∠DFN+∠DFH=180°，∠A+∠B=180°，∠B=∠DFN，∴∠A=∠DFH，∴∠FDH+∠DFH=90°，∴NH⊥DC，设DM=4k，DE=3k，EM=5k，∴AD=9k=DC，DF=6k，∵tanA=tan∠DFH=，则sin∠DFH=，∴DH=DF=k，∴CH=9k-k=k，∵cosC=cosA=，∴CN=CH=7k，∴BN=2k，∴．故答案为：.点睛：此题主要考查了翻折变换的性质以及解直角三角形，正确表示出CN的长是解题关键．。

2019年中考数学《特殊的四边形》总复习训练含答案解析

特殊的四边形（矩形、菱形）一、选择题1．如图，点P是矩形ABCD的边AD上的一个动点，矩形的两条边AB、BC的长分别为3和4，那么点P到矩形的两条对角线AC和BD的距离之和是（）A．B．C．D．不确定2．若矩形的一条对角线与一边的夹角是40°，则两条对角线相交所成的锐角是（）A．20°B．40°C．80°D．100°3．如图，矩形ABCD中，AB=8，BC=6，E、F是AC上的三等分点，则S△BEF为（）A．8 B．12 C．16 D．244．把一张长方形的纸片按如图所示的方式折叠，EM、FM为折痕，折叠后的C点落在B′M 或B′M的延长线上，那么∠EMF的度数是（）A．85°B．90°C．95°D．100°5．如图，在矩形ABCD中，EF∥AB，GH∥BC，EF、GH的交点P在BD上，图中面积相等的四边形有（）A．3对 B．4对 C．5对 D．6对6．如图，矩形ABCD的周长为68，它被分成7个全等的矩形，则矩形ABCD的面积为（）A．98 B．196 C．280 D．2847．如图，点O是矩形ABCD的中心，E是AB上的点，沿CE折叠后，点B恰好与点O 重合，若BC=3，则折痕CE的长为（）A．B．C．D．68．如图所示，把一长方形纸片沿MN折叠后，点D，C分别落在D′，C′的位置．若∠AMD′=36°，则∠NFD′等于（）A．144°B．126°C．108° D．72°9．将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB=3，则BC的长为（）10．如图，已知矩形纸片ABCD，点E是AB的中点，点G是BC上的一点，∠BEG＞60°．现沿直线EG将纸片折叠，使点B落在纸片上的点H处，连接AH，则与∠BEG相等的角的个数为（）A．4 B．3 C．2 D．111．如图，在矩形ABCD中，AB=12cm，BC=6cm，点E、F分别在AB、CD上，将矩形ABCD沿EF折叠，使点A、D分别落在矩形ABCD外部的点A′、D′处，则整个阴影部分图形的周长为（）A．18cm B．36cm C．40cm D．72cm12．下列识别图形不正确的是（）A．有一个角是直角的平行四边形是矩形B．有三个角是直角的四边形是矩形C．对角线相等的四边形是矩形D．对角线互相平分且相等的四边形是矩形13．四边形ABCD的对角线相交于点O，下列条件不能判定它是矩形的是（）A．AB=CD，AB∥CD，∠BAD=90°B．AO=CO，BO=DO，AC=BDC．∠BAD=∠ABC=90°，∠BCD+∠ADC=180°D．∠BAD=∠BCD，∠ABC=∠ADC=90°14．直角三角形中，两条直角边边长分别为12和5，则斜边中线的长是（）15．将一个矩形的纸对折两次，沿图中虚线将一角剪掉再打开后，得到的图形为（）A．B．C．D．16．菱形一条对角线长为8m，周长为20m，则其面积为（）A．40m2B．20m2C．48m2D．24m217．用直尺和圆规作一个菱形，如图，能得到四边形ABCD是菱形的依据是（）A．一组邻边相等的四边形是菱形B．四边相等的四边形是菱形C．对角线互相垂直的平行四边形是菱形D．每条对角线平分一组对角的平行四边形是菱形18．已知DE∥AC、DF∥AB，添加下列条件后，不能判断四边形DEAF为菱形的是（）A．AD平分∠BAC B．AB=AC且BD=CD C．AD为中线D．EF⊥AD二、填空题19．矩形ABCD中，对角线AC=10cm，AB：BC=3：4，则它的周长是cm．20．矩形ABCD的两条对角线相交于点O，如果矩形的周长是34cm，又△AOB的周长比△ABC的周长少7cm，则AB=cm，BC=cm．21．在矩形ABCD中，对角线AC、BD相交于点O，若∠AOB=110°，则∠OAB=度．22．如图所示，把两个大小完全一样的矩形拼成“L”形图案，则∠FAC=度，∠FCA=度．23．如图，在矩形ABCD中，点E是BC上一点，AE=AD，DF⊥AE，垂足为F，线段DF 与图中的哪一条线段相等？先将猜想出的结论填写在下面的横线上，然后再加以证明．即DF=．（写出一条线段即可）24．将矩形ABCD沿AE折叠，得到如图所示图形．若∠CED′=56°，则∠AED的大小是°．25．菱形ABCD的周长为36，其相邻两内角的度数比为1：5，则此菱形的面积为．26．已知菱形的两条对角线长为6cm和8cm，菱形的周长是cm，面积是cm2．27．如图，四边形ABCD中，E，F，G，H分别是边AB，BC，CD，DA的中点．请你添加一个条件，使四边形EFGH为矩形，应添加的条件是．28．已知菱形的两条对角线的长分别是4cm和8cm，则它的边长为cm．29．若四边形ABCD是平行四边形，使四边形ABCD是菱形，请补充条件（写一个即可）．30．已知菱形ABCD的边长为6，∠A=60°，如果点P是菱形内一点，且PB=PD=2，那么AP的长为．31．已知四边形ABCD为菱形，∠BAD=60°，E为AD中点，AB=6cm，P为AC上任一点．求PE+PD的最小值是．32．如图，在菱形ABCD中，对角线AC=6，BD=8，点E、F分别是边AB、BC的中点，点P在AC上运动，在运动过程中，存在PE+PF的最小值，则这个最小值是．33．已知四边形ABCD为平行四边形，要使四边形ABCD为菱形，还应添加条件．34．用两张对边平行的纸条交叉重叠放在一起，则四边形ABCD为；两张纸条互相垂直时，四边形ABCD为；若两张纸条的宽度相同，则四边形ABCD为．三、解答题35．如图1中的矩形ABCD，沿对角线AC剪开，再把△ABC沿着AD方向平行移动，得到图2．在图2中，△ADC≌△C′BA′，AC∥A′C′，A′B∥DC．除△DAC与△C′BA′外，指出有哪几对全等的三角形（不能添加辅助线和字母）？选择其中一对加以证明．36．如图，在▱ABCD的纸片中，AC⊥AB，AC与BD相交于点O，将△ABC沿对角线AC 翻转180°，得到△AB′C．（1）以A，C，D，B′为顶点的四边形是矩形吗（请填“是”、“不是”或“不能确定”）；=cm2．（2）若四边形ABCD的面积S=12cm2，求翻转后纸片重叠部分的面积，即S△ACE37．如图，四边形ABCD中，∠ABC=∠ADC=90°，M、N分别是AC、BD的中点，那么MN⊥BD成立吗？试说明理由．38．如图所示，两个全等菱形的边长为1厘米，一只蚂蚁由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动，行走2010厘米后停下，则这只蚂蚁停在点．39．如图，在平行四边形ABCD中，O是对角线AC的中点，过点O作AC的垂线与边AD、BC分别交于E、F．求证：四边形AFCE是菱形．特殊的四边形（矩形、菱形）参考答案与试题解析一、选择题1．如图，点P是矩形ABCD的边AD上的一个动点，矩形的两条边AB、BC的长分别为3和4，那么点P到矩形的两条对角线AC和BD的距离之和是（）A．B．C．D．不确定【考点】矩形的性质；相似三角形的判定与性质．【专题】压轴题；动点型．【分析】过P点作PE⊥AC，PF⊥BD，由矩形的性质可证△PEA∽△CDA和△PFD∽△BAD，根据和，即和，两式相加得PE+PF=，即为点P到矩形的两条对角线AC和BD的距离之和．【解答】解：法1：过P点作PE⊥AC，PF⊥BD∵矩形ABCD∴AD⊥CD∴△PEA∽△CDA∴∵AC=BD==5∴…①同理：△PFD∽△BAD∴∴…②∴①+②得：∴PE +PF=即点P 到矩形的两条对角线AC 和BD 的距离之和是．法2：连结OP ． ∵AD=4，CD=3， ∴AC==5，又∵矩形的对角线相等且互相平分， ∴AO=OD=2.5cm ，∴S △APO +S △POD =×2.5•PE +×2.5•PF=×2.5（PE +PF ）=×3×4， ∴PE +PF=．故选：A ．【点评】根据矩形的性质，结合相似三角形求解．2．若矩形的一条对角线与一边的夹角是40°，则两条对角线相交所成的锐角是（）A ．20°B ．40°C ．80°D ．100° 【考点】矩形的性质．【专题】计算题．【分析】根据矩形的性质，得△BOC 是等腰三角形，再由等腰三角形的性质进行答题．【解答】解：图形中∠1=40°，∵矩形的性质对角线相等且互相平分，∴OB=OC，∴△BOC是等腰三角形，∴∠OBC=∠1，则∠AOB=2∠1=80°．故选C．【点评】本题主要考查了矩形的性质，对角线相等且互相平分，矩形被对角线分成四个等腰三角形．3．如图，矩形ABCD中，AB=8，BC=6，E、F是AC上的三等分点，则S△BEF为（）A．8 B．12 C．16 D．24【考点】矩形的性质．【专题】压轴题．【分析】要求S△BEF只要求出底边EF以及EF边上的高就可以，高可以根据△ABC的面积得到，EF=AC，根据勾股定理得到AC，就可以求出EF的长，从而求出△EFG的面积．【解答】解：S△ABC=×8×6=24．又E、F是AC上的三等分点．∴S△BEF =S△ABC=8．故选A．【点评】本题运用了勾股定理，已知直角三角形的两直角边，求斜边上的高，这类题的解决方法是需要熟记的内容．4．把一张长方形的纸片按如图所示的方式折叠，EM 、FM 为折痕，折叠后的C 点落在B′M 或B′M 的延长线上，那么∠EMF 的度数是（）A ．85°B ．90°C ．95°D ．100°【考点】翻折变换（折叠问题）．【分析】根据折叠的性质：对应角相等，对应的线段相等，可得．【解答】解：根据图形，可得：∠EMB′=∠EMB ，∠FMB′=∠FMC ，∵∠FMC +∠FMB′+∠EMB′+∠BME=180°，∴2（∠EMB′+∠FMB′）=180°，∵∠EMB′+∠FMB′=∠FME ，∴∠EMF=90°．故选B ．【点评】本题通过折叠变换考查学生的逻辑思维能力，解决此类问题，应结合题意，最好实际操作图形的折叠，易于找到图形间的关系．5．如图，在矩形ABCD 中，EF ∥AB ，GH ∥BC ，EF 、GH 的交点P 在BD 上，图中面积相等的四边形有（）A ．3对B ．4对C ．5对D ．6对【考点】矩形的性质．【专题】压轴题．【分析】本题考查了矩形的性质，得出△EPD ≌△HDP ，则S △EPD =S △HDP ，通过对各图形的拼凑，得到的结论．【解答】解：在矩形ABCD 中，∵EF ∥AB ，AB ∥DC ，∴EF ∥DC ，则EP ∥DH ；故∠PED=∠DHP ；同理∠DPH=∠PDE ；又PD=DP ；所以△EPD ≌△HDP ；则S △EPD =S △HDP ；同理，S △GBP =S △FPB ；则（1）S 梯形BPHC =S △BDC ﹣S △HDP =S △ABD ﹣S △EDP =S 梯形ABPE ；（2）S □AGPE =S 梯形ABPE ﹣S △GBP =S 梯形BPHC ﹣S △FPB =S □FPHC ；（3）S 梯形FPDC =S □FPHC +S △HDP =S □AGPE +S △EDP =S 梯形GPDA ；（4）S □AGHD =S □AGPE +S □HDPE =S □PFCH +S □PHDE =S □EFCD ；（5）S □ABFE =S □AGPE +S □GBFP =S □PFCH +S□GBFP =S □GBCH故选C ．【点评】本题是一道结论开放题，掌握矩形的性质，很容易得到答案．6．如图，矩形ABCD 的周长为68，它被分成7个全等的矩形，则矩形ABCD 的面积为（）A ．98B ．196C ．280D ．284【考点】矩形的性质．【专题】计算题．【分析】等量关系为：5个小矩形的宽等于2个小矩形的长；6个小矩形的宽加一个小矩形的长等于大长方形周长的一半．【解答】解：设小矩形宽为x ，长为y ．则大矩形长为5x 或2y ，宽为x +y ．依题意有x +y +5x==34；5x=2y ．解得：x=4，y=10．则大矩形长为20，宽为14．所以大矩形面积为280．故选C ．【点评】本题考查了矩形的面积和一种很重要的思想：方程思想．7．如图，点O是矩形ABCD的中心，E是AB上的点，沿CE折叠后，点B恰好与点O 重合，若BC=3，则折痕CE的长为（）A．B．C．D．6【考点】翻折变换（折叠问题）；勾股定理．【分析】先根据图形翻折变换的性质求出AC的长，再由勾股定理及等腰三角形的判定定理即可得出结论．【解答】解：∵△CEO是△CEB翻折而成，∴BC=OC，BE=OE，∠B=∠COE=90°，∴EO⊥AC，∵O是矩形ABCD的中心，∴OE是AC的垂直平分线，AC=2BC=2×3=6，∴AE=CE，在Rt△ABC中，AC2=AB2+BC2，即62=AB2+32，解得AB=3，在Rt△AOE中，设OE=x，则AE=3﹣x，AE2=AO2+OE2，即（3﹣x）2=32+x2，解得x=，∴AE=EC=3﹣=2．故选：A．【点评】本题考查的是翻折变换，熟知折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等的知识是解答此题的关键．8．如图所示，把一长方形纸片沿MN折叠后，点D，C分别落在D′，C′的位置．若∠AMD′=36°，则∠NFD′等于（）A．144°B．126°C．108° D．72°【考点】翻折变换（折叠问题）；矩形的性质．【专题】计算题．【分析】根据∠AMD′=36°和折叠的性质，得∠NMD=∠NMD′=72°；根据平行线的性质，得∠BNM=∠NMD=72°；根据折叠的性质，得∠D′=∠D=90°；根据四边形的内角和定理即可求得∠NFD′的值．【解答】解：∵∠AMD′=36°，∴∠NMD=∠NMD′=72°．∵AD∥BC，∴∠BNM=∠NMD=72°．又∵∠D′=∠D=90°，∴∠NFD′=360°﹣72°×2﹣90°=126°．故选B．【点评】此题综合运用了折叠的性质、平行线的性质、四边形的内角和定理．9．将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB=3，则BC的长为（）A．1 B．2 C．D．【考点】菱形的性质；勾股定理．【专题】计算题．【分析】根据题意可知，AC=2BC，∠B=90°，所以根据勾股定理可知AC2=AB2+BC2，即（2BC）2=32+BC2，从而可求得BC的长．【解答】解：∵AC=2BC，∠B=90°，∴AC2=AB2+BC2，∴（2BC）2=32+BC2，∴BC=．故选：D．【点评】此题主要考查学生对菱形的性质及勾股定理的理解及运用．10．如图，已知矩形纸片ABCD，点E是AB的中点，点G是BC上的一点，∠BEG＞60°．现沿直线EG将纸片折叠，使点B落在纸片上的点H处，连接AH，则与∠BEG相等的角的个数为（）A．4 B．3 C．2 D．1【考点】翻折变换（折叠问题）．【分析】连BH，根据折叠的性质得到∠1=∠2，EB=EH，BH⊥EG，则∠EBH=∠EHB，又点E是AB的中点，得EH=EB=EA，于是判断△AHB为直角三角形，且∠3=∠4，根据等角的余角相等得到∠1=∠3，因此有∠1=∠2=∠3=∠4．【解答】解：连BH，如图，∵沿直线EG将纸片折叠，使点B落在纸片上的点H处，∴∠1=∠2，EB=EH，BH⊥EG，而∠1＞60°，∴∠1≠∠AEH，∵EB=EH，∴∠EBH=∠EHB，又∵点E是AB的中点，∴EH=EB=EA，∴△AHB为直角三角形，∠AHB=90°，∠3=∠4，∴∠1=∠3，∴∠1=∠2=∠3=∠4．故选B．【点评】本题考查了折叠的性质：折叠前后的两个图形全等，即对应角相等，对应线段相等．也考查了若三角形一边上的中线等于这边的一半，则此三角形为直角三角形．11．如图，在矩形ABCD中，AB=12cm，BC=6cm，点E、F分别在AB、CD上，将矩形ABCD沿EF折叠，使点A、D分别落在矩形ABCD外部的点A′、D′处，则整个阴影部分图形的周长为（）A．18cm B．36cm C．40cm D．72cm【考点】翻折变换（折叠问题）．【专题】压轴题．【分析】延长A1E交CD于点G，由题意知GE=EH，FH=GF，则阴影部分的周长与原矩形的周长相等．【解答】解：延长A1E交CD于点G，由题意知，GE=EH，FH=GF，四边形EHD1A1≌四边形EGDA，∴AD=A1D1，AE=A1E，DG=D1H，FH=FG，∴阴影部分的周长=矩形的周长=（12+6）×2=36cm．故选：B．【点评】本题利用了翻折的性质：对应图形全等，对应边相等．12．下列识别图形不正确的是（）A．有一个角是直角的平行四边形是矩形B．有三个角是直角的四边形是矩形C．对角线相等的四边形是矩形D．对角线互相平分且相等的四边形是矩形【考点】矩形的判定．【专题】证明题．【分析】矩形的判定定理有：（1）有一个角是直角的平行四边形是矩形．（2）有三个角是直角的四边形是矩形．（3）对角线互相平分且相等的四边形是矩形，据此判定．【解答】解：A、有一个角是直角的平行四边形是矩形，正确；B、有三个角是直角的四边形是矩形，正确；C、对角线相等的四边形不一定是矩形，对角线相等的平行四边形才是矩形，错误；D、对角线互相平分且相等的四边形是矩形，正确．故选C．【点评】本题主要考查的是矩形的判定定理．（1）有一个角是直角的平行四边形是矩形．（2）有三个角是直角的四边形是矩形．（3）对角线互相平分且相等的四边形是矩形，据此判定．13．四边形ABCD的对角线相交于点O，下列条件不能判定它是矩形的是（）A．AB=CD，AB∥CD，∠BAD=90°B．AO=CO，BO=DO，AC=BDC．∠BAD=∠ABC=90°，∠BCD+∠ADC=180°D．∠BAD=∠BCD，∠ABC=∠ADC=90°【考点】矩形的判定．【分析】矩形的判定定理有：（1）有一个角是直角的平行四边形是矩形．（2）有三个角是直角的四边形是矩形．（3）对角线互相平分且相等的四边形是矩形．据此判断．【解答】解：A、一个角为直角的平行四边形为矩形，故A正确．B、矩形的对角线平分且相等，故B正确．C、∠BCD+∠ADC=180°，但∠BCD不一定与∠ADC相等，根据矩形的判定定理，故C不正确．D、因为∠BAD=∠BCD，故AB∥CD，又因为，∠ABC=∠ADC=90°，根据矩形的判定（有一个角是直角的平行四边形是矩形），故D正确．故选C．【点评】本题考查的是矩形的判定定理，但考生应注意的是由矩形的判定引申出来的各图形的判定．难度一般．14．直角三角形中，两条直角边边长分别为12和5，则斜边中线的长是（）A．26 B．13 C．30 D．6.5【考点】勾股定理；直角三角形斜边上的中线．【分析】由勾股定理可以求出斜边，再根据直角三角形中斜边上的中线等于斜边的一半可以求出斜边中线的长．【解答】解：由勾股定理知，斜边c==13，∵直角三角形中斜边上的中线等于斜边的一半知，∴斜边中线的长=×13=6.5．故选D．【点评】本题考查了勾股定理和直角三角形的性质：斜边上的中线等于斜边的一半．15．将一个矩形的纸对折两次，沿图中虚线将一角剪掉再打开后，得到的图形为（）A．B．C．D．【考点】剪纸问题．【分析】根据题意知，对折实际上就是对称，对折两次的话，剪下应有4条边，并且这4条边还相等，从而可以得到剪下的图形展开后一定是菱形．【解答】解：根据题意折叠剪图可得，剪下的四边形四条边相等，根据四边形等的四边形是菱形可得剪下的图形是菱形，故选：A．【点评】此题考查了剪纸问题，关键是掌握菱形的判定方法：四边形等的四边形是菱形．16．菱形一条对角线长为8m，周长为20m，则其面积为（）A．40m2B．20m2C．48m2D．24m2【考点】菱形的性质．【专题】几何图形问题．【分析】菱形对角线互相垂直平分，所以OA2+OB2=AB2，根据已知可得AB=5，BO=4，利用勾股定理求得AO，即可求得AC的长，根据AC、BD即可求菱形ABCD的面积，即可解题．【解答】解：根据题意可得：BD=8m，则BO=DO=4m，∵菱形周长为20m，∴AB=5m，∵菱形对角线互相垂直平分，∴OA2+OB2=AB2，∴AO==3（m），∴AC=6（m），故菱形的面积S=×6×8=24（m2）．故选D．．【点评】本题考查了菱形对角线互相垂直平分的性质，菱形面积的计算，本题中根据勾股定理求AO的值是解题的关键．17．用直尺和圆规作一个菱形，如图，能得到四边形ABCD是菱形的依据是（）A．一组邻边相等的四边形是菱形B．四边相等的四边形是菱形C．对角线互相垂直的平行四边形是菱形D．每条对角线平分一组对角的平行四边形是菱形【考点】菱形的判定；作图—复杂作图．【分析】关键菱形的判定定理（有四边都相等的四边形是菱形）判断即可．【解答】解：由图形作法可知：AD=AB=DC=BC，∴四边形ABCD是菱形，故选：B．【点评】本题主要考查对作图﹣复杂作图，菱形的判定等知识点的理解和掌握，能熟练地运用性质进行推理是解此题的关键．18．已知DE∥AC、DF∥AB，添加下列条件后，不能判断四边形DEAF为菱形的是（）A．AD平分∠BAC B．AB=AC且BD=CD C．AD为中线D．EF⊥AD【考点】菱形的判定．【专题】几何图形问题．【分析】首先根据题意画出图形，然后由DE∥AC、DF∥AB，判定四边形DEAF为平行四边形，再由菱形的判定定理求解即可求得答案；注意掌握排除法在选择题中的应用．【解答】解：如图，∵DE∥AC、DF∥AB，∴四边形DEAF为平行四边形，A、∵AD平分∠BAC，DF∥AB，∴∠BAD=∠CAD，∠BAD=∠ADF，∴∠CAD=∠ADF，∴AF=DF，∴四边形DEAF为菱形；B、∵AB=AC且BD=CD，∴AD平分∠BAC，同理可得：四边形DEAF为菱形；C、∵由AD为中线，得不到AD平分∠BAC，证不出四边形DEAF的邻边相等，∴不能判断四边形DEAF为菱形；D、∵AD⊥EF，∴▱DEAF是菱形．故选C．【点评】此题考查了菱形的判定．此题难度不大，注意掌握数形结合思想的应用．二、填空题19．矩形ABCD中，对角线AC=10cm，AB：BC=3：4，则它的周长是28cm．【考点】矩形的性质；勾股定理．【专题】计算题．【分析】根据矩形的一组邻边和一条对角线组成一个直角三角形，解题即可．【解答】解：根据矩形的性质得到△ABC是直角三角形，因为对角线AC=10cm，AB：BC=3：4，根据勾股定理得到BC2=AC2﹣（BC）2=100﹣BC2解得BC=8，AB=6，故它的周长=2×8+2×6=28cm．故答案为28．【点评】本题考查对矩形的性质以及勾股定理的运用．20．矩形ABCD的两条对角线相交于点O，如果矩形的周长是34cm，又△AOB的周长比△ABC的周长少7cm，则AB=10cm，BC=7cm．【考点】矩形的性质；勾股定理．【专题】计算题．【分析】根据矩形的对边相等以及所给的三角形的周长可得到和所求线段相关的两个式子，进而求解．【解答】解：设AB=a，BC=b．∴2OA=2OB=AC=，2a+2b=34，即a+b=17．由题意可知△AOB的周长+7=△ABC的周长．∴AB+OA+OB+7=AB+BC+AC．∴a++7=a+b+．即b=7，a=17﹣7=10．即AB=10，BC=7．故答案为，10，7．【点评】本题综合考查了矩形的性质及勾股定理的运用．21．在矩形ABCD中，对角线AC、BD相交于点O，若∠AOB=110°，则∠OAB=35度．【考点】矩形的性质；三角形内角和定理．【专题】计算题．【分析】根据矩形对角线的性质得到△OAB的形状，进而求得底角的度数．【解答】解：∵矩形的对角线相等且互相平分．∴OA=OC．∴△AOB是等腰三角形．∴∠OAB=∠OBA．∵∠OAB+∠OBA+∠AOB=180°．∴2∠OAB+110°=180°．∴∠OAB=35°．故答案为35．【点评】本题考查矩形的性质以及三角形内角和定理．22．如图所示，把两个大小完全一样的矩形拼成“L”形图案，则∠FAC=90度，∠FCA= 45度．【考点】矩形的性质；全等三角形的判定与性质．【专题】计算题．【分析】两个大小完全一样的矩形拼成“L”形图案所构成的△AFG≌△CAB，所以AF=AC，∠FAC=90°，∠FCA=45度．【解答】解：由已知△AFG≌△CAB，∴∠AFG=∠CAB，AF=AC∵∠AFG+∠FAG=90°，∴∠CAB+∠FAG=90°，∴∠FAC=90°．又∵AF=AC，∴∠FCA=（180°﹣90°）×=45°．故答案为：90；45．【点评】根据矩形的性质得到全等三角形，进而求得△AFC是等腰直角三角形．23．如图，在矩形ABCD中，点E是BC上一点，AE=AD，DF⊥AE，垂足为F，线段DF 与图中的哪一条线段相等？先将猜想出的结论填写在下面的横线上，然后再加以证明．即DF=BE．（写出一条线段即可）【考点】矩形的性质；全等三角形的判定与性质．【专题】几何图形问题．【分析】根据矩形的性质得出AD∥BC，推出∠AFD=∠B，推出∠DAF=∠AEB，根据全等三角形的判定推出△AFD≌△EBA即可．【解答】解：DF=BE，理由是：∵四边形ABCD是矩形，DF⊥AE，∴∠B=∠AFD=90°，AD∥BC，∴∠DAF=∠AEB，在△AFD和△EBA中∴△AFD≌△EBA（AAS），∴DF=BE，故答案为：DF=BE．【点评】本题考查了全等三角形的性质和判定，平行线的性质，全等三角形的性质和判定的应用，关键是推出△AFD≌△EBA，注意：矩形的四个角都是直角，矩形的对边平行．24．将矩形ABCD沿AE折叠，得到如图所示图形．若∠CED′=56°，则∠AED的大小是62°．【考点】翻折变换（折叠问题）．【专题】压轴题；操作型．【分析】易得∠DED′的度数，除以2即为所求角的度数．【解答】解：∵∠CED′=56°，∴∠DED′=180°﹣56°=124°，∵∠AED=∠AED′，∴∠AED=∠DED′=62°．故答案为：62．【点评】考查翻折变换问题；用到的知识点为：翻折前后得到的角相等．25．菱形ABCD的周长为36，其相邻两内角的度数比为1：5，则此菱形的面积为40.5．【考点】菱形的性质．【分析】根据相邻两内角的度数比为1：5，可求出一个30°角，根据周长为36，求出菱形的边长，根据直角三角形里30°角的性质求出高，从而求出面积．【解答】解：作AE⊥BC于E点，∵其相邻两内角的度数比为1：5，∴∠B=180°×=30°，∵菱形ABCD的周长为36，∴AB=BC=×36=9．∴AE=×9=．∴菱形的面积为：BC•AE=9×=40.5．故答案为：40.5．【点评】本题考查菱形的性质，菱形的邻角互补，四边相等．26．已知菱形的两条对角线长为6cm和8cm，菱形的周长是20cm，面积是24cm2．【考点】菱形的性质；勾股定理．【分析】根据菱形的面积等于两对角线乘积的一半可得到其面积，根据菱形的性质可求得其边长，从而可得到其周长．【解答】解：如图，四边形ABCD是菱形，BD，AC分别是其对角线且BD=6，AC=8，求其面积和周长．∵四边形ABCD是菱形，BD，AC分别是其对角线，∴BD⊥AC，BO=OD=3cm，AO=CO=4cm，∴AB=5cm，∴菱形的周长=5×4=20cm；S菱形=×6×8=24cm2．故本题答案为：20cm；24cm2．【点评】此题主要考查学生对菱形的性质及勾股定理的理解及运用．27．如图，四边形ABCD中，E，F，G，H分别是边AB，BC，CD，DA的中点．请你添加一个条件，使四边形EFGH为矩形，应添加的条件是AC⊥BD．【考点】中点四边形．【分析】根据三角形的中位线定理，可以证明所得四边形的两组对边分别和两条对角线平行，所得四边形的两组对边分别是两条对角线的一半，再根据平行四边形的判定就可证明该四边形是一个平行四边形；所得四边形要成为矩形，则需有一个角是直角，故对角线应满足互相垂直．【解答】解：如图，∵E，F分别是边AB，BC的中点，∴EF∥AC，EF=AC，同理HG∥AC，HG=AC，∴EF∥HG，EF=HG，∴四边形EFGH是平行四边形；要使四边形EFGH是矩形，则需EF⊥FG，即AC⊥BD；故答案为：AC⊥BD．【点评】此题主要考查了三角形的中位线定理的运用．同时熟记此题中的结论：顺次连接四边形各边中点所得四边形是平行四边形；顺次连接对角线互相垂直的四边形各边中点所得四边形是矩形．28．已知菱形的两条对角线的长分别是4cm和8cm，则它的边长为2cm．【考点】菱形的性质．【专题】计算题．【分析】根据菱形的性质及勾股定理即可求得其边长的值．【解答】解：菱形的两条对角线分别是4cm，8cm，得到两条对角线相交所构成的直角三角形的两直角边是×4=2和×8=4，那么根据勾股定理得到它的斜边即菱形的边长=2cm．故答案为2【点评】本题考查菱形的性质以及勾股定理．29．若四边形ABCD是平行四边形，使四边形ABCD是菱形，请补充条件此题答案不唯一，如AC⊥BD或AB=AD等（写一个即可）．【考点】菱形的判定．【专题】开放型．【分析】由四边形ABCD是平行四边形，根据菱形的判定定理求解即可求得答案．【解答】解：∵四边形ABCD是平行四边形，∴当AC⊥BD或AB=AD时，四边形ABCD是菱形．故答案为：此题答案不唯一，如AC⊥BD或AB=AD等．【点评】此题考查了菱形的判定．此题难度不大，注意熟记定理是解此题的关键．30．已知菱形ABCD的边长为6，∠A=60°，如果点P是菱形内一点，且PB=PD=2，那么AP的长为或．【考点】菱形的性质．【专题】压轴题；分类讨论．【分析】根据题意得，应分P与A在BD的同侧与异侧两种情况进行讨论．【解答】解：当P与A在BD的异侧时：连接AP交BD于M，∵AD=AB，DP=BP，∴AP⊥BD（到线段两端距离相等的点在垂直平分线上），在直角△ABM中，∠BAM=30°，∴AM=AB•cos30°=3，BM=AB•sin30°=3，∴PM==，∴AP=AM+PM=4；当P与A在BD的同侧时：连接AP并延长AP交BD于点MAP=AM﹣PM=2；当P与M重合时，PD=PB=3，与PB=PD=2矛盾，舍去．AP的长为4或2．故答案为4或2．【点评】本题注意到应分两种情况讨论，并且注意两种情况都存在关系AP⊥BD，这是解决本题的关键．31．已知四边形ABCD为菱形，∠BAD=60°，E为AD中点，AB=6cm，P为AC上任一点．求PE+PD的最小值是3．【考点】轴对称﹣最短路线问题；菱形的性质．【专题】几何图形问题．【分析】根据菱形的性质，可得AC是BD的垂直平分线，可得AC上的点到D、B点的距离相等，连接BE交AC与P，可得答案．【解答】解：∵菱形的性质，∴AC是BD的垂直平分线，AC上的点到B、D的距离相等．连接BE交AC于P点，PD=PB，PE+PD=PE+PB=BE，在Rt△ABE中，由勾股定理得BE==3，故答案为：3．【点评】本题考查了轴对称，对称轴上的点到线段两端点的距离相等是解题关键．32．如图，在菱形ABCD中，对角线AC=6，BD=8，点E、F分别是边AB、BC的中点，点P在AC上运动，在运动过程中，存在PE+PF的最小值，则这个最小值是5．【考点】轴对称﹣最短路线问题；勾股定理；菱形的性质．【专题】计算题．【分析】AC交BD于O，作E关于AC的对称点N，连接NF，交AC于P，则此时EP+FP 的值最小，根据菱形的性质推出N是AD中点，P与O重合，推出PE+PF=NF=AB，根据勾股定理求出AB的长即可．【解答】解：AC交BD于O，作E关于AC的对称点N，连接NF，交AC于P，则此时EP+FP的值最小，∴PN=PE，∵四边形ABCD是菱形，∴∠DAB=∠BCD，AD=AB=BC=CD，OA=OC，OB=OD，AD∥BC，∵E为AB的中点，∴N在AD上，且N为AD的中点，∵AD∥CB，。

2019届中考数学复习第五章四边形52特殊平行四边形练习.docx

特殊平行四边形命题点1矩形的性质与判定（8年1考）命题解读：题型为选择题，分值为3分。

考查利用•矩形的性质求线段的长。

1. （2017 •陕西中考）如图，在矩形ABCD 中，AB 二2., BC 二3。

若E 是边CD 的中点，连接AE, 过点B 作BF 丄AE 交AE 于点F,则BF 的长为（）2. （2018 •某高新一屮模拟）如图，在矩形ABCD 屮，AD 二5, AB 二3, E 是BC 上一点，且AE二AD, 过点D 作DF 丄AE 于点F,则tan ZCDF 的值为（） 1)・命题点2菱形的性质与判定（8年5考）命题解读：题型为选择题或填空题，分值均为3分，考查形式有：（1）利用菱形的性质判断所给结论的正确•性；（2）利用菱形的性质求线段的长、线段的比值、两点间的最小距离；（3）利用菱形的性质求角度。

3. （2012 •陕西中考）如图，在菱形ABCD 中,对角线AC 与BD 相交于点0, 0E 丄AB,垂足为E,若ZADC=130° ,则ZAOE 的大小为（） A. 75° B. 65° C. 55° D. 50°4. （2014 •陕西中考）如图，在菱形ABCD 中，AB 二5,对角线AC 二6。

若过点A 作AE 丄BC,垂足为E,则AE 的长为（）1224 A. 4 B.—— C. — D. 55 5 5. （2013 •陕西中考）如图，在矩形ABCD 中，AD 二2AB,点M, N 分别在边AD, BC 上，连接 BM, DNo 若四边形MBND 是菱形，则如等于（）MD B 3,/To第1题图DC E第2题图第3题图6. （2.018 •陕西，中考）如图，在菱形ABCD 中，E, F, G, H 分别是边AB, BC, CD 和D.A 的中点，连接EF, FG, GH 和HE 。

若EII 二2EF,则下列结论正确的是（）B F C第6题图A. AB-V2EF 二巧 E”F C. AB 二2EF D.AB 二石 EF7. （2016 •陕西中考）如图，在菱形ABCD 中，ZABC=60° , AB=2, P 是这个菱形内部或边上的一点，若以点P, B,・C 为顶点的三角形是等腰三角形，则P, D （P, D 两点不重合）两点间的最短距.离为。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2019年中考数学总复习【特殊的平行四边形】专项精练题一、选择题1.(2018·上海)已知ABCD Y ，下列条件中，不能判定这个平行四边形为矩形的是()A.A B ∠=∠B.A C ∠=∠C.AC BD =D.AB BC⊥2.(2018.杭州)如图，P 是矩形ABCD 内一点(不含边界)，设1PAD θ∠=，2PBA θ∠=，3PCB θ∠=，4PDC θ∠=.若80APB ∠=︒，50CPD ∠=︒，则()A.1423()()30θθθθ+-+=︒B.2413()()40θθθθ+-+=︒C.1234()()70θθθθ+-+=︒D.1234()()180θθθθ+++=︒3.(2018·遵义)如图，P 是矩形ABCD 的对角线AC 上一点，过点P 作//EF BC ，分别交,AB CD 于点,E F ，连接,PB PD .若2,8AE PF ==，则图中涂色部分的面积为()A.10B.12C.16D.184.(2018·威海)矩形ABCD 与矩形CEFG 如图放置，点,,B C E 共线，点,,C D G 共线，连接AF ，取AF 的中点H ，连接GH .若2,1BC EF CD CE ====，则GH 的长为()A.1B.23 C.22 D.525.(2018·十堰)菱形不具备的性质是()A.四条边都相等B.对角线一定相等C.是轴对称图形D.是中心对称图形6.(2018·淮安)如图，菱形ABCD 的对角线,AC BD 的长分别为6和8，则这个菱形的周长是()A.20 B.24 C.40 D.487.(2018·大连)如图，在菱形ABCD 中，对角线,AC BD 相交于点O .若5,6AB AC ==，则BD 的长是()A.8 B.7 C.4 D.38.(2018·舟山)用尺规在一个平行四边形内作菱形ABCD ，下列作法中错误的是()9.(2018·宿迁)如图，菱形ABCD 的对角线,AC BD 相交于点O ，E 为边CD 的中点.若菱形ABCD 的周长为16，60BAD ∠=︒，则OCE ∆的面积是()10.(2018·湘西州)下列说法:①对顶角相等;②两直线平行，同旁内角相等;③对角线互相垂直的四边形为菱形;④对角线互相垂直平分且相等的四边形为正方形.其中正确的有()A.1个B.2个C.3个D.4个11.(2018·宜昌)如图，正方形ABCD 的边长为1，,E F 分别是对角线AC 上的两点，EG AB ⊥，EI AD ⊥，FH AB ⊥，FJ AD ⊥，垂足分别为,,,G I H J ，则图中涂色部分的面积为()A.1 B.12 C.13 D.1412.(2018·河南)如图①，点F 从菱形ABCD 的顶点A 出发，沿A D B →→以1cm/s 的速度匀速运动到点B ，图②是点F 运动时，FBC ∆的面积y (cm 2)随时间x (s)变化的图象，则a 的值为() A.5 B.2 C.52 D.25二、填空题13.(2018·株洲)如图，矩形ABCD 的对角线AC 与BD 相交点O ，10,,AC P Q =分别为,AO AD 的中点，则PQ 的长度为.14.(2018·成都)如图，在矩形ABCD 中，按以下步骤作图:①分别以点A 和C 为圆心，以大于12AC 的长为半径作弧，两弧相交于点M 和N ;②作直线MN 交CD 于点E .若2,3DE CE ==，则矩形的对角线AC 的长为.15.(2018·徐州)若菱形两条对角线的长分别是6cm 和8cm ，则其面积为cm 2.16.(2018·广州)如图，若菱形ABCD 的顶点,A B 的坐标分别为(3,0)，(2,0)-，点D 在y 轴上，则点C 的坐标是.17.(2018·葫芦岛)如图，在菱形OABC 中，点B 在x 轴上，点A 的坐标为(2,3)，则点C 的坐标为.18.(2018·黔西南州)已知一个菱形的边长为2，较长的对角线长为23，则这个菱形的面积是.19.(2018·双鸭山)如图，在ABCD Y 中，添加一个条件，使ABCD Y 是菱形.20.(2018·南通)如图，在ABC ∆中，,AD CD 分别平分BAC ∠和ACB ∠，//AE CD ，//CE AD .若从三个条件:①AB AC =;②AB BC =;③AC BC =中选择一个作为已知条件，则能使四边形ADCE 为菱形的是.(填序号)21.(2018·随州)如图，在平面直角坐标系xOy 中，菱形OABC 的边长为2，点A 在第一象限，点C 在x 轴正半轴上，60AOC ∠=︒.若将菱形OABC 绕点O 顺时针旋转75º，得到四边形'''OA B C ，则点B 的对应点'B 的坐标为.22.(2018·荆门)如图，在平面直角坐标系xOy 中，函数(0,0)k y k x x=>>的图象经过菱形OACD 的顶点D 和边AC 的中点E .若菱形OACD 的边长为1，则k 的值为.23.(2018·镇江)如图，点,,E F G 分别在菱形ABCD 的边,,AB BC AD 上，13AE AB =，13CF CB =，13AG AD =.已知EFG ∆的面积等于6，则菱形ABCD 的面积等于.24.(2018·乐山)如图，四边形ABCD 是正方形，延长AB 到点E ，使AE AC =，连接CE ，则BCE∠的度数是.25.(2018·咸宁)如图，将正方形OEFG 放在平面直角坐标系中，O 是坐标原点，点E 的坐标为(2,3)，则点F 的坐标为.26.(2018·上海)对于一个位置确定的图形，如果它的所有点都在一个水平放置的矩形内部或边上，且该图形与矩形的每条边都至少有一个公共点(如图①)，那么这个矩形水平方向的边长称为该图形的宽，铅垂方向的边长称为该矩形的高.如图②，菱形ABCD 的边长为1，边AB 水平放置.如果该菱形的高是宽的23，那么它的宽的值是.27.(2018·武汉)以正方形ABCD 的边AD 作等边三角形ADE ，则BEC ∠的度数是.28.(2018·青岛)如图，正方形ABCD 的边长为5，点,E F 分别在,AD DC 上，AE DF =2=，BE 与AF 相交于点,G H 为BF 的中点，连接GH ，则GH 的长为.29.(2018·呼和浩特)如图，在正方形ABCD 中，M 是边BA 延长线上的动点(不与点A 重合)，且AM AB <，CBE ∆由DAM ∆平移得到.若过点E 作EH AC ⊥，H 为垂足，则有以下结论:①点M 位置变化，使得60DHC ∠=︒时，2BE DM =;②无论点M 运动到何处，都有2DM HM =;③无论点M 运动到何处，CHM ∠一定大于135º.其中正确的结论为.(填序号)30.(2018·江西)在正方形ABCD 中，6AB =，连接,,AC BD P 是正方形边上或对角线上一点.若2PD AP =，则AP 的长为.三、解答题31.(2018·湘西州)如图，在矩形ABCD 中，E 是AB 的中点，连接,DE CE .(1)求证:ADE BCE ∆≅∆;(2)若6,4AB AD ==，求CDE ∆的周长.32.(2018连云港)如图，在矩形ABCD 中，E 是AD 的中点，延长,CE BA 交于点F ，连接,AC DF .(1)求证:四边形ACDF 是平行四边形;(2)当CF 平分BCD ∠时，写出BC 与CD 的数量关系，并说明理由.33.(2018·河南)如图，反比例函数(0)k y x x =>的图象过格点(网格线的交点)P .(1)反比例函数的解析式为.(2)在图中用直尺和2B 铅笔画出两个矩形(不写画法)，要求每个矩形均需满足下面两个条件:①四个顶点均在格点上.且其中两个顶点分别是,O P ;③矩形的面积等于k 的值.34.(2018·青岛)如图，四边形ABCD 是平行四边形，对角线AC 与BD 相交于点,E G 为AD 的中点，连接,CG CG 的延长线交BA 的延长线于点F ，连接FD .(1)求证:AB AF =;(2)若AG AB =，120BCD ∠=︒，判断四边形ACDF 的形状，并证明你的结论.35.(2018·广东)如图，BD 是菱形ABCD 的对角线，75CBD ∠=︒.(1)请用尺规作图法，作AB 的垂直平分线EF ，垂是为E ，交AD 于点F ;(不要求写作法，保留作图痕迹)(2)在(1)的条件下，连接BF ，求DBF ∠的度数.36.(2018·娄底)如图，在四边形ABCD 中，对角线,AC BD 相交于点O ，且,OA OC OB OD ==，过点O 作EF BD ⊥，分别交,AD BC 于点,E F .(1)求证:AOE COF ∆≅∆;(2)判断四边形BEDF 的形状，并说明理由.37.(2018·南京)如图，在四边形ABCD 中，BC CD =，2C BAD ∠=∠.O 是四边形ABCD 内一点，且OA OB OD ==.求证:(1)BOD C ∠=∠;(2)四边形ABCD 是菱形.38.(2018·乌鲁木齐)如图，在四边形ABCD 中，90BAC ∠=︒，E 是BC 的中点，//AD BC ，//AE DC ，EF CD ⊥于点F .(1)求证:四边形AECD 是菱形;(2)若6,10AB BC ==，求EF 的长.39.(2018·广安)如图，四边形ABCD 是正方形，M 为BC 上一点，连接AM ，延长AD 至点E ，使得AE AM =，过点E 作EF AM ⊥，垂足为F ，求证:AB EF =.40.(2018·盐城)如图，在正方形ABCD 中，对角线BD 所在的直线上有两点,E F 满足BE DF =，连接,,,AE AF CE CF .(1)求证:ABE ADF ∆≅∆;(2)试判断四边形AECF 的形状，并说明理由.41.(2018·长春)在正方形ABCD 中，E 是边CD 上一点(点E 不与点,C D 重合)，连接BE .[感知]如图①，过点A 作AF BE ⊥交BC 于点F .易证ABF BCE ∆≅∆.(不需要证明)[探究]如图②，取BE 的中点M ，过点M 作FG BE ⊥交BC 于点F ，交AD 于点G .(1)求证:BE FG =.(2)连接CM ，若1CM =，则FG 的长为.[应用]如图③，取BE 的中点M ，连接CM .过点C 作CG BE ⊥交AD 于点G ，连接,EG MG .若3CM =，则四边形GMCE 的面积为.42.(2018·潍坊)如图，M 是正方形ABCD 边CD 上一点，连接AM ，作DE AM ⊥于点E ，BF AM⊥于点F ，连接BE .(1)求证:AE BF =;(2)已知2AF =，四边形ABED 的面积为24，求EBF ∠的正弦值.43.(2018·吉林)如图①，在ABC ∆中，AB AC =，过AB 上一点D 作//DE AC 交BC 于点E ，以E为顶点，ED 为一边，作DEF A ∠=∠，另一边EF 交AC 于点F .(1)求证:四边形ADEF 为平行四边形;(2)当D 为AB 的中点时，ADEF Y 的形状为;(3)延长图①中的DE 到点G ，使EG DE =，连接,,AE AG FG ，得到图②，若AD AG =，判断四边形AEGF 的形状，并说明理由.44.(2018·绍兴)小敏思考解决如下问题:原题:如图①，点,P Q 分别在菱形ABCD 的边,BC CD 上，PAQ B ∠=∠，求证:AP AQ =.(1)小敏进行探索，将点,P Q 的位置特殊化:把PAQ ∠绕点A 旋转得到EAF ∠，使AE BC ⊥，点,E F 分别在边,BC CD 上，如图②.此时她证明了AE AF =.请你证明.(2)受以上(1)的启发，在原题中，添加辅助线:如图③，作AE BC ⊥，AF CD ⊥，垂足分别为,E F .请你继续完成原题的证明.(3)如果在原题中添加条件:4AB =，60B ∠=︒，如图①，请你编制一个计算题(不标注新的字母)，并直接给出答案.(根据编出的问题层次，给不同的得分)参考答案一、1.B 2.A3.C4.C5.B6.A7.A8.C9.A 10.B 11.B12.C 二、13. 2.514.3015.2416.(5,4)-17.(2,3)-18.2319.答案不唯一，如：AB BC=20.②21.(6,6)-22.2523.2724.22.5º25.(1,5)-26.181327.30º或150º28.34229.①②③30.2或23或142-三、解答题31.(1)点拨：由AD BCA B AE BE=⎧⎪∠=∠⎨⎪=⎩，可得()ADE BCE SAS ∆≅∆.(2)CDE ∆的周长是16.32.(1)点拨：由()FAE CDE ASA ∆≅∆，可得FA CD =.又∵//CD AF ，∴四边形ACDF 是平行四边形.(2)2BC CD=33.(1)反比例函数的解析式为4y x=(2)答案不唯一，如图，矩形OAPB ，矩形OCDP 即为所求作的图形34.(1)点拨：由AGF DGC ∆≅∆，可得AF DC =.∵四边形ABCD 是平行四边形，∴AB CD =，∴AB AF =.(2)四边形ACDF 是矩形点拨：由(1)可知四边形ACDF 是平行四边形.由AGF DGC ∆≅∆，可得2AD AG =，2CF FG =.由AG AB =，120BCD ∠=︒，AB AF =，可得AFG ∆是等边三角形，∴AG FG =，∴AD CF =.∴四边形ACDF 是矩形35.(1)如图所示，直线EF 即为所求(2)45DBF ∠=︒36.(1)点拨：由题意得到四边形ABCD 是平行四边形，∴EAO FCO ∠=∠，又∵OA OC =，OEA COF ∠=∠，∴AOE COF∆≅∆(2)四边形BEDF 是菱形37.(1)如图，延长线段AO 到点E .由题意可得，2BOD BAD ∠=∠.(2)如图，连接OC .证明OBC ODC ∆≅∆.得到12BOC DOC BOD∠=∠=∠，12BCO DCO BCD ∠=∠=∠，∵BOD BCD ∠=∠，∴BOC BCO ∠=∠，∴OB CB =，∴OB CB CD OD ===，∴四边形ABCD 是菱形.38.(1)点拨：AE CE=(2)245EF =39.点拨：EFA ABM∆≅∆40.(1)点拨：AB ADABE ADF BE DF=⎧⎪∠=∠⎨⎪=⎩(2)点拨：连接AC ，交BD 于点O .可知OC OA =，OE OF =，AC EF ⊥，∴四边形AECF 是菱形.41.[探究](1)点拨如图，过点G 作GP BC ⊥于点P .由PGF CBEPG CB FPG ECB∠=∠⎧⎪=⎨⎪∠=∠⎩，得到PGF CBE∆≅∆(2)2[应用]942.(1)点拨：由AFB DEAAB DA ABF DAE∠=∠⎧⎪=⎨⎪∠=∠⎩，可得ABF DAE∆≅∆(2)213sin 13EBF ∠=43.(1)点拨：//AD EF(2)菱形(3)四边形AEGF 是矩形.点拨：//AF EGAF EG AE DG⎧⎪=⎨⎪⊥⎩44.(1)点拨：由AEB AFDAB AD B D∠=∠⎧⎪=⎨⎪∠=∠⎩，得到AEB AFD∆≅∆(2)点拨：由AEP AFQ AE AF EAP FAQ∠=∠⎧⎪=⎨⎪∠=∠⎩，得到AEP AFQ∆≅∆(3)答案不唯一，如：求D ∠的度数.答案：60D ∠=︒.。