初一下数学解方程组练习题
七年级下册50道解二元一次方程组含答案

七年级下册50道解二元一次方程组含答案1、求解方程组:begin{cases} x+y= \\ x-y=2 \end{cases}$$改写为:begin{cases} x+y=a \\ 2x=a+2y \end{cases}$$其中,$a$为待求解的常数。
解得:$x=\frac{a+2}{2}$,$y=\frac{a-2}{2}$,因此方程的解为$(\frac{a+2}{2},\frac{a-2}{2})$。
2、求解方程组:begin{cases} y=2x \\ x+y=3 \end{cases}$$将第一个方程代入第二个方程,得到$3x=3$,解得$x=1$,因此$y=2$,方程的解为$(1,2)$。
3、求解方程组:begin{cases} x-y=6 \\ 2x+31y=-11 \end{cases}$$将第一个方程变形为$x=6+y$,代入第二个方程得到$2(6+y)+31y=-11$,解得$y=-\frac{23}{33}$,因此$x=\frac{55}{33}$,方程的解为$(\frac{55}{33},-\frac{23}{33})$。
4、求解方程组:begin{cases} x+y=1 \\ 3x-y=3 \end{cases}$$将第一个方程变形为$y=1-x$,代入第二个方程得到$3x-(1-x)=3$,解得$x=1$,因此$y=0$,方程的解为$(1,0)$。
5、求解方程组:begin{cases} y=2x-3 \\ 3x+2y=8 \end{cases}$$将第一个方程代入第二个方程,得到$3x+2(2x-3)=8$,解得$x=2$,因此$y=1$,方程的解为$(2,1)$。
6、求解方程组:begin{cases} x+y=1 \\ 4x+y=10 \end{cases}$$将第一个方程变形为$y=1-x$,代入第二个方程得到$4x+(1-x)=10$,解得$x=3$,因此$y=-2$,方程的解为$(3,-2)$。
初一下解方程组练习题

初一下解方程组练习题解方程组是初中数学中的重要内容,也是数学建模和解决实际问题的基础。
下面将为大家提供一些初一下学期解方程组的练习题,帮助大家巩固和提高解方程组的能力。
练习题1:已知方程组:$\begin{cases}2x+y=7 \\3x-2y=1\end{cases}$求解方程组。
解答:首先,我们可以使用消元法解这个方程组。
为了消去y的系数,在第一个方程的两边同时乘以2,得到新的方程:$\begin{cases}4x+2y=14 \\3x-2y=1\end{cases}$将这两个方程相加,可以得到:$7x=15$解得$x=\frac{15}{7}$将$x$的值代入第一个方程,可以得到:$2(\frac{15}{7})+y=7$解得$y=7-\frac{30}{7}=-\frac{1}{7}$因此,方程组的解为$x=\frac{15}{7}$,$y=-\frac{1}{7}$。
练习题2:已知方程组:$\begin{cases}3x-4y=10 \\5x+2y=2\end{cases}$解答:这个方程组也可以使用消元法解。
为了消去y的系数,在第二个方程的两边同时乘以2,得到新的方程:$\begin{cases}3x-4y=10 \\10x+4y=4\end{cases}$将这两个方程相加,可以得到:$13x=14$解得$x=\frac{14}{13}$将$x$的值代入第一个方程,可以得到:$3(\frac{14}{13})-4y=10$解得$y=-\frac{12}{13}$因此,方程组的解为$x=\frac{14}{13}$,$y=-\frac{12}{13}$。
练习题3:$\begin{cases}7x-3y=1 \\3x+5y=11\end{cases}$求解方程组。
解答:这个方程组我们可以使用消元法来解。
为了消去y的系数,在第一个方程的两边同时乘以5,得到新的方程:$\begin{cases}35x-15y=5 \\3x+5y=11\end{cases}$将这两个方程相加,可以得到:$38x=16$解得$x=\frac{8}{19}$将$x$的值代入第一个方程,可以得到:$7(\frac{8}{19})-3y=1$解得$y=\frac{33}{19}$因此,方程组的解为$x=\frac{8}{19}$,$y=\frac{33}{19}$。
七年级下册数学二元一次方程组的实际运用练习题含答案

七年级下册数学二元一次方程组的实际运用练习题含
答案
1.某校积极开展课外兴趣活动,已知参加球类项目的学生与参加艺术类的共32人,切参加球类的比参加艺术的多4人求球类和艺术的学生个几人?
2.某班有40民同学购买甲乙门票共用去370元,甲票每张10元,已每张8元.甲乙各买多少张?
3.李明骑车每分钟600米,跑步每分钟200米,自行车和长跑路程共25千米,求自行车和长跑路程长度?
答案:
1.设参加球类项目的学生为x人,参加艺术类的有y人
x+y=32
x-y=4
解得x=18
y=14
2.设甲门票买了x张,乙门票买了y张
x+y=40
10x+8y=370
解得x=25
y=15
3.若题目中给定一共用时t分钟.(即t已知)
设骑自行车t1分钟,跑步t2分钟
t1+t2=t
600t1+200t2=25000
t1=(125-t)/2
t2=(3t-125)/2
自行车:600t1=300(125-t)跑步:200t2=100(3t-125)。
七年级下册数学二元一次方程组题

七年级下册数学二元一次方程组题一、基础题型。
1. 已知方程2x + y = 5,当x = 2时,求y的值。
- 解析:将x = 2代入方程2x+y = 5中,得到2×2 + y=5,即4 + y = 5,解得y = 5 - 4=1。
2. 解方程组x + y = 3 x - y = 1- 解析:将两个方程相加,可得(x + y)+(x - y)=3 + 1,即2x=4,解得x = 2。
把x = 2代入x + y = 3中,得到2+y = 3,解得y = 1。
所以方程组的解为x = 2 y = 1。
3. 若x = 1 y = - 1是方程ax - 2y = 3的解,则a的值是多少?- 解析:将x = 1,y=-1代入方程ax-2y = 3中,得到a×1-2×(-1)=3,即a + 2 = 3,解得a=1。
4. 解方程组2x+3y = 8 3x - 2y=-1- 解析:给第一个方程乘以2,第二个方程乘以3,得到4x + 6y = 16 9x-6y=-3。
将这两个新方程相加,可得(4x + 6y)+(9x - 6y)=16+( - 3),即13x = 13,解得x = 1。
把x = 1代入2x+3y = 8中,得到2 + 3y = 8,解得3y = 6,y = 2。
所以方程组的解为x = 1 y = 2。
5. 已知x = 2m y = 3m满足方程2x + y = 14,求m的值。
- 解析:将x = 2m,y = 3m代入方程2x + y = 14中,得到2×2m+3m = 14,即4m+3m = 14,7m = 14,解得m = 2。
二、应用题类型。
6. 一个长方形的周长是40,长比宽多4,设长为x,宽为y,求这个长方形的长和宽。
- 解析:根据长方形周长公式C = 2(x + y),已知周长C = 40,可得方程2(x + y)=40,即x + y = 20。
又因为长比宽多4,所以x-y = 4。
初一数学方程练习题

初一数学方程练习题一、一元一次方程1. 解方程:3x 7 = 112. 解方程:5 2x = 3x + 13. 解方程:4(x 2) = 84. 解方程:7 3(x + 1) = 25. 解方程:2(3x 4) + 5 = 21二、二元一次方程组1. 解方程组:\[\begin{cases}2x + 3y = 8 \\x y = 1\end{cases}\]2. 解方程组:\[\begin{cases}3x 4y = 7 \\2x + y = 6\end{cases}\]3. 解方程组:\[\begin{cases}5x + 2y = 15 \\4x 3y = 2\end{cases}\]4. 解方程组:\[\begin{cases}2x 3y = 9 \\x + 4y = 8\end{cases}\]5. 解方程组:\[\begin{cases}4x + 5y = 23 \\3x 2y = 7\end{cases}\]三、分式方程1. 解方程:$\frac{2x 3}{5} = \frac{x + 1}{2}$2. 解方程:$\frac{3}{x 2} = \frac{4}{x + 1}$3. 解方程:$\frac{1}{x + 3} + \frac{2}{x 1} = 1$4. 解方程:$\frac{2}{x 4} \frac{3}{x + 2} = 1$5. 解方程:$\frac{5}{2x + 3} = \frac{2}{x 3}$四、一元二次方程1. 解方程:$x^2 5x + 6 = 0$2. 解方程:$2x^2 4x 6 = 0$3. 解方程:$3x^2 + 12x + 9 = 0$4. 解方程:$4x^2 12x + 9 = 0$5. 解方程:$5x^2 + 10x 3 = 0$五、应用题1. 某数的2倍与3的和等于13,求这个数。
2. 甲、乙两人年龄之和为35岁,甲的年龄是乙的2倍,求甲、乙的年龄。
专题 解二元一次方程组(计算题50题)(原卷版)
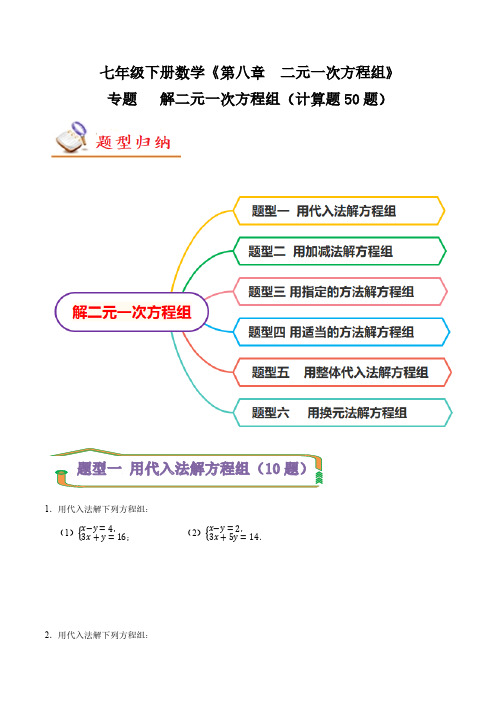
七年级下册数学《第八章二元一次方程组》专题解二元一次方程组(计算题50题)1.用代入法解下列方程组:(1)x−y=4,3x+y=16;(2)x−y=2,3x+5y=14.2.用代入法解下列方程组:(1)2x−y=33x+2y=8;(2)u+v=103u−2v=5.3.用代入法解下列方程组:(1)3x−y=2,9x+8y=17;(2)3x−4y=10x+3y=12.4.用代入法解下列方程组.(1)x+2y=4y=2x−3;(2)x−y=44x+2y=−2.5.用代入法解下列方程组:(1)5x+4y=−1.52x−3y=4(2)4x−3y−10=03x−2y=06.用代入法解下列方程组:(1)x−y=42x+y=5;(2)3x−y=29x+8y=17;(3)3x+2y=−8 6x−3y=−9.7.用代入法解下列方程组:(1)3x+2y=11,①x=y+3,②(2)4x−3y=36,①y+5x=7,②(3)2x−3y=1,①3x+2y=8,②8.用代入法解下列方程组:(1)5x+2y=15①8x+3y=−1②;(2)3(y−2)=x−172(x−1)=5y−8.9.用代入法解下列方程组:(1)x=6−5y3x−6y=4(2)5x+2y=15x+y=6(3)3x+4y=22x−y=5(4)2x+3y=73x−5y=110.用代入法解下列方程组:(1)2x+y=3x+2y=−6;(2)x+5y=43x−6y=5;(3)2x−y=63x+2y=2;(4)5x+2y=113y−x=−9;1.用加减法解下列方程组:(1)4x−y =143x +y =7 (2x−2y =7x−3y =−82.用加减法解下列方程组:(1)2m +7n =53m +n =−2(2)2u−5v =124u +3v =−2(3y 7=12+y 7=133.用加减法解下列方程组:(1)x−y =52x +y =4;(2)x−2y =33x +4y =−1.4.用加减法解下列方程组:(1)4x−3y =11,2x +y =13;(2)x−y =3,2y +3(x−y)=115.用加减法解下列方程组:(1)3μ+2t =76μ−2t =11 (2)2a +b =33a +b =4.6.(2023•市北区校级开学)用加减法解下列方程组:(1)3y−4x =04x +y =8; (2+y =3x−32y =−1.7.(2022秋•陕西期末)用加减法解下列方程组:(1)x−y =33x−8y =14; (2+2y =10=1+y 13.8.用加减法解下列方程组:(1)x +3=y ,2(x +1)−y =6; (2)x +y =2800,96%x +64%y =2800×92%.9.用加减法解下列方程组:(1)x−y =5,①2x +y =4;②(2)x−2y =1,①x +3y =6;②(3)2x−y =5,①x−1=12(2y−1).②10.用加减法解下列方程组:(1)x +3y =62x−3y =3 (2)7x +8y =−57x−y =4(3)y−1=3(x−2)y+4=2(x+1)(4+y4=1−y3=−1.1.(2022春•新田县期中)用指定的方法解下列方程组:(1)2x−5y=14①y=−x②(代入法);(2)2x+3y=9①3x+5y=16②(加减法).2.(2022春•安岳县校级月考)解下列方程组:(1)3x−y=75x+2y=8(用代入法);(2+n3=10−n4=5(用加减法).3.(2022春•大连期中)用指定的方法解下列方程组:(1)x−3y=42x+y=13(代入法);(2)5x+2y=4x+4y=−6(加减法).4.(2022春•宁远县月考)请用指定的方法解下列方程组(1)5a−b=113a+b=7(代入消元法);(2)2x−5y=245x+2y=31(加减消元法).5.(2021秋•蒲城县期末)请用指定的方法解下列方程组:(1)2x+3y=11①x=y+3②(代入消元法);(2)3x−2y=2①4x+y=10②(加减消元法).6.(2022秋•历下区期中)请用指定的方法解下列方程组:(1)m−n2=22m+3n=12(代入法);(2)6s−5t=36s+t=−15(加减法).7.(2022春•泰安期中)用指定的方法解下列方程组(1)3x+4y=19x−y=4(代入消元法);(2)2x+3y=−53x−2y=12(加减消元法);(35(x−9)=6(y−2)−y13=2.8.(2021秋•历下区期中)请用指定的方法解下列方程组:(1)3x+2y=14x=y+3;(代入法)(2)2x+3y=123x+4y=17.(加减法)9.(2021春•沙河口区期末)用指定的方法解下列方程组:(1)y=2x−33x+2y=8(代入法);(2)3x+4y=165x−6y=33(加减法).10.用指定的方法解下列方程组:(1)3x+4y=19x−y=4(代入法);(2)2x+3y=−53x−2y=12(加减法).1.(2022•苏州模拟)用适当的方法解下列方程组.(1)x+2y=9y−3x=1;(2x−34y=1=4.2.(2022秋•锦江区校级期末)用适当的方法解下列方程组.(1)x=2y−14x+3y=7;(2)3x+2y=22x+3y=28,.3.用适当的方法解下列方程组:(1)x+2y=0,3x+4y=6;(2=2y1)−y=11(3)x+0.4y=40,0.5x+0.7y=35;(4+n−m4=−14,5(n1)12=2.4.(2022•天津模拟)用适当的方法解下列方程组:(1)x +y =52x−y =4; (2=y 24−y−33=112.5.(2021•越城区校级开学)用适当的方法解下列方程组:(1)2x−3y =7x−3y =7. (2)0.3p +0.4q =40.2p +2=0.9q .6.(2022春•东城区校级月考)用适当的方法解下列方程组(1)x +y =52x +y =8; (2)2x +3y =73x−2y =4.7.(2021春•哈尔滨期末)用适当的方法解下列方程组(1)x +2y =93x−2y =−1 (2)2x−y =53x +4y =28.(2022春•椒江区校级期中)用适当的方法解下列方程组:(1)2x +3y =16①x +4y =13②; (2)2s t 3=3s−2t 8=3.9.(2022春•诸暨市期中)用适当的方法解下列方程组:(1)y=2x−1x+2y=−7(2+y3=7+y2=810.(2021春•南湖区校级期中)用适当的方法解下列方程组:(1)3x+2y=9x−y=8;(2=x y2=7.1.先阅读材料,然后解方程组:材料:解方程组x+y=4①3(x+y)+y=14②在本题中,先将x+y看作一个整体,将①整体代入②,得3×4+y=14,解得y=2.把y=2代入①得x=2,所以x=2 y=2这种解法称为“整体代入法”,你若留心观察,有很多方程组可采用此法解答,请用这种方法解方程组x−y−1=0①4(x−y)−y=5②.2.(2021秋•乐平市期末)解方程组3x−2y=8⋯⋯⋯①3(3x−2y)+4y=20⋯.②时,可把①代入②得:3×8+4y=20,求得y=﹣1,从而进一步求得x=2y=−1这种解法为“整体代入法“,请用这样的方法解下列方程组2x−3y=123(2x−3y)+5y=26.3.先阅读,然后解方程组.解方程组x−y−1=0①4(x−y)−y=5②时,可由①得x﹣y=1.③,然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得x=0y=−1这种方法被称为“整体代入法”,请用这样的方法解下列方程组:=0=2y+1.4.(2022春•太和县期末)先阅读,然后解方程组.解方程组x−y−1=0①4(x−y)−y=5②时,可由①得x﹣y=1,③然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得x=0①y=−1②这种方法被称为“整体代入法”,+2y=9.5.先阅读,然后解方程组.解方程组x−y−1=0①4(x−y)−y=5②时,可由①得x﹣y=1③,然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得x这种方法被称为“整体代入法”,请用这样的方法解下列方程组:2x−3y−2=03(2x−3y)+y=7.1.用换元法解下列方程组+2y=12−1y=342.用换元法解下列方程组:(1)3(x+y)+2(x−y)=36(x+y)−4(x−y)=−16(2+x5y3=2−(x+5y)=5.3.(2022春•云阳县期中)阅读探索:解方程组(a−1)+2(b+2)=62(a−1)+(b+2)=6解:设a﹣1=x,b+2=y原方程组可以化为x+2y=62x+y=6,解得x=2y=2,即:a−1=2b+2=2∴a=3b=0,此种解方程组的方法叫换元法.(1)拓展提高运用上述方法解下列方程组(a4−1)+2(b5+2)=102(a4−1)+(b5+2)=11;(2)能力运用已知关于x,y的方程组a1x+b1y=c1a2x+b2y=c2的解为x=6y=7,求关于m、n的方程组a1(m−2)+b1(n+3)=c1a2(m−2)+b2(n+3)=c2的解.4+x−y10=3①−x−y10=−1②,你会解这个方程组吗?小明、小刚、小芳争论了一会儿,他们分别写出了一种方法:小明:把原方程组整理得8x+2y=90③2x+8y=−30④④×4﹣③得30y=﹣210,所以y=﹣7把y=﹣7代入③得8x=104,所以x=13,即x=13y=−7小刚:设x y6=m,x−y10=n,则m+n=3③m−n=−1④③+④得m=1,③﹣④得m=2,=1=2,所以x+y=6x−y=20,所以x=13y=−7.小芳:①+②得2(x y)6=2,即x+y=6.③①﹣②得2(x−y)10=4,即x﹣y=20.④③④组成方程组得x=13③﹣④得y =﹣7,即x =13y =−7.老师看过后,非常高兴,特别是小刚的方法独特,像小刚的这种方法叫做换元法,你能用换元法解下列方程组吗?+2x 3y 7=1−2x 3y 7=5.5.(2022春•卧龙区校级月考)阅读探索(1)知识积累解方程组(a−1)+2(b +2)=62(a−1)+(b +2)=6.解:设a ﹣1=x ,b +2=y .原方程组可变为x +2y =62x +y =6,解这个方程组得x =2y =2,即a−1=2b +2=2,所以a =3b =0,这种解方程组的方法叫换元法.(2)拓展提高运用上述方法解下列方程组:(m 3−1)+2(n 5+2)=43(m 3−1)−(n 5+2)=5.(3)能力运用已知关于x ,y 的方程组a 1x +b 1y =c 1a 2x +b 2y =c 2的解为x =3y =4,请直接写出关于m 、n 的方程组a 1(m +2)−b 1n =c 1a 2(m +2)−b 2n =c 2的解是 .。
初一解方程组练习题及答案
初一解方程组练习题及答案解方程1、4+2-2=2-62、1-2=33、/3+1=/、4x-3=6x-7、5x-2=-7x+6、11x-3=2x+37、16=y/2+8、/7+/14=-/28+/119、mx-2=3x+n 10、3x-5=7x-11 11、2x+=15- 12、3/4x+2=3-1/4x 13、3/4-x=5/6-2/3x 14、2-3=9 15、2-3=716、x-3/2[2/3-2]=-217、x/3-1=x/2-218、x=/2-/319、/3=1-/0、/3-/6=/4-11、3/2-/6=122、1/3-1/2=2 23、-2-4=124、5-3=425、/2-/6=/6、2x-7+8x=10x-3-4x27、1/3[x-1/2]=2/3 8、1/2[x/3-1/2]=x/129、1/3[2-3]+3/2=1230、x/0.7-/0.03=131、/4-/6=12、/5-/18=/6-/153、1/2[x-1/2]=2/3、1/9{1/7[1/5/3+2)+6]+8}35、/0.02-/0.5=36、-2=8-x/237、/2-/5=18、/0.5-/0.2=1.639、x-=3 0、x-/2=2-/3应用题1.某车间有工人100名,每人平均每天可加工螺栓18个或螺母24个,要是每天加工的螺栓和螺母配套,应该如何分配工人?2.一项工作,甲单独做药8天完成,乙单独做要12天完成,丙单独做要24天完成。
现在甲乙丙合作3天后,甲因故离开,由乙丙合做,问还需多少天完成?3.某商品进价2000元,标价为3000元,商店以利润不低于5%的售价出售,则此商品最低可打几折?4.一辆汽车以40km/h的速度由甲地驶向乙地,车行了3小时后,因下雨被迫减少10km/h,结果比预计到达时间晚了45分钟,求甲乙两地距离?5.甲工程队有28人,乙工程队有35人,先从甲队抽调若干?a href=“http:///fanwen/shuoshuodaquan/” target=“_blank” class=“keylink”>说揭叶裕 挂叶尤耸 羌锥拥牧奖叮 Υ蛹锥映榈鞫嗌偃耍?/p>6.一个两位数,个位数字是十位数字的两倍,若把个位数字和十位数字对换,则所得数比原来数大36,求原数。
初一解方程组练习题50道
初一解方程组练习题50道解方程组是初中数学中的一种重要知识点,对学生的运算能力和逻辑思维能力有很好的培养作用。
为了帮助初一的同学们加深对解方程组的理解,我为大家准备了50道初一解方程组练习题。
请同学们认真思考并运用所学知识解答。
1. 某糖果店有两种糖果,甲袋中有红色圆形糖果5颗、黄色圆形糖果3颗,乙袋中有红色圆形糖果4颗、黄色圆形糖果6颗,两袋共计有18颗红色圆形糖果和24颗黄色圆形糖果。
求甲袋、乙袋各颜色圆形糖果的数量。
2. 某商店购进若干只笔和若干只橡皮共计79元。
已知笔每只10元,橡皮每只5元,若购进笔多六只,则每只笔4元,每只橡皮5元;若购进笔少六只,则每只笔6元,每只橡皮4元。
求购进的笔和橡皮各有几只?3. 一根木棍分成甲、乙两段,甲段比乙段长18cm。
如果把甲段减短9cm,乙段增长9cm,两段正好一样长。
求原来的木棍长度。
4. 一枝蜡烛和一本书的总重量是80g,蜡烛比书轻64g。
如果蜡烛变重或者书变轻4倍,它们的总重量将相等。
求蜡烛和书各自的重量。
5. 小明和小红共有钱30元。
已知小红比小明多5元,若小明钱增加10元,小红钱减少10元,则两人钱数相等。
求小明和小红各有多少钱?6. 一根绳子分成甲、乙两段,甲段比乙段长30米。
现在甲段增加了20米,乙段减少了10米,两段正好一样长。
求原来的绳子长度。
7. 某地的气温周一比周二高7℃,周二比周三低5℃,周三比周四低3℃,周四是-1℃,周一比周五高多少℃?8. 小明和小李正在玩一种游戏。
经过一天的游戏后,小明还剩下小李的一半多8个馒头。
第二天,经过一天的游戏后,小明还剩下小李的三分之一多10个馒头。
已知小明每天剩下的馒头数是基数,小李每天剩下的馒头数是偶数。
求小明和小李开始时的馒头数各为多少?9. 某地有红、蓝两种小球,共有球50个。
如果用两个红球和三个蓝球组成一个小组,则剩下一个球;如果用四个红球和一个蓝球组成一个小组,则少两个球。
求红球和蓝球各有几个?10. 某公司购进红、蓝两种花束共计24个,红色花束比蓝色花束多4个。
初一下数学解方程组练习题
初一下册青岛版数学解方程演习题1.(每题5分,共10分)解方程组:(1)⎩⎨⎧=+=-1732623y x y x ;(2)⎪⎩⎪⎨⎧=---=+1213343144y x y x . 2.解方程组⎪⎩⎪⎨⎧=-+=++=++1232721323z y x z y x z y x3.解方程组:(1)33(1)022(3)2(1)10x y x y -⎧--=⎪⎨⎪---=⎩ (2)04239328a b c a b c a b c -+=⎧⎪++=⎨⎪-+=⎩4.解方程(组) (1)3221+=--x x x (2)⎩⎨⎧-=+=+12332)13(2y x yx 5.⎪⎪⎩⎪⎪⎨⎧=++-=+--3423174231y x y x6.已知x,y 是有理数,且(│x│-1)2+(2y+1)2=0,则x -y 的值是若干? 7.二元一次方程组437(1)3x y kx k y +=⎧⎨+-=⎩的解x,y 的值相等,求k .8..当y=-3时,二元一次方程3x+5y=-3和3y -2ax=a+2(关于x,y 的方程)•有雷同的解,求a 的值.9.⎪⎩⎪⎨⎧=---=+-=+-.441454y x z x z y z y x10.若42x y =⎧⎨=⎩是二元一次方程ax -by=8和ax+2by=-4的公共解,求2a -b 的值. 11.解下列方程: (1).(2)(3)(4)⎪⎩⎪⎨⎧=-+=+-=+321236z -y x z y x z y x12.(凋谢题)是否消失整数m,使关于x 的方程2x+9=2-(m -2)x 在整数规模内有解,你能找到几个m 的值?你能求出响应的x 的解吗?13.方程组2528x y x y +=⎧⎨-=⎩的解是否知足2x -y=8?知足2x -y=8的一对x,y 的值是否是方程组2528x y x y +=⎧⎨-=⎩的解?14.甲乙两车间临盆一种产品,原筹划两车间共临盆300件产品,现实甲车间比原筹划多临盆10%,乙车间比原筹划多临盆20%,成果共临盆了340件产品,问原筹划甲.乙两车间各临盆了若干件产品? 15.(本题满分14分)(1)解方程组25211x y x y -=-⎧⎨+=⎩,(2)解方程组 ⎩⎨⎧=-=+)2.(633)1(,844y x y x16.⎪⎩⎪⎨⎧=++-=+--.6)(2)(3152y x y x yx y x参考答案 1.(1)⎩⎨⎧==34y x ;(2)⎪⎩⎪⎨⎧==4113y x . 【解析】试题剖析:(1)运用加减消元法消去未知数y,得到关于未知数x 的方程,解得x 的值,然后再求出y 的值,得到方程组的解; (2)起首把方程②进行变形,从新构成方程组,运用代入消元法求解. 试题解析:(1)解:3262317x y x y -=⎧⎨+=⎩①②,①×3+②×2得,13x=52, 解得x=4,把x=4代入①得,12-2y=6, 解得y=3,所以方程组的解为43x y =⎧⎨=⎩;(2)解:4143314312x y x y +=⎧⎪⎨---=⎪⎩①②,由②整顿得,3x-4y=-2③,由①得x=14-4y④,把④代入③得,3(14-4y )-4y= -2,解得y=114, 把y=114代入④,解得x=3,所以原方程组的解为3114x y =⎧⎪⎨=⎪⎩.考点:二元一次方程组的解法.2.原方程组的解231x y z =⎧⎪=⎨⎪=⎩【解析】试题剖析:3213.........(1)27............(2)2312.........(3)x y z x y z x y z ++=⎧⎪++=⎨⎪+-=⎩(1)(3)+得5525x y +=得 5.......................(4)x y +=(1)2⨯得64226....(5)x y z ++= (5)(2)-得5319..........(6)x y += (4)3⨯得3315............(7)x y += (6)(7)2x -= 3y =1z =∴原方程组的解231x y z =⎧⎪=⎨⎪=⎩考点:三元一次方程组点评:本题难度较低,重要考核学生对三元一次方程组常识点的控制.为中考罕有题型,要肄业生控制解题技能.3.(1)92x y =⎧⎨=⎩ ; (2)325a b c =⎧⎪=-⎨⎪=-⎩【解析】 试题剖析: 考点:二元一次方程组的解法,及三元一次方程组的解法. 点评:考核二元(三元)一次方程组的解法,可先整顿化简,由加减,或代入消元法求之,本题属于基本题,难度不大,但解答时易出错,需留意.4.去分母,得:6x-3(x-1)=2(x+2) ………………2分 去括号,得:6x-3x+3=2x+4 ………………4分 整顿,得:x=1 ………………6分 原方程组变形,得⎩⎨⎧=++=+)2(213)1(32)13(2y x y x ………………2分(2)把(2) 代入(1)得:4y=2+3y 解得:y=2………………4分把y=2代入(2) 得:x=1………………5分 ∴ ⎩⎨⎧==21y x 【解析】先去分母,然后去括号得出成果.(2)运用代入消元法求解.5.⎩⎨⎧-==1016y x【解析】两方程相加解得x=16, 把x=16代入随意率性一方程解得y=-10, 所以方程组的解为⎩⎨⎧-==1016y x6.解:由(│x│-1)2+(2y+1)2=0,可得│x│-1=0且2y+1=0,∴x=±1,y=-12.当x=1,y=-12时,x -y=1+12=32;当x=-1,y=-12时,x -y=-1+12=-12.【解析】任何有理数的平方都长短负数,且题中两非负数之和为0,则这两非负数(│x│-1)2与(2y+1)2都等于0,从而得到│x│-1=0,2y+1=0.7.由题意可知x=y,∴4x+3y=7可化为4x+3x=7,∴x=1,y=1.将x=1,y=•1•代入kx+(k -1)y=3中得k+k -1=3, ∴k=2【解析】由两个未知数的特别关系,可将一个未知数用含另一个未知数的代数式代替,化“二元”为“一元”,从而求得两未知数的值. 8.∴a=-119. 【解析】.解:∵y=-3时,3x+5y=-3,∴3x+5×(-3)=-3,∴x=4,∵方程3x+5y=•-•3•和3x -2ax=a+2有雷同的解, ∴3×(-3)-2a×4=a+2,∴a=-119. 9.⎪⎪⎪⎩⎪⎪⎪⎨⎧=-==.15451z y x【解析】 将三个方程左,右双方分离相加,得4x -4y +4z =8,故x -y +z =2 ④,把④分离与第一.二个方程联立,然后用加.减消元法即可求得x.z 的值. 10.4 【解析】试题剖析:把42x y =⎧⎨=⎩分离代入ax -by=8和ax+2by=-4得:4a-2b=8和4a+4b=-4.树立二元一次方程组,解得a=1,b=-2.所以2a-b=4 考点:二元一次方程组点评:本题难度中等,重要考核学生对二元一次方程组常识点的控制.为中考常考题型,要肄业生稳固控制解题技能.11.(1)x=1(2)方程组的解是;(3)原方程组的解是.(4)原方程组的解是⎪⎪⎩⎪⎪⎨⎧-=-==3173310z y x【解析】试题剖析:(1)去分母得:6﹣2(x+2)=3(x ﹣1), 去括号得:6﹣2x ﹣4=3x ﹣3, 移项归并得:﹣5x=﹣5, 解得:x=1.. (2)(1),①+②得,6x=12, 解得x=2,把x=2代入①得,2×2﹣y=5,解得y=﹣1, 所以,方程组的解是;(3)方程组可化为,①+②得,5x+5y=40,所以,x+y=8③,①﹣②得,x ﹣y=﹣16④, ③+④得,2x=﹣8, 解得x=﹣4,③﹣④得,2y=24, 解得y=12,所以,原方程组的解是.;(4).解① - ③得,-y=3,解得y=-3 ① - ②得,4y-3z=5 ④ 把y=-3代入④得,-3×4-3z=5解得z=-317 把y=-3, z=-317代入①得,x-3-(-317)=6解得x=310所以,原方程组的解是⎪⎪⎩⎪⎪⎨⎧-=-==3173310z y x考点:一元一次方程和一元二次方程组点评:本题难度较低,重要考核学生对一元一次方程和一元二次方程组常识点的控制.为中考常考题型,要肄业生稳固控制.12.24.解:消失,四组.∵原方程可变形为-mx=7, ∴当m=1时,x=-7;m=-1时,x=7;m=•7时,x=-1;m=-7时x=1. 【解析】略13.解:知足,不必定. 【解析】解析:∵2528x y x y +=⎧⎨-=⎩的解既是方程x+y=25的解,也知足2x -y=8,•∴方程组的解必定知足个中的任一个方程,但方程2x -y=8的解有很多组,如x=10,y=12,不知足方程组2528x y x y +=⎧⎨-=⎩.14.解:设甲.乙两车间分离临盆了x 件产品, y 件产品,则405001210{=+=+y x y x解这个方程得200100{==x y答:甲.乙两车间分离临盆了200件产品, 100件产品. 【解析】略 15.(1)34x y =⎧⎨=⎩(2)⎩⎨⎧==.0,2y x【解析】略 16.⎩⎨⎧-==.11y x【解析】用换元法,设x -y =A,x +y =B,解关于A.B 的方程组⎪⎩⎪⎨⎧=+=-623152B A B A ,进而求得x,y .。
数学七下解方程组练习题
数学七下解方程组练习题解方程组是数学中的重要内容之一,通过解方程组可以找到多个未知数的值。
在数学七下的学习中,我们会遇到一些解方程组的练习题,让我们来看几个例子。
1. 题目一:已知方程组:2x + 3y = 74x - y = 1要求解出方程组的解。
解析:首先,我们可以通过消元法来解这个方程组。
将第二个方程的系数乘以2,得到:8x - 2y = 2现在我们有两个方程:2x + 3y = 78x - 2y = 2接下来,我们可以通过相减消元法来求解。
将第一个方程的两倍减去第二个方程,可以消去x的项:(2x + 3y) - (8x - 2y) = 7 - 22x + 3y - 8x + 2y = 5-6x + 5y = 5我们得到一个新的方程:-6x + 5y = 5现在我们有两个方程:-6x + 5y = 54x - y = 1继续使用消元法,将第一个方程的系数乘以4,得到:-24x + 20y = 20现在我们有两个方程:-24x + 20y = 204x - y = 1再次使用相减消元法,可以消去y的项:(-24x + 20y) - (4x - y) = 20 - 1-24x + 20y - 4x + y = 19-28x + 21y = 19我们得到一个新的方程:-28x + 21y = 19现在我们有两个方程:-28x + 21y = 194x - y = 1继续使用消元法,将第一个方程的系数乘以7,得到:-196x + 147y = 133现在我们有两个方程:-196x + 147y = 1334x - y = 1再次使用相减消元法,可以消去y的项:(-196x + 147y) - (28x - 7y) = 133 - 7-196x + 147y - 28x + 7y = 126-224x + 154y = 126我们得到一个新的方程:-224x + 154y = 126现在我们有两个方程:-224x + 154y = 1264x - y = 1继续使用消元法,将第一个方程的系数乘以7,得到:-1568x + 1078y = 882现在我们有两个方程:-1568x + 1078y = 8824x - y = 1再次使用相减消元法,可以消去y的项:(-1568x + 1078y) - (28x - 7y) = 882 - 7-1568x + 1078y - 28x + 7y = 875-1596x + 1085y = 875我们得到一个新的方程:-1596x + 1085y = 875现在我们有两个方程:-1596x + 1085y = 8754x - y = 1继续使用消元法,将第一个方程的系数乘以7,得到:-11172x + 7595y = 6125现在我们有两个方程:-11172x + 7595y = 61254x - y = 1再次使用相减消元法,可以消去y的项:(-11172x + 7595y) - (28x - 7y) = 6125 - 7-11172x + 7595y - 28x + 7y = 6118-11184x + 7602y = 6118我们得到一个新的方程:-11184x + 7602y = 6118现在我们有两个方程:-11184x + 7602y = 61184x - y = 1继续使用消元法,将第一个方程的系数乘以11184,得到:-125209856x + 85072248y = 68445512现在我们有两个方程:-125209856x + 85072248y = 684455124x - y = 1再次使用相减消元法,可以消去y的项:(-125209856x + 85072248y) - (28x - 7y) = 68445512 - 7-125209856x + 85072248y - 28x + 7y = 68445505-125209884x + 85072255y = 68445505我们得到一个新的方程:-125209884x + 85072255y = 68445505现在我们有两个方程:-125209884x + 85072255y = 684455054x - y = 1继续使用消元法,将第一个方程的系数乘以1,得到:-125209884x + 85072255y = 68445505现在我们有两个方程:-125209884x + 85072255y = 684455054x - y = 1将第二个方程中的y用4x - 1代替,得到:-125209884x + 85072255(4x - 1) = 68445505-125209884x + 340289020x - 85072255 = 68445505 214079136x = 253117760x ≈ 1.182将x的值代入第二个方程,得到:4(1.182) - y = 14.728 - y = 1-y = 1 - 4.728y ≈ 3.728所以,方程组的解为:x ≈ 1.182y ≈ 3.7282. 题目二:已知方程组:3x + 4y = 105x - y = 7要求解出方程组的解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【解析】任何有理数的平方都是非负数,且题中两非负数之和为0,
则这两非负数(│x│-1)2与(2y+1)2都等于0,从而得到│x│-1=0,2y+1=0.
7.由题意可知x=y,∴4x+3y=7可化为4x+3x=7,
∴x=1,y=1.将x=1,y= 1 代入kx+(k-1)y=3中得k+k-1=3,
解得y=12,
所以,原方程组的解是 .;
(4).解①- ③得,-y=3,
解得y=-3
①-②得,4y-3z=5 ④
把y=-3代入④得,-3×4-3z=5
解得z=-
把y=-3, z=- 代入①得,x-3-(- )=6
解得x=
所以,原方程组的解是
考点:一元一次方程和一元二次方程组
点评:本题难度较低,主要考查学生对一元一次方程和一元二次方程组知识点的掌握。为中考常考题型,要求学生牢固掌握。
解得x=4,
把x=4代入①得,12-2y=6,
解得y=3,
所以方程组的解为 ;
(2)解: ,
由②整理得,3x-4y=-2③,
由①得x=14-4y④,
把④代入③得,3(14-4y)-4y= -2,
解得y= ,
把y= 代入④,解得x=3,
所以原方程组的解为 .
考点:二元一次方程组的解法.
2.原方程组的解
~
13.方程组 的解是否满足2x-y=8满足2x-y=8的一对x,y的值是否是方程组 的解
14.甲乙两车间生产一种产品,原计划两车间共生产300件产品,实际甲车间比原计划多生产10%,乙车间比原计划多生产20%,结果共生产了340件产品,问原计划甲、乙两车间各生产了多少件产品
!
15.(本题满分14分)
12.24.解:存在,四组.∵原方程可变形为-mx=7,
∴当m=1时,x=-7;m=-1时,x=7;m= 7时,x=-1;m=-7时x= 的解既是方程x+y=25的解,也满足2x-y=8,
∴方程组的解一定满足其中的任一个方程,但方程2x-y=8的解有无数组,
如x=10,y=12,不满足方程组 .
14.解:设甲、乙两车间分别生产了x件产品, y件产品,则
解这个方程得
答:甲、乙两车间分别生产了200件产品, 100件产品.
【解析】略
15.(1)
(2)
【解析】略
16.
【解析】用换元法,设x-y=A,x+y=B,解关于A、B的方程组 ,
进而求得x,y.~
#
8..当y=-3时,二元一次方程3x+5y=-3和3y-2ax=a+2(关于x,y的方程) 有相同的解,求a的值.
9.
}
10.若 是二元一次方程ax-by=8和ax+2by=-4的公共解,求2a-b的值.
@
11.解下列方程:
{
(1) .
(2)
(3)
|
(4)
。
12.(开放题)是否存在整数m,使关于x的方程2x+9=2-(m-2)x在整数范围内有解,你能找到几个m的值你能求出相应的x的解吗
考点:二元一次方程组
点评:本题难度中等,主要考查学生对二元一次方程组知识点的掌握。为中考常考题型,要求学生牢固掌握解题技巧。
11.(1)x=1(2)方程组的解是 ;(3)原方程组的解是 .
(4)原方程组的解是
【解析】
试题分析:(1)去分母得:6﹣2(x+2)=3(x﹣1),
去括号得:6﹣2x﹣4=3x﹣3,
移项合并得:﹣5x=﹣5,
解得:x=1..
(2)(1) ,
①+②得,6x=12,
解得x=2,
把x=2代入①得,2×2﹣y=5,
解得y=﹣1,
所以,方程组的解是 ;
(3)方程组可化为 ,
①+②得,5x+5y=40,
所以,x+y=8③,
①﹣②得,x﹣y=﹣16④,
③+④得,2x=﹣8,
解得x=﹣4,
③﹣④得,2y=24,
【解析】
试题分析:
得
得
得
得
∴原方程组的解
考点:三元一次方程组
点评:本题难度较低,主要考查学生对三元一次方程组知识点的掌握。为中考常见题型,要求学生掌握解题技巧。
3.(1) ; (2)
【解析】
试题分析:
考点:二元一次方程组的解法,及三元一次方程组的解法。
点评:考查二元(三元)一次方程组的解法,可先整理化简,由加减,或代入消元法求之,本题属于基础题,难度不大,但解答时易出错,需注意。
∴k=2
【解析】由两个未知数的特殊关系,可将一个未知数用含另一个未知数的代数式代替,化“二元”为“一元”,从而求得两未知数的值.
8.∴a=- .
【解析】.解:∵y=-3时,3x+5y=-3,∴3x+5×(-3)=-3,∴x=4,
∵方程3x+5y= - 3 和3x-2ax=a+2有相同的解,
∴3×(-3)-2a×4=a+2,∴a=- .
4.去分母,得:6x-3(x-1)=2(x+2) ………………2分
去括号,得:6x-3x+3=2x+4………………4分
整理,得:x=1………………6分
原方程组变形,得 ………………2分
(2)把(2)代入(1)得:4y=2+3y
解得:y=2………………4分
把y=2代入(2)得:x=1………………5分
∴
(1)解方程组
·
(2)解方程组
16.
参考答案
1.(1) ;(2) .
【解析】
试题分析:(1)应用加减消元法消去未知数y,得到关于未知数x的方程,解得x的值,然后再求出y的值,得到方程组的解;
(2)首先把方程②进行变形,重新组成方程组,应用代入消元法求解.
试题解析:(1)解: ,
①×3+②×2得,13x=52,
9.
【解析】 将三个方程左,右两边分别相加,得4x-4y+4z =8,故x-y+z=2④,把④分别与第一、二个方程联立,然后用加、减消元法即可求得x、z的值.
10.4
【解析】
试题分析:把 分别代入ax-by=8和ax+2by=-4得:4a-2b=8和4a+4b=-4.
建立二元一次方程组,解得a=1,b=-2.所以2a-b=4
初一下册青岛版数学解方程练习题
1.(每题5分,共10分)解方程组:
(1) ;
#
(2) .
@
2.解方程组
:
3.解方程组:
(1)
…
(2)
/
4.解方程(组)
(1) (2)
(
5.
6.已知x,y是有理数,且(│x│-1)2+(2y+1)2=0,则x-y的值是多少
】
7.二元一次方程组 的解x,y的值相等,求k.
【解析】先去分母,然后去括号得出结果。(2)利用代入消元法求解。
5.
【解析】两方程相加解得x=16, 把x=16代入任意一方程解得y=-10, 所以方程组的解为
6.解:由(│x│-1)2+(2y+1)2=0,可得│x│-1=0且2y+1=0,∴x=±1,y=- .
当x=1,y=- 时,x-y=1+ = ;
