桂林理工大学博文管理学院 弯矩图的一些规律 陈贤超
快速绘制弯矩图的一些规律及示例
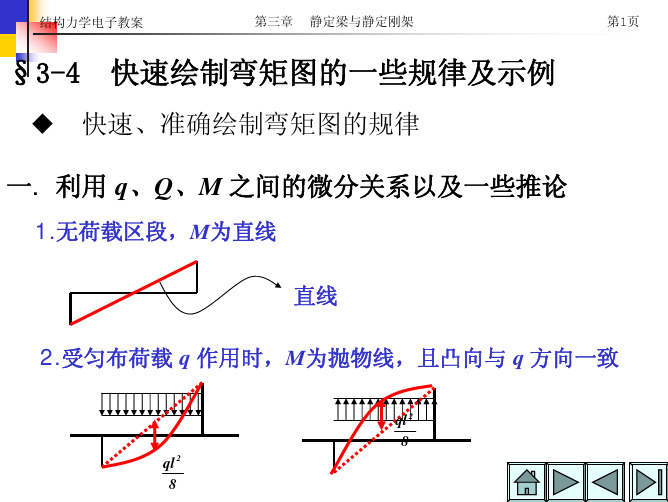
P Q= 0,M为一直线 3Pa
结构力学电子教案
第三章
静定梁与静定刚架
第11页
例6 试作图示多跨静定梁的弯矩图.
4kN 4kN.m 1kN/m
4 8 2
铰处的M为零,且梁上无集中荷载作用, M图为一无斜率变化的斜直线.
2
ql 2 =2 2
4 2
ql 2 =2 8
2
4
2Leabharlann 结构力学电子教案第三章
静定梁与静定刚架
第三章
静定梁与静定刚架
第2页
3. 受集中荷载P作用时,M为折线,折点在集中力作用点处, 且凸向与P方向一致.
P P
4. 受集中力偶 m 作用时,在m作用点处M有跳跃(突变),跳 跃量为m,且左右直线均平行.
m
m
平行
结构力学电子教案
第三章
静定梁与静定刚架
第3页
二. 铰处 M = 0
M=0 M=0 ?
三. 刚结点力矩平衡
40 20 10 30 20 20
20
∑M =0
∑M =0
结构力学电子教案
第三章
静定梁与静定刚架
第4页
四. 集中力 P 与某些杆轴线重合时,M为零
P
M=0
P
M=0
剪力Q为零时, M图为直线.
五. 剪力Q为常值时, M图为斜线;剪力Q为零 时, M为常值, M图为 直线. 剪力Q为常值
P
P
时,M图为斜线
结构力学电子教案
第三章
静定梁与静定刚架
第5页
六. 平衡力系的影响 当由平衡力系组成的荷载作用在静定结构的某一本 身为几何不变的部分上时,则只有此部分受力,其余部分 的反力内力皆为零. P
超静定结构与弯矩分配法

一、由杆端位移求杆端弯矩
杆端力和杆端位移的正负规定
MAB
EI
①杆端转角θA、θB ,弦转角 β=Δ/l都以顺时针为正。
A
l
B
MBA
②杆端弯矩对杆端以顺时针为正 对结点或支座以逆时针为正。
MAB
A
(1)由杆端弯矩M A和 BM B引 A 起 A和 的 B
B
MBA
MBA
利用单位荷载法可求得
A
E1I12MABl32MBAl
SAB与杆的i(材料的性质、横截面的形状和尺寸、杆长)及远
端支承有关, 而与近端支承无关。
超静定结构与弯矩分配法
二、分配系数 设A点有力矩M,求MAB、MAC和MAD
SAB = 4i
D
MA
B
如用位移法求解:
于1 是可得
iAD
i A AB
iAC
M AB 4 iAB AS AB A
M AC iAC ASAC A
固端弯矩之和 (第一轮第一结点)
结点不平 衡力矩
固端弯矩之和 (第一轮第二、三……结点) 加传递弯矩
传递弯矩
(其它轮次各结点)
总等于附加刚臂上的约束力矩
5)不能同时放松相邻结点(因定不出其转动刚度和传递系数),但可 以同时放松所有不相邻的结点,以加快收敛速度。
超静定结构与弯矩分配法
例2. q=20kN/m
的单跨梁,这样的梁在各种外荷载作用下的杆端弯矩叫做固
端弯矩。
超静定结构与弯矩分配法
单结点的弯矩分配 ——基本运算
A M AB
B
M BA
M BC
固端弯矩带本身符号 C
MB
=
MB
M BA
昆明理工大学材料力学第十章 弯曲变形

C
2 w 2
w1
bF 6lEI z
3l 2 2 2 2 ( l b 3 x ) ( x a ) (2) 2 2 b
bF 3 ( l 2 x1 b 2 x1 3 x 1 ) (3) 6lEI z
bF w2 6lEI z
C
∴ =0的截面应在AC段上
0,得 令w1
x0
l 2 b2 3
x0代入w1方程即可求出wmax
●结论:在简支梁上,若挠曲线无拐点,则最大挠度 wmax可用中点处的挠度值来代替。
1a
F
2
b
B
A
x1
x2 l
C
求wmax
l 把x1 代入w1方程即可求出w max 2
w A左 w A右 0
A左 A右
w A左 w A右
w A左 w A右
A左 A右
讨论: dFS ( x ) q( x ) dx
dM ( x ) FS ( x ) dx
d M ( x) q( x ) 2 dx
2
EI z w M ( x )
挠曲线近似微分方程
1 F 3 Fl 2 m 2 w x x x EI z 6 2 2
从方程可看出挠度和转角与载荷是成线性齐次关系 ∴ 可用叠加原理求梁的变形
●叠加原则: 当梁上同时作用几个载荷时,如果梁的变形很小, 且应力不超过比列极限,则梁上任一横截面的总位移即 等于各载荷单独作用时在该截面引起的位移的代数和。
讨论: ①AB是轴线,就是中性层,既不伸长也不缩短, 变形后C点在 x方向也有位移,但在小变形条件下, 挠曲线是一条很平坦的曲线,x方向的位移相对挠度 很小,所以略去不计。 挠度w就是轴线上 x的函数
《弯矩二次分配法》课件

确定结构模型: 选择合适的结 构模型,如梁、
板、柱等
计算内力:根 据结构模型和 受力情况,计 算内力,如弯
矩、剪力等
确定分配系数: 根据结构模型 和内力分布情 况,确定分配
系数
计算分配弯矩: 根据分配系数 和内力,计算
分配弯矩
绘制分配弯矩 图:将分配弯 矩绘制成图, 以便于分析和
设计
桥梁结构分析:利用弯矩二次分配法进行桥梁结构分析,提高计算精度
加强与建筑设 计院的合作, 推广弯矩二次 分配法在建筑 设计中的应用
开展弯矩二次 分配法在桥梁、 隧道等大型结 构工程中的应
用研究
推广弯矩二次 分配法在抗震 设计中的应用, 提高建筑物的
抗震性能
加强与高校、科 研机构的合作, 培养更多的弯矩 二次分配法专业 人才,提高市场
占有率
加强理论研究: 深入研究弯矩二 次分配法的原理 和应用,提高理 论水平
桥梁设计优化:利用弯矩二次分配法进行桥梁设计优化,提高桥梁承载能力和安全性
桥梁施工监控:利用弯矩二次分配法进行桥梁施工监控,确保施工质量和安全
桥梁健康监测:利用弯矩二次分配法进行桥梁健康监测,及时发现和修复桥梁缺陷,延 长桥梁使用寿命
结构设计:用 于计算结构构 件的弯矩和剪
力
抗震设计:用 于评估结构在 地震作用下的
进行传递
确定结构类型:确定结构 是静定结构还是超静定结 构
计算各杆件的内力:根据 结构类型,计算各杆件的 内力
确定各杆件的杆端弯矩: 根据内力,计算各杆件的 杆端弯矩
计算各杆件的杆端弯矩: 根据内力,计算各杆件的 杆端弯矩
计算各杆件的杆端弯矩: 根据内力,计算各杆件的 杆端弯矩
计算各杆件的杆端弯矩: 根据内力,计算各杆件的 杆端弯矩
11-1渐近法(弯矩分分配法)

=
MB
MBA
MBC
A MABP
MBAP B MBCP
+
C
-MB
MB= MBA+MBC -MB
A
M AB
M B A B M B C
最后杆端弯矩:
C 0
MBA = MBAP+ M B A
MBC = MBCP+ M B C
M B A
M B C
M B A BA (M B ) M B C BC (M B )
15 k N.m
C
CA
CH
0.4
0.2
E
CE
CH
0.4
结点7.11
20kN/m
↓↓↓↓↓↓A↓↓↓↓
7.11
杆端 AG
AC
CA
μ
0.5
0.5
0.4
0m.78 -2.6135 2.63
7.5 7.5 1.58 -1.508.75
3.75 -1.50
0.37 0.38 M图(kN.m)
0.19
0.79
- 0.04 0.79-0.08
0.02 0.02
M -7.11 7.11
2.36
C CH 0.2
-0.75 -0.03
-0.78
E
CE
CH
0.4
-1.50 - 0.75 -0.08 - 0.04 -1.58 -0.79
例、 求矩形衬砌在上部土压力作用下的弯矩图。
q
↓↓↓↓↓↓↓↓↓↓↓↓↓↓
A I1 E
20 62 8
90kN m
200kN 60 20kN/m
MB= MBA+ MBC= 60kN m
快速绘制弯矩图的一些规律及示例15页文档

41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
42、只有在人群中间,才能认识自 己。——德国
43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
快速绘制弯矩图的一些规律及示例
36、如果我们国家的法律中只有某种 神灵, 而不是 殚精竭 虑将神 灵揉进 宪法, 总体上 来说ቤተ መጻሕፍቲ ባይዱ 法律就 会更好 。—— 马克·吐 温 37、纲纪废弃之日,便是暴政兴起之 时。— —威·皮 物特
38、若是没有公众舆论的支持,法律 是丝毫 没有力 量的。 ——菲 力普斯 39、一个判例造出另一个判例,它们 迅速累 聚,进 而变成 法律。 ——朱 尼厄斯
材料力学与结构力学中关于快速做出弯矩图的讨论

材料力学与结构力学中关于快速做出弯矩图的讨论作者:李帅郭永博来源:《农家科技下旬刊》2014年第06期摘要:本来通过对材料力学,结构力学中做弯矩图的方法进行讨论,提出在材料力学中运用“走路法”做剪力图再做弯矩图的讨论,在结构力学中运用“斜率支反力叠加法”做弯矩图,避免繁琐的平衡方程的求解。
关键词:弯矩图;走路法;斜率支反力叠加法材料力学,结构力学中做内力图的先后顺序不同,导致了做内力图的方法也就不同。
材料力学中一般是做剪力图后座弯矩图,而结构力学一般是先做弯矩图再做剪力图,荷载剪力,弯矩本身存在着微积分关系,在一定的条件下,可以由其中的一个图来做其他图。
本文针对材料力学,结构力学中做弯矩图的常规顺序,提出在材料力学中运用走路法做弯矩图,其形象生动。
在结构力学中运用斜率支反力叠加法做弯矩图,避免繁琐的的绘制杆端受力图,平衡方程求解弯矩的过程。
一、内力图的形状特征1.1荷载与内力之间的关系在荷载连续分布的直杆段内,取微段dx为隔离体,如图所示,其中分布荷载集度q向下取正,有平衡条件可导出微分关系如下M为弯矩,F为剪力。
dF/dx=-qdM/dx=F1.2内力图的形状特征由微分关系可得到内力图在一段直杆上的形状特征(零、平、斜、抛。
)1.2.1无非布荷载区段(q=0)。
剪力图为一平行轴线弯矩图为一斜直线(即零、平、斜)。
如果在一段各截面的剪力都为零,弯矩图为平行轴线,即各截面弯矩为一常数。
1.2.2均匀荷载作用区段(荷载图为平直线)。
剪力图为一斜直线。
(斜直线两端截面的剪力差为分布荷载的合力。
)弯矩图为一抛物线。
(抛物线的凸向即为荷载的指向)即(平、斜、抛。
)剪力为零处,弯矩达到极值。
1.2.3横向力集中处,剪力图有突变,突变值等于集中力的值。
弯矩图连续,但发生转折,形成尖点。
尖点的指向与集中力的指向相同。
1.2.4集中力偶作用处剪力图无变化,弯矩图有突变。
突变的值为该集中力偶的值。
因为集中力偶作用处两侧的剪力值相等。
结构力学含有轴向载荷超静定结构弯矩计算新方法

22ft工科拭2020年•第11期结构力竽金有轴向裁荷超静定结构弯矩计算新方法◊长江大学机械工程学院夏成宇方永吕志鹏黄壮王志亮陈银超静定梁的求解相对复杂,含有轴向载荷的超静定梁问题则更难求解。
为解决含有轴向载荷的超静定梁问题,本文建立了含有轴向载荷的梁弯曲变形的力学模型,运用微元法建立了弯曲拓展方程。
结合梁的边界条件,通过中心差分法对弯曲拓展方程进行求解,运用计算机计算获得梁上任意截面的剪力、弯矩、转角和挠度。
通过与文献中的实例进行对比,验证了本文方法的准确性。
在此基础上,分析了轴向载荷对梁弯曲变形的影响,分析结果表明轴向载荷对梁变形的影响不能忽略,轴向压力会增加梁的挠度,轴向拉力与之相反,且轴向载荷越大,作用效果越明显。
该方法通用性强,能够求解复杂载荷下的超静定问题,同时也适用于多次超静定以及变刚度梁的求解。
超静定梁的弯曲变形问题一直是材料力学、结构力学和工程力学等学科的重点和难点,其求解过程通常要判断静不定次数、解除多余约束、选定静定基、列变形协调方程等X,求解过程十分复杂,极易出错。
为了寻求更好的方法计算梁的弯曲变形问题,学者们提岀了多种算法,诸如初参数法旳、有限单元法曲、积分法固定端法问、差分法X"等。
这些方法能够求解一定情况下的超静定问题,但均没有考虑轴向载荷对梁弯曲变形的影响,而实际上轴向载荷对梁弯曲变形的影响很大。
本文运用微元法建立了梁的弯曲拓展方程式,通过中心差分法,结合梁的边界条件和载荷情况,求岀了梁上各截面的挠度,进而求得梁的剪力、弯矩、转角。
该方法利用计算机进行计算,将计算结果与参考文献冲算例的解析解进行对比分析,验证了本方法的准确性,说明了本文方法适用于多次超静定问题的求解。
同时,分析了轴向载荷对梁弯曲变形的影响,结果表明轴向载荷越大,其对梁弯曲变形的影响越明显,并且在轴向载荷为压力时,随着轴向载荷的增大,梁上的最大剪力、最大弯矩、最大转角、最大挠度随之增大;在轴向载荷为拉力时,随着轴向载荷的增大,梁上的最大剪力、最大弯矩、最大转角、最大挠度随之减小。
