储层表征与建模
《储层表征与建模》确定性建模

n
z* x0 i zxi i 1
第一节 克里金插值方法
克里金方法(Kriging), 是以南非矿业 工程师D.G.Krige (克里格)名字命名的一项 实用空间估计技术,是地质统计学 (Matheron,1963) 的重要组成部分,是地质 统计学的核心。
地质统计学
空间函数的相关性分析 克里金估计 随机模拟
克里金插值
根据待估点周围的
若干已知信息,应用变
差函数的性质,对待估
点的未知值作出无偏、 最优的估计。
x0
n
z* x0 i zxi i 1
无偏 E Zx0 Z * x0 0 最优 Var Zx0 Z * x0 min
c为基台值,a为变程, h为滞后距。
接近原点处,变差函 数呈线性形状,在变
程处达到基台值。
原点处变差函数的切 线在变程的2/3处与 基台值相交。
h0 ha
ha
指数模型:
h
c
Exp
h a
c
1
exp
3h a
变差函数渐近地逼近 基台值。
第四章
确定性建模
Deterministic Modeling
确定性建模概述 地质统计学克里金方法
三维地质建模
数据库
油藏数模
模型粗化
三维构造建模 三维相建模
三维储层参数建模
地层-构造建模
构造模型反映储层的空间格架。在建立储层 属性的空间分布之前,应进行构造建模。
三维断层(fault)模型 三维层面(horizon)模型
储层宏观表征与建模

储层表征与建模
2020/8/3
Reservoir Characterization and Model building
4、储层宏观非均质性表征
层内非均质性
指单砂层垂向上储层性质的变化,是控制和影响砂层组内一个 单砂层垂向上注入剂波及体积的关键因素。
粒度的韵律性:单砂体内部粒度大小在垂向的变化序列
储层表征与建模
2020/8/3
Reservoir Characterization and Model building
一、宏观表征与建模 的研究内容与流程
储层表征与建模
2020/8/3
Reservoir Characterization and Model building
1、储层地质概念模型
储层表征与建模
2020/8/3
Reservoir Characterization and Model building
储层结构模型
碎屑沉积环境的三种基本储层类型 (K.J.Weber和L.C.Van Geuns,1989)
陆相
海岸相
海相
千层饼 状
席状洪积物 湖泊席状砂 风成砂丘
障壁坝 海岸沙脊沉积物
有效厚度系数:有效厚度与砂层厚度的比值,反映层内油 气的饱满程度,越大越均质。
储层表征与建模
2020/8/3
Reservoir Characterization and Model building
平均砂层厚度:砂层总厚度与总层数的比值,反映 砂体的分散程度,越大越均质。 砂岩钻遇率:钻遇砂岩的井数与总井数的比值,其 值越大砂体分布越广。 连通系数:砂厚大于平均厚度的井数与总井数的比 值,反映砂层厚度的变化,越大连通性越好。 分布系数:钻遇油层的井数与钻遇砂层的井数的比 值,反映油层的分布范围,越大油层分布越广。
《储层表征与建模》-储层表征与建模的基本步骤

(回顾内容)
相对与绝对 规模与层层间非均质 平面非均质 层内非均质 微观非均质
储层纵向分布的复杂程度 分层系数 砂岩密度
层间渗透率非均质程度
层间隔层 层间裂缝
(2)平面非均质性
砂体的平面差异性
砂体几何形态 砂体规模与各向连续性 砂体连通性 渗透率平面变化 平面渗透率的方向性
(3)低渗近致密储层(1-0.1)
孔喉半径小,接近油层下限;
几无自然产能,需大型压裂投产
(4) 低渗致密储层 (<0.1)
只能作为储气层(非常规气层),
标准致密储层(0.1-0.01) 非常致密储层 (0.01-0.001) 超致密储层 (0.001-0.0001)
标准岩心分析和测井解释不能提供可靠的资料, 需进行大型压裂等措施才能获得工业产能
总孔隙: 有效孔隙:连通的毛管孔隙及超毛管孔隙
(D= 0.2~500m) (D>500m)
无效孔隙:微毛管孔隙、死孔隙
(D=< 0.2m)
总孔隙度和有效孔隙度
测定手段:岩心 测井 ( ?) 地震 ( ?)
渗透性
在一定压差下流体可在其中流动
绝对渗透率 有效渗透率 相对渗透率
110-3m2 1.013md
≥2000 md 2000> k ≥500 500 > k ≥50 50 > k ≥10
<10
低渗透储层
低渗储层的渗透率上限?
100? 50? 10?
分类
依据:渗透率大小、渗流特征、开采方式
(1)常规低渗储层(50-10)
具自然产能,储层敏感性一般较强
(2)特低渗储层(10-1)
微孔隙发育,束缚水饱和度高,测井解释有难度; 自然产能一般达不到工业标准,需压裂投产
《储层表征与建模》期末考试试卷及答案

《储层表征与建模》A卷答题时间:2小时专业年级姓名学号分数一、判断题(对的打 ,错的打 ;每题3分,共30分)1.按照Miall(1996)的观点,曲流河点坝的顶界面属于5级界面。
()2.高岭石易发育于碱性水成岩环境,方解石易发育于酸性水成岩环境()3.钙质胶结带一般平行于地层层面分布。
()。
4.收缩裂缝的分布受控于局部构造。
()5.在其它条件相同的情况下,孔喉分布越均匀,原油的微观采出程度越高。
()6.含铁方解石的油层在低矿化度水的影响下容易发生水敏性。
()7.流动单元的分布受控于沉积相,但与成岩作用关系不大。
()8.基于目标的随机建模方法的不足之一是不能忠实于井资料。
()9.基于变差函数的估值方法属于多点统计学的范畴。
()10.序贯指示模拟可建立三维沉积相模型,因此属于基于目标的建模方法。
()二、简述题(30分)1.简述Miall(1996)构型界面的划分(6级划分)及基本特征。
(15分)2.简述储层随机建模的流程(15分)三、论述题(40分)试论述曲流河储层的宏观非均质特征。
《储层表征与建模》A卷参考答案一、判断题(对的打✓,错的打⨯;每题3分,共30分)1.按照Miall(1996)的观点,曲流河点坝的顶界面属于5级界面。
(⨯)是4级的界面。
2.高岭石易发育于碱性水成岩环境,方解石易发育于酸性水成岩环境(⨯)反了3.钙质胶结带一般平行于地层层面分布。
(⨯)。
4.收缩裂缝的分布受控于局部构造。
(⨯)5.在其它条件相同的情况下,孔喉分布越均匀,原油的微观采出程度越高。
(✓)6.含铁方解石的油层在低矿化度水的影响下容易发生水敏性。
(⨯)盐敏性7.流动单元的分布受控于沉积相,但与成岩作用关系不大。
(⨯)8.基于目标的随机建模方法的不足之一是不能忠实于井资料。
(⨯)9.基于变差函数的估值方法属于多点统计学的范畴。
(⨯)地质统计学10.序贯指示模拟可建立三维沉积相模型,因此属于基于目标的建模方法。
(⨯)二、简述题(30分)1.简述Miall(1996)构型界面的划分(6级划分)及基本特征。
【课程思政教学案例】《储层表征与建模》课程

课程名称:《储层表征与建模》课程性质:专业核心课所属一级学科:地质资源与地质工程总学时:48学时一、课程简介《储层表征与建模》课程是国家一流学科“地质资源与地质工程”(A+学科)的重要支撑课程,是油气田开发地质领域研究生的一门专业核心课。
本课程主要阐述地下非均质储层描述、预测和三维建模的理论、方法和技术。
主要教学内容包括:①储层表征内涵、信息解析与科学思维;②储层构型样式与研究方法;③储层质量差异机理与研究方法;④确定性建模原理与方法;⑤随机建模原理与方法。
采用启发性讲授、实训、研讨、习题、自学相结合的教学方式。
二、课程思政典型教学案例(一)案例名称多元融合课程思政教学模式构建与实践(二)教学目标课程教学目标:使学生掌握综合应用多学科信息和方法进行地下非均质储层描述、预测和三维建模的理论、方法和技术,并提升分析和解决复杂问题的能力、创新思维能力、团队合作能力、表达能力、自主学习能力等可迁移能力,为今后从事油气田开发地质研究工作奠定必要的基础,并为终身发展、适应和引领未来社会奠定良好的基础。
课程思政教学目标:在培养学生掌握油气储层表征与建模的基本理论和方法、提高地下地质分析和预测能力的同时,增强学生家国情怀和使命担当,坚定“我为祖国献石油”的理想与信念,使他们成为新时代“铁人精神”的传承者;同时具备创新思维能力、团队合作能力、自主学习能力等可迁移能力,为祖国石油工业培养德才兼备的合格接班人。
(三)教学过程与方法紧密围绕课程教学目标,坚持“以学生发展为中心”的原则,遵循“知识、思维、能力、素质教育并重”的课程教学理念,创新形成了一套多元融合的教学方法。
1.思维导引式授课课内理论教学环节实施思维导引式授课。
不同于传统的“单向传递”知识,思维导引式授课是根据学生课前自学测试结果构建问题链,进行层层递进的问题解析,引导学生思考,进行互动交流,得到合理认识,融知识建构与思维训练于一体,提升创新意识和高阶思维。
《储层表征与建模》储层构型模式

3st BS within a sandstone-dominated lateral-accretion deposits
Allen(1977)在第一届国际河流沉积学会议(卡尔 加里)明确提出了Fluvial architecture的概念,描述河流
层序中河道和溢岸沉积的几何形态(geometry)及内部组合 (internal arrangement )。
Reservoir architecture
不同级次储层构成 单元的几何形态、大小 、方向及其相互关系。
第二章
储层构型
Reservoir architecture
储层构型基本概念 储层构型模式(河流相) 储层构型分析
储层沉积类型
回顾内容
•冲积扇砂砾岩体 •河流砂体
滩坝 浊积岩 冲积扇
1.5 4.5
6
•湖泊砂体 •风成砂体 •海岸 砂体 •海洋三角洲砂体
42
三角洲
46
河流
我国陆相储油砂体成因类型
•陆棚(浅海)砂体
碳酸盐岩台地-盆地
第一代模式
First generation model
第二代模式
Second generation model 内部构型
第一节 储层构型基本概念
Reservoir architecture
Architecture:
日常用语: 建筑学、建筑结构、 体系结构、结构格式
地质学用语: 构型、构形、结构、 建筑结构、构成单元
构型界面 构型规模 构型要素 岩相分类
储层微观表征与建模

储层表征与建模
2020/8/3
Reservoir Characterization and Model building
泥质岩的分析鉴定 X衍射:粘土矿物含量及矿物混层比 热解分析:矿物最大热峰 镜质体反射率:有机岩成熟度
4、微观表征与建模的重点和难点
微观参数众多,如何挑选最具代表性的参数
微观参数获取困难,目前主要依靠岩心进行各种分 析化验来获得,应拓宽微观参数的获取途径,使得 其规律能够反映地下储层变化规律。
微观参数的分辨率相差悬殊
如何使得微观参数的研究和表征与宏观参数的表征 相结合,只有微观与宏观相结合,才能使微观表征 直接应用于生产。
储层表征与建模
2020/8/3
Reservoir Characterization and Model building
一、微观表征与建模概述
储层表征与建模
2020/8/3
Reservoir Characterization and Model building
微观表征与建模的研究目的意义 微观表征与建模的研究内容 微观表征与建模的研究方法 微观表征与建模的研究流程 微观表征与建模的重点和难点
一种矿物被另一种矿物所置换
方
颗 粒 边 缘 交 代
解 石 大 面 积 交 代
粘
土
储层表征与建模
2020/8/3
重结晶作用
Reservoir Characterization and Model building
储层表征与建模
2020/8/3
破裂作用
Reservoir Characterization and Model building
中国石油大学《储层表征与建模》吴胜和 第四章
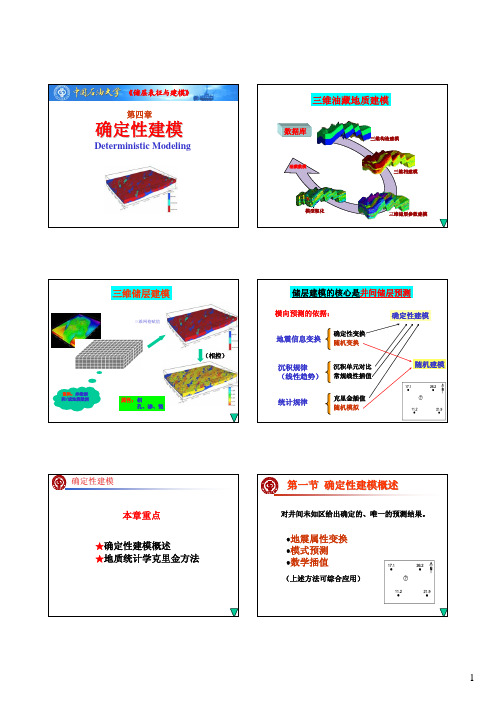
变差函数及结构分析
克里金插值方法
变差函数及结构分析
地质变量相关性的各向异性
☼1 ☼3 ☼3
☼3 ☼1 ☼1
☼3 ☼2 ☼1
h a
γ (h) = C(0) – C(h)
基台值(Sill):代表变量在空间上的总变异性大小。
即为变差函数在h大于变程时的值, 为块金值c0和拱高cc之和。 (拱高:在取得的有效数据的尺度上,可观测得到的 变异性幅度大小)。
克里金插值方法 平稳假设
二阶平稳
任何统计学均 要求平稳性假设
• 空间各点处随机变量的集合构成一个随机函数。
(将空间位置作为随机函数的自变量)
P
① 在研究区内有Z(u)的数学期望存在, 且等于常数,即:E[Z(u)] = E[Z(u+h)] = m(常数) ② 在研究区内,Z(u)的协方差函数 Cov{Z(u),Z(u+h)}存在且平稳 (即只依赖于滞后距h,而与u无关)
三维空间的水道迁移
A7 A2 A6 A1 A4 A3 A5
单井侧积层界面点提取
侧积面三维视图
确定性建模概述
地质模式拟合
确定性建模概述
三、数学插值
1. 传统数学插值
侧积层镂空视图
传统数学插值 克里金插值
如:三角剖分法(三角网方法)、 距离反比加权法等 将变量视为纯随机变量, 未考虑变量的空间结构性 仅考虑待估点位置与已知数 据位置的相互关系。
i =1
最小的估计方差,即克里金方差,可用以下公式求解:
当随机函数不满足二阶平稳,而满足内蕴(本征)假设时, 可用变差函数来表示克里金方程组: ⎧n γ (xi − x j )λi + μ = γ (x0 − x j ) ( j = 1,K, n ) ⎪ ⎪∑ i =1 ⎨ n ⎪ λi = 1 ∑ Z*(x0) ⎪ i =1 ⎩
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中国石油大学(北京)研究生考试答题纸姓名:_____________ 学号:_____________ 所属专业:___________________________考试课程:______________________________________________多点地质统计学研究进展课程名称:储层表征与建模专业年级:地质工程07级姓名:徐斌学号:S070010247任课教师:吴胜和分数:多点地质统计学研究进展摘要:本文系统的介绍了多点地质统计学的基本原理及建模方法。
在详细解释了多点地质统计学相关基本概念的基础上,阐明了Snesim算法及Simpat算法的原理及建模流程。
该类方法综合了基于象元的方法易忠实条件数据以及基于目标的方法易再现目标几何形态的优点, 同时克服了传统的基于变差函数的二点统计学不能表达复杂空间结构和再现目标几何形态的不足。
通过理论研究及结合应用实例,分析了多点地质统计学目前存在的问题及未来发展方向。
关键词:多点地质统计学随机建模Snesim算法Simpat算法多点地质统计学研究进展多点地质统计学是相对于两点地质统计学而言的。
地质统计学最初是以变差函数为工具来研究空间上既有随机性又有相关性的变量(即区域化变量)分布的一门学科,它是由法国巴黎国立高等矿业学院马特隆教授(G. Matheron)于1962年创立的,最初应用于采矿业中,主要解决矿床普查勘探、矿山设计到矿山开采整个过程中各种储量计算和误差估计问题。
近半个世纪以来,地质统计学获得了巨大的发展,其应用范围早已超出了采矿领域,气象学、生物学等学科中有可以看到它成功应用的案例,尤其是在石油工业中的应用,使它获得了进一步发展的动力。
和其它成熟的学科一样,地质统计学吸纳了其它相关学科(如人工智能、专家系统、分形系统等)的概念、理论和方法,早已超越了它最初的定义范畴。
现在的地质统计学产生了许多分支,其应用的广度和深度都有了很大的提高。
1 传统地质统计学在储层表征中的不足传统的地质统计学在储层建模中主要应用于两大方面:其一,应用各种克里金方法建立确定性的模型,这类方法主要有简单克里金、普通克里金、泛克里金、协同克里金、贝叶斯克里金、指示克里金等;其二,应用各种随机建模方法建立可选的、等可能的地质模型,这类方法主要有高斯模拟(如序贯高斯模拟)、截断高斯模拟、指示模拟(如序贯指示模拟)等。
上述方法的共同特点是空间赋值单元为象元(即网格),故在储层建模领域将其归属为基于象元的方法。
同时,这些方法均以变差函数为工具,亦可将其归属为基于变差函数的方法。
这种方法应用某一种随机模拟算法(如序贯模拟算法)以变差函数为工具求取未取样点模拟值的条件分布函数。
这种方法很灵活,易于条件化任何数据。
然而,变差函数作为传统地质统计学中研究地质变量空间相关性的重要工具,它的最大不足之处在于只能把握空间上两点之间的相关性,亦即在二阶平稳或本征假设的前提下空间上任意两点之间的相关性,对于表征复杂的空间结构和再现复杂目标的几何形态(如弯曲河道)比较困难。
如图1-1所示,三种不同的空间结构(黑色图元和白色图元的空间分布,图1-1a至图1-1c)在横向上(东西方向,图1-1d)和纵向上(南北方向,图1-1e)的变差函数十分相似,这说明应用变差函数不能区分这三种不同的空间结构及几何形态。
(a)(b)(c)(d) 三种结构东西方向的变差函数 (e) 三种结构南北方向的变差函数图1-1变差函数不能充分反映空间各向异性(Caers J, 2002)变差函数是从已有数据中推算得出,但是在实际情况中,井数据的数量通常很少,不足以获得一个可靠的三维变差函数模型,在横向上尤其如此。
即便井数据足够多,因为井通常被部署在有利于油气聚集的地方,因而并不能代表整个储层。
因此,以变差函数为工具来捕获所要研究对象的空间变化性,无论从质和量的角度来说都是不合适的。
以它为基础的传统地质统计学的插值和模拟方法因而难于精确表征具有复杂空间结构和几何形态的地质体。
而基于目标的方法虽然可以很好地再现目标体的几何形态,但是它是一种迭代算法,存在收敛性的问题,同时在条件化数据等方面也有不足。
为了建立更加合理的地质模型,多点地质统计学方法应运而生。
多点地质统计学是相对于传统的两点地质统计学而言的。
在多点地质统计学中,应用“训练图像”代替变差函数表达地质变量的空间结构性,因为可以考虑到多个点的相关性,可以克服传统地质统计学不能再现目标体几何形态的不足。
2 多点地质统计学基本概念多点地质统计学从上世纪90年代开始发展,是从传统的两点地质统计学中引申出来。
传统的地质统计学以变差函数为工具研究空间两点的相关性,但随着研究深入,逐渐发现两点之间的变化性不足以体现储层非均质的复杂性。
因而要求研究多于两点的变化性。
为此,多点地质统计学应运而生。
在多点地质统计学中使用训练图像来描述先验地质概念,可以用多个训练图像来反映不同规模的储层非均质性。
为了解多点地质统计学的思想,首先要了解几个相关概念:(1) 数据事件鉴于两点统计学只能考虑空间两点之间的相关性这一不足,多点统计学着重表达多点之间的相关性。
“多点”的集合用一个新的概念,即数据事件(data event )来表述(Strebelle and Journel,2001)。
考虑一种属性S (如沉积相),可取K 个状态(如不同相类型),即{S k , k=1,2,…K},则一个以u 为中心,大小为n 的“数据事件”d n 由以下两部分组成:①由n 个向量{h α, α=1,2,…n}确定的几何形态(数据构形),亦称为数据样板(data template ),记为τn ;②n 个向量终点处的n 个数据值。
如图2-2(a)为一个五点构形的数据事件,由一个中心点和四个向量及数值组成。
多点统计可表述为一个数据事件}n ,...1,s ){S(u d k n ===ααα出现的概率,即数据事件中n 个数据点s (u 1)…s (u n )分别处于s k 1…s k n 状态时的概率,也可表述为n 个数据指示值乘积的数学期望,即:(2)训练图像在实际建模过程中,上述多点统计或概率难于通过稀疏的井资料来获取,而{}(){}()⎥⎦⎤⎢⎣⎡====∏=n k n k I n s S d 1;E ,1;Prob Prob ααααααu u (1)需要借助于训练图像。
训练图像(既可以是二维也可以是三维)是一个先验地质模式,能够表述实际储层结构、几何形态及其分布模式。
对于沉积相建模而言,训练图像相当于定量的相模式,它不必忠实于实际储层内的井信息,而只反映一种先验的地质概念,它和传统地质统计学中的变差函数所起的作用是类似的:产生目标储层的地质模式,然后应用到实际储层数据上去(测井数据、地震数据及生产数据)。
尽管从数学角度上讲,变差函数也是一种存贮地质模式的统计工具,但它的不足之处在于:①只考虑两个点的相关性,所能表示的地质模式的复杂性受到了限制;②由于它的计算方法不简洁、不直观,很难为一般地质人员所使用。
在多点地质统计学中用训练图像代替变差函数作为度量储层非均质性的工具,能够再现地质体的曲线型特征,对储层预测有重要的作用。
更为重要的是,它在进行模拟之前,就已经对将要产生什么样的模拟结果心中有数了,对于一个普通地质人员来说,判定一个训练图像是否正确比判定一个变差函数是否正确容易得多,因而更直观、更方便。
训练图像可以由以下几种方法产生:①由基于目标的算法产生的非条件实现;②储层原型的模拟实现;③露头或现代沉积照片的数字化结果。
④地质家的手绘草图。
如图1-2(b)为一个反映河道(黑色)与河道间(白色)分布的训练图像。
(3) 数据事件概率的求取一个给定的数据事件的概率可以通过应用该数据事件对训练图像进行扫描来获取。
对于任一给定的数据样板τn和一个训练图像T,定义“侵蚀的训练图像”T n为诸点的集合,使得以u为中心的数据样板τn中的所有n个结点都在训练图像T内。
“侵蚀的训练图像”T n的大小用N n表示。
而在应用任一给定的数据样板τn对一个训练图像T进行扫描的过程中,当训练图像中一个数据事件与数据样板的数据事件d n相同时,称为一个重复。
这样,在平稳假设的前提下,数据事件d n 在侵蚀的训练图像中的重复数c (d n )与侵蚀的训练图像大小N n 的比值,就相当于该数据事件d n 出现的概率,即多点统计。
(2)(4) 条件概率分布函数(cpdf )的求取任何基于象元的随机模拟算法均要求获取待模拟点的条件概率分布函数(cpdf ),即对于任一未取样点,需要确定在给定n 个条件数据(记为n ,...1,s )S(u k ==ααα)情况下,属性S (u)取K 个状态中任一个状态的概率。
在多点统计模拟中,该概率可记为Prob{s (u)=s k |d n },其中,d n 为由n 个条件数据联合构成的数据事件。
根据贝叶斯条件概率公式,该概率可表达为:(3)上式中,分母为条件数据事件(n ,...1,s )S(u k ==ααα)出现的概率,可从公式(2)获取;分子为条件数据事件及未取样点u 取s k 状态的情况下同时出现的概率,相当于在已有的c(d n )个重复中s(u)=s k 的重复的个数与侵蚀的训练图像大小N n 的比值,记为n n k )/N (d c 。
因此,局部条件概率分布函数可表达为:(4)因此,通过扫描训练图像,可获取未取样点处的条件概率分布函数。
如图1-2所示,图1-2(a)为模拟目标区内一个由未取样点及其邻近的四个井数据(u 2和u 4代表河道,u 1和u 3代表河道间)组成的数据事件,当应用该数据事件对图1-2(b)的训练图像进行扫描时,可得到4个重复,即c(d n )=4,其中,中心点为河道(黑色)的重复为3个,即c 1(d n )=3,而中心点为河道间(白色)的重复为1个,即c 2(d n )=1,因此,该未取样点为河道的概率可定为3/4,而为河道间的概率为1/4。
(){}()n n k N d c n s s ≈== ,1;Prob αααu (){}()(){}(){}n s S ns S s S d s S k k k n k ,1;Prob ,1;and Prob |Prob =======ααααααu u u u ()(){}()()n n k n k k k d c d c d s p n s S s S ≈====)|;(,1;|Prob u u u ααα(a)(b)图1-2 数据事件与训练图像示意图(a) 数据事件:由中心点u和邻近四个向量构成的五点数据事件,其中u2和u4代表河道,u1和u3代表河道间;(b) 训练图像:反映河道(黑色)与河道间(白色)的平面分布。
