第四章平面镜棱镜系统应用光学
合集下载
2019-L12-C4-4棱镜成像判断-文档资料

应用光学 Applied Optics
光信息0701-02 2009-2019第一学期
Applied optics
第四章 平面镜棱镜系统
2
Applied optics
C4. 平面镜棱镜系统 – 棱镜成像方向判断
3
Applied optics
上节内容回顾
一、屋脊棱镜 y
y x
x
z y′ z′ x′
z y′ z′
x′
4
Applied optics
上节内容回顾
二、等效空气层厚度 棱镜尺寸计算
A
A’
O
e
O’’
O’ S
S’
s s ' ( 1 1 /nL )
e L/ n
【O、L、n】相当于 【O、L/n、1】
5
Applied optics
4-6 棱镜成像方向判断
一、棱镜系统成像方向判断
二、组合系统成像方向判断
37
Applied optics
系统成像=
棱镜系统成像(镜像/一致像) + 球面系统成像(正像/倒像)
38
注意转折方向,平行并不一定同向
12
Applied optics
y & y’:主截面内方向(I) • 与是否有屋脊面无关, • 按光轴转向和光轴反射次数判断
光轴同向:Fig. 4-25(a), 4-26(a) 光轴反向:Fig. 4-25(b), 4-26(b) …… 缺点:需要判断光轴的转向性质,涉及光轴 在每个反射面的情况。繁!
物空间右手系---棱镜系统---像空间?
两种方法 • 反弹转折法 • 法则
8
Applied optics
反弹法
光信息0701-02 2009-2019第一学期
Applied optics
第四章 平面镜棱镜系统
2
Applied optics
C4. 平面镜棱镜系统 – 棱镜成像方向判断
3
Applied optics
上节内容回顾
一、屋脊棱镜 y
y x
x
z y′ z′ x′
z y′ z′
x′
4
Applied optics
上节内容回顾
二、等效空气层厚度 棱镜尺寸计算
A
A’
O
e
O’’
O’ S
S’
s s ' ( 1 1 /nL )
e L/ n
【O、L、n】相当于 【O、L/n、1】
5
Applied optics
4-6 棱镜成像方向判断
一、棱镜系统成像方向判断
二、组合系统成像方向判断
37
Applied optics
系统成像=
棱镜系统成像(镜像/一致像) + 球面系统成像(正像/倒像)
38
注意转折方向,平行并不一定同向
12
Applied optics
y & y’:主截面内方向(I) • 与是否有屋脊面无关, • 按光轴转向和光轴反射次数判断
光轴同向:Fig. 4-25(a), 4-26(a) 光轴反向:Fig. 4-25(b), 4-26(b) …… 缺点:需要判断光轴的转向性质,涉及光轴 在每个反射面的情况。繁!
物空间右手系---棱镜系统---像空间?
两种方法 • 反弹转折法 • 法则
8
Applied optics
反弹法
华中科技大学 《应用光学》课程PPT——第四章 平面镜与平面系统
第四章 平面镜与平面系统
平面镜
平行平板
反射棱镜
折射棱镜
平面镜、棱镜在光学系统中的作用:
● 倒像变为正像 ● 改变光轴位置和方向 ● 分光作用 ● 折叠系统、缩小体积、减轻重量 ● 通过旋转改变光路方向,扩大观察范围
§ 4-1 平面镜成像特性
1. 成完善像: 物点发出的同心光束经反 射镜反射后仍成同心光束。
3)表示方法:
规定:物为左手坐标系,oz轴为光轴方向,yoz面和主截面重合, ox轴垂直于主截面,并和所有的反射面平行,通过棱镜组后的坐 标为x′y′z′ 。 原则:①光轴方向 z' 不变 ②垂直于主截面的坐标 x' 视屋脊个数而 定 ③ y‘ 坐标根据总反射次数而定, (一个屋 脊棱算两次反射)而定。奇数次反射,改 变坐标系,偶数次反射坐标系不变。
作业:
4.1,4.2,4.6,4.7,4.10,4.11,4.12
1)光线经平行板折射后,虽然方向不变,但要产生位移。 2)从点A发出的具有不同入射角的各条光线经平行板折射后,具有 不同的轴向位移值,平行板成象是不完善的。
3. 近轴光成像:
sin I1 cos I1 sin I1 1 tgI1 lim I1 0 tgI sin I1 cos I1 sin I1 n 1
2
4
6
A4
8
A5
波长一般以nm为单位。
二、玻璃的选择: 1、可用性 2、透射性 3、双折射性 4、化学稳定性 5、热特性
三、塑料光学材料: 优点:较低的质量、较高的抗冲击性,能提供更多 的形状,可塑造非球面透镜和其他复杂的形状。 缺点:较低的耐温性、耐磨性,抗化学性较差,镀 膜的附着性低,膜层的耐用性也低。
平面镜
平行平板
反射棱镜
折射棱镜
平面镜、棱镜在光学系统中的作用:
● 倒像变为正像 ● 改变光轴位置和方向 ● 分光作用 ● 折叠系统、缩小体积、减轻重量 ● 通过旋转改变光路方向,扩大观察范围
§ 4-1 平面镜成像特性
1. 成完善像: 物点发出的同心光束经反 射镜反射后仍成同心光束。
3)表示方法:
规定:物为左手坐标系,oz轴为光轴方向,yoz面和主截面重合, ox轴垂直于主截面,并和所有的反射面平行,通过棱镜组后的坐 标为x′y′z′ 。 原则:①光轴方向 z' 不变 ②垂直于主截面的坐标 x' 视屋脊个数而 定 ③ y‘ 坐标根据总反射次数而定, (一个屋 脊棱算两次反射)而定。奇数次反射,改 变坐标系,偶数次反射坐标系不变。
作业:
4.1,4.2,4.6,4.7,4.10,4.11,4.12
1)光线经平行板折射后,虽然方向不变,但要产生位移。 2)从点A发出的具有不同入射角的各条光线经平行板折射后,具有 不同的轴向位移值,平行板成象是不完善的。
3. 近轴光成像:
sin I1 cos I1 sin I1 1 tgI1 lim I1 0 tgI sin I1 cos I1 sin I1 n 1
2
4
6
A4
8
A5
波长一般以nm为单位。
二、玻璃的选择: 1、可用性 2、透射性 3、双折射性 4、化学稳定性 5、热特性
三、塑料光学材料: 优点:较低的质量、较高的抗冲击性,能提供更多 的形状,可塑造非球面透镜和其他复杂的形状。 缺点:较低的耐温性、耐磨性,抗化学性较差,镀 膜的附着性低,膜层的耐用性也低。
印刷应用光学4

B Q
Q
单个平面镜成像性质: (1)平面镜能使整个空间理想成像,物点和像点对平面镜
对称; (2)物和像大小相等,但形状不同,物空间的右手坐标在
像空间变为左手坐标;如果分别对着入射和出射光线
的方向观察物平面和像平面,当物平面按逆时针方向 旋转时,像平面则按顺时针方向旋转,形成“镜像”。 奇数次反射为镜像,偶数次反射为一致像。
当棱镜中的一个或多个反射面被称做屋脊的两个 相互垂直的反射面所取代,且屋脊的顶位处于主截面 内,这种棱镜称为屋脊棱镜。
y x
z
y x
z
y′ z′ x′
y′
棱镜系统成像的物象坐标的变化
z′ x′
⑴沿着光轴的坐标轴(图中的z轴)在整个成像过程中始终保持沿着光轴.并指向光的传播方向: ⑵垂直于主截面的坐标轴(图中的x轴)在一般情况下保持垂直于主截面,并与物坐标同向。但当遇有 屋脊面时,每经过一个屋脊面反向一次. ⑶在主截面内的坐标轴(图中的y轴)由平面镜的成像性质判断,根据反射镜具有的奇次反射成镜像、 偶次反射成一致像的特点,首先确定光在棱镜中的反射次数.再按系统成镜像还是一致像来决定该坐 标轴的方向:成镜像反射时坐标左右手系改变,成一致像反射时左右手系不变。注意,在统计反射次 数时,每一屋脊面被认为是两次反射,按两次反射计数。
该性质可用于测量物体的微小转角或位移。
光学比较仪中的光学杠杆
M
L1
A
H H'
A'
M
MM为分划板
M
L1
a)
A'
2α
F'
A
H H'
M -f b)
P
支点 a
测杆 P P PP为
反射镜
Q
单个平面镜成像性质: (1)平面镜能使整个空间理想成像,物点和像点对平面镜
对称; (2)物和像大小相等,但形状不同,物空间的右手坐标在
像空间变为左手坐标;如果分别对着入射和出射光线
的方向观察物平面和像平面,当物平面按逆时针方向 旋转时,像平面则按顺时针方向旋转,形成“镜像”。 奇数次反射为镜像,偶数次反射为一致像。
当棱镜中的一个或多个反射面被称做屋脊的两个 相互垂直的反射面所取代,且屋脊的顶位处于主截面 内,这种棱镜称为屋脊棱镜。
y x
z
y x
z
y′ z′ x′
y′
棱镜系统成像的物象坐标的变化
z′ x′
⑴沿着光轴的坐标轴(图中的z轴)在整个成像过程中始终保持沿着光轴.并指向光的传播方向: ⑵垂直于主截面的坐标轴(图中的x轴)在一般情况下保持垂直于主截面,并与物坐标同向。但当遇有 屋脊面时,每经过一个屋脊面反向一次. ⑶在主截面内的坐标轴(图中的y轴)由平面镜的成像性质判断,根据反射镜具有的奇次反射成镜像、 偶次反射成一致像的特点,首先确定光在棱镜中的反射次数.再按系统成镜像还是一致像来决定该坐 标轴的方向:成镜像反射时坐标左右手系改变,成一致像反射时左右手系不变。注意,在统计反射次 数时,每一屋脊面被认为是两次反射,按两次反射计数。
该性质可用于测量物体的微小转角或位移。
光学比较仪中的光学杠杆
M
L1
A
H H'
A'
M
MM为分划板
M
L1
a)
A'
2α
F'
A
H H'
M -f b)
P
支点 a
测杆 P P PP为
反射镜
(应用光学)第四章平面镜棱镜成像

应用光学(第四版)
4 平面镜棱镜系统
两个互相垂直 的反射面称为
屋脊面
直角棱镜
屋脊棱镜
这种两个互相垂直的反射面称为屋脊面, 而带有屋脊面的棱镜称为屋脊棱镜。
应用光学(第四版)
4 平面镜棱镜系统
y x
z
y′
z′
x′
y
x z
z′ y′
x′
一次镜面反射成镜像,两次镜面反射成一致像。
一次屋脊棱镜成一致像,两次屋脊棱镜成一致像。
当两平面镜一起转动时,出射光线的 转角不变,出射光线位置发生平移。
右手坐标系经两次反射重新还原成为
右手坐标系,成一致像。
应用光学(第四版)
4 平面镜棱镜系统 4.4~4.6 棱镜的展开与棱镜外形尺寸的计算
一、平行平板的成像性质
即入射光与出射光相互平行。
应用光学(第四版)
4 平面镜棱镜系统
• 平行平面板的出射光线BS′ 和入射光线SA是平行的
4 平面镜棱镜系统
二、棱镜转动定理
考虑:像的方向 像的位置
P' P' P
P
符号规则 ;对着转轴向量观察时,逆时针 为正,顺时针为负。
棱镜转动定理
应用光学(第四版)
4 平面镜棱镜系统 1、在平行光路中工作的棱镜,绕垂直于棱镜主界面的z轴转动
y
z
x
应用光学(第四版)
y'
z'
x'
4 平面镜棱镜系统
应用光学(第四版)
∠A’OA”=2∠POP’,转动方向于平面镜转动方向相同
应用光学(第四版)
4 平面镜棱镜系统 • 平面镜的平移
A B
P
Q
h
4 平面镜棱镜系统
两个互相垂直 的反射面称为
屋脊面
直角棱镜
屋脊棱镜
这种两个互相垂直的反射面称为屋脊面, 而带有屋脊面的棱镜称为屋脊棱镜。
应用光学(第四版)
4 平面镜棱镜系统
y x
z
y′
z′
x′
y
x z
z′ y′
x′
一次镜面反射成镜像,两次镜面反射成一致像。
一次屋脊棱镜成一致像,两次屋脊棱镜成一致像。
当两平面镜一起转动时,出射光线的 转角不变,出射光线位置发生平移。
右手坐标系经两次反射重新还原成为
右手坐标系,成一致像。
应用光学(第四版)
4 平面镜棱镜系统 4.4~4.6 棱镜的展开与棱镜外形尺寸的计算
一、平行平板的成像性质
即入射光与出射光相互平行。
应用光学(第四版)
4 平面镜棱镜系统
• 平行平面板的出射光线BS′ 和入射光线SA是平行的
4 平面镜棱镜系统
二、棱镜转动定理
考虑:像的方向 像的位置
P' P' P
P
符号规则 ;对着转轴向量观察时,逆时针 为正,顺时针为负。
棱镜转动定理
应用光学(第四版)
4 平面镜棱镜系统 1、在平行光路中工作的棱镜,绕垂直于棱镜主界面的z轴转动
y
z
x
应用光学(第四版)
y'
z'
x'
4 平面镜棱镜系统
应用光学(第四版)
∠A’OA”=2∠POP’,转动方向于平面镜转动方向相同
应用光学(第四版)
4 平面镜棱镜系统 • 平面镜的平移
A B
P
Q
h
应用光学第4章
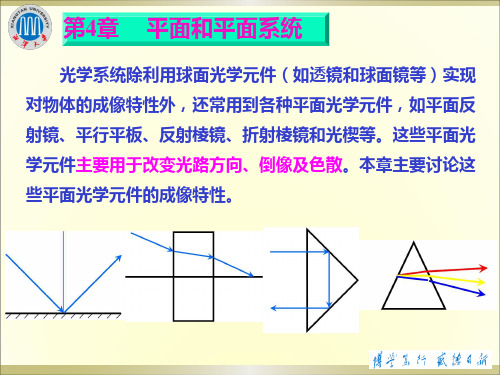
G
U2
结论2:平行平板不使物
( A2 ) A1
O1
n2 n n1
d
O2 1 n2
体放大或缩小。
光线经平行平板后方向虽然保持不变,却要 产生一定的位移,这个位移记为轴向位移ΔL′
A1F平行于GE I1 N2 EG I 2 I1 O1O2 d d ) FG FE sin(FEG) sin(N 2 EG N 2 EF ) sin(I1 I 2 ) sin(I1 I1 cos I1 cos I1 cos I1
I1
工作面 主截面
1 I 1 I 2
n
2
I2
2.偏向角的求出
sin I1 n sin I1
两式相减 n(sin I1 sin I 2 ) sin I1 sin I 2 和差化积 n sin I 2 sin I 2
sin I1 I 2 I I I I I I cos 1 2 n sin 1 2 cos 1 2 2 2 2 2
(cos cos '')i (cos cos '') j (cos cos '') k ) 2[1 (cos cos '' cos cos '' cos cos '')]
作业2.3:一玻璃球直径60mm,折射率为1.5,一束平行光 射在球上,问会聚点在什么位置?
45
最常见的是斯密特棱镜。使出射光
45
线和入射光线的夹角为45°。成 镜像,大大缩小筒长,结构紧凑。
二、 屋脊棱镜
对奇次反射的反射棱镜,为了避
U2
结论2:平行平板不使物
( A2 ) A1
O1
n2 n n1
d
O2 1 n2
体放大或缩小。
光线经平行平板后方向虽然保持不变,却要 产生一定的位移,这个位移记为轴向位移ΔL′
A1F平行于GE I1 N2 EG I 2 I1 O1O2 d d ) FG FE sin(FEG) sin(N 2 EG N 2 EF ) sin(I1 I 2 ) sin(I1 I1 cos I1 cos I1 cos I1
I1
工作面 主截面
1 I 1 I 2
n
2
I2
2.偏向角的求出
sin I1 n sin I1
两式相减 n(sin I1 sin I 2 ) sin I1 sin I 2 和差化积 n sin I 2 sin I 2
sin I1 I 2 I I I I I I cos 1 2 n sin 1 2 cos 1 2 2 2 2 2
(cos cos '')i (cos cos '') j (cos cos '') k ) 2[1 (cos cos '' cos cos '' cos cos '')]
作业2.3:一玻璃球直径60mm,折射率为1.5,一束平行光 射在球上,问会聚点在什么位置?
45
最常见的是斯密特棱镜。使出射光
45
线和入射光线的夹角为45°。成 镜像,大大缩小筒长,结构紧凑。
二、 屋脊棱镜
对奇次反射的反射棱镜,为了避
最新应用光学平面镜棱镜系统教学课件PPT教学讲义PPT

当平面镜旋转θ 角时,出射光线相对于原出射 光线将旋转2 θ 角,而且旋转的方向与镜的旋转 方向一致。
二、双平面镜的成像特性
✓θ
2θ
2θ
θ
济南大学物理学院 工程光学课件
12
证明
✓θ
β=2θ
M1
2I1 2I2
I1 I2
2
I2 I2 θ
I1
I1
M2
I1I2/2
I1I2
与入射角无关 上式恒成立
济南大学物理学院 工程光学课件
D0.33a4
(n1.516)3
D
通光口径仅有原来的1/3
D 道威棱镜
为了在一定通光口径的 条件下,减小棱镜尺寸 两个棱镜同时使用。
济南大学物理学院 工程光学课件
35
这样就组成了立方棱镜 D
D
立方棱镜的一个特点是棱镜尺寸小,通光口径大
立方棱镜的两反射面必须平行,且两反射面必须 镀膜。
立方棱镜只能工作在平行光路中
33
展开图为:
由图可求出展开长度
L AC FG D tan 600 D tan 300 4 3D
3
济南大学物理学院 工程光学课件
34
4. 立方棱镜
直角棱镜的通光口径较大,但是当采用旋转棱镜 改变光轴方向时,此时通光口径就变小了,这样 进入光学系统的光能减少,影响成像质量。
如图所示
a
由几何分析可知:
对2002年3月至2003年12 月间在我院行超声乳化人 工晶体植入手术的415例 (453眼)患者,按照民族 不同分为治疗组(维吾尔、
哈萨克族)与对照组(汉 族),治疗组共227例239 眼,对照组188例214眼。
设备及参数设置
应用光学第四章

反射棱镜(léngjìng)的类型
(2) 屋脊(wūjǐ)棱 当棱镜镜中的一个(或多个)反射面由被称作屋脊的两个互 相垂直的反射面所取代,且屋脊的顶位于主截面内(如图 4-13b),这种棱镜称为屋脊棱镜。屋脊面的作用是增加 一次反射,以改变物像的坐标系关系 。
y
z O x
y Oz
x
y' O'
x' z'
tgI1 ' sin I1 ' 1 代入式(4-7),得 l' d (1 1 ) (4-9)
tgI1 sin I1 n
n
该式表明,在近轴区,平行平板对物点的轴向
位移Δl′只与平板的厚度和折射率有关,而与物
体的位置以及孔径角无关。
精品资料
平行(píngxíng)平板的等效空气层
如图4-21所示 ,等效(děnɡ
任何情况下,维持沿光轴 的坐标轴(如z轴)方向不
变,但透镜成倒像时,将 使物面上的两个垂直于光
轴的坐标轴(如x轴和y轴)同时 反向。
y z
x z'
x' y'
x" y" z"
图4-16 复合棱镜的坐标变换
精品资料
棱镜系统(xìtǒng)成像的物像坐标
变化
例4-1:判断(pànduàn)图4-17中物体经光学 系统后的坐标方向。
前表面的折射角)
精品资料
反射棱镜的等效作用(zuòyòng)与 展开
图4-18多种棱镜的展开(zhǎn kāi) a)二次反射直角棱镜;b)道威棱镜; c)五角棱镜;
d)等边棱镜;e)半五角棱镜;f)斯密特棱镜
精品资料
反射棱镜的等效(děnɡ xiào)作用与 展开
第四章平面镜棱镜系统应用光学

将共轴系统折叠以缩小仪器的体积和减轻仪 器重量;
改变像的方向--起倒像作用; 改变共轴系统中光轴的位置和方向,形成潜 望高或使光轴转一定角度;
利用平面镜棱镜旋转,可以连续改变系统光 轴方向,以扩大观察范围
应用光学讲稿
第二节 平面镜的成像性质
一、任意物点通过单个平面镜的成像情况
求证:A点成像于A’
L e n
相当空气层的含义: 1.像面与玻璃板第二表面的距离与物平面离相当空 气层的第二表面的距离相当,即像距相当
2.投射高相当
3.像的大小相当
应用光学讲稿
例:一个薄透镜组,焦距为100,通光口径为20。利用它 使无限远物体成像,像的直径为10。在距离透镜组50处 加入一个五角棱镜,使光轴折转90°,求棱镜的尺寸和 通过棱镜后的像面位置。 由于物体位在无限远,像平面位在像方焦面上。根 据给出的条件。全部成像光束位于一个高为100,上底和 下底分别为10和20的梯形截面的锥体内,如图6-22(a)所 示。
应用光学讲稿
总结以上: 单平面镜对空间物体成像符合理想,物像关 于平面镜对称;像的大小与物的大小相等, 形状不同;成镜像。
应用光学讲稿
三、平面镜系统的成像性质 成像理想 空间对应情况:奇数个平面镜,成镜像;
偶数个平面镜,物象相似。
注意: 1、像的正、倒与相似不是一回事; 2、物体与镜像形状不同,不相似不能重合。
应用光学讲稿
第三节 平面镜的旋转及应用
一、单个平面镜的转动
A N N’ B
I
I I O
I
B’ P
Hale Waihona Puke 结论:入射光线不动,单平面镜转动 反射光线的转动量为2 转动方向与平面镜旋转方向相同
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应用光学讲稿
1:作出共轴系统的光路图 2:求棱镜第一个表面的通光直径为 D1=(20+10)/2=15
3:求棱镜展开后的平行玻璃板厚度。由“光学仪器设计 手册”可查得90°-2的五角棱镜展开以后的平行玻璃板 厚度为 L=3.414D=3.414×15=51.21
应用光学讲稿
4:求相当空气层厚度,折射率n=1.5163 e=L/n=51.21/1.5163=33.8
应用光学讲稿
第三节 平面镜的旋转及应用
一、单个平面镜的转动
A N N’ B
I
I I O
I
B’ P
结论:入射光线不动,单平面镜转动 反射光线的转动量为2 转动方向与平面镜旋转方向相同
应用光学讲稿
• 单个平面镜转动的应用 • 优点:扩大观察范围 • 缺点:转动角度引起光轴误差
应用光学讲稿
应用光学讲稿
总结以上: 单平面镜对空间物体成像符合理想,物像关 于平面镜对称;像的大小与物的大小相等, 形状不同;成镜像。
应用光学讲稿
三、平面镜系统的成像性质 成像理想 空间对应情况:奇数个平面镜,成镜像;
偶数个平面镜,物象相似。
注意: 1、像的正、倒与相似不是一回事; 2、物体与镜像形状不同,不相似不能重合。
B 1、直角棱镜 在平行光路中使用
在平行光路中只需满足 第一个条件: 展开后成平行玻璃板, 即AB // AC 则ABC ACB ACB是ACB折过去的,二者相等, ABC ACB 只要满足两角相等就能 保证AB // AC ,不一定为 45, A也不一定为直角。
应用光学讲稿
相当空气层概念
物平面经过厚度为L,折射率为n的平行玻璃板后,由平 行玻璃板的第二个表面到像平面的距离和通过厚度为 L/n的空气层后由空气层的第二个表面到像平面的距离 相等。 L ' l2 l1 n
应用光学讲稿
我们把L/n叫做厚度为L折射率为n的平行玻璃板的“相 当空气层厚度”,用e表示:
n 2 EB AB AE a(1 sin I / cos I ) 而D EB sin 45 2 2 2 将以上sin I , cos I 代入,得到 2n 2 1 若采用K 9玻璃,n 1.5163 , D 0.334a D 0.7071 a 2n 2 1 1
应用光学讲稿
结论: 单个平面镜对物点能成理想像, 物象位置相对平面镜对称,实物 成虚像,虚物成实像。
A
P
D
O O’
A’
应用光学讲稿
二、空间物体通过单平面镜反射的成像情况
y’
y
P o
z x x’ z’ o’
物像大小相等,形状不同
物空间右手坐标对应像空间左手坐标 分别迎着z、z’看xy、x’y’坐标面时,当x按逆时针方向转到y, x’按顺时针方向转到y’;物像这种对应关系称为“镜像”
应用光学讲稿
屋脊棱镜的性质:保持光轴X’和Y’的方向不变,使 垂直于主截面的方向的Z’转180度
• 作用 • 保证X’和Y’方向不变的前提下,增加了一次 反射,得到与物相似的像
应用光学讲稿
对屋脊面的要求:屋脊角必须严格等于90度,否则形成 双像 直角有一个角度误差a,出射光轴就会有4倍的误差4a
L e n
相当空气层的含义: 1.像面与玻璃板第二表面的距离与物平面离相当空 气层的第二表面的距离相当,即像距相当
2.投射高相当
3.像的大小相当
应用光学讲稿
例:一个薄透镜组,焦距为100,通光口径为20。利用它 使无限远物体成像,像的直径为10。在距离透镜组50处 加入一个五角棱镜,使光轴折转90°,求棱镜的尺寸和 通过棱镜后的像面位置。 由于物体位在无限远,像平面位在像方焦面上。根 据给出的条件。全部成像光束位于一个高为100,上底和 下底分别为10和20的梯形截面的锥体内,如图6-22(a)所 示。
缺点:体积重量较大--实心
对材料要求高--光线方向可能不只一个方向
受环境影响较大
应用光学讲稿
二、棱镜的展开——研究棱镜成像性质的方法
直角棱镜
主截面:和各个棱相垂直的截面
应用光学讲稿
1 2 3
1 2 由于折倒关系, 2 3 1 3
棱镜与反射镜的差别:光线--折射--反射--折射
应用光学讲稿
计算举例: 假设直角棱镜的口径为10,如果棱镜转动45°,则入 射和出射光轴平行,求这时的光束口径。 将棱镜展开以后玻璃板厚度L=10,棱镜材料为K9, n=1.5163,I=45°,插值求得k=0.8,将以上数值代入 公式为: E=10/1.5163×0.8=5.28
按相当空气层厚度作图, 得光束口径D为 D=MN· sin45°=(10-5.28)×0.7071=3.34
5:求像距 l2′=50-e=50-33.8=16.2
6:求棱镜第二面的口径 D2=10+(20-10)16.2/100=11.62
应用光学讲稿
光束入射角较大时的相当空气层
h1 h2 1 E O1 A NA (h1 h2 ) tg ( I1 ) tg ( I1 ) tg ( I1 )
应用光学讲稿
§4-7
确定平面镜棱镜系统成像方向的方法
平面镜棱镜系统的作用是改变光轴和像的方向。光 轴方向的改变可以直接按反射定律确定。这一节专门研 究确定平面镜棱镜系统成像方向的方法。目的有
1:已知平面镜棱镜系统,如何判断它的成像方向 2:根据对光轴方向位置以及成像方向的要求,如何 选择平面镜棱镜系统。
应用光学讲稿
1
2 3 4
2’
1’ 4’ 3’
应用光学讲稿
第五节 屋脊面和屋脊棱镜 问题的引出:
要求设计一个棱镜系统,能形成潜望高,并起倒像作用
方案1:上部直角棱镜+中间道威棱镜+下部直角棱镜
方案2:上部五角棱镜+中间道威棱镜+下部直角棱镜 或者 方案3:上部直角棱镜+中间道威棱镜+下部五角棱镜 问题:满足倒像但不能满足物像相似
第四章 平面镜棱镜系统
应用光学讲稿
本章主要解决的问题: • 平面镜、棱镜系统的成像性质及特点
• 平面镜棱镜系统与共轴球面系统配合的问题
应用光学讲稿
第一节 平面镜棱镜系统在光学仪器中的应用 • 共轴球面系统特点
所有透镜表面球心必须排列在同一条直线上 体积重量较大
应用光学讲稿
平面镜棱镜系统的主要作用:
A
N
B B’
证:任取由A点射到P的光线AO,
AOD 90 I,DOA 90 I OD OD AOD AOD AD AD
I
I
P
D O
O’
A’
由于AO是任取的,不管O点在 哪个位置,因为AD不变,A’D也 不变。所以A’的位置是确定的, 即由A点发出的任意光线经P反 射后延长线都交于一点A’,像点 是唯一的。
把棱镜的主截面沿反射面折倒,取消棱镜的反射,以平
行玻璃板的折射代替棱镜折射的方法称为“棱镜的展开” 。
应用光学讲稿
三、对棱镜的要求 1、棱镜展开后应该是一块平行玻璃板
2、如果棱镜位于会聚光束中,光轴必须和棱 镜的入射及出射表面相垂直。
棱镜展开厚度:棱镜展开以后的长度
应用光学讲稿
四、典型棱镜展开举例
h1 h2 LtgI
' 1
EtgI1 LtgI1'
sin I1' ' ' ' tgI1 cos I1 sin I1 cos I1 L cos I1 EL L L ' sin I1 tgI1 sin I1 cos I1 n cos I1' cos1
cos I1 k cos I1' L E k n
将共轴系统折叠以缩小仪器的体积和减轻仪 器重量;
改变像的方向--起倒像作用; 改变共轴系统中光轴的位置和方向,形成潜 望高或使光轴转一定角度;
利用平面镜棱镜旋转,可以连续改变系统光 轴方向,以扩大观察范围
应用光学讲稿
第二节 平面镜的成像性质
一、任意物点通过单个平面镜的成像情况
求证:A点成像于A’
应用光学讲稿
屋脊棱镜的展开 • 与普通棱镜一样沿棱展开 • 展开长度比普通棱镜长,口径大
应用光学讲稿 § 4-6 平行平板的成像性质和棱镜的外形尺寸计算
棱镜相当于在系统中多加了一块平行平板 平行平板的成像性质。
n 1 0 ' l1 l1 1 n 0 ' l2 l2
l1' nl1 l2 l n
应用光学讲稿
为了在一定通光口径下减小棱镜体积,可以把两个 同样的直角棱镜沿斜面胶合在一起,形成立方棱镜
应用光学讲稿
立方棱镜的特点 体积小:每个小棱镜的通光口径为1/3的一半 加起来为大棱镜的1/3,道威棱镜
光轴转角大:两棱镜分别工作
光束是分两束分别通过两个棱镜进入系统,过 了棱镜又合成一束,原来角度一致的平行光通过 系统后还应该角度一致,要求两个棱镜反射面严 格平行; 入射圆形光束时,出射为两个半圆;不能在圆 形光束中工作; 入射面与光轴不垂直,只能使用在平行光路中 。
满足物像相似但不能满足倒像
需要将Z方向反转
应用光学讲稿
屋脊棱镜的作用:
在不改变光轴方向和主截面内成像方向的条件 下,用两个相互垂直的反射面代替一个反射面, 增加一次反射,使系统总反射次数由奇数变成偶 数,达到物象相似的要求。
应用光学讲稿
y z
z1’
x1’ y1’
y z x
x
x2’ z2’ y2’
应用光学讲稿
双平面镜旋转:光线的转动只与两个平面镜的夹角有 关,而与入射光线的方向无关。 • 应用: • 在测距机中用双平面反射镜代替单个平面镜 • 角镜
