湖南师范大学附属中学2022-2023学年高三上学期月考(四)数学试题(解析版)
湖南省长沙市湖南师范大学附属中学2024-2025学年高三上学期月考(一)数学试题及答案

大联考湖南师大附中2025届高三月考试卷(一)数学命题人:高三数学备课组 审题人:高三数学备课组时量:120分钟 满分:150分一、选选选:本选共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,1. 已知{}()260,{lg 10}Axx x B x x =+−≤=−<∣∣,则A B = ( )A. {}32xx −≤≤∣ B. {32}x x −≤<∣ C. {12}x x <≤∣D. {12}x x <<∣2. 若复数z 满足()1i 3i z +=−+(i 是虚数单位),则z 等于( )A.B.54C.D.3. 已知平面向量()()5,0,2,1ab ==−,则向量a b +在向量b上投影向量为( )A. ()6,3−B. ()4,2−C. ()2,1−D. ()5,04. 记n S 为等差数列{}n a 的前n 项和,若396714,63a a a a +==,则7S =( ) A. 21B. 19C. 12D. 425. 某校高二年级下学期期末考试数学试卷满分为150分,90分以上(含90分)为及格.阅卷结果显示,全年级1200名学生的数学成绩近似服从正态分布,试卷的难度系数(难度系数=平均分/满分)为0.49,标准差为22,则该次数学考试及格的人数约为( )附:若()2,X Nµσ∼,记()()p k P k X k µσµσ=−≤≤+,则()()0.750.547,10.683p p ≈≈.A 136人 B. 272人C. 328人D. 820人6. 已知()π5,0,,cos ,tan tan 426αβαβαβ∈−=⋅=,则αβ+=( ) A.π6 B.π4C.π3D.2π37. 已知12,F F 是双曲线22221(0)x y a b a b−=>>的左、右焦点,以2F 为圆心,a 为半径的圆与双曲线的一条的.渐近线交于,A B 两点,若123AB F F >,则双曲线的离心率的取值范围是( )A.B.C. (D. (8. 已知函数()220log 0x a x f x x x ⋅≤= > ,,,,若关于x 的方程()()0f f x =有且仅有两个实数根,则实数a 的取值范围是( ) A. ()0,1B. ()(),00,1−∞∪C. [)1,+∞D. ()()0,11,+∞二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分9. 如图,在正方体111ABCD A B C D −中,E F M N ,,,分别为棱111AA A D AB DC ,,,的中点,点P 是面1B C 的中心,则下列结论正确的是( )A. E F M P ,,,四点共面B. 平面PEF 被正方体截得的截面是等腰梯形C. //EF 平面PMND. 平面MEF ⊥平面PMN10. 已知函数()5π24f x x=+,则( )A. ()f x 的一个对称中心为3π,08B. ()f x 的图象向右平移3π8个单位长度后得到的是奇函数的图象 C. ()f x 在区间5π7π,88上单调递增 D. 若()y f x =在区间()0,m 上与1y =有且只有6个交点,则5π13π,24m∈11. 已知定义在R 上的偶函数()f x 和奇函数()g x 满足()()21f x g x ++−=,则( )A. ()f x 的图象关于点()2,1对称B. ()f x 是以8为周期的周期函数C. ()20240g =D.20241(42)2025k f k =−=∑ 三、填空题:本题共3小题,每小题5分,共15分.12. 6(31)x y +−的展开式中2x y 的系数为______.13. 已知函数()f x 是定义域为R 的奇函数,当0x >时,()()2f x f x ′−>,且()10f =,则不等式()0f x >的解集为__________.14. 已知点C 为扇形AOB 弧AB 上任意一点,且60AOB ∠=,若(),R OC OA OB λµλµ=+∈,则λµ+的取值范围是__________.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15. ABC V 的内角,,A B C 的对边分别为,,a b c ,已知22cos a b c B +=. (1)求角C ;(2)若角C 的平分线CD 交AB于点,D AD DB =,求CD 的长.16. 已知1ex =为函数()ln af x x x =的极值点. (1)求a 的值; (2)设函数()ex kxg x =,若对()120,,x x ∀∈+∞∃∈R ,使得()()120f x g x −≥,求k 的取值范围. 17. 已知四棱锥P ABCD −中,平面PAB ⊥底面,ABCD AD∥,,,2,BC AB BC PA PB AB AB BC AD E ⊥==为AB 的中点,F 为棱PC 上异于,P C 的点.的(1)证明:BD EF ⊥;(2)试确定点F 的位置,使EF 与平面PCD18. 在平面直角坐标系xOy 中,抛物线21:2(0)C ypx p =>的焦点到准线的距离等于椭圆222:161C x y +=的短轴长,点P 在抛物线1C 上,圆222:(2)E x y r −+=(其中01r <<).(1)若1,2r Q =为圆E 上的动点,求线段PQ 长度的最小值; (2)设()1,D t 是抛物线1C 上位于第一象限的一点,过D 作圆E 的两条切线,分别交抛物线1C 于点,M N .证明:直线MN 经过定点.19. 龙泉游泳馆为给顾客更好的体验,推出了A 和B 两个套餐服务,顾客可选择A 和B 两个套餐之一,并在App 平台上推出了优惠券活动,下表是该游泳馆在App 平台10天销售优惠券情况. 日期t 12345678910销售量千张 1.9 1.98 2.2 2.36 2.43 2.59 2.68 2.76 2.7 04经计算可得:10101021111 2.2,118.73,38510i i i i i i i y y t y t ======∑∑∑ (1)因为优惠券购买火爆,App 平台在第10天时系统出现异常,导致当天顾客购买优惠券数量大幅减少,已知销售量y 和日期t 呈线性关系,现剔除第10天数据,求y 关于t 的经验回归方程结果中的数值用分数表示;(2)若购买优惠券的顾客选择A 套餐的概率为14,选择B 套餐的概率为34,并且A 套餐可以用一张优惠券,B 套餐可以用两张优惠券,记App 平台累计销售优惠券为n 张的概率为n P ,求n P ; (3)记(2)中所得概率n P 的值构成数列{}()N n P n ∗∈.①求n P 的最值;②数列收敛的定义:已知数列{}n a ,若对于任意给定的正数ε,总存在正整数0N ,使得当0n N >时,n a a ε−<,(a 是一个确定的实数),则称数列{}n a 收敛于a .根据数列收敛的定义证明数列{}n P 收敛...参考公式: ()()()1122211ˆˆ,n ni ii ii i n n i i i i x x y y x y nx yay bx x xx nx====−−−==−−−∑∑∑∑.大联考湖南师大附中2025届高三月考试卷(一)数学命题人:高三数学备课组 审题人:高三数学备课组时量:120分钟 满分:150分一、选选选:本选共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,1. 已知{}()260,{lg 10}Axx x B x x =+−≤=−<∣∣,则A B = ( )A. {}32xx −≤≤∣ B. {32}x x −≤<∣ C. {12}x x <≤∣ D. {12}x x <<∣【答案】D 【解析】【分析】通过解一元二次不等式和对数函数的定义域,求出集合,A B ,再求交集. 【详解】集合{}()32,{lg 10}{12}A x x B x x x x =−≤≤=−<=<<∣∣∣,则{12}A B xx ∩=<<∣, 故选:D .2. 若复数z 满足()1i 3i z +=−+(i 是虚数单位),则z 等于( )A.B.54C.D.【答案】C 【解析】【分析】由复数的除法运算计算可得12i z =−+,再由模长公式即可得出结果. 【详解】依题意()1i 3i z +=−+可得()()()()3i 1i 3i 24i12i 1i 1i 1i 2z −+−−+−+====−+++−,所以z =. 故选:C3. 已知平面向量()()5,0,2,1a b ==−,则向量a b +在向量b上的投影向量为( )A. ()6,3−B. ()4,2−C. ()2,1−D. ()5,0【答案】A 【解析】【分析】根据投影向量的计算公式即可求解.【详解】()()7,1,15,a b a b b b +=−+⋅==所以向量a b +在向量b 上的投影向量为()()236,3||a b b b bb +⋅==− .故选:A4. 记n S 为等差数列{}n a 的前n 项和,若396714,63a a a a +==,则7S =( ) A. 21 B. 19C. 12D. 42【答案】A 【解析】【分析】根据等差数列的性质,即可求解公差和首项,进而由求和公式求解.【详解】{}n a 是等差数列,396214a a a ∴+==,即67a =,所以67769,a a a a == 故公差76162,53d a a a a d =−=∴=−=−,()767732212S ×∴=×−+×=, 故选:A5. 某校高二年级下学期期末考试数学试卷满分为150分,90分以上(含90分)为及格.阅卷结果显示,全年级1200名学生的数学成绩近似服从正态分布,试卷的难度系数(难度系数=平均分/满分)为0.49,标准差为22,则该次数学考试及格的人数约为( )附:若()2,X Nµσ∼,记()()p k P k X k µσµσ=−≤≤+,则()()0.750.547,10.683p p ≈≈.A. 136人B. 272人C. 328人D. 820人【答案】B 【解析】【分析】首先求出平均数,即可得到学生的数学成绩2~(73.5,22)X N ,再根据所给条件求出(5790)P X ≤≤,即可求出(90)P X ≥,即可估计人数.【详解】由题得0.4915073.5,22µσ=×==,()()(),0.750.547p k P k X k p µσµσ=−≤≤+≈ ,()5790P X ∴≤≤ ()0.750.547p ≈,()()900.510.5470.2265P X ≥×−,∴该校及格人数为0.22651200272×≈(人),故选:B . 6. 已知()π5,0,,cos ,tan tan 426αβαβαβ∈−=⋅=,则αβ+=( ) A.π6 B.π4C.π3D.2π3【答案】D 【解析】【分析】利用两角差的余弦定理和同角三角函数的基本关系建立等式求解,再由两角和的余弦公式求解即可.【详解】由已知可得5cos cos sin sin 6sin sin 4cos cos αβαβαβαβ⋅+⋅=⋅ =⋅ , 解得1cos cos 62sin sin 3αβαβ⋅=⋅=,,()1cos cos cos sin sin 2αβαβαβ∴+=⋅−⋅=−,π,0,2αβ∈,()0,παβ∴+∈, 2π,3αβ∴+=,故选:D .7. 已知12,F F 是双曲线22221(0)x y a b a b−=>>的左、右焦点,以2F 为圆心,a 为半径的圆与双曲线的一条渐近线交于,A B 两点,若123AB F F >,则双曲线的离心率的取值范围是( )A.B.C. (D. (【答案】B 【解析】【分析】根据双曲线以及圆的方程可求得弦长AB =,再根据不等式123AB F F >整理可得2259c a <,即可求得双曲线的离心率的取值范围.【详解】设以()2,0F c 为圆心,a 为半径的圆与双曲线的一条渐近线0bx ay −=交于,A B 两点, 则2F 到渐近线0bx ay −=的距离d b,所以AB =, 因为123AB F F >,所以32c ×>,可得2222299a b c a b −>=+, 即22224555a b c a >=−,可得2259c a <,所以2295c a <,所以e <,又1e >,所以双曲线的离心率的取值范围是 .故选:B8. 已知函数()220log 0x a x f x x x ⋅≤= > ,,,,若关于x 的方程()()0f f x =有且仅有两个实数根,则实数a 的取值范围是( ) A. ()0,1 B. ()(),00,1−∞∪C. [)1,+∞D. ()()0,11,+∞【答案】C 【解析】【分析】利用换元法设()u f x =,则方程等价为()0f u =,根据指数函数和对数函数图象和性质求出1u =,利用数形结合进行求解即可. 【详解】令()u f x =,则()0f u =.�当0a =时,若()0,0u f u ≤=;若0u >,由()2log 0f u u==,得1u =. 所以由()()0ff x =可得()0f x ≤或()1f x =.如图所示,满足()0f x ≤的x 有无数个,方程()1f x =只有一个解,不满足题意;�当0a ≠时,若0≤u ,则()20uf u a =⋅≠;若0u >,由()2log 0f u u==,得1u =. 所以由()()0ff x =可得()1f x =,当0x >时,由()2log 1f x x==,可得2x =, 因为关于x 的方程()()0f f x =有且仅有两个实数根,则方程()1f x =在(,0∞−]上有且仅有一个实数根,若0a >且()(]0,20,xx f x a a ≤=⋅∈,故1a ≥; 若0a <且()0,20xx f x a ≤=⋅<,不满足题意.综上所述,实数a 的取值范围是[)1,+∞, 故选:C .二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分9. 如图,在正方体111ABCD A B C D −中,E F M N ,,,分别为棱111AA A D AB DC ,,,的中点,点P 是面1B C 的中心,则下列结论正确的是( )A. E F M P ,,,四点共面B. 平面PEF 被正方体截得的截面是等腰梯形C. //EF 平面PMND. 平面MEF ⊥平面PMN【答案】BD 【解析】【分析】可得过,,E F M 三点的平面为一个正六边形,判断A ;分别连接,E F 和1,B C ,截面1C BEF 是等腰梯形,判断B ;分别取11,BB CC 的中点,G Q ,易证EF 显然不平行平面QGMN ,可判断C ;EM ⊥平面PMN ,可判断D.【详解】对于A :如图经过,,E F M 三点的平面为一个正六边形EFMHQK ,点P 在平面外,,,,E F M P ∴四点不共面,∴选项A 错误;对于B :分别连接,E F 和1,B C ,则平面PEF 即平面1C BEF ,截面1C BEF 是等腰梯形,∴选项B 正确;对于C :分别取11,BB CC 的中点,G Q ,则平面PMN 即为平面QGMN , 由正六边形EFMHQK ,可知HQ EF ,所以MQ 不平行于EF ,又,EF MQ ⊂平面EFMHQK ,所以EF MQ W = ,所以EF I 平面QGMN W =, 所以EF 不平行于平面PMN ,故选项C 错误;对于D :因为,AEM BMG 是等腰三角形,45AME BMG ∴∠=∠=°, 90EMG ∴∠=°,EMMG ∴⊥,,M N 是,AB CD 的中点,易证MN AD ∥,由正方体可得AD ⊥平面11ABB A ,MN ∴⊥平面11ABB A ,又ME ⊂平面11ABB A ,EM MN ∴⊥,,MG MN ⊂ 平面PMN ,EM ∴⊥平面GMN ,EM ⊂ 平面MEF ,∴平面MEF ⊥平面,PMN 故选项D 正确.���BD .10. 已知函数()5π24f x x=+,则( )A. ()f x 的一个对称中心为3π,08B. ()f x 的图象向右平移3π8个单位长度后得到的是奇函数的图象 C. ()f x 在区间5π7π,88上单调递增 D. 若()y f x =在区间()0,m 上与1y =有且只有6个交点,则5π13π,24m∈【答案】BD 【解析】【分析】代入即可验证A ,根据平移可得函数图象,即可由正弦型函数的奇偶性求解B ,利用整体法即可判断C ,由5πcos 24x+求解所以根,即可求解D.【详解】对于A ,由35π3π2π0848f =+×=≠,故A 错误;对于B ,()f x 的图象向右平移3π8个单位长度后得: 3π3π5ππ228842y f x x x x=−−++,为奇函数,故B 正确; 对于C ,当5π7π,88x∈时,则5π5π2,3π42x +∈ ,由余弦函数单调性知,()f x 在区间5π7π,88 上单调递减,故C 错误;对于D ,由()1f x =,得5πcos 24x+ππ4x k =+或ππ,2k k +∈Z , ()y f x =在区间()0,m 上与1y =有且只有6个交点,其横坐标从小到大依次为:ππ5π3π9π5π,,,,,424242, 而第7个交点的横坐标为13π4, 5π13π24m ∴<≤,故D 正确. 故选:BD11. 已知定义在R 上的偶函数()f x 和奇函数()g x 满足()()21f x g x ++−=,则( )A. ()f x 的图象关于点()2,1对称B. ()f x 是以8为周期的周期函数C. ()20240g =D.20241(42)2025k f k =−=∑ 【答案】ABC 【解析】【分析】根据函数奇偶性以及所满足的表达式构造方程组可得()()222f x f x ++−=,即可判断A 正确;利用对称中心表达式进行化简计算可得B 正确,可判断()g x 也是以8为周期的周期函数,即C 正确;根据周期性以及()()42f x f x ++=计算可得20241(42)2024k f k =−=∑,可得D 错误. 【详解】由题意()()()(),f x f x g x g x −=−=−,且()()()00,21g f x g x =++−=, 即()()21f x g x +−=①, 用x −替换()()21f x g x ++−=中的x ,得()()21f x g x −+=②, 由①+②得()()222f x f x ++−=, 所以()f x 的图象关于点(2,1)对称,且()21f =,故A 正确;由()()222f x f x ++−=,可得()()()()()42,422f x f x f x f x f x ++−=+=−−=−, 所以()()()()82422f x f x f x f x +=−+=−−= , 所以()f x 是以8为周期的周期函数,故B 正确; 由①知()()21g x f x =+−,则()()()()882121g x f x f x g x +=++−=+−=,故()()8g x g x +=,因此()g x 也是以8为周期的周期函数, 所以()()202400g g ==,C 正确;又因为()()42f x f x ++−=,所以()()42f x f x ++=, 令2x =,则有()()262f f +=,令10x =,则有()()10142,f f +=…, 令8090x =,则有()()809080942f f +=, 所以1012(2)(6)(10)(14)(8090)(8094)2222024f f f f f f ++++++=+++=个所以20241(42)(2)(6)(10)(14)(8090)(8094)2024k f k f f f f f f =−=++++++=∑ ,故D 错误.故选:ABC【点睛】方法点睛:求解函数奇偶性、对称性、周期性等函数性质综合问题时,经常利用其中两个性质推得第三个性质特征,再进行相关计算.三、填空题:本题共3小题,每小题5分,共15分.12. 6(31)x y +−的展开式中2x y 的系数为______. 【答案】180− 【解析】【分析】根据题意,由条件可得展开式中2x y 的系数为213643C C (1)⋅−,化简即可得到结果. 【详解】在6(31)x y +−的展开式中, 由()2213264C C 3(1)180x y x y ⋅⋅−=−,得2x y 的系数为180−. 故答案为:180−.13. 已知函数()f x 是定义域为R 的奇函数,当0x >时,()()2f x f x ′−>,且()10f =,则不等式()0f x >的解集为__________.【答案】()()1,01,−∪+∞ 【解析】【分析】根据函数奇偶性并求导可得()()f x f x ′′−=,因此可得()()2f x f x ′>,可构造函数()()2xf x h x =e并求得其单调性即可得()f x 在()1,+∞上大于零,在()0,1上小于零,即可得出结论. 【详解】因为()f x 为奇函数,定义域为R ,所以()()f x f x −=−,两边同时求导可得()()f x f x ′′−−=−,即()()f x f x ′′−=且()00f =,又因为当0x >时,()()2f x f x ′−>,所以()()2f x f x ′>. 构造函数()()2xf x h x =e,则()()()22x f x f x h x ′−′=e , 所以当0x >时,()()0,h x h x ′>在()0,∞+上单调递增,又因为()10f =,所以()()10,h h x =在()1,+∞上大于零,在()0,1上小于零, 又因为2e 0x >,所以()f x 在()1,+∞上大于零,在()0,1上小于零, 因为()f x 为奇函数,所以()f x 在(),1∞−−上小于零,在()1,0−上大于零, 综上所述,()0f x >的解集为()()1,01,−∪+∞. 故答案为:()()1,01,−∪+∞14. 已知点C 为扇形AOB 的弧AB 上任意一点,且60AOB ∠=,若(),R OC OA OB λµλµ=+∈,则λµ+的取值范围是__________.【答案】【解析】【分析】建系设点的坐标,再结合向量关系表示λµ+,最后应用三角恒等变换及三角函数值域求范围即可. 【详解】方法一:设圆O 的半径为1,由已知可设OB 为x 轴的正半轴,O 为坐标原点,过O 点作x 轴垂线为y 轴建立直角坐标系,其中()()1,1,0,cos ,sin 2A B C θθ ,其中π,0,3BOC θθ ∠=∈ , 由(),R OC OA OB λµλµ=+∈,即()()1cos ,sin 1,02θθλµ =+,整理得1cos sin 2λµθθ+=,解得cos λµθ=,则ππcos cos ,0,33λµθθθθθ+=++=+∈,ππ2ππ,,sin 3333θθ+∈+∈所以λµ +∈ . 方法二:设k λµ+=,如图,当C 位于点A 或点B 时,,,A B C 三点共线,所以1k λµ=+=; 当点C 运动到AB的中点时,k λµ=+,所以λµ +∈故答案为:四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15. ABC V 的内角,,A B C 的对边分别为,,a b c ,已知22cos a b c B +=. (1)求角C ;(2)若角C 的平分线CD 交AB于点,D AD DB =,求CD 的长.【答案】(1)2π3C = (2)3CD = 【解析】【分析】(1)利用正弦定理及两角和的正弦定理整理得到()2cos 1sin 0C B +=,再利用三角形的内角及正弦函数的性质即可求解;(2)利用正弦定理得出3b a =,再由余弦定理求出4a =,12b =,再根据三角形的面积建立等式求解. 【小问1详解】 由22cos a b c B +=,根据正弦定理可得2sin sin 2sin cos A B C B +=,则()2sin sin 2sin cos B C B C B ++=,所以2sin cos 2cos sin sin 2sin cos B C B C B C B ++=,整理得()2cos 1sin 0C B +=, 因为,B C 均为三角形内角,所以(),0,π,sin 0B C B ∈≠, 因此1cos 2C =−,所以2π3C =. 【小问2详解】因为CD 是角C的平分线,AD DB=所以在ACD 和BCD △中,由正弦定理可得,,ππsin sin sin sin 33AD CD BD CDA B ==, 因此sin 3sin BADA BD==,即sin 3sin B A =,所以3b a =, 又由余弦定理可得2222cos c a b ab C =+−,即222293a a a =++, 解得4a =,所以12b =.又ABCACD BCD S S S =+△△△,即111sin sin sin 222ab ACB b CD ACD a CD BCD ∠∠∠=⋅⋅+⋅⋅, 即4816CD =,所以3CD =. 16. 已知1ex =为函数()ln af x x x =的极值点. (1)求a 的值; (2)设函数()ex kxg x =,若对()120,,x x ∀∈+∞∃∈R ,使得()()120f x g x −≥,求k 的取值范围. 【答案】(1)1a = (2)(]()10,−∞−+∞ , 【解析】【分析】(1)直接根据极值点求出a 的值;(2)先由(1)求出()f x 的最小值,由题意可得是求()g x 的最小值,小于等于()f x 的最小值,对()g x 求导,判断由最小值时的k 的范围,再求出最小值与()f x 最小值的关系式,进而求出k 的范围. 【小问1详解】()()111ln ln 1a a f x ax x x x a x xα−−==′+⋅+,由1111ln 10e e e a f a −=+=′,得1a =, 当1a =时,()ln 1f x x =′+,函数()f x 在10,e上单调递减,在1,e∞ +上单调递增, 所以1ex =为函数()ln af x x x =的极小值点, 所以1a =. 【小问2详解】由(1)知min 11()e ef x f ==−. 函数()g x 的导函数()()1e xg x k x −=−′ �若0k >,对()1210,,x x k ∞∀∈+∃=−,使得()()12111e 1e k g x g f x k=−=−<−<−≤,即()()120f x g x −≥,符合题意. �若()0,0kg x =,取11ex =,对2x ∀∈R ,有()()120f x g x −<,不符合题意.�若0k <,当1x <时,()()0,g x g x ′<在(),1∞−上单调递减;当1x >时,()()0,g x g x ′>在(1,+∞)上单调递增,所以()min ()1ekg x g ==, 若对()120,,x x ∞∀∈+∃∈R ,使得()()120f x g x −≥,只需min min ()()g x f x ≤, 即1e ek ≤−,解得1k ≤−. 综上所述,k 的取值范围为(](),10,∞∞−−∪+.17. 已知四棱锥P ABCD −中,平面PAB ⊥底面,ABCD AD ∥,,,2,BC AB BC PA PB AB AB BC AD E ⊥==为AB 的中点,F 为棱PC 上异于,P C 的点.(1)证明:BD EF ⊥;(2)试确定点F 的位置,使EF 与平面PCD【答案】(1)证明见解析 (2)F 位于棱PC 靠近P 的三等分点 【解析】【分析】(1)连接,,PE EC EC 交BD 于点G ,利用面面垂直的性质定理和三角形全等,即可得证; (2)取DC 的中点H ,以E 为坐标原点,分别以,,EB EH EP 所在直线为,,x y z 轴建立,利用线面角公式代入即可求解.小问1详解】如图,连接,,PE EC EC 交BD 于点G .因为E 为AB 的中点,PA PB =,所以PE AB ⊥.因为平面PAB ⊥平面ABCD ,平面PAB ∩平面,ABCD AB PE =⊂平面PAB , 所以PE ⊥平面ABCD ,因为BD ⊂平面ABCD ,所以PE BD ⊥.因为ABD BCE ≅ ,所以CEB BDA ∠∠=,所以90CEB ABD ∠∠+= , 所以BD EC ⊥,因为,,PE EC E PE EC ∩=⊂平面PEC , 所以BD ⊥平面PEC .因为EF ⊂平面PEC ,所以BD EF ⊥. 【小问2详解】如图,取DC 的中点H ,以E 为坐标原点,分别以,,EB EH EP 所在直线为,,x y z 轴建立空间直角坐标系,【设2AB =,则2,1,BC AD PA PB ====则()()()()0,0,1,1,2,0,1,1,0,0,0,0P C D E −,设(),,,(01)F x y z PF PC λλ=<<, 所以()(),,11,2,1x y z λ−=−,所以,2,1x y z λλλ===−,即(),2,1F λλλ−.则()()()2,1,0,1,2,1,,2,1DC PC EF λλλ==−=−,设平面PCD 的法向量为(),,m a b c =,则00DC m PC m ⋅=⋅=,,即2020a b a b c += +−= ,,取()1,2,3m =−− , 设EF 与平面PCD 所成的角为θ,由cos θ=sin θ=.所以sin cos ,m EF m EF m EF θ⋅===整理得2620λλ−=,因为01λ<<,所以13λ=,即13PF PC = ,故当F 位于棱PC 靠近P 的三等分点时,EF 与平面PCD18. 在平面直角坐标系xOy 中,抛物线21:2(0)C ypx p =>的焦点到准线的距离等于椭圆222:161C x y +=的短轴长,点P 在抛物线1C 上,圆222:(2)E x y r −+=(其中01r <<).(1)若1,2r Q =为圆E 上的动点,求线段PQ 长度的最小值;(2)设()1,D t 是抛物线1C 上位于第一象限的一点,过D 作圆E 的两条切线,分别交抛物线1C 于点,M N .证明:直线MN 经过定点.【答案】(1(2)证明见解析【解析】【分析】(1)根据椭圆的短轴可得抛物线方程2y x =,进而根据两点斜率公式,结合三角形的三边关系,即可由二次函数的性质求解,(2)根据两点坐标可得直线,MN DM 的直线方程,由直线与圆相切可得,a b 是方程()()()2222124240r x r x r −+−+−=的两个解,即可利用韦达定理代入化简求解定点. 【小问1详解】 由题意得椭圆的方程:221116y x +=,所以短半轴14b = 所以112242p b ==×=,所以抛物线1C 的方程是2y x =. 设点()2,P t t ,则111222PQ PE ≥−=−=≥, 所以当232ι=时,线段PQ . 【小问2详解】()1,D t 是抛物线1C 上位于第一象限的点,21t ∴=,且()0,1,1t D >∴设()()22,,,M a a N b b ,则: 直线()222:b a MN y a x a b a −−=−−,即()21y a x a a b −=−+,即()0x a b y ab −++=. 直线()21:111a DM y x a −−=−−,即()10x a y a −++=. 由直线DMr =,即()()()2222124240r a r a r −+−+−=..同理,由直线DN 与圆相切得()()()2222124240r b r b r −+−+−=. 所以,a b 是方程()()()2222124240r x r x r −+−+−=的两个解, 22224224,11r r a b ab r r −−∴+==−− 代入方程()0x a b y ab −++=得()()222440x y r x y +++−−−=, 220,440,x y x y ++= ∴ ++= 解得0,1.x y = =− ∴直线MN 恒过定点()0,1−.【点睛】圆锥曲线中定点问题的两种解法(1)引进参数法:先引进动点的坐标或动线中系数为参数表示变化量,再研究变化的量与参数何时没有关系,找到定点.(2)特殊到一般法:先根据动点或动线的特殊情况探索出定点,再证明该定点与变量无关.技巧:若直线方程为()00y y k x x −=−,则直线过定点()00,x y ;若直线方程为y kx b =+ (b 为定值),则直线过定点()0,.b 19. 龙泉游泳馆为给顾客更好的体验,推出了A 和B 两个套餐服务,顾客可选择A 和B 两个套餐之一,并在App 平台上推出了优惠券活动,下表是该游泳馆在App 平台10天销售优惠券情况. 日期t 1 2 3 4 5 6 7 8 9 10 销售量千张 1.9 1.98 2.2 2.36 2.43 259 2.68 2.76 2.7 0.4经计算可得:10101021111 2.2,118.73,38510i i i i i i i y y t y t ======∑∑∑. (1)因为优惠券购买火爆,App 平台在第10天时系统出现异常,导致当天顾客购买优惠券数量大幅减少,已知销售量y 和日期t 呈线性关系,现剔除第10天数据,求y 关于t 的经验回归方程结果中的数值用分数表示;..(2)若购买优惠券的顾客选择A 套餐的概率为14,选择B 套餐的概率为34,并且A 套餐可以用一张优惠券,B 套餐可以用两张优惠券,记App 平台累计销售优惠券为n 张的概率为n P ,求n P ;(3)记(2)中所得概率n P 的值构成数列{}()Nn P n ∗∈. ①求n P 的最值;②数列收敛的定义:已知数列{}n a ,若对于任意给定的正数ε,总存在正整数0N ,使得当0n N >时,n a a ε−<,(a 是一个确定的实数),则称数列{}n a 收敛于a .根据数列收敛的定义证明数列{}n P 收敛.参考公式: ()()()1122211ˆˆ,n ni ii i i i n n ii i i x x y y x y nx y ay bx x x x nx ====−−−==−−−∑∑∑∑. 【答案】(1)673220710001200y t + (2)433774n n P =+⋅−(3)①最大值为1316,最小值为14;②证明见解析 【解析】 【分析】(1)计算出新数据的相关数值,代入公式求出 ,ab 的值,进而得到y 关于t 的回归方程; (2)由题意可知1213,(3)44n n n P P P n −−=+≥,其中12113,416P P ==,构造等比数列,再利用等比数列的通项公式求解;(3)①分n 为偶数和n 为奇数两种情况讨论,结合指数函数的单调性求解;②利用数列收敛的定义,准确推理、运算,即可得证. 【小问1详解】 解:剔除第10天的数据,可得2.2100.4 2.49y ×−==新, 12345678959t ++++++++=新, 则9922111119.73100.4114,73,38510285i i i i t y t = =−×==−= ∑∑新新,所以912922119114,7395 2.4673ˆ2859560009i i i i t y t y b t t == − −×× ==−× − ∑∑新新新新新, 可得6732207ˆ 2.4560001200a =−×=,所以6732207ˆ60001200y t +. 【小问2详解】 解:由题意知1213,(3)44n n n P P P n −−=+≥,其中12111313,444416P P ==×+=, 所以11233,(3)44n n n n P P P P n −−−+=+≥,又由2131331141644P P ++×, 所以134n n P P − +是首项为1的常数列,所以131,(2)4n n P P n −+=≥ 所以1434(),(2)747n n P P n −−=−−≥,又因为1414974728P −=−=−, 所以数列47n P − 是首项为928−,公比为34−的等比数列, 故1493()7284n n P −−=−−,所以1934433()()2847774n n n P −=−−+=+−. 【小问3详解】 解:①当n 为偶数时,19344334()()28477747n n n P −=−−+=+⋅>单调递减, 最大值为21316P =; 当n 为奇数时,19344334()()28477747n n n P −=−−+=−⋅<单调递增,最小值为114P =, 综上可得,数列{}n P 的最大值为1316,最小值为14. ②证明:对任意0ε>总存在正整数0347[log ()]13N ε=+,其中 []x 表示取整函数, 当 347[log ()]13n ε>+时,347log ()34333333()()()7747474n n n P εε−=⋅−=⋅<⋅=, 所以数列{}n P 收敛.【点睛】知识方法点拨:与新定义有关的问题的求解策略:1、通过给出一个新的定义,或约定一种新的运算,或给出几个新模型来创设新问题的情景,要求在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实心信息的迁移,达到灵活解题的目的;2、遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、运算、验证,使得问题得以解决.方法点拨:与数列有关的问题的求解策略:3、若新定义与数列有关,可得利用数列的递推关系式,结合数列的相关知识进行求解,多通过构造的分法转化为等差、等比数列问题求解,求解过程灵活运用数列的性质,准确应用相关的数列知识.。
湖南省长沙市2023-2024学年高三上学期月考(四)数学试题(解析版)

大联考2024届高三月考试卷(四)数学(答案在最后)注意事项:1.答卷前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设集合{}{13},2,1,0,1M x x N =-<<=--∣,则M N ⋂=()A.{}1,0,1- B.{}0,1 C.{11}x x -<<∣ D.{11}xx -<≤∣【答案】B 【解析】【分析】根据交集的知识求得正确答案.【详解】由已知得{}0,1M N = .故选:B2.已知i 是虚数单位,若()()2i 1i 4i a ++=,则实数=a ()A.2B.0C.1- D.2-【答案】A 【解析】【分析】利用复数乘法运算法则,根据复数相等列方程组即可求.【详解】因为R a ∈,()()()2i 1i 22i 4i a a a ++=-++=,所以2024a a -=⎧⎨+=⎩,解得2a =.故选:A3.设随机变量2(,)X N μσ ,且()3()P X a P X a <=≥,则()P X a ≥=()A .0.75B.0.5C.0.3D.0.25【答案】D 【解析】【分析】利用对立事件的意义,结合正态分布列式计算即得.【详解】随机变量2(,)XN μσ ,显然()()1P X a P X a <+≥=,而()3()P X a P X a <=≥,所以()0.25P X a ≥=.故选:D4.已知43log log 5,log 2a b c ===,则下列结论正确的是()A.<<b c aB.c b a <<C.b a c <<D.<<c a b【答案】B 【解析】【分析】利用1作为中间量,判断b 、c 的大小,利用换底公式判断a 、b 的大小.【详解】因为2234422log 62log log 21log 5log 6==log log 42c b a =<<=<=,即c b a <<.故选:B .5.已知圆锥的高为3,若该圆锥的内切球的半径为1,则该圆锥的表面积为()A.6πB. C.9πD.12π【答案】C 【解析】【分析】利用圆锥与其内切球的轴截面,由已知数据计算出圆锥底面半径和母线长,可求圆锥的表面积.【详解】圆锥与其内切球的轴截面如下图所示,由已知111,2O D SO ==,可知130O SD ∠=,所以圆锥的轴截面为正三角形,因为3SO =,所以圆锥底面圆半径tan 30AO SO =⋅=cos 06AOSA ==o,则圆锥的表面积为2ππ9πS =⨯+=.故选:C .6.已知角π02α⎛⎫∈ ⎪⎝⎭,,且满足cos 4παα⎛⎫-= ⎪⎝⎭,则sin 2cos αα+=()A.2-B.2516 C.2516-D. 2【答案】D 【解析】【分析】根据题意,由条件可得tan α的值,从而可得sin ,cos αα,即可得到结果.【详解】由已知得π4α⎛⎫-= ⎪⎝⎭3(sin cos )cos ααα-=,∴4tan 3α=,∵π(0,2α∈,∴43sin ,cos ,sin 2cos 255αααα==+=.故选:D7.在等腰ABC 中,2,30,AC CB CAB ABC ∠===︒ 的外接圆圆心为O ,点P 在优弧 AB 上运动,则2PA PB PO PC PA PB⎡⎤⎛⎫⎢⎥ ⎪-+⋅⎢⎥⎪⎝⎭⎣⎦的最小值为()A.4B.2C.-D.6-【答案】D 【解析】【分析】根据题意,由正弦定理可得圆O的外接圆直径,从而可得PA PB PA PB += ,代入计算,即可得到结果.【详解】由已知2,30AC CB CAB ∠===︒,所以圆O 的外接圆直径为24sin BCR A==,因为30APC ABC BPC BAC ∠∠∠∠====︒,所以PA PB PA PB += ,所以22112||2(2622PA PB PO PC PO PC PC PC PA PB PC ⎡⎤⎛⎫⎛⎫⎢⎥⎪ ⎪-+⋅=-⋅=-=--⎢⎥⎪ ⎪⎝⎭⎝⎭⎣⎦,因为2AC PC R <≤ ,即24PC <≤,所以PC = 时,取到最小值6-.故选:D .8.已知椭圆E :22221(0)x y a b a b+=>>的右焦点为()3,0F ,过点F 的直线交椭圆E 于,A B 两点,若AB的中点坐标为()1,1-,则椭圆E 的方程为()A.221189x y += B.2212718x y += C.2213627x y += D.2214536x y +=【答案】A 【解析】【分析】利用弦中点坐标由点差法即可计算出222a b =,利用焦点坐标即可得2218,9a b ==,即得出椭圆方程.【详解】根据题意设()()1122,,,A x y B x y ,代入椭圆方程可得22112222222211x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩;两式相减可得22221212220x x y y a b --+=,整理可得2221211122y y x x b a x x y y --++=-;又因为AB 的中点坐标为()1,1-,可得12122,2x x y y +=+=-;因此过,A B 两点的直线斜率为212212ABy y b k x x a -==-,又()3,0F 和AB 的中点()1,1-在直线上,所以101132AB k --==-,即2212b a =,可得222a b =;又易知3c =,且22229a b c b =+=+,计算可得2218,9a b ==;所以椭圆E 的方程为221189x y +=,代入AB 的中点坐标为()1,1-,得()22113118918-+=<,则其在椭圆内部,则此时直线AB 与椭圆相交两点.故选:A二、多选题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)9.党的二十大报告提出,要加快发展数字经济,促进数字经济与实体经济的深度融合,数字化构建社区服务新模式成为一种时尚.某社区为优化数字化社区服务,问卷调查调研数字化社区服务的满意度,满意度采用计分制(满分100分),统计满意度绘制成如下频率分布直方图,图中3b a =.则下列结论正确的是()A.0.01a =B.满意度计分的众数为80分C.满意度计分的75%分位数是85分D.满意度计分的平均分是76.5【答案】ACD 【解析】【分析】根据频率之和为1即可求解A ,根据众数,中位数以及平均数的计算即可分别求解BCD.【详解】由频率分布直方图可知()0.0150.035101a b a ++++⨯=,即20.05b a +=,又3b a =,所以0.01a =,所以选项A 正确;满意度计分的众数为75分,所以选项B 错误;前三组的频率之和为0.10.150.350.6++=<0.75,前四组的频率之和为0.60.30.90.75+=>,则75%分位数[80,90)m ∈,故0.750.68010850.90.6m -=+⨯=-,满意度计分的75%分位数为85,所以选项C 正确;满意度计分的平均分为:550.1650.15750.35850.3950.176.5x =⨯+⨯+⨯+⨯+⨯=分,所以选项D 正确.故选:ACD .10.已知函数()sin2(0)f x a x x a =+>的最大值为,则下列结论正确的是()A.函数()f x 的最小正周期为π2B.3a =C.函数()f x 的图象关于直线π12x =-对称D.函数()f x =在区间()0,π内有两个不同实根【答案】BD 【解析】【分析】利用三角恒等变换化简()sin2(0)f x a x x a =+>,求出最大值,根据最大值为a 的值,然后利用正弦型函数的性质依次判断即可.【详解】因为()()sin22,sin f x a x x x ϕϕϕ=+=+==所以max 2ππ,()2T f x ===又()f x的最大值是=,又0a >,所以3a =,所以选项A 错误,B 正确;由于()313sin2sin2cos22226f x x x x x x π⎫⎛⎫==+=+⎪ ⎪⎪⎝⎭⎭,因为πππ2012126f ⎡⎤⎛⎫⎛⎫-=⨯-+= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,所以函数()f x 的图象关于点π,012⎛⎫-⎪⎝⎭对称,所以选项C 错误;当()00,πx ∈时,0ππ13π2,666x ⎛⎫+∈ ⎪⎝⎭,由()00π26f x x ⎛⎫=+= ⎪⎝⎭即0π1sin 262x ⎛⎫+=- ⎪⎝⎭,求得0π2x =或05π6x =,所以选项D 正确.故选:BD .11.已知数列{}n a 满足()*111,N 12nn na a a n a +==∈-,数列{}nb 满足1n n n b a a +=,记数列{}n b 的前n 项和为n S ,则下列结论正确的是()A.数列1n a ⎧⎫⎨⎬⎩⎭是等差数列B.10218211a a a =+C.12n S <-D.1n S ≥-【答案】ABC 【解析】【分析】由题意可得1112n na a +-=-,再根据等差数列的定义及性质即可判断AB ;求出数列{}n a 和{}nb 的通项,再利用裂项相消法即可求出n S ,从而可判断CD .【详解】因为111,12n n n a a a a +==-,所以112112n n n na a a a +-==-,所以1112n na a +-=-,且111a =,所以数列1n a ⎧⎫⎨⎬⎩⎭是等差数列,且该数列的首项为1,公差为2-,所以10218211a a a =+,所以选项AB 正确;因为()112132n n n a =--=-,所以132n a n=-,所以()()()()1111113212232122321n n n b a a n n n n n n +⎛⎫====- ⎪------⎝⎭,所以11111111111211133525232321n S n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++-+- ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥-----⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ 11112212n ⎛⎫=--<- ⎪-⎝⎭,所以选项C 正确,D 错误.故选:ABC .12.如图,在多面体ABCDEF 中,底面ABCD的正方形,1,DE BF DE == ,BF DE ⊥平面ABCD ,动点P 在线段EF 上,则下列说法正确的是()A.AC DP⊥B.存在点P ,使得DP 平面ACFC.当动点P 与点F 重合时,直线DP 与平面AFC 所成角的余弦值为31010D.三棱锥A CDE -的外接球被平面ACF 所截取的截面面积是92π【答案】ABC 【解析】【分析】由面面垂直的性质定理可判断选项A ;由线面平行的判定定理和性质定理可判断选项B ;由面面垂直的判定定理、面面垂直的性质及余弦定理可判断选项C ;由截面是ACF △的外接圆及正弦定理可判断选项D .【详解】令AC BD O = ,连接FO ,令EF 中点为G ,连接DG ,如图所示:由底面ABCD 是正方形可得:O 是,BD AC 的中点,且AC BD ⊥;由DE ⊥平面ABCD ,DE ⊂平面DEFB ,BD ⊂平面ABCD 可得:平面ABCD ⊥平面DEFB ,DE BD ⊥;由1,DE BF DE ==BF ,DE BD ⊥可得:四边形BDEF 为矩形.对于选项A :由AC BD ⊥,平面ABCD ⊥平面DEFB ,平面ABCD ⋂平面DEFB BD =,AC ⊂平面ABCD ,可得AC ⊥平面DEFB .又DP ⊂平面DEFB ,所以AC DP ⊥,故A 正确;对于选项B :因为在矩形BDEF 中,DO ,FG DO FG =,所以四边形DOFG 是平行四边形,则直线DG OF .因为OF ⊂平面,ACF DG ⊄平面ACF ,则DG 平面ACF .故当P 是线段EF 中点G 时,直线DP 平面ACF ,故B 正确;对于选项C :因为AC ⊥平面DEFB ,AC ⊂平面AFC ,所以平面BDEF ⊥平面AFC ,所以()DP DF 在平面AFC 内射影在直线OF 上,直线DP 与平面AFC 所成角为()OFD OPD ∠∠.在OFD △中,2223101,210OF DF DO OD OF DF OFD OF DF ∠+-=====⋅,故C 正确;对于选项D :因为在ACF △中,2,AC AF ==CF FO ==,则6sin 3OF FAC AF ∠==.由正弦定理得:ACF △的外接圆直径2sin FC r FAC ∠==,则半径r =29ππ8S r ==.因为三棱锥A CDE -的外接球的球心在过点O 且与平面ACD 垂直的直线上,四边形BDEF 为矩形,所以点F 在三棱锥A CDE -的外接球上.所以三棱锥A CDE -的外接球被平面ACF 所截取的截面是ACF △的外接圆,因此三棱锥A CDE -的外接球被平面ACF 所截取的截面面积是98π,故D 错误.故选:ABC .【点睛】关键点点睛:本题主要考查空间中线线垂直的证明、线面平行的证明、线面角的求法及球的截面问题.解题关键在于熟练灵活掌握空间线面位置关系的判断方法.选项D 先判断出截面的形状,再利用正弦定理求出半径即可求解判断.三、填空题(本大题共4小题,每小题5分,共20分.)13.已知函数()()32,2log 2,2xx f x x x ⎧≤⎪=⎨+>⎪⎩,则()()7f f 的值为__________.【答案】4【解析】【分析】运用代入法,结合对数的运算性质进行求解即可.【详解】由题意可得,()()37log 272f =+=,所以()()()27224f f f ===.故答案为:414.2023年10月国庆节旅游黄金周期间,自驾游爱好者甲、乙、丁3家组团自驾去杭州旅游,3家人分别乘坐3辆车,沪昆高速杭州入口有,,A B C 共3个不同的窗口,则每个窗口恰好都有一位该团的自驾车在等候的概率为__________.【答案】29【解析】【分析】根据给定条件,求出该团的3辆自驾车在3个窗口等候的基本事件总数,再求出3个窗口各有1辆车在等候的事件含有的基本事件数,利用古典概率公式计算得解.【详解】该团的3辆自驾车在3个窗口等候的基本事件总数为33,3个窗口各有1辆车在等候的事件含有33A 个基本事件,所以每个窗口恰好都有一位该团的自驾车在等候的概率为333A 329P ==.故答案为:2915.已知双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别为12,F F ,过2F 作一条直线与双曲线右支交于,A B两点,坐标原点为O ,若1|||5OA BF a ==,则该双曲线的离心率为___________.【答案】2【解析】【分析】由12OA OF OF ==得出12AF AF ⊥,由定义结合勾股定理得出m a =,再由勾股定理得出离心率.【详解】解:如图,1212,OA OF OF c AF AF ===∴⊥因为15BF a =,则21||||23BF BF a a =-=,设2AF m =,则12AF m a =+,则3AB m a =+,由勾股定理可得22211||||||AF AB BF +=,即()()()222235m a m a a +++=,整理可得22560m am a +-=,因为0m >,解得m a =,所以,2AF a =,13AF a =,由勾股定理可得2221212||||||AF AF F F +=,即()22292a a c +=,整理可得210c a =,因此,该双曲线的离心率为10c e a ==.故答案为:10216.已知关于x 的不等式()21e 0xx k x -+>恰有3个不同的正整数解,则实数k 的取值范围是__________.【答案】43169,5e 4e ⎡⎫⎪⎢⎣⎭【解析】【分析】由题意知,关于x 的不等式()21e x x k x >+恰有3个不同的正整数解.设函数()2e x x f x =,()1y k x =+,作出函数图象,由图象观察,可得实数的k 取值范围.【详解】当0k =时,不等式20x >有无数个正整数解,不满足题意;当0k <时,当0x >时,不等式()21e 0xx k x -+>恒成立,有无数个不同的正整数解,不满足题意;当0k >时,不等式()21e 0xx k x -+>等价于()21ex x k x >+,令()2e x x f x =,所以()()222e ex x x x x x f x --==',当0x <时,()0f x '<,函数()f x 单调递减,当02x <<时,()0f x ¢>,函数()f x 单调递增,当2x >时,()0f x '<,函数()f x 单调递减,又()()2400,2ef f ==,结合单调性可知,当0x >时,()0f x >恒成立,而()1y k x =+表示经过点()1,0-的直线,由图像可知,关于x 的不等式()21e 0xx k x -+>恰有3个不同的正整数解,故只需满足以下条件:()()()34111,e 931,e 1641,e k k k ⎧+<⎪⎪⎪+<⎨⎪⎪+≥⎪⎩解得431695e 4e k ≤<.则实数k 的取值范围是43169,5e 4e ⎡⎫⎪⎢⎣⎭,故答案为:43169,5e 4e ⎡⎫⎪⎢⎣⎭.【点睛】用数形结合思想解决不等式解的问题一般有以下几类:(1)解含参不等式:在解决含有参数不等式时,由于涉及参数,往往需要讨论,导致演算过程复杂,若利用数形结合的方法,问题将简单化;(2)确定参数范围:在确定不等式参数的范围时,几何图形更能使问题直观;(3)证明不等式:把证明的不等式赋予一定的几何意义,将复杂的证明问题明快解决.四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.在ABC 中,,,a b c 分别为内角,,A B C 的对边,且2sin sin sin 2sin 2sin a A c B b C b B c C ++=+.(1)求角A 的大小;(2)设角A 的内角平分线交BC 于点M ,若ABC的面积为AM =b c +的值.【答案】(1)π3A =(2)8+=b c【解析】【分析】(1)利用正弦定理角化边,然后结合余弦定理可得;(2)根据=+ ABC ABM ACM S S S 化简整理可得.【小问1详解】由2sin sin sin 2sin 2sin a A c B b C b B c C ++=+及正弦定理得:222222a cb bc b c ++=+,即222b c a bc +-=.由余弦定理得2221cos 22b c a A bc +-==,又0πA <<,所以π3A =.【小问2详解】由角A 的内角平分线交BC 于点M 可知π6BAM CAM ∠=∠=,11sin sin 22ABC ABM ACM S S S AM c BAM AM b CAM ∠∠=+=⋅+⋅()1133sin sin 224BAM CAM b c ∠∠=⨯+⨯=+=所以8+=b c.18.已知等差数列{}n a 的前n 项和为n S ,且满足74349,29S a a ==+,数列{}n b 满足114,3n n n b b b a +==-.(1)证明:数列{}n b n -是等比数列,并求{}{},n n a b 的通项公式;(2)已知数列{}n c 满足,,,,n n n b n n c a n -⎧=⎨⎩为奇数为偶数求数列{}n c 的前2n 项和2n T .【答案】(1)证明见解析;21n a n =-,3nn b n=+(2)21233288n n n +++-【解析】【分析】(1)设数列{}n a 的公差为d ,根据题意求得47a =和35a =,得到1d =,得到21n a n =-,再由()()113n n b n b n +-+=-,得到{}n b n -为等比数列,进而得到数列{}n b 的通项公式;(2)由(1)得到3,21,n n n c n n ⎧=⎨-⎩为奇数为偶数,结合分组求和,即可求解.【小问1详解】解:依题意,设数列{}n a 的公差为d ,因为749=S ,所以()17477492a a a +==,则47a =,因为4329a a =+,即3149a =+,所以35a =,所以43132,21d a a a a d =-==-=,所以()112n a n =+-⨯,即21n a n =-.所以()13321n n n n b b a b n +=-=--,所以()()113n n b n b n +-+=-,又因为14b =,所以1130b -=≠,故数列{}n b n -是首项为3,公比为3的等比数列,所以()11133n n n b n b --=-⋅=,所以3n n b n =+.【小问2详解】解:由(1)知21n a n =-,3nn b n =+,可得3,21,n n n c n n ⎧=⎨-⎩为奇数为偶数,所以2123212n n nT c c c c c -=+++++ ()()()()135213333221241221n n -⎡⎤=+++++⨯-+⨯-++⨯-⎣⎦()()21231934133219288n n n n n n +-+-=+=++--.19.如图,四棱柱1111ABCD A B C D -中,底面ABCD 为正方形,AC 与BD 交于点O ,平面11AC CA ⊥平面11,2,ABCD AB AA CC ==与底面ABCD 所成的角为60 .(1)求证:1C O ⊥平面ABCD ;(2)求平面1ACB 与平面11CDD C 的夹角的余弦值.【答案】(1)证明见解析(2)77【解析】【分析】(1)过1C 作11C O AC ⊥于1O ,利用面面垂直证明线面垂,再结合线面角证明1,O O 为同一点即可;(2)建立空间直角坐标系,利用向量法求两个平面夹角的余弦值.【小问1详解】过1C 作11C O AC ⊥于1O ,因为平面11AC CA ⊥平面ABCD ,又平面11A C CA ⋂平面ABCD AC =,11C O ⊂平面11A C CA ,所以11C O ⊥平面ABCD ,所以11C CO ∠为直线1CC 与平面ABCD 所成的角,所以1160C CO ∠=,112CC AA ==,则11CO =,又因为底面ABCD 为正方形,2AB =,所以2AC =,O 是AC 中点,1CO =,可知1,O O 为同一点,所以1C O ⊥平面ABCD .【小问2详解】因为底面ABCD 是正方形,所以AC BD ⊥,以O 为原点,1,,OB OC OC 所在直线分别为,,x y z 轴建立空间直角坐标系.2==AC BD ,1CO =,112CC AA ==,3CO =,则()()(()()10,1,0,0,1,0,3,1,0,0,1,0,0A C C B D --.又(110,3BB CC ==-,所以(11,3B -,所以()(10,2,0,3AC AB ==,设平面1ACB 的法向量是(),,n x y z =r ,由120,30,n AC y n AB x z ⎧⋅==⎪⎨⋅=+=⎪⎩令1z =,则3,0x y =-=,得()3,0,1n =,因为(()10,3,1,1,0CC CD =-=--,设平面11CDD C 的法向量为()111,,m x y z =r ,所以1111130,0,m CC y z m CD x y ⎧⋅=-+=⎪⎨⋅=--=⎪⎩令11z =,则3,3x y ==,得()3,3,1m =-,所以2222223330117cos ,7(3)01(3)(3)1n m n m n m++⨯⋅==-++-++,所以平面1ACB 与平面11CDD C 的夹角的余弦值为277.20.已知圆22:2C x y x +=,动点P 在y 轴的右侧,P 到y 轴的距离比它到的圆心C 的距离小1.(1)求动点P 的轨迹E 的方程;(2)过圆心C 作直线l 与轨迹E 和圆C 交于四个点,自上而下依次为A ,M ,N ,B ,若2AM NB MN +=,求AB 及直线l 的方程.【答案】(1)24(0)y x x =>(2)||6AB =,2(1)y x =-【解析】【分析】(1)易得圆的半径1r =,圆心(1,0)C ,由题意得到点P 到定点(1,0)C 的距离与到定直线=1x -的距离相等,再利用抛物线的定义求解;(2)由圆C 的半径为1,得到||2MN =,再由||||||||2||AM NB AB MN MN +=-=,得到36AB MN ==,易知直线l 的斜率不为0,设直线:1l x my =+,与抛物线方程联立,利用弦长公式求解.【小问1详解】22:2C x y x +=化为()2211x y -+=,可得半径1r =,圆心(1,0)C ,因为动点P 在y 轴的右侧,P 到y 轴的距离比它到的圆心C 的距离小1,所以点P 到定点(1,0)C 的距离与到定直线=1x -的距离相等,∴由抛物线的定义得(,)P x y 的轨迹E 方程为24(0)y x x =>;【小问2详解】如图所示:由圆C 的半径为1,可得||2MN =,||||2||4AM NB MN ∴+==又||||||||2||AM NB AB MN MN +=-=,36AB MN ∴==,当直线l 的斜率为0时,直线l 与抛物线只有1个交点,不合题意;所以直线l 的斜率不为0,可设直线:1l x my =+,联立2214404x my y my y x=+⎧⇒--=⎨=⎩,216160m ∆=+>恒成立,12124,4y y m y y +==-,因为||6AB =,126y -==,解得212m =,所以直线l 的方程为11)2x y y x =±+⇒=-.21.在上海举办的第五届中国国际进口博览会中,一款无导线心脏起搏器引起广大参会者的关注,成为了进博会的“明星展品”.体积仅有维生素胶囊大小,体积比传统心脏起搏器减小93%,重量仅约2克,拥有强大的电池续航能力,配合兼容1.5T/3.0T 全身核磁共振扫描检查等创新功能.在起搏器研发后期,某企业快速启动无线充电器主控芯片生产,试产期每天都需同步进行产品检测,检测包括智能检测和人工检测,选择哪种检测方式的规则如下:第一天选择智能检测,随后每天由计算机随机等可能生成数字“0”和“1”,连续生成4次,把4次的数字相加,若和小于3,则该天的检测方式和前一天相同,否则选择另一种检测方式.(1)求该企业前三天的产品检测选择智能检测的天数X 的分布列;(2)当地政府为了检查该企业是否具有一定的智能化管理水平,采用如下方案:设()*n p n ∈N 表示事件“第n 天该企业产品检测选择的是智能检测”的概率,若12n p >恒成立,认为该企业具有一定的智能化管理水平,将给予该企业一定的奖励资金,否则将没有该项奖励资金.请问该企业能拿到奖励资金吗?请说明理由.【答案】(1)答案见解析(2)可以;理由见解析【解析】【分析】(1)根据题意,由条件可得X 的可能取值为1,2,3,然后分别求出其所对应的概率,即可得到分布列.(2)根据题意,由条件可得12n P ⎧-⎫⎨⎬⎩⎭是以12为首项,38为公比的等比数列,然后结合等比数列的通项公式即可得到结果.【小问1详解】设计算机4次生成的数字之和为ξ,则14,2B ξ⎛⎫ ⎪⎝⎭,则()444012444111113C C C 22216P ξ⎛⎫⎛⎫⎛⎫<=++= ⎪ ⎪ ⎝⎭⎝⎭⎝⎭,()()531316P P ξξ≥=-<=,X 的可能取值为1,2,3,则()5115511616256P X ==⨯=,()25511805216161625616P X ⎛⎫==+⨯==⎪⎝⎭,()211121316256P X ⎛⎫===⎪⎝⎭,所以X 的分布列为X123P55256516121256【小问2详解】设1n A -表示事件第n 1-天该企业产品检测选择的是智能检测,n A 表示事件第n 天该企业产品检测选择的是智能检测,由全概率公式可知()()()()()()11111111153511616816n n n n n n n n n n n P P A P A A P A P A A P A P P P -------==+=+-=+则153168n n P P -=+,2n ≥,即1131282n n P P -⎛⎫-=- ⎪⎝⎭,2n ≥,且11122P -=,所以12n P ⎧-⎫⎨⎬⎩⎭是以12为首项,38为公比的等比数列,则1113228n n P -⎛⎫-= ⎪⎝⎭,所以111312282n n P -⎛⎫=+⋅>⎪⎝⎭恒成立,所以该企业具有一定的智能化管理水平,能拿到奖金.22.已知函数()()e 11xf x a x =+--,其中a ∈R .(1)讨论函数()f x 的单调性;(2)当1a >时,证明:()ln cos f x x x a x >-.【答案】(1)答案见解析(2)证明见解析【解析】【分析】(1)先求得()f x ',然后对a 进行分类讨论,从而求得()f x 的单调区间.(2)将要证明的不等式转化为()()e cos 1ln 0,0,xa x x x x x x ∞++--->∈+,利用构造函数法、放缩法,结合多次求导来研究所构造函数的单调性,进而证得不等式成立.【小问1详解】因为()()e 11xf x a x =+--,所以()e 1xf x a =+-',当1a ≥时,()e 10xf x a =+->',函数()f x 在R 上单调递增;当1a <时,由()e 10xf x a =+->',得()ln 1x a >-,函数()f x 在区间()()ln 1,a ∞-+上单调递增,由()()e 10xf x a =+-<',得()ln 1x a <-,函数()f x 在区间()(),ln 1a -∞-上单调递减.【小问2详解】要证()ln cos f x x x a x >-,即证()()e 11ln cos ,0,xa x x x a x x ∞+-->-∈+,即证()()e cos 1ln 0,0,xa x x x x x x ∞++--->∈+,设()()cos ,1sin 0k x x x k x x =-'=+≥,故()k x 在()0,∞+上单调递增,又()010k =>,所以()1k x >,又因为1a >,所以()cos cos a x x x x +>+,所以()e cos 1ln e cos 1ln xxa x x x x x x x x ++--->+--,①当01x <≤时,因为e cos 10,ln 0x x x x +->≤,所以e cos 1ln 0x x x x +-->;②当1x >时,令()e cos ln 1xg x x x x =+--,则()e ln sin 1xg x x x '=---,设()()h x g x '=,则()1e cos xh x x x=--',设()1e cos x m x x x =--,则()21e sin xm x x x=++',因为1x >,所以()0m x '>,所以()m x 即()h x '在()1,+∞上单调递增,所以()()1e 1cos10h x h >=--'>',所以()h x 在()1,+∞上单调递增,所以()()1e sin110h x h >=-->,即()0g x '>,所以()g x 在()1,+∞上单调递增,()()1e cos110g x g >=+->,即e cos 1ln 0x x x x +-->.综上可知,当1a >时,()e cos 1ln e cos 1ln 0x x a x x x x x x x x ++--->+-->,即()ln cos f x x x a x >-.【点睛】方法点睛;求解函数单调区间的步骤:(1)确定()f x 的定义域;(2)计算导数()f x ';(3)求出()0f x '=的根;。
2022届湖南师范大学附属中学高三上学期第二次月考数学试题解析

不存在 ,使得 ,可知 不正确;
B选项: 为锐角三角形, ,即 ,
, ,又 ,且 在 上单调递增
;若 ,满足 ,但 , 不锐角△ABC的内角,可知B正确;
C选项: ,则 ,则 为偶函数,可知C正确;
D选项: 向右平移 个单位得 ,可知D错误.
故选:BC.
11. 设 同时为椭圆 与双曲线 的左右焦点,设椭圆 与双曲线 在第一象限内交于点 ,椭圆 与双曲线 的离心率分别为 为坐标原点,若()
由 为等比数列,可得 是以 为首项,公比为 的等比数列,
则原不等式等价为: ,
因为 ,把 , 代入整理得: ,
可得: , ,即: ,
由 ,故答案为:18.
【点睛】本题主要考查数列与不等式的综合,计算量大,属于中档题型.
16. 已知函数 ,若 , , .则 的最大值为___________.
答案:
首先确定函数的对称性,然后利用倒序相加法求和,最后利用几何意义求得 的最大值即可.
A. ,则
B. ,则
C. ,则 的取值范围是
D. ,则 的取值范围是
答案:BD
先设 ,焦距为 ,根据椭圆与双曲线的定义,求出 , ;当 ,得 ,进而可判断B正确,A错;当 时,得到 ,推出 ,利用换元法,结合函数单调性,即可判断D正确,C错.
解:
如图,设 ,焦距为 ,由椭圆定义可得 ,由双曲线定义可得 ,解得 , ,
A. B. C. D.
答案:B
分析可知 个阴数即 个偶数为 、 、 、 , 个阳数为 、 、 、 、 ,然后对所选的 个数进行分类讨论,结合分类加法计数原理可得结果.
解:根据题意, 个阴数即 个偶数: 、 、 、 ; 个阳数即 、 、 、 、 ,
湖南师范大学附属中学2022-2023学年高三上学期月考(三)数学试题

(1)证明:
①AD平分∠BAC,
② ;
(2)若 ,求 的最大值.
19.汽车尾气排放超标是全球变暖、海平面上升的重要因素.我国近几年着重强调可持续发展,加大在新能源项目的支持力度,积极推动新能源汽车产业发展,某汽车制造企业对某地区新能源汽车的销售情况进行调查,得到下面的统计表:
年份
2017
2018
2019
2020
2021
年份代码
1
2
3
4
5
销量 万辆
10
12
17
20
26
(1)统计表明销量 与年份代码 有较强的线性相关关系,求 关于 的线性回归方程,并预测该地区新能源汽车的销量最早在哪一年能突破50万辆;
(2)为了解购车车主的性别与购车种类(分为新能源汽车与传统燃油汽车)的情况,该企业心随机调查了该地区200位购车车主的购车情况作为样本其中男性车主中购置传统燃油汽车的有 名,购置新能源汽车的有45名,女性车主中有20名购置传统燃油汽车.
14.已知定圆 ,点A是圆M所在平面内一定点,点P是圆M上的动点,若线段PA的中垂线交直线PM于点Q,则点Q的轨迹:①椭圆;②双曲线;③抛物线;④圆;⑤直线;⑥一个点.其中所有可能的结果有______个.
15.已知点O是△ABC的外心,a,b,c分别为内角A,B,C的对边, ,且 ,则 的值为________.
湖南师大附中2023届高三月考试卷(三)
数学
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合 ,若 ,则实数 的取值范围为()
湖南省湖南师范大学附属中学2020届高三数学上学期月考试题(四) 理(含解析)

湖南省湖南师范大学附属中学2020届高三数学上学期月考试题(四)理(含解析)时量:120分钟 满分:150分一、选择题:本大题共12小题,每小题5分,共60分,在每小题的四个选项中,只有一项是符合题目要求的.1.已知集合A ={x∈R |x 2-x -2<0},B ={x∈Z |x =2t +1,t ∈A},则A∩B=(C) A .{-1,0,1} B .{-1,0} C .{0,1} D .{0} 【解析】A ={x∈R |x 2-x -2<0}={x|-1<x <2}, 则x =2t +1∈(-1,5),所以B ={0,1,2,3,4}, 所以A∩B={0,1},故选C.2.已知复数z =21-i ,给出下列四个结论:①|z|=2;② z 2=2i ;③z 的共轭复数z =-1+i ;④z 的虚部为i.其中正确结论的个数是(B)A .0 B. 1 C .2 D .3【解析】由已知z =1+i ,则|z|=2,z 2=2i ,z =1-i ,z 的虚部为1.所以仅结论②正确,故选B.3.若向量a 与b 满足()a +b ⊥a ,且||a =1,||b =2,则向量a 在b 方向上的投影为(B) A. 3 B .-12 C .-1 D.33【解析】利用向量垂直的充要条件有:()a +b ·a =a 2+a ·b =0,∴a ·b =-1,向量a在b 方向上的投影为a ·b ||b =-12.4.五进制是以5为底的进位制,主因乃人类的一只手有五只手指. 中国古代的五行学说也是采用的五进制,0代表土,1代表水,2代表火,3代表木,4代表金,依此类推,5又属土,6属水,……,减去5即得. 如图,这是一个把k 进制数a(共有N 位)化为十进制数b 的程序框图,执行该程序框图,若输入的k ,a ,n 分别为5,1 203,4,则输出的b =(A)A .178B .386C .890D .14 303【解析】模拟执行程序框图,可得程序框图的功能是计算并输出b =3·50+0·51+2·52+1·53=178.故选A.5.若(1-x)5=a 0+a 1x +a 2x 2+a 3x 3+a 4x 4+a 5x 5,则|a 0|-|a 1|+|a 2|-|a 3|+|a 4|-|a 5|=(A)A .0B .1C .32D .-1【解析】由二项展开式的通项公式T r +1=C r5(-x)r=C r5(-1)r x r,可知a 1,a 3,a 5都小于0,则|a 0|-|a 1|+|a 2|-|a 3|+|a 4|-|a 5|=a 0+a 1+a 2+a 3+a 4+a 5,在原二项展开式中令x =1,可得a 0+a 1+a 2+a 3+a 4+a 5=0.故选A.6.若实数x ,y 满足⎩⎪⎨⎪⎧2x -y≥0,y ≥x ,y ≥-x +b ,且z =2x +y 的最小值为3,则实数b 的值为(C)A .1 B. 2 C.94 D.52【解析】画出可行域如图阴影部分所示,当目标函数z =2x +y 过点B 时取得最小值,由⎩⎪⎨⎪⎧y =-x +b ,2x -y =0得B ⎝ ⎛⎭⎪⎫b 3,2b 3,则2×b 3+2b 3=3,解得b =94.故选C.7.气象意义上从春季进入夏季的标志为:“连续5天的日平均温度均不低于22 ℃”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数):①甲地:5个数据的中位数为24,众数为22; ②乙地:5个数据的中位数为27,总体均值为24;③丙地:5个数据中有一个数据是32,总体均值为26,总体方差为10.8. 则肯定进入夏季的地区有(B)A .①②③B .①③C .②③D .①【解析】 由统计知识,①甲地:5个数据的中位数为24,众数为22,可知①符合题意;②乙地:5个数据的中位数为27,总体均值为24,有可能某一天的气温低于22 ℃,所以不符合题意;③丙地:5个数据中有一个数据是32,总体均值为26,总体方差为10.8.若某一天的气温低于22 ℃,则总体方差就大于10.8,所以满足题意,故选B.8.平面α过正方体ABCD -A 1B 1C 1D 1的顶点A ,平面α∥平面A 1BD ,平面α∩平面ABCD =l ,则直线l 与直线A 1C 1所成的角为(D)A .30°B .45°C .60°D .90°【解析】如图所示,平面α过正方体ABCD -A 1B 1C 1D 1的顶点A ,平面α∥平面A 1BD ,平面α∩平面ABCD =l =AF ,平面A 1BD ∩平面ABCD =BD ,∴BD ∥AF ,又∵A 1C 1∥AC ,则直线l 与直线A 1C 1所成的角即为直线BD 与直线AC 所成的角,为90°.故选D.9.对于数列{}a n ,定义H n =a 1+2a 2+…+2n -1a nn为{}a n 的“优值”,现已知某数列的“优值”H n =2n,记数列{}a n 的前n 项和为S n ,则S 2 0192 019=(B)A .2 022B .1 011C .2 020D .1 010 【解析】由H n =a 1+2a 2+…+2n -1a n n =2n,得a 1+2a 2+…+2n -1a n =n ·2n, ①a 1+2a 2+…+2n -2a n -1=(n -1)·2n -1, ② ①-②得2n -1a n =n·2n-(n -1)·2n -1=(n +1)·2n -1,即a n =n +1,S n =n (n +3)2,所以S 2 0192 019=1 011.故选B.10.在锐角△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若cos B b +cos C c =23sin A3sin C ,cos B +3sin B =2,则a +c 的取值范围是(B)A.⎝⎛⎦⎥⎤32,3 B.⎝ ⎛⎦⎥⎤32,3 C.⎣⎢⎡⎦⎥⎤32,3 D.⎣⎢⎡⎦⎥⎤32,3【解析】由题意cos B b +cos C c =23sin A3sin C可得:ccos B +bcos C bc =sin Ccos B +sin Bcos C bsin C =sin (B +C )bsin C =23sin A 3sin C ,∴b =32. cos B +3sin B =2⎝ ⎛⎭⎪⎫12cos B +32sin B =2sin ⎝ ⎛⎭⎪⎫B +π6=2,∴B +π6=π2,B =π3,bsin B =1,∴A +C =2π3,0<C =2π3-A<π2,0<A<π2,∴π6<A<π2,a +c =sin A +sin C =sin A +sin ⎝ ⎛⎭⎪⎫2π3-A =32sin A +32cos A =3sin ⎝⎛⎭⎪⎫A +π6,∵π6<A<π2,∴π3<A +π6<2π3, ∴32<3sin ⎝ ⎛⎭⎪⎫A +π6≤ 3.故答案选B.11.已知函数f(x)=⎩⎨⎧log 2()2-x ,0≤x <k ,x 3-3x 2+3,k ≤x ≤a ,若存在实数k ,使得函数f(x)的值域为[-1,1],则实数a的取值范围是(B)A.⎣⎢⎡⎦⎥⎤32,1+3 B.[]2,1+3 C.[]1,3 D.[]2,3【解析】由于y=log2(2-x)在[0,k)上是单调递减函数,当x=0时,y=1,当x=32时,y=-1,所以0<k≤32.令g(x)=x3-3x2+3,则g′(x)=3x2-6x=0,解得x=0或x=2,当x=2时,函数取得极小值-1,当x3-3x2+3=1时,解得x1=1,x2=1+3,x3=1-3<0(舍),所以2≤a≤1+3,故选B.12.设A,B是抛物线y=x2上的两点,O是坐标原点,若OA⊥OB,则以下结论恒成立的结论个数为(C)①|OA|·|OB|≥2;②直线AB过定点(1,0);③O到直线AB的距离不大于1.A.0 B.1 C.2 D.3【解析】设A(x1,x21),B(x2,x22),OA→·OB→=x1x2(1+x1x2)=0x2=-1x1,|OA|·|OB|=x21()1+x211x21⎝⎛⎭⎪⎫1+1x21=1+x21+1x21+1≥2,①正确;直线AB的斜率x22-x21x2-x1=x2+x1=x1-1x1,方程为y-x21=⎝⎛⎭⎪⎫x1-1x1(x-x1),过定点(0,1),②错误;原点到直线AB:⎝⎛⎭⎪⎫x1-1x1x-y+1=0的距离d=1⎝⎛⎭⎪⎫x1-1x12+1≤1,③正确.故选C.二、填空题:本大题共4小题,每小题5分,共20分.13.已知函数f(x)=sin⎝⎛⎭⎪⎫2ωx-π3(x∈R,ω>0)图象的相邻两条对称轴之间的距离为π2,则ω=__1__.【解析】由T2=π2,T=2π2ω得ω=1.14.已知函数f(x)=⎩⎨⎧x +1(-1≤x≤0),1-x 2(0<x≤1),则⎠⎛-11f(x)dx 的值为__12+π4__. 【解析】⎠⎛-11f(x)dx =⎠⎛-10(x +1)dx +⎠⎛011-x 2dx =⎝ ⎛⎭⎪⎫12x 2+x |0-1+π4=12+π4.15.已知双曲线x 2a 2-y2b 2=1(a>0,b>0),过x 轴上点P 的直线与双曲线的右支交于M ,N 两点(M 在第一象限),直线MO 交双曲线左支于点Q(O 为坐标原点),连接QN.若∠MPO=120°,∠MNQ =150°,则该双曲线的渐近线方程为__y =±x __ .【解析】由题意可知:M ,Q 关于原点对称,∴k MN · k QN =b2a 2,∵k MN =3,k QN =33,∴b2a2=1,渐近线方程为y =±x.16.某几何体的三视图如图所示,正视图是直角三角形,侧视图是等腰三角形,俯视图是边长为32的等边三角形,若该几何体的外接球的体积为36π,则该几何体的体积为__9__.【解析】根据几何体的三视图,得出该几何体如图所示,由该几何体的外接球的体积为36π,即43πR 3=36π,R =3,则球心O 到底面等边△ABC 的中心O′的距离||OO′=R 2-⎝ ⎛⎭⎪⎫33×322=3,可得三棱锥的高h =2||OO′=23,故三棱锥的体积V =13×34×(32)2×23=9.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.(本小题满分12分)已知等比数列{a n }的前n 项和为S n ,满足S 4=2a 4-2,S 3=2a 3-2. (Ⅰ)求{a n }的通项公式;(Ⅱ)记b n =log 2()a n -1·a n ,数列⎩⎨⎧⎭⎬⎫b n a n 的前n 项和为T n ,求使T n >177-2n60成立的正整数n的最小值.【解析】(Ⅰ)设{a n }的公比为q ,由S 4-S 3=a 4得,2a 4-2a 3=a 4,所以a 4a 3=2,所以q =2.2分又因为S 3=2a 3-2,所以a 1+2a 1+4a 1=8a 1-2,所以a 1=2. 所以a n =2n.5分(Ⅱ)由(Ⅰ)知b n =log 2(a n -1·a n )=log 2(2n -1×2n)=2n -1,所以b n a n =2n -12n ,6分T n =121+322+523+…+2n -12n ,则12T n =122+323+524+……+2n -32n +2n -12n +1,T n -12T n =12T n =12+⎝ ⎛⎭⎪⎫121+122+123+…+12n -1-2n -12n +1=12+⎝ ⎛⎭⎪⎫1-12n -1-2n -12n +1=32-2n +32n +1,所以T n =3-2n +32n ,10分由T n =3-2n +32n >177-2n 60,得2n +32n <3-177-2n 60=2n +360,即2n>60,则n≥6,所以n 的最小值是6.12分 18.(本小题满分12分)如图,在四棱锥P -ABCD 中,底面ABCD 是边长为2的菱形,∠DAB =60°,∠ADP =90°,平面ADP⊥平面ABCD ,点F 为棱PD 的中点.(Ⅰ)在棱AB 上是否存在一点E ,使得AF∥平面PCE ,并说明理由;(Ⅱ)当二面角D -FC -B的余弦值为24时,求直线PB 与平面ABCD 所成的角. 【解析】(Ⅰ)在棱AB 上存在点E ,使得AF∥平面PCE ,点E 为棱AB 的中点.理由如下:取PC 的中点Q ,连结EQ 、FQ , 由题意,FQ ∥DC 且FQ =12CD ,AE ∥CD 且AE =12CD ,故AE∥FQ 且AE =FQ.所以,四边形AEQF 为平行四边形.3分所以,AF∥EQ,又EQ 平面PEC ,AF 平面PEC , 所以,AF ∥平面PEC.5分(Ⅱ)由题意知△ABD 为正三角形,所以ED⊥AB,亦即ED⊥CD,又∠ADP=90°,所以PD⊥AD,且平面ADP⊥平面ABCD ,平面ADP∩平面ABCD =AD , 所以PD⊥平面ABCD ,故以D 为坐标原点建立如图空间直角坐标系,7分设FD =a ,则由题意知D ()0,0,0,F ()0,0,a ,C ()0,2,0,B ()3,1,0, FC →=()0,2,-a ,CB →=()3,-1,0, 设平面FBC 的法向量为m =()x ,y ,z ,则由⎩⎪⎨⎪⎧m ·FC →=0,m ·CB →=0 得⎩⎨⎧2y -az =0,3x -y =0,令x =1,则y =3,z =23a ,所以取m =⎝ ⎛⎭⎪⎫1,3,23a ,显然可取平面DFC 的法向量n =()1,0,0,由题意:24=||cos 〈m ,n 〉=11+3+12a2,所以a = 3.10分由于PD⊥平面ABCD ,所以PB 在平面ABCD 内的射影为BD , 所以∠PBD 为直线PB 与平面ABCD 所成的角,易知在Rt △PBD 中,tan ∠PBD =PDBD=a =3,从而∠PBD=60°,所以直线PB 与平面ABCD 所成的角为60°.12分 19.(本小题满分12分)为了引导居民合理用水,某市决定全面实施阶梯水价.阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:阶梯级别 第一阶梯水量第二阶梯水量第三阶梯水量月用水量范围(单位:立方米) [0,10)[10,15)[15,+∞)从本市随机抽取了10户家庭,统计了同一月份的月用水量,得到如图茎叶图: (Ⅰ)现要在这10户家庭中任意选取3户,求取到第二阶梯水量的户数X 的分布列与数学期望;(Ⅱ)用抽到的10户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取10户,若抽到k 户月用水量为一阶的可能性最大,求k 的值.【解析】(1)由茎叶图可知抽取的10户中用水量为一阶的有3户,二阶的有5户,三阶的有2户.第二阶段水量的户数X 的可能取值为0,1,2,3,P(X =0)=C 05C 35C 310=112,P(X =1)=C 15C 25C 310=512,P(X =2)=C 25C 15C 310=512,P(X =3)=C 35C 05C 310=112,4分所以X 的分布列为X 0 1 2 3 P112512512112X 的数学期望E(X)=0×112+1×512+2×512+3×112=32.6分(2)设Y 为从全市抽取的10户中用水量为一阶的家庭户数,依题意得Y ~B ⎝⎛⎭⎪⎫10,310,P(X =k)=C k 10⎝ ⎛⎭⎪⎫310k⎝ ⎛⎭⎪⎫71010-k(k =0,1,2,3,…,10),9分由⎩⎪⎨⎪⎧C k 10⎝ ⎛⎭⎪⎫310k⎝ ⎛⎭⎪⎫71010-k ≥C k +110⎝ ⎛⎭⎪⎫310k +1⎝ ⎛⎭⎪⎫7109-k,Ck 10⎝ ⎛⎭⎪⎫310k ⎝ ⎛⎭⎪⎫71010-k ≥C k -110⎝ ⎛⎭⎪⎫310k -1⎝ ⎛⎭⎪⎫71011-k,解得2310≤k≤3310,又k∈N *,所以当k =3时概率最大.即从全市依次随机抽取10户,抽到3户月用水量为一阶的可能性最大.12分 20.(本小题满分12分)已知点F 是椭圆x 21+a2+y 2=1(a>0)的右焦点,点M(m ,0),N(0,n)分别是x 轴,y 轴上的动点,且满足MN →·NF →=0.若点P 满足OM →=2ON →+PO →(O 为坐标原点).(Ⅰ)求点P 的轨迹C 的方程;(Ⅱ)设过点F 任作一直线与点P 的轨迹交于A ,B 两点,直线OA ,OB 与直线x =-a 分别交于点S ,T ,试判断以线段ST 为直径的圆是否经过点F ?请说明理由.【解析】(Ⅰ) ∵椭圆x 21+a 2+y 2=1(a>0)右焦点F 的坐标为(a ,0),1分∴NF →=(a ,-n).∵MN →=(-m ,n), ∴由MN →·NF →=0,得n 2+am =0. 3分设点P 的坐标为(x ,y),由OM →=2ON →+PO →,有(m ,0)=2(0,n)+(-x ,-y), ⎩⎪⎨⎪⎧m =-x ,n =y2.代入n 2+am =0,得y 2=4ax. 即点P 的轨迹C 的方程为y 2=4ax.5分(Ⅱ)解法一:设直线AB 的方程为x =ty +a ,A ⎝ ⎛⎭⎪⎫y 214a ,y 1,B ⎝ ⎛⎭⎪⎫y 224a ,y 2,则l OA :y =4a y 1x ,l OB :y =4ay 2x. 6分由⎩⎪⎨⎪⎧y =4a y 1x ,x =-a ,得S ⎝ ⎛⎭⎪⎫-a ,-4a 2y 1,同理得T ⎝ ⎛⎭⎪⎫-a ,-4a 2y 2. 8分∴FS →=⎝ ⎛⎭⎪⎫-2a ,-4a 2y 1,FT →=⎝⎛⎭⎪⎫-2a ,-4a 2y 2,则FS →·FT →=4a 2+16a 4y 1y 2.9分由⎩⎪⎨⎪⎧x =ty +a ,y 2=4ax ,得y 2-4aty -4a 2=0,∴y 1y 2=-4a 2.10分 则FS →·FT →=4a 2+16a 4(-4a 2)=4a 2-4a 2=0. 因此,以线段ST 为直径的圆经过点F.12分解法二:①当AB⊥x 时,A(a ,2a),B(a ,-2a),则l OA :y =2x ,l OB :y =-2x. 由⎩⎪⎨⎪⎧y =2x ,x =-a ,得点S 的坐标为S(-a ,-2a),则FS →=(-2a ,-2a). 由⎩⎪⎨⎪⎧y =-2x ,x =-a ,得点T 的坐标为T(-a ,2a),则FT →=(-2a ,2a). ∴FS →·FT →=(-2a)×(-2a)+(-2a)×2a=0. 7分②当AB 不垂直x 轴时,设直线AB 的方程为y =k(x -a)(k≠0),A ⎝ ⎛⎭⎪⎫y 214a ,y 1,B ⎝ ⎛⎭⎪⎫y 224a ,y 2, 同解法一,得FS →·FT →=4a 2+16a 4y 1y 2.8分 由⎩⎪⎨⎪⎧y =k (x -a ),y 2=4ax ,得ky 2-4ay -4ka 2=0,∴y 1y 2=-4a 2.9分 则FS →·FT →=4a 2+16a 4(-4a 2)=4a 2-4a 2=0. 11分 因此,以线段ST 为直径的圆经过点F. 12分21.(本小题满分12分)已知函数f(x)=a(x -1),g(x)=(ax -1)e x ,a ∈R .(Ⅰ)若直线y =f(x)与曲线y =g(x)相切于点P(x 0,y 0),证明:0<x 0<1;(Ⅱ)若不等式f(x)>g(x)有且仅有两个整数解,求a 的取值范围.【解析】(Ⅰ)g′(x)=(ax +a -1)e x ,由导数的几何意义可知,(ax 0+a -1)ex 0=a , ①1分又直线y =f(x)的图象过定点(1,0),因此(ax 0-1)ex 0x 0-1=a , 即(ax 0-1)ex 0=a(x 0-1), ②2分联立①②消去a 有ex 0+x 0-2=0.3分设φ(x)=e x +x -2,则φ′(x)=e x +1>0,所以φ(x)在R 上单调递增.而φ(0)=-1<0,φ(1)=e -1>0,φ(0)φ(1)<0,由函数零点存在性定理知 0<x 0<1.5分(Ⅱ)由f(x)>g(x)得a ⎝⎛⎭⎪⎫x -x -1e x <1, 令h(x)=x -x -1e x ,则h′(x)=1+x -2e x =e x+x -2ex ,6分 由(Ⅰ)知φ(x)=e x +x -2在R 上单调递增,且x∈(-∞,x 0)时,φ(x 0)<0;在x∈(x 0,+∞),φ(x 0)>0,故h(x)在(-∞,x 0)上单调递减,在(x 0,+∞)上单调递增.∴h(x)min =h(x 0)=x 0-x 0-1ex 0=x 0ex 0-x 0+1ex 0. 易证e x ≥x +1,∴h(x 0)=x 0ex 0-x 0+1ex 0>x 20+1ex 0>0,8分 当x≤0时,h (x)≥h(0)=1>0;当x≥1时,h (x)≥h(1)=1.(1)若a≤0,则ah(x)≤0<1,此时ah(x)<1有无穷多个整数解,不合题意;9分(2)若a≥1,即1a≤1,因为h(x)在(]-∞,0上单调递减,在[)1,+∞上单调递增, 所以x∈Z ,h (x)≥min {}h (0),h (1)=1≥1a, 所以h(x)<1a无整数解,不合题意;10分 (3)若0<a<1,即1a >1,此时h(0)=h(1)=1<1a ,故0,1是h(x)<1a 的两个整数解,又h(x)<1a只有两个整数解,因此⎩⎪⎨⎪⎧h (-1)≥1a ,h (2)≥1a ,解得a≥e 22e 2-1,所以a∈⎣⎢⎡⎭⎪⎫e 22e 2-1,1.12分 (二)选考题:共10分.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题计分.22.(本小题满分10分)选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,曲线C 1:⎩⎪⎨⎪⎧x =a +acos φ,y =asin φ(φ为参数,实数a >0),曲线C 2:⎩⎪⎨⎪⎧x =bcos φ,y =b +bsin φ(φ为参数,实数b >0).在以O 为极点,x 轴的正半轴为极轴的极坐标系中,射线l :θ=α⎝⎛⎭⎪⎫ρ≥0,0≤α≤π2与C 1交于O ,A 两点,与C 2交于O ,B 两点.当α=0时,|OA|=2;当α=π2时,|OB|=4. (Ⅰ)求a ,b 的值;(Ⅱ)求2|OA|2+|OA|·|OB|的最大值.【解析】(Ⅰ)由曲线C 1:⎩⎪⎨⎪⎧x =a +acos φ,y =asin φ(φ为参数,实数a >0), 化为普通方程为(x -a)2+y 2=a 2,展开为:x 2+y 2-2ax =0,其极坐标方程为ρ2=2aρcos θ,即ρ=2acos θ,由题意可得当θ=0时,|OA|=ρ=2,∴a =1.2分曲线C 2:⎩⎪⎨⎪⎧x =bcos φ,y =b +bsin φ(φ为参数,实数b >0), 化为普通方程为x 2+(y -b)2=b 2,展开可得极坐标方程为ρ=2bsin θ,由题意可得当θ=π2时,|OB|=ρ=4,∴b =2.5分 (Ⅱ)由(Ⅰ)可得C 1,C 2的极坐标方程分别为ρ=2cos θ,ρ=4sin θ.∴2|OA|2+|OA|·|OB|=8cos 2θ+8sin θcos θ=4sin 2θ+4cos 2θ+4=42sin ⎝⎛⎭⎪⎫2θ+π4+4,8分 ∵2θ+π4∈⎣⎢⎡⎦⎥⎤π4,5π4,∴42sin ⎝⎛⎭⎪⎫2θ+π4+4的最大值为42+4, 当2θ+π4=π2,θ=π8时取到最大值.10分 23.(本小题满分10分)选修4-5:不等式选讲 已知函数f(x)=2||x +a +⎪⎪⎪⎪⎪⎪x -1a ()a≠0. (Ⅰ)当a =1时,解不等式f(x)<4;(Ⅱ)求函数g(x)=f(x)+f(-x)的最小值.【解析】(Ⅰ)∵ a=1,∴原不等式为2|x +1|+|x -1|<4,∴⎩⎪⎨⎪⎧x <-1,-2x -2-x +1<4或⎩⎪⎨⎪⎧-1≤x≤1,2x +2-x +1<4或⎩⎪⎨⎪⎧x>1,2x +2+x -1<4,3分∴-53<x <-1或-1≤x<1或, ∴原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪-53<x <1.5分 (Ⅱ)由题意得g(x)=f(x)+f(-x)=2()|x +a|+|x -a|+⎝ ⎛⎭⎪⎫⎪⎪⎪⎪⎪⎪x +1a +⎪⎪⎪⎪⎪⎪x -1a ≥2|2a|+2|a|=4||a +2|a|≥42,8分 当且仅当2||a =1||a ,即a =±22,且-22≤x≤22时,g(x)取最小值4 2.10分。
2024届湖南师范大学附属中学高三上学期月考卷(四)数学及答案

湖南师大附中2024届高三月考试卷(四)数学审题人:高三备课组时量:120分钟 满分:150分一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数12i z =+,其中i 为虚数单位,则复数2z 在复平面内对应的点的坐标为( )A.(4,5)- B.(4,3)C.(3,4)- D.(5,4))2.若随机事件A ,B 满足1()3P A =,1()2P B =,3()4P A B = ,则(|)P A B =( )A.29B.23C.14D.168.设{}n a 是公比不为1的无穷等比数列,则“{}n a 为递减数列”是“存在正整数0N ,当0n N >时,1n a <”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.设0,2πα⎛⎫∈ ⎪⎝⎭,0,2πβ⎛⎫∈ ⎪⎝⎭,且1tan tan cos αβα+=,则( )A.22παβ+=B.22παβ-=C.22πβα-=D.22πβα+=5.若52345012345(12)(1)(1)(1)(1)(1)x a a x a x a x a x a x -=+-+-+-+-+-,则下列结论中正确的是( )A.01a = B.480a =C.50123453a a a a a a +++++= D.()()10024135134a a a a a a -++++=6.函数1()2cos[(2023)]|1|f x x x π=++-在区间[3,5]-上所有零点的和等于( )A.2B.4C.6D.87.点M 是椭圆22221x y a b+=(0a b >>)上的点,以M 为圆心的圆与x 轴相切于椭圆的焦点F ,圆M 与y 轴相交于P ,Q ,若PQM △是钝角三角形,则椭圆离心率的取值范围是()A.(0,2B.⎛ ⎝C.⎫⎪⎪⎭D.(2-8.已知函数22,0,()4|1|4,0,x x f x x x ⎧=⎨-++<⎩…若存在唯一的整数x ,使得()10f x x a -<-成立,则所有满足条件的整数a 的取值集合为( )A.{2,1,0,1}-- B.{2,1,0}-- C.{1,0,1}- D.{2,1}-二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分、9.已.知双曲线C过点且渐近线为y x =,则下列结论正确的是( )A.C 的方程为2213x y -= B.CC.曲线2e1x y -=-经过C 的一个焦点D.直线10x --=与C 有两个公共点10.已知向量a ,b满足|2|||a b a += ,20a b a ⋅+= 且||2a = ,则( )A.||8b = B.0a b += C.|2|6a b -=D.4a b ⋅= 11.如图、正方体1111ABCD A B C D -的棱长为2,点M 是其侧面11ADD A 上的一个动点(含边界),点P 是线段1CC 上的动点,则下列结论正确的是()A.存在点P ,M ,使得二面角M DC P --大小为23πB.存在点P ,M ,使得平面11B D M 与平面PBD 平行C.当P 为棱1CC的中点且PM =时,则点M 的轨迹长度为23πD.当M 为1A D 中点时,四棱锥M ABCD -12.若存在实常数k 和b ,使得函数()F x 和()G x 对其公共定义域上的任意实数x 都满足:()F x kx b +…和()G x kx b +…恒成立,则称此直线y kx b =+为()F x 和()G x 的“隔离直线”.已知函数2()f x x =(x ∈R ),1()g x x=(0x <),()2eln h x x =(e 2.718≈),则下列选项正确的是( )A.()()()m x f x g x =-在x ⎛⎫∈ ⎪⎝⎭时单调递增B.()f x 和()g x 之间存在“隔离直线”,且b 的最小值为–4C.()f x 和()g x 之间存在“隔离直线”,且k 的取值范围是[4,1]-D.()f x 和()h x之间存在唯一的“隔离直线”ey =-三、填空题:本题共4小题,每小题5分,共20分.13.已知函数()y f x =的图象在点(1,(1))M f 处的切线方程是122y x =+,则(1)(1)f f +'=___________.14.如图,由3个全等的钝角三角形与中间一个小等边三角形DEF 拼成的一个较大的等边三角形ABC ,若3AF =,sin ACF ∠=,则DEF △的面积为___________.15.已知数列{}n a 的首项132a =,且满足1323n n n a a a +=+.若123111181n a a a a ++++< ,则n 的最大值为___________.16.在棱长为3的正方体1111ABCD A B C D -中,点E 满足112A E EB =,点F 在平面1BC D 内,则|1||A F EF +的最小值为___________.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)已知函数2()2cos 2xf x x m ωω=++(0ω>)的最小值为–2.(1)求函数()f x 的最大值;(2)把函数()y f x =的图象向右平移6πω个单位长度,可得函数()y g x =的图象,且函数()y g x =在0,8π⎡⎤⎢⎥⎣⎦上单调递增,求ω的最大值.18.(12分)为了丰富在校学生的课余生活,某校举办了一次趣味运动会活动,学校设置项目A “毛毛虫旱地龙舟”和项目B “袋鼠接力跳”.甲、乙两班每班分成两组,每组参加一个项目,进行班级对抗赛.第一个比赛项目A 采取五局三胜制(即有一方先胜3局即获胜,比赛结束);第二个比赛项目B 采取领先3局者获胜。
湖南师范大学附属中学高三上学期月考数学(文科)试卷(四)有答案

A. B. C. D.
3.已知等差数列 的前 项和为 ,若 , ,则 取最大值时, 的值为()
A.3B.4C.5D.6
4.函数 的图像大致为()
5.过抛物线 的焦点的直线交抛物线于 , 两点,且 ,这样的直线可以作2条,则 的取值范围是()
恒成立,求实数 的取值范围.
请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.
22.选修4-4:坐标系与参数方程
已知曲线 的极坐标方程是 ,以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,在平面直角坐标系 ,直线 经过点 ,倾斜角 .
(1)写出曲线 的直角坐标方程和直线 的参数方程;
(1)证明数列 为等比数列,并求出数列 的通项公式;
(2)若 ,求数列 的前 项和 .
19.如图,在底面是菱形的四棱柱 中, , , ,点 在 上.
(1)求证: 平面 ;
(2)当 为何值时, 平面 ,并求出此时直线 与平面 之间的距离.
20.已知椭圆 的中心在原点,离心率为 ,其右焦点是圆 : 的圆心.
(2)设 与曲线 相交于 , 两点,求 的值.
23.选修4-5:不等式选讲
已知函数 , ,若 恒成立,实数 的最大值为 .
(1)求实数 ;
(2)已知实数 、 、 满足 ( ),且 的最大值是 ,求 的值.
湖南师范大学附属中学高三上学期月考数学(文科)试卷(四)
答案
一、选择题
1~5.ABCBD6~10.CBADA11~12.CD
(1)求椭圆 的标准方程;
(2)如图,过椭圆 上且位于 轴左侧的一点 作圆 的两条切线,分别交 轴于点 、 .试推断是否存在点 ,使 ?若存在,求出点 的坐标;若不存在,请说明理由.
2022-2023学年湖南省长沙市湖南师范大学附属中学高三上学期月考卷物理试题(四)(解析版)
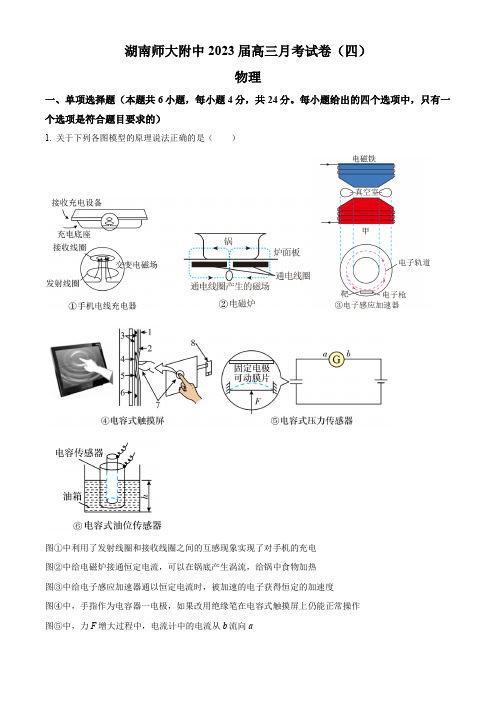
C.a、b两颗星的半径之比为 D.a、b两颗星的质量之比为
【答案】B
【解析】
【详解】A.两颗星绕它们连线上的某一点在万有引力作用下做匀速圆周运动,则角速度相同,由公式
可知两颗星的周期相等,故A错误;
BC.由于
两式联立解得
a、b两颗星的半径之比为
a星的线速度大小为
故选BC。
8.一列简谐横波沿x轴负方向传播,t=0时刻的波形如图中实线所示,t=0.7s时刻的波形如图中的虚线所示,则下列叙述正确的是( )
A.该波的波长为8m
B.波的周期可能为0.4s
C.波的传播速度可能为30m/s
D.质点P在t=0.7s时刻向下运动
【答案】ABD
【解析】
【详解】A.由波形图可知,该波的波长为λ=8m,选项A正确;
图③中给电子感应加速器通以恒定电流时,被加速的电子获得恒定的加速度
图④中,手指作为电容器一电极,如果改用绝缘笔在电容式触摸屏上仍能正常操作
图⑤中,力F增大过程中,电流计中的电流从b流向a
图⑥中,油箱液位上升时,电容变大
A.①②④B.②③⑥C.①⑤⑥D.②④⑤
【答案】C
【解析】
【详解】图①利用两线圈的互感现象在接收线圈中产生感应电流对手机充电,故①正确;
A.小滑环在D点的速度大小为
B.大圆环在B点产生的场强大小为
C.小滑环从B到C的过程中电场力所做的功为
D.小滑环在B点的加速度大小为
【答案】AD
【解析】
【详解】A.由对称性可得库仑力做功
从A到O,由动能定理得
解得
A正确;
B.由题意可知
圆环上电荷分布均匀,取环上一点,设其电荷量为 ,该点到B点的距离为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
则由1,2,3,4,5,6组成没有重复数字的六位数种,奇数不相邻,4位于第四位共有 个,
所以由1,2,3,4,5,6组成没有重复数字的六位数中,要求奇数不相邻,且4不在第四位的个数共有 个.
故答案为:120
14.已知函数 的定义域是 ,则函数 的单调增区间为______.
【详解】对于A,连接 、 .
∵ 、 分别为 、 的中点,∴ ∥EF,
易知AB∥ ,且AB= ,∴四边形 是平行四边形,
∴ ∥ ,∴ ∥EF.
∵ ⊥ ,∴ ⊥EF,故A正确;
对于B,设点 与点 到平面 的距离分别为 、 ,
∵ ,
又 ,
∴ ,故B错误;
对于C,取 的中点 ,连接 、 、EQ、 ,
易知EF∥ ∥GQ,GQ 平面AEF,EF 平面AEF,∴GQ∥平面AEF;
A.72B.74C.76D.78
【答案】B
【解析】
【分析】根据已知条件列方程,可得 ,再由 ,结合指对数关系和对数函数的性质求解即可.
【详解】由于 ,所以 ,
依题意 ,则 ,
则 ,
由 ,
所以,即 ,
所以所需的训练迭代轮数至少为74次.
故选:B
5.已知 ,则 ()
A. B.2C.4D.12
【答案】C
【解析】
【答案】①. ②.
【解析】
【分析】求出 所过 定点,结合 始终垂直,从而得到点 的轨迹为以 为直径的圆 ,数形结合求出最值,求出 的取值范围,由双曲线的离心率为 ,当 取得最大值时,离心率最大,由点到直线距离公式得到 ,求出 ,得到离心率.
【详解】 变形为 ,故经过定点 ,
变形为 ,过经过定点 ,
又 ,所以 与 始终垂直,
易知 ∥ ∥EQ,且 = =EQ,∴四边形 为平行四边形,
∴ ,同理可得 ∥平面AEF,
∵ ∩GQ=Q, 、GQ 平面 ,∴平面 ∥平面 ,
又∵ 平ቤተ መጻሕፍቲ ባይዱ ,∴ ∥平面 ,故C错误;
对于D,连接 、 、 ,
由选项A知 ∥EF,且 =2EF,故过A、E、F三点的平面截正方体的截面为等腰梯形AEFD,故D正确.
故选:A.
8.若实数 , 满足 ,则()
A. B. C. D.
【答案】A
【解析】
【分析】对不等式变形得到 ,换元后得到 ,构造 ,求导研究其单调性,极值最值情况,得到 ,从而只有 时,即 时,满足要求,从而解出 ,依次判断四个选项.
【详解】因为 ,
所以 ,即 ,
所以 ,
令 ,
则 ,即 ,
所以 ,
令 ,则 ,
当 时,函数 在 上单调递增;
所以函数 在 上单调递减,在 上单调递增,故A错误;
,
,
,
所以 ,故B正确;
将 图象左移 个单位长度后得到的图象的解析式为 ,
又 ,所以函数 为奇函数,
所以 的图象关于原点对称,故C正确;
关于 对称的区间为 ,
当 时, ,所以 ,
所以当 时, 的值域为 ,故D正确.
故选:BCD
故选:AD.
12.已知 ,具有下面三个性质:①将 的图象右移 个单位得到的图象与原图象重合;② , ;③ 在 时存在两个零点,给出下列判断,其中正确的是()
A. 在 时单调递减
B.
C.将 的图象左移 个单位长度后得到的图象关于原点对称
D.若 与 图象关于 对称,则当 时, 的值域为
【答案】BCD
【解析】
如图3,当 与圆 相切于点 时, 取得最大值,
由点到直线距离得: ,
即 ,方程两边同除以 得:
,解得: ,
其中 为图4中的情况,舍去,
故 ,此时离心率 .
故双曲线的离心率的最大值为 .
故答案为: ,
四、解答题
17.已知 是等差数列 前 项和, .
(1)求 的通项公式;
(2)在 中,去掉以 为首项,以 为公比的数列的项,剩下的项按原来顺序构成的数列记为 ,求 前100项和
【答案】C
【解析】
【分析】利用导数的几何意义确定切线斜率,则可得 ,再利用和差公式与二倍角公式以及同角三角函数关系切化弦化简所求式子,得到含 的式子,即可得结果.
【详解】解:因为 ,则
则曲线 在点 处的切线的斜率为 ,又倾斜角为
所以
则
.
故选:C.
4.深度学习是人工智能的一种具有代表性的实现方法,它是以神经网络为出发点的,在神经网络优化中,指数衰减的学习率模型为 ,其中 表示每一轮优化时使用的学习率, 表示初始学习率, 表示衰减系数, 表示训练迭代轮数, 表示衰减速度.已知某个指数衰减的学习率模型的初始学习率为 ,衰减速度为18,且当训练迭代轮数为18时,学习率衰减为 ,则学习率衰减到 以下(不含 )所需的训练迭代轮数至少为()(参考数据: )
三、填空题
13.由1,2,3,4,5,6组成没有重复数字的六位数,要求奇数不相邻,且4不在第四位,则这样的六位数共有______个.
【答案】120
【解析】
【分析】先排偶数,再使用插空法得到组成没有重复数字的六位数,奇数不相邻的个数为144个,再计算出这144个六位数中,4在第四位的个数,相减后得到答案.
由于 对称轴为 ,开口向下,所以在 上的单调递减区间为 ,
从而函数 的单调增区间为 .
故答案为: .
15.已知正方体 的棱长为 ,点E为棱 上一动点,点F为棱 上一动点,且满足 ,则三棱锥 的体积取最大值时,三棱锥 外接球的表面积为___________.
【答案】
【解析】
【分析】根据正方体的性质可知 进而利用直角三角形的性质得到外接球的球心为EF的中点O,从而得到球的半径,利用表面积公式计算得到球的表面积.
【答案】(1)
(2)
【解析】
【分析】(1)利用基本量代换列方程组求出首项与公差,即可得到通项公式;
【详解】 ,
将 右移 个单位得到的函数解析式为 ,
又该函数的图象与原图象重合,所以 ,
所以 ,
又 在 时存在两个零点,所以 ,
所以 ,即 ,所以 ,所以 ,
所以 ,
又 , ,所以 ,
所以 ,所以 ,
又 ,所以 ,所以 ,
由 得 ,
所以函数 的单调递减区间为
当 时,函数 在 上单调递减;
由 得 ,
所以函数 的单调递增区间为
C.直线 与平面 不平行
D.过A、E、F三点的平面截正方体的截面为等腰梯形
【答案】AD
【解析】
【分析】A:连接 、 ,证明 ∥EF∥ , ⊥ 即可;B:设点 与点 到平面 的距离分别为 、 ,利用等体积法 和 即可判断 、 是否相等;C:取 的中点 ,连接 、 、EQ、 ,证明平面 ∥平面 即可;D:连接 、 、 ,易知过A、E、F三点的平面截正方体的截面为等腰梯形AEFD.
A.
B.
C.
D.
【答案】A
【解析】
【分析】连接 、 ,取 的中点 , 的中点 ,连接 、 ,即可得到 , ,在 利用锐角三角函数求出 ,再在 利用锐角三角函数计算可得;
【详解】解:连接 、 ,取 的中点 , 的中点 ,连接 、 ,
由已知及双曲线的定义得 , , ,
∵ ,∴ 中, ,
又 ,∴ ,∴ ,
【分析】令 ,直接根据二项式定理求解即可.
【详解】令 ,则 ,
故 ,
中 得系数 , 中 得系数为 ,
所以 ,
故选:C.
6.已知函数 满足 ,且对任意的 ,都有 ,则满足不等式 的 的取值范围是()
A. B. C. D.
【答案】A
【解析】
【分析】 可化为 ,构造函数 ,再结合奇偶性可知该函数在R上单调递增,又将所求不等式变形,即可由单调性解该抽象不等式.
故点 的轨迹为以 为直径的圆 ,如图所示:
其中 ,即 ,且 ,
所以圆 的半径为 ,
连接 ,如图1,此时 取得最小值,长度为圆心距减去两圆半径,
即 ,
如图2,此时 取得最大值,长度为圆心距加上两圆半径,
即 ,
综上: 的取值范围是 ;
双曲线 的渐近线为 ,
由于点 在第一象限,所以渐近线 必过点 ,
双曲线的离心率为 ,当 取得最大值时,离心率最大,
【分析】根据①可得 ,再根据③可得 ,由此可得 ,从而可求得 的值,再由②可知 ,可求得 的值,从而可求出函数 的解析式.求出函数 的单调区间,即可判断A的正误;计算出 的值,可判断B的正误;求出函数左移 个单位长度后的解析式,判断其奇偶性,即可判断C的正误;根据对称性求出 的对称区间后,再求函数 的值域,可判断D的正误.
【详解】先排偶数,有 种方法,3个偶数,共有4个空格,再将奇数插空,共有 种情况,
故组成没有重复数字的六位数,奇数不相邻的个数为 种情况,
若4位于第四位,则第二位必须为偶数,可从数字2和6中二选一,有 种选择,
第五位与第六位,其中之一为偶数,故从两个位置中选择一个放入2和6中剩余的一个偶数,有 种选择,
(3) ;
(4) ,
本题难点在于 变形为 ,换元后得到 ,从而构造 解决问题.
二、多选题
9.已知 , 是平面内两个夹角为120°的单位向量,点C在以O为圆心的 上运动,若 =x +y (x,y∈R).下列说法正确的有()
A.当C位于 中点时,x=y=1
B.当C位于 中点时,x+y的值最大
C. 在 上的投影向量的模的取值范围为
B:由 得,
, ,∴ ,
∴ ,
∵ ,∴ ,
∴当 时, 的最大值为2,此时C为弧AB的中点,∴B正确,
C:当OC⊥OA时, 在 上的投影为0,∴C错误,
D:∵
,
∵ ,∴ ,
