大物实验电子逸出功数据处理
物理实验技术中的电子能谱实验数据处理方法

物理实验技术中的电子能谱实验数据处理方法一、引言电子能谱实验是物理学研究中常用的一种实验手段,它可以通过测量物质中电子的能量分布来研究材料的结构和性质。
然而,如何准确地处理电子能谱实验所得到的海量数据成为了一个重要的问题。
本文将探讨物理实验技术中的电子能谱实验数据处理方法。
二、数据获取与处理1. 数据获取电子能谱实验常用的手段是通过光电发射或电子能量损失来获取电子能谱数据。
在光电发射实验中,实验者将材料暴露在激光或X射线等辐射源下,测量出逸出电子的能量分布。
在电子能量损失实验中,实验者将电子束与样品相互作用,通过测量散射电子的能量损失来获得能谱数据。
2. 数据处理电子能谱实验得到的数据通常是一个能谱曲线或离散的能量分布数据。
为了准确地从这些数据中提取有用的信息,需要进行一系列的数据处理操作。
首先,对于能谱曲线,实验者需要进行背景扣除。
实验过程中,背景噪音常常会混入信号之中,影响实验结果的准确性。
通过对背景噪音的适当建模和拟合,可以准确地还原出原始信号。
其次,实验者需要对能谱数据进行能量标定。
能量标定是将实验得到的电子能谱与已知能量标准进行对比,建立能量与通道数(或时间)的对应关系。
这样可以将实验数据转化为实际物理量。
最后,实验者需要进行峰形拟合和积分。
能谱中常常包含多个峰,每一个峰代表特定能量的电子。
通过对峰形进行拟合,可以得到峰的能量、峰强度、峰宽度等信息。
这是分析材料结构和性质的重要依据。
三、常见的电子能谱数据处理方法1. 傅里叶变换傅里叶变换是一种常用的信号处理方法,在电子能谱实验中也有广泛的应用。
对于离散的能谱数据,可以通过傅里叶变换将其转化为频谱。
通过分析频谱的峰位和峰宽,可以得到电子态的能量和分布情况。
2. 数据插值数据插值是一种通过已有数据点来拟合新数据点的方法。
在电子能谱实验中,由于实验噪音和采样误差的存在,得到的能谱数据常常是离散的。
通过数据插值可以在离散点之间估计出新的数据点,提高数据的精确度。
实验311 金属电子逸出功的测定

但其电流不计入阳极电流中,这样使其成为
理想二极管。
图2 理想二极管的结构
大学物理实验
实验原理:
1.电子的逸出功及热电子发射
(1)逸出功:电子逸出金属表面至少需要从外界得到的能
量为 E0Eb ,EF称为e金属E电0 子的逸出功,
也称功函数
e是电子电荷, 称为逸出电位,EF 称为费密能级, Eb 势阱的深度。
If值时为何要预热几分钟才测量?
大学物理实验
作业:
完成本次实验的数据处理,预习下一次实验内容。
大学物理实验
3.从加速场外延求零场电流
肖脱基效应:外加电场Ea使逸出功减小,发射电流 增大的现象
Ia I0e x p (0 .4 3 9E a/T )
(3 )
式中Ia和I0分别是加速电场为Ea和零时的发射电流
对(3)式取对数得
0 .4 3 9 lgIa lgI02 .3 0E a/T
(4 )
0.550A 。 4.调节理想二极管的阳极电压,使阳极电压分别为
25.0V、36.0V、49.0V、64.0V……144.0V电压,分
别测出对应的阳极电流Ia,记录相应的数据.
大学物理实验
5.二极管的灯丝电流,每次增加0.050A,重复上述测 量,直至0.800A。每改变一次灯丝电流都要预热5 分钟 。
大学物理实验
将电场E用电压V来代替得:
lgIalgI002.4 .3309
1 r1lnrr1 2
Va/T
(5)
当阴极的温度T一定时,lgIa和 V a 成线性关系
大学物理实验
如果以lgIa为纵坐标,以
Va
V a为横坐标作图,如图
T5
5所示,此直线的延长 lgI0
逸出功的测量

逸出功的测量【实验目的】1. 用里查孙直线法测定阴极材料(钨)的电子逸出功。
2. 通过实验了解热电子发射的规律和掌握逸出功的测量方法。
【实验原理】关于热电子发射的里查孙—德西曼公式为:()()2121i W W kTe e J R AT e a --=-其中,()22013260.09k me A A cm K hp ==?,k 为玻尔兹曼常数,m 为电子质量,h 为普朗克常数,e R 为金属表面对发射电子的反射系数,T 为热力学温度。
若令()121e R A A -=则02e kTe J AT e f-=于是发射电流02e kTe I AST e f-=其中,S 为阴极金属的有效发射面积。
【测量及数据处理】1. A 与S 两个量的处理处理02e kTe I AST e f-=,并采用国际单位制,代入数据得到:()32lglg 5.03910e I AS T Tf =-? 这样2lge I T 和1T成线性关系,进行线性拟合获得斜率即可得到f 。
这样就解决了A 、S 无法测量的问题。
2. 发射电流I e 的测量电子逸出后将形成空间电荷阻碍后续电子的逸出,从而影响了发射电流的测量。
解决方法是在两极之间加一个加速场a E ,使电子一旦逸出就能迅速飞往阳极。
但这样又将对发射电流形成附加影响,此时发射电流为:4.39'a E Te e I I e=两边取对数得:4.39lg 'lg 2.303e e a I I E T=+若把阳极作为圆柱形并与阴极共轴,并利用'U U a a ?,则有:()1214.391lg 'lg 2.303ln e e I I U Tr r r a =+这样只要做出lg 'e I 和U a 的关系曲线,其在纵轴上的截距就是lg e I 。
这就解决了发射电流的测量问题。
3. 温度T 的测量一定的比加热电流I 1和阴极温度的关系已知。
而()321f K I I d =,其中I f 为阴极加热电流,d K 为阴极钨丝直径。
金属电子逸出功的测定实验报告

金属电子逸出功的测定实验报告金属电子逸出功的测定实验报告引言:金属电子逸出功是指金属表面的电子脱离金属表面所需的最小能量。
测定金属电子逸出功对于理解金属的电子结构以及应用于光电子学等领域具有重要意义。
本实验旨在通过测定金属电子逸出功的实验方法,探究金属电子的逸出行为,并分析其与金属表面性质的关系。
实验材料与仪器:本实验使用的材料为常见的金属样品,如铜、铝等。
实验所需仪器包括电子能谱仪、真空系统、光源等。
实验步骤:1. 准备金属样品:选择适当的金属样品,并将其表面清洗干净,以确保实验结果的准确性。
2. 搭建实验装置:将金属样品放置于真空系统中,确保系统处于良好的真空状态。
调整光源的位置和强度,以保证实验的可靠性。
3. 测定电子能谱:通过电子能谱仪测定金属样品的电子能谱曲线。
在实验过程中,可以调整光源的波长和强度,以获得不同能量下的电子能谱数据。
4. 分析数据:根据电子能谱曲线,确定金属电子的逸出功。
通过计算能量差值,可以得到电子逸出所需的最小能量。
结果与讨论:根据实验数据,我们可以得到不同金属样品的电子逸出功数值。
通过对比不同金属的逸出功,我们可以发现金属的电子逸出功与其物理性质之间存在一定的关系。
首先,金属的电子逸出功与其导电性能有关。
一般来说,导电性能较好的金属具有较低的电子逸出功,因为其电子更容易脱离金属表面。
相反,导电性能较差的金属则具有较高的电子逸出功,因为其电子与金属原子之间的束缚力较强。
其次,金属的电子逸出功与其晶格结构有关。
晶格结构较紧密的金属通常具有较高的电子逸出功,因为其表面原子对电子的束缚力较大。
相反,晶格结构较疏松的金属则具有较低的电子逸出功,因为其表面原子对电子的束缚力较小。
此外,金属的电子逸出功还与其表面的化学性质有关。
金属表面的氧化物、硫化物等化学物质会影响金属电子的逸出行为。
一般来说,金属表面存在氧化物等化学物质时,电子逸出功会增加,因为这些化学物质会增加电子与金属原子之间的相互作用力。
金属电子逸出测定实验报告(精)

实验22 金属电子逸出功的测定【实验目的】1.用里查逊(Richardson)直线法测定金属钨的电子逸出功。
2.了解光测高温计的原理和学习高温计的使用。
3.学习数据处理的方法。
【实验原理】若真空二极管的阴极(用被测金属钨丝做成)通以电流加热,并在阳极上加以正电压时,在连接这二个电极的外电路中将有电流通过,如图3—22—1所示。
这种电子从加热金属丝发射出来的现象,称为热电子发射。
研究热电子发射的目的之一可以选择合适的阴极材料。
诚然,可以在相同加热温度下测不同阳极材料的二极管的饱和电流,然后相互比较,加以选择。
但通过对阴极材料物理性质的研究来掌握其热电子发射的性能,这是带有根本性的工作,因而更为重要。
1.电子的逸出功根据固体物理学中金属电子理论,金属中的传导电子能量的分布是按费米——狄拉克(Fermi-Dirac)分布的。
即3—22—1式中称费米能级。
图3—22—1 图3—22—2在绝对零度时电子的能量分布如图3—22—2中曲线(1)所示。
这时电子所具有的最大能量为。
当温度升高时电子的能量分布曲线如图3—22—2中曲线(2)所示。
其中能量较大的少数电子具有比更高的能量,而其数量随能量的增加而指数减少。
在通常温度下由于金属表面与外界(真空)之间存在一个势垒,所以电子要从金属中逸出必须至少具有能量从图3—22—2可见,在绝对零度时电子逸出金属至少需要从外界得到的能量为:称为金属电子的逸出功,其常用单位为电子伏特(ev),它表征要使处于绝对零度下的金属中具有最大能量的电子逸出金属表面所需要给予的能量。
称为逸出电位,其数值等于以电子伏特表示的电子逸出功。
可见,热电子发射就是用提高阴极温度的办法以改变电子的能量分布,使其中一部分电子的能量大于,这样能量大于的电子就可以从金属中发射出来。
因此,逸出功的大小,对热电子发射的强弱,具有决定性作用。
2.热电子发射公式根据费米—狄拉克能量分布公式3—22—1,可以导出热电子发射的里查逊—杜什曼(Richar-dson-Dushman)公式3—22—2式中——热电子发射的电流强度,单位为安培。
逸出功的测定
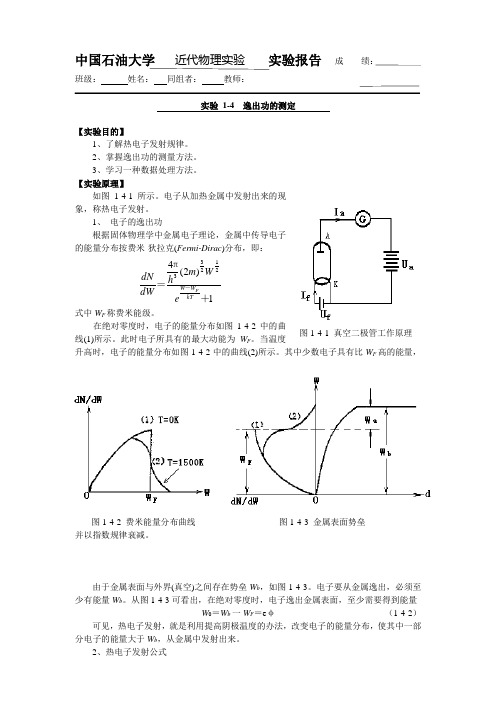
中国石油大学 近代物理实验 实验报告 成 绩:班级: 姓名: 同组者: 教师:实验 1-4 逸出功的测定【实验目的】1、了解热电子发射规律。
2、掌握逸出功的测量方法。
3、学习一种数据处理方法。
【实验原理】如图1-4-1所示。
电子从加热金属中发射出来的现象,称热电子发射。
1、 电子的逸出功根据固体物理学中金属电子理论,金属中传导电子的能量分布按费米-狄拉克(Fermi-Dirac )分布,即:1)2(421233+π=-kT W W Fe W m hdWdN 式中W F 称费米能级。
在绝对零度时,电子的能量分布如图1-4-2中的曲线(1)所示。
此时电子所具有的最大动能为W F 。
当温度升高时,电子的能量分布如图1-4-2中的曲线(2)所示。
其中少数电子具有比W F 高的能量,并以指数规律衰减。
由于金属表面与外界(真空)之间存在势垒W b ,如图1-4-3。
电子要从金属逸出,必须至少有能量W b 。
从图1-4-3可看出,在绝对零度时,电子逸出金属表面,至少需要得到能量W 0=W b 一W F =e φ (1-4-2)可见,热电子发射,就是利用提高阴极温度的办法,改变电子的能量分布,使其中一部分电子的能量大于W b ,从金属中发射出来。
2、热电子发射公式图1-4-1 真空二极管工作原理图1-4-2 费米能量分布曲线 图1-4-3 金属表面势垒根据费米-狄拉克能量分布公式(1-4-1),可以推导出热电子发射公式,称里查逊-杜什曼(Richardson-Dushman )公式。
kTe eAST I Φ-=20 (1-4-3)将(1-4-3)式两边除以T 2,再取对数,得到T 1004.5AS lg kT 30.2e AS lg TI lg320Φ-=Φ-= (1-4-4) 从得到的直线斜率即可求出电子的逸出功e φ值。
4、发射电流I 0的测量(1-4-3)式中的I 0是不存在外电场时的阴极热发射电流并在空间堆积。
逸出功的测量实验报告
逸出功的测量实验报告
《逸出功的测量实验报告》
在物理学中,逸出功是指从金属表面逸出的最小能量。
测量逸出功对于理解金
属的电子结构和性质具有重要意义。
本实验旨在通过实验方法测量金属的逸出功,并对实验结果进行分析。
实验过程中,我们选择了几种常见金属作为实验样品,包括铜、铝、铁等。
首先,我们将金属样品放置在真空室中,并通过加热或光照的方式激发金属表面
的电子。
随后,我们使用逸出功仪器测量金属表面逸出的电子能量,并记录实
验数据。
通过实验数据的分析,我们发现不同金属的逸出功存在一定的差异。
这一结果
与理论预期相符,因为不同金属的电子结构和束缚能会影响逸出功的大小。
此外,我们还发现逸出功与金属的表面特性和处理方式有关,例如金属的晶格结构、表面粗糙度等因素也会对逸出功产生影响。
通过本次实验,我们不仅成功测量了几种常见金属的逸出功,还深入了解了逸
出功与金属性质之间的关系。
这些实验结果对于深入理解金属的电子结构和应
用于光电器件等领域具有重要意义。
总的来说,本次实验为我们提供了一种简单而有效的方法来测量金属的逸出功,并为我们提供了更深入的认识金属性质的机会。
我们相信通过不断的实验探索
和理论分析,我们将能够更好地理解金属的电子结构和性质,为相关领域的研
究和应用提供更多的参考和支持。
金属电子逸出功测定实验数据处理系统
第 6卷
第 3期
Exper i m ent Sc ience & T echno logy
! 93!
触 , 而使用这些技术产品也是理解技术原理的最好 学习方法。 ( 5) 协议源代码是理解网络协议原理的最好 实例。互联网上很容易找到 BSD Un ix o r L inux 下 TCP / IP 协议源代码, 对于学习兴趣浓厚、求知欲 强烈的学生完全可以鼓励他们选择性的阅读 TCP / IP 协议源代码。 ( 6) RFC 文档是 公开的最权威、最详尽的网 络协议参考资料。有关计算机网络的教材和著作对 计算机网络协议的描 述难免有不祥 , 甚至错误之 处 , 应该鼓励学生根据需要查考 RFC 文档。 ( 7) 仿真工 具可 以让 学生学 会研 究和 探索。 例如像 OPNET 这样的网络仿真工具软件 , 可以帮 助有探索能力的学生仿真模拟一些 复杂的原理实 现 , 从而让学生成为研究性、创新人才。
4项 , 单击下一步。图表标题、坐标轴名称可通过 图生成后插入文本框来添加 ; ( 5) 点击 完成 按 钮, 至此实验数据点就在图表上描绘出来了。再通 过添加趋势线 , 在类型中选择线性类, 在选项中选 中复选框 显示公式 和 显示 R 平方值 , 单击确 定。一条线性回归拟合线和对应的直线方程就显示
! 6!
实验科学与技术
2008年 6 月
金属电子逸出功测定实验数据处理系统
陈玉林, 徐 飞, 丁留贯, 张雅男
210044) ( 南京信息工程大学物理实验教学中心 , 南京
摘要 : 大学物理实验教学中存 在着繁杂的数据处理问题 , 结合 Excel 软 件的特 点和优 势 , 文章介 绍了利 用 Ex ce l 2003 建立 金属电子逸出功测定实验数据 处理系统 。 实践表 明 , 用 Exce l软 件处理 大学 物理实 验数 据具 有快捷 、 直观 、 简 易的优 点 , 掌握它能有效提高学 生物理实验数据处理能力 。 关 键 词 : Excel软件 ; 金属电子逸出功 ; 数据处理 中图分类号 : T P274 ; O 48 文献标识码 : B 文章编号 : 1672- 4550( 2008) 03- 0006- 03
金属电子逸出功实验报告
金属电子逸出功实验报告篇一:《金属电子逸出功的测定》实验指导与报告要求1 《金属电子逸出功的测定》实验指导与报告要求一、电子发射 1、电子发射的分类:⑴、光电发射:靠光照射金属表面引起电子发射。
⑵、热电子发射:加热金属使其中大量电子克服表面势垒而逸出。
⑶、二次电子发射:靠电子流或离子流轰击金属表面产生电子发射⑷、场效应发射:靠外加强电场引起电子发射 2、热电子发射⑴、无线电电子学的基础⑵、真空管中从通电加热的金属丝阴极表面逸出电子的现象二、实验目的和要求1、了解热2、掌握逸出功的测量方法。
2、学习一种数据处理方法。
V三、金属电子逸出功的测定原理简述 1、真空二极管的结构a) 阴极K 通以电流 If 加热b) 阳极A上加以正电压,在连接这两个电极的外电路中将有电流 Ia 通过2、金属电子逸出功⑴金属中电子能量分布根据固体物理学中金属电子理论,金属中传导电子的能量分布按费米-狄拉克(Fermi-Dirac)分布,即:dN=dW314π223(2m)WeW-WFkT+1式中WF称费米能级。
c) 金属-真空界面表面势垒曲线 (x为电子距离金属表面的距离) d) 逸出功定义:E0?Eb?EF?eV⑵、根据费米-狄拉克能量分布公式,可以推导出热电子发射公式,称里查逊-杜什曼(Richardson-Dushman)公式。
I=ASTe式中:I-热电子发射的电流强度(A) S-阴极金属的有效发射面积(cm2) k-玻尔兹曼常数 T-绝对温度eV-金属的逸出功A-与阴极化学纯度有关的系数2-eVkT3、肖脱基效应I=AST2eeΦkT式中的I是不存在外电场时的阴极热发射电流。
无外场时,电子不断地从阴极发射出来,在飞向阳极的途中,必然形成空间电荷,空间电荷在阴极附近形成的电场,正好阻止热电子的发射,这就严重地影响发射电流的测量。
为了消除空间电荷的影响,在阳极加一正电压,于是阳极和阴极之间形成一加速电场Ea,使电子加速飞向阳极。
金属电子逸出功与电子比荷测量数据处理(完结)
lgIa-√Ua关系曲线图
由图读出gIa-√Ua直线延长线与纵坐标的截距,得到不同不同阴极温度时的零场热电子 发射电流I的对数值lgI0,如下所示 lgI01 -4.5312 lgI02 -4.3164 lgI03 -4.0993 lgI04 -3.9024 lgI05 -3.7121 lgI06 -3.5874 lgI07 -3.3577
-9.4 -9.6 -9.8 -10 -10.2 -10.4 -10.6 -10.8 -11 -11.2 y = -0.177x - 9.811 系列1 线性 (系列1) 1 2 3 4 5 6 7
lgI0-1/T的关系图
2.阳极电压Ua与Ic2的数据 Ua 6 5 4 3 2 1 0.044944 0.038025 0.031684 0.025281 0.019321 0.013456 Ic2
关系图如下:
0 1 -0.5 -1 -1.5 -2 -2.5 -3 -3.5 -4 -4.5 -5 y = 0.008x - 3.357 y = 0.017x - 3.587 y = 0.008x - 3.712 y = 0.008x - 3.902 y = 0.008x - 4.099 y = 0.009x - 4.316 y = 0.009x - 4.531 2 3 4 5 6 7 8 系列1 系列2 系列3 系列4 系列5 系列6 系列7 线性 (系列1) 线性 (系列2) 线性 (系列3) 线性 (系列4) 线性 (系列5) 线性 (系列6) 线性 (系列7)
【数据处理】 1.由实验数据得到√Ua-lgIa的数据记录如下所示: √Ua 4 5 6 7 8 9 10 11 lgIa1 -4.52288 -4.50864 -4.50864 -4.49485 -4.48149 -4.48149 -4.46852 -4.45593 lgIa2 -4.3098 -4.30103 -4.284 -4.27572 -4.26761 -4.25964 -4.25181 -4.24413 lgIa3 -4.09151 -4.08092 -4.07572 -4.0655 -4.05552 -4.05061 -4.04096 -4.03152 lgIa4 -3.8962 -3.88606 -3.87615 -3.86967 -3.86012 -3.85387 -3.84466 -3.83863 lgIa5 -3.70553 -3.69465 -3.68613 -3.67778 -3.66959 -3.66154 -3.65365 -3.64589 lgIa6 -3.64016 -3.51286 -3.50446 -3.49621 -3.48945 -3.48149 -3.47496 -3.46725 lgIa7 -3.35262 -3.34008 -3.33068 -3.32239 -3.31515 -3.30715 -3.30016 -3.29158
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-3.69037
-3.50724
-3.33536
11
-4.50864
-4.284
-4.07572
-3.87615
-3.68403
-3.49894
-3.32883
根据 直线的延长线与纵坐标上得截距,从图上直接读出不同阴极温度时的零场热电子发射电流I的对数值 的值为
-4.57
-4.3545
128
200
305
455
100
31
51
83
131
204
311
462
121
31
52
84
133
207
317
469
表2:lg(Ia)与Ua½关系表
0.6
0.62
0.64
0.66
0.68
0.7
0.72
4
-4.56864
-4.34679
-4.13077
-3.93554
-3.74232
-3.55909
-3.38195
-4.1375
-3.9428
-3.7502
-3.5668
-3.3878
表3:I 与T. . 关系表
I
0.60
0.62
0.64
0.66
0.68
0.70
0.72
1.880
1.914
1.945
1.978
2.010
2.040
2.074
-11.1352
-10.9304
-10.7374
-10.5415
-10.3705
-3.53165
-3.35655
8
-4.52288
-4.30103
-4.10237
-3.89963
-3.70553
-3.52433
-3.34969
9
-4.52288
-4.30103
-4.09151
-3.89279
-3.69897
-3.5157
-3.34199
10
-4.50864
-4.29243
-4.08092
再由公式
得
表5:Ua为6V时,Ia与Is关系
Is/A
0
0.05
0.1
0.12
0.14
0.16
0.18
0.2
0.22
0.24
0.26
0.28
0.3
Ia/uA
378
378
378
375
371
370
246
100
14
3
1
0
0
表6:Ua为5V时,Ia与Is关系
Is/A
0
0.05
0.1
0.12
0.14
0.16
0.18
48.5
27
12.75
Ic/A
0.201
0.183
0.109
Ic²/A²
0.040401
0.033489
0.027889
0.021316
0.015376
0.011881
斜率K=170.77
已知参数阳极半径 ,线圈匝数N=987匝,励磁线圈长度L=4.0 cm,真空磁导率 ,线圈内半径 ,线圈外半径 ,根据公式计算K’为
97
95
92
电压/%
1.01
1.04
1.07
1.1
1.2
1.3
1.4
1.5
1.6
1.7
水平透射率/%
84
80
75
69
50
34
21
12
7
4
垂直透射率/%
88
84
79
74
57
39
25
14
8
4
电压/v
1.8
1.9
2
3
水平透射率/%
3
1
0
0
垂直透射率/%
2
1
0
0
五.数据处理
表1:原始数据记录表
0.6
0.62
0.64
0.66
0.68
0.7
0.72
16
27
45
74
116
181
276
415
25
28
46
76
119
185
282
424
36
29
47
77
121
188
288
432
49
29
48
78
123
192
294
440
64
30
50
79
126
197
299
447
81
30
50
81
-10.1999
-10.0405
5.3191
5.2247
5.1414
5.0556
4.9751
4.9020
4.8216
图2: 关系曲线
直线斜率为 。
逸出电位为
所以
相对误差为
.表4:阳极电压Ua与I 的数据
Ua/V
6
5
4
3
2
1
Ia/uA
378
351
282
194
108
51
Ia/4/uA
94.5
87.75
70.5
5
-4.55284
-4.33724
-4.11919
-3.92445
-3.73283
-3.54975
-3.37263
6
-4.5376
-4.3279
-4.11351
-3.91721
-3.72584
-3.54061
-3.36452
7
-4.5376
-4.31876
-4.10791
-3.91009
-3.7167
0.2
0.22
0.24
0.26
0.28
0.3
Ia/uA
351
351
351
340
338
252
108
21
3
1
0
0
0
电压/v
0
0.5
0.7
0.8
0.83
0.86
0.89
0.92
0.95
0.98
水平透射率/%
100
100
100
100
98
97
96
94
92
88
垂直透射率/%
100
100
100
100
100
99
99
