高中数学《导数的概念及其几何意义》公开课教学设计
导数的概念及其几何意义教案

导数的概念及其几何意义教案导数的概念及其几何意义一、导数的定义和基本概念1. 导数的定义导数是微积分学中一个非常重要的概念,它描述了函数在某一点附近的变化率。
在数学上,对于给定的函数f(x),它在某一点x0处的导数可以用极限的概念来定义,即:\[ f'(x_0) = \lim_{\Delta x \to 0} \frac{f(x_0 + \Delta x) -f(x_0)}{\Delta x} \]其中,f'(x0)表示函数f(x)在点x0处的导数。
2. 导数的基本概念根据导数的定义可以知道,导数可以理解为函数图像在某一点的切线的斜率,也就是函数在该点的瞬时变化率。
导数的概念是微积分的基础,它在物理、经济、生物等领域有着广泛的应用。
二、导数的几何意义1. 切线和切线斜率在几何意义上,导数可以理解为函数图像在某一点的切线的斜率。
对于函数f(x),在点x0处的切线斜率即为该点处的导数值f'(x0)。
通过求导可以获得函数曲线在任意点的切线斜率,从而更好地理解函数图像在各个点的变化趋势。
2. 导数与函数图像的关系导数还可以帮助我们理解函数曲线的凹凸性、极值点以及拐点等性质。
对于函数f(x),如果在某一点的导数值为0,那么这个点可能是函数的极值点或者拐点。
通过导数,我们可以更直观地理解函数的整体形态和特性。
三、深入理解导数的意义1. 导数的局部性导数反映了函数在某一点附近的变化情况,是一种局部性的量。
通过导数,我们可以得知函数在某一点处的瞬时变化率,从而对函数的局部特性有更深入的理解。
2. 导数与积分的关系在微积分中,导数和积分是密切相关的。
导数描述了函数的瞬时变化率,而积分则描述了函数在一定区间内的累积效应。
导数和积分是微积分学中最重要的两个概念,它们相互补充,共同构成了微积分学的核心内容。
结语:导数作为微积分学中的重要概念,在数学和应用领域都有着广泛的意义。
通过深入理解导数的概念及其几何意义,我们可以更好地理解函数图像的变化规律,为后续的微积分学习打下扎实的基础。
《导数的几何意义》示范公开课教案【高中数学北师大】

第二章 导数及其应用2.2.2 导数的几何意义1. 理解割线逼近切线的过程,了解曲线上一点处的切线的意义;2. 理解由平均变化率到瞬时变化率与由割线到切线的斜率之间的关系.重点:曲线上一点处的切线概念的形成过程. 难点:用运动变化的观点认识导数的几何意义.一、新课导入问题1:我们学习了函数在某区间上的平均变化率,它的几何意义是什么呢?答案:几何意义为割线的斜率,反映了直线的“陡峭”程度.近似地刻画了曲线在这一区间上的变化趋势. 设计意图:这一段的内容既是对平均变化率与瞬时变化率进一步的概括,又是对本节课要研究内容的适时切入,展现了数学知识发生与发展的过程,更重要的是,这种发生、发展的规律,与人们认识事物的规律是吻合的,即数学知识的发生往往是从原有知识的基础发展而来的.问题2 有些时候我们需要研究曲线上某一点处的变化趋势,比如我们熟悉的幂函数,如图,这些幂函数在[0,1]区间上的平均变化率是相同的,但是在点P (1,1)处的变化趋势是相同的吗?答案:不相同.设计意图:提出研究方向,感受研究的必要性.其实在我们生活中也有这样的例子.在2010年广州亚运会的链球决赛中,我国选手张文秀技压群芳,获得了冠军,为国争光,作为一个专业运动员,她很好地掌握了链球在抛出点处的运动趋势,把握了链球出手的最佳时机.这些都告诉我们,确实有必要来研究曲线上一点处的变化趋势.设计意图:数学知识的产生往往离不开生产和生活的实际需要,从生活背景出发,提出◆教学目标◆教学过程◆教学重难点 ◆研究问题的必要性.二、新知探究问题3怎样在图形中表示由平均变化率到瞬时变化率?如图,设Q为曲线C上不同于点P的一点,则直线PQ称为曲线的割线.随着点Q沿曲线C向点P运动,当点Q无限逼近点P时,直线PQ最终成为点P处最逼近曲线的直线l,这时直线l称为曲线在点P处的切线.设计意图:通过类似放大镜观察图形的过程,可以近似地把曲线在一点处的变化趋势看成直线,用信息技术表达.问题4对于一般的曲线C,如抛物线f (x)=x2,如何定义它在某一点,如P0 (1,1)处的切线呢?追问1:如果一条直线与一条曲线只有一个公共点,那么这条直线与这条曲线一定相切吗?答案:不一定. 例如,二次函数f (x)=x2的图象和直线x=1只有一个交点,但它们显然不相切.追问2:如果一条直线与一条曲线相切,那么它们一定只有一个公共点吗?答案:不一定. 例如,正弦函数f (x)=sin x的图象和直线y=1相切,但它们显然不止一个交点.因此不能再像在研究直线和圆的位置关系时那样,通过交点个数来定义相切.追问3:对于抛物线f (x)=x2,应该如何定义它在点P0(1,1)处的切线的切线呢?答案:与研究瞬时速度类似,为了研究抛物线f (x)=x2在点P0(1,1)处的切线,我们在点P0(1,1)的附近任取一点P(x,x2),考察抛物线的割线P0 P的变化情况.我们可以借助几何画板工具来观察.通过演示可以看到,当点P无限趋近于点P0时,割线P0P无限趋近于一个确定的位置,这个确定位置的直线P0T称为抛物线f (x)=x2在点P0(1,1)处的切线.这样,我们得到抛物线f(x)=x2在点P0(1,1)处的切线的含义.从几何上看,抛物线在点P0的切线,是由过这一点的割线P0P,当P无限接近P0时的极限位置确定的.我们知道,斜率是确定直线的一个要素.在已知切点的情况下,如果我们再能确定切线的斜率,就能确定切线的方程.追问4:如何求抛物线f (x)=x2在点P0(1,1)处的切线P0T的斜率呢?答案:从上述切线的定义可见,抛物线f (x)=x2在点P0(1,1)处的切线P0T的斜率与割线P0P的斜率有内在联系.既然切线是割线的极限位置确定的,那么切线的斜率也就应该是割线斜率当P无限接近P0时的极限值.我们记点P的横坐标x=1+Δx,则点P的坐标为(x,(1+Δx)2).于是割线P0P的斜率k=f(x)−f(1)x−1=(1+Δx)2−1Δx=Δx+2我们可以通过割线P0P的斜率近似地表示切线的斜率,并且通过不断缩短横坐标间隔|Δx来提高近似表示的精确度.我们可以借助电脑的excel计算,来观察当P无限接近P0时,割线P0P的斜率变化情况.当Δx无限趋近于0时,无论x从小于1的一边还是大于1的一边无限趋近于1,割线斜率都无限趋近于2.事实上,由k=f(1+Δx)−f(1)Δx=Δx+2可以直接看出,当Δx无限趋近于0时,Δx+2无限趋近于2. 我们把2叫做“当Δx无限趋近于0时,k=f(1+Δx)−f(1)Δx的极限”,记做lim Δx→0f(1+Δx)−f(1)Δx=2.问题5曲线上一点处切线的斜率与导数是什么关系?答案:由导函数的定义可知,曲线上一点处切线的斜率就是曲线对应的函数在这一点的导数,可以通过割线的斜率逼近切线的斜率.问题6 在曲线上怎样反映出从平均变化率到瞬时变化率?答案:点Q 沿着曲线向点P 无限靠近时,也就是说Δx →0.即:切线的斜率为k ,那么当Δx →0,f(x 0+Δx)−f (x 0)Δx→k .总结:函数y=f (x )在x 0处的导数f′(x 0),是曲线y=f (x )在点(x 0,f (x 0))处的切线的斜率.函数y=f (x )在x 0处切线的斜率反映了导数的几何意义.三、应用举例例1 已知函数y =x 2及自变量x 0=−2.(1) 分别对Δx =1,0.5,0.1求y =x 2在区间[x 0,x 0+Δx]上的平均变化率,并画出过点(x 0,f (x 0))的相应割线;(2) 求函数y =x 2在x 0处的导数,并画出曲线y =x 2在点(x 0,f (x 0))处的切线. 解:(1)当Δx =1,0.5,0.1时,区间[x 0,x 0+Δx]相应为[−2,−1],[−2,−1.5],[−2,−1.9],y =x 2在这些区间上的平均变化率分别为f (−1)−f (−2)1=(−1)2−(−2)21=−3, f (−1.5)−f (−2)0.5=(−1.5)2−(−2)20.5=−3.5, f (−1.9)−f (−2)0.1=(−1.9)2−(−2)20.1=−3.9.如图,其相应割线分别是经过点(−2,4)和点(−1,1)的直线l 1,经过点(−2,4)和点(−1.5,2.25)的直线l 2,经过点(−2,4)和点(−1.9,3.61)的直线l 3.(2) y =x 2在区间[−2,−2+Δx]上的平均变化率为(−2+Δx)2−(−2)2Δx=−4Δx+(Δx)2Δx=−4+Δx .令Δx 趋于0,可知函数y =x 2在x 0=−2处的导数为−4.因此,曲线y =x 2在点(−2,4)处的切线为经过点(−2,4),斜率为−4的直线l .例2 求函数y =f (x )=2x 3在x =1处的切线方程. 解:f(1+Δx)−f (1)Δx=2(1+Δx)3−2×13Δx=2[1+3Δx+3(Δx)2+(Δx)3]−2Δx=6+6Δx +2(Δx)2.令Δx 趋于0,可知y =2x 3在x =1处的导数为f ′(1)=6.于是,函数y =2x 3在点(1,f(1))即(1,2)处的切线斜率为6,即该切线经过点(1,2),且斜率为6.因此,函数y =f (x )=2x 3在x =1处的切线方程为:y −2=6(x −1),即y =6x −4.四、课堂练习1.曲线f (x )=−2x 在点A (1,-2)处的切线方程为( ) A .y =-2x +4 B .y =-2x -4 C .y =2x -4 D .y =2x +42.如图,函数y =f (x )的图象在点P 处的切线方程是y =-x +8,则f (5)+f′(5)=___________.3. 直线y =−14x +b 是函数f (x )=1x图象的切线,则切点是_________,实数b =________.4.曲线y =f (x )=x 2−1在x =x 0处的切线与曲线y =g (x )=1−x 3在x =x 0处的切线互相平行.(1)求x 0的值;(2)求曲线y =f (x )在x =x 0处的切线方程. 参考答案:1.答案 C 解析:ΔyΔx =−21+Δx+2Δx=21+Δx ,所以当Δx →0时,f′(x)=2,故直线方程为y +2=2(x -1),即y =2x -4.2.答案:2解析:点P 横坐标为5,故由在点P 处切线为y =-x +8,得f′(5)=-1,f(5)=-5+8=3.∴f(5)+f′(5)=2.3.答案:(−2,−12)或(2,12),1或-1. 解析:f ′(x )=limΔx→01x+Δx −1xΔx=−1x 2=−14 ,解得x =±2.当x =-2时,y =-12,b =-1;当x =2时,y =12,b =1.4.解:(1) f′(x 0)=lim Δx→0f(x 0+Δx)−f (x 0)Δx=limΔx→0(x 0+Δx)2−1−(x 02−1)Δx =2x 0,g′(x 0)=limΔx→0g(x 0+Δx)−g (x 0)Δx=limΔx→01−(x 0+Δx)3−(1−x 03)Δx=−3x 02.由题意得2x 0=−3x 02,解得x 0=0或-23.(2)当x 0=0时,f′(x 0)=0,又f (0)=-1,故所求切线方程为y =-1;当x 0=-23时,f′(x 0)=-43,又f (-23)=−59,故所求切线方程为y +59=-43(x +23),即y =-43x -139.五、课堂小结1.切线的定义:设Q 为曲线C 上不同于点P 的一点,则直线PQ 称为曲线的割线.随着点Q 沿曲线C 向点P 运动,当点Q 无限逼近点P 时,直线PQ 最终成为点P 处最逼近曲线的直线l ,这时直线l 称为曲线在点P 处的切线.2.导数的几何意义:函数y=f (x )在x 0处的导数f′(x 0),是曲线y=f (x )在点(x 0,f (x 0))处的切线的斜率.函数y=f (x )在x 0处切线的斜率反映了导数的几何意义.六、布置作业教材第56页A 组练习第3,4,5题.。
导数的概念及其几何意义(1)教学设计
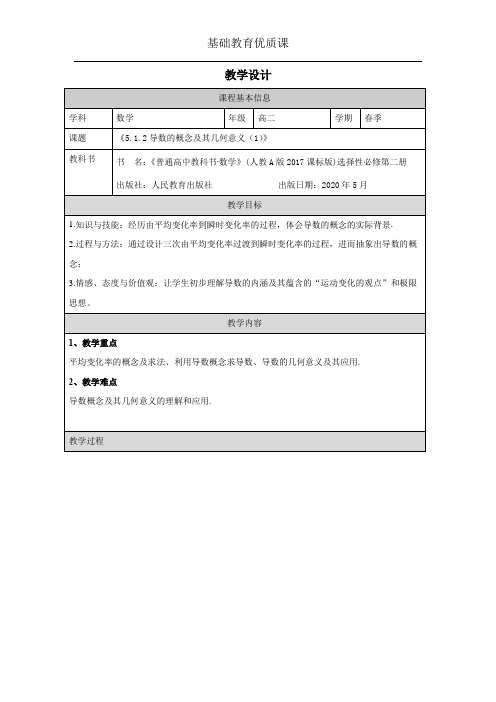
根据导数的定义,
,
所以 .
同理可得 .
在第2h与第6h时,原油温度的瞬时变化率分别为 与 .说明在第2h附近,原油温度大约以 的速率下降;在第6h附近,原油温度大约以 的速率上升.一般地, 反映了原油温度在时刻 附近的变化情况.
例3一辆汽车在公路上沿直线变速行驶,假设 时汽车的速度(单位: )为 ,求汽车在第2s与第6s时的瞬时加速度,并说明它们的意义.
教学过程
1、新课导入
在上节课的学习中,我们研究了平均速度和瞬时速度的物理问题,以及割线斜率和切线斜率的几何问题,在解决问题时,都采用了由“平均变化率”逼近“瞬时变化率”的思想方法,这节课我们就来探究一下平均变化率、导数的概念及其几何意义.
2、探索新知
一、平均变化率的概念
对于函数 ,设自变量 从 变化到 ,相应地,函数值 就从 变化到 .这时, 的变化量为 , 的变化量为 .我们把比值 ,即 叫做函数 从 到 的平均变化率.
2.过程与方法:通过设计三次由平均变化率过渡到瞬时变化率的过程,进而抽象出导数的概念;
3.情感、态度与价值观:让学生初步理解导数的内涵及其蕴含的“运动变化的观点”和极限思想。
教学内容
1、教பைடு நூலகம்重点
平均变化率的概念及求法、利用导数概念求导数、导数的几何意义及其应用.
2、教学难点
导数概念及其几何意义的理解和应用.
二、瞬时变化率(导数)的概念
如果当 时,平均变化率 无限趋近于一个确定的值,即 有极限,则称 在 处可导,并把这个确定的值叫做 在 处的导数(也称为瞬时变化率),记作 或 ,即 .
三、求函数在 处的导数(瞬时变化率)
例1设 ,求 .
马丽娜-导数的概念及其几何意义【2018年第9届全国高中数学优质课比赛教学设计、课件】

理解导数的概念, 明确求导数的基本方法, 能够运用导数的概念和 几何意义解决与瞬时变 化率有关的问题.
感受数学源于生活、 用于生活.激发求知欲, 提高课堂参与度,增强 成就感.培养敢于质疑、 勇于探索的学习习惯.引 导学生会用数学的眼光 观察世界,用数学的思 维思考世界,用数学的 语言表达世界.
学情分析
教学过程
学以致用 解决典型问题——活动4.例2
引导学生再次感受从具体到一般的抽象过程.理解导数的本质就 是瞬时变化率. 导数可以表示任何运动变化事物的瞬时变化率.
教学过程
自主探究 获得几何意义——探究2
上一分讲学生已经探究了特殊曲线的切线斜率,结合本课时“导数的概念”,学生不难 发现抛物线f(x)=x2在点(0,0)处的切线斜率就是函数f(x)=x2在x=0处的导数,这就是特殊函 数的f(x)=x2导数的几何意义. 本课时教师意在让学生抽象生成一般函数y=f(x)的导数的几何意义. 教师要关注学生的动手实践过程.教师引导学生用运动变化的观点研究问题,体会割线 的极限位置就是切线,体会割线斜率的极限就是切线斜率,割线斜率的极限的数学表达就是 导数.感受从特殊到一般、类比的研究方法.
教学目标
内容解析
教学策略 教学目标
学情分析
教学策略
经历由不同实例的 数学共性,抽象生成导 数的概念.通过类比探 究,抽象概括一般函数 导数的几何意义,生成 一般曲线的切线的定义.
体会“数形结合” 的思想方法.体会从特殊 到一般、从具体到抽象 在解决问题中的一般性 和有效性.发展学生观察、 类比、概括的数学能力, 提升数学抽象、直观想 象、逻辑推理的数学核 心素养.
1.用运动变化的观点解 决问题. 2.导数概念的建构过程. 3.导数几何意义的探究.
高中数学《导数的概念及其几何意义》公开课教学设计

《导数的概念及其几何意义》一、教材内容分析本节课的教学内容选自人教社普通高中课程标准实验教科书(A 版)数学选修2-2第一章第一节的《变化率与导数》,《导数的概念及几何意义》是在学习了函数平均变化率以后,过渡到瞬时变化率,从而得出导数的概念,再从平均变化率的几何意义,迁移至瞬时变化率即导数的几何意义.在中学数学中,导数具有相当重要的地位和作用。
从横向看,导数在现行高中教材体系中处于一种特殊的地位。
它是众多知识的交汇点,是解决函数、不等式、数列、几何等多章节相关问题的重要工具,它以更高的观点和更简捷的方法对中学数学的许多问题起到以简驭繁的处理.从纵向看,导数是函数一章学习的延续和深化,也是对极限知识的发展,同时为后继研究导数的几何意义及应用打下必备的基础,具有承前启后的重要作用. 二、学生学情分析1.导数是对变化率的一种“度量”实际生活中,学生最为熟悉的一种变化率就是物体的运动速度.学生在1.1.1小结学习了导数的物理意义,掌握了变化率,在高一年级的物理课程中学习过瞬时速度,因此,学生已经具备了一定的认知基础,他们不会对新知识感到无所适从. 2.可能存在的问题:(1)“逼近”的思想对于学生而言,还是比较陌生,需要精心设计教学活动,比如借助物理知识等,激发学生的兴趣,从学生已有的知识背景出发,帮助学生经历从平均速度到瞬时速度,从平均变化率到瞬时变化率的过渡.(2)使学生能通过观察发现:运动的物体在某一时刻的平均速度在时间间隔越来越小时,逐渐趋于一个不变的常数,而且这个常数就是物体在这一时刻的瞬时速度.这个过程学生难以想象,同时数值逼近的运算繁琐,但又不能采取简单的方式告知学生,而是要学生通过实际的计算,在计算过程中,充分感知当||t ∆趋于0时,t h ∆∆趋于一个定值;当||x ∆趋于0时,xy∆∆趋于一个定值.(3)在实际教学中,学生需要用到思想方法和表达形式的迁移,即把从平均速度到瞬时速度过渡中所运用的“逼近”的思想方法迁移到从平均变化率到瞬时变化率的过渡,从对一个具体函数在一个确定点的瞬时变化率的表达式迁移到任意一个函数在任意一点的瞬时变化率的表达,这样的探究方法可能会导致学生的不适应而产生困难.因此,如何引导学生根据生活中具体的实例,结合已有的知识经验,通过“逼近”的方法,由特殊到一般,用类比的方法归纳探究出导数的概念是本节课的难点. 而在第一课时平均变化率的学习中,课本给出了一个思考,观察函数)(x f y =的图像,平均变化xy∆∆表示什么?这个思考为研究导数的几何意义埋下了伏笔。
导数的概念及其几何意义教案

导数的概念及其几何意义教案导数的概念及其几何意义导数是微积分学中的一个基本概念,它不仅具有重要的理论意义,而且在实际应用中也有着广泛的用途。
本文将通过深入的理论探讨和几何意义的解释,帮助读者全面理解导数的概念及其应用。
一、导数的概念导数是函数的一种基本性质,它描述了函数在某一点上的变化率。
具体地说,设函数y=f(x),在某一点x=a处有定义,若存在极限lim_[h→0] (f(a+h)-f(a))/h ,那么这个极限就称为函数f(x)在点a处的导数,记作f'(a)或dy/dx|_(x=a)。
从定义中可以看出,导数表示了函数在某一点上的瞬时变化率,也即函数的斜率。
导数的绝对值越大,表示函数在该点上的变化越剧烈;导数为零表示函数在该点上没有变化;导数为正表示函数在该点上单调递增;导数为负表示函数在该点上单调递减。
二、导数的几何意义导数的几何意义可以通过理解切线的概念来解释。
对于一个函数,取其中一点P(x,y),在这一点上作一条切线,使得切线与曲线只有一个公共点P。
那么这条切线的斜率就是函数在点P处的导数。
通过这种解释,我们可以把导数理解为函数曲线在某一点上的局部近似线性化描述。
切线的近似线性特征使得我们可以使用直线的性质来研究函数曲线的性质。
我们可以通过判断切线的斜率的正负来确定函数的单调性;通过判断切线与x轴的交点来确定函数的根的存在性等等。
三、导数的应用导数在实际应用中具有广泛的用途。
下面列举几个典型的应用场景:1. 曲线的拟合与插值:通过函数的导数可以获得曲线的斜率信息,进而进行曲线的拟合和插值,从而更好地描述和预测曲线的变化。
2. 最优化问题:很多最优化问题可以通过导数的求解来解决。
求函数在某一范围内的最大值或最小值,我们可以通过求解导数为零的位置来得到答案。
3. 物理学中的速度和加速度:在物理学中,速度和加速度是描述物体的运动的重要概念。
通过对位移和时间的关系进行导数运算,我们可以得到速度和加速度的函数表达式,从而更好地分析物体的运动规律。
《导数的概念及其几何意义》教学设计

《导数的概念及其几何意义》教学设计课题:导数的概念及其几何意义教材分析:微积分是人类思维的伟大成果之一,是人类经历了2000多年的智慧成果,开创了数学向近代数学过渡的新时期,其中牛顿和莱布尼茨功不可没,他们各自独立创立了微积分,单凭这一项成就,就足以奠定两人科学史上的伟大地位。
而导数的概念是微积分核心概念之一,它具有极其丰富的实际背景和广泛应用。
导数的概念及其几何意义一课是在学生已经学习了解了一些实际问题的平均变化率的基础上对于瞬时变化率的确切的再认识,同时也是高中数学与大学数学衔接的重要内容章节。
考虑到教材对于本节的安排过于支离,而且缺乏典型的实际情境问题的分析引入,因此我整合教材内容,从实际问题中抽象出导数概念后,再回到实际问题中去,趁热打铁进一步研究导数的几何意义。
因此,本节课主要内容是抽象概括导数的一般概念以及发现学习导数的几何意义。
教学设计上是紧紧围绕一个问题:跳水运动员的瞬时速度问题,以提出问题,形成问题串,然后合作、交流、分析问题,进而解决问题的方式展开教学。
教学目标:1.知识与技能:抽象概括并理解导数的概念,发现并学习导数的几何意义。
2.过程与方法:体会瞬时变化率,归纳形成导数概念。
观察函数曲线的变化趋势,发现形成导数的几何意义。
3.情感态度价值观:学习的过程中养成数学抽象和数学建模的核心素养,渗透不断逼近和以直代曲的数学思想,以有限认识无限,体会量变和质变的辩证关系,感受数学思想的无限魅力。
教学重点:导数的概念以及导数的几何意义。
教学难点:导数的概念以及导数的几何意义。
教学过程:【复习回顾,创设情境】:回顾什么是平均变化率?情境1、吹气球的时候,随着气球的不断膨胀,吹起来,会越来越难,这是怎么回事?怎样用数学知识解释这一现象?情境2、巍峨的珠穆朗玛峰,攀登珠峰的队员两幅不同的陡峭状态的图片,当陡峭程度不同时,登山运动员的感受程度是不一样的,如何用数学反映山势的陡峭程度,给我们的登山运动员一些有益的技术参考?情境3、观看跳水视频,运动员从10米高台跳水时,从腾空到进入水面的过程中,设运动员相对于水面的高度h与起跳后的时间t存在函数关系为。
高中数学一对一教案 导数的概念及几何意义

教学内容导数的概念及几何意义教学目标1、了解导数的概念2、理解导数的几何意义,并由此求切线的方程3、掌握基本初等函数的导数公式和导数的运算法则教学重、难点 重点:函数导数的计算和导数的几何意义的应用。
难点:导数几何意义的应用扫清障碍1、若某个问题中的函数关系用()f x 表示,问题中的变化率用式子()()2121f x f x x x --fx ∆=∆表示,则式子()()2121f x f x x x --称为函数()f x 从1x 到2x 的平均变化率.2、函数()f x 在0x x =处的瞬时变化率是()()210021limlimx x f x f x fx x x∆→∆→-∆=-∆,则称它为函数()y f x =在0x x =处的导数,记作()0f x '或0x x y =',即()()()0000limx f x x f x f x x∆→+∆-'=∆.3、函数()y f x =在点0x 处的导数的几何意义是曲线()y f x =在点()()00,x f x P 处的切线的斜率. 曲线()y f x =在点()()00,x f x P 处的切线的斜率是()0f x ',切线的方程为:()()()000y f x f x x x '-=-.若函数在0x 处的导数不存在,则说明斜率不存在,切线的方程为0x x =. 特别的,若质点运动的位移S 是时间t 的函数,则(),()S t v v t a ''==。
4、若当x 变化时,()f x '是x 的函数,则称它为()f x 的导函数(导数),记作()f x '或y ',即()()()limx f x x f x f x y x∆→+∆-''==∆5、基本初等函数的导数公式②求出函数在点0x 处的导数0()f x '得到曲线在点00(,())x f x 的切线的斜率k,即0()k f x '=; ③利用点斜式写出切线方程并化简.变式练习:1.(2009江西卷理)设函数2()()f x g x x =+,曲线()y g x =在点(1,(1))g 处的切线方程为21y x =+,则曲线()y f x =在点(1,(1))f 处切线的斜率为( )A .4B .14-C .2D .12-2.已知函数3()f x x =的切线的斜率等于1,则切线有( )A .1条B .2条C .3条D .不确定3.(11年全国理)曲线y=2x e -+1在点(0,2)处的切线与直线y=0和y=x 围成的三角形的面积为( )A .13B .12C .23D .14.曲线2y x =在点P 处的切线斜率为1,则点P 的坐标为_________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《导数的概念及其几何意义》
一、教材内容分析
本节课的教学内容选自人教社普通高中课程标准实验教科书(A 版)数学选修2-2第一章第一节的《变化率与导数》,《导数的概念及几何意义》是在学习了函数平均变化率以后,过渡到瞬时变化率,从而得出导数的概念,再从平均变化率的几何意义,迁移至瞬时变化率即导数的几何意义.
在中学数学中,导数具有相当重要的地位和作用。
从横向看,导数在现行高中教材体系中处于一种特殊的地位。
它是众多知识的交汇点,是解决函数、不等式、数列、几何等多章节相关问题的重要工具,它以更高的观点和更简捷的方法对中学数学的许多问题起到以简驭繁的处理.
从纵向看,导数是函数一章学习的延续和深化,也是对极限知识的发展,同时为后继研究导数的几何意义及应用打下必备的基础,具有承前启后的重要作用. 二、学生学情分析
1.导数是对变化率的一种“度量”
实际生活中,学生最为熟悉的一种变化率就是物体的运动速度.学生在1.1.1小结学习了导数的物理意义,掌握了变化率,在高一年级的物理课程中学习过瞬时速度,因此,学生已经具备了一定的认知基础,他们不会对新知识感到无所适从. 2.可能存在的问题:
(1)“逼近”的思想对于学生而言,还是比较陌生,需要精心设计教学活动,比如借助物理知识等,激发学生的兴趣,从学生已有的知识背景出发,帮助学生经历从平均速度到瞬时速度,从平均变化率到瞬时变化率的过渡.
(2)使学生能通过观察发现:运动的物体在某一时刻的平均速度在时间间隔越来越小时,逐渐趋于一个不变的常数,而且这个常数就是物体在这一时刻的瞬时速度.这个过程学生难以想象,同时数值逼近的运算繁琐,但又不能采取简单的方式告知学生,而是要学生通过实际的计算,在计算过程中,充分感知当||t ∆趋于0时,t h ∆∆趋于一个定值;当||x ∆趋于0时,x
y
∆∆趋于一个定值.
(3)在实际教学中,学生需要用到思想方法和表达形式的迁移,即把从平均速度到瞬时速度过渡中所运用的“逼近”的思想方法迁移到从平均变化率到瞬时变化率的过渡,从对一个具体函数在一个确定点的瞬时变化率的表达式迁移到任意一个函数在任意一点的瞬时变化率
的表达,这样的探究方法可能会导致学生的不适应而产生困难.
因此,如何引导学生根据生活中具体的实例,结合已有的知识经验,通过“逼近”的方法,由特殊到一般,用类比的方法归纳探究出导数的概念是本节课的难点. 而在第一课时平均变化率的学习中,课本给出了一个思考,观察函数)(x f y =的图像,平均变化
x
y
∆∆表示什么?这个思考为研究导数的几何意义埋下了伏笔。
因此,在将瞬时变化率定义为导数之后,立即让学生继续探索导数的几何意义,学生会对导数的几何意义有更为深刻的认识. 三、教学目标
1、会从物理意义、数值意义、几何意义三个不同角度理解导数的本质;
2、应用导数的定义求简单函数在某点处的导数;
3、理解函数在一点处的导数的几何意义. 四、教学重点 导数的概念及导数的几何意义 五、教学难点 导数的几何解释及切线概念的形成. 六、数学核心素养
1、通过动手计算培养学生观察、分析、比较和归纳能力,养成数学抽象、直观想象和数学建模的核心素养.
2、通过问题的探究不断渗透逼近和以直代曲的数学思想,以及用已知探求未知、从特殊到一般及数形结合等数学思想方法. 七、教学策略分析
考虑到教材对于本节的安排过于支离,而且缺乏典型的实际情境问题的分析引入,因此我整合教材内容,从实际问题中抽象出导数概念后,再回到实际问题中去,趁热打铁进一步研究导数的几何意义。
因此,本节课主要内容是抽象概括导数的一般概念以及发现学习导数的几何意义。
教学设计上是紧紧围绕一个问题:跳水运动员的瞬时速度问题,以提出问题,形成问题串,然后合作、交流、分析问题,进而解决问题的方式展开教学.
采用“教师适时引导和学生自主探究发现相结合”的教学方式.课堂教学始终贯彻“教师为主导、学生为主体,探究为主线,思维为核心”的教学思想.
将学生分组,让学生更好的进行合作探究活动,通过手机同屏提取分组学生的计算结果,让学生感受逼近的思想方法.
简单介绍微积分的发展史,介绍牛顿和莱布尼兹的贡献,提高学生对学习导数的兴趣欲望,以已知探求未知,激发学生的学习热情;提前通过导学案引导学生自主计算跳水运动员任意时刻的平均速度,课堂上分组汇报各组数据,教师利用EXCEL 快速计算更多的数据,让
学生直观感受数值逼近的思想,求出瞬时速度,从而得到导数的定义,注重抽象概念不同意
义间的转换,再用几何画板进行动态演示,让学生探索出导数的几何意义.
八、教学过程设计
(一)设置问题情境
295年前,中国古代数学家刘徽利用割圆术计算出圆周率为3.1416,他们已经具备了微积分的思想,离研究出微积分只有一步之遥!
17世纪初,四类科学问题急待解决,这四类问题是:
第一类,求变速运动的即时速度的问题;
第二类,求曲线的切线的问题;
第三类,求函数的最大值和最小值问题;
第四类,求曲线长、曲边梯形面积、不规则物体的体积、物体的重心、压强等问题.
几百年来,为了解决这些科学问题,许多著名的科学家,如古希腊的阿基米德;法国的费马、笛卡尔、柯西;德国的开普勒;意大利的卡瓦列利等人都提出许多有建树的理论,为微积
分的创立做出了贡献.
直到17世纪中叶,英国物理学家牛顿和德国数学家菜布尼茨在前人探索与研究的基础上,凭着他们敏锐的直觉和丰富的想象力,在不同的国度,不同的领域,各自独立地创立了微积分.
微积分是数学发展史上继欧氏几何后的又一个具有划时代意义的伟大创造,被誉为数学史上的里程碑!
微积分是人类经历了2000多年的智慧成果,它极大地推动了数学的发展,过去很多束手无策的数学问题运用微积分就会迎刃而解.
微积分也极大的推动了天文学、力学、物理学、化学、生物学、工程学、经济学等自然科学、社会科学及应用科学各个分支中的发展,并在这些学科中应用越来越广泛.
物理学家牛顿是从运动学,即瞬时速度的方向去研究的,而莱布尼茨则是在几何学的角
度去研究的.他们的最大功绩是把两个貌似毫不相关的问题联系在一起,实现了数与形的结合!数形结合自古就不分家!今天我们就先从“数”的方向大致沿着牛顿的路线研究导数,然后
再从“形”的方向沿着莱布尼兹的路线研究导数.下面我们来看这样一个物理问题:设计意图:通过简单介绍微积分的发展史及牛顿的成就激发学生学习导数的兴趣
(二)问题情境,数学探究
在高台跳水运动中,运动员相对于水面的高度为h(单位:m)与起跳后的时间t(单位:s )存在函数关系h(t)=-4.9t2+6.5t+10,求t=2时的瞬时速度.
问题1、你能够设计一个方案,求运动员的在某时刻的瞬时速度吗?
如果我们想求高台跳水运动员在s t 2=时的瞬时速度,可以先考察s t 2=附近的情况. 问题2:那么t 在[2,2.1],[2,2.01],[2,2.001]……内的平均速度分别是多少?请各小组汇报你们的计算结果,用手机同屏学生的实验结果. 我们先看运动员在]2,2[t ∆+内的平均速度.请完成表格: 问题3:大家发现了什么特点? 再看运动员在内在]2,2[t ∆+的平均速度.请完成表格:
问题4:大家发现了什么特点?
这种现象我们还可以通过电子表格来观察到。
