222管内强制对流换热计算示例-空气
空气强迫对流换热系数

空气强迫对流换热系数一、概述空气强迫对流换热系数是指在自然或强制的气流条件下,通过气体与固体表面之间的热传递过程中,单位面积上的热量传递率与温度差之比。
该系数是描述气体与固体表面间传热特性的重要参数,广泛应用于空调、暖通、化工等领域。
二、影响因素1. 气体性质:不同气体的密度、粘度、导热系数等物理特性不同,会影响气体在表面附近的速度分布和温度分布,从而影响换热系数;2. 流动状态:流动状态分为层流和湍流两种情况。
层流时,气体流动方向和速度分布均匀,换热系数较小;湍流时,气体速度分布不均匀且存在涡旋运动,换热系数较大;3. 表面状态:表面粗糙度会影响气体在表面附近的速度分布和温度分布,进而影响换热系数;4. 气体速度:当气体速度增加时,交换界面上形成的边界层变薄,气体与固体表面的接触面积增加,从而换热系数增大;5. 温度差:温度差越大,热传递速率越快,换热系数也就越大。
三、计算方法1. 热传递方程在对流传热中,根据牛顿冷却定律,热量传递率与温度差成正比。
因此可将气体与固体表面间的热传递方程表示为:q= hA(θs-θ∞)其中,q为单位时间内通过单位面积的热量;h为换热系数;A为交换界面积;θs为固体表面温度;θ∞为气体流动远离固体表面时的温度。
2. 换热系数计算公式(1)对于层流状态下的空气强迫对流换热系数:h = 0.664 × (ρuμ)/λ其中,ρ为空气密度;u为空气速度;μ为空气动力粘性系数;λ为空气导热系数。
(2)对于湍流状态下的空气强迫对流换热系数:h = 0.037 × (ρu^0.8μ^0.2)/λ其中,ρ、u、μ和λ的含义同上。
四、实验方法1. 实验装置实验装置包括:空气流量计、温度计、热电偶、电源和数据采集系统等组成。
其中,空气流量计用于测量空气流速,温度计和热电偶用于测量固体表面温度和气体远离表面时的温度。
2. 实验步骤(1)将试样固定在实验台上,并连接好电源和数据采集系统;(2)开启空气流量计,调节空气流速,并记录下对应的流速值;(3)打开数据采集系统,并将温度计和热电偶插入试样中相应位置;(4)记录下固体表面温度和气体远离表面时的温度值;(5)根据公式计算出空气强迫对流换热系数。
实验五 空气在圆形直管中强制对流传热膜系数的测定

实验五 空气在圆形直管中强制对流传热膜系数的测定一、实验目的1、通过实验掌握传热膜系数α的测定方法,并分析影响α的因素;2、掌握确定传热膜系数准数关联式中的系数C 和指数m 、n 的方法;3、通过实验提高对α关联式的理解,了解工程上强化传热的措施;4、掌握测温热电偶的使用方法。
二、实验原理对流传热的核心问题是求算传热膜系数α,当流体无相变化时对流传热准数关联式一般形式为:Nu = C Re m Pr n Gr p对强制湍流,Gr 准数可以忽略。
Nu = C Re m Pr n本实验中,可用图解法和最小二乘法两种方法计算准数关联式中的指数m 、n 和系数C 。
用图解法对多变量方程进行关联时,要对不同变量Re 和Pr 分别回归。
为了便于掌握这类方程的关联方法,可取n = 0.4(实验中流体被加热)。
这样就简化成单变量方程。
两边取对数,得到直线方程:Re lg lg Pr lg4.0m C Nu+= 在双对数坐标系中作图,找出直线斜率,即为方程的指数m 。
在直线上任取一点的函数值代入方程中得到系数C ,即mNu C Re Pr 4.0=用图解法,根据实验点确定直线位置,有一定的人为性。
而用最小二乘法回归,可以得到最佳关联结果。
应用计算机对多变量方程进行一次回归,就能同时得到C 、m 、n 。
可以看出对方程的关联,首先要有Nu 、Re 、Pr 的数据组。
雷诺准数 μρdu =Re努塞尔特准数 λαd Nu 1=普兰特准数 λμp C =Prd —换热器内管内径(m )α1—空气传热膜系数(W/m 2·℃)ρ—空气密度(kg/m 3)λ—空气的导热系数(W/m·℃) Cp —空气定压比热(J/kg·℃) 实验中改变空气的流量以改变准数Re 之值。
根据定性温度计算对应的Pr 准数值。
同时由牛顿冷却定律,求出不同流速下的传热膜系数α值。
进而算得Nu 准数值。
因为空气传热膜系数α1远小于蒸汽传热膜系数α2,所以传热管内的对流传热系数α1约等于冷热流体间的总传热系数K 。
求空气和管壁面间对流换热系数

求空气和管壁面间对流换热系数对流换热是热工学中一个重要的研究对象,对流换热系数是描述流体和固体壁面之间换热效果的一个重要参数。
而在许多工程领域中,空气和管壁面间的对流换热系数更是备受关注。
本文将围绕这一主题展开讨论,探讨空气和管壁面间对流换热系数的相关影响因素和计算方法。
一、对流换热系数的定义对流换热系数是指单位面积上的传热功率与温差之比,通常用符号"h"表示。
在对流换热过程中,对流换热系数的大小直接影响着传热效果,因此对其的研究和计算具有重要意义。
二、空气和管壁面间对流换热系数的影响因素1. 管道材质管道的材质直接影响着管壁面的导热性能和表面粗糙度,从而影响对流换热系数的大小。
一般来说,导热性能好、表面粗糙度小的管道对流换热系数会较高。
2. 流体性质空气的流体性质,如密度、粘度和导热系数等,也会对空气和管壁面间对流换热系数产生影响。
这些性质与空气的温度、压力等因素密切相关,在对流换热系数的计算中需要综合考虑。
3. 流体流动状态流体的流动状态对对流换热系数有明显影响。
层流和湍流的流动状态下,对流换热系数的大小会有所不同。
在实际工程中需根据流体流动状态的不同进行对流换热系数的计算和分析。
4. 管道几何形状管道的几何形状也会对对流换热系数产生影响。
不同形状的管道在对流换热过程中,由于流体流动状态的差异,其对流换热系数也会有所不同。
在计算对流换热系数时需要考虑管道的几何形状。
5. 表面温度差表面温度差是影响空气和管壁面间对流换热系数的重要因素。
一般来说,温度差越大,对流换热系数也会相应增大。
在工程实践中需要合理控制表面温度差,以提高对流换热系数。
三、空气和管壁面间对流换热系数的计算方法对于空气和管壁面间对流换热系数的计算,通常采用经验公式或数值模拟的方法。
常用的经验公式包括Dittus-Boelter公式、Sieder-Tate 公式等,这些公式都是根据大量实验数据拟合得到的经验公式,适用范围较广。
管内强迫对流换热计算.

qm qv uA u
注意 注意 注意
d
4
2
一定要使用国际通用单位!!! 一定要使用国际通用单位!!! 一定要使用国际通用单位!!!
CDPC-pony
传热学 Heat Transfer
Chengde Petroleum College
1、计算步骤
(1)定性温度的选取
tf 1 t f t f 2
tf 1 1 t f t f 50 60 55℃ 2 2
(2)查物性参数:查得水的物性参数为:
=0.6535W / (m ℃, ) Pr 3.265, v 0.517 106 m2 fer
(4) 格尼林斯基(Gnilinski)公式(1976)
2/3 f 8 Ref 1000 Prf d Nuf 1 ct 1/2 2/3 1 12.7 f 8 Prf 1 l
适用条件:
0.6 Prf 105 , 2300 Ref 106
Nuf 0.021Re Pr
0.8 f
0.43 f
适用条件:
4
Prf Prw
0.25
0.6 Prf 700, 10 Ref 1.7510 , l / d 60
6
CDPC-pony
传热学 Heat Transfer
Chengde Petroleum College
Chengde Petroleum College
(3)计算Re数为
Re ud 0.8 0.05 4 7.74 10 v 0.517 106
属于旺盛稳流阶段
空气横掠单圆管时强迫对流换热实验1

空气横掠单圆管时强迫对流换热实验报告一、实验原理 可根据相似理论,空气横掠单圆管强迫对流的换热规律可用下列准则关系式来表示:n Nu CRe = (1)式中,努谢尔特准则数为: /Nu hD λ= (2)雷诺准则数为: /Re uD v = (3) 这里,λ为空气的导热系数, ν为空气的运动粘度,是平均温度2)/(m f w t t t =+的函数,其中w t 为管外壁温,f t 为空气温度;D 为实验管的外径,u 为空气的流速。
关键的是对流换热平均表面传热系数h 的确定。
由对流换热平均表面传热系数h 的定义:(/)w f h Qa F t t =-式中,Qa 为管外表面与周围空气之间的对流换热量,管的外表面积F DL π=,L 为横管的有效长度。
考虑到管外表面在与周围空气对流换热同时,与周围环境间存在辐射换热。
即管实际传出热量为:4480+10()()a f w f w f Q Q Q hF t t C F T T ε-=+=⨯--其中,ε为实验管外表面的黑度,黑体辐射系数240 5.67C Wm K --= 。
这里,假定环境温度即空气温度。
因此, 横管外表面对流换热平均表面传热系数就可以由下式确定:4480[()/10/ ]()w f w f h Q F C T T t t ε-=⨯---因此,对给定实验管,通过测量管的实际传出热量Q 、管外壁温w t 、来流空气的温度f t 就可通过实验确定管外表面与周围空气之间对流换热平均表面传热系数h 。
由式(2)和(3)通过改变气流速度或实验管直径,就可得到一系列Nu-Re 对应数据。
在数据足够多、Re 变化范围足够大的条件下,就可确定式(1)中的C 和n 的值。
二、实验数据列表一、实验结果及分析作出lg~lg ReNu拟合曲线如下拟合公式log0.5814log Re0.5748Nu=-,则得到0.58140.2662ReNu=即0.2662,0.581C n==产生偏差的原因可能是:(1)准则方程式在Re=4000~40000时的情况较为接近,而实验中有部分Re 值小于4000造成了误差;(2)管内存在阻力损失使压力测量有偏差,导致速度测量不准确;(3)管壁也不是严格的等壁温条件,在tf、tw的计算上会产生误差。
实验8 空气横掠单管强迫对流换热系数测定实验
实验8 空气横掠单管强迫对流换热系数测定实验一、实验目的1. 测算空气横掠单管时的平均换热系数h 。
2. 测算空气横掠单管时的实验准则方程式13Re Pr nNu C =⋅⋅。
3. 学习对流换热实验的测量方法。
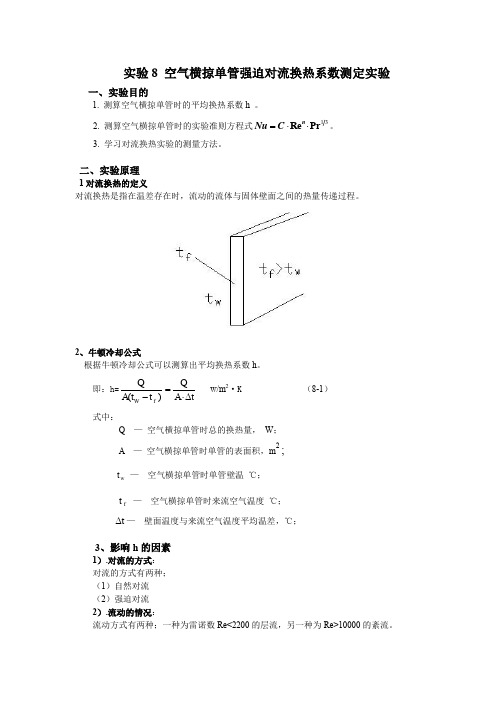
二、实验原理 1对流换热的定义对流换热是指在温差存在时,流动的流体与固体壁面之间的热量传递过程。
2、牛顿冷却公式根据牛顿冷却公式可以测算出平均换热系数h 。
即:h=)(f W t t A Q-Q A t=⋅∆ w/m 2·K (8-1)式中:Q — 空气横掠单管时总的换热量, W ; A — 空气横掠单管时单管的表面积,m2;w t — 空气横掠单管时单管壁温 ℃;f t — 空气横掠单管时来流空气温度 ℃;t ∆— 壁面温度与来流空气温度平均温差,℃;3、影响h 的因素1).对流的方式: 对流的方式有两种; (1)自然对流 (2)强迫对流 2).流动的情况:流动方式有两种;一种为雷诺数Re<2200的层流,另一种为Re>10000的紊流。
Re — 雷诺数, Re vud =, 雷诺数Re 的物理定义是在流体运动中惯性力对黏滞力比值的无量纲数。
上述公式中,d —外管径(m ),u —流体在实验测试段中的流速(m/s ),v —流体的运动粘度(㎡/s )。
3).物体的物理性质: Pr — 普朗特数,Pr=αν= cpμ/k 其中α为热扩散率, v 为运动粘度, μ为动力粘度;cp 为等压比热容;k 为热导率; 普朗特数的定义是:运动粘度与导温系数之比 4).换面的形状和位置 5).流体集体的改变 相变换热 :凝结与沸腾4、对流换热方程的一般表达方式强制对流:由外力(如:泵、风机、水压头)作用所产生的流动 强迫对流公式为(Re,Pr)Nu f =自然对流:流体因各部分温度不同而引起的密度差异所产生的流动。
自然对流公式为Nu=f (Gr ,Pr ) 1).Re=vul =雷诺数Re 的定义是在流体运动中惯性力对黏滞力比值的无量纲数Re=UL/ν 。
对流换热公式整理

/2 1/3 , 0.664 Re1 x Pr x
(0.6<Pr<60)
/5 1/3 恒热流: Nu x 0.0308 Re 4 Pr x x
3 1 0.14
Pr f Prw
) 0.25 _________。
1.3 过渡流: Nu 格尼林斯基公式: f
Pr f 修正:①温差(加热或冷却): Pr w
f Tf 或 或 T w w
k
0.7
l d ②入口段(短管 l/d<60): 或 c l 1 d l
d 列齐德-泰特公式:__ Nu 1.86 Re Pr l f ________ w ( f 8 )(Re - 1000)Pr f d = 1 + ct 1 + 12.7 f 8(Pr f 2 3 - 1) l
③弯管:
d 气体:c R 1 1.77 R
d 液体: c R 1 10 .3 R
3
④非圆管:当量径:de = 4Ac/P 2.外部流: 2.1 平板:
1/3 2.1.1 层流: Nu x 0.332 Re 1x/ 2 Pr x /5 1/3 2.1.2 湍流: Nu x 0.0296 Re 4 Pr x x
对流换热公式
一、强制对流换热
l l 粘性流体强制流: Nu f l , Re, Pr l , Re, Pe 或 Nu f 0 0 l/d>60,短管 1.内部流(管内流,(长管 l/d&s-Boelter 公式:_ Nu 0.023 Re 0.8 Pr n _, 条件:__气体≤50℃,水≤20~40℃,油类≤10℃。 Re=104-1.2×105_, 定性温度为:流体平均温度,定性尺寸为:管内径。 ②温差大:修正或 米海耶夫公式:_ Nu f 0.021 Re 0f.8 Pr f0.43 ( 1.2 层流
自然对流与强制对流及计算实例

自然对流与强制对流及计算实例热设计就是电子设备开发中必不可少得环节。
本连载从热设计得基础——传热着手,介绍基本得热设计方法。
前面介绍得热传导具有消除个体内温差得效果。
上篇绍得热对流,则具有降低平均温度得效果。
下面就通过具体得计算来分别说明自然对流与强制对流得情况。
首先,自然对流得传热系数可以表述为公式(2)。
热流量=自然对流传热系数×物体表面积×(表面温度-流体温度) (2)很多文献中都记载了计算传热系数得公式,可以把流体得特性值带入公式中进行计算,可以适用于所有流体。
但每次计算得时候,都必须代入五个特性值。
因此,公式(3)事先代入了空气得特性值,简化了公式。
自然对流传热系数h=2 、51C(⊿T/L)0、25(W/m2K) (3)2、51就是代入空气得特性值后求得得系数。
如果就是向水中散热,2、51需要换成水得特性值。
公式(3)出现了C、L、⊿T三个参数。
C与L从表1中选择。
例如,发热板竖立与横躺时,周围空气得流动各不相同。
对流传热系数也会随之改变,系数C就负责吸收这一差异。
代表长度L与C就是成对定义得。
计算代表长度得公式因物体形状而异,因此,在计算得时候,需要从表1中选择相似得形状。
需要注意得就是,表示大小得L位于分母。
这就表示物体越小,对流传热系数越大。
⊿T就是指公式(2)中得(表面温度-流体温度)。
温差变大后,传热系数也会变大。
物体与空气之间得温差越大,紧邻物体那部分空气得升温越大。
因此,风速加快后,传热系数也会变大。
公式(3)叫做“半理论半实验公式”。
第二篇中介绍得热传导公式能够通过求解微分方程得方式求出,但自然对流与气流有关,没有完全适用得理论公式。
能建立理论公式得,只有产生得气流较简单得平板垂直放置得情况。
因为在这种情况下,理论上得温度边界线得厚度可以计算出来。
但就是,如果发热板水平放置,气流就会变得复杂,计算得难度也会增加。
这种情况下,就要根据原始得理论公式,通过实验求出系数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
222管内强制对流换热计算示例-空气
222 管内强制对流换热计算示例-空气
说明
流体在换热过程中无相变。
流体在管内用泵、风机、压缩机等强制流动。
雷诺数
Re=ud/v
式中,u为流体速度,m/s;d为管路直径,m;v为流体的运动黏度,m2/s。
计算方程(流体与管内壁温差不太大、管路不太短时)
当2300>R e>13,且dR e P r/L>10时(R e为流体流动的雷诺数,无因次;d为管路的当量直径,m;P r为流体的普朗特数,无因次;L 为管路长度,m),
N u=1.86(dR e P r/L)0.333
当10000>R e>2300,且流体为气体,气体普朗特数1.5>P r>0.6时,
N u=0.0214P r0.4(R e0.8-100)
当10000>R e>2300,且流体为液体,液体普朗特数100>P r>1.5时,
N u=0.012P r0.4(R e0.87-280)
当12*104>R e>104,普朗特数120>P r>0.7,L/d>60时,
如流体被加热,则:
N u=0.023P r0.4R e0.8
如流体被冷却,则:
N u=0.023P r0.3R e0.8
上述公式中流体物性的定性温度为流体进出管路的平均温度。
换热系数:
a fa=N u d ao/d
式中,a fa为流体的对流换热系数,W/(m2.K);N u为努谢尔特数,
无因次;d ao为流体的热导率,W/(m.K);d为管路当量直径,m。
流体与管路的换热量为:
Q=a fa FT d
式中,Q为换热量,W;a fa为流体的对流换热系数,W/(m2.K); F 为流体与管路壁面的接触面积,m2;T d为流体与管壁表面温度之差;K。
计算示例
空气在膜管-壳体型膜组件的壳侧(膜管与壳体之间的空间)流动,壳体内直径为40mm,膜管有100根,膜管外直径为1.3mm,膜管长度为1500mm,膜管外壁温度约为80℃;空气在膜管外的流速为6.6m/s,空气在膜管外的平均温度为78℃,计算膜组件给空气的加热量和空气流经膜组件的温升。
查78℃时空气的热物性,有:
运动黏度v=20.5*10-6m2/s
普朗特数P r=0.69
热导率d ao=0.03W/(m.K)
比热c=1009J/(kg.K)
密度r ou=1.02kg/m3
具体计算如下:
当量直径为:
d=(D2-Nd o2)/(D+Nd o)=(0.042-
100*0.00132)/(0.04+100*0.0013)=0.00842m
流动雷诺数:
Re=ud/v=6.6*0.00842/(20.5*10-6)=2711
N u=0.0214P r0.4(R e0.8-100)
=0.0214*0.690.4(27110.8-100)
=0.01845*458=8.45
对流换热系数:
a fa=N u d ao/d=8.45*0.03/0.00842=30W/(m2.K)
换热面积:
F=3.14d o LN=3.14*0.0013*1.5*100=0.6123m2
换热量:
Q=a fa F T d =30*0.6123*(80-78)=37W
空气的质量流量:
m=(0.25*3.14*D2-0.25*3.14*N*d o2)ur ou=(0.25*3.14*0.042-0.25*3.14*100*0.00132)*6.6*1.02=0.00756kg/s
空气在流经膜组件过程中温升为:
T s=Q/(mc)=37/(0.00756*1009)=5℃
●研讨
6m/s多的空气吹到膜管上,膜管受力为多少?是否会造成膜管振动而使根部损坏?如何通过结构设计避免膜管明显受力或振动?
空气在膜管外流动近似按轴向均流,实际的流动可能出现哪些情况?如何分析实际流动因素对换热的影响?如何使空气较好地实现均匀轴向流动?
空气的流动阻力主要受哪些因素影响?如何计算?。
