博弈论与信息不对称(精选)
博弈论经典案例

重复博弈囚徒困境,砸了传统经济学的场子。
因为个人的自利行为,并不一定导致集体利益的最大化,“看不见的手”拉不住,人类向堕落之城下滑的趋势,难道这真是一个悲哀?索性并非如此,撇去博弈论的理性假设不说。
博弈论者很快发现囚徒困境只在单次博弈情形下明显,一旦博弈的开始陷入重复,合作将到来。
因为,未来的收益将左右目前的决策。
以牙还牙重复的博弈理论上导致了合作的产生,但是谁也不能保证合作的继续,因为之前已经说过,合作的代价是建立在损害个人利益基础之上的。
如果个人放弃未来收益或当前背叛收益大于未来收益,背叛的风险仍然存在。
那么在重复博弈中怎样的策略才是最优。
若干睿智而复杂在经过计算机中PK之后,极其原始的“以牙换牙”策略脱颖而出,固然这个策略简单至极,其威力却无穷,以至于人们在短暂的欣喜之后,发现这把太阿指之剑倒持的可怕,一旦重复链条中出现一次(也许不经意的)背叛,那据此原则行事的博弈将永无止境的背叛下去,个人利益极度膨胀的同时,集体利益无限衰微。
幸好,这个世界不是模型,也不是如此简单。
很多时候,我们不必以牙还牙,第三方的规范:道德与法律就是我们的假牙,他们更加有利、有理、有节。
人质困境一场憋屈的博弈。
抢打出头鸟,人质联合固然可以制服歹徒,但是谁愿出头。
这一点给了无数处于劫持者地位的一方以机会,类似于秦的远交近攻、各个击破的策略,将最终全盘赢下。
人质可有反制的策略,当然有,不过艰难至极。
人质可以选择沉默,这样他有一定时间苟延残喘;或者联合劫持者对付人质,结局还是取决于劫持者,万一他过河拆桥怎么办;同时反抗,集体将获得左右策略,但是这需要壮士断腕的勇气,部分人可能因此受伤。
这里是实力与勇气的较量,而且实力暂居上风。
酒吧博弈如果人人理性,那么每一天到达酒吧的人数将是差不多正好的,但是人非圣贤,往往是有限理性的。
第一次到酒吧的人多,那么大多人人认为酒吧人太多,太挤。
第二次决定的时候,参考前次而不去酒吧。
少数去的人发现酒吧的人第二天很少,感觉很爽,第三次将继续回来,并重新带回许多人……循环就此开始。
博弈论与信息经济学

博弈论与信息经济学一、引言博弈论与信息经济学是现代经济学中重要的研究领域之一。
博弈论研究的是决策者在互动中面临的策略选择问题,致力于解决各种冲突和合作关系中涉及的决策问题。
信息经济学则侧重于分析信息在经济活动中的作用,特别是信息不对称情况下的市场行为和结果。
本文将就博弈论与信息经济学的主要概念、方法和应用展开论述。
二、博弈论博弈论是一种数学工具,用于分析决策者在互动中的行为和选择。
博弈论中的“博弈”指的是参与者之间的相互作用,每个参与者都试图通过选择最优策略来达到个人利益最大化。
1.基本概念在博弈论中,最基本的概念是“博弈”,即参与者之间的互动行为。
每个参与者在博弈中都会考虑其他参与者的选择,以制定自己的策略。
博弈可以分为合作博弈和非合作博弈两种形式。
2.关键元素博弈论中的关键元素包括参与者、策略和支付。
参与者是指在博弈中做出决策的个体或组织,策略是指参与者的选择或行动,支付是参与者根据策略和其他参与者的选择所获得的利益或成本。
3.博弈模型博弈论通过建立数学模型来描述博弈中的参与者、策略和支付之间的关系。
常见的博弈模型包括正规博弈和扩展博弈。
正规博弈是指参与者同时或依次选择策略,而扩展博弈则考虑了时间因素,并将博弈过程分为不同阶段。
三、信息经济学信息经济学研究的是在市场经济中信息的获取、传递和利用。
在现实经济中,信息通常是不对称的,即买方和卖方在交易中拥有不同的信息水平。
信息经济学探讨了信息不对称对市场行为和经济结果的影响。
1.信息不对称信息经济学的核心概念是信息不对称,即市场参与者在交易中所拥有的信息水平不同。
信息不对称会导致市场效率下降,因为交易双方无法完全了解对方的信息,从而影响了市场的决策和结果。
2.逆向选择和道德风险逆向选择和道德风险是信息不对称的两个主要问题。
逆向选择指的是交易中买方无法获得完全信息,导致买方从卖方处选择低质量产品或服务。
道德风险则是指卖方在交易完成后可能会改变行为,损害买方的利益。
风投家与风险企业——信息不对称下的博弈分析

本文试 图借 助博 弈论 中 不完 全 信息 静 态博 弈 的分 析 方
法, 从信息不对称 的角度 来 阐述风 险投 资家与 风险企 业在 签 订协议前相互选择过程中的博弈过 程。文章第一 部分对 国 内 外风投活动 中的博 弈进行 了回顾 和总结 ; 第二 部分 基于 文章 相关理论建立相应 的博弈模型 , 并对模 型进行分析 ; 第 三部分
2 博 弈 模 型 建 立及 分 析
2 . 1 基 本 假 设
在资本市场 中, 风 险投资 越来 越受 到投融 资者 的 广泛关 注, 对风险投资相关 理论 问题 的研究 也不 断受 到学术 界 的重
视, 尤其是影响风 险投资 市场 有效发 展却 广泛存 在 的信息 不
对称 问题 。风险投 资 活动 的直接参 与者 包括 投 资者 、 风 险投 资家和风险企业三方。相应的 , 在 风险投 资整个 活动过程 中 ,
总结模型分析所 得到 的结论 , 并 结合结 论提 出相关 的一 些建
议。 ,
1 文 献 综 述
在 上述 假设 下 , 可 以拟 出双方 的支付矩阵如表 1 所示 。
表 1
风 险 企 业
项 目高质 量
隐瞒 不 隐 瞒
项 目低 质 量
隐瞒 不 隐 瞒
风险投资 的信 息不对 称f n ] 题、 代 理 问题 是 目前 国内学 术
4 ) 风险企业 有两 种策 略 , 隐 瞒和不 隐 瞒。风险 投 资家有
两种策略 , 调查和不调查。
5 ) 博弈双方信息不对称。假设风 险投 资机构无 法调查 出 企业 隐瞒下 的真实情 况。 6 ) 风险投资家在不调查 的情 况下会 对 申请 企业 均注 人 S 的风险资金 , 且若投入到低质量 的项 目中, 本 金无法收 回。 7 ) 高质量项 目才可盈利 。
对称均衡 非对称均衡 博弈论

对称均衡非对称均衡博弈论
对称均衡和非对称均衡是博弈论中的重要概念,用于描述博弈中各方的策略选择和结果。
在博弈论中,博弈是指一种决策情形,其中参与者的利益受到彼此的影响。
对称均衡和非对称均衡都是描述博弈中可能出现的情况的概念。
首先,让我们来看看对称均衡。
在博弈论中,对称均衡是指参与者采取相同的策略,并且没有动机去改变自己的策略,因为任何一方的单方面改变都不会使其获益。
对称均衡的一个经典例子是“囚徒困境”博弈,其中两名囚犯面临合作或者背叛的选择。
在对称均衡中,如果两名囚犯都选择背叛,那么他们都会受到最严厉的惩罚,而如果两名囚犯都选择合作,那么他们都会受益。
因此,对称均衡发生在他们都选择背叛或者都选择合作的情况下。
其次,非对称均衡是指参与者采取不同的策略,并且在当前策略下没有动机去改变自己的策略,因为任何一方的单方面改变都不会使其获益。
非对称均衡的一个例子是“买方市场”博弈,其中卖方和买方在价格谈判中采取不同的策略。
在非对称均衡中,如果卖方设定了一个最低价格,而买方愿意接受这个价格,那么双方都没有动机改变自己的策略。
总的来说,对称均衡和非对称均衡是博弈论中用于描述参与者策略选择和结果的重要概念。
通过研究对称均衡和非对称均衡,我们可以更好地理解博弈中参与者的决策行为,以及他们可能达到的结果。
这些概念对于经济学、政治学以及其他社会科学领域都具有重要意义。
希望这个回答能够帮助你更好地理解对称均衡、非对称均衡和博弈论的相关概念。
博弈论与信息经济学精选全文
可编辑修改精选全文完整版1、理性的人不一定是自私主义者,也有可能是利他主义者。
2、博弈论:game theory。
是研究决策主体的行为发生直接相互作用时候的决策以及这种决策的均衡问题。
博弈论研究的是在存在相互外部经济条件下的个人选择问题。
3、博弈论:合作博弈和非合作博弈,现在经济学家谈到的博弈论一般指得非合作博弈论。
合作博弈强调的是团体理性-----collective rationality,强调的是效率efficiency,、公正fairness、公平equality。
非合作博弈强调的是个人理性、个人最优决策。
(纳什和tucker基本上奠定了现代非合作博弈论的基石)4、博弈论的基本概念包括:参与人、行动、信息战略、支付、函数、结果和均衡。
5、博弈----动态博弈和静态博弈。
静态博弈(static game)指的是博弈中,参与人同时选择行动或虽非同时但后行动者并不知道前行动者采取了什么具体行动;动态博弈(dynamic)指的是参与人的行动有先后顺序,且后行动者能够观察到先行动者所选择的行动。
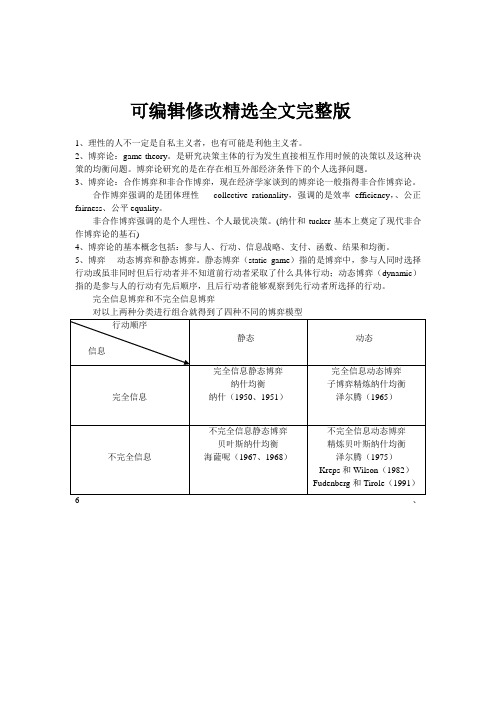
完全信息博弈和不完全信息博弈对以上两种分类进行组合就得到了四种不同的博弈模型行动顺序信息静态动态完全信息完全信息静态博弈纳什均衡纳什(1950、1951)完全信息动态博弈子博弈精炼纳什均衡泽尔腾(1965)不完全信息不完全信息静态博弈贝叶斯纳什均衡海薩呢(1967、1968)不完全信息动态博弈精炼贝叶斯纳什均衡泽尔腾(1975)Kreps和Wilson(1982)Fudenberg和Tirole(1991)6、。
博弈论与信息经济学

博弈论与信息经济学引言博弈论和信息经济学是现代经济学中两个重要的分支领域。
博弈论研究决策者在相互影响的环境中作出决策的数学模型,而信息经济学则关注信息不对称对经济行为和市场结果的影响。
本文将对博弈论和信息经济学的基本概念和应用进行介绍和讨论。
一、博弈论1.1 基本概念博弈论是由数学家冯·诺伊曼和经济学家莫里斯·贝克利于20世纪40年代提出的一种分析决策制定者行为的数学方法。
博弈论涉及多个决策者之间的相互作用,每个决策者根据其他决策者的行为来制定自己的策略。
在博弈论中,决策者被称为“玩家”,玩家可利用数学模型来描绘他们之间的相互作用。
博弈论主要研究决策者在特定的决策环境下作出最优决策的方法。
不同的决策环境可以分为正和零和博弈。
正和博弈是指玩家的利益完全一致,而零和博弈是指玩家的利益完全相反,一方的利益得到的增加,另一方的利益就会减少。
1.2 博弈论的应用博弈论在现代经济学中有广泛的应用。
在市场竞争中,企业之间的定价策略和广告策略可以通过博弈论模型来分析。
此外,博弈论还可以应用于股市、政治决策和国际贸易等领域。
通过博弈论的分析,我们可以预测不同玩家的最优策略,并对市场结果进行预测和解释。
二、信息经济学2.1 基本概念信息经济学研究在信息不对称的情况下,信息对决策者行为和市场结果的影响。
在现实生活中,决策者通常无法获得所有相关的信息,而且有些信息可能被其他决策者所掌握。
信息经济学通过研究不完全信息的决策环境来分析决策者的行为。
在信息经济学中,主要包括代理理论、道德风险以及契约理论等概念。
代理理论用于研究委托人与代理人之间的关系,道德风险则探讨行为者的操纵和欺诈行为,契约理论研究经济交易中的合同设计和执行。
2.2 信息经济学的应用信息经济学在现代经济学中有广泛的应用。
在公司治理中,代理理论被用于分析委托人与代理人之间的冲突和激励机制的设计。
在金融市场中,对信息的不对称和不完全的研究有助于理解金融市场的运行机制。
博弈论经典案例(2篇)

第1篇囚徒困境是博弈论中一个著名的案例,由梅里尔·弗里德曼(Merrill Flood)和莫顿·哈特(Morton Hall)在1950年提出。
这个案例旨在揭示个体理性行为可能导致集体非理性的结果,从而揭示了合作与竞争之间的复杂关系。
一、案例背景假设有两个犯罪嫌疑人甲和乙,他们被关押在两个分开的牢房中,彼此无法沟通。
警方分别向他们提出以下指控:1. 如果甲和乙都保持沉默,那么他们都将被判无罪释放。
2. 如果甲和乙都认罪,那么他们都将被判刑3年。
3. 如果甲保持沉默而乙认罪,那么甲将被判刑10年,乙将被判无罪释放。
4. 如果甲认罪而乙保持沉默,那么乙将被判刑10年,甲将被判无罪释放。
二、个体理性决策从个体理性角度出发,每个犯罪嫌疑人都会选择认罪。
原因如下:1. 如果对方保持沉默,自己认罪可以减少3年的刑期。
2. 如果对方认罪,自己保持沉默将面临10年的刑期。
3. 如果自己认罪,无论对方是否认罪,自己都能获得较轻的刑期。
因此,从个体理性角度来看,每个犯罪嫌疑人都会选择认罪。
三、集体非理性结果然而,当两个犯罪嫌疑人同时考虑对方的行为时,他们都会发现,无论对方是否认罪,自己选择认罪都能获得较轻的刑期。
这种情况下,两人都会选择认罪,导致最终结果是他们都将被判刑3年。
这种结果看似合理,但实际上却是一个集体非理性的结果。
如果两人都能保持沉默,他们都将被判无罪释放,这显然是一个更好的结果。
然而,由于个体理性行为,他们最终都选择了认罪,导致了一个集体非理性的结果。
四、案例分析囚徒困境案例揭示了以下博弈论原理:1. 合作与竞争的矛盾:个体理性可能导致集体非理性。
在这个案例中,每个犯罪嫌疑人都从个体理性角度出发,选择了认罪,但最终导致了一个集体非理性的结果。
2. 信息不对称:由于甲和乙无法沟通,他们无法获取对方的信息,这导致他们无法进行有效的合作。
3. 信任缺失:在囚徒困境中,即使双方都从集体理性角度出发,但由于缺乏信任,他们仍然会选择认罪。
完全信息和不完全信息-博弈论相关

3、完全信息和不完全信息:完全信息博弈的基本假设:所有参与人都知道博弈的结构、博弈的规则,知道博弈支付函数.在不完全信息博弈里,至少有一个参与人不知道其他参与人的支付函数.温泉信息是指自然不首先行动或自然的促使行动被所有参与人观测到的情况,即没有事前的不确定性。
显然不完全信息意味着不完美信息,但逆命题不成立。
12、完美和不完美信息:不完美信息指的是自然做出了它的选择,但是其他选择人并不知道它的具体选择是什么,金知道各种选择的概率分布。
完美信息:指一个参与人对其他参与人(包括虚拟参与人“自然")的行动选择有准确了解的情况,即每一个信息集只包含一个值。
2、贝叶斯均衡:是纳什均衡在不完全信息博弈中的自然扩展。
在静态不完全信息博弈中,参与人同时行动么有机会观察到别人的选择.给定别人的战略选择,每个参与人的概率分布而不知道其真实类型不可能准确的知道其他参与人实际上会选择什么策略,但是它能正确预测到其他参与人的选择如何以来与其各自的类型.这样,他决策的目标就是在给定自己的类型和别人的类型已从战略情况下最大化自己的期望效用14、PBNE贝叶斯纳什均衡是这样一种类型依从战略组合:给定自己的类型和别人类型的概率分布的情况下,每个参与人的期望效用达到了最大化,也就是说没有人有积极性选择其他战略。
贝叶斯纳什均衡:P1474、有限次重复博弈:16、重复博弈是指同样结构的博弈重复多次,其中每次博弈成为“阶段博弈”。
定理:令G是阶段博弈,G(T)是G重复T次的重复博弈(T小于正无穷)。
那么,如果G有唯一的纳什均衡,重复博弈G(T)的唯一的子博弈纳什均衡结果是阶段博弈G的纳什均衡重复T次(即每个阶段博弈出现的都是一次性博弈的均衡结果)。
7、激励相容:当参与人之间存在信息不对称时,任何一种有效的制度安排都必须满足“激励相容”条件。
激励相容约束也是委托人设计机制时要考虑的第二个约束:给定委托人不知道代理人的类型时,代理人在所涉及的机制下必须有积极性选择委托人希望他选择的行动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
不做广告 (6,8)(20,2)
博弈论与信息不对称
15
占优策略
v 从经过修改的支付矩阵可以发现,A厂商不存在占 优策略,其决策将依赖B厂商的决策,因为当B厂商 选择(不)做广告时,A厂商选择(不)做广告将 获得最大支付。
v 虽然A厂商不存在占优策略,但是该博弈仍然存在 均衡。因为B厂商存在占优策略即做广告,如果A厂 商按照B厂商必将做广告的事实进行决策,A厂商也 将做广告,所以两个厂商都做广告为该博弈的均衡。
v 在解析奥曼和谢林获奖原因时,经济学奖评委会主 席表示:“为什么有些国家、团体和个人可以和平 地解决冲突,而另一些国家、团体和个人却不断地 被冲突困扰呢?感谢奥曼和谢林的研究,为这一自 古以来困扰我们的问题带来启迪。”
博弈论与信息不对称
4
引言
v 斯蒂格利茨:“中国改革二个阶段, 第一个阶段构建市场框架,第二个 阶段是制度设计”。博弈论对社会 福利的意义正在于制度设计
者加入市场时,各厂商如何作出定价决策? v 博弈论为这些问题提供了合理的分析框架。
博弈论与信息不对称
6
1、博弈论和竞争策略
v 博弈论的应用是微观经济学 的重要发展,这里我们将阐 述其部分内容,并说明它能 如何被应用于理解市场的发 展和运作,以及经营者应怎 样考虑他们不断面临的决策 问题。
博弈论与信息不对称
v 当每个参与者都有占优策略时,我们把 博弈的结果叫做占优策略均衡。上面广 告博弈的例子存在占优策略均衡,即A和 B厂商都做广告。
博弈论与信息不对称
14
占优策略
v 需要注意,并非每个博弈的各个参与者都有一个
占优策略。如果将前面广告博弈的支付矩阵进行
修改如下:
厂商A\厂 做广告 不做广
商B
告
做广告 (10,5)(15,0)
7
1.1、博弈和决策
v 博弈是参与者在其中作出策略性决策的情境——也 就是考虑到其他人的行为和反应后作出的决策。
v 策略性决策将给予参与者和某一具体结果相联系的 价值即支付。
v 策略是参与者在博弈中遵循的行动规则或者计划。 而博弈论的关键目标是决定每个参与者的最优策 略——参与者的最优策略是能够最大化他的期望的 支付策略。
博弈论与信息不对称
此课件下载后可自行编辑修改 关注我 每天分享干货
博弈论与信息不对称
1
引言
v 在经济学史上,曾经发生过三次重大的 “革 命”,分别是 “边际分析革命”、“凯恩斯 革命”与“博弈论革命 ”。博弈论与信息经 济学的产生与发展引发了一场深刻的经济学 革命,因为它代表着一种新概念、新方法和 一种全新的思想。
v 非合作博弈的例子: v 1、两竞争的厂商互相考虑到对方可能的行为,并独立确定
价格或广告策略,以夺取市场份额。 v 2、拍卖中,每一个投标者在作出自己的最优投标策略时,
都必须考虑其他投标者可能的行动。
博弈论与信息不对称
11
非合作与合作博弈
v 合作与非合作博弈之间的区别在于签订合同 的可能性。
v 我们主要关心非作博弈,而在任何博弈中, 策略设计最重要的方面是理解你的对手的观 点,并推断他对你的行为大概如何反应。
博弈论与信息不对称
2
引言
v 萨缪尔森:你可以将一只鹦鹉训 练成经济学家,因为它所要学习 的只有两个词:供给与需求。博 弈论专家坎多瑞引申说:要成为 现代经济学家,这只鹦鹉必须再 多学一个词,这个词就是“纳什 均衡”。
博弈论与信息不对称
3
引言
v 瑞典皇家科学院 10月 10日宣布,将2005年诺贝尔 经济学奖授予有以色列和美国双重国籍的罗伯特·奥 曼和美国人托马斯·谢林,以表彰他们通过博弈理论 分析增加了世人对合作与冲突的理解。
小区A\小区B
修建
不修建
修建
(100,100) (-100,300)
不修建 (300,-100) (0,0)
博弈论与信息不对称
18
公路的博弈
v 对于小区A或B来说,其占优策略是不参与公 路的修建。
v 以小区A为例,无论小区B是否参与公路的修 建,它都可以通过不参与修建,节省成本支 出,从获得现成利益或者避免损失。ຫໍສະໝຸດ 博弈论与信息不对称8
博弈和决策
v 这里主要讨论参与者是理性的博弈,即他们 完全认识到了自己行动的重要性。
v 如下问题应该受到关注:如果某个参与者相 信其他竞争者是理性的和追求最大利润的, 那么在他作出自身利润最大化决策时,他应 该如何考虑到其他人的行为?
博弈论与信息不对称
9
非合作与合作博弈
v 合作博弈:参与人可以谈判并制定具 有约束力的,共同策略行为的契约的博 弈。
v 合作博弈的例子: v 1、当买方对商品评价高于卖方生产成
本,买卖双方的经过讨价还价达成交易 价格使得双方都获得好处。 v 2、一个行业中两个厂商谈判进行联合 投资开发各自无法独立完成新技术。
博弈论与信息不对称
10
非合作与合作博弈
v 非合作博弈:不能达成具有约束力的协议的博弈,并且该博 弈方之间不能相互协调。
博弈论与信息不对称
16
公路的博弈
v 假设存在两个小区A和B,现 在需要修建一条连接两个小 区的公路。
v 修建该公路的成本为400,而 公路修建完毕则能为各小区 带来300的利益。当然小区A 和B都有权拒绝公路的修建公 路,等对方修建完毕以坐享 其成。
博弈论与信息不对称
17
公路的博弈
v 该问题的支付矩阵如下:
v 博弈论也是很好的思维训练,它能 提高思维能力和思维素养,因为博 弈论研究策略的互动和利益依存, 从而能够进行换位思考
博弈论与信息不对称
5
1、博弈论和竞争策略
v 一些有关市场结构和厂商行为的问题: v 为什么有些市场的厂商倾向于共谋而另一些
市场的厂商倾向于激烈竞争? v 有些厂商是怎样阻止潜在的竞争者加入? v 需求和成本条件发生变化,或者有新的竞争
博弈论与信息不对称
12
1.2、占优策略
v 占优策略是不管竞争者如何行动,该策略都是最 优的策略。
v 下表为竞争厂商A和B的广告博弈支付矩阵: 厂商A\厂商B 做广告 不做广告
做广告 (10,5) (15,0)
不做广告 (6,8) (10,2)
博弈论与信息不对称
13
占优策略
v 从该支付矩阵可以看出,无论B厂商做不 做广告,A厂商选择做广告所获得的支付 都将大于不做广告所获得的支付。因此 不论B厂商如何行动,A厂商一定会选择 做广告的策略, 做广告也就是A厂商的 占优策略。
