单纯形法 计算对偶变量值
运筹学-单纯形法灵敏度对偶
若新增约束如下:
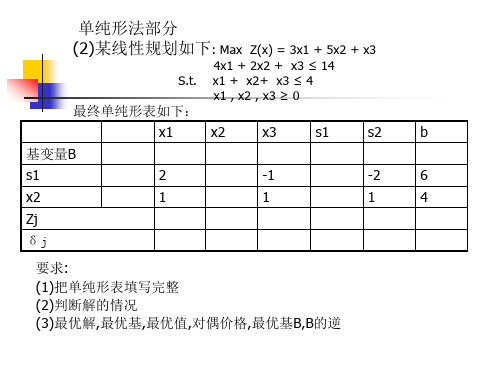
max z 50x1 100x2 x1 x2 300 2x1 x2 400 x2 250 10x1 30x2 5000(电力约束) x1, x2 , 0
x1 x2 s1
把最优解x1=50,x2 =250代入电力约束 1050+30 250=80005000 新约束不满足,最优解变化
例题:已知某线性规划初始可行基是(S1 S2 S3 a1), 最终单纯形表如下,求对偶价格不变时的△bi变化范围
x1 x2 s1
50 100 0
X1 50
1
0
0
S3 0
0
0
0
X2 100 0
1
0
s1 0
0
0
1
Zj
50 100 0
δj
0
0
0
(1) △b1的变化范围: ?
(2) △b2的变化范围:?
(3) △b3的变化范围: ? (4) △b4的变化范围:?
1 0 1 2 0.5
B1 p6'
2
1
1
0.5
2
0 0 1 1.5 1.5
Z6' 50 0.5 0 (2) 100 1.5 175
' 6
C6
Z6'
150 175
25
δ6´<0,最优解不变,即仍生产Ⅰ50件,Ⅱ100件。
2、变量xk系数列由pk变为pk´,在最终单纯形表 上xk是基变量
x1 x2 s1
50 100 0
X1 50 1
0
0
S3 0
0
0
0
X2 100 0
1
0
s1 0
0
运筹学 对偶单纯形法

=min{j’ / akj’┃akj’<0}=r’/akr’那么 xr为进基变量,转4; 4.以akr’为转轴元,作矩阵行变换使其变为1,该
列其他元变为0,转2。
2.对偶单纯形法
例3.2:求解线性规划问题:
1.线性规划对偶问题
对称形式: (P) Max z = cT x s.t. Ax ≤ b x ≥0 “Max -- ≤ ”
互为对偶 (D) Min f = bT y s.t. AT y ≥ c y ≥0 “Min-- ≥”
线性规划的对偶模型
原问题(或对偶问题) 约束条件右端项 目标函数变量的系数 目标函数 max 约 束 条 件 m个 ≤ ≥ = n个 变 量 ≥0 ≤0 无约束 对偶问题(或原问题) 目标函数变量的系数 约束条件右端项 目标函数 min m个 ≥0 ≤0 无约束 n个 ≥ ≤ = 约 束 条 件 变 量
否
所有aik
计算
0
否
是
Hale Waihona Puke 0 bi be min aik 0 aik aek
计算
j min aej 0 k < aej aek
以为中心元素进行迭代
以为中心元素进行迭代
单纯形法和对偶单纯形法步骤
2.对偶单纯形法 对偶单纯形法的适用范围 对偶单纯形法适合于解如下形式 的线性规划问题
0 x4 0 1 0 0 0 1 0 0 0 1 0 0
0 x5 0 0 1 0 -1 -1 1 -100 -1 1 1 -50
I
θ i 300 400 250 50 75
对偶单纯形法
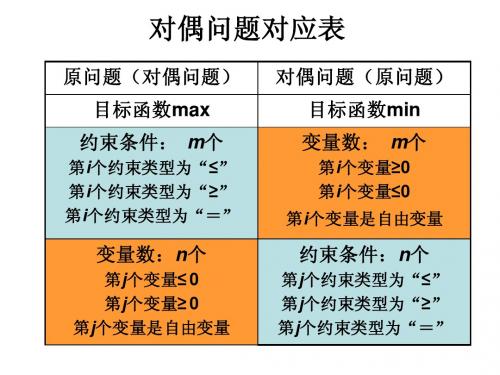
y4 y5 cj
-2 -1 0
15 24 5 y1 y2 y3 0 [-6] [- ] -1 -2 -1 -5 15 0 -5 15 -5/4 15/2 15/2 24 1 0 0 1 0 0 5 1/6 [-2/3] 1 0 1 0
0 y4 1 0 0 -1/6 -1/3 4
0 y5 0 1 0 0 1 0
C-CBB-1A≥0
对于标准线性规划问题:
min f = CX
max z = bY
s.t. AT Y ≥ C
AX = b s.t. X ≥ 0
最优基B
可行基B 对偶可行基B 单纯形法 保持可行性 对偶单纯形法 保持对偶可行性
可行基B
对偶可行基B
可行基B
对偶可行基B
对于标准线性规划问题:
min f = CX AX = b s.t. X ≥ 0
•
下面通过例题说明对偶单纯形法的步骤:
例3 用对偶单纯形法求解线性规划问题: min w = 15 y1 + 24 y2 + 5 y3
6 y2 + y3 ≥ 2 y1 + 2 y2 + y3 ≥ 1 :先将问题改写为:
' min w = 15 y1 + 24 y2 + 5 y3 min w = 15 y1 + 24 y2 + 5 y3 + 0 y4 + 0 y5
对偶单纯形法
对偶单纯形法并不是求解对偶问题解的方法,而是利 用对偶理论求解原问题的解的方法。 对于标准线性规划问题:
min f = CX AX = b s.t. X ≥ 0
max z = bY T s.t. A Y ≥ C
对偶单纯形法

把上述思想移植到对偶问题上。
对偶单纯形法迭代过程的实质是:保持对偶问题的可行性(只要检验数≤0即可), 通过改变对偶问题的可行基,使原问题由不可行变为可行。根据对偶理论,这两 个可行解就是原始和对偶问题的最优解。
例2.4.1 用对偶单纯形法求解下列线性规划问题。 min z = 15x1+24 x2 +5 x3
6 x2 + x3 ≥2
st.
5x1+2 x2 + x3 ≥1
x1 , x2 , x3 ≥0
解:把线性规划问题化为标准形式。
max z′ = -15x1-24 x2 - x3 +0 x4 +0 x5
-2/3是主元素, x3是换入变量。
ቤተ መጻሕፍቲ ባይዱj
-15 -24 - 5
CB
XB
b
x1
x2
x3
-24
x2 1/4
-5/4
1
0
表 11
0
0
x4
x5
-1/4 1/4
5
x3 1/2 15/2
0
1
1/2 -3/2
(cj-zj) 或 j
-15/2 0
0
-7/2 -3/2
由于原始,对偶都已经可行,所以,表11对应的解是最优解。
求极大为标准形式时
min j
c
j
arj
z
j
arj
0
cs zs ars
求极小为标准形式时
min j
z
j c arj
j
arj
0
用对偶单纯形法求解线性规划问题

用对偶单纯形法求解线性规划问题对偶单纯形法是一种常用于求解线性规划问题的方法。
它通过对原始线性规划问题进行对偶化,将原问题转化为对偶问题,并通过迭代的方式逐步优化,最终得到最优解。
本文将详细介绍对偶单纯形法的基本原理和步骤,并通过一个实例来演示其具体应用。
对偶单纯形法的基本原理是基于线性规划的对偶性理论。
根据对偶性理论,对于原始线性规划问题的最优解,一定存在一个对偶问题,其最优解与原问题的最优解相等。
因此,我们可以通过求解对偶问题来得到原问题的最优解。
对偶问题的形式如下:最大化 W = b'y约束条件为:A'y ≤ c其中,A是原始线性规划问题的约束矩阵,b是原始问题的目标函数系数矩阵,c是原始问题的约束条件矩阵,y是对偶问题的变量向量。
对偶单纯形法的步骤如下:步骤1: 初始化将原始线性规划问题转化为标准型,并初始化基变量和非基变量的初始解。
步骤2: 计算对偶变量值根据对偶问题的约束条件,计算对偶变量的初始值。
步骤3: 计算对偶目标函数值根据对偶问题的目标函数,计算初始的对偶目标函数值。
步骤4: 检验最优性判断当前解是否为最优解。
如果是,则终止算法;否则,进入下一步。
步骤5: 选择入基变量和出基变量根据当前解,选择一个入基变量和一个出基变量。
步骤6: 更新解通过列生成法或其他方法,更新当前解。
步骤7: 更新对偶变量和对偶目标函数值根据更新后的解,更新对偶变量和对偶目标函数值。
步骤8: 转至Step 4重复步骤4至步骤7,直到找到最优解。
下面以一个具体的线性规划问题为例来演示对偶单纯形法的应用。
假设有以下线性规划问题:最大化 Z = 3x1 + 5x2约束条件为:2x1 + x2 ≤ 10x1 + 3x2 ≤ 15x1, x2 ≥ 0首先,将原始问题转化为标准型:最大化 Z = 3x1 + 5x2约束条件为:2x1 + x2 + s1 = 10x1 + 3x2 + s2 = 15x1, x2, s1, s2 ≥ 0初始化基变量和非基变量的初始解为:x1 = 0, x2 = 0, s1 = 10, s2 = 15根据对偶问题的约束条件,计算对偶变量的初始值:y1 = 0, y2 = 0根据对偶问题的目标函数,计算初始的对偶目标函数值:W = 0检验最优性,发现当前解不是最优解,需要进入下一步。
16.对偶理论(三)对偶单纯形法

16.对偶理论(三)对偶单纯形法⼉童节快乐呀这⼀部分我们考虑原问题是标准型的问题,并且介绍对偶单纯形法。
在上⼀节的强对偶定理的证明中,对标准型问题使⽤单纯形法,定义了对偶变量p为p T=c T B B−1。
然后由原问题最优性条件c T−c T B B−1A≥0T得到了等价表达的对偶可⾏性条件p T A≤c T。
那么我们之前介绍的单纯形法可以看作是在保证原问题可⾏的前提下去寻找对偶可⾏的解。
那么反过来,我们也可以从对偶可⾏的前提下去寻找原问题可⾏的解,这种算法称为对偶算法。
在接下来,将介绍对偶单纯形法。
并且说明这个算法事实上求解了对偶问题,更近⼀步,它是从对偶问题的⼀个基本可⾏解移动到另⼀个。
对偶单纯形法考虑⼀个标准型的线性规划问题,假设矩阵A是⾏满秩(为什么这个假设具有⼀般性,可参考线性规划中的⼏何(三))。
记B为基本矩阵,它包含了矩阵A的m个线性⽆关的列。
考虑下表(与之前介绍的单纯形法中的表⼀样)更详细的有不过,在这⾥不再要求B−1b是⾮负的,那就说明此时的解是⼀个原问题的基本解但不⼀定是可⾏解。
但是,我们要求¯c≥0成⽴,也相当于p T A≤c T成⽴(具体见上⼀节强对偶定理证明)。
这说明现在有了⼀个对偶问题的可⾏解,并且对偶问题的⽬标函数值为p T b=c T B B−1b=c T B x B,这恰好就是上表中的左上⾓元素的相反数。
如果不等式B−1b≥0也成⽴,那么这个解也将是⼀个原问题的可⾏解,并且⽬标函数值相同,这说明我们找到了原问题和对偶问题的最优解。
如果不等式B−1b≥0并不成⽴,那么我们将寻找下⼀个基矩阵。
找到满⾜x B(l)<0的l,考虑表中的第l⾏为pivot ⾏(x B(l)),v1,⋯,v n),其中v i为B−1A i的第l个元素。
对于满⾜v i<0的所有i(如果存在的话),我们计算⽐率¯c i/|v i|,然后记j为这些⽐率中最⼩的那个的下标(为什么这么选呢,后⾯会说),也就是说v j<0且¯cj|v j|=min{i∣v i<0}¯ci|v i|.称v j为pivot 元素。
数学LP对偶单纯形法

4
4
12
MRT
0
20 11
0 0 4 4 2 -14
1 -4 4 1 -1 1 0 4 -2 -1 1/2 1/2
用对偶单纯性算法计算
min x1 2 x2
s.t .
x1
1,
x2 1,
x1
x2
1.5,
x 0.
初始对偶基本可行解的基为B {1,2,5}
第一个对偶基本可行解的求法
任选基矩阵AB ,则典式为
min z cBT AB1b (cN T cBT AB1 AN ) xN
s.t. xB AB1b AB1 AN xN , xB 0, xN 0. 若 j 0, j N;则yB ABTcB为对偶bfs.
若 j 0, j N;增 加 一 个 变 量xn1和 一 个 约 束
x j xn1 M (充 分 大).
注意到:(1) 0; (2)(AB1b)o 0
(1)aoi 0, i N .增加任何一个非基变量xe (e N )都不能改善 基本解x的不可行性,即原问题不可行。
(2)j N , 使得aoj 0, 从0开始慢慢增加对应的非基变量x j
则基本解xB的第o个分量也会增加,直到为非负数。
xj能增加到多少?要保持 0,
2 x1 2 x2 4x4 3, x0
解: 标准型为 min 12x1 8x2 16x3 12x4 s.t. 2x1 x2 4x3 - x5 2,
2x1 2x2 4x4 x6 3, x0
解: 标准型为
min 12x1 8x2 16x3 12x4
s.t. 2x1 x2 4x3 - x5 2,
若 sN的所有分量均不为零,称 y是非退化的。
若 AB 对应的原始基本解和对偶基本解都是非退化的, 称AB 为非退化基。
2对偶单纯形法

对偶问题的经济解释-影子价格
3)影子价格在资源利用中的应用 根据对偶理论的互补松弛性定理: Y*Xs=0 , YsX*=0
Page 5
表明生产过程中如果某种资源bi未得到充分利用时,该种 资源的影子价格为0;若当资源资源的影子价格不为0时,表明 该种资源在生产中已耗费完。
对偶问题的经济解释-影子价格
Page 15
学习要点:
1. 线性规划解的概念以及3个基本定理
2. 熟练掌握单纯形法的解题思路及求解步骤
λj
对偶单纯形法
cj cB xB -9 x1 -12 x2 -15 x3 0 x4 0 x5 0 x6 b
Page 11
i
0
0 -15
x4
x5 x3
-9/5
-9/5 1/5 -6
-9/5
-14/5 1/5 -9 -12 -15
0
0 1 0 0
1
0 0 0 0
0
1 0 0
-1/5
-1/5 -1/5 -3 0
初始表中一定要满足对偶问题可行,也就是说检验数满足最优判别 准则
最小比值中
aij<0 这时必须取绝对值。在极大化问题中,σj≤0,分母aij<0, 写成
aij
的绝对值是使得比值非负,在极小化问题σj≥0,分母
总满 a
ij
j
j
足非负,这时绝对值符号不起作用,可以去掉。如在本例中将目标函数
max z' 4 x1 x2 3 x3
max Z CX AX b P X 0 minW Yb YA C D Y 0
n m j 1 i 1
由对偶问题得基本性质可得: z c j x j bi yi
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单纯形法计算对偶变量值
以单纯形法计算对偶变量值
在线性规划中,单纯形法是一种常用的求解最优解的方法。
对于一个线性规划问题,除了求出最优解外,还可以通过单纯形法计算对偶变量的值。
本文将介绍单纯形法的基本原理,并详细讲解如何计算对偶变量的值。
单纯形法的基本原理是通过不断迭代改进当前解,直到找到最优解。
在这个过程中,我们需要引入对偶问题。
对偶问题是原始问题的一种等价形式,通过对原始问题进行变换得到。
对偶问题可以用来检验原始问题的最优解,并且可以计算出对偶变量的值。
我们需要了解什么是对偶问题。
对于一个线性规划问题,如果原始问题是最大化问题,则对偶问题是最小化问题;如果原始问题是最小化问题,则对偶问题是最大化问题。
对偶问题的约束条件是原始问题的目标函数的系数,而对偶问题的目标函数的系数是原始问题的约束条件。
通过这种变换,我们可以得到原始问题和对偶问题之间的对应关系。
在单纯形法中,我们首先需要求解原始问题的最优解。
通过迭代的方式,不断改进当前解,直到找到最优解。
在每一次迭代过程中,我们需要计算对偶变量的值。
对偶变量是对偶问题中的变量,表示对应约束条件的价格。
计算对偶变量的值的方法是通过计算最终的单纯形表格得到。
单纯形表格是单纯形法中用来记录每一次迭代过程的表格,其中包含了原始问题和对偶问题的所有信息。
通过对最终的单纯形表格进行分析,我们可以得到对偶变量的值。
在单纯形表格中,对偶变量的值可以通过检查对应约束条件的松弛变量的值来计算。
松弛变量是为了将约束条件转化为等式形式而引入的变量。
如果松弛变量的值为0,则对应约束条件的对偶变量的值为非零;如果松弛变量的值不为0,则对应约束条件的对偶变量的值为0。
通过以上步骤,我们可以计算出对偶变量的值。
对偶变量的值可以用来检验原始问题的最优解的可行性,并且可以提供额外的信息来解释最优解。
对偶变量的值越大,说明对应约束条件的限制越紧,对最优解的影响越大;对偶变量的值越小,说明对应约束条件的限制越松,对最优解的影响越小。
通过单纯形法可以求解线性规划问题的最优解,并且可以计算出对偶变量的值。
对偶变量的值可以用来检验最优解的可行性,并且可以提供额外的信息来解释最优解。
通过对最终的单纯形表格进行分析,我们可以得到对偶变量的值,并且可以进一步优化我们的决策过程。
在实际应用中,单纯形法是一种非常有效的求解线性规划问题的方
法。
通过计算对偶变量的值,我们可以更好地理解问题,并且可以得到更全面的解释和分析。
因此,掌握单纯形法并能够计算对偶变量的值对于线性规划问题的求解非常重要。
希望本文能够对读者有所帮助,谢谢阅读!。
