单纯形法基本原理
单纯形法原理
单纯形法原理单纯形法，求解线性规划问题的通用方法。
单纯形是美国数学家G.B.丹齐克于1947年首先提出来的。
它的理论根据是：线性规划问题的可行域是n维向量空间Rn中的多面凸集，其最优值如果存在必在该凸集的某顶点处达到。
顶点所对应的可行解称为基本可行解。
单纯形法的基本思想是：先找出一个基本可行解，对它进行鉴别，看是否是最优解；若不是，则按照一定法则转换到另一改进的基本可行解,再鉴别；若仍不是，则再转换,按此重复进行。
因基本可行解的个数有限，故经有限次转换必能得出问题的最优解。
如果问题无最优解也可用此法判别。
单纯形法是从某一基可行解出发，连续地寻找相邻的基可行解，直到达到最优的迭代过程，其实质是解线性方程组。
概述：根据单纯形法的原理，在线性规划问题中，决策变量（控制变量）某1，某2，…某n的值称为一个解,满足所有的约束条件的解称为可行解。
使目标函数达到最大值（或最小值）的可行解称为最优解。
这样，一个最优解能在整个由约束条件所确定的可行区域内使目标函数达到最大值（或最小值）。
求解线性规划问题的目的就是要找出最优解。
最优解可能出现下列情况之一：①存在着一个最优解；②存在着无穷多个最优解；③不存在最优解，这只在两种情况下发生，即没有可行解或各项约束条件不阻止目标函数的值无限增大（或向负的方向无限增大）。
单纯形法的一般解题步骤可归纳如下：①把线性规划问题的约束方程组表达成典范型方程组，找出基本可行解作为初始基本可行解。
②若基本可行解不存在，即约束条件有矛盾，则问题无解。
③若基本可行解存在，从初始基本可行解作为起点，根据最优性条件和可行性条件，引入非基变量取代某一基变量，找出目标函数值更优的另一基本可行解。
④按步骤3进行迭代,直到对应检验数满足最优性条件（这时目标函数值不能再改善），即得到问题的最优解。
⑤若迭代过程中发现问题的目标函数值无界，则终止迭代。
用单纯形法求解线性规划问题所需的迭代次数主要取决于约束条件的个数。
单纯形法基本原理
否
含 有xa
是 无可行解
(a对ik
0 任一
j 0)
否
是 无界解
有某个 否 非基变量的
j 0
唯一 最优解
是
无穷多
最优解
循
环
停止
计 算 i
( bi alk
alk
0)
用 非 基 变 量xk 替 换 基 变 量xl
列出下一个 新单纯形表
单纯形法的进一步讨论－人工变量法 Page 17
解的判别： 1）唯一最优解判别：最优表中所有非基变量的检验数非零, 则线 规划具有唯一最优解。 2）多重最优解判别：最优表中存在非基变量的检验数为零, 则线则性规划具有多重最优解（或无穷多最优解）。 3）无界解判别：某个λk>0且aik≤０（i=1，2,…,m）则线性 规划具有无界解。 4）无可行解的判断：当用大M单纯形法计算得到最优解并 且存在Ri>0时，则表明原线性规划无可行解。 5）退化解的判别：存在某个基变量为零的基本可行解。
max Z 3 x1 4 x2
2x1 x2 40
x1
3x2
30
x1
,
x2
0
解：1）将问题化为标准型，加入松驰变量x3、x4则标准型为:
max Z 3 x1 4 x2
2 x1 x2 x3 40
ቤተ መጻሕፍቲ ባይዱ
x
1
3x2
x4
30
x1
,
x2
,
x3
换
x3
x4
出
1
0
40 行
0
1
1-3 单纯形法原理
由于任意系数列向量均可由基向量组线性表示，则非基向 量中的 Pj 用基向量组线性表示为：
Pj a ijPi
i 1
2017/5/5
m
Pj a ijPi 0,
i 1
m
( j m 1,...,n )
12
设有 0，则
( Pj aij Pi ) 0
i 1
只要取
(0) (0) x x min i aij 0 l 为
正，于是非零分量的个数
m
，并可证得
P P2 ... Pl 1 Pl 1 ... Pm , Pj 1
线性无关，所以 X (1) 是新的基可行解。
2017/5/5
a12 a22
a1n a2 n
am 2 amn
1 0 0 0 1 0 0 0 1
9
由于该矩阵含有一个单位子矩阵，因此，这个单位阵就是一组 基，就可以求出一个基可行解：
X 0,,0, b1,, bm
令：X X (1) (1 ) X ( 2 )
0 1
则AX A(X (1) (1 ) X ( 2 ) ) AX (1) AX ( 2 ) AX ( 2 ) b
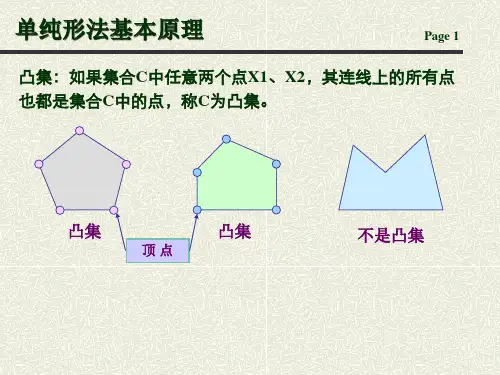
X C C 为凸集
引理：线性规划问题的可行解X＝(x1,x2,……xn)为基可行解的充要条件是 X的正分量所对应的系数列向量是线性独立的（所组成的矩阵是非奇 异的）。
11
由构造初始可行基的方法知前m 个基向量恰好是一个单位
阵，所以约束方程组的增广矩阵为
P1 P2 ... Pm Pm1 ... Pj ... Pn b
1 0 ... 0 0 ... 0 1 ... 0 ... ... ... 0 ... 1 a1,m 1 ... ... a1, j ... ... a2,m 1 ... a2, j am,m 1 ... am , j ... a1,n b1 ... a2,n b2 ... ... ... ... am,n bm
单纯形法的基本原理
单纯形法的基本原理单纯形法是一种用于求解线性规划问题的数学方法，它的基本原理是通过不断地移动解空间中的顶点来逼近最优解。
在解决实际问题中，我们经常会遇到一些资源有限，而需要在这些资源限制下最大化或最小化某个指标的情况，这时就需要用到线性规划问题。
而单纯形法正是针对这类问题提出的一种高效的求解方法。
单纯形法的基本原理可以用几个关键步骤来概括。
首先，我们需要将线性规划问题转化为标准型，即目标函数为最大化，约束条件为等式的形式。
接着，我们需要找到一个初始可行解，这个可行解需要满足所有的约束条件。
然后，我们通过一系列的基本变量的替换，不断地移动解空间中的顶点，直到找到最优解为止。
在单纯形法中，我们需要利用单纯形表来进行计算。
单纯形表是一个表格，其中包含了目标函数、约束条件、基本变量等信息。
通过对单纯形表的不断变换和计算，我们可以逐步逼近最优解。
在每一步的计算中，我们需要选择一个入基变量和一个出基变量，通过一系列的行变换和列变换来更新单纯形表，直到找到最优解为止。
单纯形法的基本原理虽然看起来比较复杂，但实际上它是建立在一些简单的数学原理之上的。
通过对解空间中的顶点进行移动，我们可以逐步逼近最优解，这是单纯形法能够高效求解线性规划问题的关键所在。
在实际应用中，单纯形法已经被证明是一种非常有效的方法，它可以帮助我们在资源有限的情况下做出最优的决策。
总的来说，单纯形法是一种用于求解线性规划问题的高效方法，它的基本原理是通过不断地移动解空间中的顶点来逼近最优解。
通过对单纯形表的计算和变换，我们可以逐步找到最优解。
在实际应用中，单纯形法已经被广泛地应用于各个领域，它为我们解决资源有限的最优化问题提供了一个强大的工具。
希望本文对单纯形法的基本原理有所帮助，谢谢阅读！。
运筹学-第一章-单纯形法基本原理
X ( 0) ( x1 , x2 ,, xm ,0,0,...,0)T (b1 , b2 ,......,bm ,0,0,...,0)T
0
0
0
单纯形法基本原理
2、基变换 定义：两个基可行解称为相邻的，如果它们之间变换 且仅变换一个基变量。 初始基可行解的前m个为基变量，
X
凸集
顶点
凸集
不是凸集
顶点：如果凸集C中不存在任何两个不同的点X1，X2，使X 成为这两个点连线上的一个点
单纯形法基本原理
定理1：若线性规划问题存在可行解，则该问题的可行域是 凸集。 定理2：线性规划问题的基可行解X对应可行域(凸集)的顶 点。 定理3：若问题存在最优解，一定存在一个基可行解是最优 解。（或在某个顶点取得）
的左边变成一个单位矩阵，
b (b1 a1 j ,.,bl 1 al 1 j , , bl 1 al 1 j ,.,bm am1 j , ) ( x1 , x2 ,..., xl 1 , x j , xl 1 ,..., xm )
X
(1)
T
与X
( 0)
是相邻的基可行解。
M M bm 0 L
M M
M M
L 1 am,m1 L L 00
M , M amn m
bi 其中： i a kj 0 a kj
j c j ci aij c j z j
单纯形法的计算步骤
例1.12 用单纯形法求下列线性规划的最优解
max Z 3 x1 4 x 2 2 x1 x 2 40 x1 3 x 2 30 x , x 0 1 2
xi0 aij 0, aij 0,取值无限，
运筹学第5章 单纯形法
0 0 1
在第一次找可行基时，所找到的基或为单位矩阵或为由单位矩阵的 各列向量所组成，称之为初始可行基，其相应的基本可行解叫初始基 本可行解。如果找不到单位矩阵或由单位矩阵的各列向量组成的基作 为初始可行基，我们将构造初始可行基，具体做法在以后详细讲述。
8Leabharlann §1 单纯形法的基本思路和原理
二、 最优性检验 所谓最优性检验就是判断已求得的基本可行解是否是最优解。
5
§1 单纯形法的基本思路和原理
线性规划解之间的关系：
1.可行解与最优解： 最优解一定是可行解，但可行解不一定是最优解。
2. 可行解与基本解： 基本解不一定是可行解，可行解也不一定是基本解。
3. 可行解与基本可行解： 基本可行解一定是可行解，但可行解不一定是基本可行解。
4. 基本解与基本可行解： 基本可行解一定是基本解， 但基本解不一定是基本可行解。
9
§1 单纯形法的基本思路和原理
2.最优解判别定理
对于求最大目标函数的问题中，对于某个基本可行解，如
果所有检验数 j≤0，则这个基本可行解是最优解。 下面我
们用通俗的说法来解释最优解判别定理。设用非基变量表示
的目标函数为: z z0 j xj jJ 由于所有的xj的取值范围为大于等于零，当所有的 j都小
由线性代数的知识知道，如果我们在约束方程组系数矩阵中找
到一个基，令这个基的非基变量为零，再求解这个m元线性方程组就
可得到唯一的解了，这个解我们称之为线性规划的基本解。
在此例中我们不妨找到
1 1 0 B3 1 0 0
为A的一个基，令这个基的非
1 0 1
基变量x１，s2为零。这时约束方程就变为基变量的约束方程：
第五章 单 纯 形 法
运筹学单纯形法
单纯形表
max z=x1+2x2 s.t. x1+x23 x2 1 x1, x2 0
Cj CB XB b 0 0 Z X3 3 X4 1 0 1 2 0 0
标准化
max z=x1+2x2 s.t. x1+x2+ x3 =3 x2 +x4=1 x1, x2 ,x3, x40
X1 X2 X3 X4 1 0 1 1 1 2 1 0 0 0 1 0
Z=x1+2x2 x1+x2+ x3 =3 x2 +x4=1 单纯形表
Cj
1
2
0
0
单纯形法原理 单纯形表 CB XB b
z=x1+2x2 x3 =3-x1-x2 x4=1 -x2
x2进基，x4离基
X1 X2 X3 X4
3/1 11
0
1 0
1 1
1 1
2 2 0 1 0 2 0 1 0 0 1 0 -1 0
max z=x1+2x2 s.t. x1+x2+x3 =3 x2 +x4=1 x1, x2, x3, x40
x1=0
(x1,x2,x3,x4)= (0,1,2,0), z=2 C (x1,x2,x3,x4)= (2,1,0,0), z=4,最优解
B
x4=0 x3=0
(x1,x2,x3,x4)= (0,0,3,1), z=0
1 0
0 0
0 1
0
CB XB b 0 2 Z Cj CB XB b 1 2 Z X1 2 X2 1 4 X3 2 X2 1 2 1 1 0 0
X1 X2 X3 X4 1 0 1 1 0 0 0 -1 1 -1
单纯形法原理 单纯形表
单纯形法原理单纯形表单纯形法原理与单纯形表的详实解析在数学领域中，特别是在线性规划问题的研究中，单纯形法是一种十分重要的求解方法。
它是由美国数学家乔治·丹齐格在1947年提出的一种迭代算法，用于解决具有多个变量和约束条件的优化问题。
本文将围绕单纯形法的原理和单纯形表这两个核心概念进行详细的解析。
一、单纯形法原理单纯形法的基本思想是通过一系列可行解逐步逼近目标函数的最大值或最小值。
这些可行解形成一个点集，称为单纯形。
每次迭代过程中，算法都会选择一个新的顶点作为下一个单纯形的顶点，这个新的顶点应该使目标函数有所改进。
重复这一过程，直到达到最优解或者满足停止准则为止。
单纯形法的步骤如下：1. 构造初始单纯形：首先，需要找到一个包含至少两个可行解的多边形，这就是初始单纯形。
2. 判断是否达到最优解：如果当前顶点的目标函数值已经是全局最优解，那么算法结束。
3. 选择换入变量：如果当前顶点不是最优解，那么需要选择一个非基变量来替换基变量。
这个被选中的非基变量应该是能够使目标函数最大化的变量。
4. 计算换出变量：确定了换入变量后，需要计算相应的换出变量。
这可以通过解一个线性方程组来实现。
5. 更新单纯形：用新选出的变量替换旧的变量，得到新的单纯形。
6. 回到第二步，继续判断是否达到最优解。
二、单纯形表单纯形表是单纯形法的重要工具，它记录了单纯形法每一步的详细信息。
每个列代表一个基变量，而每个行则代表一个约束条件。
表中还包括目标函数的系数、常数项以及松弛变量和剩余变量的系数。
在单纯形表中，每一行代表一个约束条件，包括它的系数、常数项以及松弛变量和剩余变量的系数。
每一列则代表一个基变量，包括它的系数和该变量对应的值。
在每一步迭代过程中，单纯形表都会被更新以反映当前的解状态。
通过观察单纯形表的变化，我们可以清楚地看到迭代过程是如何进行的，以及如何通过调整基变量来改进目标函数的值。
总结来说，单纯形法是一种有效的解决线性规划问题的方法，其核心在于构造并不断更新单纯形表，通过迭代寻找最优解。
simplex 单纯形法
simplex 单纯形法单纯形法（Simplex Algorithm）是一种用于线性规划问题求解的有效算法。
它由美国运筹学家Dantzig于1947年提出，被广泛应用于工业生产优化、资源分配、物流管理等领域。
本文将介绍单纯形法的基本原理、步骤与应用，并探讨其优缺点。
一、基本原理单纯形法是通过不断地在可行解空间中移动来逼近最优解的方法。
该方法从一个初始可行解出发，通过一系列迭代操作，每次改变一个基本变量以达到更优的目标函数值。
最终，算法将找到一个全局最优解或者判断问题无界或无可行解。
二、基本步骤1. 线性规划标准形式化：将线性规划问题转化为标准形式，即目标函数最小化，约束条件为线性等式。
2. 初始可行解：找到一个满足约束条件的初始可行解，并将其称为基本可行解。
3. 进行迭代操作：通过改变基本变量来改善目标函数值，直到达到最优解或者判断问题无界或无可行解。
4. 基本变量的选择：在每一次迭代中，选择一个非基本变量作为入基变量，并选取一个基本变量作为出基变量。
5. 确定迭代终止条件：判断是否终止迭代，若目标函数值无法继续改善或者判断问题无界或无可行解，则终止迭代。
6. 输出最优解：若找到了最优解，输出最优解及最优目标函数值。
若判断问题无界或无可行解，则给出相应的判断结果。
三、应用领域单纯形法广泛应用于工业生产优化、资源分配、物流管理等领域。
以下是一些典型应用案例：1. 生产计划优化：通过使用单纯形法，可以优化生产计划以最大化产出，同时考虑资源约束和成本限制。
这对于提高生产效率和降低成本非常重要。
2. 物流网络优化：单纯形法可以帮助优化物流网络的设计和运作，以最小化物流成本、最大化物流效率，并满足客户需求。
3. 能源系统调度：单纯形法可以应用于能源系统的调度问题，包括电力系统、天然气输送网络等，以最大化供应效率，并解决资源分配和运营问题。
4. 金融投资组合优化：通过单纯形法，可以优化金融投资组合以最大化收益或最小化风险，并满足投资者的需求。
运筹学单纯形法
16
三、其他解旳情况 1、无穷多种解 例2 解LP问题：
min Z x1 2 x2 x3 0 x4 0 x5
xx51
1 2c 5 3c
其中c是满足非负性旳任意常数。
21
再由
x1,
x5
旳非负性，知：
x1 x2
1 2c c
0 0
x5 5 3c 0
解出 0 c 5 3
最优解为：
(2c 1, c,0,0,5 3c)T （其中0 c 5 ）
3
最优值为：max S 1.
22
2、无最优解旳两种情况：
相应地，将 X 0代入目的函数得 Z ( X 0 ) 0
从数学角度看，若让非基变量 x1, x2 取值从零增长，
6
min Z 2x1 x2 0x3 0x4 0x5
相应旳目旳函数值Z也将随之降低。所以有可能找到一种 新旳基本可行解，使其目旳函数值有所改善。即进行基变
换，换一种与它相邻旳基。再注意到 x1 前旳系数－2比 x2
x3
6 x1 x1
2x2 x2
x4 x5
xi 0
i 1,,5
15 24 5
目前可行基{ x3, x4 , x5 }所相应旳基本可行解
X 0 (0,0,15,24,5)T
(相应可行域旳 o(0,0) )
显然不是最优。 因为从经济意义上讲， x1 0, x2 0
意味着该厂不安排生产，所以没有利润。
2
单纯形法原理及例题
单纯形法原理及例题
单纯形法原理：
单纯形法是求解线性规划问题的一种数学方法，它是由美国数学家卢克·单纯形于1947年发明的。
用单纯形法求解线性规划的过程，往往利用线性规划的对偶形式，将原问题变换为无约束极大化问题，逐步把极大化问题转换为标准型问题，最后利用单纯形法的搜索方法求解满足所有约束条件的最优解。
例题：
问题：求解最小化目标函数z=2x1+x2的线性规划问题，约束条件如下：
x1+2x2≥3
3x1+x2≥6
x1,x2≥0
解：将上述线性规划问题转换为无约束极大化问题，可得：
极大化问题：
Max z=-2x1-x2
s.t. x1+2x2≤3
3x1+x2≤6
x1,x2≥0
将极大化问题转换为标准型问题，可得：
Max z=-2x1-x2
s.t. x1+2x2+s1=3
3x1+x2+s2=6
x1,x2,s1,s2≥0
运用单纯形法的搜索方法求解：
令x1=0,x2=0，则可得s1=3,s2=6，即(0,0,3,6)是单纯形的初始解；
令z=-2x1-x2=0，代入约束条件，可得x1=3,x2=3，则可得s1=0,s2=0，即(3,3,0,0)是新的单纯形解。
由于s1=s2=0，说明x1=3,x2=3是线性规划问题的最优解，且最小值为z=2*3+3=9。
单纯形法原理
单纯形法原理
单纯形法是线性规划中常用的一种方法，用于求解极值问题。
它的基本思想是通过不断迭代的方式，逐渐接近最优解。
单纯形法的基本步骤如下：
1. 将线性规划问题转化为标准型。
标准型的约束条件为≤，目标函数为最大化，且所有变量的取值范围为非负数。
2. 利用人为变量引入的方法，将标准型问题转化为初始单纯形表。
3. 选择合适的初始基变量，并计算出对应的基变量解。
4. 计算单纯形表中的评价函数。
如果所有评价函数中的系数都为非负数，则当前基变量解为最优解，过程结束。
否则，继续进行下一步。
5. 选择进入变量和离开变量。
进入变量是指取值为负的评价函数系数对应的变量，离开变量是指进入变量在当前基变量解中最先达到0的变量。
6. 迭代计算，通过变换基变量，逐渐接近最优解。
具体的计算方式为将进入变量对应列调整为单位向量，同时更新初始单纯形表中其它列的数值。
7. 重复步骤4至步骤6，直至得到最优解为止。
值得注意的是，单纯形法的执行依赖于初始基变量的选择，不同的初始基变量可能会得到不同的最优解。
因此，在实际应用中，需要通过灵活选择初始基变量来提高求解效果。
单纯形法
矩阵A表示为： A = ( p1 ，p2 ，…，pn ) ， 其中 pj = ( a1j ，a2j ，…，amj )T。若找 到一个可行基，无防设 B = ( p1 ，p2 ，…，pm ) ，则m个基变 量为 x1 , x2 , …, xm，n-m个非基变量 为 xm+1 ，xm+2 ，…，xn 。通过运算， 所有的基变量都可以用非基变量来表 示：
f(x
6 )=3
二、单纯形法的基本思路 要找到线性规划问题的最优解，只要在基本 可行解中寻找就可以了。虽然基本可行解的数 目是有限个（不超过Cnm个），但当m,n较大时， 要用“穷举法”求出所有基本可行解是行不通 的。利用LP问题基本可行解（极点）的方法来 求解较大规模的问题是不可行的。 单纯形法的基本思路是：从线性规划问题的 一个基本可行解开始，沿边界转换到另一个使 目标函数值增大的基本可行解。反复迭代，直 到目标函数值达到最大时，就得到了最优解。
基本解 对于基B，令非基变量为零，求得满足AX=b的解,称 为基B对应的基本解。若得到的基变量的值均非负， 则称为基本可行解，同时称这个基B为可行基。 令非基变量 XN = 0，求得基变量 XB的值称为基本解 即 XB = B1 b XB 是基本解的必要条件为XB 的非零分量个数 m 基本可行解 基本解 XB 的非零分量都 0 时，称为基本可行解， 否则为基本非可行解 基本可行解的非零分量个数 < m 时，称为退化解
2.线性规划的基、基本解与基本可行解
基：设B是A矩阵中的一个非奇异（可逆）的 m×m子矩阵，则称B为线性规划的一个基。 与B中的这些列向量对应的变量称为基变量， m Cm n 个基。 其余变量称为非基变量。最多有
在标准型中，技术系数矩阵有 n×m 列，即 A = ( P1, P2 , … , Pn×m ) A中线性独立的 m 列，构成该标准型的一个基， 即 B = ( P1 , P2 , … , Pm )， | B | 0 P1 , P2 , … , Pm 称为基向量 与基向量对应的变量称为基变量，记为 XB = ( x1 , x2 , … , xm )T，其余的变量称为非基变 量，记为 XN = ( xm+1 , xm+2 , … , xm+n ) T ， 故有 X = XB + XN m Cm n 个基 最多有
单纯形算法的一般原理
单纯形算法的一般原理单纯形法的基本思路是有选择地取基本可行解，即是从可行域的一个极点出发，沿着可行域的边界移到另一个相邻的极点，要求新极点的目标函数值不比原目标函数值差。
考虑到如下线性规划问题：其中Ａ一个m ×n 矩阵，且秩为m ，ｂ总可以被调整为一个m 维非负列向量，Ｃ为n 维行向量，Ｘ为n 维列向量。
根据线性规划基本定理：如果可行域Ｄ={ Ｘ∈Ｒn / ＡＸ=ｂ，Ｘ≥0}非空有界，则Ｄ上的最优目标函数值Ｚ=ＣＸ一定可以在Ｄ的一个顶点上达到。
这个重要的定理启发了Dantzig 的单纯形法，即将寻优的目标集中在D 的各个顶点上。
Dantzig 的单纯形法把寻优的目标集中在所有基本可行解（即可行域顶点）中。
其基本思路是从一个初始的基本可行解出发，寻找一条达到 最优基本可行解的最佳途径。
单纯形法的一般步骤如下：（1）寻找一个初始的基本可行解。
（2）检查现行的基本可行解是否最优，如果为最优，则停止迭代，已找到最优解，否则转一步。
（3）移至目标函数值有所改善的另一个基本可行解，然后转会到步骤（2）。
求解思想如下图所示：maxZ=CX AX=b X 0⎧⎨≥⎩确定初始的基本可行解等价于确定初始的可行基，一旦初始的可行基确定了，那么对应的初始基本可行解也就唯一确定为了讨论方便，不妨假设在标准型线性规划中，系数矩阵Ａ中前m 个系数列向量恰好构成一个可行基，即Ａ=（ＢＮ），其中Ｂ=（Ｐ1，Ｐ2，…Ｐm ）为基变量x1，x2，…xm 的系数列向量 构成的可行基，Ｎ=(Ｐm+1，Pm+2， …Pn)为非基变量xm+1，xm+2， …xn 的 系数列向量构成的矩阵。
那么约束方程AX=b 就可表示为：用可行基Ｂ的逆阵Ｂ-1左乘等式两端，再通过移项可推得：若令所有非基变量 ，则基变量由此可得初始的基本可行解B B N N X AX=(BN)=BX +NX =b X ⎛⎫ ⎪⎝⎭-1-1B N X =B b-B NX N X =0-1B X =B b 1B b X=0-⎛⎫ ⎪⎝⎭-1-1-1B N B N N B AX=b BX +NX =b X =B b-B NX X =0,X =B b →→→● 问题：要判断m 个系数列向量是否恰好构成一个基并不是一件容易的事。
单纯形法的原理
单纯形法是一种线性规划的求解方法，其基本思想是在线性规划问题的可行域内，通过不断迭代，逐步找到最优解。
单纯形法的原理可以概括为以下几个步骤：1. 确定线性规划问题的可行域：对于一个线性规划问题，首先需要确定其可行域，即所有满足约束条件的解的集合。
可行域通常是一个凸多边形，也可以表示为一个凸锥。
2. 确定初始基：在单纯形法中，我们需要选取一个初始基，即一个初始的可行解，来开始迭代过程。
初始基可以是一个非基变量为零的点，也可以是通过某种启发式算法得到的一个初始可行解。
3. 判断最优解：在得到初始基之后，我们需要判断该基是否是最优解。
如果该基对应的目标函数值已经满足要求，则该基是最优解。
否则，我们需要找到一个非基变量，其对应的系数在约束条件下最小，来继续迭代。
4. 确定换入变量：在找到一个非基变量后，我们需要确定一个换入变量，即需要被替换掉的那个基变量。
通常情况下，我们选择当前基中对应的系数最小的非基变量作为换入变量。
5. 进行迭代：在确定了换入变量之后，我们需要进行迭代，将当前基中的某个基变量替换为非基变量，得到一个新的基。
具体来说，我们可以使用高斯消元法来计算新的基变量的系数，并更新当前基的矩阵表示。
6. 判断收敛：在完成一次迭代后，我们需要判断当前基是否已经收敛到最优解。
如果当前基已经满足精度要求，或者达到了一定的迭代次数上限，我们可以认为已经找到了最优解，停止迭代。
否则，我们需要回到步骤3，继续迭代过程。
单纯形法的原理比较简单，其核心思想是通过不断迭代，逐步逼近最优解。
该方法具有良好的数值稳定性和广泛的应用范围，是求解线性规划问题的一种常用方法之一。
需要注意的是，在实际应用中，单纯形法可能会面临一些问题，例如初始基的选择、系数矩阵的奇异性等问题，需要进行一定的处理和优化。
除了单纯形法外，还有许多其他的线性规划求解方法，例如内点法、外点法、椭球算法等。
这些方法各有优缺点和适用范围，可以根据具体问题的特点进行选择和组合使用。
单纯形法、大M法
单纯形法、大M法单纯形法是一种线性规划算法，通常用于寻找线性规划问题的最优解。
它的基本思想是在约束条件下，寻找目标函数的最大值或最小值。
单纯形法是由美国数学家乔治·达内在1947年提出的，是目前应用最广泛的解线性规划问题的方法之一。
单纯性法的原理是基于一个立方体模型的，该模型由各种小三角形组成。
每个三角形都是由原问题的一个约束条件所定义的平面，当这些平面被绘制时，它们会将立方体分成多个小三角形。
在这个模型中，每个小三角形代表了原问题的一个可行解，即满足所有约束条件的解。
最初的解法是从任意一个可行解作为起始点，通过一系列变形（称为单纯形变换）来寻找可行解中的最优解。
这个过程可以看作是在不断地将一个小三角形变形成另一个小三角形的过程。
具体而言，我们会找到一个角点（即可行解的某个顶点），然后对它进行变形，通过不断调整其他的角点直到得到一个更优的可行解。
在单纯性法的过程中，还有一些其他的要点需要注意。
首先，我们需要选择一个合适的起始点。
通常情况下，我们会选择一个位于可行域的角点，这可以通过求解一个最小化问题来实现。
其次，每一次变形都会改变模型中三角形表面的形状，从而使得原来的角点可能不再是新的最优解。
因此，在每次变形后，我们需要重新计算通过各个角点可以到达的最优解，然后再进行变换。
最后，为了保证算法能够收敛，需要对一些特殊情况进行处理，比如出现无界解或无可行解的情况。
尽管单纯性法是目前应用最广泛的线性规划算法之一，但它也存在一些问题。
比如，它对于非特定类型的问题来说，可能会产生较低的收敛速度，尤其是在高维空间中更为明显。
此外，如果问题的可行域非常大，那么单纯形法可能需要很长的计算时间才能找到最优解。
因此，针对这些问题，研究人员提出了一些改进的方法，比如内点法、动态规划等。
大M法是一种针对线性规划问题的算法，它可以将不等式约束转化为等式约束，从而使问题更容易求解。
大M法是一种通用方法，可以用于解决任何线性规划问题，不论其约束条件是等式还是不等式形式。
5-1-单纯形法-方法原理
Y
D扩张到E，PD=DE
D比B好
E比B好 N
Y
Y
ABD
ABE
…
AFD
…
…
…
N
D比C好
Y
收缩 DG=GP
ABG
… …
y
F
E
A
D
G P
N
H C
B
x
收缩 PH=HC
ABH
… …
图6-2 单纯形规则示意图
单纯形法——方法原理
在单纯形的推移过程中，新实验点在空间的位 置坐标按以下方法计算：
[新试点的坐标]＝(1+a)
[留下各点的坐标和] n源自a [去掉点的坐标]a＝1，反射，基本单纯形 a>1， 扩张 -1<a<0，内收缩 0<a<1，收缩
单纯形表
有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）
单纯形法——程序框图
课程教案
最优化方法在化学化工中的应用简介
单纯形法——方法原理
单纯形法——方法原理
单纯形法是一种优化设计方法
特点：
计算简便 不受因素数的限制 因素数的增加不会导致试验次数大量增加
单纯形法——方法原理
发展简史
1962年，Spendley提出基本单纯形法 1965年，Nelder等提出改进单纯形法 之后，Routh提出加权形心法与控制加权形心 法
不用求导，甚至没有目标函数表达式时也可使用。
单纯形法——方法原理
单纯形的寻查 方向逐步逼近极 值点 。
F E
D
有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）
图6-1 单纯形的寻查方向
单纯形法原理
单纯形法原理
单纯形法是一种用于求解线性规划问题的经典方法。
它基于一个重要的原理，即通过不断地改变可行解来寻找最优解。
首先，我们需要将线性规划问题转化为标准形式，即目标函数最小化的约束条件下的线性等式约束问题。
然后，我们引入一组基变量，用它们来表示约束条件中的不等式。
这样，我们就可以将问题表示为一个矩阵方程。
通过逐步迭代的过程，单纯形法从初始可行解开始，在每一步中选择合适的基变量进入基组合，同时选择一个离开基变量离开基组合。
这个选择过程基于目标函数的增益最大化。
在每一步中，我们计算一个指标称为换入变量的相对利润。
然后，我们选择具有最大相对利润的变量作为新的基变量。
接下来，我们计算每个基变量的换出变量，以确定哪个变量将离开基组合。
换出变量的选择基于非基变量进入基变量的限制条件。
通过不断地魔法步骤，我们可以逐渐靠近最优解。
当达到最优解时，指标函数的值为最小值，而最终的基变量和非基变量的值则保存了最优解的解。
需要注意的是，单纯形法并不总是在有限时间内结束。
在某些情况下，它可能会进入一个无穷循环，无法找到最优解。
为了解决这个问题，我们可以添加一些人工变量，并进行二阶段法来确保最优解的存在。
总之，单纯形法是一种有效的线性规划求解方法，它通过不断改变可行解来寻找最优解。
通过选择合适的基变量和换出变量，单纯形法能够逐步逼近最优解。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
工程优化设计中单纯形法的基本原理张云龙（大连海洋大学土木工程学院辽宁大连116023)摘要：从实例出发提出线性规划的数学模型，给出图解法的基本原理，进而重点讲述它的标准解法——单纯形法。
在此基础上进一步讨论单纯形法的推广，即大M法和两相法。
关键词：线性规划图解法单纯形法大M法THE BASIC PRINCIPLES OF SIMPLEX METHOD TO THE ENGINEERING OPTIMIZE DESIGNZHANG Yun-long(Dalian Ocean University, College of Civil Engineering, Liaoning, Dalian 16023)Abstract: From the instance of the starting linear programming mathematical model of the basic principles of the graphic method, and then focus on the standard solution - simplex method. To promote further discussion on this basis, the simplex method, that is, the big M method and two-phase method.Key Words: Linear programming；Graphic method；Simplex Method; Big M Method1引言在工程优化设计问题中，当约束集由一组线性函数所确定时，其最优化问题的求解已有比较系统的技巧。
如果连目标函数也是线性的，也即线性规划问题，则是目前对规划问题研究最透彻最完善的一类问题，而且有比较成熟的解法。
线性规划在工程实例中的应用已相当广泛。
虽然大多数设计问题是非线性的，但对线性规划的研究仍然占据突出地位。
其原因是：有一部分实际问题，诸如运输问题，分配问题等，确实可以用线性规划问题来求解。
尤为重要的是，对于几乎所有规划问题的讨论都与线性规划有关，有时用线性逼近法去直接求解非线性问题；有时则利用线性规划，作为求解在最优化过程中所提出的那些子问题的一个工具，例如，可用来求解可行方向法中的方向寻求问题等错误!未找到引用源。
因此，深刻理解线性规划问题及其标准解法——单纯形法，显得尤为关键。
2线性规划问题2.1数学模型线性规划主要解决：如何利用现有的资源，使得预期目标达到最优。
例如，美佳公司计划制造Ⅰ、Ⅱ两种家电产品。
已知各制造一件时分别占用的设备A、B的台时、调试工序及每天可用于这两种家电的能力、各售出一件时的获利情况，如表1-1所示。
问该公司应制造两种家电各多少件，使获取的利润最大？表1-1 工时及利润简表解题过程：设公司制造Ⅰ、Ⅱ两种家电分别为1,x 2x 件。
问题：1?x = 2?x =可使得利润Z 最大？ 设备A 的工时限制： 2515x ≤ 设备B 的工时限制： 126224x x +≤ 调试工序的时间限制：125x x +≤ 利润： 122Z x x =+ 即要求：12max 2Z x x =+ 目标函数即为：12max 2Z x x =+约束条件：s.t. 212121251562245,x x x x x x x ≤⎧⎪+≤⎪⎨+≤⎪⎪≥⎩其中，约束条件可记 s. t. (subject to), 意思为“以…为条件”、“假定”、“满足”之意。
从数学的角度来看上述的例子①每一个问题都有一组变量—称为决策变量，一般记为12,,,.n x x x 对决策变量每一组值：(0)(0)(0)12(,,)T n x x x 代表了一种决策方案。
通常要求决策变量取值非负，即0,(1,2,).i x i n ≥=②每个问题中都有决策变量需满足的一组约束条件—线性的等式或不等式。
③都有一个关于决策变量的线性函数—称为目标函数。
要求这个目标函数在满足约束条件下实现最大化或最小化。
将约束条件及目标函数都是决策变量的线性函数的规划问题称为线性规划。
有时也将线性规划问题简记为LP （linear programming)其数学模型为：1122max(min)n n Z c x c x c x =+++11112211211222221122(,)(,)..(,)0,(1,2,,)n n n n m m mn n mj a x a x a x b a x a x a x b s t a x a x a x bx j n +++≤=≥⎧⎪+++≤=≥⎪⎪⎨⎪+++≤=≥⎪≥=⎪⎩上述模型的简写形式为：1max(min)nj jj Z c x==∑1(,)(1,2,,).0(1,2,,)nij j i j j a x b i m s t x j n =⎧≤=≥=⎪⎨⎪≥=⎩∑若令12(,,,);n C c c c =12;n x x X x ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭12;m b b b b ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭11121212221212(,,,)n n n m m mn a a a a a a A P P P a a a ⎛⎫ ⎪ ⎪== ⎪ ⎪⎝⎭则线性规划问题的矩阵形式：max(min)Z CX =(,).0AX bs t X ≤=≥⎧⎨≥⎩2.2 线性规划问题的标准形式LP 问题的数学模型的标准形式为：1122max n n Z c x c x c x =+++1(1,2,,,0).0(1,2,,)nij j i i j j a x b i m b s t x j n =⎧==≥⎪⎨⎪≥=⎩∑且⑴ 若目标函数为 1122min n n Z c x c x c x =+++，则可以引进新的目标函数,Z Z '=-则Z 的最小值即为Z ’的最大值，即：min max Z Z '=。
从而目标函数变换为：1122max n n Z c x c x c x '=----⑵ 当约束条件中含有不等式时， 如：12max 33Z x x =+()()12122101.21420(1,2)ix x s t x x x i +≤→⎧⎪+≤→⎨⎪≥=⎩此时，对⑴ 12210x x +≤，引入变量30,x ≥ 使得⑴式变为：123210x x x ++=，同理对⑵式12214x x +≤引入变量40,x ≥使得⑵式变为：124214x x x ++= 于是原LP 问题化为标准形式：12max 33Z x x =+123124210.2140(1,2,3,4)i x x x s t x x x x i ++=⎧⎪++=⎨⎪≥=⎩引进变量x 3,x 4称为松弛变量。
⑶ 若约束条件中线性方程式的常数项为负数，则将该线性方程式两端乘以-1，使得常数项为正数。
⑷ 若变量l x 无约束，则引进两个非负变量0,l x '≥0l x ''≥将l x 表示为：l l l x x x '''=- 所有的线性规划问题，总可以通过这四步将其化为标准形式，这样便于利用图解法或单纯形法进一步求解。
3 线性规划的图解法线性规划的图解法是解决两个变量LP 问题的一种简单实用的方法。
图解法步骤：⑴ 根据约束条件画出可行域。
⑵ 根据目标函数Z 的表达式画出目标直线Z=0，并表明目标函数增加的方向，即目标函数原点处的梯度方向，可通过求偏导数得到。
⑶ 在可行域中，找符合要求的距离目标直线Z=0的最远或最近点，并求出该点坐标。
例如，解LP 问题：12max 3Z x x =+12128.601,2i x x s t x x i +≤⎧⎪≤⎨⎪≥=⎩解：123Z x x =+在原点的梯度：13,xZ '=21x Z '= 所以，(3,1)Z ∇=。
随着直线213x x =-沿梯度方向去扫可行域，目标函数123Z x x =+中的Z 在增加。
如：经过点(1,1)时， 4.Z =由此可见，当目标函数沿梯度的方向去扫可行域时，在顶点(6,1)处取得最大值。
目标函数的最优值为：max 36119.Z =⨯+=图1 线性规划图解法实际上，如果利用图解法解决很多的类似的题目后，我们可以得到以下事实： ①若线性规划问题的可行域存在，则可行域一定是凸集。
②若线性规划问题的最优解存在，则最优解或最优解之一（如果有无穷多最优解的话）一定是可行域凸集的某个顶点。
4 单纯形法4.1 单纯形法中的一些基本概念在一个非齐次线性方程组中，例如：非其次方程组2312412551562245x x x x x x x x +=⎧⎪++=⎨⎪++=⎩，其增广矩阵为 称3,x 4,x 5x 为基变量（括号中的数字所对应的变量）。
基变量个数=()()3r A r A ==。
此方程组的解为3241251215524625x x x x x x xx =-⎧⎪=--⎨⎪=--⎩。
其中1,x 2x 为任意实数。
称它们为非基变量，或自由变量。
称非基变量1,x 2x 为0的解(0,0,15,24,5) 叫基解。
如果一个解的每个分量都是非负数，就叫做可行解。
如果基解是可行的，就叫基可行解，如0(0,0,15,24,5)TX =即为基可行解。
基可行解所对应的基称为2x ()()()0510********2411015A ⎛⎫ ⎪= ⎪ ⎪⎝⎭1x 2x 3x 4x 5x b可行基，如345{,,}x x x 即为可行基。
基可行解很重要，可以证明以下定理：定理1：若线性规划问题存在最优解，则问题的可行域是凸集。
定理2：线性规划问题的基可行解对应线性规划问题可行域（凸集）的顶点。
定理3：若线性规划问题最优解存在，则最优解一定在可行域顶点处取得[2]。
由此可看出，最优解要在基可行解（可行域顶点）中找。
通过以上分析，我们也可以得到以下几个结论：（1）线性规划问题的可行域是一个凸集，可行域可能有界，也可能无界，但其顶点数是有限个。
（2）线性规划问题每个基本可行解对应于可行域的一个顶点。
（3）若线性规划问题有最优解，则必可在其可行域的某个（或多个）顶点上达到最优值。
4.2 单纯形法基本原理首先说明什么是基变换。
例如，对于LP 问题：12345max 2000Z x x x x x =++++23124125515622451,,5i x x xx x x x x x i +=⎧⎪++=⎪⎨++=⎪⎪≥=⎩当前可行基345{,,}x x x 所对应的基可行解0(0,0,15,24,5)TX =。
这个解显然不是最优。
因为，当10,x =20x =时是没有现实意义的。