随机实验理想白噪声和带限白噪声的产生与分析
白噪声的产生与测试实验

3)正态随机随机数,从中取 1024、10240、20480 个点的功率普密度,做比较,
观察这些随机数的功率谱密度随长度的变化。实际的白噪声功率普密度不是常 数。 ⑷ 根据白噪声的特性,确定哪些随机信号属于白噪声范畴。根据分析确定 白噪声与概率分布有关系吗? ⑸ 通过编程分别确定当5个均匀分布过程、5个指数分布分别叠加时,结果 是否是高斯分布。叠加次数对结果的影响?
Sn ( f ) N0 2
其中 N 0 /2就是白噪声的均方值。 白噪声的自相关函数位:
R ( ) N0 N ( ) 白噪声的自相关函数是位于τ=0处、强度为 0 的冲击函数。 2 2
这表明白噪声在任何两个不同的瞬间的取值是不相关的。同时也意味着白噪声能
随时间无限快的变化,因为它的带宽是无限宽的。下面我们给出几种分布的白噪 声。 随机过程的几种分布 均匀分布随机信号、正态分布(高斯分布)随机信号、指数分布随机信号等。
lim
T
(5)
取20480个点时的功率谱密度和自相关函数,如下图 (1) 功率谱密度:
(2) 随机信号叠加:
4.随机信号检验:
五、实验总结
这次试验让我们对白噪声有了很大的理解,最主要是在实验过程中用到了好 久不用的matlab软件,由于好长时间不用好多的函数的功能都忘记了,而且实验 过程中用到的好多函数以前都没接触过,所以还得花好长时间去查阅相关资料。 这次试验的目的其实让我们学会是利用matlab软件对信号分析,同时加深我们 对信号和噪声参数处理的理解,锻炼我们的实践动手能力。 参考文献:
均值表达了信号变化的中心趋势,或称之为直流分量。 在 MATLAB 中,可以用 mean()函数来计算。 (1)
白噪声的产生

σ 2 , ω ≤ ω0 ( ω0 为给定的远大于过程的截止频率) 谱密度: SW (ω ) = 0, ω > ω0 σ 2ω0 sin ω0τ 相关函数: RW (τ ) = ⋅
π
ω0τ
讨论白噪声时,还要涉及到白噪声的概率分布,服从正态分布的白噪声称为 高斯白噪声。 n 维白噪声:一个 n 维随机过程 W (t ) 满足: E{W (t )} = 0 Cov{W (t ),W (t + τ )} = E{W (t )W (t + τ )} = Qδ (τ ) 其中 Q 为正定常数矩阵,则称 W (t ) 为 n 维白噪声过程。 ● 白噪声序列 白噪声序列是白噪声过程的离散形式。如果序列 {W (k )} 满足: 相关函数: RW (l ) = σ 2δ l , l = 0,±1,±2,L 则称为白噪声序列。 谱密度: SW (ω ) =
N 2 = i =1 N / 12
∑ξ
N
i
−
N 12 2 由此可得正态分布η ~ N ( µη ,σ η ) 的随机数。
取 N = 12 时,有
η = µη + σ η
∑ξ
i =1
N
i
−
N 2
η = µη + σ η ∑ ξi − 6
i =1
● 变换抽样法 理论依据:设 ξ1 和 ξ 2 是相互独立的(0,1)均匀分布随机变量,则
● M 序列的生成结构图 ● M 序列的波形 1.2.3 特征多项式 解决如何选取反馈通道的问题,以保证生成 M 序列。 ● 定义多项式: G ( s ) = ∑ x i s i (无限阶)
i =0 P 1 , F ( s ) = 1 ⊕ ∑ a j s j (有限阶) F ( s) j =1 称 F ( s ) 为 M 序列的特征多项式。 注意 1:此时选取 M 序列初始状态为: x1 = 1, x 2 = 0, L , x P = 0 。 注意 2:生成 M 序列的结构图完全由特征多项式 F ( s ) 确定。 ∞
第2章随机信号与噪声

●随机过程:尽管随机信号和随机噪声是不可预测的、随机 的,但它们具有一定的统计规律。从统计学的观点看,均可 表示为随机过程。
随机过程是一类随时间作随机变化的过程,它不能用确切的时
间函数描述。
统计学中的有关随机过程的理论可以运用到随机信号和噪声分
析中来。
2021/5/12
通信原理
3
பைடு நூலகம்
第2章 随机信号与噪声分析
2021/5/12
通信原理
5
第2章 随机信号与噪声分析
x1 (t)
角度1:对应不同随机试验结
果的时间过程的集合。
x2 (t)
角度2:随机过程是随机变量
概念的延伸。
xn (t)
讨论:
t1
t2
t
图 2- 1 n图 图 图 图 图 图 图 图 图
●在任一给定时刻t1上,每一个样本函数xi (t)都有一个确定的
●全部随机函数的集合--随 机过程:
X(t) ={x1(t), x2(t), …, xn(t)} ●每一条曲线xi(t)都是随机过 程的一个实现/样本--为确 定的时间函数。
角度1:对应不同随机试验结果的时间过程的集合。 角度2:随机过程是随机变量概念的延伸。
●在某一特定时刻t1观察各台接收机的输出噪声值x(t1) ,发现 他们的值是不同的-- 是一个随机量(随机变量)。
过程。
意义: ●具有各态历经性平稳随机过程--十分有趣,非常有用。 ●通信系统中所遇到的信号与噪声,大多数可视为平稳、具 有各态历经性的随机过程。
2021/5/12
通信原理
21
第2章 随机信号与噪声分析
2.3.2 平稳随机过程的各态历经性
●问题的提出 随机过程的数字特征(均值、相关函数)是对随机过程的 所有样本函数的统计平均,但在实际中常常很难测得大量 的样本。 问题:能否从一次试验而得到的一个样本函数x(t)来决定平 稳过程的数字特征呢?
白噪声
4.3 理想白噪声、带限白噪声比较分析1、实验原理若一个具有零均值的平稳随机过程,其功率谱密度在某一个有限频率范围内均匀分布,而在此范围外为零,则称这个过程为带限白噪声。
带限白噪声分为低通型和带通型。
白噪声详细描述可参考马文平、李兵兵等编著.随机信号分析与应用.科学出版社,2006出版的书第2章节。
朱华、黄辉宁、李永庆、梅文博.随机信号分析.北京理工大学出版社,2000出版的书第4章节。
以及与随机信号分析相关的参考书籍。
2、实验任务与要求⑴通过实验掌握白噪声的特性以及带限白噪声的意义,重点在于系统测试与分析。
算法选用matlab或c/c++语言之一编写和仿真程序。
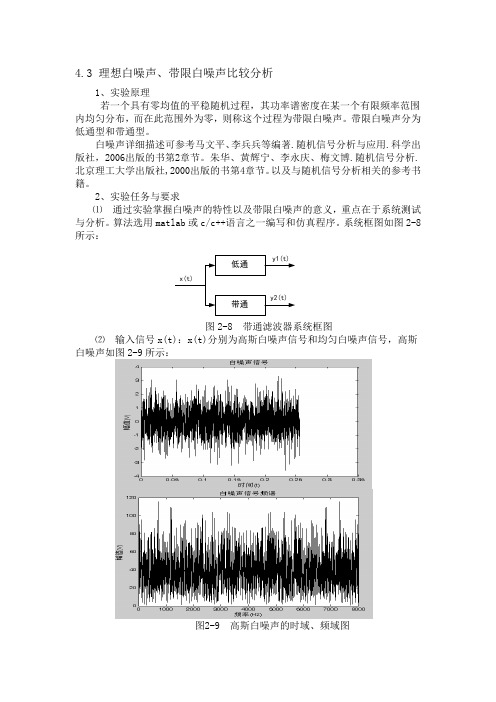
系统框图如图2-8所示:低通带通x(t)y1(t)y2(t)图2-8带通滤波器系统框图⑵输入信号x(t):x(t)分别为高斯白噪声信号和均匀白噪声信号,高斯白噪声如图2-9所示:图2-9 高斯白噪声的时域、频域图要求测试白噪声的均值、均方值、方差,自相关函数、概率密度、频谱及功率谱密度并绘图。
分析实验结果,搞清楚均值、均方值、方差,自相关函数、频谱及功率谱密度的物理意义。
例:均值除了表示信号的平均值,它还表示信号中有了什么成分。
相关函数当τ=0时为什么会有一个冲击,表示什么,它又等于什么。
信号的时域波形有哪些特征,频域又有哪些特征。
频谱及功率谱密度有什么差异,什么噪声是白噪声,这个噪声符合白噪声的定义吗等等。
⑶设计一个低通滤波器和一个带通滤波器。
要求白噪声分别通过低通滤波器和带通滤波器后的信号能够表现出带限白噪声的特点。
测试低通滤波器和一个带通滤波器的时频特性和频域特性以验证其正确性。
⑷分别计算高斯白噪声、均匀白噪声经低通滤波、带通滤波器后的均值、均方值、方差、概率密度、自相关函数、频谱及功率谱密度,并加以分析。
⑸所有结果均用图示法来表示。
⑹白噪声在什么情况下为带限白噪声?⑺按要求写实验报告。
3.7理想白噪声及特性

随机信号分析目录CONTENTS白噪声的定义白噪声的时频域特性物理可实现的白噪声小结随机过程的分类⚫按分布函数或概率密度函数特性:正态过程、马尔可夫过程、独立增量过程等;⚫按功率谱特性:宽带过程、窄带过程;白噪声、色噪声等。
定义:若N(t)为一个具有零均值的平稳随机过程,其功率谱密度均匀的分布在整个频率区间,即其中,N0为一个正实常数,则称N(t)为白噪声过程或简称白噪声。
“白”字借用光学中的“白光”术语。
N 120S N ω()白噪声的功率谱ω0=ωS N N 2()10∈−∞+∞ω(,)结论:功率谱在整个频率轴上满足均匀分布。
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)根据维纳-辛钦定理,白噪声的自相关函数为00111()()222j N R N e d N ωττωδτπ+∞−∞==⎰0)(τN R 021N 结论:白噪声的自相关函数是一个δ函数,其面积等于功率谱密度。
白噪声的时频域特征白噪声的自相关系数为⎩≠⎨===⎧=τττττK R r K R N N N N N (0)(0)0 0()()() 1 0 结论:白噪声在任何两个相邻时刻的取值都是不相关的,白噪声过程随时间的起伏极快,过程的功率谱密度极宽。
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)物理可实现的白噪声实际上,白噪声是不存在的,因为在实际应用中,当研究随机过程通过某一系统时,只要过程的功率谱密度在一个比系统带宽大得多的频率范围内近似均匀分布,就可以把它作为白噪声来处理。
2(0)(0)N N R σδ==→∞白噪声的功率谱在整个频率轴上满足均匀分布。
白噪声的自相关函数是一个δ函数,其面积等于功率谱密度,在任何两个相邻时刻的取值都是不相关的。
理想白噪声不存在,但某些情况下随机过程可近似看作白噪声。
对于一个具有零均值的平稳随机过程,其功率谱密度均匀的分布在整个频率区间,则称其为白噪声。
中心极限定理和高斯噪声的产生、白噪声的分析、色噪声的产生。

高斯噪声的自相关函数 10000
0.45 0.4
高斯噪声的概率密度
8000
0.35
6000
0.3 0.25
4000
0.2
2000
0.15 0.1
0
0.05
-2000
0
0.2
0.4
0.6
0.8
1 t
1.2
1.4
1.6
1.8 x 10
2
4
0 -5
-4
-3
-2
-1
0
1
2
3
4
5
实 验 分 析 : 用 matlab 计 算 得 此 高 斯 信 号 的 均 值 为 5.95076876663825e-14 ,约等于 0 。自相关函数近似为一冲击, 功率谱在某一值附近波动,在整个频率轴上均匀分布。这些数学 特征表明该高斯随机信号满足白噪声的相关特性。
d
d d
四、实验总结
1.通过本次实验,我们了解了如何利用同余法中 心极限定理产生白噪声,分析了白噪声的一些数 字特征。 2.对白噪声进行低通滤波后的信号进行功率谱密 度和相关时间的分析,发现此信号较好地符合限 带型高斯白噪声的特性,从而很好地验证了白噪 声理论。
输出信号的功率谱密度函数 0 -5 -10 -15 -20 -25 -30 -35 -40 -45 -50
Power/frequency (dB/rad/sample)
0
0.1
0.2
0.3 0.4 0.5 0.6 0.7 0.8 Normalized Frequency ( rad/sample)
高斯噪声 4 3 2 1 0 -1 -2 -3 -4
0
1000
高斯随机过程高斯白噪声和带限白噪声

(x) 1
x
ez2 / 2dz
2
(2.5.9)
则正态分布函数可表示为:
F (x) ( x a )
(2.5.8)
通信原理
第2章 随机过程
xa
x
x
F(x) f (z)dz
1 exp[ (z a)2 ]dz 1
et2 / 2dt
2
2 2
2
(3) 用误差函数表示
正态分布函数更常表示成与误差函数相联系的形式。
---窄带随机过程: nc(t)---n(t)之同相分量; ns(t)---n(t)之正交分量。
通信原理
第2章 随机过程
代入,整理:
r(t) Acos (ct ) n(t) Acos cosct Asin sin ct nc (t) cosct ns (t) sin ct
Acos nc (t)cosct [Asin ns (t)]sin ct
当输入是随机过程ξ (t)的一个实现ξi1(t)--随机函 数时,便有输出随机过程ξo1(t)。 进一步:当输入是随机过程ξi(t)时,便有输出随机过程 ξo(t)。且有:
0 (t) h( ) i (t )d 2.8.4 0
通信原理
第2章 随机过程
0 (t) h( ) i (t )d 2.8.4 0
R c s (0)=0 , f (c ,s )=f (c ) f (s )
通信原理
第2章 随机过程
2.5.3 已知ξ(t)的统计特性,求 aξ(t)、φξ(t)的统计特性
结论2
(t) a (t) cos ct (t) , a 0
若ξ(t):均值为0、方差为δ2、窄带平稳高斯随机过程。
则:
白噪声检验的方法及原理

白噪声检验的方法及原理咱得明白啥是白噪声。
白噪声啊,就像是一种杂乱无章但又有规律可循的声音信号。
在统计学和时间序列分析里,白噪声可是个重要的概念呢。
它具有一些特定的性质,比如说均值为零,方差是一个常数,不同时间点的取值相互独立。
简单来说,白噪声就是一种随机的、没有明显趋势和规律的信号。
那为啥要进行白噪声检验呢?这可重要啦!如果一个时间序列是白噪声,那就意味着它没有可预测的模式,是完全随机的。
在很多情况下,我们需要确定一个时间序列是不是白噪声,因为这关系到我们后续的分析和预测方法的选择。
如果一个时间序列不是白噪声,那就可能存在某种趋势、季节性或者周期性,我们就可以利用这些特征来进行预测和分析。
但如果它是白噪声,那我们就知道用传统的预测方法可能不太管用啦。
接下来,咱说说白噪声检验的方法。
常见的方法有好几种呢,比如说自相关函数检验、Ljung-Box 检验和单位根检验等。
自相关函数检验呢,就是看时间序列的自相关函数。
如果一个时间序列是白噪声,那么它的自相关函数在所有的滞后阶数上都应该接近于零。
啥意思呢?就是说不同时间点的取值之间没有明显的相关性。
我们可以通过计算时间序列的自相关函数,并观察它在不同滞后阶数上的值来判断是不是白噪声。
如果自相关函数的值都很小,接近零,那很可能就是白噪声;如果自相关函数在某些滞后阶数上有较大的值,那就不是白噪声啦。
Ljung-Box 检验也是个常用的方法。
这个检验主要是通过计算统计量来判断时间序列的自相关性。
它会比较实际的自相关系数和在白噪声假设下的预期自相关系数。
如果统计量的值很大,那就说明时间序列不是白噪声;如果统计量的值比较小,那就有可能是白噪声。
Ljung-Box 检验通常会给出一个p 值,我们可以根据p 值来判断是否拒绝白噪声假设。
如果p 值小于某个显著性水平,比如0.05,那就拒绝白噪声假设,说明时间序列不是白噪声;如果p 值大于显著性水平,那就不能拒绝白噪声假设,可能是白噪声。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验八理想白噪声和带限白噪声的产生与分析
1.实验目的
了解理想白噪声和带限白噪声的基本概念并能够区分它们,掌握用matlab或c/c++软件仿真和分析理想白噪声和带限白噪声的方法。
⒉实验原理
所谓白噪声是指它的概率统计特性服从某种分布而它的功率谱密度又是均匀的。
确切的说,白噪声只是一种理想化的模型,因为实际的噪声功率谱密度不可能具有无限宽的带宽,否则它的平均功率将是无限大,是物理上不可实现的。
然而白噪声在数学处理上比较方便,所以它在通信系统的分析中有十分重要的作用。
一般地说,只要噪声的功率谱密度的宽度远大于它所作用的系统的带宽,并且在系统的带内,它的功率谱密度基本上是常数,就可以作为白噪声处理了。
白噪声的功率谱密度为:其中为单边功率谱密度。
2 ) ( 0 N f S n 0 N
白噪声的自相关函数位:白噪声的自相关函数是位于τ =0 处,强度为的冲击函数。
这表明白噪声在任何两个不同的瞬间的取值是不相关的。
同时也意味着白噪声能随时间无限快的变化,因为它含一切频率分量而无限宽的带宽。
) ( 20 N R )( 20 N
若一个具有零均值的平稳随机过程,其功率谱密度在某一个有限频率范围内均匀分布,而在此范围外为零,则称这个过程为带限白噪声。
带限白噪声分为低通型和带通型。
⒊实验任务与要求
⑴用matlab 或c/c++语言编写和仿真程序。
系统框图如图19、图20 所示:
特性测试绘制图形低通滤波特性测试绘制图形白噪声
图1 低通滤波器系统框图
特性测试绘制图形带通滤波特性测试绘制图形白噪声
图2 带通滤波器系统框图
⑵输入信号为:高斯白噪声信号和均匀白噪声信号,图为高斯白噪声。
⑶设计一个低通滤波器和一个带通滤波器。
要求低通滤波器的通带为0KHz-2KHz、通带衰减小于1db、阻带衰减大于35db。
带通滤波器的通带为10KHz-20KHz、通带衰
减小于1db、阻带衰减大于35db。
⑷首先计算白噪声的均值、均方值、方差、概率密度、频谱及功率谱密度、自相关函数。
然后分别经低通滤波、带通滤波器后,计算它们的均值、均方值、方差、概率密度、频谱及功率谱密度。
⑸所有结果均用图示法来表示。
⑹白噪声在什么情况下为带限白噪声?
⑺按要求写实验报告。
4.实验步骤与结果:
高斯白噪声
ts=-100:.0001:100;
s=sin(ts);
y=awgn(s,1);
x=y-s;
subplot(2,1,1);
plot(x);
a=xcorr(x);
subplot(2,1,2);
plot(a)
g=fft(a,512);
p=g.*conj(g)/512;
plot(p(1:256));
xm=mean(x)%均值
xm =3.7253e-005
xv=var(x)%方差
xv =0.7935
xs=xv+xm.^2%均方值
xs=0.7935
[x_pdf,x1]=ksdensity(x);
figure(4)
plot(x1,x_pdf);%画出高斯白噪声的一维概率密度grid on
title('白噪声的一维概率密度')
低通滤波器
Fs=10000;
fp=2000;fs=2200;
rp=0.5;rs=50;
wp=2*pi*fp/Fs;
ws=2*pi*fs/Fs;
wap=tan(wp/2);
was=tan(ws/2);
Fs=1;
[N,Wn]=buttord(wap,was,rp,rs,'s');%估计滤波器的阶数
[z,p,k]=buttap(N);
[bp,ap]=zp2tf(z,p,k);
[bs,as]=lp2lp(bp,ap,wap);
[bz,az]=bilinear(bs,as,Fs/2);
[H,w]=freqz(bz,az,512,Fs*10000);%计算数字滤波器的频率响应figure(6)
plot(w,abs(H));%低通滤波器的频谱
title('0-2KHz的低通滤波器的频谱')
xlabel('Frequency/Hz')
ylabel('Mag of frequency response')
grid on
带通滤波器
Fs=100000
[b,a]=ellip(10,0.5,50,[10000,20000]*2/Fs); [H,w]=freqz(b,a,512);
figure(6)
plot(w*Fs/(2*pi),abs(H));
title('带通滤波器幅频响应');
set(gcf,'color','white')
xlabel('Frequency Hz');
ylabel('Mag of frequency response');
grid on
经过低通滤波器
ts=-100:.0001:100;
s=sin(ts);
y=awgn(s,1);
x=y-s;
Fs=10000;
fp=2000;fs=2200;
rp=0.5;rs=50;
wp=2*pi*fp/Fs;
ws=2*pi*fs/Fs;
wap=tan(wp/2);
was=tan(ws/2);
Fs=1;
[N,Wn]=buttord(wap,was,rp,rs,'s');%估计滤波器的阶数
[z,p,k]=buttap(N);
[bp,ap]=zp2tf(z,p,k);
[bs,as]=lp2lp(bp,ap,wap);
[bz,az]=bilinear(bs,as,Fs/2);
[H,w]=freqz(bz,az,512,Fs*10000);%计算数字滤波器的频率响应
figure(6)
plot(w,abs(H));%低通滤波器的频谱
title('0-2KHz的低通滤波器的频谱')
xlabel('Frequency/Hz')
ylabel('Mag of frequency response')
y=filter(bz,az,x);%白噪声通过滤波器
y_mean=mean(y) %y的均值
y_std=std(y); %标准差
y_var=y_std.^2 %方差
y_msv=y_var+y_mean.^2
y_mean =3.8098e-005
y_var = 0.3187
y_msv =0.3187
[y_c,lags1]=xcorr(y,200,'unbiased');%计算y的相关函数figure(8)
plot(lags1,y_c);%画出y的相关函数的图形
title('y的自相关函数')
grid on
g=fft(y_c,512);
p=g.*conj(g)/512;
plot(p(1:256));%功率谱密度
y_msv =经过带通滤波器后:
ts=-100:.0001:100;
s=sin(ts);
y=awgn(s,1);
x=y-s;
Fs=100000
[b,a]=ellip(10,0.5,50,[10000,20000]*2/Fs); [H,w]=freqz(b,a,512);
figure(1)
plot(w*Fs/(2*pi),abs(H));
title('带通滤波幅频响应');
set(gcf,'color','white')
xlabel('Frequency Hz');
ylabel('Mag of frequency response');
y=filter(b,a,x);
ym=mean(y)
ym =-4.6823e-006%均值
y_std=std(y);
y_std =0.3878%方差
ys=y_std+ym;
ys=0.3878%均方值
[y_c,lags1]=xcorr(y,200,'unbiased');%计算y的相关函数figure(8)
plot(lags1,y_c);%画出y的相关函数的图形
title('y的自相关函数')
grid on
g=fft(y_c,512);
>> p=g.*conj(g)/512;
plot(p(1:256));%功率谱密度。
