高考数学函数专题习题集答案
高考数学专题复习-2.1函数及其表示-高考真题练习(附答案)

专题二函数的概念与基本初等函数2.1函数及其表示考点一函数的概念及表示1.(2015湖北文,7,5分)设x∈R,定义符号函数sgnx=1,>0,0,=0,-1,<0.则()A.|x|=x|sgnx|B.|x|=xsgn|x|C.|x|=|x|sgnxD.|x|=xsgnx答案D 由已知可知xsgnx=s >0,0,=0,-s <0,而|x|=s >0,0,=0,-s <0,所以|x|=xsgnx,故选D.2.(2014江西理,3,5分)已知函数f(x)=5|x|,g(x)=ax 2-x(a∈R).若f[g(1)]=1,则a=()A.1B.2C.3D.-1答案A 由已知条件可知:f[g(1)]=f(a-1)=5|a-1|=1,∴|a-1|=0,得a=1.故选A.评析本题主要考查函数的解析式,正确理解函数的定义是解题关键.3.(2015重庆文,3,5分)函数f(x)=log 2(x 2+2x-3)的定义域是()A.[-3,1]B.(-3,1)C.(-∞,-3]∪[1,+∞)D.(-∞,-3)∪(1,+∞)答案D 由x 2+2x-3>0,解得x<-3或x>1,故选D.4.(2015湖北文,6,5分)函数f(x)=4−|U +lg 2-5x+6t3的定义域为()A.(2,3)B.(2,4]C.(2,3)∪(3,4]D.(-1,3)∪(3,6]答案C 要使函数f(x)有意义,0,0,>0,解之得2<x<3或3<x≤4,故选C.5.(2014山东理,3,5分)函数()A. B.(2,+∞)C. D.答案C 要使函数f(x)有意义,需使(log 2x)2-1>0,即(log 2x)2>1,∴log 2x>1或log 2x<-1.解之得x>2或0<x<12.故f(x)的定义域为0,6.(2016课标Ⅱ文,10,5分)下列函数中,其定义域和值域分别与函数y=10lgx的定义域和值域相同的是()A.y=xB.y=lgxC.y=2x答案D函数y=10lgx的定义域、值域均为(0,+∞),而y=x,y=2x的定义域均为R,排除A,C;y=lgx的值域为R,排除B,故选D.易错警示利用对数恒等式将函数y=10lgx变为y=x,将其值域认为是R是失分的主要原因.评析本题考查函数的定义域和值域,熟练掌握基本初等函数的图象和性质是解题的关键.7.(2022北京,4,4分)已知函数f(x)=11+2,则对任意实数x,有()A.f(-x)+f(x)=0B.f(-x)-f(x)=0C.f(-x)+f(x)=1D.f(-x)-f(x)=13答案C∵f(x)=11+2,∴f(-x)=11+2−=22+1,∴f(x)+f(-x)=11+2+22+1=1.故选C.一题多解:若对任意实数x,使得选项中式子成立,则可任取x值,代入验证,进行排除.当x=0时,f(0)+f(0)=12+12=1,f(0)-f(0)=0,故A,D选项错误.当x=1时,f(-1)-f(1)=11+2−1−11+21≠0,故B选项错误.根据排除法可知选C.8.(2022北京,11,5分)函数f(x)=1+1−的定义域是.答案(-∞,0)∪(0,1]解析由题意得≠0,1−≥0,解得x≤1且x≠0,所以函数f(x)的定义域为(-∞,0)∪(0,1].9.(2016江苏,5,5分)函数y=3−2t2的定义域是.答案[-3,1]解析若函数有意义,则3-2x-x2≥0,即x2+2x-3≤0,解得-3≤x≤1.考点二分段函数1.(2019天津理,8,5分)已知a∈R.设函数f(x)=2-2ax+2a,x≤1,tEns>1.若关于x的不等式f(x)≥0在R上恒成立,则a的取值范围为()A.[0,1]B.[0,2]C.[0,e]D.[1,e]答案C本题主要考查分段函数及不等式恒成立问题,考查学生推理论证能力及运算求解能力,将恒成立问题转化为求最值问题,考查了学生化归与转化思想及分类讨论思想.(1)当x≤1时,f(x)=x 2-2ax+2a=(x-a)2+2a-a 2,①若a>1,则f(x)在(-∞,1]上是减函数,所以f(x)≥f(1)=1>0恒成立;②若a≤1,则f(x)≥f(a)=2a-a 2,要使f(x)≥0在(-∞,1]上恒成立,只需2a-a 2≥0,得0≤a≤2,∴0≤a≤1,综合①②可知,a≥0时,f(x)≥0在(-∞,1]上恒成立.(2)当x>1时,lnx>0,f(x)=x-alnx≥0恒成立,即a≤ln 恒成立.令g(x)=ln ,g'(x)=lnt1(lnp 2,令g'(x)=0,得x=e,当x∈(1,e)时,g'(x)<0,g(x)为减函数,当x∈(e,+∞)时,g'(x)>0,g(x)为增函数,∴g(x)min =g(e)=e,∴a≤e.综合(1)(2)可知,a 的取值范围是0≤a≤e,故选C.解后反思求不等式恒成立时的参数取值范围的方法:一是分离参数法,不等式f(x)≥a 在R 上恒成立⇔f(x)min ≥a,f(x)≤a 在R 上恒成立⇔f(x)max ≤a;二是讨论分析法,根据参数取值情况进行分类讨论,从而确定参数的取值范围.2.(2019天津文,8,5分)已知函数≤x ≤1,x >1.若关于x 的方程f(x)=-14x+a(a∈R)恰有两个互异的实数解,则a 的取值范围为()答案D 本题以分段函数和方程的解的个数为背景,考查函数图象的画法及应用.画出函数y=f(x)的图象,如图.方程f(x)=-14x+a 的解的个数,即为函数y=f(x)的图象与直线l:y=-14x+a 的公共点的个数.当直线l 经过点A 时,有2=-14×1+a,a=94;当直线l 经过点B 时,有1=-14×1+a,a=54.由图可知,函数y=f(x)的图象与l 恰有两个交点.另外,当直线l 与曲线y=1,x>1相切时,恰有两个公共点,此时a>0.联立=1,=−14x +a,得1=-14x+a,即14x 2-ax+1=0,由Δ=a 2-4×14×1=0,得a=1(舍去负根).综上故选D.一题多解令g(x)=f(x)+14x=4(0≤x ≤1),>1),当0≤x≤1时,g(x)=2+4为增函数,其值域为0,当x>1时,g(x)=1+4,对g(x)求导得g'(x)=-12+14,令g'(x)=0,得x=2,当x∈(1,2)时,g'(x)<0,g(x)单调递减,当x∈(2,+∞)时,g'(x)>0,g(x)单调递增,∴当x=2时,g(x)min =g(2)=1,函数g(x)的简图如图所示:方程f(x)=-14x+a 恰有两个互异的实数解,即函数y=g(x)的图象与直线y=a 有两个不同的交点,由图可知54≤a≤94或a=1满足条件,故选D.易错警示本题入手时,容易分段研究方程2=-14x+a(0≤x≤1)与1=-14x+a(x>1)的解,陷入相对复杂的运算过程.利用数形结合时,容易在区间的端点处出现误判.3.(2015课标Ⅰ文,10,5分)已知函数f(x)=2t1-2,x ≤1,-log 2(x +1),x >1,且f(a)=-3,则f(6-a)=()A.-74 B.-54 C.-34 D.-14答案A 当a≤1时,f(a)=2a-1-2=-3,即2a-1=-1,不成立,舍去;当a>1时,f(a)=-log 2(a+1)=-3,即log 2(a+1)=3,得a+1=23=8,∴a=7,此时f(6-a)=f(-1)=2-2-2=-74.故选A.评析本题主要考查分段函数,指数与对数的运算,考查分类讨论的思想,属中等难度题.4.(2015陕西文,4,5分)设f(x)=1−sx ≥0,2,x <0,则f(f(-2))=()A.-1B.14C.12D.32答案C ∵f(-2)=2-2=14,∴f(f(-2))=f =12,选C.5.(2015山东文,10,5分)设函数f(x)=3ts x <1,2,x ≥1.若f 则b=()A.1B.78C.34D.12答案D=3×56-b=52-b,当52-b≥1,即b≤32时-b=252-b,即252-b=4=22,得到52-b=2,即b=12;当52-b<1,即b>32时-b=152-3b-b=152-4b,即152-4b=4,得到b=78<32,舍去.综上,b=12,故选D.6.(2014江西文,4,5分)已知函数f(x)=·2,x≥0,2-,x<0(a∈R),若f[f(-1)]=1,则a=() A.14 B.12 C.1 D.2答案A由f[f(-1)]=f(2)=4a=1,得a=14,故选A.7.(2014课标Ⅰ文,15,5分)设函数f(x)=e t1,x<1,13,x≥1,则使得f(x)≤2成立的x的取值范围是.答案(-∞,8]解析f(x)≤2⇒<1,e t1≤2或≥1,13≤2⇒<1,≤ln2+1或≥1,≤8⇒x<1或1≤x≤8⇒x≤8,故填(-∞,8].8.(2022浙江,14,6分)已知函数f(x)=−2+2,≤1,+1−1,>1,则f=;若当x∈[a,b]时,1≤f(x)≤3,则b-a的最大值是.答案3728;3+3解析∵+2=74,∴f==74+47−1=3728.f(x)的大致图象如图.∵当x∈[a,b]时,1≤f(x)≤3,∴由图可得b>1且b+1-1=3,∴b=2+3,∵f(a)=1,∴-a2+2=1,解得a=1或a=-1,∴(b-a)max=2+3-(-1)=3+3.一题多解:第二空:∵当x≤1时,y=-x2+2≤2,∴f(x)=3⇒x+1-1=3(x>1),故x=2+3,令-x2+2=1(x≤1),解得x=1或x=-1,令x+1-1=1(x>1),无解,∴a min=-1,b=2+3,∴(b-a)max=2+3-(-1)=3+3.。
高考数学专题《对数与对数函数》习题含答案解析
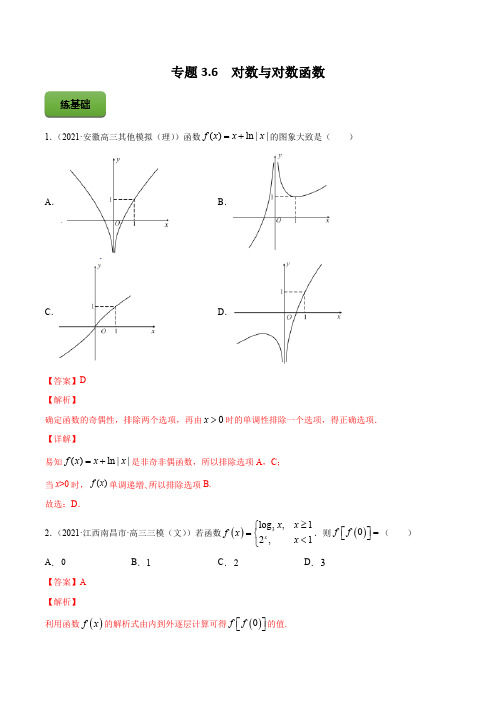
专题3.6 对数与对数函数1.(2021·安徽高三其他模拟(理))函数()ln ||f x x x =+的图象大致是()A .B .C .D .【答案】D 【解析】确定函数的奇偶性,排除两个选项,再由0x >时的单调性排除一个选项,得正确选项.【详解】易知()ln ||f x x x =+是非奇非偶函数,所以排除选项A ,C ;当x >0时,()f x 单调递増、所以排除选项B.故选:D .2.(2021·江西南昌市·高三三模(文))若函数()3log ,12,1x x x f x x ≥⎧=⎨<⎩.则()0f f ⎡⎤=⎣⎦( )A .0B .1C .2D .3【答案】A 【解析】利用函数()f x 的解析式由内到外逐层计算可得()0f f ⎡⎤⎣⎦的值.练基础()3log ,12,1x x x f x x ≥⎧=⎨<⎩,则()0021f ==,因此,()()301log 10f f f ===⎡⎤⎣⎦.故选:A.3.(2021·浙江高三其他模拟)已知a 为正实数,则“1a >”是“32212log log a a ->”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】C 【解析】利用充分、必要条件的定义,即可推出“1a >”与“32212log log a a ->”的充分、必要关系.【详解】因为32212log log a a ->等价于3222log log a a >,由a 为正实数且1a >,故有32a a >,所以3222log log a a >成立;由a 为正实数,3222log log a a >且函数2log y x =是增函数,有32a a >,故()210aa ->,所以1a >成立.故选:C .4.(2021·浙江高三专题练习)已知函数f (x )=1331,,log 1x x x x ⎧≤⎪⎨>⎪⎩则函数y =f (1-x )的大致图象是( )A .B .C .D .【答案】D 【解析】由()f x 得到()1f x -的解析式,根据函数的特殊点和正负判断即可.因为函数()f x 133,1log ,1x x x x ⎧≤⎪=⎨>⎪⎩,所以函数()1f x -()1133,0log 1,0x x x x -⎧≥⎪=⎨-<⎪⎩,当x =0时,y =f (1)=3,即y =f (1-x )的图象过点(0,3),排除A ;当x =-2时,y =f (3)=-1,即y =f (1-x )的图象过点(-2,-1),排除B ;当0x <时,()1311,(1)log 10x f x x ->-=-<,排除C ,故选:D .5.(2021·江苏南通市·高三三模)已知1331311log 5,,log 26a b c ⎛⎫=== ⎪⎝⎭,则a ,b ,c 的大小关系为( )A .a b c >>B .b a c >>C .c b a>>D .c a b>>【答案】D 【解析】由于1331log g 66lo c ==,再借助函数3log y x =的单调性与中间值1比较即可.【详解】1331log g 66lo c ==,因为函数3log y x =在()0,∞上单调递增,所以333131log 31log 5log 6log 6a c =<=<<=,因为函数12xy ⎛⎫= ⎪⎝⎭在R 上单调递减,所以10312112b <⎛⎫⎛⎫= ⎪ ⎪⎝⎝⎭=⎭,所以c a b >>故选:D6.(2021·辽宁高三月考)某果农借助一平台出售水果,为了适当地给鲜杏保留空气呼吸,还会在装杏用的泡沫箱用牙签戳上几个小洞,同时还要在鲜杏中间放上冰袋,来保持泡沫箱内部的温度稳定,这样可以有效延长水果的保鲜时间.若水果失去的新鲜度h 与其采摘后时间t (小时)满足的函数关系式为t h m a =⋅.若采摘后20小时,这种杏子失去的新鲜度为10%,采摘后40小时,这种杏子失去的新鲜度为20%.在这种条件下,杏子约在多长时间后会失去一半的新鲜度( )(已知lg 20.3≈,结果取整数)A .42小时B .53小时C .56小时D .67小时【答案】D 【解析】利用指数的运算得出1202a =,再利用对数的运算即可求解.【详解】由题意可得200010m a =⋅,①400020m a =⋅,②②÷①可得202a =,解得1202a =,所以0050t m a =⋅,③ ③÷①可得205t a -=,所以202025t -=,即20lg 2lg 51lg 20.720t -==-=,解得67t ≈(小时).故选:D7.【多选题】(2021·辽宁高三月考)已知2log 3a =,34b =,22log 31c =+,则下列结论正确的是( )A .a c <B .2ab =C .1abc a =+D .22bc b =+【答案】BCD 【解析】先判断1a >,即可判断A ; 利用222log 3b a==判断B ;利用B 的结论判断C ;利用C 的结论判断D.【详解】因为2log 31a =>,所以22log 3112c a a c a =+=+<⇒<,即A 不正确;因为33222log 42log 2log 3b a====,所以2ab =,即B 正确;由2ab =可知,21abc c a ==+,C 正确;由1abc a =+可知,2ab c ab b =+,则22bc b =+,即D 正确.故选:BCD.8.【多选题】(2021·山东日照市·高三一模)已知113log 0x x +=,222log 0xx +=,则( )A .2101x x <<<B .1201x x <<<C .2112lg lg 0x x x x -<D .2112lg lg 0x x x x ->【答案】BC 【解析】根据对数函数的性质可判断AB 正误,由不等式的基本性质可判断CD 正误.【详解】由131log 0x x =->可得101x <<,同理可得201x <<,因为(0,1)x ∈时,恒有23log log x x<所以122231log log 0x x x x -=-<,即12x x <,故A 错误B 正确;因为1201x x <<<,所以12lg lg 0x x <<,即210lg lg x x <-<-,由不等式性质可得1221lg lg x x x x -<-,即2112lg lg 0x x x x -<,故C 正确D 错误.故选:BC9.(2021·浙江高三期末)已知2log 3a =,则4a =________.【答案】9【解析】把2log 3a =代入4a 可得答案.【详解】因为2log 3a =,所以222log 3log 34429a ===.故答案为:9.10.(2021·河南高三月考(理))若41log 32a =,则39a a +=___________;【答案】6【解析】首先利用换底公式表示3log 2a =,再代入39a a +求值.【详解】由条件得331log 4log 22a ==,所以3333log 2log 2log 2log 4393933246a a +=+=+=+=.故答案为:61.(2021·浙江高三专题练习)如图,直线x t =与函数()3log f x x =和()3log 1g x x =-的图象分别交于点A ,B ,若函数()y f x =的图象上存在一点C ,使得ABC V 为等边三角形,则t 的值为( )ABCD.3+【答案】C 【解析】由题意得()3,log A t t ,()3,log 1B t t -,1AB =,根据等边三角形的性质求得C点的横坐标x t =-,结合A ,B两点的纵坐标和中点坐标公式列方程t =,解方程即可求得t 的值.【详解】由題意()3,log A t t ,()3,log 1B t t -,1AB =.设()3,log C x x ,因为ABC V 是等边三角形,所以点C 到直线AB所以t x -=,x t =-根据中点坐标公式可得练提升33333log log 11log log log 22t t t t ⎛+-==-= ⎝,所以t -=,解得t =故选:C2.(2021·安徽高三其他模拟(文))已知函数()()14,12ln 1,1xx f x x x ⎧⎛⎫-≤-⎪ ⎪=⎨⎝⎭⎪+>-⎩,若()0f f x <⎡⎤⎣⎦,则x 的取值范围为( )A .()2,0-B .21,1e ⎛⎫-∞- ⎪⎝⎭C .212,1e ⎛⎫-- ⎪⎝⎭D .()212,11,0e ⎛⎫--⋃-⎪⎝⎭【答案】D 【解析】先由()0f f x <⎡⎤⎣⎦可得出()20f x -<<,然后再分1x ≤-、1x >-两种情况解不等式()20f x -<<,即可得解.【详解】若()1f x ≤-,则()()1402f x f f x ⎛⎫=-<⎡⎤ ⎪⎣⎦⎝⎭,解得()2f x >-,此时,()21f x -<≤-;若()1f x >-,则()()ln 10f f x f x =+<⎡⎤⎡⎤⎣⎦⎣⎦,可得()011f x <+<,解得()10f x -<<.综上,()20f x -<<.若1x ≤-,由()20f x -<<可得12402x ⎛⎫-<-< ⎪⎝⎭,可得1242x⎛⎫<< ⎪⎝⎭,解得21x -<<-,此时21x -<<-;若1x >-,由()20f x -<<可得()2ln 10x -<+<,可得2111x e <+<,解得2110x e -<<,此时,2110x e -<<.综上,满足()0f f x <⎡⎤⎣⎦的x 的取值范围为()212,11,0e ⎛⎫--⋃- ⎪⎝⎭.故选:D.3.(2021·全国高三三模)已知函数()xxf x e e-=+,若()()4561log ,log 6,log 45a f b f c f ⎛⎫=== ⎪⎝⎭,则,,a b c 的大小关系正确的是( )A .b a c >>B .a b c >>C .c b a >>D .c a b>>【答案】B 【解析】先判断函数的奇偶性,再利用导数判断函数的单调性,最后根据对数函数的性质,结合基本不等式、比较法进行判断即可.【详解】因为()()xx f x ee f x --=+=,所以()f x 为偶函数,()21x xxxe x ee f e --=='-,当0x >时,()0f x '>,函数单调递增,当0x <时,()0f x '<,函数单调递减,()()()()444561log log 5log 5,log 6,log 45a f f f b f c f ⎛⎫==-=== ⎪⎝⎭,因为lg4lg6+>故2222lg4lg6lg 24lg25lg4lg6(lg5)242+⎛⎫⎛⎫⋅<=<= ⎪ ⎪⎝⎭⎝⎭245lg5lg6lg 5lg4lg6log 5log 60lg4lg5lg4lg5-⋅-=-=>⋅所以456log 5log 61log 40>>>>,则.a b c >>故选:B.4.【多选题】(2021·辽宁高三月考)若1a b >>,则( )A .log 3log 3a b <B .33a b <C .11log ()log 21ab ab a b+≥-D .11+11a b <+【答案】ACD 【解析】由已知,A 选项,借助对数换底公式及对数函数单调性可判断;B 选项,利用幂函数单调性可判断;C 选项,利用对数函数单调性可判断;D 选项,利用反比例函数单调性可判断.【详解】对于A 选项:3log y x =在(0,+∞)上单调递增,1a b >>,则333311log log 0log log a b a b>>⇒<,即log 3log 3a b <,A 正确;对于B 选项:函数y =x 3在R 上递增,则33a b >,B 错误;对于C 选项:1a b >>,则ab >1,a +b >2,11log ()log log ()1ab ab ab a ba b a b ab++==+-log 21ab >-,有11log (log 21ab ab a b+≥-成立,即C 正确;对于D 选项:1112a b a b >>⇒+>+>,而函数1y x =在(0,+∞)上递减,则有11+11a b <+,即D 正确.故选:ACD5.【多选题】(2021·全国高三专题练习(理))已知0a b >>,且4ab =,则( )A .21a b ->B .22log log 1a b ->C .228a b +>D .22log log 1a b ⋅<【答案】ACD 【解析】利用不等式的性质和基本不等式的应用,结合指数函数与对数函数的单调性,对选项逐一分析判断.【详解】因为0a b >>,且4ab =,对A ,0a b ->,所以0221a b ->=,故A 正确;对B ,取83,32a b ==,所以2222216log log log log log 219a ab b -==<=,故B 错误;对C,22a b ≥+,当且仅当a b =取等号,又因为4a b +≥=,当且仅当a b =取等号,所以228a b ≥≥=+,当且仅当a b =取等号,因为0a b >>,所以不能取等号,故C 正确;对D ,当10>>>a b ,22log 0,log 0a b ><,所以22log log 1a b ⋅<;当1a b >>,22log 0,log 0a b >>,所以()()2222222log log log log log 144a b ab a b +⋅≤==,当且仅当a b =取等号,因为0a b >>,所以不能取等号,故D 正确.故选:ACD.6.【多选题】(2021·湖南高三二模)若正实数a ,b 满足a b >且ln ln 0a b ⋅>,下列不等式恒成立的是( )A .log 2log 2a b >B .ln ln a a b b ⋅>⋅C .122ab a b ++>D .log 0a b >【答案】CD 【解析】由已知不等式,求出,a b 之间的关系,结合选项一一判断即可.【详解】由ln ln 0a b ⋅>有01b a <<< 或1a b >> ,对于选项A ,当01b a <<<或1a b >>都有log 2log 2a b < ,选项A 错误;对于选项B ,比如当11,24a b == 时,有211111111ln ln 2ln ln 44424222⎛⎫==⨯= ⎪⎝⎭故ln ln a a b b ⋅>⋅不成立,选项B 错误;对于C ,因为()()1110ab a b a b +--=-->,所以1ab a b +>+ ,则122ab a b ++> ,选项C 正确;对于选项D ,因为ln ln 0a b ⋅>,所以ln log 0ln a bb a=>,选项D 正确,故选:CD .7.【多选题】(2021·山东临沂市·高三二模)若5log 2a =,1ln 22b =,1ln 55c =,则( )A .a b >B .b c>C .c a>D .2a b>【答案】AB 【解析】对四个选项一一验证:对于A :利用换底公式,化为同底结构,利用函数的单调性比较大小;对于B :利用换底公式,化为同底结构,利用函数的单调性比较大小;对于C :利用不等式的传递性比较大小;对于D :利用换底公式,化为同底结构,利用函数的单调性比较大小;【详解】对于A :522221111ln o 21l g 2,log 522log log a b e e ====⨯=,又25e >,且2log y x =为增函数,所以222l l g 5og o e <,所以22251l og 1l og e <,即a b >.故A 正确;对于B:1ln 22b ==,1ln 55c ==因为101052232,525,ln y x =====为增函数,所以b c >;故B 正确;对于C :因为a b >,b c >,所以a c >,故C 错误;对于D :因为1ln 22b =,所以212ln 2log b e ==,而521log 2,log 5a ==又5e <,所以22log log 5e <,所以2211log log 5e >,所以2b a >,故D 错误.故选:AB.8.(2021·浙江高三专题练习)已知函数()f x 满足()(1)f x f x =-+,当(0,1)x ∈时,函数()3x f x =,则13(log 19)f =__________.【答案】2719-【解析】由()(1)f x f x =-+得函数的周期为2,然后利用周期和()(1)f x f x =-+对13(log 19)f 化简可得13(log 19)f 33927(log 1)(log 1919f f =-+=-,从而可求得结果【详解】解:由题意,函数()f x 满足()(1)f x f x =-+,化简可得()(2)f x f x =+,所以函数()f x 是以2为周期的周期函数,又由(0,1)x ∈时,函数()3x f x =,且()(1)f x f x =-+,则133339(log 19)(log 19)(log 192)(log 19f f f f =-=-+=327log 193392727(log 1)(log 3191919f f =-+=-=-=-.故答案为:2719-.9.(2021·千阳县中学高三其他模拟(文))已知函数()()()11330log 0x x f x x x +⎧≤⎪=⎨>⎪⎩,则不等式()1f x >的解集为___________.【答案】11,3⎛⎫- ⎪⎝⎭【解析】根据分段函数的定义,分段讨论即可求解.【详解】解:()()()11330log 0x x f x x x +⎧≤⎪=⎨>⎪⎩ ,()10131x x f x +≤⎧∴>⇔⎨>⎩或130log 1x x >⎧⎪⎨>⎪⎩,解得10-<≤x 或103x <<,即113x -<<,∴不等式()1f x >的解集为11,3⎛⎫- ⎪⎝⎭.故答案为:11,3⎛⎫- ⎪⎝⎭.10.(2021·浙江丽水市·高三期末)已知()()()1log 1log 01a a a a a ++<<<,则a 的取值范围是__________.【答案】⎫⎪⎪⎭【解析】通过作差将()()()1log 1log 01a a a a a ++<<<转化为(1)log (1)log 0++-<a a a a ,利用换底公式计算可得[][](1)lg(1)lg lg(1)lg log (1)log lg lg(1)++-+++-=+a a a a a a a a a a ,分别判断每个因式的正负,最终转化为211()124+->a 成立,结合二次函数图像,即可求得a 的取值范围.【详解】∵(1)lg(1)lg log (1)log lg lg(1)a a a aa a a a +++-=-+22lg (1)lg lg (1)a aalg a +-=+[][]lg(1)lg lg(1)lg lg lg(1)a a a a a a +-++=+而当01a <<时,lg 0a <,g(0)l 1a +>,1lg(1)lg lglg10a a a a++-=>=211lg(1)lg lg (1)lg (24a a a a a ⎡⎤++=+=+-⎢⎥⎣⎦,所以()()()1log 1log 01a a a a a ++<<<即为211lg ()024⎡⎤+->⎢⎥⎣⎦a ,由于lg u 单调递增,所以211(124+->a .211()24u a =+-的图象如图,当1u =时,0a =,1a <<时,12u <<,lg 0u >,可得()()log 1log 10a a a a a +-+<.故答案为:⎫⎪⎪⎭1.(2020·全国高考真题(文))设3log 42a =,则4a-=( )练真题A .116B .19C .18D .16【答案】B 【解析】由3log 42a =可得3log 42a=,所以49a =,所以有149a-=,故选:B.2.(2020·全国高考真题(理))设函数()ln |21|ln |21|f x x x =+--,则f (x )( )A .是偶函数,且在1(,)2+∞单调递增B .是奇函数,且在11(,22-单调递减C .是偶函数,且在1(,)2-∞-单调递增D .是奇函数,且在1(,2-∞-单调递减【答案】D 【解析】由()ln 21ln 21f x x x =+--得()f x 定义域为12x x ⎧⎫≠±⎨⎬⎩⎭,关于坐标原点对称,又()()ln 12ln 21ln 21ln 21f x x x x x f x -=----=--+=-,()f x ∴为定义域上的奇函数,可排除AC ;当11,22x ⎛⎫∈-⎪⎝⎭时,()()()ln 21ln 12f x x x =+--,()ln 21y x =+Q 在11,22⎛⎫- ⎪⎝⎭上单调递增,()ln 12y x =-在11,22⎛⎫- ⎪⎝⎭上单调递减,()f x ∴在11,22⎛⎫- ⎪⎝⎭上单调递增,排除B ;当1,2x ⎛⎫∈-∞-⎪⎝⎭时,()()()212ln 21ln 12ln ln 12121x f x x x x x +⎛⎫=----==+ ⎪--⎝⎭,2121x μ=+- 在1,2⎛⎫-∞- ⎪⎝⎭上单调递减,()ln f μμ=在定义域内单调递增,根据复合函数单调性可知:()f x 在1,2⎛⎫-∞- ⎪⎝⎭上单调递减,D 正确.故选:D.3.(2020·天津高考真题)设0.80.70.713,,log 0.83a b c -⎛⎫=== ⎪⎝⎭,则,,a b c 的大小关系为( )A .a b c <<B .b a c <<C .b c a<<D .c a b<<【答案】D 【解析】因为0.731a =>,0.80.80.71333b a -⎛⎫==>= ⎪⎝⎭,0.70.7log 0.8log 0.71c =<=,所以1c a b <<<.故选:D.4.(2019年高考全国Ⅲ卷理)设是定义域为R 的偶函数,且在单调递减,则A .(log 3)>()>()B .(log 3)>()>()C .()>()>(log 3)D .()>()>(log 3)【答案】C【解析】是定义域为的偶函数,.,又在(0,+∞)上单调递减,∴,即.故选C .5.(2020·全国高考真题(理))若2233x y x y ---<-,则( )()f x ()0,+∞f 14f 322-f 232-f 14f 232-f 322-f 322-f 232-f 14f 232-f 322-f 14()f x R 331(log (log 4)4f f ∴=223303322333log 4log 31,1222,log 422---->==>>∴>> ()f x 23323(log 4)22f f f --⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭23323122log 4f f f --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭A .ln(1)0y x -+>B .ln(1)0y x -+<C .ln ||0x y ->D .ln ||0x y -<【答案】A 【解析】由2233x y x y ---<-得:2323x x y y ---<-,令()23t t f t -=-,2x y = 为R 上的增函数,3x y -=为R 上的减函数,()f t ∴为R 上的增函数,x y ∴<,0y x ->Q ,11y x ∴-+>,()ln 10y x ∴-+>,则A 正确,B 错误;x y -Q 与1的大小不确定,故CD 无法确定.故选:A.6.(2019·天津高考真题(文))已知a =log 27,b =log 38,c =0.30.2,则a ,b ,c 的大小关系为( )A.c <b <a B.a <b <c C.b <c <a D.c <a <b【答案】A 【解析】c =0.30.2<0.30=1;log 27>log 24=2;1<log 38<log 39=2.故c <b <a .故选A.。
高考数学专题《函数的图象》习题含答案解析

专题3.7 函数的图象1.(2021·全国高三专题练习(文))已知图①中的图象是函数()y f x=的图象,则图②中的图象对应的函数可能是()A.(||)y f x=B.|()|y f x=C.(||)y f x=-D.(||)y f x=--【答案】C【解析】根据函数图象的翻折变换,结合题中条件,即可直接得出结果.【详解】图②中的图象是在图①的基础上,去掉函数()y f x=的图象在y轴右侧的部分,然后将y轴左侧图象翻折到y轴右侧,y轴左侧图象不变得来的,∴图②中的图象对应的函数可能是(||)y f x=-.故选:C.2.(2021·浙江高三专题练习)函数()lg1y x=-的图象是()A.B.C.练基础D .【答案】C【解析】将函数lg y x =的图象进行变换可得出函数()lg 1y x =-的图象,由此可得出合适的选项.【详解】将函数lg y x =的图象先向右平移1个单位长度,可得到函数()lg 1y x =-的图象,再将所得函数图象位于x 轴下方的图象关于x 轴翻折,位于x 轴上方图象不变,可得到函数()lg 1y x =-的图象.故合乎条件的图象为选项C 中的图象.故选:C.3.(2021·全国高三专题练习(理))我国著名数学家华罗庚先生曾说:“数缺形时少直观,形缺数时难入微,数形结合百般好,隔离分家万事休.”在数学的学习和研究中,经常用函数的图象来研究函数的性质,也经常用函数的解析式来研究函数图象的特征.若函数()y fx =在区间[],a b 上的图象如图,则函数()y f x =在区间[],a b 上的图象可能是( )A .B .C .D .【答案】D【解析】先判断出函数是偶函数,根据偶函数的图像特征可得选项.【详解】 函数()y f x =是偶函数,所以它的图象是由()y f x =把0x ≥的图象保留,再关于y 轴对称得到的.结合选项可知选项D 正确,故选:D .4.(2021·全国高三专题练习(文))函数()5xf x x x e =-⋅的图象大致是( ). A . B .C .D .【答案】B【解析】由()20f >和()20f -<可排除ACD ,从而得到选项.【详解】由()()2223222160f e e =-=->,可排除AD ;由()()2223222160f e e ---=-+=-<,可排除C ;故选:B.5.(2021·陕西高三三模(理))函数x y b a =⋅与()log a y bx =的图像在同一坐标系中可能是()A .B .C .D .【答案】C【解析】根据指数函数和对数函数的单调性,以及特殊点函数值的范围逐一判断可得选项.【详解】令x f x b a ,()()log a g x bx =,对于A 选项:由x f xb a 得>1a ,且()00>1f b a b ==⋅,所以log >0a b ,而()1log 0a g b =<,所以矛盾,故A 不正确;对于B 选项:由x f xb a 得>1a ,且()001f b a b ⋅=<=,所以log 0a b <,而()1log >0a g b =,所以矛盾,故B 不正确;对于C 选项:由x f xb a 得>1a ,且()001f b a b ⋅=<=,所以log 0a b <,又()1log 0a g b =<,故C 正确;对于D 选项:由x f xb a 得>1a ,且()00>1f b a b ==⋅,而()()log a g x bx =中01a <<,所以矛盾,故D 不正确;故选:C . 6.(2021·宁夏吴忠市·高三其他模拟(文))已知函数()()()ln 2ln 4f x x x =-+-,则( ). A .()f x 的图象关于直线3x =对称B .()f x 的图象关于点()3,0对称C .()f x 在()2,4上单调递增D .()f x 在()2,4上单调递减【答案】A【解析】先求出函数的定义域.A :根据函数图象关于直线对称的性质进行判断即可;B :根据函数图象关于点对称的性质进行判断即可;C :根据对数的运算性质,结合对数型函数的单调性进行判断即可;D :结合C 的分析进行判断即可.【详解】 ()f x 的定义域为()2,4x ∈,A :因为()()()()3ln 1ln 13f x x x f x +=++-=-,所以函数()f x 的图象关于3x =对称,因此本选项正确;B :由A 知()()33f x f x +≠--,所以()f x 的图象不关于点()3,0对称,因此本选项不正确;C :()()()2ln 2ln 4ln(68)x x x f x x =-+-=-+- 函数2268(3)1y x x x =-+-=--+在()2,3x ∈时,单调递增, 在()3,4x ∈时,单调递减,因此函数()f x 在()2,3x ∈时单调递增,在()3,4x ∈时单调递减,故本选项不正确;D :由C 的分析可知本选项不正确,故选:A7.(2021·安徽高三二模(理))函数()n xf x x a =,其中1a >,1n >,n 为奇数,其图象大致为( ) A . B .C .D .【答案】B【解析】分析()f x 在()0,∞+、(),0-∞上的函数值符号,及该函数在()0,∞+上的单调性,结合排除法可得出合适的选项.【详解】对任意x ∈R ,0x a >,由于1n >,n 为奇数,当0x <时,0n x <,此时()0f x <,当0x >时,0n x >,此时()0f x >,排除AC 选项;当0x >时,任取1x 、()20,x ∈+∞且12x x >,则120x x a a >>,120n n x x >>,所以()()12f x f x >,所以,函数()f x 在()0,∞+上为增函数,排除D 选项.故选:B.8.(2021·浙江高三专题练习)已知函数f (x )=1331,,log 1x x x x ⎧≤⎪⎨>⎪⎩则函数y =f (1-x )的大致图象是( ) A . B .C .D .【答案】D【解析】由()f x 得到()1f x -的解析式,根据函数的特殊点和正负判断即可.【详解】因为函数()f x 133,1log ,1x x x x ⎧≤⎪=⎨>⎪⎩, 所以函数()1f x -()1133,0log 1,0x x x x -⎧≥⎪=⎨-<⎪⎩, 当x =0时,y =f (1)=3,即y =f (1-x )的图象过点(0,3),排除A ;当x =-2时,y =f (3)=-1,即y =f (1-x )的图象过点(-2,-1),排除B ;当0x <时,()1311,(1)log 10x f x x ->-=-<,排除C ,故选:D .9.【多选题】(2021·浙江高一期末)如图,某池塘里浮萍的面积y (单位:2m )与时间t (单位:月)的关系为t y a =.关于下列法正确的是( )A .浮萍每月的增长率为2B .浮萍每月增加的面积都相等C .第4个月时,浮萍面积不超过280mD .若浮萍蔓延到22m 、24m 、28m 所经过的时间分别是1t 、2t 、3t ,则2132t t t =+【答案】AD【解析】根据图象过点求出函数解析式,根据四个选项利用解析式进行计算可得答案.【详解】由图象可知,函数图象过点(1,3),所以3a =,所以函数解析式为3ty =, 所以浮萍每月的增长率为13323233t t tt t +-⨯==,故选项A 正确; 浮萍第一个月增加的面积为10332-=平方米,第二个月增加的面积为21336-=平方米,故选项B 不正确;第四个月时,浮萍面积为438180=>平方米,故C 不正确;由题意得132t =,234t =,338t =,所以13log 2t =,23log 4t =,33log 8t =,所以2133333332log 2log 8log (28)log 16log 42log 42t t t +=+=⨯====,故D 正确.故选:AD10.(2020·全国高一单元测试)函数()2x f x =和()3g x x =的图象如图所示,设两函数的图象交于点11(,)A x y ,22(,)B x y ,且12x x <.(1)请指出图中曲线1C ,2C 分别对应的函数;(2)结合函数图象,比较(3)f ,(3)g ,(2020)f ,(2020)g 的大小.【答案】(1)1C 对应的函数为()3g x x =,2C 对应的函数为()2x f x =;(2)(2020)(2020)(3)(3)f g g f >>>.【解析】(1)根据指数函数和一次函数的函数性质解题;(2)结合函数的单调性及增长快慢进行比较.【详解】(1)1C 对应的函数为()3g x x =,2C 对应的函数为()2x f x =.(2)(0)1f =,(0)0g =,(0)(0)f g ∴>,又(1)2f =,(1)3g =,(1)(1)f g ∴<,()10,1x ∴∈;(3)8f =,(3)9g =,(3)(3)f g ∴<,又(4)16f =,(4)12g =,(4)(4)f g ∴>,()23,4x ∴∈.当2x x >时,()()f x g x >,(2020)(2020)f g ∴>.(2020)(2020)(3)(3)f g g f ∴>>>.1.(2021·湖南株洲市·高三二模)若函数()2()mx f x e n =-的大致图象如图所示,则( )A .0,01m n ><<B .0,1m n >>C .0,01m n <<<D .0,1m n <>【答案】B【解析】令()0f x =得到1ln x n m =,再根据函数图象与x 轴的交点和函数的单调性判断.【详解】令()0f x =得mx e n =,即ln mx n =,解得1ln x n m =,由图象知1l 0n x m n =>,当0m >时,1n >,当0m <时,01n <<,故排除AD ,当0m <时,易知mx y e =是减函数,当x →+∞时,0y →,()2f x n →,故排除C故选:B2.(2021·甘肃高三二模(理))关于函数()ln |1|ln |1|f x x x =++-有下列结论,正确的是( ) A .函数()f x 的图象关于原点对称 B .函数()f x 的图象关于直线1x =对称 练提升C .函数()f x 的最小值为0D .函数()f x 的增区间为(1,0)-,(1,)+∞【答案】D 【解析】A.由函数的奇偶性判断;B.利用特殊值判断;C.利用对数函数的值域求解判断;D.利用复合函数的单调性判断. 【详解】2()ln |1|ln |1|ln |1|f x x x x =++-=-,由1010x x ⎧+>⎪⎨->⎪⎩,解得1x ≠±,所以函数的定义域为{}|1x x ≠±, 因为()ln |1|ln |1|ln |1|ln |1|()f x x x x x f x -=-++--=++-=,所以函数为偶函数,故A 错误. 因为(0)ln |1|0,(3)ln8f f =-==,所以(0)(3)f f ≠,故B 错误;因为 ()2|1|0,x -∈+∞,所以()f x ∈R ,故C 错误;令2|1|t x =-,如图所示:,t 在(),1,[0,1)-∞-上递减,在()(1,0],1,-+∞上递增,又ln y t =在()0,∞+递增,所以函数()f x 的增区间为(1,0)-,(1,)+∞,故D 正确; 故选:D3.(2021·吉林长春市·东北师大附中高三其他模拟(理))函数ln xy x=的图象大致为( )A .B .C .D .【答案】C 【解析】 求出函数ln xy x=的定义域,利用导数分析函数的单调性,结合排除法可得出合适的选项. 【详解】 对于函数ln xy x =,则有0ln 0x x >⎧⎨≠⎩,解得0x >且1x ≠, 所以,函数ln xy x=的定义域为()()0,11,+∞,排除AB 选项;对函数ln x y x =求导得()2ln 1ln x y x -'=.当01x <<或1x e <<时,0y '<;当x e >时,0y '>. 所以,函数ln xy x=的单调递减区间为()0,1、()1,e ,单调递增区间为(),e +∞, 当01x <<时,0ln xy x =<,当1x >时,0ln x y x=>,排除D 选项. 故选:C.4.(2021·海原县第一中学高三二模(文))函数2xx xy e+=的大致图象是( )A .B .C .D .【答案】D 【解析】利用导数可求得2xx xy e+=的单调性,由此排除AB ;根据0x >时,0y >可排除C ,由此得到结果. 【详解】 由题意得:()()222211x xxxx e x x e x x y e e +-+-++'==,令0y '=,解得:1x =,2x =,∴当11,,22x ∞∞⎛⎛⎫+∈-⋃+ ⎪ ⎪⎝⎭⎝⎭时,0y '<;当11,22x ⎛+∈ ⎝⎭时,0y '>;2x x x y e +∴=在1,2⎛--∞ ⎝⎭,1,2⎛⎫++∞ ⎪ ⎪⎝⎭上单调递减,在1122⎛⎫-+ ⎪ ⎪⎝⎭上单调递增,可排除AB ; 当0x >时,0y >恒成立,可排除C. 故选:D.5.(2021·天津高三三模)意大利画家列奥纳多·达·芬奇的画作《抱银鼠的女子》(如图所示)中,女士颈部的黑色珍珠项链与她怀中的白貂形成对比.光线和阴影衬托出人物的优雅和柔美.达·芬奇提出:固定项链的两端,使其在重力的作用下自然下垂,形成的曲线是什么?这就是著名的“悬链线问题”.后人研究得出,悬链线并不是抛物线,而是与解析式为2x x e e y -+=的“双曲余弦函数”相关.下列选项为“双曲余弦函数”图象的是( )A .B .C .D .【答案】C 【解析】分析函数2x xe e y -+=的奇偶性与最小值,由此可得出合适的选项.【详解】令()e e 2x x f x -+=,则该函数的定义域为R ,()()2x xe ef x f x -+-==,所以,函数()e e 2x xf x -+=为偶函数,排除B 选项.由基本不等式可得()112f x ≥⨯=,当且仅当0x =时,等号成立,所以,函数()f x 的最小值为()()min 01f x f ==,排除AD 选项. 故选:C.6.(2021·浙江高三月考)函数()3log 01a y x ax a =-<<的图象可能是( )A .B .C .D .【答案】B 【解析】先求出函数的定义域,判断函数的奇偶性,构造函数,求函数的导数,利用是的导数和极值符号进行判断即可. 【详解】根据题意,()3log a f x x ax =-,必有30x ax -≠,则0x ≠且x ≠即函数的定义域为{|0x x ≠且x ≠,()()()()33log log a a x a x x f f x ax x ---=--==,则函数3log a y x ax =-为偶函数,排除D ,设()3g x x ax =-,其导数()23g x x a '=-,由()0g x '=得x =±,当3x >时,()0g x '>,()g x 为增函数,而()f x 为减函数,排除C ,在区间,33⎛⎫- ⎪ ⎪⎝⎭上,()0g x '<,则()g x 在区间,33⎛⎫- ⎪ ⎪⎝⎭上为减函数,在区间3⎛⎫+∞ ⎪ ⎪⎝⎭上,()0g x '>,则()g x 在区间3⎛⎫+∞ ⎪ ⎪⎝⎭上为增函数,0g=,则()g x 存在极小值33339g a ⎛⎛⎫=-⨯=- ⎪ ⎪⎝⎭⎝⎭,此时()g x ()0,1,此时()0f x >,排除A , 故选:B.7.(2019·北京高三高考模拟(文))当x∈[0,1]时,下列关于函数y=2(1)mx -的图象与y =的图象交点个数说法正确的是( ) A .当[]m 0,1∈时,有两个交点 B .当(]m 1,2∈时,没有交点 C .当(]m 2,3∈时,有且只有一个交点 D .当()m 3,∞∈+时,有两个交点【答案】B 【解析】设f (x )=2(1)mx -,g (x ) ,其中x∈[0,1]A .若m=0,则()1f x =与()g x =[0,1]上只有一个交点(1,1),故A 错误.B .当m∈(1,2)时,111()(0)1,()(0)1()()2f x f g x g f x g x m<<∴≤=≥=>∴<即当m∈(1,2]时,函数y=2(1)mx -的图象与y =x∈[0,1]无交点,故B 正确,C .当m∈(2,3]时,2111()(1)(1),()(1)32f x f mg x g m <<∴≤=-≤=2(1)m >-时()()f x g x <,此时无交点,即C 不一定正确.D .当m∈(3,+∞)时,g (0)1,此时f (1)>g (1),此时两个函数图象只有一个交点,故D 错误,故选:B.8.(2021·浙江高三专题练习)若关于x的不等式34log2xax-≤在10,2x⎛⎤∈ ⎥⎝⎦恒成立,则实数a的取值范围是()A.1,14⎡⎫⎪⎢⎣⎭B.10,4⎛⎤⎥⎝⎦C.3,14⎡⎫⎪⎢⎣⎭D.30,4⎛⎤⎥⎝⎦【答案】A 【解析】转化为当10,2x⎛⎤∈ ⎥⎝⎦时,函数342xy=-的图象不在log ay x=的图象的上方,根据图象列式可解得结果.【详解】由题意知关于x的不等式34log2xax-≤在10,2x⎛⎤∈ ⎥⎝⎦恒成立,所以当10,2x⎛⎤∈ ⎥⎝⎦时,函数342xy=-的图象不在log ay x=的图象的上方,由图可知0111log 22a a <<⎧⎪⎨≥⎪⎩,解得114a ≤<. 故选:A9.对a 、b ∈R ,记{},max ,,a a b a b b a b⎧=⎨<⎩≥,函数{}2()max ||,24()f x x x x x =--+∈R .(1)求(0)f ,(4)f -.(2)写出函数()f x 的解析式,并作出图像.(3)若关于x 的方程()f x m =有且仅有3个不等的解,求实数m 的取值范围.(只需写出结论) 【答案】见解析.【解析】解:(1)∵{},max ,,a a b a b b a b⎧=⎨<⎩≥,函数{}2()max ||,24f x x x x =--+,∴{}(0)max 0,44f ==,{}(4)max 4,44f -=-=.(2)(3)5m =或m 10.(2021·全国高一课时练习)函数()2xf x =和()()30g x xx =≥的图象,如图所示.设两函数的图象交于点()11A x y ,,()22B x y ,,且12x x <.(1)请指出示意图中曲线1C ,2C 分别对应哪一个函数;(2)结合函数图象,比较()8f ,()8g ,()2015f ,()2015g 的大小. 【答案】(1)1C 对应的函数为()()30g x xx =≥,2C 对应的函数为()2x f x =;(2)()()()()2015201588f g g f >>>.【解析】(1)根据图象可得结果;(2)通过计算可知1282015x x <<<,再结合题中的图象和()g x 在()0+∞,上的单调性,可比较()8f ,()8g ,()2015f ,()2015g 的大小.【详解】(1)由图可知,1C 的图象过原点,所以1C 对应的函数为()()30g x xx =≥,2C 对应的函数为()2x f x =.(2)因为11g =(),12f =(),28g =(),24f =(),()9729g =,()9512f =,()101000g =,()101024f =,所以11f g >()(),22f g <()(),()()99f g <,()()1010f g >.所以112x <<,2910x <<.所以1282015x x <<<.从题中图象上知,当12x x x <<时,()()f x g x <;当2x x >时,()()f x g x >,且()g x 在()0+∞,上是增函数,所以()()()()2015201588f g g f >>>.1. (2020·天津高考真题)函数241xy x =+的图象大致为( ) 练真题A .B .C .D .【答案】A 【解析】由函数的解析式可得:()()241xf x f x x --==-+,则函数()f x 为奇函数,其图象关于坐标原点对称,选项CD 错误; 当1x =时,42011y ==>+,选项B 错误. 故选:A.2.(2019年高考全国Ⅲ卷理)函数3222x xx y -=+在[]6,6-的图像大致为( ) A . B .C .D .【答案】B【解析】设32()22x xx y f x -==+,则332()2()()2222x x x x x x f x f x ----==-=-++,所以()f x 是奇函数,图象关于原点成中心对称,排除选项C .又34424(4)0,22f -⨯=>+排除选项D ; 36626(6)722f -⨯=≈+,排除选项A , 故选B .3.(2020·天津高考真题)已知函数3,0,(),0.x x f x x x ⎧=⎨-<⎩若函数2()()2()g x f x kx xk =--∈R 恰有4个零点,则k 的取值范围是( ) A .1,(22,)2⎛⎫-∞-+∞ ⎪⎝⎭B .1,(0,22)2⎛⎫-∞- ⎪⎝⎭C .(,0)(0,22)-∞D .(,0)(22,)-∞+∞【答案】D 【解析】注意到(0)0g =,所以要使()g x 恰有4个零点,只需方程()|2|||f x kx x -=恰有3个实根 即可, 令()h x =()||f x x ,即|2|y kx =-与()()||f x h x x =的图象有3个不同交点. 因为2,0()()1,0x x f x h x x x ⎧>==⎨<⎩, 当0k =时,此时2y =,如图1,2y =与()()||f x h x x =有2个不同交点,不满足题意; 当k 0<时,如图2,此时|2|y kx =-与()()||f x h x x =恒有3个不同交点,满足题意; 当0k >时,如图3,当2y kx =-与2yx 相切时,联立方程得220x kx -+=,令0∆=得280k -=,解得k =,所以k >综上,k 的取值范围为(,0)(22,)-∞+∞.故选:D.4.(2019年高考全国Ⅱ卷理)设函数()f x 的定义域为R ,满足(1) 2 ()f x f x +=,且当(0,1]x ∈时,()(1)f x x x =-.若对任意(,]x m ∈-∞,都有8()9f x ≥-,则m 的取值范围是A .9,4⎛⎤-∞ ⎥⎝⎦B .7,3⎛⎤-∞ ⎥⎝⎦C .5,2⎛⎤-∞ ⎥⎝⎦D .8,3⎛⎤-∞ ⎥⎝⎦【答案】B【解析】∵(1) 2 ()f x f x +=,()2(1)f x f x ∴=-. ∵(0,1]x ∈时,1()(1)[,0]4f x x x =-∈-;∴(1,2]x ∈时,1(0,1]x -∈,1()2(1)2(1)(2),02f x f x x x ⎡⎤=-=--∈-⎢⎥⎣⎦; ∴(2,3]x ∈时,1(1,2]x -∈,()2(1)4(2)(3)[1,0]f x f x x x =-=--∈-,如图:当(2,3]x ∈时,由84(2)(3)9x x --=-解得173x =,283x =,若对任意(,]x m ∈-∞,都有8()9f x ≥-,则73m ≤.则m 的取值范围是7,3⎛⎤-∞ ⎥⎝⎦.故选B.5.(2017·天津高考真题(文))已知函数f(x)={|x|+2,x <1x +2x ,x ≥1.设a ∈R ,若关于x 的不等式f(x)≥|x 2+a|在R 上恒成立,则a 的取值范围是 A .[−2,2] B .[−2√3,2] C .[−2,2√3] D .[−2√3,2√3] 【答案】A【解析】满足题意时f (x )的图象恒不在函数y =|x2+a|下方,当a =2√3时,函数图象如图所示,排除C,D 选项;当a =−2√3时,函数图象如图所示,排除B 选项,本题选择A 选项.6.(2018·全国高考真题(文))设函数()2010x x f x x -⎧≤=⎨>⎩,,,则满足()()12f x f x +<的x 的取值范围是( )A .(]1-∞-,B .()0+∞,C .()10-,D .()0-∞,【答案】D 【解析】分析:首先根据题中所给的函数解析式,将函数图像画出来,从图中可以发现若有()()12f x f x +<成立,一定会有2021x x x <⎧⎨<+⎩,从而求得结果.详解:将函数()f x 的图像画出来,观察图像可知会有2021x x x <⎧⎨<+⎩,解得0x <,所以满足()()12f x f x +<的x 的取值范围是()0-∞,,故选D .。
高考数学专题《函数的概念及其表示》习题含答案解析

专题3.1 函数的概念及其表示1.(2021·四川达州市·高三二模(文))已知定义在R 上的函数()f x 满足,2(1)2()1f x f x x -+=+,则(1)f =( )A .1-B .1C .13-D .13【答案】B 【解析】当0x =时,f (1)2(0)1f +=①;当1x =时,(0)2f f +(1)2=②,由此进行计算能求出f (1)的值. 【详解】定义在R 上的函数()f x 满足,2(1)2()1f x f x x -+=+,∴当0x =时,f (1)2(0)1f +=,①当1x =时,(0)2f f +(1)2=,②②2⨯-①,得3f (1)3=,解得f (1)1=. 故选:B2.(2021·浙江高一期末)已知231,1,()3,1,x x f x x x +⎧=⎨+>⎩则(3)f =( )A .7B .2C .10D .12【答案】D 【解析】根据分段函数的定义计算. 【详解】由题意2(3)3312f =+=.故选:D .练基础3.(2021·全国高一课时练习)设3,10()(5),10x x f x f x x +>⎧=⎨+≤⎩,则(5)f 的值为( )A .16B .18C .21D .24【答案】B 【解析】根据分段函数解析式直接求解. 【详解】因为3,10()(5),10x x f x f x x +>⎧=⎨+≤⎩,所以(5)(10)(15)15318f f f ===+=. 故选:B.4.(2021·浙江湖州市·湖州中学高一开学考试)若函数213()22f x x x =-+的定义域和值域都是[1,]b ,则b =( ) A .1 B .3C .3-D .1或3【答案】B 【解析】 根据函数213()22f x x x =-+在[1,]b 上为增函数,求出其值域,结合已知值域可求出结果. 【详解】 因为函数213()22f x x x =-+21(1)12x =-+在[1,]b 上为增函数,且定义域和值域都是[1,]b , 所以min ()(1)f x f =1=,2max 13()()22f x f b b b b ==-+=,解得3b =或1b =(舍),故选:B5.(上海高考真题)若是的最小值,则的取值范围为( ).A .[-1,2]B .[-1,0]C .[1,2]D .[0,2]【答案】D 【详解】由于当0x >时,1()f x x a x=++在1x =时取得最小值2a +,由题意当0x ≤时,2()()f x x a =-应该是递减的,则0a ≥,此时最小值为2(0)f a =,因此22a a ≤+,解得02a ≤≤,选D .6.(广东高考真题)函数()f x x=的定义域是______. 【答案】[)()1,00,∞-⋃+ 【解析】由根式内部的代数式大于等于0且分式的分母不等于0联立不等式组求解x 的取值集合得答案. 【详解】由{100x x +≥≠,得1x ≥-且0x ≠.∴函数()f x =的定义域为:[)()1,00,-⋃+∞; 故答案为[)()1,00,-⋃+∞.7.(2021·青海西宁市·高三一模(理))函数()f x 的定义域为[]1,1-,图象如图1所示,函数()g x 的定义域为[]1,2-,图象如图2所示.若集合()(){}0A x f g x ==,()(){}0B x g f x ==,则A B 中有___________个元素.【答案】3 【解析】利用数形结合分别求出集合A 与集合B ,再利用交集运算法则即可求出结果. 【详解】若()()0f g x =,则()0g x =或1-或1,∴{}1,0,1,2A =-, 若()()0g f x =,则0f x 或2,∴{}1,0,1B =-,∴{}1,0,1=-AB .故答案为:3.8.(2021·湖北襄阳市·襄阳五中高三二模)已知函数22211x x y f x x ⎛⎫+-= ⎪+-⎝⎭的定义域是[)1,+∞,则函数()y f x =的定义域是_______.【答案】(]1,2 【解析】令()()222111x x g x x x x +-=≥+-,根据函数值域的求解方法可求得()g x 的值域即为所求的()f x 的定义域.【详解】令()()222111x x g x x x x +-=≥+-,则()()222111111111x x x x g x x x x x x x x+-+==+=+≥+-+--+, 1y x x =-在[)1,+∞上单调递增,10x x∴-≥,10111x x∴<≤-+,()12g x ∴<≤,()f x ∴的定义域为(]1,2.故答案为:(]1,2.9.(2021·黑龙江哈尔滨市第六中学校高三二模(文))已知函数()221,01,0x x f x x x⎧+≥⎪=⎨<⎪⎩,若()2f a =,则实数a =___________. 【答案】1或- 【解析】分别令212a +=,212a=,解方程,求出方程的根即a 的值即可. 【详解】当0a ≥,令212a +=,解得:1a =,当0a <,令212a =,解得:2a =-, 故1a =或2-, 故答案为:1或2-. 10.(2021·云南高三二模(理))已知函数231,1()1,1x x f x x x +≤⎧=⎨->⎩,若n m >,且()()f n f m =,设t n m =-,则t 的取值范围为________.【答案】171,12⎤⎥⎦【解析】用n 表示出m ,结合二次函数的性质求得t n m =-的取值范围. 【详解】画出()f x 图象如下图所示,3114⨯+=,令()2140x x -=>,解得x =由()(),n m f n f m >=得2311m n +=-,223n m -=,且1n <≤所以(222121333n t n m n n n n -=-=-=-++<≤,结合二次函数的性质可知,当131223n =-=⎛⎫⨯- ⎪⎝⎭时,t 取得最大值为2133217322312⎛⎫-⨯++= ⎪⎝⎭,当n =时,t取得最小值为212133-⨯=. 所以t的取值范围是171,12⎤⎥⎦.故答案为:171,12⎤⎥⎦1.(2021·云南高三二模(文))已知函数231,1()1,1x x f x x x +≤⎧=⎨->⎩,若n m >,且()()f n f m =,设t n m =-,则( ) A .t 没有最小值 B .t 1 C .t 的最小值为43D .t 的最小值为1712【答案】B 【解析】先作出分段函数图象,再结合图象由()()f n f m =,得到m 与n 的关系,消元得关于n 的函数,最后求最值. 【详解】如图,作出函数()f x 的图象,练提升()()f n f m =且n m >,则1m ,且1n >,2311m n ∴+=-,即223n m -=.由21014n n >⎧⎨<-≤⎩,解得1n <≤222211317(32)()333212n n m n n n n -⎡⎤∴-=-=---=--+⎢⎥⎣⎦,又1n <≤∴当n =()min 1n m -=.故选:B.2.(2020·全国高一单元测试)已知函数21,0,()2,0,x x f x x x ⎧+≤=⎨->⎩,若()05f x =,则0x 的取值集合是( )A .{2}-B .5,22⎧⎫-⎨⎬⎩⎭C .{2,2}-D .52,2,2⎧⎫--⎨⎬⎩⎭【答案】A 【解析】根据分段函数值的求解方法,对00x ≤与00x >两种情况求解,可得答案. 【详解】若00x ≤,可得2015x +=,解得02x =-,(02x =舍去);若00x >,可得02x -=5,可得052x =-,与00x >相矛盾,故舍去,综上可得:02x =-. 故选:A.3.【多选题】(2021·全国高一课时练习)(多选题)下列函数中,定义域是其值域子集的有( )A .865y x =+ B .225y x x =--+ C .y =D .11y x=- 【答案】AC 【解析】分别求得函数的定义域和值域,利用子集的定义判断. 【详解】A 函数的定义域和值域都是R ,符合题意;B.定义域为R ,因为2225(1)66y x x x =--+=-++≤,所以函数值域为(,6]-∞,值域是定义域的真子集不符合题意;C.易得定义域为[1,)+∞,值域为[0,)+∞,定义域是值域的真子集;D.定义域为{|0}x x ≠,值域为{|1}x x ≠-,两个集合只有交集; 故选:AC4.【多选题】(2021·全国高一课时练习)已知f (x )=2211x x +-,则f (x )满足的关系有( )A .()()f x f x -=-B .1f x ⎛⎫⎪⎝⎭= ()f x - C .1f x ⎛⎫⎪⎝⎭=f (x ) D .1()()f f x x-=-【答案】BD 【解析】根据函数()f x 的解析式,对四个选项逐个分析可得答案. 【详解】因为f (x )= 2211x x+-, 所以()f x -=221()1()x x +---=2211x x +-()f x =,即不满足A 选项;1f x ⎛⎫ ⎪⎝⎭=221111x x ⎛⎫+ ⎪⎝⎭⎛⎫- ⎪⎝⎭=2211x x +-,1f x ⎛⎫⎪⎝⎭=()f x -,即满足B 选项,不满足C 选项, 1()f x -=221111x x ⎛⎫+- ⎪⎝⎭⎛⎫-- ⎪⎝⎭=2211x x +-,1()()f f x x -=-,即满足D 选项. 故选:BD5.【多选题】(2021·全国高三其他模拟)已知函数21,0,()2,0,x x f x x x x +<⎧=⎨-+≥⎩令()()()g x f f x =,则下列说法正确的是( ) A .()10g -=B .方程()2g x =有3个根C .方程()2g x =-的所有根之和为-1D .当0x <时,()()f x g x ≤【答案】ACD 【解析】由题意知()10f -=可得()10g -=;令()f x u =,因为方程()2f u =没有实根,即()2g x =没有实根;令()u f x =,则方程()2g x =-,即()2f u =-,通过化简与计算即可判断C ;当0x <时,()(1)g x f x =+,则将函数()f x 在(,1)-∞的图象向左平移1个单位长度可得函数()g x 的图象,即可判断D . 【详解】对于A 选项,由题意知()10f -=,则()()()()1100g f f f -=-==,所以A 选项正确; 对于B 选项,令()f x u =,则求()()()2g x f f x ==的根,即求()2f u =的根, 因为方程()2f u =没有实根,所以()2g x =没有实根,所以选项B 错误;对于C 选项,令()u f x =,则方程()2g x =-,即()2f u =-,得112,03u u u +=-<⇒=-,2222,01u u u u -+=-≥⇒=由方程1()f x u =得13(0)x x +=-<或223(0)x x x -+=-≥,解得4x =-或3x =,易知方程2()f x u =,没有实数根,所以方程()2g x =-的所有根之和为-1,选项C 正确;对于D 选项,当0x <时,()(1)g x f x =+,则将函数()f x 在(,1)-∞的图象向左平移1个单位长度可得函数()g x 的图象,当0x <时,函数()g x 的图象不在()f x 的图象的下方,所以D 选项正确,故选:ACD .6.【多选题】(2021·全国高三专题练习)已知函数()f x ,(,0)(0,)x ∈-∞⋃+∞,对于任意的,(,0)(0,)x y ∈-∞+∞,()()()f xy f x f y =+,则( )A .()f x 的图象过点()1,0和()1,0-B .()f x 在定义域上为奇函数C .若当1x >时,有()0f x >,则当10x -<<时,()0f x <D .若当01x <<时,有()0f x <,则()0f x >的解集为()1,+∞ 【答案】AC 【解析】根据抽象函数的性质,利用特殊值法一一判断即可; 【详解】解:因为函数()f x ,(,0)(0,)x ∈-∞⋃+∞,对于任意的,(,0)(0,)x y ∈-∞+∞,()()()f xy f x f y =+,令1x y ==,则()()()111f f f =+,则()10f =,令1x y ==-,则()()()111f f f =-+-,则()10f -=,所以()f x 过点()1,0和()1,0-,故A 正确;令1y =-,则()()()1f x f x f -=+-,即()()f x f x -=,所以()f x 为偶函数,故B 错误; 令1y x =-,则()()110f f x f x ⎛⎫-=+-= ⎪⎝⎭,则()1f f x x ⎛⎫-=- ⎪⎝⎭当1x >时,所以()11,0x -∈-,又()0f x >,则10f x ⎛⎫-< ⎪⎝⎭,即当10x -<<时,()0f x <,故C 正确;令1y x =,则()()110f f x f x ⎛⎫=+= ⎪⎝⎭,则()1f f x x ⎛⎫=- ⎪⎝⎭,当01x <<时,所以()11,x ∈+∞,又()0f x <,则10f x ⎛⎫> ⎪⎝⎭,即当1x >时,()0f x >,因为()f x 是偶函数,所以1x <-时,()0f x >,所以()0f x >的解集为()(),11,-∞-+∞,故D 错误;故选:AC7.【多选题】(2021·全国高三专题练习)已知函数()22,023,0x x x f x x x ⎧-<=⎨-+≥⎩,则( )A .()13f f -⎡⎤⎣=-⎦B .若()1f a =-,则2a =C .()f x 在R 上是减函数D .若关于x 的方程()f x a =有两解,则(]0,3a ∈ 【答案】ABD 【解析】根据函数解析式,代入数据可判断A 、B 的正误,做出()f x 的图象,可判断C 、D 的正误,即可得答案. 【详解】对于A :由题意得:2(1)(1)2(1)3f -=--⨯-=, 所以()(3)23331f f f -==-⨯+=-⎡⎤⎣⎦,故A 正确;对于B :当0a <时,2()21f a a a =-=-,解得a =1,不符合题意,舍去当0a ≥时,()231f a a =-+=-,解得2a =,符合题意,故B 正确; 对于C :做出()f x 的图象,如下图所示:所以()f x 在R 上不是减函数,故C 错误;对于D :方程()f x a =有两解,则()y f x =图象与y a =图象有两个公共点, 如下图所示所以(]0,3a ∈,故D 正确. 故选:ABD8.(2021·浙江高三月考)已知0a >,设函数2(22),(02)(),(2)x a x x a f x ax x a ⎧-++<<+=⎨≥+⎩,存在0x 满足()()00f f x x =,且()00f x x ≠,则a 的取值范围是______.1a ≤< 【解析】求得()2x ax a y =≥+关于y x =对称所得函数的解析式,通过构造函数,结合零点存在性列不等式,由此求得a 的取值范围.【详解】由于()f x 存在0x 满足()()0f f x x =,且()00f x x ≠,所以()f x 图象上存在关于y x =对称的两个不同的点.对于()()2,2y ax x a y a a =≥+≥+,交换,x y 得x ay =, 即()()12,2y x x a a y a a=≥+≥+, 构造函数()()22111222222g x x a x x x a x x x a a a a ⎛⎫⎛⎫=-++-=-++-=-++- ⎪ ⎪⎝⎭⎝⎭(()22a a x a +≤<+),所以()g x 的零点122a a +-满足()12222a a a a a+≤+-<+, 由1222a a a +-<+得()()21111001a a a a a a a a+---==<⇒<<,由()1222a a a a+≤+-得3210a a -+≤,即()()()()31111a a a a a a a --+=+---()()()21110a a a a a a ⎛=+--=--≤ ⎝⎭⎝⎭,由于01a <<1a ≤<.故答案为:112a ≤< 9. (2021·浙江高一期末)已知函数()1f x x =-+,()()21g x x =-,x ∈R .(1)在图1中画出函数()f x ,()g x 的图象;(2)定义:x R ∀∈,用()m x 表示()f x ,()g x 中的较小者,记为()()(){}min ,m x f x g x =,请分别用图象法和解析式法表示函数()m x .(注:图象法请在图2中表示,本题中的单位长度请自己定义且标明)【答案】(1)图象见解析;(2)()(][)()()21,,01,1,0,1x x m x x x ⎧-+∈-∞⋃+∞⎪=⎨-∈⎪⎩;图象见解析. 【解析】(1)由一次函数和二次函数图象特征可得结果;(2)根据()m x 定义可分段讨论得到解析式;由解析式可得图象. 【详解】(1)()f x ,()g x 的图象如下图所示:(2)当0x ≤时,()211x x -≥-+,则()()1m x f x x ==-+;当01x <<时,()211x x -<-+,则()()()21m x g x x ==-; 当1≥x 时,()211x x -≥-+,则()()1m x f x x ==-+;综上所述:()(][)()()21,,01,1,0,1x x m x x x ⎧-+∈-∞⋃+∞⎪=⎨-∈⎪⎩. ()m x 图象如下图所示:10. (2021·全国高一课时练习)已知函数()12f x x x =++-,()3g x x =-. (1)在平面直角坐标系里作出()f x 、()g x 的图象.(2)x R ∀∈,用()min x 表示()f x 、()g x 中的较小者,记作()()(){}min ,x f x g x =,请用图象法和解析法表示()min x ;(3)求满足()()f x g x >的x 的取值范围.【答案】(1)答案见解析;(2)答案见解析;(3)()(),20,-∞-+∞.【解析】(1)化简函数()f x 、()g x 的解析式,由此可作出这两个函数的图象;(2)根据函数()min x 的意义可作出该函数的图象,并结合图象可求出函数()min x 的解析式; (3)根据图象可得出不等式()()f x g x >的解集. 【详解】(1)()21,2123,1212,1x x f x x x x x x -≥⎧⎪=++-=-<<⎨⎪-≤-⎩,()3,333,3x x g x x x x -≥⎧=-=⎨-<⎩. 则对应的图象如图:(2)函数()min x 的图象如图:解析式为()3,20312,21min 3,103,3x x x x x x x x x -<-≤<⎧⎪--≤≤-⎪=⎨-<<⎪⎪-≥⎩或;(3)若()()f x g x >,则由图象知在A 点左侧,B 点右侧满足条件,此时对应的x 满足0x >或2x <-, 即不等式()()f x g x >的解集为()(),20,-∞-+∞.1.(山东高考真题)设f (x )={√x,0<x <12(x −1),x ≥1 ,若f (a )=f (a +1),则f (1a )=( ) A .2 B .4 C .6 D .8 【答案】C【解析】由x ≥1时f (x )=2(x −1)是增函数可知,若a ≥1,则f (a )≠f (a +1),所以0<a <1,由f(a)=f(a +1)得√a =2(a +1−1),解得a =14,则f (1a )=f(4)=2(4−1)=6,故选C.2.(2018上海卷)设D 是含数1的有限实数集,f (x )是定义在D 上的函数,若f (x )的图象绕原点逆时针旋转π6后与原图象重合,则在以下各项中,f (1)的可能取值只能是( ) A .√3 B .√32 C .√33 D .0 【答案】B 【解析】由题意得到:问题相当于圆上由12个点为一组,每次绕原点逆时针旋转π6个单位后与下一个点会重合. 我们可以通过代入和赋值的方法当f (1)=√3,√33,0时,此时得到的圆心角为π3,π6,0,然而此时x=0或练真题者x=1时,都有2个y 与之对应,而我们知道函数的定义就是要求一个x 只能对应一个y ,因此只有当x=√32,此时旋转π6,此时满足一个x 只会对应一个y , 故选:B .3. (2018年新课标I 卷文)设函数f (x )={2−x , x ≤01 , x >0 ,则满足f (x +1)<f (2x )的x 的取值范围是( )A. (−∞ , −1]B. (0 , +∞)C. (−1 , 0)D. (−∞ , 0) 【答案】D【解析】将函数f(x)的图象画出来,观察图象可知会有{2x <02x <x +1,解得x <0,所以满足f (x +1)<f (2x )的x 的取值范围是(−∞ , 0),故选D.4.(浙江高考真题(文))已知函数()2,1{66,1x x f x x x x≤=+->,则()2f f ⎡⎤-=⎣⎦ ,()f x 的最小值是 .【答案】162- 【解析】如图根据所给函数解析式结合其单调性作出其图像如图所示,易知()()min 12,62f f f x f ⎡⎤-=-==⎣⎦.5. (2018·天津高考真题(文))已知a R ∈,函数()22220220x x a x f x x x a x ⎧++-≤=⎨-+->⎩,,,.若对任意x ∈[–3,+∞),f (x )≤x 恒成立,则a 的取值范围是__________. 【答案】1,28⎡⎤⎢⎥⎣⎦【解析】由题意分类讨论0x >和0x ≤两种情况,结合恒成立的条件整理计算即可求得最终结果. 【详解】分类讨论:①当0x >时,()f x x ≤即:222x x a x -+-≤, 整理可得:21122a x x ≥-+, 由恒成立的条件可知:()2max 11022a x x x ⎛⎫≥-+> ⎪⎝⎭, 结合二次函数的性质可知: 当12x =时,2max 1111122848x x ⎛⎫-+=-+= ⎪⎝⎭,则18a ≥; ②当30x -≤≤时,()f x x ≤即:222x x a x ++-≤-,整理可得:232a x x ≤--+, 由恒成立的条件可知:()()2min3230a x x x ≤--+-≤≤,结合二次函数的性质可知: 当3x =-或0x =时,()2min322x x --+=,则2a ≤;综合①②可得a 的取值范围是1,28⎡⎤⎢⎥⎣⎦,故答案为1,28⎡⎤⎢⎥⎣⎦.6.(2018·浙江高考真题)已知λ∈R,函数f (x )=24,43,x x x x x λλ-≥⎧⎨-+<⎩,当λ=2时,不等式f (x )<0的解集是___________.若函数f (x )恰有2个零点,则λ的取值范围是___________. 【答案】(1,4) (1,3](4,)⋃+∞ 【解析】分析:根据分段函数,转化为两个不等式组,分别求解,最后求并集.先讨论一次函数零点的取法,再对应确定二次函数零点的取法,即得参数λ的取值范围.详解:由题意得240x x ≥⎧⎨-<⎩或22430x x x <⎧⎨-+<⎩,所以24x ≤<或12x <<,即14x <<,不等式f (x )<0的解集是(1,4),当4λ>时,()40f x x =->,此时2()430,1,3f x x x x =-+==,即在(,)λ-∞上有两个零点;当4λ≤时,()40,4f x x x =-==,由2()43f x x x =-+在(,)λ-∞上只能有一个零点得13λ<≤.综上,λ的取值范围为(1,3](4,)⋃+∞.。
高考数学函数题库(含答案)

2009——20XX 高考题1.〔2012高考XX 文3〕〔2log 9〕·〔3log 4〕= 〔A 〕14 〔B 〕12〔C 〕2 〔D 〕4 [答案]D2.〔2012高考新课标文11〕当0<x ≤12时,4x <log a x ,则a 的取值X 围是〔A 〕(0,22) 〔B 〕(22,1) 〔C 〕(1,2) 〔D 〕(2,2) [答案]B3.〔2012高考XX 文3〕函数21()4ln(1)f x x x =+-+的定义域为(A)[2,0)(0,2]- (B)(1,0)(0,2]- (C)[2,2]- (D)(1,2]-[答案]B4.〔2012高考XX 文10〕函数cos622x xxy -=-的图象大致为[答案]D5.〔2012高考XX 文12〕设函数1()f x x=,2()g x x bx =-+.若()y f x =的图象与()y g x =的图象有且仅有两个不同的公共点1122(,),(,)A x y B x y ,则下列判断正确的是 (A)12120,0x x y y +>+> (B)12120,0x x y y +>+< (C)12120,0x x y y +<+> (D)12120,0x x y y +<+<[答案]B[解析]方法一:在同一坐标系中分别画出两个函数的图象,要想满足条件,则有如图,做出点A 关于原点的对称点C,则C 点坐标为),(11y x --,由图象知,,2121y y x x >-<-即0,02121<+>+y y x x ,故答案选B.方法二:设32()1F x x bx =-+,则方程()0F x =与()()f x g x =同解,故其有且仅有两个不同零点12,x x .由()0F x '=得0x =或23x b =.这样,必须且只须(0)0F =或2()03F b =,因为(0)1F =,故必有2()03F b =由此得3322b =.不妨设12x x <,则32223x b ==.所以231()()(2)F x x x x =--,比较系数得3141x -=,故31122x =-.3121202x x +=>,由此知12121212110x x y y x x x x ++=+=<,故答案为B. 6.〔2012高考XX 文7〕已知22log 3log 3a =+,22log 9log 3b =-,3log 2c =则a,b,c 的大小关系是〔A 〕 a b c =< 〔B 〕a b c => 〔C 〕a b c << 〔D 〕a b c >>[答案]B7.〔2012高考全国文11〕已知ln x π=,5log 2y =,12z e -=,则〔A 〕x y z << 〔B 〕z x y << 〔C 〕z y x << 〔D 〕y z x <<[答案]D8.〔2012高考全国文2〕函数1(1)y x x =+≥-的反函数为〔A 〕)0(12≥-=x x y 〔B 〕)1(12≥-=x x y 〔C 〕)0(12≥+=x x y 〔D 〕)1(12≥+=x x y [答案]B9.〔2012高考XX 文4〕函数(0,1)xy a a a a =->≠的图象可能是〔 〕[答案]C10.〔2012高考XX 文2〕下列函数中,既是奇函数又是增函数的为〔 〕 A. 1y x =+ B. 2y x =- C. 1y x= D. ||y x x = [答案]D.11.〔2012高考XX 文9〕设定义在R 上的函数f(x)是最小正周期为2π的偶函数,()f x '是f(x)的导函数,当[]0,x π∈时,0<f(x)<1;当x ∈〔0,π〕 且x ≠2π时 ,()()02x f x π'->,则函数y=f(x)-sinx 在[-2π,2π] 上的零点个数为 A .2 B .4 C.5 D. 8 [答案]B12.〔2012高考XX 文3〕函数f(x)=xcos2x 在区间[0,2π]上的零点个数为 A 2 B 3 C 4 D 5 [答案]D13.〔2012高考XX 文3〕设函数211()21x x f x x x ⎧+≤⎪=⎨>⎪⎩,则=))3((f f[答案]D14.〔2012高考XX 文10〕如右图,OA=2〔单位:m 〕,OB=1(单位:m),OA 与OB 的夹角为6π,以A 为圆心,AB 为半径作圆弧BDC 与线段OA 延长线交与点C.甲。
2024年高考数学真题分类汇编(三角函数篇,解析版)

专题三角函数1(新课标全国Ⅰ卷)已知cos (α+β)=m ,tan αtan β=2,则cos (α-β)=()A.-3mB.-m3C.m 3D.3m【答案】A【分析】根据两角和的余弦可求cos αcos β,sin αsin β的关系,结合tan αtan β的值可求前者,故可求cos α-β 的值.【详解】因为cos α+β =m ,所以cos αcos β-sin αsin β=m ,而tan αtan β=2,所以=12×2b ×kb ×sin A 2+12×kb ×b ×sin A2,故cos αcos β-2cos αcos β=m 即cos αcos β=-m ,从而sin αsin β=-2m ,故cos α-β =-3m ,故选:A .2(新课标全国Ⅰ卷)当x ∈[0,2π]时,曲线y =sin x 与y =2sin 3x -π6 的交点个数为()A.3B.4C.6D.8【答案】C【分析】画出两函数在0,2π 上的图象,根据图象即可求解【详解】因为函数y =sin x 的的最小正周期为T =2π,函数y =2sin 3x -π6 的最小正周期为T =2π3,所以在x ∈0,2π 上函数y =2sin 3x -π6有三个周期的图象,在坐标系中结合五点法画出两函数图象,如图所示:由图可知,两函数图象有6个交点.故选:C3(新课标全国Ⅱ卷)设函数f (x )=a (x +1)2-1,g (x )=cos x +2ax ,当x ∈(-1,1)时,曲线y =f (x )与y =g (x )恰有一个交点,则a =()A.-1B.12C.1D.22024年高考数学真题分类汇编——三角函数篇【分析】解法一:令F x =ax 2+a -1,G x =cos x ,分析可知曲线y =F (x )与y =G (x )恰有一个交点,结合偶函数的对称性可知该交点只能在y 轴上,即可得a =2,并代入检验即可;解法二:令h x =f (x )-g x ,x ∈-1,1 ,可知h x 为偶函数,根据偶函数的对称性可知h x 的零点只能为0,即可得a =2,并代入检验即可.【详解】解法一:令f (x )=g x ,即a (x +1)2-1=cos x +2ax ,可得ax 2+a -1=cos x ,令F x =ax 2+a -1,G x =cos x ,原题意等价于当x ∈(-1,1)时,曲线y =F (x )与y =G (x )恰有一个交点,注意到F x ,G x 均为偶函数,可知该交点只能在y 轴上,可得F 0 =G 0 ,即a -1=1,解得a =2,若a =2,令F x =G x ,可得2x 2+1-cos x =0因为x ∈-1,1 ,则2x 2≥0,1-cos x ≥0,当且仅当x =0时,等号成立,可得2x 2+1-cos x ≥0,当且仅当x =0时,等号成立,则方程2x 2+1-cos x =0有且仅有一个实根0,即曲线y =F (x )与y =G (x )恰有一个交点,所以a =2符合题意;综上所述:a =2.解法二:令h x =f (x )-g x =ax 2+a -1-cos x ,x ∈-1,1 ,原题意等价于h x 有且仅有一个零点,因为h -x =a -x 2+a -1-cos -x =ax 2+a -1-cos x =h x ,则h x 为偶函数,根据偶函数的对称性可知h x 的零点只能为0,即h 0 =a -2=0,解得a =2,若a =2,则h x =2x 2+1-cos x ,x ∈-1,1 ,又因为2x 2≥0,1-cos x ≥0当且仅当x =0时,等号成立,可得h x ≥0,当且仅当x =0时,等号成立,即h x 有且仅有一个零点0,所以a =2符合题意;故选:D .4(全国甲卷数学(理)(文))已知cos αcos α-sin α=3,则tan α+π4=()A.23+1 B.23-1C.32D.1-3【答案】B【分析】先将cos αcos α-sin α弦化切求得tan α,再根据两角和的正切公式即可求解.【详解】因为cos αcos α-sin α=3,所以11-tan α=3,⇒tan α=1-33,所以tan α+π4 =tan α+11-tan α=23-1,故选:B .5(新高考北京卷)已知f x =sin ωx ω>0 ,f x 1 =-1,f x 2 =1,|x 1-x 2|min =π2,则ω=()A.1B.2C.3D.4【分析】根据三角函数最值分析周期性,结合三角函数最小正周期公式运算求解.【详解】由题意可知:x 1为f x 的最小值点,x 2为f x 的最大值点,则x 1-x 2 min =T 2=π2,即T =π,且ω>0,所以ω=2πT=2.故选:B .6(新高考天津卷)已知函数f x =sin3ωx +π3ω>0 的最小正周期为π.则函数在-π12,π6 的最小值是()A.-32B.-32C.0D.32【答案】A【分析】先由诱导公式化简,结合周期公式求出ω,得f x =-sin2x ,再整体求出x ∈-π12,π6时,2x 的范围,结合正弦三角函数图象特征即可求解.【详解】f x =sin3ωx +π3 =sin 3ωx +π =-sin3ωx ,由T =2π3ω=π得ω=23,即f x =-sin2x ,当x ∈-π12,π6 时,2x ∈-π6,π3,画出f x =-sin2x 图象,如下图,由图可知,f x =-sin2x 在-π12,π6上递减,所以,当x =π6时,f x min =-sin π3=-32故选:A7(新高考上海卷)下列函数f x 的最小正周期是2π的是()A.sin x +cos xB.sin x cos xC.sin 2x +cos 2xD.sin 2x -cos 2x【答案】A【分析】根据辅助角公式、二倍角公式以及同角三角函数关系并结合三角函数的性质一一判断即可 .【详解】对A ,sin x +cos x =2sin x +π4,周期T =2π,故A 正确;对B ,sin x cos x =12sin2x ,周期T =2π2=π,故B 错误;对于选项C ,sin 2x +cos 2x =1,是常值函数,不存在最小正周期,故C 错误;对于选项D ,sin 2x -cos 2x =-cos2x ,周期T =2π2=π,故D 错误,故选:A .8(新课标全国Ⅱ卷)对于函数f(x)=sin2x和g(x)=sin2x-π4,下列说法正确的有() A.f(x)与g(x)有相同的零点 B.f(x)与g(x)有相同的最大值C.f(x)与g(x)有相同的最小正周期D.f(x)与g(x)的图像有相同的对称轴【答案】BC【分析】根据正弦函数的零点,最值,周期公式,对称轴方程逐一分析每个选项即可.【详解】A选项,令f(x)=sin2x=0,解得x=kπ2,k∈Z,即为f(x)零点,令g(x)=sin2x-π4=0,解得x=kπ2+π8,k∈Z,即为g(x)零点,显然f(x),g(x)零点不同,A选项错误;B选项,显然f(x)max=g(x)max=1,B选项正确;C选项,根据周期公式,f(x),g(x)的周期均为2π2=π,C选项正确;D选项,根据正弦函数的性质f(x)的对称轴满足2x=kπ+π2⇔x=kπ2+π4,k∈Z,g(x)的对称轴满足2x-π4=kπ+π2⇔x=kπ2+3π8,k∈Z,显然f(x),g(x)图像的对称轴不同,D选项错误.故选:BC9(新课标全国Ⅱ卷)已知α为第一象限角,β为第三象限角,tanα+tanβ=4,tanαtanβ=2+1,则sin(α+β)=.【答案】-22 3【分析】法一:根据两角和与差的正切公式得tanα+β=-22,再缩小α+β的范围,最后结合同角的平方和关系即可得到答案;法二:利用弦化切的方法即可得到答案.【详解】法一:由题意得tanα+β=tanα+tanβ1-tanαtanβ=41-2+1=-22,因为α∈2kπ,2kπ+π2,β∈2mπ+π,2mπ+3π2,k,m∈Z,则α+β∈2m+2kπ+π,2m+2kπ+2π,k,m∈Z,又因为tanα+β=-22<0,则α+β∈2m+2kπ+3π2,2m+2kπ+2π,k,m∈Z,则sinα+β<0,则sinα+βcosα+β=-22,联立sin2α+β+cos2α+β=1,解得sinα+β=-223.法二:因为α为第一象限角,β为第三象限角,则cosα>0,cosβ<0,cosα=cosαsin2α+cos2α=11+tan2α,cosβ=cosβsin2β+cos2β=-11+tan2β,则sin(α+β)=sinαcosβ+cosαsinβ=cosαcosβ(tanα+tanβ)=4cosαcosβ=-41+tan2α1+tan2β=-4(tanα+tanβ)2+(tanαtanβ-1)2=-442+2=-223故答案为:-22 3.10(全国甲卷数学(文))函数f x =sin x-3cos x在0,π上的最大值是.【答案】2【分析】结合辅助角公式化简成正弦型函数,再求给定区间最值即可.【详解】f x =sin x -3cos x =2sin x -π3 ,当x ∈0,π 时,x -π3∈-π3,2π3,当x -π3=π2时,即x =5π6时,f x max =2.故答案为:2一、单选题1(2024·宁夏石嘴山·三模)在平面直角坐标系中,角θ的顶点与原点重合,始边与x 轴的非负半轴重合,终边经过点P 1,2 ,则7cos 2θ-2sin2θ=()A.-15B.15C.-2D.2【答案】A【分析】由题意可知:tan θ=2,根据倍角公式结合齐次化问题分析求解.【详解】由题意可知:tan θ=2,所以7cos 2θ-2sin2θ=7cos 2θ-4sin θcos θsin 2θ+cos 2θ=7-4tan θtan 2θ+1=7-4×222+1=-15.故选:A .2(2024·广东茂名·一模)已知cos α+π =-2sin α,则sin 2α-3cos α+π2cos αcos2α+1=()A.-1B.-25C.45D.78【答案】D【分析】根据给定条件,求出tan α,再结合诱导公式及二倍角的余弦公式,利用正余弦齐次式法计算得解.【详解】由cos α+π =-2sin α,得cos α=2sin α,则tan α=12,所以sin 2α-3cos α+π2 cos αcos2α+1=sin 2α+3sin αcos α2cos 2α=12tan 2α+32tan α=18+34=78.故选:D3(2024·河北保定·二模)函数f (x )=1-e x1+e xcos2x 的部分图象大致为()A. B.C. D.【答案】A【分析】根据函数的奇偶性判断即可.【详解】设g x =1-e x1+e x,则g-x=1-e-x1+e-x=e x-11+e x=-g x ,所以g x 为奇函数,设h x =cos2x,可知h x 为偶函数,所以f x =1-e x1+e xcos2x为奇函数,则B,C错误,易知f0 =0,所以A正确,D错误.故选:A.4(2024·山东济宁·三模)已知函数f(x)=(3sin x+cos x)cos x-12,若f(x)在区间-π4,m上的值域为-3 2,1,则实数m的取值范围是()A.π6,π2B.π6,π2C.π6,7π12D.π6,7π12【答案】D【分析】利用二倍角公式、辅助角公式化简函数f(x),再借助正弦函数的图象与性质求解即得.【详解】依题意,函数f(x)=3sin x cos x+cos2x-12=32sin2x+12cos2x=sin2x+π6,当x∈-π4,m时,2x+π6∈-π3,2m+π6,显然sin-π3=sin4π3=-32,sinπ2=1,且正弦函数y=sin x在π2,4π3上单调递减,由f(x)在区间-π4,m上的值域为-32,1,得π2≤2m+π6≤4π3,解得π6≤m≤7π12,所以实数m的取值范围是π6,7π12.故选:D5(2024·江西景德镇·三模)函数f x =cosωx x∈R在0,π内恰有两个对称中心,fπ=1,将函数f x 的图象向右平移π3个单位得到函数g x 的图象.若fα +gα =35,则cos4α+π3=()A.725B.1625C.-925D.-1925【答案】A【分析】根据y轴右边第二个对称中心在0,π内,第三个对称中心不在0,π内可求得32≤ω<52,结合fπ=1可得ω=2,再利用平移变换求出g x ,根据三角变换化简fα +gα =35可得sin2α+π6=35,然后由二倍角公式可解.【详解】由x∈0,π得ωx∈0,ωπ,因为函数f x 在0,π内恰有两个对称中心,所以3π2≤ωπ5π2>ωπ,解得32≤ω<52,又fπ=cosωπ=1,所以ωπ=kπ,k∈Z,即ω=k,k∈Z,所以ω=2,将函数f x 的图象向右平移π3个单位得到函数y=cos2x-π3=cos2x-2π3,即g x =cos2x-2π3,因为fα +gα =cos2α+cos2α-2π3=32sin2α+12cos2α=sin2α+π6=35,所以cos4α+π3=1-2sin22α+π6=1-2×35 2=725.故选:A6(2024·安徽马鞍山·三模)已知函数f(x)=sin2ωx+cos2ωx(ω>1)的一个零点是π2,且f(x)在-π6,π16上单调,则ω=()A.54B.74C.94D.114【答案】B【分析】整理可得f(x)=2sin2ωx+π4,以2ωx+π4为整体,根据单调性分析可得1<ω≤2,再结合零点分析求解.【详解】因为f(x)=sin2ωx+cos2ωx=2sin2ωx+π4,x∈-π6,π16,且ω>1时,可得2ωx+π4∈-π3ω+π4,π8ω+π4,且-π3ω+π4<0<π8ω+π4,若f(x)在-π6,π16上单调,则-π3ω+π4≥-π2π8ω+π4≤π2,解得1<ω≤2,又因为f(x)的一个零点是π2,则πω+π4=kπ,k∈Z,解得ω=k-14,k∈Z,所以k=2,ω=7 4 .故选:B.7(2024·山东临沂·二模)已知函数f x =sin2x+φϕ <π2图象的一个对称中心为π6,0,则()A.f x 在区间-π8,π3上单调递增B.x=5π6是f x 图象的一条对称轴C.f x 在-π6,π4上的值域为-1,32D.将f x 图象上的所有点向左平移5π12个长度单位后,得到的函数图象关于y轴对称【答案】D【分析】借助整体代入法结合正弦函数的性质可得A、B;结合正弦函数最值可得C;得到平移后的函数解析式后借助诱导公式即可得D.【详解】由题意可得2×π6+φ=kπk∈Z,解得φ=-π3+kπk∈Z,又ϕ <π2,故φ=-π3,即f x =sin2x-π3;对A :当x ∈-π8,π3 时,2x -π3∈-7π12,π3,由函数y =sin x 在-7π12,π3上不为单调递增,故f x 在区间-π8,π3上不为单调递增,故A 错误;对B :当x =5π6时,2x -π3=4π3,由x =4π3不是函数y =sin x 的对称轴,故x =5π6不是f x 图象的对称轴,故B 错误;对C :当x ∈-π6,π4 时,2x -π3∈-2π3,π6,则f x ∈-1,12,故C 错误;对D :将f x 图象上的所有点向左平移5π12个长度单位后,可得y =sin 2x +2×5π12-π3 =sin 2x +π2=cos2x ,该函数关于y 轴对称,故D 正确.故选:D .8(2024·广东广州·二模)已知函数f (x )=2sin (ωx +φ)ω>0,|φ|<π2的部分图象如图所示,若将函数f (x )的图象向右平移θ(θ>0)个单位后所得曲线关于y 轴对称,则θ的最小值为()A.π8B.π4C.3π8D.π2【答案】A【分析】根据给定的图象特征,结合五点法作图列式求出ω和φ,再根据图象的平移变换,以及图象的对称性即可得解.【详解】由f π4=1,得sin π4ω+φ =22,又点π4,1 及附近点从左到右是上升的,则π4ω+φ=π4+2k π,k ∈Z ,由f 5π8 =0,点5π8,0 及附近点从左到右是下降的,且上升、下降的两段图象相邻,得5π8ω+φ=π+2k π,k ∈Z ,联立解得ω=2,φ=-π4+2k π,k ∈Z ,而|φ|<π2,于是φ=-π4,f (x )=2sin 2x -π4,若将函数f (x )的图像向右平移θ(θ>0)个单位后,得到y =sin 2x -2θ-π4,则-2θ-π4=π2-k π,k ∈Z ,而θ>0,因此θ=-3π8+k π2,k ∈N ,所以当k =1时,θ取得最小值为π8.故选:A9(2024·四川雅安·三模)已知函数f x =sin ωx +3cos ωx (ω>0),则下列说法中正确的个数是()①当ω=2时,函数y =f x -2log πx 有且只有一个零点;②当ω=2时,函数y =f x +φ 为奇函数,则正数φ的最小值为π3;③若函数y =f x 在0,π3 上单调递增,则ω的最小值为12;④若函数y =f x 在0,π 上恰有两个极值点,则ω的取值范围为136,256.A.1 B.2C.3D.4【答案】B【分析】利用辅助角公式化简函数,由图象分析判断①;由正弦函数的性质判断②③;由极大值的意义结合正弦函数的性质判断④.【详解】依题意,ω>0,函数f (x )=212sin ωx +32cos ωx =2sin ωx +π3,对于①:f (x )=2sin 2x +π3,令y =f x -2log πx =0,即f x =2log πx ,作出函数y =f (x )和函数y =2log πx 的图象,如图,观察图象知,两个函数在0,7π12 上只有一个零点,f 13π12 =2sin 5π2=2,当x =13π12时,y =2log π13π12=2log π1312+2log ππ=2+2log π1312>2,当x >13π12时,2log πx >2≥f (x ),因此函数y =f x 与函数y =2log πx 的图象有且只有一个交点,①正确;对于②:f (x +φ)=2sin 2x +2φ+π3 为奇函数,则2φ+π3=k π,k ∈Z ,φ=-π6+k π2,k ∈Z ,即正数φ的最小值为π3,②正确;对于③:当x ∈0,π3 时,ωx +π3∈π3,π(ω+1)3,由y =f x 在0,π3 上单调递增,得π(ω+1)3≤π2ω>0,解得0<ω≤12,正数ω有最大值12,③错误;对于④:当x ∈(0,π)时,ωx +π3∈π3,ωπ+π3,而y =f x 在(0,π)上恰有两个极值点,由正弦函数的性质得3π2<ωπ+π3≤5π2,解得76<ω≤136,因此ω的取值范围是76,136,④错误.综上,共2个正确,故选:B .10(2024·河北保定·二模)已知tan α=3cos αsin α+11,则cos2α=()A.-78B.78C.79D.-79【答案】B【分析】利用切化弦和同角三角函数的关系,解出sin α,再结合二倍角公式即可求解.【详解】因为sin αcos α=3cos αsin α+11,所以4sin 2α+11sin α-3=0,解得sin α=14或sin α=-3(舍去),所以cos2α=1-2sin 2α=78.故选:B .11(2024·河北衡水·三模)已知sin (3α-β)=m sin (α-β),tan (2α-β)=n tan α,则m ,n 的关系为()A.m =2nB.n =m +1mC.n =m m -1D.n =m +1m -1【答案】D【分析】利用和差角的正弦公式化简,结合已知列出方程即可求解.【详解】依题意,sin (3α-β)=sin [(2α-β)+α]=sin (2α-β)cos α+cos (2α-β)sin α,sin (α-β)=sin [(2α-β)-α]=sin (2α-β)cos α-cos (2α-β)sin α,则sin (2α-β)cos α+cos (2α-β)sin α=m sin (2α-β)cos α-m cos (2α-β)sin α,即sin (2α-β)cos αcos (2α-β)sin α=m +1m -1,即tan (2α-β)tan α=m +1m -1=n .故选:D12(2024·辽宁沈阳·三模)已知tan α2=2,则sin 2α2+sin α的值是()A.25B.45C.65D.85【答案】D【分析】利用二倍角公式和同角之间的转化,进行求解判断选项【详解】当tan α2=2,则sin 2α2+sin α=sin 2α2+2sin α2cos α2sin 2α2+cos 2α2=tan 2α2+2tan α2tan 2α2+1=22+2×222+1=85故选:D13(2024·贵州黔东南·二模)已知0<α<β<π,且sin α+β =2cos α+β ,sin αsin β-3cos αcos β=0,则tan α-β =()A.-1 B.-32C.-12D.12【答案】C【分析】找出tan α和tan β的关系,求出tan α和tan β即可求解.【详解】∵sin αsin β-3cos αcos β=0,∴sin αsin β=3cos αcos β,∴tan αtan β=3①,∵sin α+β =2cos α+β ,∴tan α+β =2⇒tan α+tan β1-tan αtan β=2⇒tan α+tan β1-3=2,∴tan α+tan β=-4②,由①②解得tan α=-1tan β=-3或tan α=-3tan β=-1 ,∵0<α<β<π,∴tan α<tan β,∴tan α=-3tan β=-1 ,∴tan α-β =tan α-tan β1+tan αtan β=-12.故选:C .二、多选题14(2024·河北张家口·三模)已知函数f (x )=23cos 2x +2sin x cos x ,则下列说法正确的是()A.函数f (x )的一个周期为2πB.函数f (x )的图象关于点π3,0 对称C.将函数f (x )的图象向右平移φ(φ>0)个单位长度,得到函数g (x )的图象,若函数g (x )为偶函数,则φ的最小值为5π12D.若f 12α-5π24 -3=12,其中α为锐角,则sin α-cos α的值为6-308【答案】ACD【分析】利用三角恒等变换公式化简,由周期公式可判断A ;代入验证可判断B ;根据平移变化求g (x ),由奇偶性可求出φ,可判断C ;根据已知化简可得sin α-π12 =14,将目标式化为2sin α-π12 -π6 ,由和差角公式求解可判断D .【详解】对于A ,因为f (x )=31+cos2x +sin2x =2sin 2x +π3+3,所以f (x )的最小值周期T =2π2=π,所以2π是函数f (x )的一个周期,A 正确;对于B ,因为f π3 =2sin 2×π3+π3 +3=3,所以,点π3,0 不是函数f (x )的对称中心,B 错误;对于C ,由题知,g x =f (x -φ)=2sin 2(x -φ)+π3 +3=2sin 2x +π3-2φ +3,若函数g (x )为偶函数,则π3-2φ=π2+k π,k ∈Z ,得φ=-π12-k π2,k ∈Z ,因为φ>0,所以φ的最小值为5π12,C 正确;对于D ,若f 12α-5π24-3=2sin 212α-5π24 +π3 =2sin α-π12 =12,则sin α-π12 =14,因为α为锐角,-π12<α-π12<5π12,所以cos α-π12 =154,所以sin α-cos α=2sin α-π4 =2sin α-π12 -π6=232sin α-π12 -12cos α-π12=232×14-12×154=6-308,D 正确.故选:ACD 15(2024·辽宁鞍山·模拟预测)已知函数f x =sin x ⋅cos x ,则()A.f x 是奇函数B.f x 的最小正周期为2πC.f x 的最小值为-12D.f x 在0,π2上单调递增【答案】AC【分析】首先化简函数f x =12sin2x ,再根据函数的性质判断各选项.【详解】f x =sin x ⋅cos x =12sin2x ,函数的定义域为R ,对A ,f -x =-12sin2x =-f x ,所以函数f x 是奇函数,故A 正确;对B ,函数f x 的最小正周期为2π2=π,故B 错误;对C ,函数f x 的最小值为-12,故C 正确;对D ,x ∈0,π2 ,2x ∈0,π ,函数f x 不单调,f x 在0,π4 上单调递增,在π4,π2上单调递减,故D 错误.故选:AC16(2024·安徽·三模)已知函数f x =sin x -3cos x ,则()A.f x 是偶函数B.f x 的最小正周期是πC.f x 的值域为-3,2D.f x 在-π,-π2上单调递增【答案】AC【分析】对于A ,直接用偶函数的定义即可验证;对于B ,直接说明f 0 ≠f π 即可否定;对于C ,先证明-3≤f x ≤2,再说明对-3≤u ≤2总有f x =u 有解即可验证;对于D ,直接说明f -5π6>f -2π3 即可否定.【详解】对于A ,由于f x 的定义域为R ,且f -x =sin -x -3cos -x =-sin x -3cos x =sin x -3cos x =f x ,故f x 是偶函数,A 正确;对于B ,由于f 0 =sin0 -3cos0=-3,f π =sinπ -3cosπ=3,故f 0 ≠f π ,这说明π不是f x 的周期,B 错误;对于C ,由于f x =sin x -3cos x ≤sin x +3cos x =sin x +3cos x 2≤sin x +3cos x 2+3sin x -cos x 2=sin 2x +3cos 2x +23sin x cos x +3sin 2x +cos 2x -23sin x cos x =4sin 2x +4cos 2x =4=2,且f x =sin x -3cos x ≥-3cos x ≥-3,故-3≤f x ≤2.而对-3≤u ≤2,有f 0 =-3≤u ,f 5π6 =2≥u ,故由零点存在定理知一定存在x ∈0,5π6使得f x =u .所以f x 的值域为-3,2 ,C 正确;对于D ,由于-π<-5π6<-2π3<-π2,f -5π6 =2>3=f -2π3 ,故f x 在-π,-π2上并不是单调递增的,D 错误.故选:AC .17(2024·山西太原·模拟预测)已知函数f x =sin 2x +φ 0<φ<π2 的图象关于直线x =π12对称,且h x =sin2x -f x ,则()A.φ=π12B.h x 的图象关于点π6,0中心对称C.f x 与h x 的图象关于直线x =π4对称 D.h x 在区间π6,5π12内单调递增【答案】BCD【分析】根据正弦函数的对称性求解φ判断A ,先求出h x =sin 2x -π3,然后利用正弦函数的对称性求解判断B ,根据对称函数的性质判断C ,结合正弦函数的单调性代入验证判断D .【详解】由题意得2×π12+φ=π2+k π,k ∈Z ,解得φ=π3+k π,k ∈Z ,又因为0<φ<π2,所以φ=π3,A 错误;由φ=π3可知f x =sin 2x +π3,则h x =sin2x -sin 2x +π3 =12sin2x -32cos2x =sin 2x -π3,令2x -π3=k π,k ∈Z ,解得x =π6+k π2,k ∈Z ,令k =0,得x =π6,所以点π6,0 是曲线y =h x 的对称中心,B 正确;因为f π2-x =sin 2π2-x +π3 =sin 4π3-2x =sin 2x -π3=h x ,所以f x 与h x 的图象关于直线x =π4对称,C 正确;当x ∈π6,5π12 时,2x -π3∈0,π2 ,故h x 在区间π6,5π12内单调递增,D 正确.故选:BCD 18(2024·浙江金华·三模)已知函数f x =sin2ωx cos φ+cos2ωx sin φω>0,0<φ<π2的部分图象如图所示,则()A.φ=π6B.ω=2C.f x +π6为偶函数 D.f x 在区间0,π2的最小值为-12【答案】ACD【分析】先由正弦展开式,五点法结合图象求出f x =sin 2x +π6,可得A 正确,B 错误;由诱导公式可得C 正确;整体代入由正弦函数的值域可得D 正确.【详解】由题意得f x =sin 2ω+φ ,由图象可得f 0 =12⇒sin φ=12,又0<φ<π2,所以φ=π6,由五点法可得ω×4π3+π6=3π2⇒ω=1,所以f x =sin 2x +π6 .A :由以上解析可得φ=π6,故A 正确;B :由以上解析可得ω=1,故B 错误;C :f x +π6 =sin 2x +π6 +π6=cos2x ,故C 正确;D :当x ∈0,π2 ⇒2x +π6∈π6,7π6 时,sin 2x +π6 ∈-12,1,所以最小值为-12,故D 正确;故选:ACD .19(2024·浙江温州·二模)已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,P -3,4 为其终边上一点,若角β的终边与角2α的终边关于直线y =-x 对称,则()A.cos π+α =35B.β=2k π+π2+2αk ∈Z C.tan β=724D.角β的终边在第一象限【答案】ACD【分析】根据三角函数的定义,可求角α的三角函数,结合诱导公式判断A 的真假;利用二倍角公式,求出2α的三角函数值,结合三角函数的概念指出角2α的终边与单位圆的交点,由对称性确定角β终边与单位圆交点,从而判断BCD 的真假.【详解】因为角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边经过点P -3,4 ,所以:OP =5,所以sin α=45,cos α=-35,所以cos π+α =-cos α=35,故A 对;又sin2α=2sin α⋅cos α=2×45×-35 =-2425,cos2α=cos 2α-sin 2α=-35 2-45 2=-725,所以2α的终边与单位圆的交点坐标为:-725,-2425 ,因为角β的终边与角2α的终边关于直线y =-x 对称,所以角β的终边与单位圆的交点为2425,725,所以tan β=724,且β的终边在第一象限,故CD 正确;又因为终边在直线y =-x 的角为:k π-π4,k ∈Z ,角2α的终边与角β的终边关于y =-x 对称,所以2α+β2=k π-π4⇒β=2k π-π2-2αk ∈Z ,故B 错误.故选:ACD20(2024·广东佛山·二模)已知函数f x =sin x +cos2x 与g x =sin2x +cos x ,记h x =λf x +μg x ,其中λ,μ∈R 且λ2+μ2≠0.下列说法正确的是()A.h x 一定为周期函数B.若λ⋅μ>0,则h x 在0,π2上总有零点C.h x 可能为偶函数 D.h x 在区间0,2π 上的图象过3个定点【答案】ABD【分析】对于A :计算h x +2π ,化简即可;对于B :求出h x ,然后计算h 0 h π2的正负即可;对于C :计算h x ,h -x 是否恒相等即可;对于D :令f x =0g x =0,求解x 即可.【详解】对于A ,∀x ∈R ,h x +2π =λf x +2π +μg x +2π =λf x +μg x =h x ,A 正确;对于B ,h x =λcos x -2sin2x +μ2cos2x -sin x ,则h 0 =λ+2μ,h π2=-3μ,因为λμ>0,即λ,μ同号,所以h 0 h π2<0,由零点存在定理知h x 在0,π2上总有零点,故B 正确;对于C ,h x =λsin x +λcos2x +μsin2x +μcos x ,h -x =-λsin x +λcos2x -μsin2x +μcos x ,由h x =h -x 得2λsin x +2μsin2x =2λsin x +2μ⋅2sin x cos x =2sin x λ+2μcos x =0对x ∈R 恒成立,则λ=μ=0与题意不符,故C 错误;对于D ,令f x =0g x =0 ,则sin x +cos2x =1-2sin 2x +sin x =-sin x -1 2sin x +1 =0sin2x +cos x =cos x 2sin x +1 =0 ⇒sin x =1或sin x =-12cos x =0或sin x =-12,即x ∈-π6+2k π,π2+2k π,7π6+2k π ,k ∈Z ,故所有定点坐标为-π6+2k π,0 ,π2+2k π,0 ,7π6+2k π,0 ,k ∈Z ,又因为x ∈0,2π ,所以函数h x 的图象过定点π2,0 ,7π6,0 ,11π6,0 ,故D 正确;故选:ABD .21(2024·湖南·二模)已知函数f x =12cos 2x -π3 ,把y =f x 的图象向右平移π3个单位长度,得到函数y =g x 的图象,以下说法正确的是()A.x =π6是y =f x 图象的一条对称轴B.f x 的单调递减区间为k π+π6,k π+2π3k ∈Z C.y =g x 的图象关于原点对称D.f x +g x 的最大值为12【答案】ABD【分析】根据题意,求得g x =-12cos2x 的图象,结合三角函数的图象与性质,以及两角差的正弦公式,逐项判定,即可求解.【详解】将函数f x =12cos 2x -π3 的图象向右平移π3个单位长度,得到函数y =g x =12cos 2x -π =-12cos2x 的图象,对于A 中,令x =π6,求得f x =12,即为函数y =f x 最大值,所以直线x =π6是函数f x 图象的一条对称轴,所以A 正确;对于B 中,令2k π≤2x -π3≤2k π+π,k ∈Z ,解得k π+π6≤x ≤k π+2π3,k ∈Z ,可得f x 的单调减区间为k π+π6,k π+2π3,k ∈Z ,所以B 正确.对于C 中,由于g x =-12cos2x 是偶函数,可得函数g x 的图象关于y 轴对称,所以C 错误.对于D 中,由f x +g x =12cos 2x -π3 +-12cos2x =1212cos2x +32sin2x -12cos2x =34sin2x -14cos2x =12sin 2x -π6 ≤12,即f x +g x 的最大值为12,所以D 正确.故选:ABD .22(2024·广东江门·一模)已知函数f (x )=sin 2ωx +π3 +sin 2ωx -π3+23cos 2ωx -3(ω>0),则下列结论正确的是()A.若f x 相邻两条对称轴的距离为π2,则ω=2B.当ω=1,x ∈0,π2时,f x 的值域为-3,2 C.当ω=1时,f x 的图象向左平移π6个单位长度得到函数解析式为y =2cos 2x +π6D.若f x 在区间0,π6上有且仅有两个零点,则5≤ω<8【答案】BCD【分析】根据三角恒等变换化简f x =2sin 2ωx +π3,进而根据周期可判断A ,根据整体法求解函数的值域判断B ,根据函数图象的平移可判断C ,根据零点个数确定不等式满足的条件可判断D .【详解】f (x )=sin 2ωx +π3 +sin 2ωx -π3+23cos 2ωx -3=sin2ωx cos π3+cos2ωx sin π3+sin2ωx cos π3-cos2ωx sin π3+3cos2ωx=sin2ωx +3cos2ωx =2sin 2ωx +π3,对于A ,若f x 相邻两条对称轴的距离为π2,则T =2×π2=π=2π2ω,故ω=1,A 错误,对于B ,当ω=1,f x =2sin 2x +π3 ,当x ∈0,π2 时,2x +π3∈π3,4π3,则f x 的值域为-3,2 ,B 正确,对于C ,当ω=1,f x =2sin 2x +π3,f x 的图象向左平移π6个单位长度得到函数解析式为f x +π6 =2sin 2x +π6 +π3 =2sin 2x +2π3 =2cos 2x +π6,C 正确,对于D ,当x ∈0,π6 时,2ωx +π3∈π3,2ωπ6+π3,若f x 在区间0,π6 上有且仅有两个零点,则2π≤2ωπ6+π3<3π,解得5≤ω<8,故D 正确,故选:BCD 三、填空题23(2024·北京·三模)已知函数f (x )=sin x cos ωx ,x ∈R .①若ω=1,则f (x )的最小正周期是;,②若ω=2,则f (x )的值域是.【答案】π[-1,1]【分析】把ω=1代入,t 明智二倍角的正弦,结合正弦函数的周期求出f (x )的最小正周期;把ω=2代入,利用二倍角的余弦公式,借助换元法,利用导数求出f (x )的值域.【详解】当ω=1时,f (x )=sin x cos x =12sin2x ,函数f (x )的最小正周期为2π2=π;当ω=2时,f (x )=sin x cos2x =sin x (1-2sin 2x ),令sin x =t ∈[-1,1],g (t )=t (1-2t 2)=-2t 3+t ,求导得g (t )=-6t 2+1,当-1≤t <-66或66<t ≤1时,g (t )<0,当-66<t <66时,g (t )>0,函数g (t )在-1,-66 ,66,1 上单调递减,在-66,66上单调递增,g (-1)=1,g 66 =69,g (1)=-1,g -66 =-69,所以g (t )min =-1,g (t )max =1,f (x )的值域是[-1,1].故答案为:π;[-1,1]24(2024·北京·模拟预测)已知函数f (x )=sin ωx -2cos ωx (ω>0),且f α+x =f α-x .若两个不等的实数x 1,x 2满足f x 1 f x 2 =5且x 1-x 2 min =π,则sin4α=.【答案】-45/-0.8【分析】利用辅助角公式化简f (x )的解析式,再由题意可得函数关于x =α对称,且最小正周期T =π,即可求出ω的值,从而得到2α=φ+π2+k π,k ∈Z ,再由二倍角公式及同角三角函数的基本关系计算可得.【详解】因为f (x )=sin ωx -2cos ωx =5sin ωx -φ ,其中tan φ=2,由f α+x =f α-x ,可得f x 关于x =α对称,又两个不等的实数x 1,x 2满足f x 1 f x 2 =5且x 1-x 2 min =π,所以f x 的最小正周期T =π,又ω>0,所以2πω=π,解得ω=2,所以f x =5sin 2x -φ ,所以2α-φ=π2+k π,k ∈Z ,则2α=φ+π2+k π,k ∈Z ,所以sin4α=sin2φ+π2+k π =sin 2φ+π+2k π =-sin2φ=-2sin φcos φsin 2φ+cos 2φ=-2tan φtan 2φ+1=-2×222+1=-45.故答案为:-4525(2024·湖北荆州·三模)设0<α<β<π2,tan α=m tan β,cos α-β =35,若满足条件的α与β存在且唯一,则m =,tan αtan β=.【答案】191【分析】由tan α=m tan β得到sin αcos β=m cos αsin β,再结合cos α-β =35,利用sin α-β =-45,得到cos αsin β=-45m -1 ,sin αcos β=-4m5m -1 ,从而sin α+β =-4m +1 5m -1,再由满足条件的α与β存在且唯一,得到α+β唯一,从而sin α+β =-4m +15m -1=1,求得m 即可.【详解】解:由tan α=m tan β,得sin αcos α=m sin βcos β,即sin αcos β=m cos αsin β,因为0<α<β<π2,tan α=m tan β,所以-π2<α-β<0,0<m <1,又cos α-β =35,所以sin α-β <0,从而sin α-β =sin αcos β-cos αsin β=m -1 cos αsin β=-45,所以cos αsin β=-45m -1,所以sin αcos β=m cos αsin β=-4m5m -1,所以sin α+β =sin αcos β+cos αsin β=-4m +15m -1,因为α,β∈0,π2,所以α+β∈0,π ,因为满足条件的α与β存在且唯一,所以α+β唯一,所以sin α+β =-4m +1 5m -1=1,所以m =19,经检验符合题意,所以tan α=19tan β,则tan α-β =-43=tan α-tan β1+tan αtan β=tan α-9tan α1+9tan 2α,解得tan α=13,所以tan αtan β=9tan 2α=1.故答案为:19,1【点睛】关键点点睛:关键是结合已知得出sin α+β =-4m +15m -1 =1,求出m ,由此即可顺利得解.。
历年(2020-2024)全国高考数学真题分类(函数及其基本性质)汇编(附答案)

历年(2020-2024)全国高考数学真题分类(函数及其基本性质)汇编考点01 直接求函数值1.(2024∙全国新Ⅰ卷∙高考真题)已知函数()f x 的定义域为R ,()(1)(2)f x f x f x >-+-,且当3x <时()f x x =,则下列结论中一定正确的是( ) A .(10)100f > B .(20)1000f > C .(10)1000f <D .(20)10000f <2.(2024∙上海∙高考真题)已知()0,1,0x f x x >=≤⎪⎩则()3f = . 3.(2023∙北京∙高考真题)已知函数2()4log xf x x =+,则12f ⎛⎫= ⎪⎝⎭.4.(2021∙全国甲卷∙高考真题)设()f x 是定义域为R 的奇函数,且()()1f x f x +=-.若1133f ⎛⎫-= ⎪⎝⎭,则53f ⎛⎫= ⎪⎝⎭( )A .53-B .13-C .13D .535.(2021∙浙江∙高考真题)已知R a ∈,函数24,2()3,2,x x f x x a x ⎧->⎪=⎨-+≤⎪⎩若3f f ⎡⎤=⎣⎦,则=a .考点02 函数的定义域与值域1.(2022∙北京∙高考真题)函数1()f x x=的定义域是 . 2.(2020∙山东∙高考真题)函数()1lg f x x=的定义域是( ) A .()0,∞+B .()()0,11,+∞C .[)()0,11,+∞UD .()1,+∞考点03 函数单调性的判断及其应用1.(2024∙全国新Ⅰ卷∙高考真题)已知函数22,0()e ln(1),0x x ax a x f x x x ⎧---<=⎨++≥⎩在R 上单调递增,则a 的取值范围是( ) A .(,0]-∞B .[1,0]-C .[1,1]-D .[0,)+∞2.(2023∙北京∙高考真题)下列函数中,在区间(0,)+∞上单调递增的是( ) A .()ln f x x =-B .1()2xf x =C .1()f x x=-D .|1|()3x f x -=3.(2023∙全国甲卷∙高考真题)已知函数()2(1)e x f x --=.记,,a f b f c f ===⎝⎭⎝⎭⎝⎭,则( )A .b c a >>B .b a c >>C .c b a >>D .c a b >>4.(2023∙全国新Ⅰ卷∙高考真题)设函数()()2x x a f x -=在区间()0,1上单调递减,则a 的取值范围是( )A .(],2-∞-B .[)2,0-C .(]0,2D .[)2,+∞5.(2021∙全国甲卷∙高考真题)下列函数中是增函数的为( )A .()f x x =-B .()23xf x ⎛⎫= ⎪⎝⎭C .()2f x x = D .()f x 6.(2020∙山东∙高考真题)已知函数()f x 的定义域是R ,若对于任意两个不相等的实数1x ,2x ,总有()()21210f x f x x x ->-成立,则函数()f x 一定是( )A .奇函数B .偶函数C .增函数D .减函数7.(2020∙全国∙高考真题)设函数331()f x x x=-,则()f x ( ) A .是奇函数,且在(0,+∞)单调递增 B .是奇函数,且在(0,+∞)单调递减 C .是偶函数,且在(0,+∞)单调递增D .是偶函数,且在(0,+∞)单调递减考点04 函数的奇偶性及其应用1.(2024∙天津∙高考真题)下列函数是偶函数的是( )A .22e 1x x y x -=+ B .22cos 1x x y x +=+C .e 1x x y x -=+D .||sin 4e x x xy +=2.(2024∙上海∙高考真题)已知()3f x x a =+,x ∈R ,且()f x 是奇函数,则=a .3.(2023∙全国甲卷∙高考真题)若()()2π1sin 2f x x ax x ⎛⎫=-+++ ⎪⎝⎭为偶函数,则=a .4.(2023∙全国乙卷∙高考真题)已知e ()e 1xax x f x =-是偶函数,则=a ( )A .2-B .1-C .1D .25.(2023∙全国新Ⅱ卷∙高考真题)若()()21ln 21x f x x a x -=++为偶函数,则=a ( ). A .1-B .0C .12D .16.(2022∙全国乙卷∙高考真题)若()1ln 1f x a b x++-=是奇函数,则=a ,b = . 7.(2021∙全国甲卷∙高考真题)设()f x 是定义域为R 的奇函数,且()()1f x f x +=-.若1133f ⎛⎫-= ⎪⎝⎭,则53f ⎛⎫= ⎪⎝⎭( )A .53-B .13-C .13D .538.(2021∙全国新Ⅱ卷∙高考真题)写出一个同时具有下列性质①②③的函数():f x . ①()()()1212f x x f x f x =;②当(0,)x ∈+∞时,()0f x '>;③()f x '是奇函数.9.(2021∙全国新Ⅰ卷∙高考真题)已知函数()()322x x x a f x -=⋅-是偶函数,则=a .10.(2021∙全国乙卷∙高考真题)设函数1()1xf x x-=+,则下列函数中为奇函数的是( ) A .()11f x --B .()11f x -+C .()11f x +-D .()11f x ++11.(2020∙山东∙高考真题)若定义在R 的奇函数f (x )在(,0)-∞单调递减,且f (2)=0,则满足(10)xf x -≥的x 的取值范围是( )A .[)1,1][3,-+∞B .3,1][,[01]--C .[1,0][1,)-⋃+∞D .[1,0][1,3]-⋃12.(2020∙全国∙高考真题)设函数()ln |21|ln |21|f x x x =+--,则f (x )( )A .是偶函数,且在1(,)2+∞单调递增B .是奇函数,且在11(,)22-单调递减C .是偶函数,且在1(,)2-∞-单调递增D .是奇函数,且在1(,2-∞-单调递减考点05 函数的周期性及其应用1.(2022∙全国新Ⅱ卷∙高考真题)已知函数()f x 的定义域为R ,且()()()(),(1)1f x y f x y f x f y f ++-==,则221()k f k ==∑( )A .3-B .2-C .0D .12.(2021∙全国新Ⅱ卷∙高考真题)已知函数()f x 的定义域为R ,()2f x +为偶函数,()21f x +为奇函数,则( ) A .102f ⎛⎫-= ⎪⎝⎭B .()10f -=C .()20f =D .()40f =3.(2021∙全国甲卷∙高考真题)设函数()f x 的定义域为R ,()1f x +为奇函数,()2f x +为偶函数,当[]1,2x ∈时,2()f x ax b =+.若()()036f f +=,则92f ⎛⎫= ⎪⎝⎭( )A .94-B .32-C .74D .52考点06 函数的对称性及其应用1.(2024∙全国新Ⅱ卷∙高考真题)(多选)设函数32()231f x x ax =-+,则( ) A .当1a >时,()f x 有三个零点 B .当0a <时,0x =是()f x 的极大值点C .存在a ,b ,使得x b =为曲线()y f x =的对称轴D .存在a ,使得点()()1,1f 为曲线()y f x =的对称中心2.(2022∙全国新Ⅰ卷∙高考真题)(多选)已知函数()f x 及其导函数()f x '的定义域均为R ,记()()g x f x '=,若322f x ⎛⎫- ⎪⎝⎭,(2)g x +均为偶函数,则( )A .(0)0f =B .102g ⎛⎫-= ⎪⎝⎭C .(1)(4)f f -=D .(1)(2)g g -=3.(2022∙全国乙卷∙高考真题)已知函数(),()f x g x 的定义域均为R ,且()(2)5,()(4)7f x g x g x f x +-=--=.若()y g x =的图像关于直线2x =对称,(2)4g =,则()221k f k ==∑( )A .21-B .22-C .23-D .24-4.(2020∙全国∙高考真题)已知函数f (x )=sin x +1sin x,则() A .f (x )的最小值为2B .f (x )的图象关于y 轴对称C .f (x )的图象关于直线x π=对称D .f (x )的图象关于直线2x π=对称参考答案 考点01 直接求函数值1.(2024∙全国新Ⅰ卷∙高考真题)已知函数()f x 的定义域为R ,()(1)(2)f x f x f x >-+-,且当3x <时()f x x =,则下列结论中一定正确的是( ) A .(10)100f > B .(20)1000f > C .(10)1000f < D .(20)10000f <【答案】B【答案分析】代入得到(1)1,(2)2==f f ,再利用函数性质和不等式的性质,逐渐递推即可判断. 【答案详解】因为当3x <时()f x x =,所以(1)1,(2)2==f f , 又因为()(1)(2)f x f x f x >-+-,则(3)(2)(1)3,(4)(3)(2)5f f f f f f >+=>+>,(5)(4)(3)8,(6)(5)(4)13,(7)(6)(5)21f f f f f f f f f >+>>+>>+>, (8)(7)(6)34,(9)(8)(7)55,(10)(9)(8)89f f f f f f f f f >+>>+>>+>, (11)(10)(9)144,(12)(11)(10)233,(13)(12)(11)377f f f f f f f f f >+>>+>>+> (14)(13)(12)610,(15)(14)(13)987f f f f f f >+>>+>,(16)(15)(14)15971000f f f >+>>,则依次下去可知(20)1000f >,则B 正确;且无证据表明ACD 一定正确. 故选:B.【名师点评】关键点名师点评:本题的关键是利用(1)1,(2)2==f f ,再利用题目所给的函数性质()(1)(2)f x f x f x >-+-,代入函数值再结合不等式同向可加性,不断递推即可.2.(2024∙上海∙高考真题)已知()0,1,0x f x x >=≤⎪⎩则()3f = .【答案分析】利用分段函数的形式可求()3f .【答案详解】因为()0,1,0x f x x >=≤⎪⎩故()3f =3.(2023∙北京∙高考真题)已知函数2()4log xf x x =+,则12f ⎛⎫= ⎪⎝⎭ .【答案】1【答案分析】根据给定条件,把12x =代入,利用指数、对数运算计算作答. 【答案详解】函数2()4log xf x x =+,所以12211()4log 21122f =+=-=.故答案为:14.(2021∙全国甲卷∙高考真题)设()f x 是定义域为R 的奇函数,且()()1f x f x +=-.若1133f ⎛⎫-= ⎪⎝⎭,则53f ⎛⎫= ⎪⎝⎭( )A .53-B .13-C .13D .53【答案】C【答案分析】由题意利用函数的奇偶性和函数的递推关系即可求得53f ⎛⎫⎪⎝⎭的值.【答案详解】由题意可得:522213333f f f f⎛⎫⎛⎫⎛⎫⎛⎫=+=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 而21111133333f f f f⎛⎫⎛⎫⎛⎫⎛⎫=-==--=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 故5133f ⎛⎫= ⎪⎝⎭.故选:C.【名师点评】关键点名师点评:本题主要考查了函数的奇偶性和函数的递推关系式,灵活利用所给的条件进行转化是解决本题的关键.5.(2021∙浙江∙高考真题)已知R a ∈,函数24,2()3,2,x x f x x a x ⎧->⎪=⎨-+≤⎪⎩若3f f ⎡⎤=⎣⎦,则=a . 【答案】2【答案分析】由题意结合函数的答案解析式得到关于a 的方程,解方程可得a 的值.【答案详解】()()642233f f f f a ⎡⎤=-==-+=⎣⎦,故2a =, 故答案为:2.考点02 函数的定义域与值域1.(2022∙北京∙高考真题)函数1()f x x=的定义域是 . 【答案】()(],00,1-∞⋃【答案分析】根据偶次方根的被开方数非负、分母不为零得到方程组,解得即可;【答案详解】解:因为()1f x x =100x x -≥⎧⎨≠⎩,解得1x ≤且0x ≠, 故函数的定义域为()(],00,1-∞⋃; 故答案为:()(],00,1-∞⋃2.(2020∙山东∙高考真题)函数()1lg f x x=的定义域是( ) A .()0,∞+ B .()()0,11,+∞C .[)()0,11,+∞UD .()1,+∞【答案】B【答案分析】根据题意得到0lg 0x x >⎧⎨≠⎩,再解不等式组即可.【答案详解】由题知:0lg 0x x >⎧⎨≠⎩,解得0x >且1x ≠. 所以函数定义域为()()0,11,+∞ . 故选:B考点03 函数单调性的判断及其应用1.(2024∙全国新Ⅰ卷∙高考真题)已知函数22,0()e ln(1),0x x ax a x f x x x ⎧---<=⎨++≥⎩在R 上单调递增,则a 的取值范围是( ) A .(,0]-∞ B .[1,0]- C .[1,1]- D .[0,)+∞【答案】B【答案分析】根据二次函数的性质和分界点的大小关系即可得到不等式组,解出即可.【答案详解】因为()f x 在R 上单调递增,且0x ≥时,()()e ln 1xf x x =++单调递增,则需满足()02021e ln1aa -⎧-≥⎪⨯-⎨⎪-≤+⎩,解得10a -≤≤, 即a 的范围是[1,0]-. 故选:B.2.(2023∙北京∙高考真题)下列函数中,在区间(0,)+∞上单调递增的是( ) A .()ln f x x =- B .1()2xf x =C .1()f x x=-D .|1|()3x f x -=【答案】C【答案分析】利用基本初等函数的单调性,结合复合函数的单调性判断ABC ,举反例排除D 即可. 【答案详解】对于A ,因为ln y x =在()0,∞+上单调递增,y x =-在()0,∞+上单调递减, 所以()ln f x x =-在()0,∞+上单调递减,故A 错误;对于B ,因为2x y =在()0,∞+上单调递增,1y x=在()0,∞+上单调递减,所以()12xf x =在()0,∞+上单调递减,故B 错误; 对于C ,因为1y x=在()0,∞+上单调递减,y x =-在()0,∞+上单调递减, 所以()1f x x=-在()0,∞+上单调递增,故C 正确;对于D ,因为111221332f -⎛⎫=== ⎪⎝⎭()()112101331,233f f --=====,显然()13x f x -=在()0,∞+上不单调,D 错误.故选:C.3.(2023∙全国甲卷∙高考真题)已知函数()2(1)e x f x --=.记,,222a f b f c f ⎛⎫=== ⎪⎝⎭⎝⎭⎝⎭,则( ) A .b c a >> B .b a c >> C .c b a >> D .c a b >>【答案】A【答案分析】利用作差法比较自变量的大小,再根据指数函数的单调性及二次函数的性质判断即可. 【答案详解】令2()(1)g x x =--,则()g x 开口向下,对称轴为1x =,4112⎛-= ⎝⎭,而22491670-=+=>,41102⎛-=> ⎝⎭,即1122->-由二次函数性质知g g <,4112⎛-= ⎝⎭,而22481682)0-=+-=-=-<,112<-,所以(2g g >,综上,(2g g g <<, 又e x y =为增函数,故a c b <<,即b c a >>. 故选:A.4.(2023∙全国新Ⅰ卷∙高考真题)设函数()()2x x a f x -=在区间()0,1上单调递减,则a 的取值范围是( )A .(],2-∞-B .[)2,0-C .(]0,2D .[)2,+∞【答案】D【答案分析】利用指数型复合函数单调性,判断列式计算作答.【答案详解】函数2x y =在R 上单调递增,而函数()()2x x a f x -=在区间()0,1上单调递减,则有函数22()()24a a y x x a x =-=--在区间()0,1上单调递减,因此12a ≥,解得2a ≥,所以a 的取值范围是[)2,+∞. 故选:D5.(2021∙全国甲卷∙高考真题)下列函数中是增函数的为( )A .()f x x =-B .()23xf x ⎛⎫= ⎪⎝⎭C .()2f x x = D .()f x 【答案】D【答案分析】根据基本初等函数的性质逐项判断后可得正确的选项. 【答案详解】对于A ,()f x x =-为R 上的减函数,不合题意,舍. 对于B ,()23xf x ⎛⎫= ⎪⎝⎭为R 上的减函数,不合题意,舍.对于C ,()2f x x =在(),0∞-为减函数,不合题意,舍.对于D ,()f x =R 上的增函数,符合题意, 故选:D.6.(2020∙山东∙高考真题)已知函数()f x 的定义域是R ,若对于任意两个不相等的实数1x ,2x ,总有()()21210f x f x x x ->-成立,则函数()f x 一定是( )A .奇函数B .偶函数C .增函数D .减函数【答案】C【答案分析】利用函数单调性定义即可得到答案. 【答案详解】对于任意两个不相等的实数1x ,2x ,总有()()21210f x f x x x ->-成立,等价于对于任意两个不相等的实数12x x <,总有()()12f x f x <. 所以函数()f x 一定是增函数. 故选:C7.(2020∙全国∙高考真题)设函数331()f x x x =-,则()f x ( ) A .是奇函数,且在(0,+∞)单调递增 B .是奇函数,且在(0,+∞)单调递减 C .是偶函数,且在(0,+∞)单调递增 D .是偶函数,且在(0,+∞)单调递减【答案】A【答案分析】根据函数的答案解析式可知函数的定义域为{}0x x ≠,利用定义可得出函数()f x 为奇函数,再根据函数的单调性法则,即可解出.【答案详解】因为函数()331f x x x =-定义域为{}0x x ≠,其关于原点对称,而()()f x f x -=-, 所以函数()f x 为奇函数. 又因为函数3y x =在()0,+?上单调递增,在(),0-?上单调递增,而331y x x -==在()0,+?上单调递减,在(),0-?上单调递减,所以函数()331f x x x =-在()0,+?上单调递增,在(),0-?上单调递增.故选:A .【名师点评】本题主要考查利用函数的答案解析式研究函数的性质,属于基础题.考点04 函数的奇偶性及其应用1.(2024∙天津∙高考真题)下列函数是偶函数的是( )A .22e 1x x y x -=+ B .22cos 1x x y x +=+C .e 1x xy x -=+D .||sin 4e x x xy +=【答案】B【答案分析】根据偶函数的判定方法一一判断即可.【答案详解】对A ,设()22e 1x xf x x -=+,函数定义域为R ,但()112e 1f ---=,()112e f -=,则()()11f f -≠,故A 错误;对B ,设()22cos 1x x g x x +=+,函数定义域为R , 且()()()()()2222cos cos 11x x x x g x g x x x -+-+-===+-+,则()g x 为偶函数,故B 正确;对C ,设()e 1x xh x x -=+,函数定义域为{}|1x x ≠-,不关于原点对称, 则()h x 不是偶函数,故C 错误; 对D ,设()||sin 4e x x x x ϕ+=,函数定义域为R,因为()sin141e ϕ+=,()sin141e ϕ---=, 则()()11ϕϕ≠-,则()x ϕ不是偶函数,故D 错误. 故选:B.2.(2024∙上海∙高考真题)已知()3f x x a =+,x ∈R ,且()f x 是奇函数,则=a .【答案】0【答案分析】根据奇函数的性质可求参数a .【答案详解】因为()f x 是奇函数,故()()0f x f x -+=即()330x a x a ++-+=,故0a =, 故答案为:0.3.(2023∙全国甲卷∙高考真题)若()()2π1sin 2f x x ax x ⎛⎫=-+++ ⎪⎝⎭为偶函数,则=a .【答案】2【答案分析】利用偶函数的性质得到ππ22f f ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭,从而求得2a =,再检验即可得解.【答案详解】因为()()()22π1sin 1cos 2y f x x ax x x ax x ⎛⎫==-+++=-++ ⎪⎝⎭为偶函数,定义域为R ,所以ππ22f f ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭,即22ππππππ222222s 1co 1cos a a ⎛⎫⎛⎫⎛⎫-+=-+ ⎪ -⎪ ⎪⎝⎭⎝⎭--⎝+⎭,则22πππ2π1212a -⎛⎫⎛⎫=+- ⎪⎪⎭⎝⎭= ⎝,故2a =,此时()()2212cos 1cos f x x x x x x =-++=++, 所以()()()()221cos s 1co f x x x x x f x -=-++++-==, 又定义域为R ,故()f x 为偶函数, 所以2a =. 故答案为:2.4.(2023∙全国乙卷∙高考真题)已知e ()e 1xaxx f x =-是偶函数,则=a ( ) A .2- B .1- C .1 D .2【答案】D【答案分析】根据偶函数的定义运算求解.【答案详解】因为()e e 1x ax x f x =-为偶函数,则()()()()1e e e e 0e 1e 1e 1a x x x x ax ax axx x x f x f x ---⎡⎤--⎣⎦--=-==---, 又因为x 不恒为0,可得()1e e 0a x x --=,即()1e e a x x -=, 则()1x a x =-,即11a =-,解得2a =. 故选:D.5.(2023∙全国新Ⅱ卷∙高考真题)若()()21ln 21x f x x a x -=++为偶函数,则=a ( ). A .1- B .0C .12D .1【答案】B【答案分析】根据偶函数性质,利用特殊值法求出a 值,再检验即可.【答案详解】因为()f x 为偶函数,则 1(1)(1)(1)ln (1)ln 33f f a a =-∴+=-+,,解得0a =, 当0a =时,()21ln21x x x f x -=+,()()21210x x -+>,解得12x >或12x <-,则其定义域为12x x ⎧⎨⎩或12x ⎫<-⎬⎭,关于原点对称.()()()()()()()121212121ln ln ln ln 21212121f x x x x x x x x x f x x x x x ---+⎫-=---⎛==== ⎪-+-++⎝-⎭-, 故此时()f x 为偶函数. 故选:B.6.(2022∙全国乙卷∙高考真题)若()1ln 1f x a b x++-=是奇函数,则=a ,b = . 【答案】 12-; ln 2.【答案分析】根据奇函数的定义即可求出. 【答案详解】[方法一]:奇函数定义域的对称性 若0a =,则()f x 的定义域为{|1}x x ≠,不关于原点对称0a ∴≠若奇函数的1()||1f x ln a b x =++-有意义,则1x ≠且101a x+≠- 1x ∴≠且11x a≠+,函数()f x 为奇函数,定义域关于原点对称,111a ∴+=-,解得12a =-, 由(0)0f =得,102ln b +=,2b ln ∴=,故答案为:12-;2ln .[方法二]:函数的奇偶性求参 111()111a ax ax a f x ln a b ln b ln b x x x-+--=++=+=+--- 1()1ax a f x lnb x++-=++函数()f x 为奇函数11()()2011ax a ax a f x f x lnln b x x--++∴+-=++=-+2222(1)201a x a lnb x -+∴+=-22(1)1210112a a a a +∴=⇒+=⇒=- 1222241,22b ln b ln a b ln ln -==-⇒=∴=-=[方法三]:因为函数()1ln 1f x a b x++-=为奇函数,所以其定义域关于原点对称. 由101a x+≠-可得,()()110x a ax -+-≠,所以11a x a +==-,解得:12a =-,即函数的定义域为()()(),11,11,-∞-⋃-⋃+∞,再由()00f =可得,ln 2b =.即()111ln ln 2ln 211x f x x x+=-++=--,在定义域内满足()()f x f x -=-,符合题意. 故答案为:12-;ln 2.7.(2021∙全国甲卷∙高考真题)设()f x 是定义域为R 的奇函数,且()()1f x f x +=-.若1133f ⎛⎫-= ⎪⎝⎭,则53f ⎛⎫= ⎪⎝⎭( )A .53-B .13-C .13D .53【答案】C【答案分析】由题意利用函数的奇偶性和函数的递推关系即可求得53f ⎛⎫⎪⎝⎭的值.【答案详解】由题意可得:522213333f f f f⎛⎫⎛⎫⎛⎫⎛⎫=+=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 而21111133333f f f f⎛⎫⎛⎫⎛⎫⎛⎫=-==--=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 故5133f ⎛⎫= ⎪⎝⎭.故选:C.【名师点评】关键点名师点评:本题主要考查了函数的奇偶性和函数的递推关系式,灵活利用所给的条件进行转化是解决本题的关键.8.(2021∙全国新Ⅱ卷∙高考真题)写出一个同时具有下列性质①②③的函数():f x . ①()()()1212f x x f x f x =;②当(0,)x ∈+∞时,()0f x '>;③()f x '是奇函数.【答案】()4f x x =(答案不唯一,()()2*n x N f n x =∈均满足)【答案分析】根据幂函数的性质可得所求的()f x .【答案详解】取()4f x x =,则()()()()44421121122x f x f x x x x f x x ===,满足①, ()34f x x '=,0x >时有()0f x ¢>,满足②, ()34f x x '=的定义域为R ,又()()34f x x f x ''-=-=-,故()f x '是奇函数,满足③.故答案为:()4f x x =(答案不唯一,()()2*n x N f n x =∈均满足)9.(2021∙全国新Ⅰ卷∙高考真题)已知函数()()322x xx a f x -=⋅-是偶函数,则=a .【答案】1【答案分析】利用偶函数的定义可求参数a 的值.【答案详解】因为()()322x x x a f x -=⋅-,故()()322x xf x x a --=-⋅-,因为()f x 为偶函数,故()()f x f x -=,时()()332222x x x x x a x a --⋅-=-⋅-,整理得到()()12+2=0x xa --,故1a =, 故答案为:110.(2021∙全国乙卷∙高考真题)设函数1()1xf x x-=+,则下列函数中为奇函数的是( ) A .()11f x -- B .()11f x -+C .()11f x +-D .()11f x ++【答案】B【答案分析】分别求出选项的函数答案解析式,再利用奇函数的定义即可. 【答案详解】由题意可得12()111x f x x x-==-+++, 对于A ,()2112f x x--=-不是奇函数; 对于B ,()211f x x-=+是奇函数; 对于C ,()21122f x x +-=-+,定义域不关于原点对称,不是奇函数; 对于D ,()2112f x x ++=+,定义域不关于原点对称,不是奇函数. 故选:B【名师点评】本题主要考查奇函数定义,考查学生对概念的理解,是一道容易题.11.(2020∙山东∙高考真题)若定义在R 的奇函数f (x )在(,0)-∞单调递减,且f (2)=0,则满足(10)xf x -≥的x的取值范围是( )A .[)1,1][3,-+∞B .3,1][,[01]--C .[1,0][1,)-⋃+∞D .[1,0][1,3]-⋃【答案】D【答案分析】首先根据函数奇偶性与单调性,得到函数()f x 在相应区间上的符号,再根据两个数的乘积大于等于零,分类转化为对应自变量不等式,最后求并集得结果.【答案详解】因为定义在R 上的奇函数()f x 在(,0)-∞上单调递减,且(2)0f =, 所以()f x 在(0,)+∞上也是单调递减,且(2)0f -=,(0)0f =,所以当(,2)(0,2)x ∈-∞-⋃时,()0f x >,当(2,0)(2,)x ∈-+∞ 时,()0f x <, 所以由(10)xf x -≥可得:0210x x <⎧⎨-≤-≤⎩或0012x x >⎧⎨≤-≤⎩或0x = 解得10x -≤≤或13x ≤≤,所以满足(10)xf x -≥的x 的取值范围是[1,0][1,3]-⋃, 故选:D.【名师点评】本题考查利用函数奇偶性与单调性解抽象函数不等式,考查分类讨论思想方法,属中档题. 12.(2020∙全国∙高考真题)设函数()ln |21|ln |21|f x x x =+--,则f (x )( )A .是偶函数,且在1(,)2+∞单调递增B .是奇函数,且在11(,)22-单调递减C .是偶函数,且在1(,)2-∞-单调递增D .是奇函数,且在1(,2-∞-单调递减【答案】D【答案分析】根据奇偶性的定义可判断出()f x 为奇函数,排除AC ;当11,22x ⎛⎫∈- ⎪⎝⎭时,利用函数单调性的性质可判断出()f x 单调递增,排除B ;当1,2x ⎛⎫∈-∞- ⎪⎝⎭时,利用复合函数单调性可判断出()f x 单调递减,从而得到结果.【答案详解】由()ln 21ln 21f x x x =+--得()f x 定义域为12x x ⎧⎫≠±⎨⎬⎩⎭,关于坐标原点对称,又()()ln 12ln 21ln 21ln 21f x x x x x f x -=----=--+=-, ()f x \为定义域上的奇函数,可排除AC ;当11,22x ⎛⎫∈- ⎪⎝⎭时,()()()ln 21ln 12f x x x =+--,()ln 21y x =+Q 在11,22⎛⎫- ⎪⎝⎭上单调递增,()ln 12y x =-在11,22⎛⎫- ⎪⎝⎭上单调递减,()f x \在11,22⎛⎫- ⎪⎝⎭上单调递增,排除B ;当1,2x ⎛⎫∈-∞- ⎪⎝⎭时,()()()212ln 21ln 12ln ln 12121x f x x x x x +⎛⎫=----==+ ⎪--⎝⎭,2121x μ=+- 在1,2⎛⎫-∞- ⎪⎝⎭上单调递减,()ln f μμ=在定义域内单调递增,根据复合函数单调性可知:()f x 在1,2⎛⎫-∞- ⎪⎝⎭上单调递减,D 正确.故选:D.【名师点评】本题考查函数奇偶性和单调性的判断;判断奇偶性的方法是在定义域关于原点对称的前提下,根据()f x -与()f x 的关系得到结论;判断单调性的关键是能够根据自变量的范围化简函数,根据单调性的性质和复合函数“同增异减”性得到结论.考点05 函数的周期性及其应用1.(2022∙全国新Ⅱ卷∙高考真题)已知函数()f x 的定义域为R ,且()()()(),(1)1f x y f x y f x f y f ++-==,则221()k f k ==∑( )A .3-B .2-C .0D .1【答案】A【答案分析】法一:根据题意赋值即可知函数()f x 的一个周期为6,求出函数一个周期中的()()()1,2,,6f f f 的值,即可解出. 【答案详解】[方法一]:赋值加性质因为()()()()f x y f x y f x f y ++-=,令1,0x y ==可得,()()()2110f f f =,所以()02f =,令0x =可得,()()()2f y f y f y +-=,即()()f y f y =-,所以函数()f x 为偶函数,令1y =得,()()()()()111f x f x f x f f x ++-==,即有()()()21f x f x f x ++=+,从而可知()()21f x f x +=--,()()14f x f x -=--,故()()24f x f x +=-,即()()6f x f x =+,所以函数()f x 的一个周期为6.因为()()()210121f f f =-=-=-,()()()321112f f f =-=--=-,()()()4221f f f =-==-,()()()5111f f f =-==,()()602f f ==,所以一个周期内的()()()1260f f f +++= .由于22除以6余4, 所以()()()()()221123411213k f k f f f f ==+++=---=-∑.故选:A .[方法二]:【最优解】构造特殊函数由()()()()f x y f x y f x f y ++-=,联想到余弦函数和差化积公式()()cos cos 2cos cos x y x y x y ++-=,可设()cos f x a x ω=,则由方法一中()()02,11f f ==知2,cos 1a a ω==,解得1cos 2ω=,取3πω=, 所以()2cos3f x x π=,则()()()()2cos 2cos 4cos cos 333333f x y f x y x y x y x y f x f y ππππππ⎛⎫⎛⎫++-=++-== ⎪ ⎪⎝⎭⎝⎭,所以()2cos 3f x xπ=符合条件,因此()f x 的周期263T ππ==,()()02,11f f ==,且()()()()()21,32,41,51,62f f f f f =-=-=-==,所以(1)(2)(3)(4)(5)(6)0f f f f f f +++++=, 由于22除以6余4,所以()()()()()221123411213k f k f f f f ==+++=---=-∑.故选:A .【整体点评】法一:利用赋值法求出函数的周期,即可解出,是该题的通性通法;法二:作为选择题,利用熟悉的函数使抽象问题具体化,简化推理过程,直接使用具体函数的性质解题,简单明了,是该题的最优解.2.(2021∙全国新Ⅱ卷∙高考真题)已知函数()f x 的定义域为R ,()2f x +为偶函数,()21f x +为奇函数,则( ) A .102f ⎛⎫-= ⎪⎝⎭B .()10f -=C .()20f =D .()40f =【答案】B【答案分析】推导出函数()f x 是以4为周期的周期函数,由已知条件得出()10f =,结合已知条件可得出结论.【答案详解】因为函数()2f x +为偶函数,则()()22f x f x +=-,可得()()31f x f x +=-, 因为函数()21f x +为奇函数,则()()1221f x f x -=-+,所以,()()11f x f x -=-+, 所以,()()()311f x f x f x +=-+=-,即()()4f x f x =+, 故函数()f x 是以4为周期的周期函数,因为函数()()21F x f x =+为奇函数,则()()010F f ==, 故()()110f f -=-=,其它三个选项未知. 故选:B.3.(2021∙全国甲卷∙高考真题)设函数()f x 的定义域为R ,()1f x +为奇函数,()2f x +为偶函数,当[]1,2x ∈时,2()f x ax b =+.若()()036f f +=,则92f ⎛⎫= ⎪⎝⎭( )A .94-B .32-C .74D .52【答案】D【答案分析】通过()1f x +是奇函数和()2f x +是偶函数条件,可以确定出函数答案解析式()222f x x =-+,进而利用定义或周期性结论,即可得到答案. 【答案详解】[方法一]:因为()1f x +是奇函数,所以()()11f x f x -+=-+①; 因为()2f x +是偶函数,所以()()22f x f x +=-+②.令1x =,由①得:()()()024f f a b =-=-+,由②得:()()31f f a b ==+, 因为()()036f f +=,所以()462a b a b a -+++=⇒=-,令0x =,由①得:()()()11102f f f b =-⇒=⇒=,所以()222f x x =-+.思路一:从定义入手.9551222222f f f f ⎛⎫⎛⎫⎛⎫⎛⎫=+=-+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ 1335112222f f f f ⎛⎫⎛⎫⎛⎫⎛⎫-=-+=-+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ 511322=2222f f f f ⎛⎫⎛⎫⎛⎫⎛⎫-=-+=--+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭所以935222f f⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭. [方法二]:因为()1f x +是奇函数,所以()()11f x f x -+=-+①; 因为()2f x +是偶函数,所以()()22f x f x +=-+②.令1x =,由①得:()()()024f f a b =-=-+,由②得:()()31f f a b ==+, 因为()()036f f +=,所以()462a b a b a -+++=⇒=-,令0x =,由①得:()()()11102f f f b =-⇒=⇒=,所以()222f x x =-+.思路二:从周期性入手由两个对称性可知,函数()f x 的周期4T =. 所以91352222f f f⎛⎫⎛⎫⎛⎫==-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 故选:D .【名师点评】在解决函数性质类问题的时候,我们通常可以借助一些二级结论,求出其周期性进而达到简便计算的效果.考点06 函数的对称性及其应用1.(2024∙全国新Ⅱ卷∙高考真题)(多选)设函数32()231f x x ax =-+,则( ) A .当1a >时,()f x 有三个零点 B .当0a <时,0x =是()f x 的极大值点C .存在a ,b ,使得x b =为曲线()y f x =的对称轴D .存在a ,使得点()()1,1f 为曲线()y f x =的对称中心【答案】AD【答案分析】A 选项,先答案分析出函数的极值点为0,x x a ==,根据零点存在定理和极值的符号判断出()f x 在(1,0),(0,),(,2)a a a -上各有一个零点;B 选项,根据极值和导函数符号的关系进行答案分析;C 选项,假设存在这样的,a b ,使得x b =为()f x 的对称轴,则()(2)f x f b x =-为恒等式,据此计算判断;D 选项,若存在这样的a ,使得(1,33)a -为()f x 的对称中心,则()(2)66f x f x a +-=-,据此进行计算判断,亦可利用拐点结论直接求解.【答案详解】A 选项,2()666()f x x ax x x a '=-=-,由于1a >,故()(),0,x a ∞∞∈-⋃+时()0f x '>,故()f x 在()(),0,,a ∞∞-+上单调递增, (0,)x a ∈时,()0f x '<,()f x 单调递减,则()f x 在0x =处取到极大值,在x a =处取到极小值, 由(0)10=>f ,3()10f a a =-<,则(0)()0f f a <, 根据零点存在定理()f x 在(0,)a 上有一个零点,又(1)130f a -=--<,3(2)410f a a =+>,则(1)(0)0,()(2)0f f f a f a -<<,则()f x 在(1,0),(,2)a a -上各有一个零点,于是1a >时,()f x 有三个零点,A 选项正确; B 选项,()6()f x x x a '=-,a<0时,(,0),()0x a f x '∈<,()f x 单调递减, ,()0x ∈+∞时()0f x '>,()f x 单调递增,此时()f x 在0x =处取到极小值,B 选项错误;C 选项,假设存在这样的,a b ,使得x b =为()f x 的对称轴,即存在这样的,a b 使得()(2)f x f b x =-, 即32322312(2)3(2)1x ax b x a b x -+=---+,根据二项式定理,等式右边3(2)b x -展开式含有3x 的项为303332C (2)()2b x x -=-,于是等式左右两边3x 的系数都不相等,原等式不可能恒成立, 于是不存在这样的,a b ,使得x b =为()f x 的对称轴,C 选项错误; D 选项,方法一:利用对称中心的表达式化简(1)33f a =-,若存在这样的a ,使得(1,33)a -为()f x 的对称中心,则()(2)66f x f x a +-=-,事实上,32322()(2)2312(2)3(2)1(126)(1224)1812f x f x x ax x a x a x a x a +-=-++---+=-+-+-,于是266(126)(1224)1812a a x a x a -=-+-+-即126012240181266a a a a -=⎧⎪-=⎨⎪-=-⎩,解得2a =,即存在2a =使得(1,(1))f 是()f x 的对称中心,D 选项正确. 方法二:直接利用拐点结论任何三次函数都有对称中心,对称中心的横坐标是二阶导数的零点,32()231f x x ax =-+,2()66f x x ax '=-,()126f x x a ''=-,由()02af x x ''=⇔=,于是该三次函数的对称中心为,22a a f ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭, 由题意(1,(1))f 也是对称中心,故122aa =⇔=, 即存在2a =使得(1,(1))f 是()f x 的对称中心,D 选项正确. 故选:AD【名师点评】结论名师点评:(1)()f x 的对称轴为()(2)x b f x f b x =⇔=-;(2)()f x 关于(,)a b 对称()(2)2f x f a x b ⇔+-=;(3)任何三次函数32()f x ax bx cx d =+++都有对称中心,对称中心是三次函数的拐点,对称中心的横坐标是()0f x ''=的解,即,33b b f a a ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭是三次函数的对称中心 2.(2022∙全国新Ⅰ卷∙高考真题)(多选)已知函数()f x 及其导函数()f x '的定义域均为R ,记()()g x f x '=,若322f x ⎛⎫- ⎪⎝⎭,(2)g x +均为偶函数,则( )A .(0)0f =B .102g ⎛⎫-= ⎪⎝⎭C .(1)(4)f f -=D .(1)(2)g g -=【答案】BC【答案分析】方法一:转化题设条件为函数的对称性,结合原函数与导函数图象的关系,根据函数的性质逐项判断即可得解.【答案详解】[方法一]:对称性和周期性的关系研究对于()f x ,因为322f x ⎛⎫- ⎪⎝⎭为偶函数,所以332222f x f x ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭即3322f x f x ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭①,所以()()3f x f x -=,所以()f x 关于32x =对称,则(1)(4)f f -=,故C 正确; 对于()g x ,因为(2)g x +为偶函数,(2)(2)g x g x +=-,(4)()g x g x -=,所以()g x 关于2x =对称,由①求导,和()()g x f x '=,得333333222222f x f x f x f x g x g x ''⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫''-=+⇔--=+⇔--=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦,所以()()30g x g x -+=,所以()g x 关于3(,0)2对称,因为其定义域为R ,所以302g ⎛⎫= ⎪⎝⎭,结合()g x 关于2x =对称,从而周期34222T ⎛⎫=⨯-= ⎪⎝⎭,所以13022g g ⎛⎫⎛⎫-== ⎪ ⎪⎝⎭⎝⎭,()()()112g g g -==-,故B 正确,D 错误; 若函数()f x 满足题设条件,则函数()f x C +(C 为常数)也满足题设条件,所以无法确定()f x 的函数值,故A 错误.故选:BC.[方法二]:【最优解】特殊值,构造函数法.由方法一知()g x 周期为2,关于2x =对称,故可设()()cos πg x x =,则()()1sin ππf x x c =+,显然A ,D 错误,选BC.故选:BC.[方法三]: 因为322f x ⎛⎫- ⎪⎝⎭,(2)g x +均为偶函数, 所以332222f x f x ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭即3322f x f x ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭,(2)(2)g x g x +=-, 所以()()3f x f x -=,(4)()g x g x -=,则(1)(4)f f -=,故C 正确;函数()f x ,()g x 的图象分别关于直线3,22x x ==对称, 又()()g x f x '=,且函数()f x 可导, 所以()()30,32g g x g x ⎛⎫=-=- ⎪⎝⎭, 所以()(4)()3g x g x g x -==--,所以()(2)(1)g x g x g x +=-+=, 所以13022g g ⎛⎫⎛⎫-== ⎪ ⎪⎝⎭⎝⎭,()()()112g g g -==-,故B 正确,D 错误; 若函数()f x 满足题设条件,则函数()f x C +(C 为常数)也满足题设条件,所以无法确定()f x 的函数值,故A 错误.故选:BC.【点评】方法一:根据题意赋值变换得到函数的性质,即可判断各选项的真假,转化难度较高,是该题的通性通法;方法二:根据题意得出的性质构造特殊函数,再验证选项,简单明了,是该题的最优解.3.(2022∙全国乙卷∙高考真题)已知函数(),()f x g x 的定义域均为R ,且()(2)5,()(4)7f x g x g x f x +-=--=.若()y g x =的图像关于直线2x =对称,(2)4g =,则()221k f k ==∑( )A .21-B .22-C .23-D .24-【答案】D【答案分析】根据对称性和已知条件得到()(2)2f x f x +-=-,从而得到()()()352110f f f +++=- ,()()()462210f f f +++=- ,然后根据条件得到(2)f 的值,再由题意得到()36g =从而得到()1f 的值即可求解.【答案详解】因为()y g x =的图像关于直线2x =对称,所以()()22g x g x -=+,因为()(4)7g x f x --=,所以(2)(2)7g x f x +--=,即(2)7(2)g x f x +=+-,因为()(2)5f x g x +-=,所以()(2)5f x g x ++=,代入得[]()7(2)5f x f x ++-=,即()(2)2f x f x +-=-,所以()()()()35212510f f f +++=-⨯=- ,()()()()46222510f f f +++=-⨯=- .因为()(2)5f x g x +-=,所以(0)(2)5f g +=,即()01f =,所以()(2)203f f =--=-.因为()(4)7g x f x --=,所以(4)()7g x f x +-=,又因为()(2)5f x g x +-=,联立得,()()2412g x g x -++=,所以()y g x =的图像关于点()3,6中心对称,因为函数()g x 的定义域为R ,所以()36g =因为()(2)5f x g x ++=,所以()()1531f g =-=-.所以()()()()()()()()221123521462213101024()k f f f f f f f f f k =+++++++++=----=-⎡⎤⎡⎤⎣⎦⎣⎦=∑ . 故选:D【名师点评】含有对称轴或对称中心的问题往往条件比较隐蔽,考生需要根据已知条件进行恰当的转化,然后得到所需的一些数值或关系式从而解题.4.(2020∙全国∙高考真题)已知函数f (x )=sin x +1sin x ,则() A .f (x )的最小值为2B .f (x )的图象关于y 轴对称C .f (x )的图象关于直线x π=对称D .f (x )的图象关于直线2x π=对称【答案】D【答案分析】根据基本不等式使用条件可判断A;根据奇偶性可判断B;根据对称性判断C,D.【答案详解】sin x 可以为负,所以A 错;1sin 0()()sin ()sin x x k k Z f x x f x x π≠∴≠∈-=--=-∴Q Q ()f x 关于原点对称; 11(2)sin (),()sin (),sin sin f x x f x f x x f x x x ππ-=--≠-=+=Q 故B 错; ()f x ∴关于直线2x π=对称,故C 错,D 对故选:D【名师点评】本题考查函数定义域与最值、奇偶性、对称性,考查基本答案分析判断能力,属中档题.。
2023-2024学年高考数学指数函数与对数函数专项练习题(含答案)

2024....二、多选题.函数,若对任意实数、,,则下列结论错误的是()(32log f x x x =++a b 0a b +>A .方程有且只有6个不同的解B .方程()()0f g x =解C .方程有且只有5个不同的解D .方程()()0f f x =解的零点个数为 .()4log =-y f x x16.已知函数,若方程有4个不同的实根,,,22log (1),13()1357,322x x f x x x x ⎧-<≤⎪=⎨-+>⎪⎩()34f x =1x 2x 3x 且,则.4x 1234x x x x <<<()341211x x x x ⎛⎫++=⎪⎝⎭答案:1.C【分析】根据函数的单调性,借助中间值比较大小.【详解】因为函数在单调递增,且,所以,即,2log y x =()0,∞+π2>22log π>log 21=1a >因为函数在单调递减,且,所以,即,0.5log y x =()0,∞+π1>0.50.5log π<log 1=00b <因为函数在单调递增,且,所以,即,πxy =(),-∞+∞20-<200<ππ1-<=01c <<所以,a c b >>故选:C 2.A【分析】由提供的数据知,描述西红柿种植成本与上市时间的变化关系函数不可能是单Q t 调函数,故选取二次函数进行描述,将表格所提供的三组数据代入,即得函2Q at bt c =++Q 数解析式,进而求解.【详解】因为随着时间的增加,种植成本先减少后增加,所以函数不单调,所以选取,且开口向上,2Q at bt c =++将表格中的三组数据分别代入,2Q at bt c =++得解得116360060,8410000100,11632400180,a b c a b c a b c =++⎧⎪=++⎨⎪=++⎩0.01,2.4,224,a b c =⎧⎪=-⎨⎪=⎩即,对称轴,开口向上,20.01 2.4224Q t t =-+ 2.412020.01t -=-=⨯在对称轴处即120天时函数取最小值.∴t =西红柿种植成本最低时的上市天数是120天.∴故选:A.3.C【分析】由指数函数的性质分别对和的情况讨论单调性并求值域,从而列方程组01a <<1a >即可得到答案.【详解】函数(且)的值域为,2x y a =-0a >1,11a x ≠-≤≤5,13⎡⎤-⎢⎥⎣⎦又由指数函数的单调性可知,当时,函数在上单调递减,值域是01a <<2xy a =-[]1,1-12,2a a -⎡⎤--⎣⎦所以有,即,解得;110152321a a a -<<⎧⎪⎪-=-⎨⎪-=⎪⎩101133a a a -<<⎧⎪⎪=⎨⎪=⎪⎩13a =当时,函数在上单调递增,值域是1a >2x y a =-[]1,1-12,2a a -⎡⎤--⎣⎦所以有,即 ,解得.11152321a a a ->⎧⎪⎪-=-⎨⎪-=⎪⎩11133a a a ->⎧⎪⎪=⎨⎪=⎪⎩3a =综上所述,或.13a =3a =故选:C.4.B【分析】结合已知条件,利用抽象函数的定义域以及对数、分式的定义域求法求解即可.【详解】因为函数的定义域是,()f x [1,2022]所以对于有:,(1)()lg f x g x x +=1120220lg 0x x x ≤+≤⎧⎪>⎨⎪≠⎩解得:且,02021x <≤1x ≠故函数的定义域是,()()1ln f x g x x+=(01)(1],,2021⋃故选:B .5.A【分析】根据题意,求得,得到,结合零点的存在性定理,3()0,(2)02f f >>3(1)()02f f ⋅<即可求解.【详解】由函数,且,可得,()348f x x x =+-()()10,30f f <>3()70,(2)2602f f =>=>所以,根据零点的存在性定理,3(1)()02f f ⋅<可得方程的近似解落在区间为.3480x x +-=31,2⎛⎫⎪⎝⎭故选:A.6.C【分析】根据给定条件,可得函数在R 上单调递增,再利用分段函数及对数函数单调性()f x 列出不等式求解即得.【详解】函数的定义域为R ,(2)1,1()log ,1a a x x f x x x --≤⎧=⎨>⎩由对任意,都有,得函数在R 上单调递增,12x x ≠1212()()f x f x x x ->-()f x 于是,解得,20130a a a ->⎧⎪>⎨⎪-≤⎩23a <≤所以实数的取值范围为.a (]2,3故选:C 7.B【分析】利用对数的换底公式和运算法则即可得解.【详解】,,,230x y k ==>Q 23log ,log x k y k ==∴11log 2,log 3k k x y ∴==,,则.12log 2log 3log 61k k k x y ∴=+=+=∴26k =6k =故选:B.8.A【分析】由函数的定义域排除C ,由函数的奇偶性排除D ,由特殊的函数值排除B ,结合奇偶性和单调性判断A.【详解】由得,则函数的定义域为,排除选项C ;30x ->33x -<<()ln 3y x =-()3,3-又,所以为偶函数,则图象关于y 轴对称,排除选项D ;()()ln 3ln 3x x --=-()ln 3y x =-当时,,排除选项B ,52x =1ln 02y =<因为为偶函数,且当时,函数单调递减,()ln 3y x =-30x >>()()ln 3ln 3y x x =-=-选项A 中图象符合.故选:A 9.ACD【分析】分析函数的奇偶性与单调性,由已知可得出,结合函数的奇偶性()f x a b >-()f x与单调性可得出合适的选项.【详解】令,对任意的,,即,()()22log 1g x x x =++x ∈R 21x x x+>≥-210x x ++>所以,函数的定义域为,()g x R 则.()()()()2222221log 1log 1log1g x x x x x g x x x⎛⎫-=+--=+-==- ⎪⎝⎭++所以,函数是定义域为的奇函数,()g x R 因为函数、为上的增函数,1u x =221u x =+[)0,∞+所以,内层函数在上为增函数,21u x x =++[)0,∞+外层函数在上为增函数,2log y u =()0,∞+所以,函数在上为增函数,()()22log 1g x x x =++[)0,∞+由于函数是定义域为的奇函数,则该函数在上为增函数,()g x R (],0-∞所以,函数在上单调递增,()()22log 1g x x x =++R 因为的定义域为,则,()f x R ()()()()()33f x x g x x g x f x -=-+-=--=-所以,函数为奇函数,()f x 又因为函数为上的增函数,所以,函数在上单调递增.3y x =R ()f x R 因为,所以,则,即,A 错B 对,0a b +>a b >-()()()f a f b f b >-=-()()0f a f b +>又、的大小不确定,故CD 错.a b 故选:ACD.方法点睛:函数的三个性质:单调性、奇偶性和周期性,在高考中一般不会单独命题,而是常将它们综合在一起考查,其中单调性与奇偶性结合、周期性与抽象函数相结合,并结合奇偶性求函数值,多以选择题、填空题的形式呈现,且主要有以下几种命题角度;(1)函数的单调性与奇偶性相结合,注意函数的单调性及奇偶性的定义,以及奇、偶函数图象的对称性.(2)周期性与奇偶性相结合,此类问题多考查求值问题,常利用奇偶性及周期性进行交换,将所求函数值的自变量转化到已知解析式的函数定义域内求解;(3)周期性、奇偶性与单调性相结合,解决此类问题通常先利用周期性转化自变量所在的区间,然后利用奇偶性和单调性求解.10.ABC【分析】根据题意,由函数的定义,只需满足集合中的每一个元素在集合中都有唯一一P Q 个元素与之对应即可,再结合选项逐一分析,即可得到结果.【详解】选项A ,,集合中的每一个元素在集合中都有唯一一个元素与之1:2f x y x→=P Q 对应,故A 正确;选项B ,,集合中的每一个元素在集合中都有唯一一个元素与之对应,故13:f x y x →=P Q B 正确;选项C ,,集合中的每一个元素在集合中都有唯一一个元素与之对应,1:2xf x y ⎛⎫→= ⎪⎝⎭P Q 故C 正确;选项D ,,集合中的1,在集合中没有元素与之对应,故D 错误;:ln f x y x →=P Q 故选:ABC 11.ABD【分析】根据奇偶性的定义即可判断A,根据基本函数的单调性即可判断BC ,根据反函数的性质即可判断D.【详解】对于A ,定义域为,关于原点对称,又由于()f x R ()()e e e e ,,22x x x xf x f x --++=-=,所以为偶函数,A 正确,()()=f x f x -()f x 对于B ,,由于函数在单调递增,所以在()e 121e 1e 1x x x f x -==-++e 1xy =+x ∈R 1e 1x y =+单调递减,因此在单调递增,B 正确,x ∈R ()21e 1xf x =-+x ∈R 对于C ,由于函数为定义域上的偶函数,当时,在区间上单调递lg y x=0x >lg y x =()0,∞+增,故C 错误,对于D ,由于函数与互为反函数,所以两者图象关于,D 正13xy ⎛⎫= ⎪⎝⎭133log log y x x ==-y x =确,故选:ABD 12.ACD【分析】令,结合图象可得有3个不同的解,,,不妨设,()t x g =()0f t =1t 2t 3t 123t t t <<则可知,,,令,结合图象可得有2个不同的解121t -<<-2t =312t <<()m f x =()0g m =,,不妨设,则可知,,再数形结合求出复合函数的解的1m 2m 12m m <121m -<<-201m <<个数.【详解】A 选项,令,结合图象可得有3个不同的解,,,()t x g =()0f t =1t 2t 3t 不妨设,则可知,,,123t t t <<121t -<<-20t =312t <<由图可知有2个不同的解,有2个不同的解,有2个不同的解,()1g x t =()2g x t =()3g x t =即有6个不同的解,A 正确;()()0f g x =B 选项,令,结合图象可得有2个不同的解,,()m f x =()0g m =1m 2m 不妨设,则可知,,12m m <121m -<<-201m <<由图可知有1个解,有3个不同的解,()1f x m =()2f x m =即有4个不同的解,B 错误;()()0g f x =C 选项,令,结合图象可得有3个不同的解,,()m f x =()0f m =1m 2m 3m 且,,,121m -<<-20m =312m <<由图可知有1个解,有3个不同的解,有1个解,()1f x m =()2f x m =()3f x m =即有5个不同的解,C 正确;()()0f f x =D 选项,令,结合图象可得有两个不同的解,()t x g =()0g t =1t2t 不妨设,则可知,,12t t <121t -<<-201t <<由图可知有2个不同的解,有2个不同的解,()1g x t =()2g x t =即有4个不同的解,D 正确.()()0g g x =故选:ACD .13.193【分析】利用位数的定义,结合对数运算法则即可得解.k故答案为.14。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
函数专题练习(一) 选择题(12个) 1.函数1()x y ex R +=∈的反函数是( )A .1ln (0)y x x =+>B .1ln (0)y x x =->C .1ln (0)y x x =-->D .1ln (0)y x x =-+> 2.已知(31)4,1()log ,1a a x a x f x x x -+<⎧=⎨>⎩是(,)-∞+∞上的减函数,那么a 的取值范围是(A )(0,1)(B )1(0,)3(C )11[,)73(D )1[,1)73.在下列四个函数中,满足性质:“对于区间(1,2)上的任意1212,()x x x x ≠,1221|()()|||f x f x x x -<-恒成立”的只有(A )1()f x x=(B )()||f x x = (C )()2xf x =(D )2()f x x =4.已知()f x 是周期为2的奇函数,当01x <<时,()lg .f x x =设63(),(),52a f b f ==5(),2c f =则(A )a b c << (B )b a c << (C )c b a << (D )c a b <<5.函数2()lg(31)f x x =++的定义域是 A .1(,)3-+∞ B . 1(,1)3- C . 11(,)33- D . 1(,)3-∞- 6、下列函数中,在其定义域内既是奇函数又是减函数的是A .3 ,y x x R =-∈B . sin ,y x x R =∈C . ,y x x R =∈ D7、函数()y f x =的反函数1()y f x -=的图像与y 轴交于点(0,2)P (如右图所示),则方程()0f x =在[1,4]上的根是x =A .4B .3C . 2D .1 8、设()f x 是R 上的任意函数,则下列叙述正确的是(A )()()f x f x -是奇函数 (B )()()f x f x -是奇函数 (C ) ()()f x f x --是偶函数 (D ) ()()f x f x +-是偶函数 9、已知函数xy e =的图象与函数()y f x =的图象关于直线y x =对称,则)A .()22()xf x e x R =∈ B .()2ln 2ln (0)f x x x =>C .()22()xf x e x R =∈ D .()2ln ln 2(0)f x x x =+>10、设1232,2()((2))log (1) 2.x e x f x f f x x -⎧⎪=⎨-≥⎪⎩<,则的值为, (A )0 (B )1 (C )2 (D )3 11、对a ,b ∈R ,记max {a ,b }=⎩⎨⎧≥ba b ba a <,,,函数f (x )=max {|x +1|,|x -2|}(x ∈R )的最小值是(A )0 (B )12 (C ) 32(D )3 12、关于x 的方程222(1)10x x k ---+=,给出下列四个命题: ①存在实数k ,使得方程恰有2个不同的实根;②存在实数k ,使得方程恰有4个不同的实根; ③存在实数k ,使得方程恰有5个不同的实根; ④存在实数k ,使得方程恰有8个不同的实根; 其中假.命题的个数是 A .0 B .1 C .2 D .3 (二) 填空题(4个)1.函数()f x 对于任意实数x 满足条件()()12f x f x +=,若()15,f =-则()()5f f =_______________。
2设,0.(),0.x e x g x lnx x ⎧≤=⎨>⎩则1(())2g g =__________3.已知函数()1,21xf x a =-+,若()f x 为奇函数,则a =________。
4. 设0,1a a >≠,函数2()log (23)a f x x x =-+有最小值,则不等式log (1)0a x ->的解集为 。
(三) 解答题(6个) 1. 设函数54)(2--=x x x f .(1)在区间]6,2[-上画出函数)(x f 的图像;(2)设集合{}),6[]4,0[]2,(,5)(∞+-∞-=≥= B x f x A . 试判断集合A 和B 之间的关系,并给出证明;(3)当2>k 时,求证:在区间]5,1[-上,3y kx k =+的图像位于函数)(x f 图像的上方.2、设f(x)=3ax 0.2=++++c b a c bx b若,f (0)>0,f (1)>0,求证:(Ⅰ)a >0且-2<ba<-1; (Ⅱ)方程f (x )=0在(0,1)内有两个实根.3. 已知定义域为R 的函数12()2x x bf x a+-+=+是奇函数。
(Ⅰ)求,a b 的值;(Ⅱ)若对任意的t R ∈,不等式22(2)(2)0f t t f t k -+-<恒成立,求k 的取值范围;4.设函数f (x )=,22aax x c ++其中a 为实数. (Ⅰ)若f (x )的定义域为R ,求a 的取值范围; (Ⅱ)当f (x )的定义域为R 时,求f (x )的单减区间.5. 已知定义在正实数集上的函数21()22f x x ax =+,2()3ln g x a x b =+,其中0a >.设两曲线()y f x =,()y g x =有公共点,且在该点处的切线相同. (I )用a 表示b ,并求b 的最大值; (II )求证:()()f x g x ≥(0x >).6. 已知函数2()1f x x x =+-,,αβ是方程f (x )=0的两个根()αβ>,'()f x 是f (x )的导数;设11a =,1()'()n n n n f a a a f a +=-(n =1,2,……) (1)求,αβ的值;(2)证明:对任意的正整数n ,都有n a >a ; (3)记lnn n n a b a aβ-=-(n =1,2,……),求数列{b n }的前n 项和S n 。
(四) 创新试题1. 下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出路口,,A B C 的机动车辆数如图所示,图中123,,x x x 分别表示该时段单位时间通过路段、、的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则 (A )123x x x >> (B )132x x x >> (C )231x x x >> (D )321x x x >>2. 设函数f (x )=3sinx +2cosx +1。
若实数a 、b 、c 使得af (x )+bf (x −c )=1对任意实数x 恒成立,则a cb cos 的值等于( ) A . 21- B . 21C . −1D . 1解答: 一、选择题1解:由1x y e+=得:1ln ,x y +=即x=-1+lny ,所以1ln (0)y x x =-+>为所求,故选D 。
2解:依题意,有0<a <1且3a -1<0,解得0<a <13,又当x <1时,(3a -1)x +4a >7a -1,当x >1时,log a x <0,所以7a -1≥0解得x ≥17故选C 3解:2112121212x x 111|||||x x x x x x |x x |--==-|12x x 12∈,(,)12x x ∴>1121x x ∴<1∴ 1211|x x -|<|x 1-x 2|故选A 4解:已知()f x 是周期为2的奇函数,当01x <<时,()lg .f x x =设644()()()555a f f f ==-=-,311()()()222b f f f ==-=-,51()()22c f f ==<0,∴c a b <<,选D .5解:由1311301<<-⇒⎩⎨⎧>+>-x x x ,故选B .6解:B 在其定义域内是奇函数但不是减函数;C 在其定义域内既是奇函数又是增函数;D 在其定义域内不是奇函数,是减函数;故选A . 7解:0)(=x f 的根是=x 2,故选C8解:A 中()()()F x f x f x =-则()()()()F x f x f x F x -=-=,即函数()()()F x f x f x =-为偶函数,B 中()()()F x f x f x =-,()()()F x f x f x -=-此时()F x 与()F x -的关系不能确定,即函数()()()F x f x f x =-的奇偶性不确定, C 中()()()F x f x f x =--,()()()()F x f x f x F x -=--=-,即函数()()()F x f x f x =--为奇函数,D 中()()()F x f x f x =+-,()()()()F x f x f x F x -=-+=,即函数()()()F x f x f x =+-为偶函数,故选择答案D 。
9解:函数xy e =的图象与函数()y f x =的图象关于直线y x =对称,所以()f x 是xy e =的反函数,即()f x =ln x ,∴ ()2ln 2ln ln 2(0)f x x x x ==+>,选D .10解:f (f (2))=f (1)=2,选C11解:当x <-1时,|x +1|=-x -1,|x -2|=2-x ,因为(-x -1)-(2-x )=-3<0,所以2-x >-x -1;当-1≤x <12时,|x +1|=x +1,|x -2|=2-x ,因为(x +1)-(2-x )=2x -1<0,x +1<2-x ;当12≤x <2时,x +1≥2-x ;当x ≥2时,|x +1|=x +1,|x -2|=x -2,显然x +1>x -2;故2((,1)12([1,))2()11([,2))21([2,))x x x x f x x x x x -∈-∞-⎧⎪⎪-∈-⎪=⎨⎪+∈⎪⎪+∈+∞⎩据此求得最小值为32。
选C12解:关于x 的方程()011222=+---k x x 可化为()22211011x x k x x --+=≥≤(-)(或-)…(1) 或()222110x x k -+=+(-)(-1<x <1) (2)① 当k =-2时,方程(1)的解为(2)无解,原方程恰有2个不同的实根② 当k =14时,方程(1)有两个不同的实根±2(2)有两个不同的实根±2,即原方程恰有4个不同的实根③ 当k =0时,方程(1)的解为-1,+1,,方程(2)的解为x =0,原方程恰有5个不同的实根 ④ 当k =29时,方程(1)的解为,,方程(2)的解为有8个不同的实根 选A二、填空题。
