离散网格上曲率计算的综述_2016
有限元网格划分和收敛性
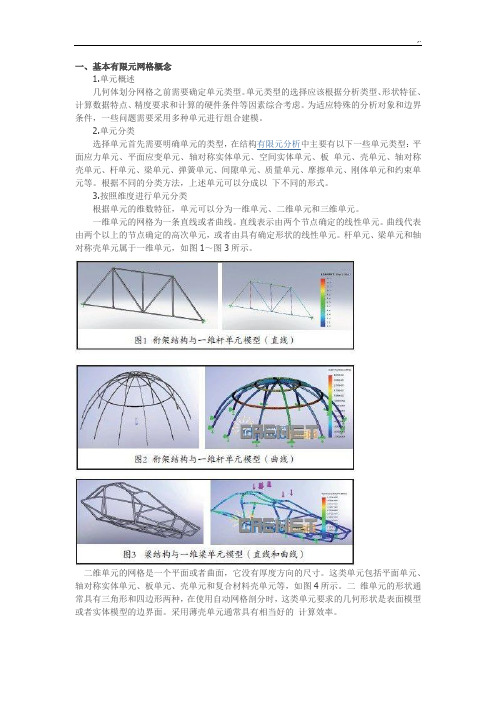
一、基本有限元网格概念1.单元概述几何体划分网格之前需要确定单元类型。
单元类型的选择应该根据分析类型、形状特征、计算数据特点、精度要求和计算的硬件条件等因素综合考虑。
为适应特殊的分析对象和边界条件,一些问题需要采用多种单元进行组合建模。
2.单元分类选择单元首先需要明确单元的类型,在结构有限元分析中主要有以下一些单元类型:平面应力单元、平面应变单元、轴对称实体单元、空间实体单元、板单元、壳单元、轴对称壳单元、杆单元、梁单元、弹簧单元、间隙单元、质量单元、摩擦单元、刚体单元和约束单元等。
根据不同的分类方法,上述单元可以分成以下不同的形式。
3.按照维度进行单元分类根据单元的维数特征,单元可以分为一维单元、二维单元和三维单元。
一维单元的网格为一条直线或者曲线。
直线表示由两个节点确定的线性单元。
曲线代表由两个以上的节点确定的高次单元,或者由具有确定形状的线性单元。
杆单元、梁单元和轴对称壳单元属于一维单元,如图1~图3所示。
二维单元的网格是一个平面或者曲面,它没有厚度方向的尺寸。
这类单元包括平面单元、轴对称实体单元、板单元、壳单元和复合材料壳单元等,如图4所示。
二维单元的形状通常具有三角形和四边形两种,在使用自动网格剖分时,这类单元要求的几何形状是表面模型或者实体模型的边界面。
采用薄壳单元通常具有相当好的计算效率。
三维单元的网格具有空间三个方向的尺寸,其形状具有四面体、五面体和六面体,这类单元包括空间实体单元和厚壳单元,如图5所示。
在自动网格划分时,它要求的是几何模型是实体模型(厚壳单元是曲面也可以)。
4.按照插值函数进行单元分类根据单元插值函数多项式的最高阶数多少,单元可以分为线性单元、二次单元、三次单元和更高次的单元。
线性单元具有线性形式的插值函数,其网格通常只具有角节点而无边节点,网格边界为直线或者平面。
这类单元的优点是节点数量少,在精度要求不高或者结果数据梯度不太大的情况下,采用线性单元可以得到较小的模型规模。
改进的曲率计算方法及其效果分析

d 五 一d z一
b r [利用 3 平面 网格拟合曲面计 算 曲率属 et 9 s] ×3 性, 给出 了详细 的计 算 公 式 , 得 曲率 属 性 成 为 地 使 震解 释 的一 大亮 点 l。Mafr等将 R brs 究 6 ] rut o et研 的成 果推 广到沿 层 曲率属 性 的提取 , 派生 出地 震属 性解 释 的新方 法 , 很快 得到 了推广 应用 E-] 并 i1 。 o2
中 图 分 类 号 : 6 1学 属性 , 应用 到地震 勘探 领 域 能够很 好地 揭示 地质构 造 [ ] 1 。褶皱 越严 重 曲率 {
一
兰 ± ± ± ! ± ± 一 ± ±
1 Az 2 6 Ax
d
第 5 卷第 2 1 期
21 0 2年 3月
石
油
物
探
Vo . 1 No 2 15 。 .
M a ., 01 r 2 2
GEOPHYS C I AL R0S ECTI P P NG 0R ETR0LEUM F P
文章编号 :0 0 4 1 2 1 ) 2 1 6 5 10 —1 4 (0 2 0 —04 —0
zx ( ,)一 a b cy+如 + + - ( ) x - y - r 4 4 厂 1
R b r 推 导 a的过 程 是 用 z , 5 点 沿 z方 向 o et s z, 2 8
Ro etE采用 3 brs 。 ×3网格单 元 作 逼 近 ( 1 , 图 ) 由一 阶和二 阶导 数 的定 义 , () 中各系 数 : 得 1式
基础 。
一
一
兰 ± ± 二兰 二叠二 !
6Ax
。
一
d
空间曲线的曲率挠率

. 故曲率中心的半径向量为 可以求出密切平面为
于是曲率圆为
Exceltek Electronics (HK) Ltd Confidential
设曲线方程为
曲率半径及曲率中心 设点M 处的曲率圆方程为
且
求曲线上点M 处的
的坐标公式 .
y
D( , )
故曲率半径公式为
R
1
(1
y2
)
3 2
y
, 满足方程组
密切平面: 法平面: 从切平面:
r(s)
v (R
rv)
v
0
v (R
rv,v,
v
)
0
密切平面
v (R
rv)
v
0
α(s)
而由三个基本向量(R和v上面rv)三 个v平面0所构成的图形叫做曲线的基本三从棱切形平面。
C β(s)
O
Exceltek Electronics (HK) Ltd Confidential
曲线。
Exceltek Electronics (HK) Ltd Confidential
1.曲线的自然参数
自然参数:我们知道曲线有不同的参数表示,能 否找一种参数使研究曲线很方便呢?回答是肯定
的这就对是于以光弧滑长曲s线为参r(t数) ((x自(t然), y参(t数), z)(t)), t A R
若曲线方程为
x ( y), 若曲线由参数方程
x x(t)
y
y(t)
x
则 (1 x 2 )32
xy xy
给出, 则 ( x2 y2 )32
Exceltek Electronics (HK) Ltd Confidential
ansys workbench 15.0 网格划分

网格修补选项只有一个三角表 面网格划分器设置选项。对于三 角表面网格划分器,存在两个选 项:程序控制和高级前缘,程序 控制选项为默认选项。
-如果选择程序控制选项,则程序根据模型表面形状,来确定是否 使用三角剖分法(Delaunay)或高级前缘(advancing front)算 法;
-如果选择高级前缘算法,则程序优先使用高级前缘算法,如果网 格划分过程中失败,则自动转换为三角剖分算法。
-参数化:参数驱动系统,可以基于优化设计 模块,研究网格对求解精度的影响;
-稳定性:模型通过系统参数进行更新; -高度自动化:仅需要有限的输入信息即可完
成基本的分析类型; -灵活性:能够对结果网格添加控制和影响(
完全控制建模/分析); -物理相关:根据物理环境的不同,系统自动
建模和分析的物理系统; -自适应结果:适应用户程序的开发系统 ——CAD neutral meshing netral solver
3.网格控制-总体尺寸控制-高级尺寸函数
Proximity尺寸控制函数
-该函数基于模型边缘特征控制网格,主要作用于 模型中的所有边缘,该函数有6个控制参数: Proximity Accuracy-临近边缘精度参数; Num Cells Across Gap-间隙截面单元数量; Proximity Min Size-边缘最小尺寸; Max Face –面上最大尺寸; Max Size-总体最大尺寸; Growth Rate-网格生长率;
网格控制总体尺寸控制高级尺寸函数曲率尺寸函数网格划分算法基于五个参数控制网格密度单元以模型中的孔洞为起始处起始处的网格大小由曲率法向角度和最小尺寸共同控制并且最小尺寸占主导即当最小尺寸小于曲率法向角度的单元尺寸时单元大小由曲率法向决定否则由单元最小尺寸控制
结构有限元分析中的网格划分技术及其应用实例

结构有限元分析中的网格划分技术及其应用实例一、前言有限元网格划分是进行有限元数值模拟分析至关重要的一步,它直接影响着后续数值计算分析结果的精确性。
网格划分涉及单元的形状及其拓扑类型、单元类型、网格生成器的选择、网格的密度、单元的编号以及几何体素。
从几何表达上讲,梁和杆是相同的,从物理和数值求解上讲则是有区别的。
同理,平面应力和平面应变情况设计的单元求解方程也不相同。
在有限元数值求解中,单元的等效节点力、刚度矩阵、质量矩阵等均用数值积分生成,连续体单元以及壳、板、梁单元的面内均采用高斯(Gauss)积分,而壳、板、梁单元的厚度方向采用辛普生(Simpson)积分。
辛普生积分点的间隔是一定的,沿厚度分成奇数积分点。
由于不同单元的刚度矩阵不同,采用数值积分的求解方式不同,因此实际应用中,一定要采用合理的单元来模拟求解。
CAD软件中流行的实体建模包括基于特征的参数化建模和空间自由曲面混合造型两种方法。
Pro/E和SoildWorks是特征参数化造型的代表,而CATIA与Unigraphics等则将特征参数化和空间自由曲面混合造型有机的结合起来。
现有CAD软件对表面形态的表示法已经大大超过了CAE软件,因此,在将CAD实体模型导入CAE软件的过程中,必须将CAD模型中其他表示法的表面形态转换到CAE软件的表示法上,转换精度的高低取决于接口程序的好坏。
在转换过程中,程序需要解决好几何图形(曲线与曲面的空间位置)和拓扑关系(各图形数据的逻辑关系)两个关键问题。
其中几何图形的传递相对容易实现,而图形间的拓扑关系容易出现传递失败的情况。
数据传递面临的一个重大挑战是,将导入CAE程序的CAD模型改造成适合有限元分析的网格模型。
在很多情况下,导入CAE程序的模型可能包含许多设计细节,如细小的孔、狭窄的槽,甚至是建模过程中形成的小曲面等。
这些细节往往不是基于结构的考虑,保留这些细节,单元数量势必增加,甚至会掩盖问题的主要矛盾,对分析结果造成负面影响。
_B样条曲面等曲率线的高阶抽取方法

参 考 文 献:
1. 2. 3. Gerald E. Farin: Class A Bézier curves. Computer Aided Geometric Design 23(7): 573-581 (2006) Juan Cao, Guozhao Wang: A note on Class A Bézier curves. Computer Aided Geometric Design 25(7): 523-528 (2008) Hughes T.J.R., Cottrell J.A., Bazilevs Y.. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry, and mesh refinement [J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(39-41): 4135-4195 4. 5. 冯结青, 叶修梓. 计算机辅助设计与制造中的外形分析. 机械工业出版社, 2005 T. Maekawa and N. M. Patrikalakis. Interrogation of differential geometry properties for design and manufacture [J]. The Visual Computer, 10(4) : 216-237, 1994. 6. 7. 蔺宏伟,王国瑾. 光滑曲面上的 G1 插值曲线. 计算机辅助设计与图形学学报, 15(5), 541-546, 2003 Octavian Soldea, Gershon Elber, Ehud Rivlin: Global Segmentation and Curvature Analysis of Volumetric Data Sets Using
第五章网壳结构

二向正交型 双曲抛物面网壳
五.网壳结构的选型
根据跨度大小、刚度要求、平面形状、支承条件、制 作安装以及技术经济指标综合考虑。
1. 双层网壳可采用铰接节点,单层网壳采用刚接节点;
2. 双层网壳适合大中跨度的结构,中小跨度可采用单层 网壳;
3. 跨度大时,宜采用矢高大的球面或柱面网壳;跨度小 时,可选用矢高较小的双曲扁壳或双曲抛物面壳;
矢跨比F/S与耗钢量W的关系
跨度S与耗钢量W的关系
(4)柱面网壳的水平推力
圆柱面网壳由于 环向力的作用而产生 较大的水平推力。水 平推力N的大小也与 矢跨比有关。
水平推力的处理可采用: ① 加水平拉杆; ② 结构落地; ③ 增加下部柱的刚度; ④ 利用下部结构吸收推力。
二.计算方法 网壳结构的分析不仅仅是强度的分析,通
正放四角锥
抽空四角锥
斜置正放四角锥
三角锥柱面网壳
抽空三角锥柱面网壳
清华大学游泳馆
柱面网壳的组合应用—— 成渝高速路二郎收费站
三.球面网壳 当跨度较小时可以 采用单层,也可采 用双层。 球面网壳的网格分 割方法很多,主要 有:
大英博物馆
肋环型球面网壳
施威德勒球面网壳
单层球 联方型球面网壳
面网壳 三向网格型球面网壳
(c) 联方型(d)三向网格型(e) 交叉斜杆型
单斜杆型与交叉斜杆型相比,前者杆件数量少, 杆件连接易于处理,但刚度稍差,适于小跨度、小 荷载网架;
联方网格杆件数量最少,杆件长度统一,节点 上只有四个杆件,节点构造简单,刚度较差;
三向网格刚度最好、杆件数量较少。
悉尼国际水上运动中心
2. 双层柱面网壳
第五章 网壳结构
一.网壳结构的形式与选型 二.网壳结构分析 三.网壳结构的杆件设计和节点构造 四.网壳结构的施工和验收
三角形网格模型顶点曲率的求解算法

・ 108・
计 算 机 应 用 研 究
2007 年
得的曲线为 r( s) 。一般地 , 曲线 r( s) 上 任意一点 , 有单位 切向 量 T ( s) 和单位法向量 N( s) , 则曲线 r( s) 上任意一点都有沿曲 线 r( s) 的 Frenet 标架 { r( s) ; T ( s) ; N ( s) } , 则点 v = r( sv ) 处 的 Frenet 标架为 { r( sv ) ; T ( sv ) ; N ( sv ) } 。由于网格 模型不是连 续 曲面 , 无法直接求得曲线 r( s) 在 顶点 v 处的曲 率, 必 须建立 其 近似求解方法。
Approach of Solving Vertex Curvature for Triangular Mesh Model
LIU Shi-qing, CHEN You-ping, YUAN Chu-ming, ZHOU Zu-de
( Natinonal Research Center of NC Engineering, Huazhong University of Science & Technology, Wuhan Hubei 430074 , China)
渊b冤边界 E轧顶点
Nv=N渊s v冤 v1
v
Nn vn T渊s v冤 Ni
v
v
将 vE 取代 vi , 求得
k( sv ) ≈ 2 ( N v ×vvE ) / ( ‖ vvE ‖ 2 )
vi N5 v5
v
( 5)
这就是曲线 r( s) 在顶点 v 处的曲率近似值 , 虽然是曲线曲
r渊s 冤
N2 v2 N3 v3
N v = N v /‖ N v ‖
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
可视化技术课程报告 ——离散网格上的曲率计算
姓名王娜 学号 201531491 院系信息科学与技术学院 专业软件工程 年级 2015级 1
离散网格上的曲率计算 摘要:离散曲面形状分析主要研究对各种离散形式曲面的进行曲率估算,设计更准确更有效率的曲率估算方法。本文主要综述了离散网格上曲率的多种估算方法,展望了这些问题的发展趋势。 关键字:离散曲面;网格曲面;曲率
1.离散曲面发展背景 随着三维数据采样技术和硬件设备的不断改善,以及图形工业对任意拓扑结构的光滑曲面造型的迫切需求,(这里的“任意拓扑”具有两个方面的含义:一是网格的亏格和相应曲面的拓扑结构的任意的;二是由网格的顶点和边法的特点所构成的图形是任意的。)使得离散曲面日益成为计算机图形学和几何设计邻域的宠儿。因此对离散曲面的估算微分量的研究逐渐成为一个新型课题。 将离散曲面估算得到的高斯曲率应用于离散曲面形状分析工具的设计,更加有效的提取其形状和特征区域,利于特征区域边界计算,区域分割。近年来,更是将离散曲面分析应用到实际生活,在医学领域,通过对大脑皮层的扫描,建立数字化模型,分析曲面形状,来获取大脑发育信息,甚至病变区域位等。成为病变检测和获取脑部发育信息的有力途径。
2.网格曲面上离散曲率的计算 三角网格模型在计算机图形学、计算机辅助几何设计中的使用日益广泛,但 是在三角网格上任意点处得到精确的法向量和曲率十分困难,主要原因是离散三角网格曲面并不是用传统微分几何中熟知的参数方程和隐式方程来定义,而是由 离散点云以及点与点之间的拓扑关系定义的,这样,传统微分几何中一阶微分和 二阶微分的计算不能简单地应用于离散三角网格曲面上。 一般来说,曲面的一阶微分量是指曲面的切平面方向和法向量,二阶微分量是指曲面的曲率等有关量。随着三维扫描技术的发展和逆向工程的兴起,三角网格曲面日益成为三维图形的一种通用表示方法,在计算机图形学,计算机辅助几 2
何设计中的使用日益广泛。但是由于三角网格曲面是由离散点云以及点与点之间的拓扑关系定义的,缺少曲面确切的解析表示,所以不再适用传统的解析曲面的曲率计算方法。 众所周知,曲率是曲面曲线的重要不变量,是传统微分几何中的重要基础。同样,三角网格的离散曲率也是离散曲面上应用的基础和前提。例如网格变形[1],网格曲面的特征提取,网格光顺[2],网格简化[3],模型分块[4]等等。在这些应用中,通常需要首先估计离散曲面上某点的法向量和曲率,然后根据这些法向量或曲率定义一个范数,作为一个优化的标准,利用这个关于曲率泛函的优化标准再进行离散网格曲面的进一步处理。例如,在网格简化应用中,曲率的估计对确保优化三角剖分起着至关重要的作用。在曲面建模中,许多技术是用来由原始粗糙网格来创建光滑曲面的,离散曲率是当前近似情形的重要度量。精确的曲率和法向量也是网格去噪问题的基础。好的平均曲率和法向量估计是无扭曲曲面光顺技术的关键。在计算机图形学、图像分析处理和几何建模等研究领域中,如自由曲面、反求工程、图像识别、三维医疗图像重构以及人脸识别等,经常需要计算主曲率、平均曲率和高斯曲率等值,用于折痕、棱边、隆起、沟壑等关键特征的提取、噪声的过滤和曲面的修补等。这样,三角网格曲面上离散曲率的各种估计方法应运而生。 对于给定的描述一些光滑曲面的三角网格,有许多估算顶点法向量和曲率的方法"曲率估计算法多种多样,例如,利用欧拉公式,采用最小二乘的估算方法(Chenandschmitt,1992)[5];曲率张量的估计方法(Taubin,1995)[6];法曲率积分公式的方法(Wa1LanabeandBelyaev,2001)[7];曲率算子的方法(Meyer,2002)[8]估计顶点的法曲率,权值的选取在不断革新,从最初Henri Gouraud(1971)的等加权平均,到角度权值以及面积权值,而后Max(l999)给出的与角度和边长度相关的新权值,Sheng一GwoChen(2004)等又提出选择点到相邻三角形重心距离平方的倒数为权值。 除此之外,还有比较不同算法估算精度的文章,Tatiana(2003)对三角网格上高斯曲率和平均曲率不同的估计方法作比较,ShuangthuangJin(2003)等对三角网格上点法向量的不同估计方法的比较。还有一些网格应用的文章,Dyn和Hormann不但给出新的高斯曲率和平均曲率估算定义,还应用估算的曲率定义范 3
数,进行网格简化。 本文主要综述了较为基础的Chen 和Schmitt的方法,以及介绍了罗良峰和齐宝明针对该问题提出的基于Taubin方法的改进,进行离散三角网格的曲率计算。
2.1 Chen 和 Schmitt 方法 三角网格模型一般情况下可以由一对线性表表示,M=(V,F);其中,表示顶点集,表示三角片集。如下图三角网格模型:
三角片fk的法向量气的计算式如下 其中,表示由顶点指向顶点的边向量;表示由顶点指向的边向量。我们称1-环邻域是与点相邻的三角形集合。图中除顶点外的其它顶
点组成的集合记为。如果顶点属于,则是的相邻点。中顶点个数称为其顶点的度,记为。包含的三角形片集合记为。如果三角形片记属于,记为,记为三角形片的面积。包含点的三角片的面积之和记为。 4
离散三角网格上法向量和法曲率也有一般的定义方法,这些几何估算的准确度对高斯曲率和平均曲率的准确度影响很大。对于离散三角网格曲面M=(V,F),
任意点的法向量一般可定义为1-环三角形某些几何的加权和。最简单的加权方法1-环三角形的法向量平均值,定义如下:
Taubin给出面积加权和的定义:
对于三角网格上任意点,法曲率通常使用公式 得到两个主曲率(k1,k2)后,进而计算平均曲率(H=(k1+k2)/2)和高斯曲率(K=k1*k2)。 Chen和Schmitt通过欧拉公式,给出了一种估计算法。他们的主要思想是
在切平面上选择合适的坐标。由欧拉公式可得
是选择的坐标系与主方向的夹角,上式可重写为:
C1,C2,C3是常数,是切向量与第一坐标向量r1的夹角。然后,他们选择,通过最小二乘的方法估计常数C1,C2,C3,
其中,是与的夹角。 5
曲率k1,k2可以由常数C1,C2,C3,和以下关系求得 主方向可以由下列公式计算获得 其中,{r1,r2}是选择的坐标系。 仿真实现了三角网格上的曲率计算,便于实验的效果观察,比较了三角网格上和矩形网格上的最大主曲率计算结果,如下图显示:
三角网格与矩形网格上的曲率计算 6
2.2改进的Taubin方法 罗良峰应用重心加权和新的法曲率估计方法改进原始的Taubin方法,使用重心权重相比于使用面积加权的方式而言,更加充分的考虑到了三角网格形状多实验结果的影响。但是估算法向量和法曲率这两个几何量,仍然是改进后的Taubin方法对于三角网格中任意一点曲率计算的首要任务。采用重心加权和的方法估计法向量,利用任意一点的1-环三角面片的法向信息来估计曲率,得到局部曲率张量矩阵,此后对该矩阵进行Householder变换和Givens变换,计算出对应的特征矩阵和特征向量,最后通过主曲率与矩阵特征值的关系得出两个主曲率,进而得到平均曲率和高斯曲率。 将改进Taubin方法与原始Taubin方法和Meyer方法作了比较。对于隐式曲面和参数曲面,给出详细的误差分析;对于自由曲面,根据曲率确定三角网格顶点颜色,从视觉上分析曲率估算结果。 使用多组测试用例,不论是单位球面的测试用例、环面的测试用例还是自由三角网格曲面测试用例,测试结果均表明改进的Taubin方法无论是在稳定性上,还是在精确度上,较原始Taubin方法都有明显改善。 齐宝明采用面积质心夹角的三角网格顶点向量法和三角片质心权值来改进Taubin离散曲率方法,同样忽略了三角面片的形状。但是如果只使用质心或者面积夹角的估计方法,也不能反应三角面片形状的影响。所以作者提出了新的加权方法,面积质心夹角的三角网格顶点向量法。相比较重心加权和面积夹角加权,更加明确的反映了三角片形状的影响。 不论是哪一种离散网格曲率计算方式,都相较于未改进之前的方法有很大的提高,通过误差分析,很明显,同一物体的测量数据重建而得到的两个三角网格中,顶点密度不同,曲率计算亦不同。顶点密度越大,计算结果越精密。可以得出曲率误差是和点的密度以及此点的曲面弯曲程度是有密切关系的。误差分析,可以直接找出误差最大点,而不必计算每个点的曲率误差。对误差最大点进行分析,减小误差,提高算法精度。 7
3.发展趋势 未来的工作,除了进一步提高计算精度以及算法的稳定性和适应性外,在该领域里有许多重要方向值得研究探索。如网格光顺、网格简化、网格分割、特征识别等等,这些方向都是以离散网格上曲率估计为基础而展开的。在不同场合,计算曲率的方法效率会有所不同,并非某一个特定的方法会占有绝对优势,寻找一种更加快速、准确地对海量数据的离散曲面的曲率计算,将成为这个研究课题不断发展的源源动力。 8
参考文献: [1] Warren J, Schaefer S, Hirani A N, Desbrun M.Barycentric coordinates for convexsets. Technical report, Rice University, 2003. [2] Taubin G. A signal processing approach to fair surface design. In:Proc. of theSIGGRAPH' 95. New York: ACM Press, 1995. p.351-358. [3] Garland M, Heckbert P S. Surface simplification using quadric error metrics[A].In:Computer Graphics Proceedings, Annual Conference Series, ACM SIGGRAPH, Los Angeles,1997. p.209-216. [4] G.Lavoue, F.Dupont and A.Baskurt, Constant. Curvature Region Decomposition of3D-Meshes by a Mixed. Approach Vertex-Triangle. Journal of WSCG, 2004, vol. 12, no.2, p. 245-252. [5]Chen,X.,Sehmitt,F.,1992.IntrinsieSurfaeePropertiesfromSurfaeeTrian即lation. ProeeedingsoftheEuroPeanConfereneeonComPuterVersion,P.739一743. [6]Taubin,G.,1995.EstimatingtheTensorofCurvatureofaSurfaeefromaPolyhedral ApproximationProeeedingsoftheFifthInternationalConfereneeonComputerVision, P.902一907. [7]K.WatanabeandA.GBelyaev.Deteetionofsalieuteurvaturefeaturesonpolygonal surfaees.In:EUROGRAPHICS2001,volume20,2001. [8]MeyerM,DesbrunM,SehloderP,BarrAH.Diseretedifferential一geometryoperatorsfor triangulatedZ,anifolds.In:VisualizationandMathematies,Berlin,Ge伽any,2002, P.52一58. [8]罗良峰.离散三角网格上的法向量和曲率估计[ D].大连:大连理工大学.硕士学位论文, 2007 [9]齐宝明.三角网格离散曲率估计和Taubin方法改进[D].大连:大连理工大学硕士学位论文,2008 [10]熊芳,方逵,欧新良.离散曲面高斯曲率估算的研究[J].长沙大学学报, 2010,2VOL.24:53-55.
