管理运筹学讲义 第6节 网络计划(6学时)
合集下载
管理运筹学讲义 网络分析
v2 4
15 9 v3 3
1
v7
37
OR:SM
第二节 最小树问题
v1 23 v6 28 v5 25 17 16 v4 1 v7 9 v3 3
20
v2 4
15
38
OR:SM
第二节 最小树问题
v1 23 v6 28 v5 25 17 16 v4 1 v7 9 v3 3 20
v2 4
15
39
OR:SM
√ √ √
√
OR:SM
第一节 图论的概念
• 解:用图来建模。把比赛项目作为研究对象,用点 表示。如果2个项目有同一名运动员参加,在代表这 两个项目的点之间连一条线,可得下图。
在图中找到一个点序 列,使得依次排列的 两点不相邻,即能满 足要求。如: 1) A,C,B,F,E,D B D
A
F
2) D,E,F,B,C,A
1 2 1 2
e1 e2 v2 e5 e6 e7 e8 v1 e4 e3 v3
V1 V2 和E1 E 2 称G1是G2的一个子图。
e4 v2 e5 e6 e8 e6 v3 v2
e2
e4
e3 v3 e8
v4
(G图)
v5
e7
v4
v5
(a)
12
v4
(b)
v5
OR:SM
第一节 图论的概念
网络(赋权图)
第二节 最小树问题
v1 23 1 v7 4 9 28 v5 25 17 16 v4 v2 15 v3 3
v1 5 v2 8 4 3 v4 v3 7 5 v5 1 v6
8
2
6
33
OR:SM
第二节 最小树问题
运筹学网络计划
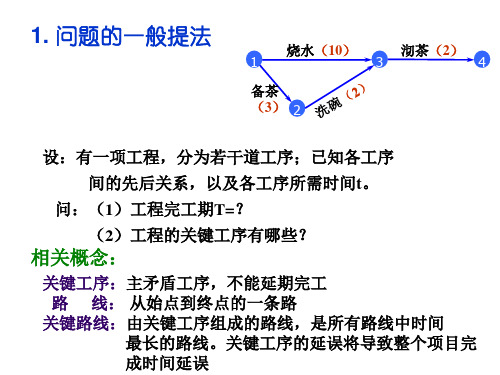
A
拆迁
/
2
B
工程设计
/
3
C
土建工程设计
B
2.5
D
采购设备
B
6
E
厂房土建
C、A
20
F
设备安装
D、E
4
G
设备调试
F
2
A(2)
1
B (3)
2
C (2.5)
3
D (6)
E (20)
G (2)
F (4)
4
5
6
用箭秆删除法标号(保证箭尾号大于箭头号)
工序
A
B
C
D
EFGHIJKL
M
N
紧前工序
_
_
_
_
D
E
A
F
G
B
由本例可见:关键工序 头尾皆有
=
关键工序时间之和=工期T。
,但反之未必。
二、工程完工期的概率分析
(计划评审技术PERT)
1、PERT与 CPM的区别:
CPM工序时间是确定的
工程工期的概率分析是是时间不确定情况下PERT
的主要工作
确定平均工序时间的三点估计法:
设工序最乐观时间为aij,最悲观时间为bij,最可能时间为m ij ,
t ij
a ij 4m ij bij
- 给任意点 i 标 Li ,
Li=Min{以 i 为箭尾的各箭之 “箭头
- 箭长tij”}
16
(3)求关键路(用标号法)
6
2
8
0
0 1
3
B '(0)
3
2)计算各工序 i
第六章-运筹学图与网络优化

9
6 3
3
4
7
2
53
4 31
5
1
7
4
4
第3节 最短路问题
一、最短路的含义
赋权有向图D (V,A),图中各弧(vi,v j )有权wij, vs,vt为图D中任意两点,求一条路P, 使它是从vs到vt的所有路中总权最小的路,
即w(
P
)
min
wij 。
(vi,vj )P
定义:路P的权是P中所有弧的权之和,记为w(P)
习题6-3:用Dijkstra方法求解下图从v1到v9的 最短‘路’。
v2
11
v7
3 6
2
5
5
v5
8
v1
v3
v9
2 4
4
3
7
v4
4
v6
6
v8
第3节 最短路问题
三、最短路问题的应用 ✓ 设备更新问题
第3节 最短路问题
例10:某工厂使用一台设备,每年年初工厂都要作出决定, 如果继续使用旧的,要付维修费;若购买一台新设备, 要付购买费。试制定一个5年的更新计划,使总支出最 少。已知设备在各年的购买费,及不同机器役龄时的 维修费如下表所示:
5
2
5 v6
v4
v7 8
习题6-2
2、
v2
2
v5
5
1
5
1
8
v1
7
5 v4 9
v6
6
v7
2
1
12
v3
第3节 最短路问题
(二)赋权无向图的最短‘路’问题的求解方 法
赋权无向图G=(V,E),边[vi,vj]表示既可以 从vi到达vj,也可以从vj到达vi,所以边[vi, vj]可以看作是两条弧(vi,vj)和(vj,vi),且 它们具有相同的权ωij。
第六章网络计划
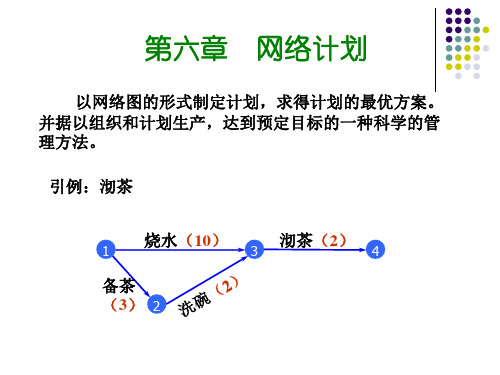
结点:表示相邻工序的时间分界点, 结点:表示相邻工序的时间分界点,称事项
连接箭尾的结点称为该工序的紧前事项 连接箭尾的结点称为该工序的紧前事项 连接箭头的结点称为该工序的紧后事项。 连接箭头的结点称为该工序的紧后事项。 紧后事项
权:工序的完成时间 相邻弧:表示工序前后衔接关系,称紧 前(后)工序; 相邻弧:表示工序前后衔接关系, 后 工序; 工序
a + 4m + b t ij = 6
p135
(1)绘制工程网络图
1 烧水( ) 烧水(10) 3 沏茶( ) 沏茶(2) 4
1)顺序:按工序先后从左至右; 备茶 )顺序:按工序先后从左至右; 2)图的结构 ) 弧(箭线 : 箭线): 箭线 表示工序; 表示工序;
(3) 2 )
为工序的起点、终点 为工序的起点、
G (4) 15 11 8 F (2) 15 H (2) 17 9 17
D (3) E (6) 7
工序时间参数的计算: 工序时间参数的计算:
1 计算最早开始时间 计算最早开始时间(ES)与最早完工 与最早完工(EF)时间 与最早完工 时间 从网络起点开始, 用下列公式计算最早开始时间(t 和最 从网络起点开始 用下列公式计算最早开始时间 ES)和最 早完工时间(t 早完工时间 EF): 最早开始时间 = (紧前活动的 最早结束时间的最大值 紧前活动的)最早结束时间的最大值 紧前活动的 =开始结点的最早时间 开始结点的最早时间 tES (i, j) = maxk tEF (k, i)=ETi 最早完工时间 = 最早开始时间 + 活动持续时间 tEF(i, j) = tES (i, j) + t (i, j)
工序时间( 工序代号 紧前工序 工序时间(周) A / 2 B / 3 C / 2 D A 3 E A 4
运筹学课件第九章网络计划

运筹学
1
2
3
4
5
6
24
22
26
24
30
18
18
上图为一个项目的网络计划,已知用于该项目的直接成本为47800元,间接成本为18000元,该项目原订74日完成,现要缩短工期,每缩短一天,间接费用可以节省330元,试求出工期较短而成本最少的最优方案。箭线下的数字为正常持续时间,括弧内为最短持续时间。相关数据见下表。 1→3→4→6为关键线路。
工作的最迟可能开工时间与最迟可能结束的时间
02
总时差
在不影响任务总工期的条件下,某工作(i,j)可以延迟其开工时间的最大幅度称为工作的总时差R(i,j) R(i,j) =tLF(i,j)-tEF(i,j)=tLS(i,j)-tES(i,j)
工作单时差
在不影响紧后工作的最早开工时间条件下,此工作可以延迟其开工时间的最大服务,r(i,j) r(i,j)= tES(j,k)-tEF(i,j)
本工作
紧后工作
紧前工作
紧后工作
双代号网络计划
双代号网络图是以箭线及其两端节点的编号表示工作的网络图
支模2
支模1
扎筋2
扎筋1
混凝土2
混凝土1
1.双代号网络图的基本符号
运筹学
工作i—j的持续时间 -------- D i—j 节点最早时间:earliest time -------- ETi 节点最迟时间:latest time -------- LTi 工作最早开始时间earliest star time -------- ES i—j 工作最早结束时间earliest finish time -------- EF i—j 工作最迟开始时间 latest star time -------- LS i—j 工作最迟结束时间 latest finish time ------- LF i—j i—j工作的自由时差 -------- FF i—j i—j工作的总时差 -------- TF i—j
运筹学第六章图与网络分析

S
2
4
7
2 A
0 5
S
5 45 B
98
14
5
13
D
T
C
E
4
4
4
7
最短路线:S AB E D T
最短距离:Lmin=13
2.求任意两点间最短距离的矩阵算法
⑴ 构造任意两点间直接到达的最短距离矩阵D(0)= dij(0)
S A B D(0)= C D E T
SABCDET 0 25 4 2 02 7 5 20 1 5 3 4 1 0 4 75 0 15 3 41 0 7 5 7 0
e1 v1
e5
v0 e2
e3
v2
e4
e6 e7
v3
v4
(4)简单图:无环、无多重边的图称为简单图。
(5)链:点和边的交替序列,其中点可重复,但边不能 重复。
(6)路:点和边的交替序列,但点和边均不能重复。
(7)圈:始点和终点重合的链。
(8)回路:始点和终点重合的路。
(9)连通图:若一个图中,任意两点之间至少存在一条 链,称这样的图为连通图。 (10)子图,部分图:设图G1={V1,E1}, G2={V2,E2}, 如果有V1V2,E1E2,则称G1是G2的一个子图;若 V1=V2,E1E2,则称G1是G2的一个部分图。 (11)次:某点的关联边的个数称为该点的次,以d(vi)表示。
步骤:
1. 两两连接所有的奇点,使之均成为偶点;
2. 检查重复走的路线长度,是否不超过其所在 回路总长的一半,若超过,则调整连线,改 走另一半。
v1
4
v4
4
1
4
v2
v5
5
网络计划2013.4.16
17 17
1
5 e 8 4
9
9
g 6
23 23
6
c 2
• 参数计算
工程期望工期 TE=23 ,关键工序的方差2 =49/9,则 (x)=-1.29,查表知 P(x)=9.9%
P(x)=90% ,查表知 (x)=1.3,则可接受的合同工期为TE+ (x) =26
19 OM:SM
直接 费用
极限完 工时间
正常完 工时间
赶进度极限完工费用 正常完工作业时间
时间
赶单位时间增加的直接
费用 (费率 )
- 正常完工费用 - 极限完工作业时间
OM:SM
22
第五节
2、工期-费用优化案例
网络计划优化
某工程作业流程及其费用统计资料
作业 A B C D E 紧前作业 B B 作业时间(天) 正常完工 3 5 5 6 5 极限完工 3 3 4 3 2 作业直接费用(万元) 正常完工 8 16 20 20 5 极限完工 8 19 23 23 8.6 费率 1.5 3 1 1.2
工序时间 t a 4m b 6 ,方差
2
(
ba 6
)
2
二、计算期望工期
• 工程期望工期等于关键路线上各道工序的时间之和 。
工期 T E
i
(
a i 4 m i bi 6
),方差
2
i
(
bi a i 6
)
2
• 设规定的工程完工时间为Tk,则完工时间的概率为 ( x )
0 0 1
6 a 6 c 4
6
15
6
OM:SM
《运筹学》课件--网络规划问题
版权所有 肖智 重庆大学经济与工商管理学院
版权所有 肖智 重庆大学经济与工商管理学院
表2.1-1 演员 1 2 3 4 节目 A B C D E F G H
5
6
7
8
9
10
版权所有 肖智 重庆大学经济与工商管理学院
分析: 把节目作为研究对象,用点表示。如果两个节目 无同一名演员参加,这说明二者可以紧排在一起,则 给相应的两点间连结一条边,得到下列图2.1-9。这 就是本例的网络模型。于是问题归结为:从图中找出 一条从A到H或从H到A且通过所有结点的链,且每一 个点只通过一次。 不难看出,这样的路有四条: (1)AFBCGDEH (2)HEDGCBFA (3)AFGCBDEH (4)HEDBCGFA 则文艺演出的节目表可按上面任一顺序安排。 肖智 版权所有
重庆大学经济与工商管理学院
B
C D E
A H G
图2.1-9
F
版权所有 肖智 重庆大学经济与工商管理学院
例2.1.2:电话线架设问题 某地7个村镇之间的现有交通道路如下图2.1-10 所示,边旁数字为各村镇之间道路的长度。现要沿交 通道路架设电话线,使各村之间均能通话。应如何架 线使总长最短?
6 1
5
最短路
1-3-2-4-6
版权所有 肖智 重庆大学经济与工商管理学院
2、标号法: 例2.3-4:以例2.3-1为例,解题步骤如下图2.3-4。
6
4 2 3 6 5
C1
8
7 4 5
5
11
B1
0
4
D1
5 12 6
3
版权所有 肖智 重庆大学经济与工商管理学院
表2.1-1 演员 1 2 3 4 节目 A B C D E F G H
5
6
7
8
9
10
版权所有 肖智 重庆大学经济与工商管理学院
分析: 把节目作为研究对象,用点表示。如果两个节目 无同一名演员参加,这说明二者可以紧排在一起,则 给相应的两点间连结一条边,得到下列图2.1-9。这 就是本例的网络模型。于是问题归结为:从图中找出 一条从A到H或从H到A且通过所有结点的链,且每一 个点只通过一次。 不难看出,这样的路有四条: (1)AFBCGDEH (2)HEDGCBFA (3)AFGCBDEH (4)HEDBCGFA 则文艺演出的节目表可按上面任一顺序安排。 肖智 版权所有
重庆大学经济与工商管理学院
B
C D E
A H G
图2.1-9
F
版权所有 肖智 重庆大学经济与工商管理学院
例2.1.2:电话线架设问题 某地7个村镇之间的现有交通道路如下图2.1-10 所示,边旁数字为各村镇之间道路的长度。现要沿交 通道路架设电话线,使各村之间均能通话。应如何架 线使总长最短?
6 1
5
最短路
1-3-2-4-6
版权所有 肖智 重庆大学经济与工商管理学院
2、标号法: 例2.3-4:以例2.3-1为例,解题步骤如下图2.3-4。
6
4 2 3 6 5
C1
8
7 4 5
5
11
B1
0
4
D1
5 12 6
3
运筹学课件——网络计划技术PPT课件
1 a1
a2
2
3
a3 4
LOGO
5 b1 6 b2 7 b3 8
作业的合并 3
B 1A2
D
E
5G
C
F
4
LOGO
6
1A2
X
5
G
6
4.绘制网络图的基本原则
两事项间只能有一项作业
A
3
改为 A
2
B
5
2
B
C
C
4
LOGO
5
LOGO
网络图应从左向右延伸,编号应从小到大,且不 重复。箭头事项编号大于箭尾事项编号
7.3 网络优化
工期限定,资源需要平衡 资源有限,工期希望最短 工期缩短,总费用最小
LOGO
一、工期限定,资源需要平衡 LOGO
工期不变,就是关键工作时间不能调整 资源不平衡将导致资源不足 利用时差,调整非关键路线上工作的开
始时间,使资源实现平衡。
例
LOGO
2(6)
00
1 B
运筹学7
讲课教师:XXX
第七章 网络计划技术
LOGO
7.1 PERT网络图 7.2 PERT网络参数计算 7.3 PERT网络优化 7.4
7.1 PERT网络图
LOGO
一、网络计划技术的基本概念
工程计划与甘特图
– 不易表现工程全貌 – 不便于对各项工作的安排进行筹划和推敲 – 不能识别影响进度的关键工作 – 不能反映一项工作不能按进度完成时对工程进度的影
C
总费用
间接费用
直接费用
TK*
T
直接成本的处理
LOGO
按线性处理,作业的费用率为
a2
2
3
a3 4
LOGO
5 b1 6 b2 7 b3 8
作业的合并 3
B 1A2
D
E
5G
C
F
4
LOGO
6
1A2
X
5
G
6
4.绘制网络图的基本原则
两事项间只能有一项作业
A
3
改为 A
2
B
5
2
B
C
C
4
LOGO
5
LOGO
网络图应从左向右延伸,编号应从小到大,且不 重复。箭头事项编号大于箭尾事项编号
7.3 网络优化
工期限定,资源需要平衡 资源有限,工期希望最短 工期缩短,总费用最小
LOGO
一、工期限定,资源需要平衡 LOGO
工期不变,就是关键工作时间不能调整 资源不平衡将导致资源不足 利用时差,调整非关键路线上工作的开
始时间,使资源实现平衡。
例
LOGO
2(6)
00
1 B
运筹学7
讲课教师:XXX
第七章 网络计划技术
LOGO
7.1 PERT网络图 7.2 PERT网络参数计算 7.3 PERT网络优化 7.4
7.1 PERT网络图
LOGO
一、网络计划技术的基本概念
工程计划与甘特图
– 不易表现工程全貌 – 不便于对各项工作的安排进行筹划和推敲 – 不能识别影响进度的关键工作 – 不能反映一项工作不能按进度完成时对工程进度的影
C
总费用
间接费用
直接费用
TK*
T
直接成本的处理
LOGO
按线性处理,作业的费用率为
管理运筹学 第6章 图与网络模型
表示。
a1
(v2)钱
a7
a2
a8
(赵v1)
a14 a15 a3
(v4) 李
a4
a9
(v3)孙
a5
a6
a12
a11
(v5) 周
a10
(v6)吴 a13
(v7)陈
图3
图(Graph)由点(Vertex)和点之间的连线所构成的集合。 不带箭头的连线称为边;带前头的连线称为弧。 点和边的集合称为无向图(Undirected graph),如图 (a), 用G={V,E}表示;
,
d (0) SC
d (0) CB
,
d (0) SD
d
(0) DB
,
d (0) SE
d
(0) EB
,
d (0) SF
d
(0) FB
,
d
(0) ST
d (0) TB
}
一般地有:
d (1) ij
min{di(r0)
d (0) rj
}
0 2 4 4 6 1 6
2
Hale Waihona Puke 0224
3
11
v7 v6
v 3
v4 v5
v1,v2 , v4 ,v7,v3, v5,v6 , v8
§6.1 图与网络的基本概念
图论中图是由点和边构成,可以反映一些对象之间的关系。 如物质结构、电路网络、城市规划、交通运输、信息传递、物 资调配等都可以用点和线连接起来的图进行模拟。
0sssasbscsdsesfstasaaabacadaeafatbsbabbbcbdbebfbtcscacbcccdcecfctdsdadbdcdddedfdteseaebecedeeefetfsfafbfcfdfefffttstatbtctdtetfttddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddddd???????????????????????????0212022420312043434071305???????????????????????????????????????6????????????????7d0为对称矩阵50160??????1sb0ss0sb0sa0ab0sb0bb0sc0cb0sd0db0se0eb0sf0fb0st0tbminddddddddddddddddd?????????因为从i到j的最短路不一定是i?j可能是i?l?ji?l?k?j
