结构力学-第三章力法PPT课件
合集下载
结构力学课件--6力法3
2
内容回顾
对称荷载:
反对称荷载:
EI
P EI
EI P P
EI
P EI
EI P P
B.有中柱对称结构(偶数跨结构) 对称荷载:
反对称荷载:
EI EI
P EI
EI P P
EI EI
P EI EI EI P P
EI/2
2019/7/14
课件
3
用力法计算下图所示结构,并作结构M图。
1 kN/m EI
EI
EI 2m
可能使: 21 = 12 = 0
即得:
课件
11X1 1P = 0 22 X 2 2P = 0 33 X 3 3P = 0
y y´
12
X2
X2 y
X1 X1 a
y
O
x
x'
1
y
x
X1 = 1
y
X2 =1
M1 =1 N1 = 0 Q1 = 0
12 =
15
4m
a
y
2EI
EI
EI
x
8m
X1 X1
X2 X2 X3
a
=
y
1 EI
ds
1 EI
ds
=
1 2EI
8 4
2( 1 EI
4 2)
=
8
=
2.667m
1 8 2( 1 4)
3
2019/7/14
2EI
EI 课件
§6-7 支座移动和温度改变时的内力计算
16
一、支座移动时的计算
(a 11
1 2
集美大学船舶结构力学(48学时)第三章 力法(3)2014(2学时)

由于: R2 v2 / A
216EI v 2 3 11l
M 2 M1 5 R2 ql l 2
因此,有方程:
216 EI M 2 M1 5 v ql 2 3 11l l 2
将此式与上面两方程联立 问题则解决。
题9 求下图 M , v , R 。 1 1 1
据3.6改 (教材52页)
梁的左半段断面惯性矩 为 I 1 ,右半段断面惯性矩 为 I 2 ,可以设想在断面变 化处加上一个柔性系数 A= ∞ 的弹性支座,如图4-27b)所示, 于是就可以按弹性支座上双跨 梁的方法来计算了。
静定基
v AR
EI1
R10
R R12
EI 2
v
静力平衡方程?
R0
A
转角连续方程式?
因此,可列出中间支座断面的 转角连续方程式:
R10
R12
3
l v1 AR1 ( R10 R12 ) 12EI 2 R ql 3
题8
(教材49页例2) 图3-26a所示的具有弹 性支座的多跨梁,试求其断 面弯矩、节点挠度和作用在 弹性支座上的力。
解:1、静定基:
M1
q 1
EI , l
M2
q
E,4I ,4l
M2
3
11l 3 A 216EI
即: 原模型:
A l3 6 EI
静定基:
EI , l EI , l
变协方: 4 4 5 q(2l ) 1 R(2l ) AR 384 EI 48 EI
由此直接解得:
R
v1 AR
可以去掉 中间的弹性支 座代以支反力 R,再利用变 形连续条件列 方程式求解。
R 5ql / 8
216EI v 2 3 11l
M 2 M1 5 R2 ql l 2
因此,有方程:
216 EI M 2 M1 5 v ql 2 3 11l l 2
将此式与上面两方程联立 问题则解决。
题9 求下图 M , v , R 。 1 1 1
据3.6改 (教材52页)
梁的左半段断面惯性矩 为 I 1 ,右半段断面惯性矩 为 I 2 ,可以设想在断面变 化处加上一个柔性系数 A= ∞ 的弹性支座,如图4-27b)所示, 于是就可以按弹性支座上双跨 梁的方法来计算了。
静定基
v AR
EI1
R10
R R12
EI 2
v
静力平衡方程?
R0
A
转角连续方程式?
因此,可列出中间支座断面的 转角连续方程式:
R10
R12
3
l v1 AR1 ( R10 R12 ) 12EI 2 R ql 3
题8
(教材49页例2) 图3-26a所示的具有弹 性支座的多跨梁,试求其断 面弯矩、节点挠度和作用在 弹性支座上的力。
解:1、静定基:
M1
q 1
EI , l
M2
q
E,4I ,4l
M2
3
11l 3 A 216EI
即: 原模型:
A l3 6 EI
静定基:
EI , l EI , l
变协方: 4 4 5 q(2l ) 1 R(2l ) AR 384 EI 48 EI
由此直接解得:
R
v1 AR
可以去掉 中间的弹性支 座代以支反力 R,再利用变 形连续条件列 方程式求解。
R 5ql / 8
结构力学讲义ppt课件

x y
x
结点自由度
y
φ
x
y
x
刚片自由度
2)一个刚片在平面内有三个自由度,因为确定 该刚片在平面内的位置需要三个独立的几何参
数x、y、φ。
4. 约束
凡是能减少体系自由度的装置就称为约束。
6
约束的种类分为:
1)链杆
简单链杆 仅连结两个结点的杆件称为简单 链杆。一根简单链杆能减少一个自由度,故一 根简单链杆相当于一个约束。
FyA
特点: 1) 结构在支座截面可以绕圆柱铰A转动 ; 2) x、y方向的反力通过铰A的中心。
29
3. 辊轴支座
A
A
FyA
特点: 1) 杆端A产生垂直于链杆方向的线位移; 2) 反力沿链杆方向作用,大小未知。
30
4. 滑动支座(定向支座)
A 实际构造
A
MA
FyA
A
MA
FyA
特点: 1)杆端A无转角,不能产生沿链杆方向的线 位移,可以产生垂直于链杆方向的线位移;
16
A
I
II
c)
B III C
形成瞬铰B、C的四根链杆相互平行(不等 长),故铰B、C在同一无穷远点,所以三个 铰A、 B、C位于同一直线上,故体系为瞬变 体系(见图c)。
17
二、举例
解题思路: 基础看作一个大刚片;要区分被约束的刚片及
提供的约束;在被约束对象之间找约束;除复 杂链杆和复杂铰外,约束不能重复使用。
高等教育出版社
4
第一章 绪 论
§1-1 结构力学的内容和学习方法
§1-2 结构计算简图
5
§1-1 结构力学的内容和学习方法
一、结构
建筑物或构筑物中 承受、传递荷载而起 骨架作用的部分称为 结构。如:房屋中的 框架结构、桥梁、大 坝等。
x
结点自由度
y
φ
x
y
x
刚片自由度
2)一个刚片在平面内有三个自由度,因为确定 该刚片在平面内的位置需要三个独立的几何参
数x、y、φ。
4. 约束
凡是能减少体系自由度的装置就称为约束。
6
约束的种类分为:
1)链杆
简单链杆 仅连结两个结点的杆件称为简单 链杆。一根简单链杆能减少一个自由度,故一 根简单链杆相当于一个约束。
FyA
特点: 1) 结构在支座截面可以绕圆柱铰A转动 ; 2) x、y方向的反力通过铰A的中心。
29
3. 辊轴支座
A
A
FyA
特点: 1) 杆端A产生垂直于链杆方向的线位移; 2) 反力沿链杆方向作用,大小未知。
30
4. 滑动支座(定向支座)
A 实际构造
A
MA
FyA
A
MA
FyA
特点: 1)杆端A无转角,不能产生沿链杆方向的线 位移,可以产生垂直于链杆方向的线位移;
16
A
I
II
c)
B III C
形成瞬铰B、C的四根链杆相互平行(不等 长),故铰B、C在同一无穷远点,所以三个 铰A、 B、C位于同一直线上,故体系为瞬变 体系(见图c)。
17
二、举例
解题思路: 基础看作一个大刚片;要区分被约束的刚片及
提供的约束;在被约束对象之间找约束;除复 杂链杆和复杂铰外,约束不能重复使用。
高等教育出版社
4
第一章 绪 论
§1-1 结构力学的内容和学习方法
§1-2 结构计算简图
5
§1-1 结构力学的内容和学习方法
一、结构
建筑物或构筑物中 承受、传递荷载而起 骨架作用的部分称为 结构。如:房屋中的 框架结构、桥梁、大 坝等。
结构力学课件 力法

(5)叠加原理作M图
M1(m)
M A 360 6 ( 22) 228 M C 6 ( 22) 132
90
228
132
桁架
P
a
(1)基本体系 —基本未知量 (2)位移协调条件 —写力法基本方程 (3)求系数和自由项 —单位荷载法
a
(4)解力法方程 —求基本未知量
P
→ X1 ↑
拆开一个单铰,相当于去掉两个联系。
X1
X 1 ← → ↑ → X2
(3) 在刚结处作一切口,或去掉一个固定端,相当于去掉 三个联系。 X
X1
←→
X2
(4)将刚结改为单铰联结,相当于去掉一个联系。
X1 X1
← →
3
例1: 确定图示结构的超静定次数。
2
1 3
n=6
例2: 确定图示结构的超静定次数。 对于具有较多框格的结构, 可按框格的数目确定,因为一
q a
A
B X1
A
2 力法的基本概念
力法的基本体系
q
A B A
q a
力法的基本未知量
a
B X1
B点的位移条件Δ1=0
变形协调条件
q
A
B A
变形协调条件
Δ1=Δ1P+Δ11=0
Δ1P:基本体系在荷载q单独
a q
A B Δ1P
Δ11 B X1
作用下沿X1方向产生的位移;
Δ11:基本体系在荷载X1单 独作用下沿X1方向产生的 位移;
X1
X1
(1)基本体系 —基本未知量 (2)位移协调条件 —写力法基本方程
a
a
1P 11 X 1 0
船舶结构力学ppt第三章力法

3-4 弹性支座与弹性固定端的概念
本节主要通过力法解杆系结构的例子引出弹性支座与弹性固定端的 实际概念。
1、弹性支座
q
I
l/2 R l/2
R
l1/2
l1/2
3-4 弹性支座与弹性固定端的概念
根据原结构节点处位移连续条件,列出力法方程为:
ql4 Rl3 Rl13 384EI 192EI 48EI1
X n
Δnp
3-3 刚性支座上连续梁与不可动节点简单刚架 计算
1、刚性支座上连续梁与三弯矩方程
1
2
i-1
M1
1
M2
2
i
i+1
n-1
n
Mn Mn-1
n-1
n
1、刚性支座上连续梁与三弯矩方程
根据原结构在固定端处转角为0和在每一个中间支座处转角连续的条件, 可列出力法方程:
l 3EI
i1
M i1
i
i
Mi
Mi
i1
M i1
li 1
i-1
i
li
i
i+1
根据中间支座i处转角连续的条件: i=(2M i1
li 3EI i
Mi
i (qi1) i
i 1
li1
li 3EI i
Mi
li1 6 EI i 1
(2)去掉多余约束后的体系,必须是几何不变的体系,因 此,某些约束是不能去掉的。
3-2 力法的基本原理及典型方程
M1
1
M2
M2
2
2
为使新静定结构与原结构等效, 必须满足以下变形协调条件:
结构力学第三章
q
2 1 0
l
3 6 7 4
l
5 图3.6
解: (1)计算弹性支座柔性系数A 首先需设在节点1处柔性系数A= ,则由下图 可求出柔性系数A。
由力的平衡知,有M4=Rl,其变形连续方程为:
R
v1 M 4l M 4l M 5l M 4l M 5l , 0 l 3EI 3EI 6 EI 6 EI 3EI
第2章 力法
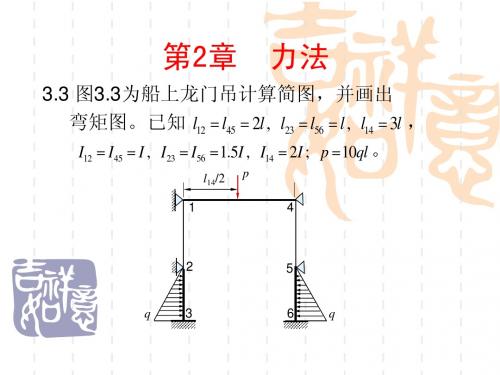
3.3 图3.3为船上龙门吊计算简图,并画出 弯矩图。已知 l12 l45 2l , l23 l56 l , l14 3l , I12 I45 I , I23 I56 1.5I , I14 2I ; p 10ql 。
l14/2 1 p 4
2
5
q
为此,将各杆取出有:
FB B FB ME p A= ME C FC
FC
R1E
MF A= MF
R1F
R2E
R2F
MA
MD RA RD
要使杆B-C轴向力平衡必有 FB=FC 由图中杆E-B和杆A-E可得:
R1E p
12 p 5M E 2M A 0 故有: 由图中杆D-F和杆F-C可得:
C D
MF
2 MD 5
(2)
3 M FB p A 5 10
FC MD 10
A
D
(3)
由式(a)、(b)得: 12M A 25M D 3EIfB 由式(c)、(d)得: 12M D 25M F 3EIfB 由式(e)、(f)得:12M A 25M E 12M D 25M F 0 将式(2)代入式(f)得:
2 1 0
l
3 6 7 4
l
5 图3.6
解: (1)计算弹性支座柔性系数A 首先需设在节点1处柔性系数A= ,则由下图 可求出柔性系数A。
由力的平衡知,有M4=Rl,其变形连续方程为:
R
v1 M 4l M 4l M 5l M 4l M 5l , 0 l 3EI 3EI 6 EI 6 EI 3EI
第2章 力法
3.3 图3.3为船上龙门吊计算简图,并画出 弯矩图。已知 l12 l45 2l , l23 l56 l , l14 3l , I12 I45 I , I23 I56 1.5I , I14 2I ; p 10ql 。
l14/2 1 p 4
2
5
q
为此,将各杆取出有:
FB B FB ME p A= ME C FC
FC
R1E
MF A= MF
R1F
R2E
R2F
MA
MD RA RD
要使杆B-C轴向力平衡必有 FB=FC 由图中杆E-B和杆A-E可得:
R1E p
12 p 5M E 2M A 0 故有: 由图中杆D-F和杆F-C可得:
C D
MF
2 MD 5
(2)
3 M FB p A 5 10
FC MD 10
A
D
(3)
由式(a)、(b)得: 12M A 25M D 3EIfB 由式(c)、(d)得: 12M D 25M F 3EIfB 由式(e)、(f)得:12M A 25M E 12M D 25M F 0 将式(2)代入式(f)得:
《力法结构力学》课件

详细描述
力的作用与反作用原理表明,当一个物体对另一个物体施加力时,另一个物体也 会对施力物体施加一个大小相等、方向相反的反作用力。这个原理是牛顿第三定 律的一部分,是理解结构力学中相互作用和平衡状态的基础。
弹性力学的基本假设
总结词
对弹性力学的基本性质和假设的概括。
详细描述
弹性力学的基本假设包括:1) 材料是线弹性的,即应力与应变之间存在线性关系;2) 材料是均匀的,即各部分具有相同的物理性质;3) 材料是无缝的,即不存在内部空隙 或缺陷;4) 材料是连续的,即物质没有离散的间隙或孔洞。这些假设为简化问题和分
来获得结构的响应。
力法结构力学的智能化技术应用
人工智能与机器学习
利用人工智能和机器学习技术对大量 数据进行处理和分析,自动识别结构
的性能特征和优化设计方案。
智能传感器与监测技术
通过智能传感器实时监测结构的性能 状态,实现结构的健康监测和预警。
优化算法与智能决策
将优化算法与人工智能相结合,实现 结构的智能优化设计,提高结构的性
能和可靠性。
感谢您的观看
THANKS03力法结 Nhomakorabea力学的基本方法
静力分析方法
静力分析方法是一种基于平衡条 件的结构分析方法,用于确定结 构在静力荷载作用下的内力和变
形。
静力分析方法主要包括:线弹性 分析、塑性分析和弹塑性分析等
。
静力分析方法广泛应用于各种工 程结构的分析和设计,如桥梁、
房屋、塔架等。
动力分析方法
动力分析方法是一种基于动力 学方程的结构分析方法,用于 确定结构在动力荷载作用下的
总结词
交通工具的力法分析是力法结构力学在交通 运输领域的应用,通过对交通工具进行力法 分析,可以提高交通工具的安全性和舒适性 。
力的作用与反作用原理表明,当一个物体对另一个物体施加力时,另一个物体也 会对施力物体施加一个大小相等、方向相反的反作用力。这个原理是牛顿第三定 律的一部分,是理解结构力学中相互作用和平衡状态的基础。
弹性力学的基本假设
总结词
对弹性力学的基本性质和假设的概括。
详细描述
弹性力学的基本假设包括:1) 材料是线弹性的,即应力与应变之间存在线性关系;2) 材料是均匀的,即各部分具有相同的物理性质;3) 材料是无缝的,即不存在内部空隙 或缺陷;4) 材料是连续的,即物质没有离散的间隙或孔洞。这些假设为简化问题和分
来获得结构的响应。
力法结构力学的智能化技术应用
人工智能与机器学习
利用人工智能和机器学习技术对大量 数据进行处理和分析,自动识别结构
的性能特征和优化设计方案。
智能传感器与监测技术
通过智能传感器实时监测结构的性能 状态,实现结构的健康监测和预警。
优化算法与智能决策
将优化算法与人工智能相结合,实现 结构的智能优化设计,提高结构的性
能和可靠性。
感谢您的观看
THANKS03力法结 Nhomakorabea力学的基本方法
静力分析方法
静力分析方法是一种基于平衡条 件的结构分析方法,用于确定结 构在静力荷载作用下的内力和变
形。
静力分析方法主要包括:线弹性 分析、塑性分析和弹塑性分析等
。
静力分析方法广泛应用于各种工 程结构的分析和设计,如桥梁、
房屋、塔架等。
动力分析方法
动力分析方法是一种基于动力 学方程的结构分析方法,用于 确定结构在动力荷载作用下的
总结词
交通工具的力法分析是力法结构力学在交通 运输领域的应用,通过对交通工具进行力法 分析,可以提高交通工具的安全性和舒适性 。
结构力学力法ppt课件

结构对称一般选取对称基本结构
19
§5-6 超静定结构自内力概念与计算
自内力 — 超静定结构在没有荷载作用情况下,由于
支座移动、温度改变、制造误差等因素产 生的内力。(这是超静定结构所特有的性质)
1. 支座移动
θ
A
EI
已知图示梁A端转动角度
为θ,B端下沉a,求在梁
l
中引起的自内力。
A
B a
B
基本结构
2EI 3 2
4
48EI
2P
M2MP EI
ds
1 (1 1.5EI 2
a
a
1 qa2 ) 2
qa4 6EI
6
④解力法方程:
52
19 48
qa
0
1 3
X1
2 9
X2
1 6
qa
0
得:
X1
7 qa, 16
X2
3 qa 32
⑤画内力图:
M M1X1 M 2X2 M p
24
2111XX112122XX22213 pX3 0 2 p二阶0(对称未(知a)力)
3121XX113222XX22332Xp 303 p 0
33 X3 3 p 0
一阶(反对称未知力)
(线性方程组降阶)
18
说明:
对称超静定结构如果选取对称基本结 构,只要未知力分为对称与反对称,则力 法方程也必然分组,该性质与荷载无关。
4
③求力法方程系数
a a
X1=1 M1图
X2=1
a
M2图
19
§5-6 超静定结构自内力概念与计算
自内力 — 超静定结构在没有荷载作用情况下,由于
支座移动、温度改变、制造误差等因素产 生的内力。(这是超静定结构所特有的性质)
1. 支座移动
θ
A
EI
已知图示梁A端转动角度
为θ,B端下沉a,求在梁
l
中引起的自内力。
A
B a
B
基本结构
2EI 3 2
4
48EI
2P
M2MP EI
ds
1 (1 1.5EI 2
a
a
1 qa2 ) 2
qa4 6EI
6
④解力法方程:
52
19 48
qa
0
1 3
X1
2 9
X2
1 6
qa
0
得:
X1
7 qa, 16
X2
3 qa 32
⑤画内力图:
M M1X1 M 2X2 M p
24
2111XX112122XX22213 pX3 0 2 p二阶0(对称未(知a)力)
3121XX113222XX22332Xp 303 p 0
33 X3 3 p 0
一阶(反对称未知力)
(线性方程组降阶)
18
说明:
对称超静定结构如果选取对称基本结 构,只要未知力分为对称与反对称,则力 法方程也必然分组,该性质与荷载无关。
4
③求力法方程系数
a a
X1=1 M1图
X2=1
a
M2图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 超静定结构的解法—力法
Methods of Analysis of Statically Indeterminate Structures - Mechanics
1
刘敬喜,2008
§ 3-1 超静定结构的组成与超静定次数的确定
概述
超静定结构是相对于静定结构而言的。静定结构 是几何不变而又没有多余约束的体系,其反力和内力 只需静力平衡方程即可求得。所谓几何不变体系是指 如果不考虑材料应变所产生的变形,体系在受到任何 载荷作用后能够保持其固有的几何形状和位置的体系。 超静定结构有以下几个特征:
vq,2lq2 2 lE 2 4 l3I2 2 ll2 2 642 2 ll2 2 ll2 2 2q4l
在vR集1l 中3R载E 1l3荷I,vRR12l1作5用6RE1l下3I:
0.713ql2
在集中载荷R2作用下:
vR2l
56RE2l3I,vR2,2l
8R2l3 3EI
几何特征:有多余约束的几何不变体系。
静力特征:仅由静力平衡方程不能求出所有内力和反力.
超静定问题的求解要同时考虑结构的“变形、本构、 平衡”.
2
刘敬喜,2008
§ 3-1 超静定结构的组成与超静定次数的确定
1)超静定结构的类型
桁架
拱
超静定梁
刚架
桁架
组合结构
3
刘敬喜,2008
§ 3-1 超静定结构的组成与超静定次数的确定
支座1处
的转角
支座2处
1 0
的转角
21 23
16
刘敬喜,2008
§ 3-2 力法的基本原理及典型方程
上式即为变形协调条件。利用两端自由支持单跨 梁的弯曲要素表,可以得到转角与弯矩和外载荷之间 的关系式,并将他们代入到上式,得到:
M
1
1
M
m1l
3 EI
2
m 2l 6 EI
q 2
m1l 6 EI
为了求出基本结构中多余的约束力,必须考虑原
结构在多余联系处的已知变形条件。下面以求M1和M2 (图3-6b)为例来说明。原结构(图3-6a)在均布载荷
q作用下在固定端处的转角为零,在中间支座处转角连
续。为使基本结构的受力和变形与原结构完全一致,
就应使基本结构在多余约束力M1 、 M2 载荷q作用下在 支座1处的转角为零,在支座2处的转角连续,即:
解
14
刘敬喜,2008
§ 3-2 力法的基本原理及典型方程
看下面简单的例子:
q
如图3-6所示的双
1 l
2
3 跨梁,它是二次超静
l
定结构。在用力法计
图3-6a
M1
(2)
M2
算时,可将其两个多 余联系去掉。
q
1 lLeabharlann 2图3-6bl
R1
l
R2
2 l
图3-6c
15
刘敬喜,2008
§ 3-2 力法的基本原理及典型方程
2)超静定次数确定 (1)超静定次数——结构多余约束或多余未知力的数
目,即为超静定次数。
(2)确定超静定次数的方法——通过去掉多余约束来
确定。(去掉n个多余约束,即为n次超静定)。
(3)去掉(解除)多余约束的方式 a、撤去一个活动铰支座、去掉或切断一根链杆——去
掉1个约束(联系);
X1
4
刘敬喜,2008
m(杆个数); r(支反力数 目); j(节点数)
10
刘敬喜,2008
§ 3-1 超静定结构的组成与超静定次数的确定
X2 X1
X3
X2 X1
X3
X5 X4
X6
一个无铰封闭框有 三个多余约束.
3×封闭框数-单铰数目 =3×3-3=6
3×封闭框数-单铰数目 =3×3-4=5
12
刘敬喜,2008
此链杆不能去掉
§ 3-1 超静定结构的组成与超静定次数的确定
b、去掉一个单铰或一个固定铰支座—— 去掉2个约束;
X1 X2
c、切断刚性联系(梁式杆)或去掉一个固定端——
去掉3个约束;
X3
X1
X1
X3
X2
X2
5
刘敬喜,2008
§ 3-1 超静定结构的组成与超静定次数的确定
d、将刚性连接改为单铰—— 去掉1个约束。
第二种等效方法
求解:
变形 v1 0
R1
条件 v2 0 R 2
在均布载荷q作用下:
R1 1.1429ql()
R2 0.3929ql()
固定端支反力
vq l q 2 2 lE 2 4 l3I2 ll2 2 6 42 ll2 ll2 2 12 q7 34 l
R0.464q2l M 0.0 7 1 3
0.071ql2
0.107ql2
-0.125ql2
-0.125ql2
0.036ql -0.5ql
0.5ql
0.036ql
-0.107ql -0.5ql
0.5ql
-0.107ql
0.713ql2
0.464ql
0.107ql2
0.536ql
0.393ql
0.607ql 18
刘敬喜,2008
§ 3-2 力法的基本原理及典型方程
X3 X1
X1 X2 X3
X2
几何可变体系不能 X 3 作为基本体系
X1
X2
7
刘敬喜,2008
§ 3-1 超静定结构的组成与超静定次数的确定
X1 X2
X3
X1
X2
X3
X1 X2
X3
平衡方程个数:2×8=16
未知数个数:16+3=19 多余约束力:19-16=3
计算桁架超静定次数的简单 公式(m+r)-2j=16+3-2×8=3
m 2l 3 EI
1
ql 4 24 EI
2
ql 4 24 EI
M2
根据变形条件
2m2l/3EI1110
q
IV 2
ql 4 24 EI
212222IV23 求解:
M1 0.071ql2
M2 0.107ql2
17
刘敬喜,2008
§ 3-2 力法的基本原理及典型方程
求出基本未知量M1和M2后,就可分别对两个静定 单跨梁进行计算,并用叠加法画出梁1-2和2-3的弯矩图 和剪力图,此即原双跨梁的弯矩图和剪力图。
X1
注意事项
(1)对于同一超静定结构,可以采取不同方式去掉多余 约束,而得到不同形式的静定结构,但去掉多余约束的 总个数应相同。
(2)去掉多余约束后的体系,必须是几何不变的体系,因
此,某些约束是不能去掉的。
6
刘敬喜,2008
§ 3-1 超静定结构的组成与超静定次数的确定
X2 X1
X3
X3
X2 X1
此两链杆任一根都不能去掉
13
刘敬喜,2008
§ 3-2 力法的基本原理及典型方程
解除多余约束,转化为静定结构。将多余 约束以多余未知力代替。这种把多余约束力 作为基本量的计算方法——力法。
力法的基本思想: 1.找出未知问题不能求解的原因, 2.将其化成能求解的问题, 3.找出改造后的问题与原问题的差别, 4.消除差别后,改造后的问题的解即为原问题的
Methods of Analysis of Statically Indeterminate Structures - Mechanics
1
刘敬喜,2008
§ 3-1 超静定结构的组成与超静定次数的确定
概述
超静定结构是相对于静定结构而言的。静定结构 是几何不变而又没有多余约束的体系,其反力和内力 只需静力平衡方程即可求得。所谓几何不变体系是指 如果不考虑材料应变所产生的变形,体系在受到任何 载荷作用后能够保持其固有的几何形状和位置的体系。 超静定结构有以下几个特征:
vq,2lq2 2 lE 2 4 l3I2 2 ll2 2 642 2 ll2 2 ll2 2 2q4l
在vR集1l 中3R载E 1l3荷I,vRR12l1作5用6RE1l下3I:
0.713ql2
在集中载荷R2作用下:
vR2l
56RE2l3I,vR2,2l
8R2l3 3EI
几何特征:有多余约束的几何不变体系。
静力特征:仅由静力平衡方程不能求出所有内力和反力.
超静定问题的求解要同时考虑结构的“变形、本构、 平衡”.
2
刘敬喜,2008
§ 3-1 超静定结构的组成与超静定次数的确定
1)超静定结构的类型
桁架
拱
超静定梁
刚架
桁架
组合结构
3
刘敬喜,2008
§ 3-1 超静定结构的组成与超静定次数的确定
支座1处
的转角
支座2处
1 0
的转角
21 23
16
刘敬喜,2008
§ 3-2 力法的基本原理及典型方程
上式即为变形协调条件。利用两端自由支持单跨 梁的弯曲要素表,可以得到转角与弯矩和外载荷之间 的关系式,并将他们代入到上式,得到:
M
1
1
M
m1l
3 EI
2
m 2l 6 EI
q 2
m1l 6 EI
为了求出基本结构中多余的约束力,必须考虑原
结构在多余联系处的已知变形条件。下面以求M1和M2 (图3-6b)为例来说明。原结构(图3-6a)在均布载荷
q作用下在固定端处的转角为零,在中间支座处转角连
续。为使基本结构的受力和变形与原结构完全一致,
就应使基本结构在多余约束力M1 、 M2 载荷q作用下在 支座1处的转角为零,在支座2处的转角连续,即:
解
14
刘敬喜,2008
§ 3-2 力法的基本原理及典型方程
看下面简单的例子:
q
如图3-6所示的双
1 l
2
3 跨梁,它是二次超静
l
定结构。在用力法计
图3-6a
M1
(2)
M2
算时,可将其两个多 余联系去掉。
q
1 lLeabharlann 2图3-6bl
R1
l
R2
2 l
图3-6c
15
刘敬喜,2008
§ 3-2 力法的基本原理及典型方程
2)超静定次数确定 (1)超静定次数——结构多余约束或多余未知力的数
目,即为超静定次数。
(2)确定超静定次数的方法——通过去掉多余约束来
确定。(去掉n个多余约束,即为n次超静定)。
(3)去掉(解除)多余约束的方式 a、撤去一个活动铰支座、去掉或切断一根链杆——去
掉1个约束(联系);
X1
4
刘敬喜,2008
m(杆个数); r(支反力数 目); j(节点数)
10
刘敬喜,2008
§ 3-1 超静定结构的组成与超静定次数的确定
X2 X1
X3
X2 X1
X3
X5 X4
X6
一个无铰封闭框有 三个多余约束.
3×封闭框数-单铰数目 =3×3-3=6
3×封闭框数-单铰数目 =3×3-4=5
12
刘敬喜,2008
此链杆不能去掉
§ 3-1 超静定结构的组成与超静定次数的确定
b、去掉一个单铰或一个固定铰支座—— 去掉2个约束;
X1 X2
c、切断刚性联系(梁式杆)或去掉一个固定端——
去掉3个约束;
X3
X1
X1
X3
X2
X2
5
刘敬喜,2008
§ 3-1 超静定结构的组成与超静定次数的确定
d、将刚性连接改为单铰—— 去掉1个约束。
第二种等效方法
求解:
变形 v1 0
R1
条件 v2 0 R 2
在均布载荷q作用下:
R1 1.1429ql()
R2 0.3929ql()
固定端支反力
vq l q 2 2 lE 2 4 l3I2 ll2 2 6 42 ll2 ll2 2 12 q7 34 l
R0.464q2l M 0.0 7 1 3
0.071ql2
0.107ql2
-0.125ql2
-0.125ql2
0.036ql -0.5ql
0.5ql
0.036ql
-0.107ql -0.5ql
0.5ql
-0.107ql
0.713ql2
0.464ql
0.107ql2
0.536ql
0.393ql
0.607ql 18
刘敬喜,2008
§ 3-2 力法的基本原理及典型方程
X3 X1
X1 X2 X3
X2
几何可变体系不能 X 3 作为基本体系
X1
X2
7
刘敬喜,2008
§ 3-1 超静定结构的组成与超静定次数的确定
X1 X2
X3
X1
X2
X3
X1 X2
X3
平衡方程个数:2×8=16
未知数个数:16+3=19 多余约束力:19-16=3
计算桁架超静定次数的简单 公式(m+r)-2j=16+3-2×8=3
m 2l 3 EI
1
ql 4 24 EI
2
ql 4 24 EI
M2
根据变形条件
2m2l/3EI1110
q
IV 2
ql 4 24 EI
212222IV23 求解:
M1 0.071ql2
M2 0.107ql2
17
刘敬喜,2008
§ 3-2 力法的基本原理及典型方程
求出基本未知量M1和M2后,就可分别对两个静定 单跨梁进行计算,并用叠加法画出梁1-2和2-3的弯矩图 和剪力图,此即原双跨梁的弯矩图和剪力图。
X1
注意事项
(1)对于同一超静定结构,可以采取不同方式去掉多余 约束,而得到不同形式的静定结构,但去掉多余约束的 总个数应相同。
(2)去掉多余约束后的体系,必须是几何不变的体系,因
此,某些约束是不能去掉的。
6
刘敬喜,2008
§ 3-1 超静定结构的组成与超静定次数的确定
X2 X1
X3
X3
X2 X1
此两链杆任一根都不能去掉
13
刘敬喜,2008
§ 3-2 力法的基本原理及典型方程
解除多余约束,转化为静定结构。将多余 约束以多余未知力代替。这种把多余约束力 作为基本量的计算方法——力法。
力法的基本思想: 1.找出未知问题不能求解的原因, 2.将其化成能求解的问题, 3.找出改造后的问题与原问题的差别, 4.消除差别后,改造后的问题的解即为原问题的
