抗震例题
建筑抗震重点考试例题

一场地类别1.覆盖层厚度≤20m2.剪切波速<500m/s3.火山岩硬夹层视为刚体,从土体中扣除Vse=d0/求和d/v二土的液化1.饱和砂土和粉土会发生液化土层液化深度很少超过15m2.初步判别法有任意一个条件满足,不考虑液化Du>D0+Db-2Dw>D0+Db-3Du+Dw>1.5D0+2Db-4.5Dw地下水位深度Du上覆非液化土层厚度Db基础埋深≥2mD0液化特征深度查表3.标准贯入试验判别法求液化系数IleWi=10 Dm≤5m=(2/3)(20-Dm)5m ≤Dm≤20m Dm所代表土层中点距地面距三振型分解反应谱法1.查表αmax,Tg2.0.1<T≤Tg α=αmaxTg<T<5Tg α=(Tg/T)的0.9次方* αmaxFxi=α*γ*Xxi*G3.每层V=各振型每层V平方和的开方四 底部剪力法1.对于重量和刚度沿高度分布比较均匀、高度不超过40m ,并以剪切变形为主(房屋高宽比小于4时)的结构。
2.查表Tg αmax 求出α3.底部剪力Fk=αGekGek=0.85*(G1+G2+…) 4.查表得顶部附加地震作用系数δn 5.ΔFn=δn*Fk6.F1=G1*H1/(GH 求和) *Fk (1-δn )7.鞭稍效应V=3F下一层V=F+F1+ΔFn例:带有突出屋面楼梯间的三层钢砼框架结构,层高均为3m,1-3层柱刚度均为280000KN/m,出屋面梯间柱的刚度为50000kN/m, 屋面恒载5700KN ,活载600kN,1层楼面恒载6000kN, 2层楼面恒载5000kN ,1-2层活载均为1000kN ,出屋面梯间恒载820kN ,活载240kN 。
已知设防烈度8度(0.2g ),II 类场地,第二组,第一自振周期T1=0.6s,要求用底部剪力法求楼层地震剪力及结构顶层位移。
解:(1)计算楼层重力荷载代表值G 1 = 6000 + 0 . 5 ´ 1000 = 6500 kN顶层重力荷载代表值包括,屋面恒荷载+50%雪荷载+纵横梁自重+半层柱自重+半层墙体自重。
抗震题库计算题

抗震题库计算题2、某建筑8层、高度为29m,丙类建筑,其场地地质钻孔资料(无剪切波速资料)如3、地地质勘察资料如下:=120m/s;①0~2.0m,淤泥质土,Vs②2.0~25.0m,密实粗砂,V=400m/s;s=800m/s③25.0~26.0m,玄武岩,Vs=350m/s④26.0~40.0m/s,密实含砾石砂,Vs=700m/s⑤40.0m以下,强风化粉砂质泥岩,Vs请分析该场地的类别?4、地底层资料如下:②0~30m,黏土,V s=150m/s;=350m/s;②3~18m,砾砂,Vs③18~20m,玄武岩,V s=600m/s④20~27m/s,黏土,V s=160m/s⑤27~32m/s,黏土,V s=420m/s⑥32m以下,泥岩,V s=600m/s请分析该场地的类别?5、地抗震设防烈度为8度,设计基本地震加速度为0.30g,设计地震分组为第一组。
土层等效剪切波速为150m/s,覆盖层厚度为60m,结构自震周期为T=0.40s,试求阻尼比为ζ=0.05时的地震影响系数α6、筑场地抗震设防烈度为8度,设计基本地震加速度为0.30g,设计地震分组为第二组。
场地类别为Ⅲ类,结构自震周期为T=1.65s,结构阻尼比ζ=0.05,试求多遇地震作用下水平地震影响系数。
7、层建筑,采用钢框架-钢筋混凝土核心筒结构,房屋高度34.0m,抗震设防烈度为=0.35s,考虑非承重墙体刚度7度,设计基本地震加速度为0.15g,场地特征周期Tg=1.82s,已知η1=0.0213,η2=1.078,试求,地震影响系影响折减后结构自震周期为T1数α。
8、20层的高层建筑,采用钢筋混凝土结构。
该建筑地抗震设防烈度为8度(0.3g),场地类别为Ⅱ类,设计地震分组为第一组。
该结构的自振周期T1=1.2s,阻尼比ξ=0.05,求地震系数α。
9、架剪力墙结构房屋,丙类建筑,场地为Ⅰ1类,设防烈度为7度,设计地震分组为第一组,设计基本地震加速度为0.15g。
抗震计算题整理
[2 0.2 1 (T 5Tg )]max
5Tg
6 .0
T ( s)
0.05 0.05 0.9 2 1 0.3 6 0.08 1.6
例:试用振型分解反应谱法计算图示框架多遇地震时的层间剪力。 抗震设防烈度为8度,Ⅱ类场地,设计地震分组为第二组。 解: (1)求体系的自振周期和振型 m 180t
K3 98MN/m
m2 270t
K 2 195MN/m
m1 270t K1 245MN/m
T1 0.467s T2 0.208s T3 0.134s
(2)计算各振型的地震影响系数 查表得 max 0.16
Tg 0.4s
2 max
T ( g ) 2 max T
K3 98MN/m
m2 270t
K 2 195MN/m
m1 270t K1 245MN/m
T1 0.467s T2 0.208s T3 0.134s
(2)计算各振型的地震影响系数 查表得 max 0.16
Tg 0.4s
地震影响系数最大值(阻尼比为0.05)
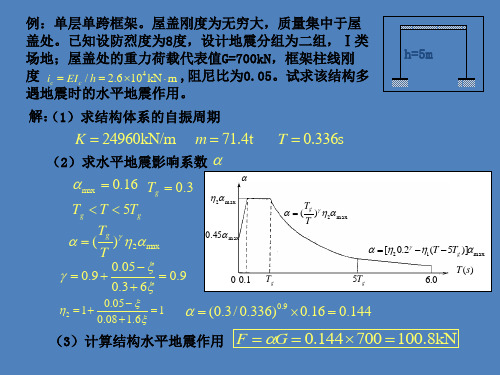
例:单层单跨框架。屋盖刚度为无穷大,质量集中于屋 盖处。已知设防烈度为8度,设计地震分组为二组,Ⅰ类 场地;屋盖处的重力荷载代表值G=700kN,框架柱线刚 度 ic EI c / h 2.6 104 kN m ,阻尼比为0.05。试求该结构多 遇地震时的水平地震作用。
h=5m
解: (1)求结构体系的自振周期
D2 (t ) 0.000534(1 cos 2t )
y1 (t ) 1 1 D1 (t ) D2 (t ) 1 / 2 y2 (t ) 2
抗震计算题

箍筋的最小直径查表得: ;
(3)但是题目已知:框架梁端纵向受拉钢筋配筋率为2.18%>2%!根据抗规-2010-6.3.3条:表中箍筋的最小直径应增大2mm,故实际采用的箍筋的最小直径为: !
由《建筑结构荷载规范》7.4.2条公式可得风振系数βz为:
βz=1+φzξv/μz=1+(Hi/H)ξv/μz
=1+(1.502×0.474/μz)(Hi/H)
=1+(0.712/μz)(Hi/H)
(4)确定风压高度变化系数μz
已知建筑场地位于大城市郊区,地面粗糙度属于B类,根据《建筑结构荷载规范》表7.2.1可查得各区段中点位置的风压高度变化系数μz为:
2-3层:ΣD2=ΣD3=2×(6.825+13.365)×103N/mm =40.38×103N/mm
4、求各楼层的总剪力Vpj
第一层:Vp1=3p=300 KN;
第二层:Vp2=2p=200 KN;
第三层:Vp3=1p=100 KN。
5、求各楼层的层间侧移(由于梁柱弯曲变形产生的)
第ቤተ መጻሕፍቲ ባይዱ层:
第二层:
解:1求各层中柱,边柱的k,α值
底层边柱: ,
α
底层中柱:
,
α
2-3层边柱:
,
α
2-3层中柱: ,
α
2、求各层中柱、边柱的D值
底层边柱:D=α
底层中柱:D=α
2-3层边柱:D=α
2-3层中柱:D=α
土木工程高层抗震计算例题

水平地震作用计算步骤:①确定计算简图并计算结构重力荷载G E;②计算结构侧向刚度K;③计算结构自振周期T;④确定地震参数:查表得a max、Tg、a;⑤计算水平地震作用:F Ek =aG E。
【例1】如图3. 11所示,单层钢筋混凝土框架,G=1200 kN,设梁刚度EI=∞,b×h=350 mm×350 mm,柱抗侧移刚度为k1=k2=3×l03 kN/m,阻尼比 =0.05。
设防烈度7度,Ⅲ类场地,该地区地震分组为第一组。
试计算该框架在多遇地震下的水平地震作用ek f【解】 (1)确定计算简图如图所示。
G=1200 kN图3.11例3.2图(2)计算结构侧向刚度k柱抗侧移刚度为两柱抗侧移刚度之和K=k1+k2=2×3.O×l03=6.0×l03kN/m (3)计算结构自振周期TT=ωπ2=2πkm =2πgk G=2π631068.9101200⨯⨯⨯=0.897s(4)确定地震参数查表得max α=0.08;Tg=0.45 s 。
因为Tg=0.45 s<T=0.897s<5Tg=5×0.45 s=2.25 s ,故a 处于反应谱曲线下降段,其地震影响系数为:α=2ηγ⎪⎪⎭⎫⎝⎛TT g maxα=9.0897.045.0⎪⎭⎫ ⎝⎛×1×0.08=0.043(5)计算水平地震作用F=αE G=0.043×1200=51.965 kNE K【例2】如图所示框架结构,设防烈度为8度,设计基本地震加速度为0.20g,I类建筑场地,地震分组为第一组。
试用底部剪力法计算该框架在多遇地震下的水平地震作用,层间地震剪力,层间位移及顶点位移计算。
解:(1)确定地震参数α=0.16,由由设防烈度8度查出maxI类场地和地震分组查出Tg=0.25。
因为Tg=0.25<T1=0.358<5Tg =1.25所以取反应谱的曲线下降段:因为Tg <T1 <5T。
抗震考试题及答案

抗震考试题及答案一、单项选择题1. 抗震设防烈度是指在一定时期内,由于地震引起的可能对建筑物产生破坏性影响的最大地震烈度。
根据我国地震区划图,抗震设防烈度为7度的地区,其基本地震加速度值为()。
A. 0.10gB. 0.15gC. 0.20gD. 0.25g答案:B2. 建筑物抗震设计的基本目标是()。
A. 小震不坏B. 中震可修C. 大震不倒D. 以上都是答案:D3. 抗震结构延性是指结构在受到地震作用时,能够吸收和耗散地震能量,避免结构发生脆性破坏的能力。
以下哪种结构的延性最差()。
A. 钢筋混凝土框架结构B. 钢结构C. 砌体结构D. 木结构答案:C4. 抗震设计中,建筑物的抗震等级是根据()来确定的。
A. 建筑物的重要性B. 建筑物的使用功能C. 建筑物的高度D. 建筑物的抗震设防烈度答案:D5. 抗震设计中,建筑物的抗震措施分为()。
A. 抗震构造措施B. 抗震性能化设计C. 抗震性能评估D. 以上都是答案:D二、多项选择题1. 抗震设计中,以下哪些因素会影响建筑物的抗震性能()。
A. 建筑物的平面和立面形状B. 建筑物的结构体系C. 建筑物的材料性能 D. 建筑物的施工质量答案:ABCD2. 抗震设计中,以下哪些措施可以提高建筑物的抗震性能()。
A. 增加结构的延性B. 增加结构的强度C. 提高结构的刚度D.增加结构的阻尼比答案:ABD三、判断题1. 抗震设计中,建筑物的抗震等级越高,其抗震性能越好。
()答案:正确2. 抗震设计中,建筑物的抗震性能只与建筑物的结构体系有关,与其他因素无关。
()答案:错误3. 抗震设计中,建筑物的抗震性能可以通过增加结构的强度来提高。
()答案:错误四、简答题1. 简述抗震设计中,建筑物的抗震性能主要取决于哪些因素?答案:建筑物的抗震性能主要取决于建筑物的结构体系、材料性能、施工质量、平面和立面形状、结构的延性和阻尼比等因素。
2. 简述抗震设计中,建筑物的抗震等级是如何确定的?答案:建筑物的抗震等级是根据建筑物所在地的抗震设防烈度来确定的。
抗震设计有关计算例题
N j= 1
= &&g ( t ) ∑ γ j x ji = &&g ( t ) x x
j =1
& & & = m ∑ xjiγ j ∆ j (t) +γ j xji & g (t)] [ x i = ∑Fji (t)
j =1 N
3
0.334 {X}1 = 0.667 1.000
− 0.667 4.019 {X}2 = − 0.666 {X}3 = −3.035 1.000 1.000
K 3 = 98MN/m
m2 = 270t
K 2 = 195MN/m
i 质点相对于基底的位移与加速度为
xi (t) = ∑xji Dj (t)
j =1
N
N
= ∑xjiγ j ∆ j (t)
j =1 N
& & & i (t) = ∑xjiγ j ∆ j (t) & x
j =1
∑
n
j =1
γ j x ji &&g ( t ) = x
n
i 质点 t 时刻的水平地震作用为 时刻的水平地震作用为
M* = {X}j [m]{X}j ---j振型广义质量 ---j j
T
K* = {X}j [k]{X}j ---j振型广义刚度 ---j j
T
C* = {X}j [c]{X}j ---j振型广义阻尼系数 ---j j
T
C* & K* & (t) + j D + j D (t) = −{X}j [M]{I} & (t) & & Dj xg j j * * * Mj Mj Mj
抗震例题
d u (m)
d u (d b 2) 5m d w (d b 2) 5.5m
需要进一步判别是否考虑液 化影响。 dw(m)
1 1 2 3 4
2
3
4
5
6
7
8
9
10
须进一步判别区
7度
5
6 7 8 9 10
8度
9度
不考虑液化影响区
砂土
8 7m 8m
9 8m 9m
粉土 砂土
d 0 8m 1.5d 0 2d b 4.5 11.5m d u d w 11.5m
需要考虑液化影响。
解:按土层液化判别图确定
dw=6m
例1 图示为某场地地基剖面图 上覆非液化土层厚度du=5.5m 其下为砂土,地下水位深度 为dw=6m.基础埋深db=2m,该 场地为8度区。确定是否考 虑液化影响。
饱和土 类别
烈度
7 6m 7m
8 7m 8m
9 8m 9m
粉土 砂土
d 0 8m 1.5d 0 2d b 4.5 12.5m d u d w 11.5m
不满足判别式,需要进一步判别是否考虑液化影响。
解:按土层液化判别图确定
dw=6m
例2 图示为某场地地基剖面图 上覆非液化土层厚度du=5.5m 其下为沙土,地下水位深度 为dw=6m.基础埋深db=2.5m, 该场地为8度区。确定是否考 虑液化影响。
解:按判别式确定
d u d w 1.5d 0 2d b 4.5
查液化土特征深度表
dw=6m
例1 图示为某场地地基剖面图 上覆非液化土层厚度du=5.5m 其下为砂土,地下水位深度 为dw=6m.基础埋深db=2m,该 场地为8度区。确定是否考 虑液化影响。
抗震与设计计算题目解析
高层建筑结构抗震与设计(练习题1)1.某单跨单层厂房如图1所示,集中于屋盖的重力荷载代表值为G= 2800kN,柱抗侧移刚度系数k1=k2=2.0 xi04kN/m,结构阻尼比Z=0.03 , n类建筑场地,设计地震分组为第一组,设计基本地震加速度为0.15g。
分别求厂房在多遇地震和罕遇地震时水平地震作用。
GG2.图2为两层房屋计算简图,楼层集中质量分别为m1=120t,m2=80t,楼板刚度无穷大,楼层剪切刚度系数分别为k1= 5 xi04kN/m , k2= 3 xi04kN/m。
求体系自振频率和振型, 并验算振型的正交性。
m2k2 k1图2两层房屋计算简图3.钢筋混凝土3层框架计算简图如图3所示。
分别按能量法和顶点位移法计算结构的基本自振周期(取填充墙影响折减系数为0.6 )。
3图3 3层框架计算简图4.钢筋混凝土 3层框架经质量集中后计算简图如图4所示。
各层高均为5米,各楼层集中质量代表值分别为:G1=G2=750kN,G3=500kN ;经分析得结构振动频率和振型如图4所示。
结构阻尼比Z= 0.05 , I 类建筑场地,设计地震分组为第一组,设计基本地震加速度为0.10g 。
试按振型分解反应谱法确定结构在多遇地震时的地震作用效应,绘出层间 地震剪力图。
图4计算简图5. 已知条件和要求同上题,试按底部剪力法计算。
1、表1为某建筑场地的钻孔资料,试确定该场地的类别。
m 3180 10 kgm 2270 103kgk39800kN / mm 1270 103kgn/" / / 才k 2195000kN/mk 1245000kN / m• G3-1.."10.22rad /s338.37rad / s[./x'J..227.94rad /s3层底深度土层厚度岩土名称土层剪切波速/(m/s)20米的丙类建筑的场地地质钻孔资料如表 2所示(无剪切波速解: 覆盖层厚度达22m ,故取20m 深度计算,共有五个土层:t3d 3V s3 V 5d 5 V s5V sl5 220 4 290平均剪切波速:—0.01875 160 0.022730.01379V sed 。
midas抗震设计例题
midas抗震设计例题一、引言地震是一种自然灾害,其能量巨大,破坏力极强。
为了提高建筑物的抗震性能,减少地震对建筑物的破坏,抗震设计是建筑设计中必不可少的一环。
本文以midas抗震设计为例,介绍如何进行抗震设计以及注意事项。
二、设计流程1.确定建筑物的用途和重要性,根据相关规范进行抗震设防分类。
2.根据地震危险性分析结果,确定建筑物所处地区的地震基本烈度。
3.根据建筑物的高度、结构形式、使用功能等因素,选择合适的抗震设计方法。
4.进行结构分析,确定结构的刚度、承载力和延性等性能指标。
5.进行抗震措施设计,包括构造措施、材料选用、施工要求等。
三、midas软件应用midas是一款广泛应用于结构工程领域的有限元分析软件,可用于抗震设计。
以下是在midas中进行抗震设计的一般步骤:1.建立模型:根据建筑物结构形式建立三维有限元模型,并进行模型验证。
2.施加地震荷载:根据地震基本烈度,施加相应地震荷载。
3.进行结构分析:对模型进行地震响应分析,得到结构的响应曲线和变形情况。
4.调整结构参数:根据分析结果,调整结构参数,优化结构性能。
5.输出结果:得到结构在地震作用下的变形、应力、损伤等结果,并进行评估。
四、注意事项1.抗震设计应遵循相关规范和标准,确保结构设计符合抗震要求。
2.在进行结构分析时,应考虑地震动的影响,选择合适的地震动输入。
3.在进行结构参数调整时,应综合考虑结构的刚度、承载力和延性等性能指标,确保结构在地震作用下具有足够的抗震性能。
4.在进行抗震设计时,应注重构造措施的设计和实施,如加强连接节点、保证梁柱截面尺寸等。
5.对于特殊结构或重要部位,应进行专门的地震响应分析,采取针对性的抗震措施。
总之,抗震设计是建筑设计中必不可少的一环,在进行抗震设计时,应注重结构分析和参数调整,确保结构在地震作用下具有足够的抗震性能。
同时,应注重构造措施的设计和实施,以保证建筑物的安全和稳定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例题2.1 已知某建筑场地的钻孔资料如下表所示,试确定该场地的类别。
土层底部深度/m
土层厚度/m 岩土名称 土层剪切波速/(m/s ) 2.00
2.00 杂填土 220 5.00
3.00 粉土 300 8.50
3.50 中砂 390 15.70 7.20 碎石土 550
解:因为距地面8.5m 以下土层的剪切波速vs=550m/s>500m/s ,故场地覆盖层厚度d0v=8.5m ,又d0v < 20m ,所以土层计算深度d0 =8.5m 。
t = 2.0/220+3.0/300+3.5/390 = 0.028(s )
vse =
d0 /t = 8.5/0.028 = 303.6(m/s )
查表2-1,vse 位于250~500m/s 之间,且d0v >5m ,因此该场地的类别为Ⅱ类。
【例题3.1】如图3.1(a)所示单跨单层厂房,屋盖刚度无穷大,屋盖自重标准值为880 kN 屋面雪荷载标准值为200kN ,雪荷载组合值系数为0.5,忽略柱自重,柱抗侧移刚度系致 k1 = k2= 3.0×103 kN/m ,结构阻尼比ζ=0.05,I 类建筑场地,设计地震分组为第二组,设计基本地震加速度为0.02g ,抗震设防烈度为8度,求厂房在多遇地震时水平地震作用。
【解】因质量集中于屋盖,所以结构计算时可简化为图3.1(b )所示的单质点体系。
⑴确定重力荷载代表值G 和自振周期T 。
已知雪荷载组合值系数为0.5,所以G = 880+200×0.5 = 980(kN )
质点集中质量
柱抗侧移刚度为两柱抗侧移刚度之和:
于是得结构自振周期为
⑵确定地震影响系数最大值αmax 和特征周期Tg 。
当设计基本地震加速度为0.20g 时,抗震设防烈度为8度。
由表3-1查得,在多遇地震时,αmax=0.16。
kg s m kN g G m 3210100/8.9980⨯===m
N m kN k k k /100.6/100.66
321⨯=⨯=+=)(811.0100.6101002263
s k m T =⨯⨯==ππ
由表3-2查得,在I 类场地、设计地震第二组时,Tg=0. 30s 。
⑶计算地震影响系数α值。
因Tg<T<5Tg ,所以α处于曲线下降段,α的计算公式为
当阻尼比 ζ = 0.05时,式3-47 和式3-49可得 γ = 0.9,η = 1,则
⑷计算水平地震作用。
由式3-50得
[例题3.2] 如图3.2(a )所示的二层框架结构,横梁刚度无限大,集中于楼面和屋面的质量分别为m1=100t ,m2=50t ,各楼层层间剪切刚度为k1=4×104kN/m ,k2=2×104kN/m 。
求结构的自振频率和振型。
[解] 将结构简化为图3.2(b )所示的两自由度弹性体系。
(a)二层框架 (b)计算简图 (c) k11、k21计算 (d )k12、k22计算 结构的质量矩阵为
根据刚度系数的定义,分别使质点1和质点2产生单位水平位移,如图3.2(c 、d ),则
于是刚度矩阵为: max 2αηαγ⎪⎪⎭⎫ ⎝⎛=T T g 065.016.00.1811.03.09.0max 2=⨯⨯⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=αηαγT T g kN kN G F 7.63980065.0=⨯=∙
=α[]()t m m m ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=50001000021)/(10642111m KN k k k ⨯=+=)/(102422112m KN k k k ⨯-=-==)
/(10242
22m KN k k ⨯==
频率方程为:
将上式展开得
解上列方程式得
体系自振圆频率为
相对于第一阶频率ω1
即:
由上式得第一振型幅值的相对比值为
同理,第一振型幅值的相对比值为
[])/(102226422211211m KN k k k k k ⨯⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡=050102102102100106244424222221122111=-⨯⨯-⨯--⨯=--ωωωωm k k k m k 010161000)(4222=⨯+-ωω800,2002221==ωωs rad s rad /28.28,/14.1421==ωω[][]{}0)(121=-X m k ω012112122221122
1111=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡--X X m k k k m k ωω1210210620010044
12112111112=⨯-⨯-⨯=-=k k m X X ω1
110210680010044
12112212122-=⨯-⨯-⨯=-=k k m X X ω
因此,第一振型为
第二振型为
振型图分别示于下图
第一振型 第二振型
3.3试用底部剪力法计算图3所示三质点体系在多遇地震下的各层地震剪力。
已知设计基本加速度为0.2g ,Ⅲ类场地一区,m1=116.62×103kg ,
m2=110.85×103kg , m3=59.45×103kg ,
T1=0.716s ,δn=0.0673。
解:查表3-2,3-3得 {}{}
⎭
⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧=11212221212111X X X X X X
又因
所以
因
s T g 45.0=16.0max =αg
T T 4.11>s T s g 55.035.0≤<0673.001.008.01=+=T n δg g T T T 51<<()1053.016.0716.045.09.0=⨯=α()kN m g G eq
04.23901045.5985.11062.1168.985.085.03
=⨯++⨯⨯==∑kN G F eq Ek 67.25104.23901053.0=⨯==α()()67.2510673.015.1745.595.1285.1105.662.1165.662.1161111⨯-⨯+⨯+⨯⨯=-=∑Ek n i i F H G H G F δkN 88.55=()()67.2510673.015.1745.595.1285.1105.662.1165.1285.1101222⨯-⨯+⨯+⨯⨯=-=∑Ek n i i F H G H G F δkN 15.102=()()67.2510673.015.1745.595.1285.1105.662.1165.1745.591333⨯-⨯+⨯+⨯⨯=-=∑Ek n i i F H G H G F δkN 7.76=kN F F Ek n n 94.1667.2510673.0=⨯==∆δkN F F V n 64.9394.167.7633=+=∆+=kN F V V 79.19515.10264.932
32=+=+=kN F V V 67.25188.5579.195121=+=+=
5.4为什么要限制框架柱的轴压比?
答:柱轴压比过大时,箍筋对柱延性的影响很小,柱多产生脆性破坏。
5.5抗震设计为什么要尽量满足“强梁弱柱”、“强剪弱弯”、“强节点弱构件”的原则?如何满足这些要求?
答:满足这些原则就能保证结构不产生危及结构安全的脆性破坏和结构的倒塌;通过调整地震下结构内力(增大柱上的设计弯矩和构件上的设计剪力,对节点进行抗震验算)来满足这些要求。
