(精品-1)贵州省六盘水市第十三中学八年级数学下学期第三次周周清(无答案) 北师大版
八年级下第三周周练数学试卷(有答案)

八年级下第三周周练数学试卷(有答案)一、选择(3*8=24)1.下列各式中,①,②,③,④﹣,⑤,⑥x+y,⑦=,⑧,分式个数为()A.3个 B.4个 C.5个 D.6个2.点M(﹣3,2)关于y轴对称的点的坐标为()A.(﹣3,﹣2)B.(3,﹣2)C.(3,2) D.(﹣3,2)3.下列可以判定两个直角三角形全等的条件是()A.斜边相等B.面积相等C.两对锐角对应相等D.两对直角边对应相等4.下列分式,,,,中,最简分式的个数是()A.1个 B.2个 C.3个 D.4个5.当x为任意实数时,下列分式一定有意义的是()A. B. C.D.6.下列式子计算正确的是()A. B.C. D.7.将中的a、b都扩大为原来的4倍,则分式的值()A.不变B.扩大原来的4倍C.扩大原来的8倍 D.扩大原来的16倍8.已知关于x的分式方程=1的解是非正数,则a的取值范围是()A.a≤﹣1 B.a≤1且a≠﹣2 C.a≤﹣1且a≠﹣2 D.a≤1二、填空(每空2分,20)9.要使分式无意义,则x的取值范围是.10.分式表示一个正整数时,整数m可取的值是.11.填写出未知的分子或分母:(1).(2).12.若,则m=,n=.13.若﹣=2,则的值是.14.已知==,则=.15.若关于x的方程有增根,则k的值为.16.若关于x的分式方程﹣2=无解,则m=.三、解答题17.计算:(1)﹣(2)•(3)÷(4)﹣a+b.18.解分式方程:(1)﹣=0(2)+1=.(3)5+=﹣.19.先化简÷(a+1)+,然后a在﹣1、1、2三个数中任选一个合适的数代入求值.20.关于x的分式方程=﹣1的解为非负数,求k的取值范围.21.已知2x﹣3y+z=0,3x﹣2y﹣6z=0,且xyz≠0,求的值.22.已知:一次函数y=2x+b.(1)如果它的图象与一次函数y=﹣2x+1和y=x+4的图象交于同一点,求b的值;(2)如果它的图象与坐标轴所围成的图象的面积等于4,求b的值.23.观察下列各式:(1)由此可推测=;(2)试猜想此类式子的一般规律.用含字母m的等式表示出来.并说明理由(m表示整数);(3)请直接用(2)中的规律计算的值.24.如图1,已知一次函数y=﹣x+6分别与x、y轴交于A、B两点,过点B的直线BC交x 轴负半轴与点C,且OC=OB.(1)求直线BC的函数表达式;(2)如图2,若△ABC中,∠ACB的平分线CF与∠BAE的平分线AF相交于点F,求证:∠AFC=∠ABC;(3)在x轴上是否存在点P,使△ABP为等腰三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.八年级(下)第三周周练数学试卷参考答案与试题解析一、选择(3*8=24)1.下列各式中,①,②,③,④﹣,⑤,⑥x+y,⑦=,⑧,分式个数为()A.3个 B.4个 C.5个 D.6个【考点】分式的定义.【分析】判断一个式子是否是分式,关键要看分母中是否含有字母,然后对分式的个数进行判断【解答】解:②,④﹣,⑤,⑧的分母中均含有字母,属于分式,其它不符合条件,故选:B.2.点M(﹣3,2)关于y轴对称的点的坐标为()A.(﹣3,﹣2)B.(3,﹣2)C.(3,2) D.(﹣3,2)【考点】关于x轴、y轴对称的点的坐标.【分析】根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变.即点P(x,y)关于y轴的对称点P′的坐标是(﹣x,y),可以直接得到答案.【解答】解:点M(﹣3,2)关于y轴对称的点的坐标为(3,2),故选:C.3.下列可以判定两个直角三角形全等的条件是()A.斜边相等B.面积相等C.两对锐角对应相等D.两对直角边对应相等【考点】直角三角形全等的判定.【分析】根据判定直角三角形全等的条件:SAS、ASA、AAS、HL进行分析即可.【解答】解:A、斜边相等,缺少一个条件,不能证明两个直角三角形全等,故此选项错误;B、面积相等,不能证明两个直角三角形全等,故此选项错误;C、两对锐角对应相等,缺少边相等的条件,不能证明两个直角三角形全等,故此选项错误;D、两对直角边对应相等,可利用SAS定理证明两个直角三角形全等,故此选项正确;故选:D.4.下列分式,,,,中,最简分式的个数是()A.1个 B.2个 C.3个 D.4个【考点】最简分式.【分析】根据分子和分母是否存在公因式进行判断,没有公因式的为最简分式.【解答】解:的分子与分母存在公因式x,此分式不是最简分式;的分母分解因式可得2(m+2),分子与分母存在公因式2,此分式不是最简分式;的分子与分母都没有公因式,这两个分式为最简分式;的分子分解因式可得(b﹣2)(b+2),分子与分母存在公因式(b+2),此分式不是最简分式;的分子可变形为﹣(b﹣a),分子与分母存在公因式(b﹣a),此分式不是最简分式.最简分式只有1个,故选A.5.当x为任意实数时,下列分式一定有意义的是()A. B. C.D.【考点】分式有意义的条件.【分析】根据分式有意义,分母不等于0对各选项分析判断即可得解.【解答】解:A、x=0时,分母等于0,分式无意义,故本选项错误;B、x=0时,分母等于0,分式无意义,故本选项错误;C、∵x2≥0,∴x2+1≥1,∴x为任意实数,分式一定有意义,故本选项正确;D、x=±2时,分母等于0,分式无意义,故本选项错误.故选C.6.下列式子计算正确的是()A. B.C. D.【考点】分式的乘除法;约分;分式的加减法.【分析】根据分式的乘除、加减运算法则,约分的知识点进行解答.【解答】解:A、,A错;B、,B正确;C、,C错;D、,D错.故选B.7.将中的a、b都扩大为原来的4倍,则分式的值()A.不变B.扩大原来的4倍C.扩大原来的8倍 D.扩大原来的16倍【考点】分式的基本性质.【分析】根据分式的分子分母都乘以(或除以)同一个不为零,分式的值不变,可得答案.【解答】解:中的a、b都扩大为原来的4倍,则分式的值扩大为原来的4倍,故选:B.8.已知关于x的分式方程=1的解是非正数,则a的取值范围是()A.a≤﹣1 B.a≤1且a≠﹣2 C.a≤﹣1且a≠﹣2 D.a≤1【考点】分式方程的解;解一元一次不等式.【分析】先解分式方程,再根据解为非正数,得出a的取值范围即可.【解答】解:a+2=x+1,解得x=a+1,∵解为非正数,∴a+1≤0,∴a≤﹣1,∵x+1≠0,∴x≠﹣1,∴a+1≠﹣1,∴a≠﹣2,∴a的取值范围是a≤﹣1且a≠﹣2故选C.二、填空(每空2分,20)9.要使分式无意义,则x的取值范围是x=﹣1.【考点】分式有意义的条件.【分析】根据分式无意义,分母等于0列方程求解即可.【解答】解:∵分式无意义,∴x+1=0,解得x=﹣1.故答案为:x=﹣1.10.分式表示一个正整数时,整数m可取的值是m=﹣2或﹣2或1或5.【考点】分式的值.【分析】根据题意把问题转化为方程即可解决问题.【解答】解:∵分式表示一个正整数,∴m+3=1或2或4或8,∴m=﹣2或﹣2或1或5.故答案为m=﹣2或﹣2或1或5.11.填写出未知的分子或分母:(1).(2).【考点】分式的基本性质.【分析】(1)分子、分母同时乘以(x﹣y);(2)分子、分母同时除以(y+1).【解答】解:(1)观察等式两边分式的分母知,原分式的分子、分母同时乘以(x﹣y),分式的值不变.故答案是:3x(x﹣y);(2)原式==.故答案是:y+1.12.若,则m=3,n=1.【考点】分式的加减法.【分析】已知等式右边通分并利用同分母分式的加法法则计算,列出关系式,求出m与n的值即可.【解答】解:∵=+=,∴4a﹣1=m(a﹣1)+n(a+2)=(m+n)a+2n﹣m,∴m+n=4,2n﹣m=﹣1,解得:m=3,n=1,故答案为:3;113.若﹣=2,则的值是.【考点】分式的加减法.【分析】先将﹣=2进行通分,然后化为x﹣y=2xy,然后将原式进行适当的变形后将x﹣y 代入即可求出答案.【解答】解:由题意可知:y﹣x=2xy即x﹣y=﹣2xy,∴原式===故答案为:14.已知==,则=4.【考点】比例的性质.【分析】根据等比性质,可得答案.【解答】解:设===k,得x=3k,y=4k,z=5k.==4,故答案为:4.15.若关于x的方程有增根,则k的值为﹣或3.【考点】分式方程的增根.【分析】增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母(x+3)(x﹣3)=0,得到x=﹣3或3,然后代入化为整式方程的方程算出k的值.【解答】解:方程两边都乘(x+3)(x﹣3),得x+3+k(x﹣3)=3+k∵原方程有增根,∴最简公分母(x+3)(x﹣3)=0,解得x=﹣3或3,当x=﹣3时,k=﹣,当x=3时,k=3,故a的值可能是﹣,3.故答案为﹣或3.16.若关于x的分式方程﹣2=无解,则m=.【考点】分式方程的解.【分析】分式方程无解的条件是:去分母后所得整式方程无解,或解这个整式方程得到的解使原方程的分母等于0.【解答】解:去分母,得x﹣2(x﹣3)=m2,把x=3代入得3﹣2(3﹣3)=m2,解得:m=±.故答案是:.三、解答题17.计算:(1)﹣(2)•(3)÷(4)﹣a+b.【考点】分式的混合运算.【分析】(1)先找出最简公分母,然后通分化简即可.(2)根据分式的乘法法则即可求出答案(3)先将分子分母进行因式分解,然后根据分式的乘法法则即可求出答案(4)先通分,然后根据分式加减运算法则即可求出答案.【解答】解:(1)原式=﹣==(2)原式=(3)原式=•=(4)原式=﹣(a﹣b)==18.解分式方程:(1)﹣=0(2)+1=.(3)5+=﹣.【考点】解分式方程.【分析】解分式方程的步骤为:①去分母;②求出整式方程的解;③检验;④得出结论.【解答】解:(1)去分母,得(x﹣5)(x﹣1)﹣(x+1)(x﹣3)=0,即﹣4x+8=0,解得x=2,经检验:x=2是原方程的解,∴原方程的解为x=2;(2)原方程可化为+1=去分母,得15x﹣12+3x﹣6=4x+10,解得x=2,经检验:x=2是原方程的增根,∴原方程无解;(3)原方程可化为5+=+去分母,得5(x+4)(x﹣4)+96=(2x﹣1)(x﹣4)+(3x﹣1)(x+4),解得x=8,经检验:x=8是原方程的解,∴原方程的解为x=8.19.先化简÷(a+1)+,然后a在﹣1、1、2三个数中任选一个合适的数代入求值.【考点】分式的化简求值.【分析】先根据分式混合运算的法则把原式进行化简,再选取合适的a的值代入进行计算即可.【解答】解:原式=•+=+=,当a=2(a≠﹣1,a≠1)时,原式==5.20.关于x的分式方程=﹣1的解为非负数,求k的取值范围.【考点】分式方程的解;解一元一次不等式.【分析】首先解关于x的方程,利用方程的解是非负数,以及分式方程的分母不等于0列不等式求得k的范围.【解答】解:方程两边同时乘以(x﹣1)(x+2)得:(5﹣x)(x﹣1)=k﹣(x﹣1)(x+2),即6x﹣x2﹣5=k﹣x2﹣x+2,移项,得﹣x2+x2+6x+x=2+5﹣k,合并同类项,得7x=7﹣k,系数华为1得x=,根据题意得:≥0且≠﹣2,≠1,解得:k≤7且k≠0.21.已知2x﹣3y+z=0,3x﹣2y﹣6z=0,且xyz≠0,求的值.【考点】分式的值;解二元一次方程组.【分析】把z看成已知数,求出x、y,然后代入所求代数式进行化简即可.【解答】解:由题可得,解得,∴===.22.已知:一次函数y=2x+b.(1)如果它的图象与一次函数y=﹣2x+1和y=x+4的图象交于同一点,求b的值;(2)如果它的图象与坐标轴所围成的图象的面积等于4,求b的值.【考点】两条直线相交或平行问题.【分析】(1)由题意可知:三条直线交于一点,所以可先根据一次函数y=﹣2x+1与y=x+4求出该交点坐标.(2)分别求出一次函数y=2x+b与坐标轴的交点,然后根据它的图象与坐标轴所围成的图象的面积等于4列出方程即可求出b的值.【解答】解:(1)联立,∴解得:把(﹣1,3)代入y=2x+b,∴3=﹣2+b,∴b=5,(2)令x=0代入y=2x+b,∴y=b,令y=0代入y=2x+b,∴x=﹣,∵y=2x+b的图象与坐标轴所围成的图象的面积等于4∴×|b|×|﹣|=4,∴b2=16,∴b=±423.观察下列各式:(1)由此可推测=;(2)试猜想此类式子的一般规律.用含字母m的等式表示出来.并说明理由(m表示整数);(3)请直接用(2)中的规律计算的值.【考点】规律型:数字的变化类.【分析】(1)由已知各等式的规律可以总结得出=﹣;(2)由已知各等式的规律可以总结得出,再根据分式通分可以计算证明结论:=﹣;(3)由(2)总结规律可以容易求出各式运算结果得零.【解答】解:(1)==﹣∴=﹣(2)猜想:=﹣.理由如下:﹣=﹣==(3)原式=﹣﹣(﹣)+﹣=024.如图1,已知一次函数y=﹣x+6分别与x、y轴交于A、B两点,过点B的直线BC交x 轴负半轴与点C,且OC=OB.(1)求直线BC的函数表达式;(2)如图2,若△ABC中,∠ACB的平分线CF与∠BAE的平分线AF相交于点F,求证:∠AFC=∠ABC;(3)在x轴上是否存在点P,使△ABP为等腰三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.【考点】一次函数综合题.【分析】(1)根据自变量与函数值的对应关系,可得A、B、C点的坐标,根据待定系数法,可得函数解析式;(2)根据角平分线的性质,可得∠FCA=∠BCA,∠FAE=∠BAE,根据三角形外角的关系,可得∠BAE=∠ABC+∠BCA,∠FAE=∠F+∠FCA,根据等式的性质,可得答案;(3)根据等腰三角形的定义,分类讨论:AB=AP=10,AB=BP=10,BP=AP,根据线段的和差,可得AB=AP=10时P点坐标,根据线段垂直平分线的性质,可得AB=BP=10时P点坐标;根据两点间的距离公式,可得BP=AP时P点坐标.【解答】解:(1)当x=0时,y=6,即B(0,6),当y=0时,﹣x+6=0,解得x﹣8,即A(8,0);由OC=OB,得OC=3,即C(﹣3,0);设BC的函数解析式为,y=kx+b,图象过点B、C,得,解得,直线BC的函数表达式y=2x+6;(2)证明:∵∠ACB的平分线CF与∠BAE的平分线AF相交于点F,∴∠FCA=∠BCA,∠FAE=∠BAE.∵∠BAE是△ABC的外角,∠FAE是△FAC的外角,∴∠BAE=∠ABC+∠BCA,∠FAE=∠F+∠FCA.∴∠ABC+∠BCA=∠F+∠BCA,∠ABC=∠F;(3)当AB=AP=10时,8﹣10=﹣2,P1(﹣2,0),8+10=18,P2(18,0);当AB=BP=10时,AO=PO=8,即P3(﹣8,0);设P(a,0),当BP=AP时,平方,得BP2=AP2,即(8﹣a)2=a2+62化简,得16a=28,解得a=,P4(,0),综上所述:P1(﹣2,0),P2(18,0),P3(﹣8,0);P4(,0).2017年4月18日。
八年级数学第三次周测试题试题

ABCDMN 图2A BCDF EO图4OD CBA 图9A BCEF尚西中学2021-2021学年八年级第三次周测数学试题〔无答案〕 新人教版创 作人:历恰面 日 期: 2020年1月1日:〔每一小题4分一共40分〕1.如图1,假设△ABC ≌△ADE ,∠EAC=35°,那么∠BAD=_________度.2.如图2,沿AM 折叠,使D 点落在BC 上的N 点处,假如AD=7cm ,DM=5cm , ∠DAM=300,那么AN= cm ,NM= cm ,∠NAM= . 3.:如图3,∠ABC =∠DEF ,AB =DE ,要说明△ABC ≌△DEF ,〔1〕假设以“SAS 〞为根据,还须添加的一个条件为________________. 〔2〕假设以“ASA 〞为根据,还须添加的一个条件为________________. 〔3〕假设以“AAS 〞为根据,还须添加的一个条件为________________.4.如图4,在△ABC 中,∠C =90°AD 平分∠BAC ,DE ⊥AB 于E ,那么△___≌△____. .如图5,在ABC ∆中,90,,A AB AC CD ∠=︒=平分ACB ∠,DE BC ⊥于E ,假设15cm BC =,那么DEB △的周长为 cm .6. 如图6,在ABC ∆中,AB=AC ,BE 、CF 是中线,那么由 可得AEB AFC ∆≅∆.AB CDE图1A BC DEFBCA DEA PCBEF D B C E P A 图15CEDBOA图 5 图6 图 7 图87. 如图7,AB=CD ,AD=BC ,O 为BD 中点,过O 点作直线与DA 、BC 延长线交于E 、 F ,假设︒=∠60ADB ,EO=10,那么∠DBC= ,FO= .8. 如图8,△DEF ≌△ABC ,且AC >BC >AB ,那么在△DEF 中,_____< _____< ___. 9.如图9,∠A=∠D=90°,AC=DB,欲使OB=OC,可以先利用“HL〞 说明 ≌ 得到AB=DC,再利用“ 〞证明△AOB≌ 得到OB=OC. △ABC的角平分线,DE⊥AB于E,且DE=3cm , 那么点D到AC的间隔 为 . 二.选择题(每一小题4分,一共40分)11.如图10,P 是∠BAC 的平分线AD 上一点,PE ⊥AB 于E ,PF ⊥AC 于F ,以下结论中不正确的选项是〔 〕 图10A .PE PF =B .AE AF =C .△APE ≌△APFD .AP PE PF =+12.如图11,在CD 上求一点P ,使它到OA ,OB 的间隔 相等 ,那么P 点是 〔 〕A. 线段CD 的中点B. OA 与OB 的中垂线的交点 图11C. OA 与CD 的中垂线的交点D. CD 与∠AOB 的平分线的交点13 假如两个三角形中两条边和其中一边上的高对应相等,那么这两个三角形的第三条边 所对的角的关系是〔 〕A. 相等 B. 不相等 C. 互余或者相等 D. 互补或者相等14. 如图13,AB =DC ,AD =BC ,E.F 在DB 上两点且BF =DE ,假设∠AEB =120°,∠ADB°°° D. 90° B C B C F_ B_ D_ O_ C_ A图13 图14 图16 图17 15.如图14.△ABC 中,AB =AC ,BD ⊥AC 于D ,CE ⊥ 16.根据以下条件,能唯一画出△ABC的是〔 〕〔A〕AB=3,BC=4,AC=8 〔B〕AB=4,BC=3,∠A=30° 〔C〕∠A=60°,∠B=45°,AB=4 〔D〕∠C=90°,AB=6 17.如图15,等边△ABC中,BD=CE,AD与BE交于点P,那么∠APE的度数为〔 〕.〔A〕70° 〔B〕60° 〔C〕40° 〔D〕30°18.三角形中到三边间隔 相等的点是〔 〕A 、三条边的垂直平分线的交点 B 、三条高的交点 C 、三条中线的交点 D 、三条角平分线的交点 19.如图16,直线l 1,l 2,l 320.如图17,OA=OB,OC=OD, ∠O=60°, ∠C=25°那么∠BED 的度数是 ( )° B. 85° C. 65° D. 以上都不对三.解答题(每一小题9分,一共36分)19.〔8分〕:如图,A 、C 、F 、D 在同一直线上,AF =D C ,AB =DE ,BC =EF ,求证:△ABC ≌△DEF .21.〔8分〕:如图,AB =AC ,BD ⊥AC ,CE ⊥AB ,垂足分别为D 、E ,BD 、CE 相交于点F ,求证:BE =CD .ACB DEF l 2l 1l 3BCDEF A22.〔8分〕如图,在△ABC 中,AD 为∠BAC 的平分线,DE ⊥AB 于E ,DF ⊥AC 于F ,△ABC面积是282cm ,AB =20cm ,AC =8cm ,求DE 的长.BDC。
贵州省六盘水市第十三中学八年级数学上册33轴对称与坐标变化导学案(无答案)(新版)北师.docx
3. 3轴对称与坐标变化
章节 3.3 轴对称与坐标变化
学生学习內容及耍求学悄预设
学习目标
法制1、了解图形的变化与相应各点的坐标变化之间的关系,发展数形结合肓•识.
2、疳寿坐标系小,以处标轴为对称轴,能写出一个己知顶点坐标的多边形的对称图形的顶点坐标,并知道对应顶点坐标Z间的关系。
《中华人民共和国国徽法》第二条:中华人民共和国国徽,中间是五星照耀下的天安门,周围是谷穗和齿轮。
第三条:中华人民
渗透点共和国国徽是中华人民共和国的象征和标志。
一切组织和公民,都应当尊重和爱护国徽。
学法指导:结合教材和预习学案,先独立思考,遇到困难小对了Z间进
行帮扶,完成学习任务。
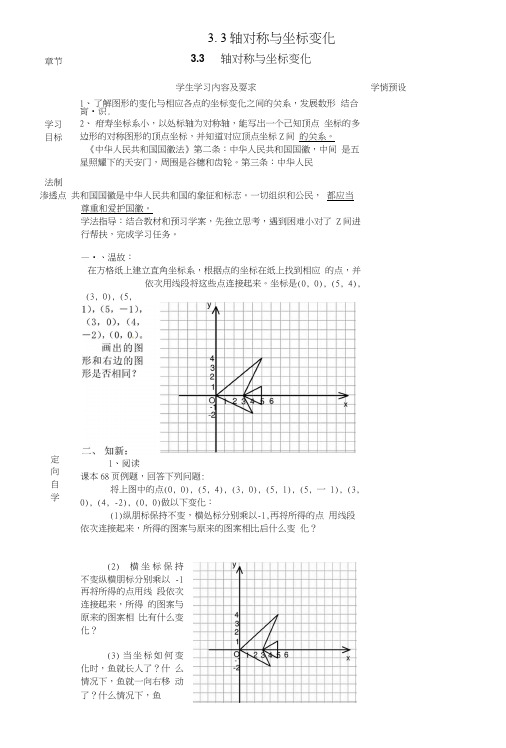
—•、温故:
在方格纸上建立直角坐标系,根据点的坐标在纸上找到相应的点,并
依次用线段将这些点连接起来。
坐标是(0, 0), (5, 4),
定向自学
(3, 0), (5,
1、阅读
课本68页例题,回答下列问题:
将上图中的点(0, 0), (5, 4), (3, 0), (5, 1), (5, 一1), (3,
0), (4, -2), (0, 0)做以下变化:
(1)纵朋标保持不变,横处标分别乘以-1,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比启什么变化?
(2)横坐标保持
不变纵横朋标分别乘以-1,
再将所得的点用线段依次
连接起来,所得的图案与
原来的图案相比有什么变
化?
(3)当坐标如何变
化时,鱼就长人了?什么
情况下,鱼就一向右移动
了?什么情况下,鱼。
贵州省六盘水市第十三中学八年级数学下册 3.3 中心对称导学案(无答案)北师大版
留给学生充足的时间讨论交流。
检查
讨论
小组合作讨论预习中出现的问题,不能解决的提交全班讨论完成。定向自学中发现的新问题提交小组讨论解决发现的问题,处理的结果
展示
反馈
小组展示(自选)定向自学的内容;课本83页的随堂练习,习题3.6的1题,2题,3题
反思
总结
预习内容:3.4简单的图案设计其它方式吗?图3—3—1
解:
二、知新:
归纳:图形变换中最基本的三种变换方式,,。
三、学点训练:
“想一想”你能将下图中的左图,通过平移或旋转得到右图吗?
答:
。
例1怎样将下图中的甲图案变成乙图案?
甲乙
解:
2、阅读课本81页理解“中心对称”和“两个图形成中心对称”这两个定义
3、观察图形3——20(课本81页),学习课本82页的例题理解中心对称的性质。
1.复习平移、旋转、轴对称、和中心对称的概念
2.掌握平移的基本性质、旋转的性质、和中心对称的性质
中心对称
章节
第三章3.3中心对称
环节
学生学习内容及要求
学情预设
学习
目标
1、
学法指导:结合教材和预习学案,先独立思考,遇到困难小对子之间进行帮扶,完成学习任务。
定
向
自
学
1、温故:
图3—3—1由四部分组成,
每部分都包括两个小“十”字,
其中一部分能经过适当的旋转
得到其他三部分吗?能经过平
移吗?能经过轴对称吗?还有
2023-2024学年贵州省六盘水市八年级(下)期末数学试卷(含答案)

2023-2024学年贵州省六盘水市八年级(下)期末数学试卷一、选择题:本题共12小题,每小题3分,共36分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.下列各实数中,无理数是( )A. 73B. π C. 9 D. 3.3⋅32.下列图形是中心对称图形的是( )A. B. C. D.3.六盘水市位于贵州西部乌蒙山区,是国家“三线”建设时期发展起来的一座能源原材料工业城市,六盘水市共辖4个县级行政区(六枝特区、盘州市、水城区、钟山区),全市总人口数约3618200人,将3618200这个数用科学记数法表示是( )A. 36.182×105B. 3.6182×105C. 3.6182×106D. 0.36182×1074.已知等腰三角形的一边长为8,另一边长为5,则它的周长是( )A. 18B. 21C. 18或21D. 265.若a<b,则下列不等式正确的是( )A. a−b<0B. a−8>b+8C. −5a<−5bD. a2>b26.下列等式从左到右的变形中,属于因式分解的是( )A. (m+n)(m−n)=m2−n2B. m2+2m+1=(m+1)2C. m2+2m−1=m(m+2)−1D. m(m−2)=m2−2m7.在平面直角坐标系中,点P(2,−3)在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限8.在一次体检中,测得某校八(1)班第一组同学的体重(单位:kg)分别为:48,55,58,55,52,50,56,60.则该组同学体重的中位数是( )A. 50kgB. 52kgC. 55kgD. 56kg9.若分式x−3x+4无意义,则实数x的值是( )A. x=3B. x=−3C. x=4D. x=−410.如图所示,在▱ABCD中,对角线AC,BD相交于点O,点E是BC的中点.若OE=6cm,则AB的长是( )A. 9cmB. 12cmC. 15cmD. 18cm11.如图,在已知的△ABC中,按以下步骤作图:①分别以点B和点C为圆心,以大于12BC的长为半径作弧,两弧相交于点M,N;②作直线MN交AB于点D,连接CD.若点D是AB的中点,则∠ACB的度数是( )A. 90°B. 95°C. 100°D. 105°12.如图,点A1,A2,A3…在直线y=x上,点C1,C2,C3…在直线y=2x上,以它们为顶点依次构造第一个正方形A1C1A2B1,第二个正方形A2C2A3B2…,若点A2的横坐标是1,则点B6的坐标是( )A. (6,6)B. (6,12)C. (32,16)D. (64,32)二、填空题:本题共4小题,每小题4分,共16分。
2024-2025学年八年级数学上学期第三次月考卷(贵州专用,人教版第十一章~第十四章)(全解全析)

2024-2025学年八年级数学上学期第三次月考卷(贵州专用)(考试时间:120分钟试卷满分:150分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:人教版八年级上册第11章~第14章(第11章24%,第12章16%,第13章32%,第14章28%)。
5.难度系数:0.58。
第一部分(选择题共36分)一、选择题:本题共12小题,每小题3分,共36分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.“二十四节气”是中华农耕文明的智慧结晶,如图四幅作品分别代表“立春”“惊蛰”“清明”“小满”,其中是轴对称图形的是( )A.B.C.D.【答案】A【详解】解:A、图形是轴对称图形,故A符合题意;B、C、D中的图形不是轴对称图形,故B、C、D不符合题意.故选:A.2.下列运算正确的是( )A .(﹣a 2b )3=a 5b 3B .(3a )2+a 2=7a 2C .(x ﹣2y )(x +2y )=x 2﹣2y 2D .(x ﹣2)2=x 2﹣4x +4【答案】D【详解】解:A 、(﹣a 2b )3=﹣a 6b 3,不符合题意;B 、(3a )2+a 2=10a 2,不符合题意;C 、(x ﹣2y )(x +2y )=x 2﹣4y 2,不符合题意;D 、(x ﹣2)2=x 2﹣4x +4,符合题意,故选:D .3.在平面直角坐标系xOy 中,点A (2,4+m )与点B (m ,n )关于y 轴对称,则m +n 的值为( )A .0B .1C .2D .﹣1【答案】A【详解】解:∵点A (2,4+m )与点B (m ,n )关于y 轴对称,∴m =﹣2,4+m =n ,解得:n =2,则m +n 的值为:﹣2+2=0.故选:A .4.如图,∠BAC =90°,且AD ,AE ,BF 分别是△ABC 的高线,中线和角平分线,下列结论错误的是( )A .∠BAD =∠CB .∠ABF =∠CBFC .S △ABE =S △AECD .AF =CF【答案】D【详解】解:∵AD 是△ABC 的高线,∴∠ADC =90°,∵∠BAC =∠BAD +∠DAC =90°,∠DAC +∠C =180°﹣∠ADC =90°,∴∠BAD =∠C ,A 正确,故该选项不符合题意;∵BF 是△ABC 的角平分线,∴∠ABF =∠CBF ,B 正确,故该选项不符合题意;∵AE 是△ABC 的中线,∴BE =EC ,∵△ABE ,△AEC 的高相同,设为h ,∴,∴S △ABE =S △AEC ,C 正确,故该选项不符合题意;根据已知条件并不能证明AF =CF ,∴D 错误,故该选项符合题意,故选:D .5.根据下列已知条件,能唯一画出△ABC 的是( )A .AB =3,BC =4,AC =8B .∠A =60°,∠B =45°,AB =4C .AB =4,BC =3,∠A =30°D .∠C =90°,AB =64【答案】B【详解】解:对于选项A ,∵AB =3,BC =4,AC =8,∴AB +BC <AC ,∴该选项中的条件不能构成三角形,∴选项A 中的条件不能唯一画出△ABC ,故选项A 不合题意;对于选项B ,∵∠A =60°,∠B =45°,AB =4,满足全等三角形的判定“ASA ”,∴该选项中的条件能唯一画出△ABC,故选项B符合题意;对于选项C,∵AB=4,BC=3,∠A=30°,不满足全等三角形的判定,∴该选项中的条件不能唯一画出△ABC,故选项C不合题意;对于选项D,∵∠C=90°,AB=64,不满足全等三角形的判定,∴该选项中的条件不能唯一画出△ABC,故选项D不合题意.故选:B.6.为方便劳动技术小组实践教学,需用篱笆围一块三角形空地,现已连接好三段篱笆AB,BC,CD,这三段篱笆的长度如图所示,其中篱笆AB,CD可分别绕轴BE和CF转动.若要围成一个三角形的空地,则在篱笆AB上接上新的篱笆的长度可以为( )A.1m B.2m C.3m D.4m【答案】D【详解】解:设在篱笆AB上接上新的篱笆长度为x,根据题意得:AB=2m,BC=8m,CD=3m,∵BC﹣CD<AB+x<BC+CD,即5m<AB+x<11m,∴3m<x<9m,∴在篱笆AB上接上新的篱笆的长度可以为4m,故选:D.7.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC,AC于点D和E,∠B=60°,∠C=25°,则∠BAD为( )A.60°B.50°C.80°D.70°【答案】D【详解】解:∵∠B=60°,∠C=25°,∴∠BAC=180°﹣60°﹣25°=95°,∵DE是AC的垂直平分线,∴AD=CD,∴∠DAC=∠C=25°,∴∠BAD=∠BAC﹣∠DAC=95°﹣25°=70°.故选:D.8.如图,在等边三角形ABC中,BC=2,D是AB的中点,过点D作DF⊥AC于点F,过点F作EF⊥BC 于点E,则BE的长为( )A.1B.C.D.【答案】B【详解】解:∵△ABC为等边三角形,∴∠A=∠C=60°,AB=AC=BC=2,∵DF⊥AC,FE⊥BC,∴∠AFD=∠CEF=90°,∴∠ADF=∠CFE=30°,∴AF=AD,CE=CF,∵点D是AB的中点,∴AD=1,∴AF=,CF=,CE=,∴BE=BC﹣CE=2﹣=,故选:C.9.已知a+b=5,ab=﹣2,则a2﹣ab+b2的值是( )A.30B.31C.32D.33【答案】B【详解】解:∵a+b=5,ab=﹣2,∴a2﹣ab+b2=(a+b)2﹣3ab=25+6=31.故选:B.10.如图,已知△ABC的内角∠A=α,分别作内角∠ABC与外角∠ACD的平分线,两条平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;……以此类推得到∠A2018,则∠A2018的度数是( )A.B.C.D.90°+【答案】B【详解】解:∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,∴∠A1BC=∠ABC,∠A1CD=∠ACD,又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,∴(∠A+∠ABC)=∠ABC+∠A1,∴∠A1=∠A,∵∠A=α,∴∠A1=;同理可得∠A2=∠A1=•α=,∴∠A n=,∴∠A2018=.故选:B.11.将一个多项式分组后,可提公因式或运用公式继续分解的方法是分组分解法.例如:am+an+bm+bn=(am+an)+(bm+bn)=a(m+n)+b(m+n)=(a+b)(m+n).以下说法:①分解因式:x2y+x2﹣y﹣1=(x2﹣1)(y+1);②若a,b,c是△ABC的三边长,且满足a2+b2+c2=ac+ab+bc,则△ABC为等边三角形;③若a,b,c是△ABC的三边长,且满足a2﹣ab+c2=2ac﹣bc,则这三边能构成等腰三角形;正确的有( )个.A.3B.2C.1D.0【答案】B【详解】解:x2y+x2﹣y﹣1=y(x2﹣1)+(x2﹣1)=(x2﹣1)(y+1)=(x+1)(x﹣1)(y+1),故①错误;∵a2+b2+c2=ac+ab+bc,∴a2+b2+c2﹣ac﹣ab﹣bc=0,∴2a2+2b2+2c2﹣2ac﹣2ab﹣2bc=0,∴(a2﹣2ab+b2)+(a2﹣2ac+c2)+(b2﹣2bc+c2)=0,∴(a﹣b)2+(a﹣c)2+(b﹣c)2=0,又∵(a﹣b)2≥0,(a﹣c)2≥0,(b﹣c)2≥0,∴a﹣b=b﹣c=a﹣c=0,∴a=b=c,∴△ABC为等边三角形,故②正确;∵a2﹣ab+c2=2ac﹣bc,∴a2﹣ab+c2﹣2ac+bc=0,∴a2﹣2ac+c2﹣ab+bc=0,∴(a﹣c)2﹣b(a﹣c)=0,∴(a﹣c)(a﹣c﹣b)=0,∵a,b,c是△ABC的三边长,∴a<c+b,则a﹣c﹣b≠0,∴a﹣c=0,∴a=c,∴这三边能构成等腰三角形,故③正确;综上,②③正确;故选:B.12.如图,已知∠AOB=120°,点D是∠AOB的平分线上的一个定点,点E,F分别在射线OA和射线OB 上,且∠EDF=60°.下列结论:①△DEF是等边三角形;②四边形DEOF的面积是一个定值;③当DE⊥OA时,△DEF的周长最小;④当DE∥OB时,DF也平行于OA.其中正确的个数是( )A.1个B.2个C.3个D.4个【答案】C【详解】解:过点D作DM⊥于点M,DN⊥OA于点N,如图所示:∵点D是∠AOB的平分线上的一点,∴DM=DN,∵∠AOB=120°,∠DNO=∠DMO=90°,∴∠MDN=60°,∵∠EDF=60°,∴∠EDN=∠FDM,∴△DEN≌△DFM(ASA),∴DE=DF,∴△DEF 是等边三角形;故①正确;∴S △DEN =S △DFM ,∴S △DEN +S 四边形DEOM =S 四边形DEOM +S △DFM ,即S 四边形DEOF =S 四边形DMON ,∵点D 是∠AOB 的平分线上的一个定点,∴四边形DMON 的面积是一个定值,∴四边形DEOF 的面积是一个定值,故②正确;∵DE ⊥OA ,∴点E 与N 重合,∵垂线段最短,∴DE 的值最小,当DE 最小时,△DEF 的周长最小,∴当DE ⊥OA 时,DE 最小,△DEF 的周长最小,故③正确,∵DE ∥OB ,∠D =∠DFB =60°,∵∠AOB =120°,∴∠DFB ≠∠AOB ,∴DF 一定与OA 不平行,故④错误.故选:C .第二部分(非选择题 共114分)二、填空题:本题共4小题,每小题4分,共16分。
贵州省六盘水市第十三中学八年级数学上册 4.3 一次函数的图象(二)导学案(无答案)(新版)北师大版
1、通过函数图象获取信息。
2、利用函数图象解决简单的实际问题。
3、初步体会方程与函数的关系。
连线:把这些点依次连接起来,得到y=2x+1的图象,它是。
作图:
小结:从刚才作图的情况来总结一下作一次函数图象有哪些步骤:
(1);(2);(3)。
3、作图分析回答以下问题
(1)满足关系式y=2x+1的x、y所对应的点(x,y)都在一 次函数y=2x +1的图象上吗?
(2)一次函数y=2x+1的图象上的点(x,y)都满足关系式y=2x+1吗?
(3)一次函数y=kx+b的图象有什么特点?
检
查
讨
论
小组合作讨论预习中出现的问题,不能解决的提交全班讨论完成。定向自学中发现的新问题提交小组讨论解决发现的问题,处理的结果
展示
反馈
小组展示(自选)定向自学的内容
中
考
链
接
在同一坐标系中作出一次函数y= x与y=-3x+9的图象。
反
思
总
结
(1)说收获:
(2)说改进方法:
(1)函数图象的概念
把 一个函数的自变量x与对应的的值作为点的坐标和坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该。
(2)作一次函数的图象
例1:作出一次函数y=2x+1的图象
解:列表:
x
…
-2
-1
0
1
2
…
y=2x+1
…
-3
-1
1
3
5
…
描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点。
贵州省六盘水市第十三中学八年级数学上册 2.21 平方根导学案(无答案)(新版)北师大版
平方根章节环节学生学习内容及要求学情预设学习目标1、掌握算术平方根的概念,会用根号表示一个数的算术平方根.2、求一个正数的算术平方根与平方是互逆的运算,会利用这个互逆运算关系求非负数的算术平方根.3、了解算术平方根的性质.学法指导:结合教材和预习学案,先独立思考,遇到困难小对子之间进行帮扶,完成学习任务。
定向自学(一)上节课学习了无理数,了解到无理数产生的实际背景和引入的必要性,掌握了无理数的概念,知道有理数和无理数的区别是:有理数是有限小数或无限循环小数,无理数是无限不循环小数.比如上一节课我们做过的:由两个边长为1的小正方形,通过剪一剪,拼一拼,得到一个边长为a的大的正方形,那么有a2=2,a= ,2是有理数,而a是无理数.在前面我们学过若x2=a,则a叫x的平方,反过来x叫a的什么呢?本节课我们一起来学习.(二)问题导入1、前面我们学习了勾股定理,请大家根据勾股定理,结合图形完成填空:x2= ,y2= ,z2= ,w2= .2、x2=2,y2=3,z2=4,w2=5,已知幂和指数,求底数x,你能求出来吗?3、在上面思考的基础上,明晰概念:一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x就叫做a的,记为“”,读作“”.特别地,我们规定0的算术平方根是0,即=.4、例1 求下列各数的算术平方根:(1)900;(2)1;(3)6449;(4)14.解:(1)(2)(3)(4)5、例2 自由下落物体的高度h(米)与下落时间t(秒)的关系为h=4.9t2.有一铁球从19.6米高的建筑物上自由下落,到达地面需要多长时间?解:6、观察我们刚才求出的算术平方根有什么特点.a的双重非负性:①②检查讨论小组合作讨论预习中出现的问题,不能解决的提交全班讨论完成。
定向自学中发现的新问题提交小组讨论解决发现的问题,处理的结果展示反馈小组展示(自选)定向自学的内容课堂练习P39随堂练习1、求下列个数的算术平方根:36,169,17,0.81,104-2、反思总结(1)说收获:(2)说改进方法:预习内容:2.2平方根(2)1、掌握平方根的概念2、知道平方根与算术平方根的区别和联系11 111ABOCDE方yzw。
贵州省六盘水市第十三中学八年级数学下册 第四章 因式分解 周周清(无答案)(新版)北师大版
因式分解(A B )姓名 班级 得分(5) 2ax 2+4axy+2a=___________ . (6) b ab b a 952+-_________________.(7) a(a+b)-b(a+b)=_________________.(8) x x x 64223-+-=__________________. 二.下列由左边到有右边的变形,___________________是分解因式(填序号)。
(本题5分)(1)(a+3)(a-3)=a 2-9; (2) m 2-4=(m+2)(m-2); (3) a 2–b 2+1=(a+b)(a-b)+1(4) 10x 2-5x=5x(2x-1); (5) y 2-4xy+4=(y-2); (6) t 2-16+3t=(t+4)(t-4)+3t三、(如图),根据两个图形中阴影部分的面积相等,可以验证( )(本题5分) A 、222()2a b a ab b +=++ B 、222()2a b a ab b -=-+C 、22()()a b a b a b -=+- D 、22(2)()2a b a b a ab b +-=+- 四、将下列各式分解因式:(每题10分)(1)5y 3+20y (2)a(x -y) -b(y -x) +c(y -x) (6)ac ab a -+2-(4) 22)()(x y y y x x --- 2)()(m n m n m mn ---八年级周周清因式分解(A B )姓名 班级 得分一.直接写出下列各式分解因式的结果(每题5分)(1)ma+mb-mc=______________. (2) 3x 2-3x=________________________. (3) 2mR+2mr =________________. (4) ax+ay=_____________. (5) 2ax 2+4axy+2a=___________ . (6) b ab b a 952+-_________________.(7) a(a+b)-b(a+b)=_________________.(8) x x x 64223-+-=__________________. 二.下列由左边到有右边的变形,___________________是分解因式(填序号)。
2024届六盘水市重点中学数学八年级第二学期期末统考试题含解析
2024届六盘水市重点中学数学八年级第二学期期末统考试题注意事项1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每小题3分,共30分)1.下列各组数中,可以构成直角三角形的三边长的是()A.1,2,3 B.2,3,4 C.1,2,3D.1,2,32.下列命题中是正确的命题为A.有两边相等的平行四边形是菱形B.有一个角是直角的四边形是矩形C.四个角相等的菱形是正方形D.两条对角线互相垂直且相等的四边形是平行四边形3.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为()A.6 B.8 C.16 D.554.下列计算正确的是()A.35﹣25=1 B.(1﹣2)(1+2)=﹣1C.(2﹣2)(3+2)=4 D.(3+2)2=5,点D在y轴上,则点C的5.如图在平面直角坐标系xOy中若菱形ABCD的顶点,A B的坐标分别为(6,0),(4,0)坐标是()A.(6,8)B.(10,8)C.(10,6)D.(4,6)6.若x 2+在实数范围内有意义,则x 的取值范围在数轴上表示正确的是( )A .B .C .D .7.在中山市举行“慈善万人行”大型募捐活动中,某班50位同学捐款金额统计如下:金额(元) 20 3035 50 100 学生数(人) 2010 5 10 5 则在这次活动中,该班同学捐款金额的众数和中位数分别是( )A .20元,30元B .20元,35元C .100元,35元D .100元,30元8.下列窗花图案中,是轴对称图形的是( )A .B .C .D .9.如图是反比例函数1k y x=和212()k y k k x =<在第一象限的图象,直线AB y ∥轴,并分别交两条曲线于A B 、两点,若4AOB S △=,则21k k -的值是( )A .1B .2C .4D .8102x -x 的取值范围为( )A .2x ≥B .2x ≠C .2x >D .0x ≥二、填空题(每小题3分,共24分)11.已知一次函数3y x m =-+的图象经过点()2,P n -,则不等式3x m n -+>的解是__________.12.如图,BD是矩形ABCD的一条对角线,点E,F分别是BD,DC的中点.若AB=4,BC=3,则AE+EF的长为_____.13.如图,在平行四边形ABCD中,对角线AC⊥BD,AC=10,BD=24 ,则AD=____________14.因式分解:2a2﹣8= .15.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的用电器,其限制电流不能超过10A,那么用电器可变电阻R应控制的范围是____.16.计算:()22-=_____________.17.在平面直角坐标系中,点P(﹣3,﹣1)到原点的距离为_____.18.函数33yx=+自变量x的取值范围是_______________ .三、解答题(共66分)19.(10分)某商店分两次购进A.B两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:(1)求A、B两种商品每件的进价分别是多少元?(2)商场决定A种商品以每件30元出售,B种商品以每件100元出售.为满足市场需求,需购进A、B两种商品共1000件,且A种商品的数量不少于B种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.20.(6分)如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE,CF相交于点D,(1)求证:BE=CF ;(2)当四边形ACDE为菱形时,求BD的长.21.(6分)一个有进水管与出水管的容器,从某时刻开始的3分内只进水不出水,在随后的9分内既进水又出水,每分的进水量和出水量都是常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图所示.①当0≤x≤3时,求y与x之间的函数关系.②3<x≤12时,求y与x之间的函数关系.③当容器内的水量大于5升时,求时间x的取值范围.22.(8分)如图中的虚线网格我们称为正三角形网格,它的每一个小三角形都是边长为1个单位长度的正三角形,这样的三角形称为单位正三角形.(1)图①中,已知四边形ABCD 是平行四边形,求△ABC 的面积和对角线AC 的长;(2)图②中,求四边形EFGH 的面积.23.(8分)如图,在方格纸中每个小方格都是边长为1的小正方形,△ABC的顶点均在格点上(1)作出△ABC以点C为旋转中心,顺时针旋转90°后的△A1B1C;(2)以点O为对称中心,作出与△ABC成中心对称的△A2B2C224.(8分)如图,在中,AD 平分交BC 于点D ,F 为AD 上一点,且,BF 的延长线交AC 于点E .备用图(1)求证:; (2)若,,,求DF 的长;25.(10分)先化简,再求值22226951222a ab b b a b a ab a b a⎛⎫-+÷--- ⎪--⎝⎭,其中a =3,b =﹣1. 26.(10分)由中宣部建设的“学习强国”学习平台正式上线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六盘第三次周周清(C ) 班级: 姓名: 得分:
一、(20分)作出右图中∠AOB 的角平分线(保留作图痕迹)
二、(20分)已知DE 为△ABC 的AB 边的垂直平分线,
D 为垂足,D
E 交BC 于E , AC = 5,BC = 8,求△AEC 的周长。
三、(30分)如图所示,CD ⊥AB ,BE ⊥AC ,垂足分别为D 、E ,BE 、CD 相交于O ,
且OB = OC 。
求证:∠1 =∠2
四、(30分)如图所示,AB ⊥BC ,DC ⊥BC ,E 是BC 的中点,AE 平分∠BAD ,
求证:DE 平分∠ADC
六盘水市第十三中学八年级下数学第三次周周清(C )
班级: 姓名: 得分:
一、(20分)作出右图中∠AOB 的角平分线(保留作图痕迹)
二、(20分)已知DE 为△ABC 的AB 边的垂直平分线, 21O
E
D A B C A F D E
C B A
B O A B
O
D 为垂足,D
E 交BC 于E , AC = 5,BC = 8,求△AEC 的周长。
四、(30分)如图所示,CD ⊥AB ,B E ⊥AC ,垂足分别为D 、E ,BE 、CD 相交于O , 且OB = OC 。
求证:∠1 =∠2
四、(30分)如图所示,AB ⊥BC ,DC ⊥BC ,E 是BC 的中点,AE 平分∠BAD ,
求证:DE 平分∠ADC
E D A
B C 21O
E D A B C
A F D E
C B。
