2020北京试题研究课件·数学3.第32课时 切线的性质及判定
《切线的性质和判定》PPT赏析(第2课时)

对于甲、乙两人的作法,下列判断正确的是( C )
A.甲正确,乙错误
B.甲错误,乙正确
C.两人都正确
D.两人都错误
知2-练
2 如图,在平面直角坐标系中,过格点A,B,C作一 圆弧,点B与下列格点的连线中,能够与该圆弧相 切的是( C ) A.点(0,3) B.点(2,3) C.点(5,1) D.点(6,1)
探究三、切线长定理的运用
命题角度: 1.利用切线长定理计算; 2.利用切线长定理证明.
例3.[2012•绵阳] 如图30-3,PA、PB分 别切⊙O于A、B两点,连接PO、AB相交 于D,C是⊙O上一点,∠C=60°. (1)求∠APB的大小; (2)若PO=20 cm,求△AOB的面积.
考点聚焦
归类探究
∴∠ADB=90°,
∴∠CDB=90°,BD⊥AC.
∵BD 平分∠ABC,
∴∠ABD=∠CBD.
┃归类探究
解析
在△ABD 和△CBD 中,
∠ADB=∠CDB, BD=BD, ∠ABD=∠CBD,
∴△ABD≌△CBD(ASA).
∴AB=CB.
∵直线 BC 与⊙O 相切于点 B,
∴∠ABC=90°,
知识点 1 切线的判定定理
知1-导
如图,在⊙O中,经过半径 OA 的外端点 A 作直线 l⊥OA,则圆心 O 到直线 l 的距离是多少?直线 l 和⊙O 有什么位置关系?
O
l A
经过半径的外端并且垂直于这条半径的直线是圆的切线.
知1-讲
例1 如图,已知AB为⊙O的直径,点D在AB的延长线上, BD=OB,点C在圆上,∠CAB=30°. 求证:DC是⊙O的切线.
知1-讲
切线的判定方法有三种: ①直线与圆有唯一公共点; ②直线到圆心的距离等于该圆的半径; ③切线的判定定理.即
冀教版九年级下册 数学 课件 切线的性质和判定PPT

13、光阴似箭,日月如梭,转眼间已经十二年了。这十二年里,我们都在成长着,心灵上,身体上,精神上,而爱,是这成长的养料。 6 、有朝一日你动了爱情,千万保守秘密,没有弄清楚对方的底细,决不能掏出你的心来。 6、如果你准备结婚的话,告诉你一句非常重要的哲学名言「你一定要忍耐包容对方的缺点,世界上没有绝对幸福圆满的婚姻,幸福只是来自 于无限的容忍与互相尊重。
29.3 切线的性质和判定
目标:
1、探索切线与过切点的半径的位置关系。
2、了解切线的性质,能判定一条直线是 不是圆的切线。
3、灵活运用切线的性质与判定解决问题,培 养学生的数学思考与表达能力。
回顾
1.直线和圆有哪些位置关系? 2.直线与圆相切时如何识别?
观察探究
如图,如果直线I是⊙O的切线,A是切点,那么半径OA与L垂直吗?
求证 (1)AC是⊙D的切线
(2) AB+BE=AC
A
E
F
B
D
C
看到切线时常用辅助线: 连接切点和圆心得垂直
证明切线时常用辅助线:
1、有点连圆心,证垂直 2、无点作垂线,证相等
中考链接:
如图 正方形ABCD是⊙O的内接正方形延 长BA到E,使AE=AB,连接ED 求证(1)ED是⊙O的切线。
(2)连接OE交AD于点F,说明 EF=2OF
1 、如果以棋喻人生,那么人生岂不是没有一点回旋的余地?一般来说,人生迈错了一步,是不能往回倒退的,已经不能重来,但事实上迈错 一步未必就是没有了希望,因为你还有下一步呢! 2 、二十一世纪工作生存法则就是:建立个人品牌,把你的名字变成钱。 11 、珍惜今天的拥有,明天才会富有。 14、别人永远对,我永远错,这样子比较没烦恼。 15 、只有自己流过血受过伤才能真正成长。 8 、驾驭命运的舵是奋斗。不抱有一丝幻想,不放弃一点机会,不停止一日努力。 6、如果你准备结婚的话,告诉你一句非常重要的哲学名言「你一定要忍耐包容对方的缺点,世界上没有绝对幸福圆满的婚姻,幸福只是来自 于无限的容忍与互相尊重。
2020春北师大版数学九年级下册第三章 圆 专题三 切线的判定和性质的综合应用
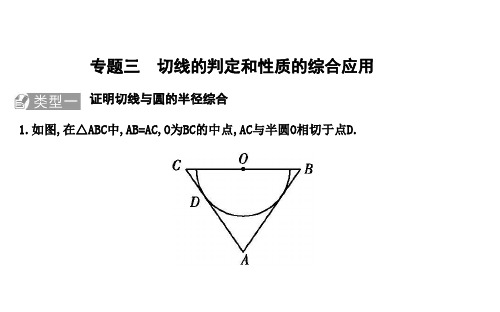
2
在 Rt△ABH 中,AH= AB2 BH 2 =1. 在 Rt△OBH 中,设 OB=r, 因为 OH2+BH2=OB2, 所以(r-1)2+( 3 )2=r2,解得 r=2, 所以 DB=2r=4.
在 Rt△ABD 中,AD= BD2 AB2 = 42 22 =2 3 , 所以 AD 的长为 2 3 .
(2)若 AE∥BC,BC=2 3 ,AC=2,求 AD 的长.
(2)解:连接 OC, 因为 AE∥BC,所以∠BAE=∠ABC. 因为∠BAE=∠ACB,所以∠ACB=∠ABC, 所以 AB=AC=2, 所以∠AOB=∠AOC, 因为 OC=OB, 所以 OA⊥BC, 所以 CH=BH= 1 BC= 3 .
(2)若 cos∠ABC= 2 ,AB=12,求半圆 O 所在圆的半径. 3
(2)解:因为 AB=AC,O 是 BC 的中点,所以 AO⊥BC. 在 Rt△AOB 中,OB=AB·cos∠ABC=12× 2 =8.OA= AB2 OB2 =4 5 .
3
由三角形的面积得 S△AOB= 1 AB·OE= 1 OB·OA,
因为∠OAE=∠ODA=90°,∠O=∠O,
所以△ODA∽△OAE,所以∠OAD=∠E,
因为 cos E= 4 ,所以 cos∠OAD= 4 ,
5
5
所以 OA=5,所以 OD=3,
所以 CD=OC-OD=5-3=2.
证明切线与求弦长综合 3.(2019滨州模拟)如图,BD为△ABC外接圆☉O的直径,且∠BAE=∠C.
(1)求证:AE与☉O相切于点A;
(1)证明:连接 AO 并延长交☉O 于点 F,连接 BF, 则 AF 为直径,∠ABF=90°,∠ACB=∠F. 因为∠BAE=∠ACB, 所以∠BAE=∠F. 因为∠FAB+∠F=90°, 所以∠FAB+∠BAE=90°, 所以 OA⊥AE, 所以 AE 与☉O 相切于点 A.
北师版数学下册3.6.2切线的性质(练习题课件)

∴ EG ∥ AC. ∴ 四 边 形 AEGC 为 平 行 四 边 形 , 四 边 形 OEGB 为 平 行 四 边 形 . ∴ CG = AE = 3 , EG = OB.∵PE⊥AO,AO∥CB,∴PG⊥CD.∴CD=2CG= 6.∴DB=BC-CD=8-6=2. ∵PD=5,DG=CG=3,∴PG=4.∴OB=EG=5+4 =9.∴D(9,2).
【点拨】∵⊙O 与 AC 相切于点 D,∴OD⊥AC.
∴∠ADO=90°.∵AD=
3OD,∴tan
A=OADD=
3 3.
∴∠A=30°.∵BD 平分∠ABC,∴∠OBD=∠CBD.
∵OB=OD,∴∠OBD=∠ODB.∴∠ODB=∠CBD.
∴OD∥BC.∴∠C=∠ADO=90°.∴∠ABC=60°,BC=12AB=6. ∴∠CBD=30°.∴CD= 33BC= 33×6=2 3. 【答案】A
(2)过点 C 作⊙O 的切线 CD,交 AP 的延长线于点 D.如果∠D =90°,DP=1,求⊙O 的直径.
解:连接PC.∵CD为⊙O的切线,∴OC⊥CD. 又 ∵ ∠ D = 90° , ∴ AD ⊥ CD , ∴ OC ∥ AD , ∴ ∠ APO = ∠ COP. ∵ ∠ AOP = ∠ COP , ∴ ∠ APO = ∠ AOP , ∴ OA = AP. 又∵OA=OP,∴△APO为等边三角形,∴∠AOP=60°. ∴∠POC=60°.
13.【2020·武汉】如图,在 Rt△ ABC 中,∠ABC=90°,以 AB 为直径的⊙O 交 AC 于点 D,AE 与过点 D 的切线互相垂直, 垂足为 E. (1)求证:AD 平分∠BAE;
证明:连接 OD,如图, ∵DE 为切线,∴OD⊥DE. ∵DE⊥AE,∴OD∥AE.∴∠1=∠ODA. ∵OA=OD,∴∠2=∠ODA.∴∠1=∠2. ∴AD 平分∠BAE.
九年级数学上册教学课件《切线的判定与性质》

d l
A
3.判定定理:经过半径的外端并且垂直于
O
这条半径的直线是圆的切线.
l
A
已 知 : 直 线 AB 经 过 ⊙ O 上 的 点 C , 并 且 OA=OB ,
CA=CB.求证:直线AB是⊙O的切线.
证明:连接OC.
∵OA=OB,CA=CB,
O
∴OC是等腰三角形OAB底边AB上的中线.
∴AB⊥OC.
证明:∵ AT=AB,
B
∴∠T=∠ABT=45°,
∴∠TAB=90°,
O.
∴BA⊥AT,
∴AT是⊙O的切线
T
A
4. 如图, AB是⊙O的直径,直线l1,l2是⊙O的切
线,A,B是切点. l1,l2有怎样的位置关系?证明你
的结论.【选自教材P98 练习第2题】
解: l1 ∥ l2.
A l1
证明:∵直线l1,l2是⊙O的切线,
⑴ 经过半径外端的直线是圆的切线.( × ) ⑵ 垂直于半径的直线是圆的切线. (× ) ⑶ 过半径的端点与半径垂直的直线是圆的切线. ( × ) ⑷ 和圆只有一个公共点的直线是圆的切线. ( √ ) ⑸ 过直径一端点且垂直于直径的直线是圆的切线. ( √ )
利用判定定理时,要注意直线须具备以下两个条件,缺一 不可: (1)直线经过半径的外端;(2)直线与这半径垂直.
课堂小结
切线的判 定方法
定义法 →1个公共点
证切线常作辅助线:
数量关系 →d=r,相切
有公共点,连半径,证垂直; 无公共点,作垂直,证半径.
经过半径的外端并 判定定理 →且垂直于这条半径
的直线是圆的切线
切线的性 质定理
→
圆的切线垂直于 经过切点的半径
人教版数学九年级上册24.2.2切线的判定与性质课件(共24张PPT)

知识回顾
直线与圆相切的判定: 1.利用定义判定:直线和圆只有一
个公共点时,直线与圆相切. 2.利用直线与圆心距离判定:当圆
心与直线的距离等于该圆的半径时,直 线与圆相切.
O
l
O d=r
l
新知探究
知识点1 切线的判定
思考:如图,在⊙O中,经过半径OA 的外端点 A 作直线 l⊥OA. (1)圆心O到直线 l 的距离是多少?
l
∴OA⊥l
ห้องสมุดไป่ตู้ 反证法证明切线的性质
如图,直线CD与⊙O相切,求证:⊙O的半径OA
与直线CD垂直.
证明:(1)假设AB与CD不垂直,过
B
点O作一条直线垂直于CD,垂足为M;
(2)则OM<OA,即圆心到直线CD的
O
距离小于⊙O的半径,因此,CD与⊙O
相交.这与已知条件“直线与⊙O相切”相 C 矛盾;
A MD
证明:连接OA,OD,作OE⊥AC 于E . ∵ ⊙O与AB相切于E, ∴OD⊥AB.
又∵△ABC为等腰三角形,
O是底边BC的中点,
B
A D
1
O
E C
∴AO平分∠BAC,
∴OD=OE ,即OE是⊙O半径.
∴AC是⊙O的切线. 方法总结:无交点,作垂直,证半径.
随堂练习
1.如图,已知⊙O的直径AB与弦AC的夹角为31°,
d l
A
3.判定定理:经过半径的外端并且垂直于
O
这条半径的直线是圆的切线.
l
A
已 知 : 直 线 AB 经 过 ⊙ O 上 的 点 C , 并 且 OA=OB ,
CA=CB.求证:直线AB是⊙O的切线.
证明:连接OC.
北师版九年级下《切线的性质定理》课件
8.(11肇庆中考)己知:如图10.△ABC内接于⊙O, AB为直径,∠CBA的平分线交AC干点F,交⊙O于 点D,DF⊥AB于点E,且交AC于点P,连结AD。
求证:(1)∠DAC=∠DBA
(2)求证:P处线段AF的中点
(3)若⊙O的半径为5,
D
AF= ,求tan∠ABF的值
(1)求证:DE⊥AC;
(2)若∠ABC=30°,求tan∠BCO的值。
5.(11芜湖中考)23. (本小题满分12分)
如图,已知直线PA交⊙0于A、B两点,AE是⊙0 的直径.点C为⊙0上一点,且AC平分∠PAE,过C 作CD⊥PA,垂足为D。
(1)求证:CD为⊙0的切线;
(2)若DC+DA=6,
⊙0的直径为l0,
求AB的长度.
6.(11淄博中考)已知:△ABC是边长为4的等边 三角形,点O在边AB上,⊙O过点B且分别与边 AB,BC相交于点D,E,EF⊥AC,垂足为F.
(1)求证:直线EF
是⊙O的切线;
(2)当直线DF与⊙O
相切时,求⊙O的半径.
7.(11甘肃中考)12.如图,⊙O过点B、C,圆心 O在等腰Rt△ABC的内部,∠BAC=90°,OA=1, BC=6.则⊙O的半径为( )
3.(11北京中考). 如图,△ABC中,AB ,AC
以AB为直径Leabharlann ⊙O分别交AC、BC于点D、E,点F
在AC的延长线上,且
CBF 1。CAB
(1)求证:直线BF是⊙O的切线; 2
(2)若,,求BC和BF的长。
A
D
O
C
E
B
F
4. (11烟台中考)24、(本题满分10分)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章 圆 第32课时 切线的性质及判定 (建议时间:45分钟)
基础过关 1. (2019重庆A卷)如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC与⊙O交于点D,连接OD,若∠C=50°,则∠AOD的度数为( ) A.40° B.50° C.80° D. 100°
第1题图 2. (2019通州区期末)如图,PA和PB是⊙O的切线,点A和B为切点,AC是⊙O的直径,已知∠P=50°,则∠ACB的大小是( ) A. 65° B. 60° C. 55° D. 50°
第2题图 3. (2019泰安)如图,△ABC是⊙O的内接三角形,∠A=119°,过点C的圆的切线交BO于点P,则∠P的度数为( ) A. 32° B. 31° C. 29° D. 61°
第3题图 4. (2019贺州)如图,在△ABC中,O是AB边上的点,以O为圆心,OB为半径的⊙O与AC相切于点D,BD平分∠ABC,AD=3OD,AB=12,CD的长是( ) A. 23 B. 2 C. 33 D. 43 第4题图 5. 如图,PA与⊙O相切于点A,线段PO交⊙O于点C,过点C作⊙O的切线交PA于点B.若PC=4,AB=3,则⊙O的半径长为 .
第5题图 6. (2019北京四中月考)如图,PA,PB是⊙O的两条切线,切点分别为A,B.连接OA,OB,AB,PO,PO与AB交于点C.若∠APB=60°,OC=1,则△PAB的周长为 .
第6题图 7. (2019东城区二模)如图,⊙O是△ABC的外接圆,连接OC,过点A作AD∥OC交BC的延长线于点D,∠ABC=45°. (1)求证:AD是⊙O的切线;
(2)若sin∠CAB=35,⊙O的半径为522,求AB的长.
第7题图 8. (2020原创)如图,在平面内给定△ABC,点O到△ABC三个顶点的距离均等于c(c为常数),到点O的距离等于c的所有点组成图形G,过点A作AB的垂线交BC于点E,交图形G于点D,延长DA,在DA的延长线上存在一点F,使得BF⊥OB,且∠ABF=∠ABC. (1)求证:AB=AC;
(2)若AD=4,cos∠ABF=45,求DE的长.
第8题图
能力提升 9. (2019海淀区期末)如图,在平面直角坐标系xOy中,P是直线y=2上的一个动点,⊙P的半径为1,直线OQ切⊙P于点Q,则线段OQ的最小值为 .
第9题图 10. (2018石景山区二模)如图,⊙O的半径为2,切线AB的长为23,点P是⊙O上的动点,则AP的长的取值范围是 .
第10题图 11. (2019朝阳区期末)如图所示的网格是正方形网格,线段AB绕点A顺时针旋转α(0°<α<180°)后与⊙O相切,则α的值为 . 第11题图 12. (2019房山区期末)如图①,将一个量角器与一张等边三角形(△ABC)纸片放置成轴对称图形,CD⊥AB,垂足为D,半圆(量角器)的圆心与点D重合,此时,测得顶点C到量角器最高点的距离CE=2 cm,将量角器沿DC方向平移1 cm,半圆(量角器)恰与△ABC的边AC,BC相切,如图②,则AB的长为 cm.
第12题图 满分冲关 13. (2019延庆区期末)如图,在Rt△ABC 中,∠C=90°,∠A=30°,AB=43.若动点 D 在线段 AC 上(不与点 A、C 重合),过点 D 作 DE⊥AC 交 AB 边于点 E.点 A 关于点 D 的对称点为点 F,以 FC 为半径作⊙C,当 DE= 时,⊙C 与直线 AB 相切.
第13题图 14. (2019西城区二模)如图,AB是⊙O的直径,CA与⊙O相切于点A,且CA=BA.连接OC,过点A作AD⊥OC于点E,交⊙O于点D,连接D B. (1)求证:△ACE≌△BAD; (2)连接CB交⊙O于点M,交AD于点N.若AD=4,求MN的长.
第14题图 参考答案 第32课时 切线的性质及判定 基础过关 1. C 【解析】由题意知∠BAC=90°,∠C=50°,∴∠B=40°,∴∠AOD=2∠B=80°. 2. A 【解析】如解图,连接OB,∵PA、PB是⊙O的切线,∴OA⊥PA,OB⊥PB,∴∠OAP=∠OBP=90°,∴∠AOB=360°-90°-90°-50°=130°,∴∠OCB=12 ×130°=65°,即∠ACB=65°.
第2题解图 3. A 【解析】如解图,设BP与⊙O交于点M,连接OC,CM.∵PC是切线,∴∠OCP=90°.∵四边形ABMC是圆内接四边形,∠A=119°,∴∠BMC=180°-119°=61°.∵OC=OM,∴∠OCM=∠OMC=61°.∴在△COM中,∠COM=58°.∴在△COP中,∠P=180°-∠COM-∠OCP=180°-58°-90°=32°.
第3题解图 4. A 【解析】∵AD是⊙O的切线,∴OD⊥AD,在Rt△AOD中,AD=3 OD,∴tan A=ODAD =OD3OD =33 ,∴∠A=30°,∴∠AOD=60°,∵OD=OB,∴∠ODB=∠ABD=12 ∠AOD=30°,∵BD平分∠ABC,
∴∠CBD=∠ABD=30°,∴∠ABC=60°,∴∠C=90°. 在Rt△ABC中,sin A=BCAB ,AB=12,∴sin 30°
=BC12 ,BC=AB·sin A=12×12 =6. 在Rt△CBD中,CD=BC·tan 30°=6×33 =23 .
5. 6 【解析】设⊙O的半径为r,由切线长定理得,BC=BA=3,∵BC是⊙O的切线,∴∠BCP=90°,∴PB=PC2+BC2 =5,∴AP=PB+AB=8,∵PA是⊙O的切线,∴∠OAP=90°,∴AP2+OA2=OP2,即82+r2=(4+r)2,解得:r=6. 6. 63 【解析】∵PA,PB是⊙O的两条切线,∴OA⊥PA,OB⊥PB,OP平分∠APB,PA=PB,∵∠APB=60°,∴△PAB是等边三角形,AB=2AC,PO⊥AB,∴∠PAB=60°,∴∠OAC=∠PAO-∠PAB=90°-60°=30°,∴AO=2OC,∵OC=1,∴AO=2,∴AC=3 ,∴AB=2AC=23 ,∴△PAB的周长=63 .
7. 解:(1)如解图,连接OA, ∵∠ABC=45°, ∴∠AOC=2∠ABC=90°, ∵AD∥OC, ∴∠DAO=∠COA=90°, ∵OA是⊙O的半径, ∴AD是⊙O的切线; (2)过C作CE⊥AB于E, ∵∠AOC=90°,
AO=OC=522 , ∴AC=5, ∵∠AEC=90°,
∴sin ∠CAE=CEAC =35 ,
∴CE=3,AE=4, ∵∠CEB=90°,∠ABC=45°, ∴∠BCE=45°, ∴CE=BE=3, ∴AB=AE+BE=7.
第7题解图 8. (1)证明:根据题意作图如解图所示; ∵BF⊥OB, ∴∠ABF=∠D,∴∠ABF=∠C, ∵∠ABF=∠ABC, ∴∠ABC=∠C, ∴AB=AC;
第8题解图 (2)解:如解图,连接BD,在Rt△ADB中,∠BAD=90°, ∵cos ∠ADB=ADBD ,∴BD=ADcos ∠ADB =ADcos ∠ABF =445
=5.
∴AB=3. 在Rt△ABE中,∠BAE=90°,
∵cos ∠ABE=ABBE ,∴BE=
ABcos ∠ABE =345 =154 .
∴AE=(154)2-32 =94 ,
∴DE=AD-AE=4-94 =74 .
能力提升 9. 3 【解析】如解图,连接PQ、OP,∵直线OQ切⊙P于点Q,∴PQ⊥OQ,在Rt△OPQ中,OQ=OP2-PQ2 =OP2-1 ,当OP最小时,OQ最小,当OP⊥直线y=2时,OP有最小值2,∴OQ
的最小值为22-1 =3 .
第9题解图 10. 2≤AP≤6 【解析】如解图,连接OB,∵AB是⊙O的切线,∴∠OBA=90°,∴OA=AB2+OB2 =4,当点P在线段AO上时,AP最小为2,当点P在线段AO的延长线上时,AP最大为6,∴AP的长的取值范围是2≤AP≤6. 第10题解图 11. 60°或120° 【解析】如解图,线段AB绕点A顺时针旋转α(0°<α<180°)后与⊙O相切,切点为C′和C″,连接OC′、OC″,则OC′⊥AB′,OC″⊥AB″,在Rt△OAC′中,∵OC′=1,OA=2,∴∠OAC′=30°,∴∠BAB′=60°,同理可得∠OAC″=30°,∴∠BAB″=120°,综上所述,α的值为60°或120°.
第11题解图 12. 23 【解析】如解图,设图中半圆的圆心为O,与BC的切点为M,连接OM,则OM⊥MC,∴∠OMC=90°,依题意知道∠DCB=30°,设AB为2x cm,∵△ABC是等边三角形,∴CD=3 x cm,在题图①中,CE=2 cm,∴半圆的半径为(3 x-2)cm,由解图可知OC=(3 x-1)cm,∴sin ∠DCB=OMOC =12 ,
∴3x-23x-1 =12 ,∴x=3 ,∴AB=2x=23 cm.
第12题解图 满分冲关 13. 32 或332 【解析】如解图,过C作CH⊥AB于H,∵∠ACB=90°,AB=43 ,BC=12 AB=23 ,AC=3 BC=6,∴由三角形面积公式得:12 BC·AC=12 AB·CH,解得CH=3,分为两种情况:①如解图①,∵CF=CH=3,∴AF=6-3=3,∵A和F关于D对称,∴DF=AD=32 ,∵DE∥BC,
∴△ADE∽△ACB,∴DEBC =ADAC ,∴DE23 =326 ,DE=32 ;
