第三章材料物理性能
合集下载
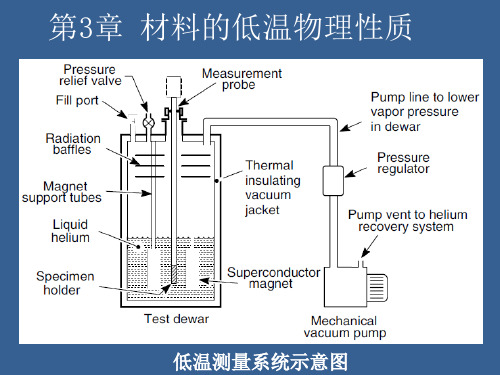
低温物理与技术-第3章 材料的低温性质
Parts pቤተ መጻሕፍቲ ባይዱr million
交流磁化率实验
温度计 样品 初级 加热 次级1 次级2
M M dc dc H H dc
通过零点的直线和很小时才有关系’dc=dc，一般两者是不同的。
磁场
H=Hdc+Hac=Hdc+hcost
磁化强度 M=Mdc+Mac，或 M=Mdc+mcos(t-) 是角频率，角标dc指直流，ac指交流，h和m分别
式中的a1,a2分别为气体分子在表面的温度适用系数
a 为总的适用系数
0
若冷表面积A1近似等于热表面积A2，则
a1 a2 a0 a1 a2 a1 a2
不同温度下几种气体的a值
温度(K) 氦气(He) 氢气(H2) 氖气(Ne) 空气(Air) 300 77 20 4 0.29 0.42 0.59 1.00 0.29 0.53 0.97 / 0.66 0.83 1.00 / 0.8～0.9 1.00 1.00 /
•
•
液体主要是分子振动能量传递，气体主要是平动 （单原子）以及平动与转动（双原子）能量传递。 由气体分子运动论，材料热导率的理论表达式
1 k t ( 9 5) cv v 8
固体热导率
固体热导率
1 k t cv v 3
液氮温度以上，纯金 属热导率基本为定值； 液氮温度以下，热导 率与T-2成正比；达到 一极值后，热导率随 温度下降而下降。无 序合金和不纯金属热 导率随温度下降而下 降，合金中无最大值 现象。
~
次级线圈输出的瞬时电压为
dI (t ) 1 (t ) 2 (t ) ( M 1 M 2 ) dt
式中M1和M2分别是线圈1和线圈2的互感系数。
材料物理性能PPT课件
参考书：
材料物理性能 哈尔滨工业大学出版社 邱成军等 TB303/Q712
材料物理性能
机械工业出版社，陈騑騢
TB303/C417
金属材料物理性能
冶金工业出版社 王润
75.211 W35
无机材料物理性能
清华大学出版社 关振铎等
71.2241/460
工程材料的性能、设计与选材 机械工业出版社，柴惠芬,石德珂编
学习材料物理性能主要是为功能材料的研究和使用打基础。
本课程学习的内容和要求
学习热学性能、电学性能、磁学性能和光学性能。 ●掌握基本概念：
有关概念与现象及表征，如热导率、磁畴、硬磁与软磁材料、热电效 应、半导体的热敏、光敏现象等等。 ●物理本质：
如热膨胀是怎么产生的，不同材料为什么有不同的磁性等。从材料原 子结构、电子层、晶格运动等内部因素认识材料物理性能的本质和机理。 ●影响因素、与化学成分及组织结构之间的关系：
1.爱因斯坦模型 1906年爱因斯坦根据普朗克质点振动量子化的观点，并假设每个质
点都在独立振动，原子间彼此无关，每个质点振动频率相同，简化、 推导而得。
推导过程：略 注意爱因斯坦温度θE 进步：能量量子化、考虑到温度因素。
1.爱因斯坦模型
讨论： （1）当高温时（T＞＞θE ），Cv≈3R
即为杜隆－伯替定律的形式，实际上杜隆－伯替定律在较高温度 时与事实符合较好。
3、质点的热振动与物体热量 构成物体各质点热运动动能的总和即为物体的热量。温度升高，质
点振动频率和振幅增加，热量增加。与热容有关。
第1节 热学性能的物理基础
4、声频支振动和光频支振动 材料中质点间存在很强的相互作用力，一个质点的振动会影响其临近
质点的振动，进而影响到其它区域质点的振动。相邻质点间的振动存在 一定相位相差，即晶格振动以弹性波的形式在整个材料内传播，这种弹 性波称为格波。弹性波是多频率振动的组合波，频率高者传播较快。
材料物理性能
腹有诗书气自华！无机材料物理性能 课件第三章材料的热学性能z第一节 材料的热容 z第二节 材料的热膨胀 z第三节 材料的热传导 z第四节 材料的热稳定性热学性能：包括热容（thermal content）， 热膨胀（thermal expansion），热传导（heat conductivity），热稳定性（thermal stability）等。
本章目的就是探讨热性能与材料宏观、微观本质 关系，为研究新材料、探索新工艺打下理论基础。
热性能的物理本质：晶格热振动（lattice heat vibration），根据牛顿第二定律，简谐振动方程 （simple harmonic vibration equation）为：式中：dx m ⋅ 2 = β ( x n +1 + x n −1 − 2 x n ) dt2β = 微观弹性模量（ micro-elastic- modulus ），m = 质点质量（mass）， x = 质点在x方向上位移（displacement）。
另外, ∑ i =1N(动能kinetic energy)i=热量 （quantity of heat）即：各质点热运动时动能总和就是该物 体的热量。
弹性波（格波）：包括振 动频率低的声频支和振动频率高的光 频支。
声频支可以看成是相邻原子具有相同的 振动方向。
由于两种原子的质量不同，振幅 也不同，所以两原子间会有相对运动。
光频支可以看成相邻原子振动方向相反， 形成一个范围很小，频率很高的振动。
如果振动着的质点中包含频率甚低的格 波，质点彼此之间的位相差不大，则格波类 似于弹性体中的应变波，称为 “ 声频支振动 ” 。
格波中频率甚高的振动波，质点彼此之间的 位相差很大，邻近质点的运动几乎相反时， 频率往往在红外光区，称为“光频支振动”。
如图3.1，其中声频支最大频率：γ max3 × 10 m / s 13 = = = 1 . 5 × 10 ( HZ ) −10 2a 2 × 10 m3υ第一节 材料的热容热容是物体温度升高1K所需要增加的能量。
第三章-材料的性能PPT学习教案
16
洛氏硬度计算
HRc
K
h1 h0
0.002
K为常数，洛氏硬度值无量纲
第16页/共129页
17
3．维氏硬度（Vickers）
维氏硬度试验法是由英国人和在1925年提出的。按照此法试制的第 一台硬度计是英国维克斯公司制作的，因此称为维氏硬度法。
它采用了布氏硬度试验的原理，但换用一个金刚石正四棱锥体作 压头，锥面夹角为，试验时在载荷P的作用下，在试样试验面上压 出一个正方形的压痕，测量压痕两对角线的平均长度d，算出压痕 的面积。
E 为杨氏模量。 第28页/共129页
大多数钢的弹性模量为～1011Pa。
29
泊松比，泊松比是垂直方向的弹性变形与水平方向 的弹性变形的比值。对理想材料来说是0.5 ，而对 真实材料一般为0.3。
侧向 纵向
比例极限（弹性极限）：表示金属材料按虎克定律 变形的最大应力。
e
Fe A0
屈服强度：是金属材料抵抗微量塑性变形（0.2%） 时的应力。
第5页/共129页
6
二氧化铀（不同氧/铀比的）导热系数随温度变 化趋势
第6页/共129页
7
常用金属和合金的导热率W/m•K
Na K Be Mg Al Fe Co Ni Cu Ag 140 100 160 172 226 94 70 62 392 415
Zr
U UO2 碳钢
23.7/473K 25/RT 8.4/RT 63.3~80.4 16.0~ 22.1
冲击韧性是应用冲击试验把规定形状的试 样用弯曲的方法，使之迅速断裂, 测定使之 断裂所需要的功。称其为冲击韧性试验， 所测得的值称为冲击韧性值。
第32页/共129页
33
洛氏硬度计算
HRc
K
h1 h0
0.002
K为常数，洛氏硬度值无量纲
第16页/共129页
17
3．维氏硬度（Vickers）
维氏硬度试验法是由英国人和在1925年提出的。按照此法试制的第 一台硬度计是英国维克斯公司制作的，因此称为维氏硬度法。
它采用了布氏硬度试验的原理，但换用一个金刚石正四棱锥体作 压头，锥面夹角为，试验时在载荷P的作用下，在试样试验面上压 出一个正方形的压痕，测量压痕两对角线的平均长度d，算出压痕 的面积。
E 为杨氏模量。 第28页/共129页
大多数钢的弹性模量为～1011Pa。
29
泊松比，泊松比是垂直方向的弹性变形与水平方向 的弹性变形的比值。对理想材料来说是0.5 ，而对 真实材料一般为0.3。
侧向 纵向
比例极限（弹性极限）：表示金属材料按虎克定律 变形的最大应力。
e
Fe A0
屈服强度：是金属材料抵抗微量塑性变形（0.2%） 时的应力。
第5页/共129页
6
二氧化铀（不同氧/铀比的）导热系数随温度变 化趋势
第6页/共129页
7
常用金属和合金的导热率W/m•K
Na K Be Mg Al Fe Co Ni Cu Ag 140 100 160 172 226 94 70 62 392 415
Zr
U UO2 碳钢
23.7/473K 25/RT 8.4/RT 63.3~80.4 16.0~ 22.1
冲击韧性是应用冲击试验把规定形状的试 样用弯曲的方法，使之迅速断裂, 测定使之 断裂所需要的功。称其为冲击韧性试验， 所测得的值称为冲击韧性值。
第32页/共129页
33
第三章材料力学性能分析
第三章材料力学性能分析
应变硬化
第三章材料力学性能分析
应变硬化
第三章材料力学性能分析
应变硬化
第三章材料力学性能分析
应变硬化
第三章材料力学性能分析
第三章材料力学性能分析
抗拉强度
抗拉强度：拉伸实验时，试样拉断过程中最大实验力所对应的 应力。其值等于最大拉力Fb除以试样的原始横截面面积A0， 抗拉强度用σb表示，即 σb=Fb/A0 抗拉强度是材料在承受拉伸载荷时的实际承载能力。高分 子材料和陶瓷材料的抗拉强度是产品设计的重要依据。
拉伸时σ=Eε，剪切时τ=Gγ，E和G分别为拉伸时的杨氏模 数和切变模数。
可视为衡量材料产生弹性变形难易程度的指标。 材料的抗弹性变形的一个量，材料刚度的一个指标。它只与
材料的化学成分有关，与其组织变化无关，与热处理状态无 关。各种钢的弹性模量差别很小，金属合金化对其弹性模量 影响也很小。
第三章材料力学性能分析
塑性变形 ：材料的塑性变形上微观结构的相邻部分产生 永久性位移，并不引起材料破裂的现象。
金属材料的塑性变形机理 金属材料常见的塑性变形机理为晶体的滑移和孪生两种。
第三章材料力学性能分析
塑性变形-滑移
定义： 滑移面：原子最密排面； 滑移向：原子最密排方向。 滑移系：滑移面和滑移向的组合。 滑移系越多，材料的塑性越好。
第三章 材料的力属在单向静拉伸载荷下的力学性能
力学实验
蠕变 疲劳 磨损
第三章材料力学性能分析
金属在单向静拉伸载荷下的力学性能
力-伸长曲线和应力应变曲线
c C
Op——直线关系与pe——偏离直线关 系，即弹性形变阶段（可逆形变）；
F到达FA至Fc点时，产生不均匀塑性变 形（不可逆的永久变形）；
应变硬化
第三章材料力学性能分析
应变硬化
第三章材料力学性能分析
应变硬化
第三章材料力学性能分析
应变硬化
第三章材料力学性能分析
第三章材料力学性能分析
抗拉强度
抗拉强度：拉伸实验时，试样拉断过程中最大实验力所对应的 应力。其值等于最大拉力Fb除以试样的原始横截面面积A0， 抗拉强度用σb表示，即 σb=Fb/A0 抗拉强度是材料在承受拉伸载荷时的实际承载能力。高分 子材料和陶瓷材料的抗拉强度是产品设计的重要依据。
拉伸时σ=Eε，剪切时τ=Gγ，E和G分别为拉伸时的杨氏模 数和切变模数。
可视为衡量材料产生弹性变形难易程度的指标。 材料的抗弹性变形的一个量，材料刚度的一个指标。它只与
材料的化学成分有关，与其组织变化无关，与热处理状态无 关。各种钢的弹性模量差别很小，金属合金化对其弹性模量 影响也很小。
第三章材料力学性能分析
塑性变形 ：材料的塑性变形上微观结构的相邻部分产生 永久性位移，并不引起材料破裂的现象。
金属材料的塑性变形机理 金属材料常见的塑性变形机理为晶体的滑移和孪生两种。
第三章材料力学性能分析
塑性变形-滑移
定义： 滑移面：原子最密排面； 滑移向：原子最密排方向。 滑移系：滑移面和滑移向的组合。 滑移系越多，材料的塑性越好。
第三章 材料的力属在单向静拉伸载荷下的力学性能
力学实验
蠕变 疲劳 磨损
第三章材料力学性能分析
金属在单向静拉伸载荷下的力学性能
力-伸长曲线和应力应变曲线
c C
Op——直线关系与pe——偏离直线关 系，即弹性形变阶段（可逆形变）；
F到达FA至Fc点时，产生不均匀塑性变 形（不可逆的永久变形）；
第三章材料的力学性能-PPT课件
屈服现象
屈服机理
影响金属材料屈服强度的因素
（1）晶体结构：金属材料的屈服过程主要是位错的运动。 （2）晶界与亚结构：晶界是位错运动的重要障碍，晶界越多， 对材料屈服强度的提高贡献越大。 （晶粒细化） （3）溶质元素：晶格畸变应力场与位错应力场产生交互作用； 溶质与溶剂之间的电学交互作用；化学交互作用；有序作用等 都使位错运动受阻，从而提高屈服强度，产生固溶增强化。
应变硬化
应变硬化
应变硬化
应变硬化
抗拉强度
抗拉强度：拉伸实验时，试样拉断过程中最大实验力所对应的 应力。其值等于最大拉力Fb除以试样的原始横截面面积A0， 抗拉强度用σb表示，即 σb=Fb/A0 抗拉强度是材料在承受拉伸载荷时的实际承载能力。高分 子材料和陶瓷材料的抗拉强度是产品设计的重要依据。
10 30
12 30
10 2.5
30 60
• 120HBS10 ／ 1000 ／ 30 代表用 10mm 钢球，在 1000kgf （ 10kN ）试验力作用下保持 30s ，测得的 布氏硬度值。 • 布氏硬度试验法一般用于试验各种硬度不高的钢材、铸 铁、有色金属等，也用于试验经淬火、回火但硬度不高 的钢件。 • 由于布氏硬度试验的压痕较大，试验结果能更好地代表 试件的硬度。
• 试验时，根据被测的材料不同，压头的类型、试验力及按 下选择，对应的洛氏硬度标尺为HRA、HRB、HRC三种
符号 压头类型 载荷/k g f 硬度有效 范围 70～85 使用范围
120
HRA 金刚石圆锥 60 体 直径为 1.588m m钢球 100
适用于测量硬质合金、 钢表、淬火层或渗碳 层
第三章 材料的力学性能
内容
金属在单向静拉伸载荷下的力学性能 力学实验
第3章 材料的力学性能1
①抗拉强度σb —表示材料最大的抵抗能力。
②屈服强度σs —材料开始发生塑性变形时对应 的应力。 ③弹性模量E —描述应力和应变之间的比例关系。 ④延伸率δ —表征材料的塑性程度。 ⑤断面伸缩率Ψ — ⑥冲击韧性αk —抗冲击的能力（主要用于低温） ⑦硬度G—描述材料软硬的程度等。 ⑧疲劳— 使用寿命。
力学性能
提高材料屈服强度的方法很多： （1）通过热处理方法—方便，但要求它在固态下发生相变， 满足这种要求的合金包括在固态下经历有序—无序转变的合 金，伴随这一过程出现的材料强化称为有序强化，它在许多 方面类似于沉淀强化。通常利用的与热处理有关的强化方式
是过饱和固溶体的沉淀强化和共析分解反应的共析强化。如
什么影响，难以去改变键合类型和结合力来强化材 料。在这方面，一般常见的方法就是形成新的相 （因为新相中的原子键合类型和结合力自然不同）。
力学性能
2. 位错 我们有很多方法来影响材料中的位错，通 过影响位错的运动来达到强化材料的目的。 所以可以说，近代金属物理领域中的最大成 果就是关于材料中的位错的研究。
min r max
疲劳
（1）对称交变应力，如图（a）所示，
σm =0，r=－1。大多数旋转轴类零件的 循环应力就是这种情况。 （2）不对称交变应力，如图如图（b）所示，
－1＜r＜0。发动机连杆的循环应力就是 这种情况。
疲劳
（3）波动应力，如图如图（c）所示，
σm＞σa，0＜r＜1。 发动机缸盖螺栓的循环应力就是这种情况。 （4）脉动应力，如图如图（d）所示， σm =σa＞0，r=0。
不同材料的应力—应变曲线
弯曲试验
a) 三点弯曲加载
b) 四点弯曲加载
硬度试验
定义：表示材料抵抗他物压入的能力。它在机械制造中具有特殊的意义。
②屈服强度σs —材料开始发生塑性变形时对应 的应力。 ③弹性模量E —描述应力和应变之间的比例关系。 ④延伸率δ —表征材料的塑性程度。 ⑤断面伸缩率Ψ — ⑥冲击韧性αk —抗冲击的能力（主要用于低温） ⑦硬度G—描述材料软硬的程度等。 ⑧疲劳— 使用寿命。
力学性能
提高材料屈服强度的方法很多： （1）通过热处理方法—方便，但要求它在固态下发生相变， 满足这种要求的合金包括在固态下经历有序—无序转变的合 金，伴随这一过程出现的材料强化称为有序强化，它在许多 方面类似于沉淀强化。通常利用的与热处理有关的强化方式
是过饱和固溶体的沉淀强化和共析分解反应的共析强化。如
什么影响，难以去改变键合类型和结合力来强化材 料。在这方面，一般常见的方法就是形成新的相 （因为新相中的原子键合类型和结合力自然不同）。
力学性能
2. 位错 我们有很多方法来影响材料中的位错，通 过影响位错的运动来达到强化材料的目的。 所以可以说，近代金属物理领域中的最大成 果就是关于材料中的位错的研究。
min r max
疲劳
（1）对称交变应力，如图（a）所示，
σm =0，r=－1。大多数旋转轴类零件的 循环应力就是这种情况。 （2）不对称交变应力，如图如图（b）所示，
－1＜r＜0。发动机连杆的循环应力就是 这种情况。
疲劳
（3）波动应力，如图如图（c）所示，
σm＞σa，0＜r＜1。 发动机缸盖螺栓的循环应力就是这种情况。 （4）脉动应力，如图如图（d）所示， σm =σa＞0，r=0。
不同材料的应力—应变曲线
弯曲试验
a) 三点弯曲加载
b) 四点弯曲加载
硬度试验
定义：表示材料抵抗他物压入的能力。它在机械制造中具有特殊的意义。
第3章 工程结构材料的物理力学性能
南航土木工程系
第3章工程结构材料物理力学性能
37
（2）轴心抗压强度（棱柱体抗压强度） f ck 立方体受压不是处于单轴受力状态！ 采用棱柱体，中间基本上是处于轴心受压。 与立方体抗压强度的关系：
南航土木工程系
第3章工程结构材料物理力学性能
9
折算应力 zs 以主应力表示：
1 zs [( 1 2 )2 ( 2 3 )2 ( 3 1 )2 2
以应力分量表示：
2 2 2 2 zs x2 y z2 ( x y y z z x ) 3( xy yz zx )
南航土木工程系 第3章工程结构材料物理力学性能 17
南航土木工程系
第3章工程结构材料物理力学性能
18
3.1.4
钢材的疲劳
疲劳破坏：在低于钢材抗拉强度的应力反复作用 下，所发生的破坏。 疲劳破坏特点： 过程：裂纹形成，缓慢发展，最后迅速断裂 疲劳破坏前没有明显的变形，脆性破坏
南航土木工程系
3.1.3 影响钢材性能的因素 （1）化学成分（铁99％＋碳） 碳：提高强度，却恶化塑性、可焊性、耐锈蚀性。 锰：有益，提高强度，弱氧化剂 硅：有益，提高强度，强氧化剂 硫：有害，高温热脆 磷：有害，低温变脆
低碳钢 低合金钢
南航土木工程系
第3章工程结构材料物理力学性能
13
南航土木工程系 第3章工程结构材料物理力学性能 14
南航土木工程系
第3章工程结构材料物理力学性能
15
（3）应力集中 现象：当构件内部缺陷或截面形状等改变时，应 力分布不均匀，出现局部高峰应力，促使 钢材变脆。 影响因素：截面变化愈剧烈，应力集中现象愈明 显。
新版材料物理性能课后习题答案_北航出版社_田莳主编-新版.pdf
=5.21 10 19 J 3.25eV
2
6.02 1023 / 8 ) 3
由E0
3 5
E
0 F
1.08eV
6. 若自由电子矢量 K 满足以为晶格周期性边界条件 试证明下式成立： eiKL =1
( x)= ( x L ) 和定态薛定谔方程 。
解：由于满足薛定谔定态方程
(x ) AeiKx
又 满足周期性边界条件
A1e( W /kT ) B 3000
13.
6
本征半导体中，从价带激发至导带的电子和价带产生的空穴共同电导，
激发的电子数 n可以近似表示为：
n N exp( E g / 2kT )
式中： N 为状态密度， k为波尔兹曼常数， T为热力学温度（ K ），试回答 （ 1）设 N =1023cm-3， k=8.6 10-5 eV k 1时， Si（ Eg 1.1eV） ,
=1.09 10 18 J 6.83eV
2
6.02 1023 / 8 ) 3
5. 计算 Na 在 0K 时自由电子的平均动能。 （Na 的摩尔质量 M=22.99 ， =1.013 103kg/m3 ）
（ P16）
2
解：由
E
0 F
h2 (3n / 8
2
)3
2m
(6.63 10 34 )2 1.013 106 = 2 9 10 31 (3 22.99
12.
实验测出离子型电导体的电导率与温度的相关数据， 经数学回归分析得出关系为 lg A B 1
T (1)试求在测量温度范围内的电导激活能表达式； (2) 若给出 T1=500K 时， 1=10-（9 m）-1，
T2 1000K时， 2=10-（6 m）-1 计算电导激活能的值。
第三章-Properties-of-Materials材料的性能PPT课件
淬火钢球或硬质合金球D(mm)压入试样表面
测量圆形压痕d, 圆形压痕表面积S
-
41
(1)布氏硬度HB：
F
2F
HB
S D(D D2d2)
淬火钢球： HBS<450 硬质合金球：HBW=450~650。
-
42
(2)HB表示方法：
数字 + 硬度符号 + 数字 /
↓
↓
↓
硬度值 (HBW或HBS) 钢球直径
溶剂都可以将其溶解； • 交联型高分子在有机溶剂中不溶解，但能溶胀，使材
料体积膨胀，性能变差； • 不同的高分子材料，其分子链以及侧基不同，对各种
有机溶剂表现出不同的耐受性； • 组织结构对耐溶剂性也有较大影响。
– 例如，作为结晶性聚合物，聚乙烯在大多数有机溶剂中都难 溶，因而具有很好的耐溶剂性。
-
• 聚四氟乙烯有极好的耐老化性能
– 氟原子与碳原子形成牢固的化学键；
– 氟原子的尺寸大小适中，一个紧挨一个，能把碳链紧紧 包围住。
• 分子链中含有不饱和双键、聚酰氨的酰氨键、聚碳酸 酯的酯键、聚砜的碳硫键、聚苯醚的苯环上的甲基等 等，都会降低高分子材料的耐老化性。
-
26
耐老化性的提高
(3) Chemical stability of polymers
• 延伸率
elongation
l f l0 100%
l0
• 断面收缩率
reduction of area
A0 Af 100%
A0
< 5%：
脆性材料
-
35
材料的一些力学性能特点：
• 很多金属材料既有高的强度，又有良好的延展性； • 多晶材料的强度高于单晶材料；