大连理工大学 秋季优化方法大作业
2016年大连理工大学优化方法上机大作业

2016年理工大学优化方法上机大作业学院:专业:班级:学号::上机大作业1:1.最速下降法:function f = fun(x)f = (1-x(1))^2 + 100*(x(2)-x(1)^2)^2; endfunction g = grad(x)g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)^2-x(2)); g(2) = 200*(x(2)-x(1)^2);endfunction x_star = steepest(x0,eps)gk = grad(x0);res = norm(gk);k = 0;while res > eps && k<=1000dk = -gk;ak =1; f0 = fun(x0);f1 = fun(x0+ak*dk);slope = dot(gk,dk);while f1 > f0 + 0.1*ak*slopeak = ak/4;xk = x0 + ak*dk;f1 = fun(xk);endk = k+1;x0 = xk;gk = grad(xk);res = norm(gk);fprintf('--The %d-th iter, the residual is %f\n',k,res); endx_star = xk;end>> clear>> x0=[0,0]';>> eps=1e-4;>> x=steepest(x0,eps)2.牛顿法:function f = fun(x)f = (1-x(1))^2 + 100*(x(2)-x(1)^2)^2; endfunction g = grad2(x)g = zeros(2,2);g(1,1)=2+400*(3*x(1)^2-x(2));g(1,2)=-400*x(1);g(2,1)=-400*x(1);g(2,2)=200;endfunction g = grad(x)g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)^2-x(2)); g(2) = 200*(x(2)-x(1)^2);endfunction x_star = newton(x0,eps)gk = grad(x0);bk = [grad2(x0)]^(-1);res = norm(gk);k = 0;while res > eps && k<=1000dk=-bk*gk;xk=x0+dk;k = k+1;x0 = xk;gk = grad(xk);bk = [grad2(xk)]^(-1);res = norm(gk);fprintf('--The %d-th iter, the residual is %f\n',k,res); endx_star = xk;end>> clear>> x0=[0,0]';>> eps=1e-4;>> x1=newton(x0,eps)--The 1-th iter, the residual is 447.213595--The 2-th iter, the residual is 0.000000x1 =1.00001.00003.BFGS法:function f = fun(x)f = (1-x(1))^2 + 100*(x(2)-x(1)^2)^2; endfunction g = grad(x)g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)^2-x(2)); g(2) = 200*(x(2)-x(1)^2);endfunction x_star = bfgs(x0,eps)g0 = grad(x0);gk=g0;res = norm(gk);Hk=eye(2);k = 0;while res > eps && k<=1000dk = -Hk*gk;ak =1; f0 = fun(x0);f1 = fun(x0+ak*dk);slope = dot(gk,dk);while f1 > f0 + 0.1*ak*slopeak = ak/4;xk = x0 + ak*dk;f1 = fun(xk);endk = k+1;fa0=xk-x0;x0 = xk;go=gk;gk = grad(xk);y0=gk-g0;Hk=((eye(2)-fa0*(y0)')/((fa0)'*(y0)))*((eye(2)-(y0)*(fa0)')/((fa0)'*( y0)))+(fa0*(fa0)')/((fa0)'*(y0));res = norm(gk);fprintf('--The %d-th iter, the residual is %f\n',k,res); endx_star = xk;End>> clear>> x0=[0,0]';>> eps=1e-4;>> x=bfgs(x0,eps)4.共轭梯度法:function f = fun(x)f = (1-x(1))^2 + 100*(x(2)-x(1)^2)^2; endfunction g = grad(x)g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)^2-x(2)); g(2) = 200*(x(2)-x(1)^2);endfunction x_star =CG(x0,eps)gk = grad(x0);res = norm(gk);k = 0;dk = -gk;while res > eps && k<=1000ak =1; f0 = fun(x0);f1 = fun(x0+ak*dk);slope = dot(gk,dk);while f1 > f0 + 0.1*ak*slopeak = ak/4;xk = x0 + ak*dk;f1 = fun(xk);endk = k+1;x0 = xk;g0=gk;gk = grad(xk);res = norm(gk);p=(gk/g0)^2;dk1=dk;dk=-gk+p*dk1;fprintf('--The %d-th iter, the residual is %f\n',k,res); endx_star = xk; end>> clear>> x0=[0,0]'; >> eps=1e-4; >> x=CG(x0,eps)上机大作业2:function f= obj(x)f=4*x(1)-x(2)^2-12;endfunction [h,g] =constrains(x) h=x(1)^2+x(2)^2-25;g=zeros(3,1);g(1)=-10*x(1)+x(1)^2-10*x(2)+x(2)^2+34;g(2)=-x(1);g(3)=-x(2);endfunction f=alobj(x) %拉格朗日增广函数%N_equ等式约束个数?%N_inequ不等式约束个数N_equ=1;N_inequ=3;global r_al pena;%全局变量h_equ=0;h_inequ=0;[h,g]=constrains(x);%等式约束部分?for i=1:N_equh_equ=h_equ+h(i)*r_al(i)+(pena/2)*h(i).^2;end%不等式约束部分for i=1:N_inequh_inequ=h_inequ+(0.5/pena)*(max(0,(r_al(i)+pena*g(i))).^2-r_al(i).^2) ;end%拉格朗日增广函数值f=obj(x)+h_equ+h_inequ;function f=compare(x)global r_al pena N_equ N_inequ;N_equ=1;N_inequ=3;h_inequ=zeros(3,1);[h,g]=constrains(x);%等式部分for i=1:1h_equ=abs(h(i));end%不等式部分for i=1:3h_inequ=abs(max(g(i),-r_al(i+1)/pena));endh1 = max(h_inequ);f= max(abs(h_equ),h1); %sqrt(h_equ+h_inequ);function [ x,fmin,k] =almain(x_al)%本程序为拉格朗日乘子算法示例算法%函数输入:% x_al:初始迭代点% r_al:初始拉格朗日乘子N-equ:等式约束个数N_inequ:不等式约束个数?%函数输出% X:最优函数点FVAL:最优函数值%============================程序开始================================ global r_al pena ; %参数(全局变量)pena=10; %惩罚系数r_al=[1,1,1,1];c_scale=2; %乘法系数乘数cta=0.5; %下降标准系数e_al=1e-4; %误差控制围max_itera=25;out_itera=1; %迭代次数%===========================算法迭代开始============================= while out_itera<max_iterax_al0=x_al;r_al0=r_al;%判断函数?compareFlag=compare(x_al0);%无约束的拟牛顿法BFGS[X,fmin]=fminunc(alobj,x_al0);x_al=X; %得到新迭代点%判断停止条件?if compare(x_al)<e_aldisp('we get the opt point');breakend%c判断函数下降度?if compare(x_al)<cta*compareFlagpena=1*pena; %可以根据需要修改惩罚系数变量elsepena=min(1000,c_scale*pena); %%乘法系数最大1000disp('pena=2*pena');end%%?更新拉格朗日乘子[h,g]=constrains(x_al);for i=1:1%%等式约束部分r_al(i)= r_al0(i)+pena*h(i);endfor i=1:3%%不等式约束部分r_al(i+1)=max(0,(r_al0(i+1)+pena*g(i)));endout_itera=out_itera+1;end%+++++++++++++++++++++++++++迭代结束+++++++++++++++++++++++++++++++++ disp('the iteration number');k=out_itera;disp('the value of constrains'); compare(x_al)disp('the opt point');x=x_al;fmin=obj(X);>> clear>> x_al=[0,0];>> [x,fmin,k]=almain(x_al)上机大作业3:1、>> clear alln=3; c=[-3,-1,-3]'; A=[2,1,1;1,2,3;2,2,1;-1,0,0;0,-1,0;0,0,-1];b=[2,5,6,0,0,0]'; cvx_beginvariable x(n)minimize( c'*x)subject toA*x<=bcvx_endCalling SDPT3 4.0: 6 variables, 3 equality constraints------------------------------------------------------------num. of constraints = 3dim. of linear var = 6*******************************************************************SDPT3: Infeasible path-following algorithms*******************************************************************version predcorr gam expon scale_dataNT 1 0.000 1 0it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime-------------------------------------------------------------------0|0.000|0.000|1.1e+01|5.1e+00|6.0e+02|-7.000000e+01 0.000000e+00| 0:0:00| chol 1 11|0.912|1.000|9.4e-01|4.6e-02|6.5e+01|-5.606627e+00 -2.967567e+01| 0:0:01| chol 1 12|1.000|1.000|1.3e-07|4.6e-03|8.5e+00|-2.723981e+00 -1.113509e+01| 0:0:01| chol 1 13|1.000|0.961|2.3e-08|6.2e-04|1.8e+00|-4.348354e+00 -6.122853e+00| 0:0:01| chol 1 14|0.881|1.000|2.2e-08|4.6e-05|3.7e-01|-5.255152e+00 -5.622375e+00| 0:0:01| chol 1 15|0.995|0.962|1.6e-09|6.2e-06|1.5e-02|-5.394782e+00 -5.409213e+00| 0:0:01| chol 1 16|0.989|0.989|2.7e-10|5.2e-07|1.7e-04|-5.399940e+00 -5.400100e+00| 0:0:01| chol 1 17|0.989|0.989|5.3e-11|5.8e-09|1.8e-06|-5.399999e+00 -5.400001e+00| 0:0:01| chol 1 18|1.000|0.994|2.8e-13|4.3e-11|2.7e-08|-5.400000e+00 -5.400000e+00| 0:0:01| stop: max(relative gap, infeasibilities) < 1.49e-08-------------------------------------------------------------------number of iterations = 8primal objective value = -5.39999999e+00dual objective value = -5.40000002e+00gap := trace(XZ) = 2.66e-08relative gap = 2.26e-09actual relative gap = 2.21e-09rel. primal infeas (scaled problem) = 2.77e-13rel. dual " " " = 4.31e-11rel. primal infeas (unscaled problem) = 0.00e+00rel. dual " " " = 0.00e+00norm(X), norm(y), norm(Z) = 4.3e+00, 1.3e+00, 1.9e+00norm(A), norm(b), norm(C) = 6.7e+00, 9.1e+00, 5.4e+00Total CPU time (secs) = 0.71CPU time per iteration = 0.09termination code = 0DIMACS: 3.6e-13 0.0e+00 5.8e-11 0.0e+00 2.2e-09 2.3e-09-------------------------------------------------------------------------------------------------------------------------------Status: SolvedOptimal value (cvx_optval): -5.42、>> clear alln=2; c=[-2,-4]'; G=[0.5,0;0,1]; A=[1,1;-1,0;0,-1]; b=[1,0,0]'; cvx_beginvariable x(n)minimize( x'*G*x+c'*x)subject toA*x<=bcvx_endCalling SDPT3 4.0: 7 variables, 3 equality constraintsFor improved efficiency, SDPT3 is solving the dual problem.------------------------------------------------------------num. of constraints = 3dim. of socp var = 4, num. of socp blk = 1dim. of linear var = 3******************************************************************* SDPT3: Infeasible path-following algorithms*******************************************************************version predcorr gam expon scale_dataNT 1 0.000 1 0it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime-------------------------------------------------------------------0|0.000|0.000|8.0e-01|6.5e+00|3.1e+02| 1.000000e+01 0.000000e+00| 0:0:00| chol 1 1 1|1.000|0.987|4.3e-07|1.5e-01|1.6e+01| 9.043148e+00 -2.714056e-01| 0:0:00| chol 1 1 2|1.000|1.000|2.6e-07|7.6e-03|1.4e+00| 1.234938e+00 -5.011630e-02| 0:0:00| chol 1 1 3|1.000|1.000|2.4e-07|7.6e-04|3.0e-01| 4.166959e-01 1.181563e-01| 0:0:00| chol 1 1 4|0.892|0.877|6.4e-08|1.6e-04|5.2e-02| 2.773022e-01 2.265122e-01| 0:0:00| chol 1 1 5|1.000|1.000|1.0e-08|7.6e-06|1.5e-02| 2.579468e-01 2.427203e-01| 0:0:00| chol 1 1 6|0.905|0.904|3.1e-09|1.4e-06|2.3e-03| 2.511936e-01 2.488619e-01| 0:0:00| chol 1 1 7|1.000|1.000|6.1e-09|7.7e-08|6.6e-04| 2.503336e-01 2.496718e-01| 0:0:00| chol 1 1 8|0.903|0.903|1.8e-09|1.5e-08|1.0e-04| 2.500507e-01 2.499497e-01| 0:0:00| chol 1 19|1.000|1.000|4.9e-10|3.5e-10|2.9e-05| 2.500143e-01 2.499857e-01| 0:0:00| chol 1 1 10|0.904|0.904|4.7e-11|1.3e-10|4.4e-06| 2.500022e-01 2.499978e-01| 0:0:00| chol 2 2 11|1.000|1.000|2.3e-12|9.4e-12|1.2e-06| 2.500006e-01 2.499994e-01| 0:0:00| chol 2 2 12|1.000|1.000|4.7e-13|1.0e-12|1.8e-07| 2.500001e-01 2.499999e-01| 0:0:00| chol 2 2 13|1.000|1.000|2.0e-12|1.0e-12|4.2e-08| 2.500000e-01 2.500000e-01| 0:0:00| chol 2 2 14|1.000|1.000|2.6e-12|1.0e-12|7.3e-09| 2.500000e-01 2.500000e-01| 0:0:00|stop: max(relative gap, infeasibilities) < 1.49e-08-------------------------------------------------------------------number of iterations = 14primal objective value = 2.50000004e-01dual objective value = 2.49999996e-01gap := trace(XZ) = 7.29e-09relative gap = 4.86e-09actual relative gap = 4.86e-09rel. primal infeas (scaled problem) = 2.63e-12rel. dual " " " = 1.00e-12rel. primal infeas (unscaled problem) = 0.00e+00rel. dual " " " = 0.00e+00norm(X), norm(y), norm(Z) = 3.2e+00, 1.5e+00, 1.9e+00norm(A), norm(b), norm(C) = 3.9e+00, 4.2e+00, 2.6e+00Total CPU time (secs) = 0.36CPU time per iteration = 0.03termination code = 0DIMACS: 3.7e-12 0.0e+00 1.3e-12 0.0e+00 4.9e-09 4.9e-09------------------------------------------------------------------------------------------------------------------------------- Status: SolvedOptimal value (cvx_optval): -3。
优化作业流程的三种方法

优化作业流程的三种方法下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!优化作业流程是提高工作效率和质量的重要手段。
以下是三种常见的优化作业流程的方法:1. 流程再造:步骤:分析现有流程:对当前的作业流程进行全面的分析,包括流程的各个环节、涉及的人员、使用的工具和资源等。
大工20秋《人机交互》大作业答案

大工20秋《人机交互》大作业答案一、项目概述本大作业旨在设计一个人机交互系统,提供便捷的交互方式,以提高用户体验和效率。
二、需求分析根据用户调研和需求分析,我们得出以下主要需求:1. 用户可以通过语音输入对系统进行操作。
2. 系统需要提供图形化界面,方便用户进行操作和导航。
3. 用户可以利用手势来进行交互和控制。
4. 系统需要支持多平台,包括移动设备和桌面设备。
三、系统设计基于以上需求,我们提出了以下系统设计方案:1. 语音输入:系统将集成语音识别功能,通过语音输入来实现用户操作和控制。
2. 图形化界面:我们将采用现代化的图形界面设计,提供直观友好的交互界面,使用户能够轻松使用系统。
3. 手势交互:系统将支持手势识别,并提供相应的手势操作指令,以增加用户的交互自由度。
4. 跨平台支持:系统将开发移动设备和桌面设备的应用程序,以满足用户在不同平台上的需求。
四、技术实现为了实现上述系统设计方案,我们将采用以下技术:1. 语音识别:使用现有的语音识别API,如Google Speech API 或微软的语音识别API,实现语音输入功能。
2. 图形界面:采用现代化的前端开发框架,如React或Angular,设计具有良好用户体验的图形界面。
3. 手势识别:利用现有的手势识别技术,如Leap Motion或Microsoft Kinect,实现手势交互功能。
4. 跨平台开发:使用跨平台开发框架,如React Native或Electron,来开发移动设备和桌面设备的应用程序。
五、测试和验证为了确保系统的正常运行和满足用户需求,我们将进行以下测试和验证:1. 功能测试:测试系统的各项功能是否正常运行,包括语音输入、图形界面和手势交互。
2. 用户测试:邀请一些用户进行系统使用测试,并收集他们的反馈和意见,以改进系统的用户体验和界面设计。
3. 跨平台测试:在不同的移动设备和桌面设备上测试应用程序的兼容性和性能。
大连理工大学20年秋季《软件工程》在线作业2附参考答案

大连理工大学20年秋季《软件工程》在线作业2附参考答案
试卷总分:100 得分:100
一、单选题 (共 10 道试题,共 50 分)
1.为了提高模块的独立性,模块内部最高程度的内聚是( )。
A.逻辑内聚
B.时间内聚
C.功能内聚
D.偶然内聚
答案:C
2.下列几种类型中,耦合性最弱的是( )耦合。
A.内容
B.控制
C.公共环境
D.数据
答案:D
更多加微boge30619
3.一个只有顺序结构的程序(含有4条边,5个顶点),其环形复杂度是( )。
A.0
B.1
C.3
D.4
答案:B
4.在详细设计阶段,经常采用的工具不包括( )。
A.PAD
B.N-S
C.PDL
D.DFD
答案:D
5.下面说法正确的是( )。
A.测试是为了表明程序是正确的
B.成功的测试是没有发现错误的测试
C.测试是为了发现程序中的错误而执行程序的过程
D.以上都不对
答案:C
6.使用程序设计的控制结构导出测试用例的测试方法是( )。
A.黑盒测试。
大连理工大学优化方法上机作业

大连理工大学优化方法上机作业本页仅作为文档页封面,使用时可以删除This document is for reference only-rar21year.March优化方法上机大作业学院:电子信息与电气工程学部姓名:学号:指导老师:上机大作业(一)%目标函数function f=fun(x)f=100*(x(2)-x(1)^2)^2+(1-x(1))^2;end%目标函数梯度function gf=gfun(x)gf=[-400*x(1)*(x(2)-x(1)^2)-2*(1-x(1));200*(x(2)-x(1)^2)]; End%目标函数Hess矩阵function He=Hess(x)He=[1200*x(1)^2-400*x(2)+2,-400*x(1);-400*x(1), 200;];end%线搜索步长function mk=armijo(xk,dk)beta=0.5; sigma=0.2;m=0; maxm=20;while (m<=maxm)if(fun(xk+beta^m*dk)<=fun(xk)+sigma*beta^m*gfun(xk)'*dk) mk=m; break;endm=m+1;endalpha=beta^mknewxk=xk+alpha*dkfk=fun(xk)newfk=fun(newxk)%最速下降法function [k,x,val]=grad(fun,gfun,x0,epsilon)%功能:梯度法求解无约束优化问题:minf(x)%输入:fun,gfun分别是目标函数及其梯度,x0是初始点,% epsilon为容许误差%输出:k是迭代次数,x,val分别是近似最优点和最优值maxk=5000; %最大迭代次数beta=0.5; sigma=0.4;k=0;while(k<maxk)gk=feval(gfun,x0); %计算梯度dk=-gk; %计算搜索方向if(norm(gk)<epsilon), break;end%检验终止准则m=0;mk=0;while(m<20) %用Armijo搜索步长if(feval(fun,x0+beta^m*dk)<=feval(fun,x0)+sigma*beta^m*gk'*dk) mk=m;break;endm=m+1;endx0=x0+beta^mk*dk;k=k+1;endx=x0;val=feval(fun,x0);>> x0=[0;0];>> [k,x,val]=grad('fun','gfun',x0,1e-4)迭代次数:k =1033x =0.99990.9998val =1.2390e-008%牛顿法x0=[0;0];ep=1e-4;maxk=10;k=0;while(k<maxk)gk=gfun(x0);if(norm(gk)<ep)x=x0miny=fun(x)k0=kbreak;elseH=inv(Hess(x0));x0=x0-H*gk;k=k+1;endendx =1.00001.0000miny =4.9304e-030迭代次数k0 =2%BFGS方法function [k,x,val]=bfgs(fun,gfun,x0,varargin) %功能:梯度法求解无约束优化问题:minf(x)%输入:fun,gfun分别是目标函数及其梯度,x0是初始点,% epsilon为容许误差%输出:k是迭代次数,x,val分别是近似最优点和最优值N=1000;epsilon=1e-4;beta=0.55;sigma=0.4;n=length(x0);Bk=eye(n);k=0;while(k<N)gk=feval(gfun,x0,varargin{:});if(norm(gk)<epsilon), break;enddk=-Bk\gk;m=0;mk=0;while(m<20)newf=feval(fun,x0+beta^m*dk,varargin{:});oldf=feval(fun,x0,varargin{:});if(newf<=oldf+sigma*beta^m*gk'*dk)mk=m;break;endm=m+1;endx=x0+beta^mk*dk;sk=x-x0;yk=feval(gfun,x,varargin{:})-gk;if(yk'*sk>0)Bk=Bk-(Bk*sk*sk'*Bk)/(sk'*Bk*sk)+(yk*yk')/(yk'*sk);endk=k+1;x0=x;endval=feval(fun,x0,varargin{:});>> x0=[0;0];>> [k,x,val]=bfgs('fun','gfun',x0)k =20x =1.00001.0000val =2.2005e-011%共轭梯度法function [k,x,val]=frcg(fun,gfun,x0,epsilon,N)if nargin<5,N=1000;endif nargin<4, epsilon=1e-4;endbeta=0.6;sigma=0.4;n=length(x0);k=0;while(k<N)gk=feval(gfun,x0);itern=k-(n+1)*floor(k/(n+1));itern=itern+1;if(itern==1)dk=-gk;elsebetak=(gk'*gk)/(g0'*g0);dk=-gk+betak*d0; gd=gk'*dk;if(gd>=0),dk=-gk;endendif(norm(gk)<epsilon),break;endm=0;mk=0;while(m<20)if(feval(fun,x0+beta^m*dk)<=feval(fun,x0)+sigma*beta^m*gk'*dk) mk=m;break;endm=m+1;endx=x0+beta^m*dk;g0=gk; d0=dk;x0=x;k=k+1;endval=feval(fun,x);>> x0=[0;0];[k,x,val]=frcg('fun','gfun',x0,1e-4,1000)k =122x =1.00011.0002val =7.2372e-009上机大作业(二)%目标函数function f_x=fun(x)f_x=4*x(1)-x(2)^2-12;%等式约束条件function he=hf(x)he=25-x(1)^2-x(2)^2;end%不等式约束条件function gi_x=gi(x,i)switch icase 1gi_x=10*x(1)-x(1)^2+10*x(2)-x(2)^2-34;case 2gi_x=x(1);case 3gi_x=x(2);otherwiseend%求目标函数的梯度function L_grad=grad(x,lambda,cigma)d_f=[4;2*x(2)];d_g(:,1)=[-2*x(1);-2*x(2)];d_g(:,2)=[10-2*x(1);10-2*x(2)];d_g(:,3)=[1;0];d_g(:,4)=[0;1];L_grad=d_f+(lambda(1)+cigma*hf(x))*d_g(:,1);for i=1:3if lambda(i+1)+cigma*gi(x,i)<0L_grad=L_grad+(lambda(i+1)+cigma*gi(x,i))*d_g(:,i+1);continueendend%增广拉格朗日函数function LA=lag(x,lambda,cee)LA=fun(x)+lambda(1)*hf(x)+0.5*cee*hf(x)^2;for i=1:3LA=LA+1/(2*cee)*(min(0,lambda(i+1)+cee*gi(x,i))^2-lambda(i+1)^2); endfunction xk=BFGS(x0,eps,lambda,cigma)gk=grad(x0,lambda,cigma);res_B=norm(gk);k_B=0;a_=1e-4;rho=0.5;c=1e-4;length_x=length(x0);I=eye(length_x);Hk=I;while res_B>eps&&k_B<=10000dk=-Hk*gk;m=0;while m<=5000if lag(x0+a_*rho^m*dk,lambda,cigma)-lag(x0,lambda,cigma)<=c*a_*rho^m*gk'*dkmk=m;break;endm=m+1;endak=a_*rho^mk;xk=x0+ak*dk;delta=xk-x0;y=grad(xk,lambda,cigma)-gk;Hk=(I-(delta*y')/(delta'*y))*Hk*(I-(y*delta')/(delta'*y))+(delta*delta')/(delta'*y);k_B=k_B+1;x0=xk;gk=y+gk;res_B=norm(gk);end%增广拉格朗日法function val_min=ALM(x0,eps)lambda=zeros(4,1);cigma=5;alpha=10;k=1;res=[abs(hf(x0)),0,0,0];for i=1:3res(1,i+1)=norm(min(gi(x0,i),-lambda(i+1)/cigma)); endres=max(res);while res>eps&&k<1000xk=BFGS(x0,eps,lambda,cigma);lambda(1)=lambda(1)+cigma*hf(xk);for i=1:3lambda(i+1)=lambda(i+1)+min(0,lambda(i+1)+gi(x0,1)); endk=k+1;cigma=alpha*cigma;x0=xk;res=[norm(hf(x0)),0,0,0];for i=1:3res(1,i+1)=norm(min(gi(x0,i),-lambda(i+1)/cigma)); endres=max(res);endval_min=fun(xk);fprintf('k=%d\n',k);fprintf('fmin=%.4f\n',val_min);fprintf('x=[%.4f;%.4f]\n',xk(1),xk(2));>> x0=[0;0];>> val_min=ALM(x0,1e-4)k=10fmin=-31.4003x=[1.0984;4.8779]val_min =-31.4003上机大作业(三)A=[1 1;-1 0;0 -1];n=2;b=[1;0;0];G=[0.5 0;0 2];c=[2 4];cvx_solver sdpt3cvx_beginvariable x(n)minimize (x'*G*x-c*x)subject toA*x<=bcvx_enddisp(x)Status: SolvedOptimal value (cvx_optval): -2.40.40000.6000A=[2 1 1;1 2 3;2 2 1;-1 0 0;0 -1 0;0 0 -1]; n=3;b=[2;5;6;0;0;0];C=[-3 -1 -3];cvx_solver sdpt3cvx_beginvariable x(n)minimize (C*x)subject toA*x<=bcvx_enddisp(x)Status: SolvedOptimal value (cvx_optval): -5.40.20000.00001.600011。
大连理工大学硕士研究生有限元课程大作业参考模板

盘轴紧配合结构分析214000000 Alex 183******** 1*********@摘要接触是一种高度非线性行为,需要较多的计算资源,为了进行有效的计算,理解问题的特性和建立合理的模型是很重要的。
在本文中,将在Ansys环境中用有限元分析方法对一个盘轴紧配合结构进行接触分析。
第一个载荷步分析轴和盘在过盈配合时的应力,第二个载荷步分析将该轴从盘心拔出时轴和盘的接触应力情况。
关键词: 接触,盘轴,有限元方法,接触应力0.前言有限元法(Finite Element Method,FEM),是计算力学中的一种重要的方法,它是20世纪50年代末60年代初兴起的应用数学、现代力学及计算机科学相互渗透、综合利用的边缘科学。
接触是一种高度非线性行为,需要较大的计算资源,为了进行有效的计算,理解问题的特性和建立合理的模型是很重要的。
本文中将通过轴盘点接触(面面接触)说明接触分析的方法。
1.问题描述在旋转机械中通常会遇到轴与轴承、轴与齿轮、轴与盘连接的问题,根据各自的不同情况可能有不同的连接形式。
但大多数连接形式中存在过盈配合,也就是涉及到接触问题的分析。
这里我们以某转子中轴和盘的连接为例,分析轴和盘的配合应力以及将轴从盘中拔出时盘轴连接处的应力情况。
本实例的轴为一等直径空心轴,盘为等厚度圆盘,其结构及尺寸如图 1.1所示。
由于模型和载荷都是轴对称的,可以用轴对称方法进行分析。
这里为了后处理时观察结果更直观,我们采用整个模型的四分之一进行建模分析,最后将其进行扩展,来观察整个结构的变形及应力分布、变化情况。
盘和轴共用同一种材料,其性质如下:弹性模量: EX=2.5E5泊松比: NUXY=0.35接触摩擦系数: MU=0.2图1.1 盘轴结构图1.系统建模2.1 建立几何模型并划分网格调整后的两个圆环几何体如图2.1所示。
读者可以单击对话框下部的动态显示选择框,然后通过鼠标右键来调整视图位置。
图 2.1 建立的盘轴几何模型对盘进行网格划分,建立的有限元模型如图2.2所示。
最优化大作业2

最优化大作业2⚫姓名:cxf⚫班级学号:****20****⚫学院:******学院⚫选择方式:方式4——撰写课程小论文⚫题目来源:附录二备选问题(计算机通信网)中文献[9]——F. Kelly. The Mathematics of Traffic in Network. Princeton University Press, 2005.⚫工作方式:独立完成⚫完成时间:2020年12月15日交通网络中的数学优化问题研究cxf(北京航空航天大学 ******学院, 北京 100191)摘要 由于交通网络流中分散控制的程度差异,人们往往需要寻求一种解决方案对系统进行继续扩展和优化。
车流量控制问题一直是交通网络所面临的重要挑战,也是研究者研究的重点。
本论文用微积分来描述拥堵如何依赖于车流量,以Wardrop 均衡和Braess’s 悖论等理论为基础,建立车流分配控制问题的数学模型,并利用Lingo 优化软件对原始问题进行求解。
最后,由优化模型的结果可知,当网络达到均衡状态时不一定是最优的车流分配方案,且达到最优解状态时能够使通信网络中的分散控制能够表现的更好。
但是,这最优方案需强制执行,否则自私车辆又会选择最短的路径,即形成新的均衡状态。
关键词 交通网络,车流分配, Wardrop 均衡, 优化模型.1.问题背景许多网络中都普遍存在着拥堵现象,其拥堵的发生方式和原因不尽相同。
然而,流量通过网络的流动方式是不同用户之间微妙而复杂交互的结果。
例如,在交通网络中,每位驾驶员都会尝试选择最方便的路径,以便节省时间和开销,而这一选择将取决于驾驶员期望在不同道路上遇到的延迟,且这些延迟反过来取决于其他人对路径的选择。
这种相互依赖关系,使得人们很难预测系统变化的影响,例如建造新的道路或在某地方实行收费等。
在电话网、互联网和交通网等大型网络系统中,主要的实际问题就是控制权的分散程度不同。
发展至今,这种分散式节点之间的流量控制方法已经显示出紧张的迹象,如果网络作为一个整体要继续扩展和进化,则需要进一步优化网络流量控制。
最优化方法大作业模板
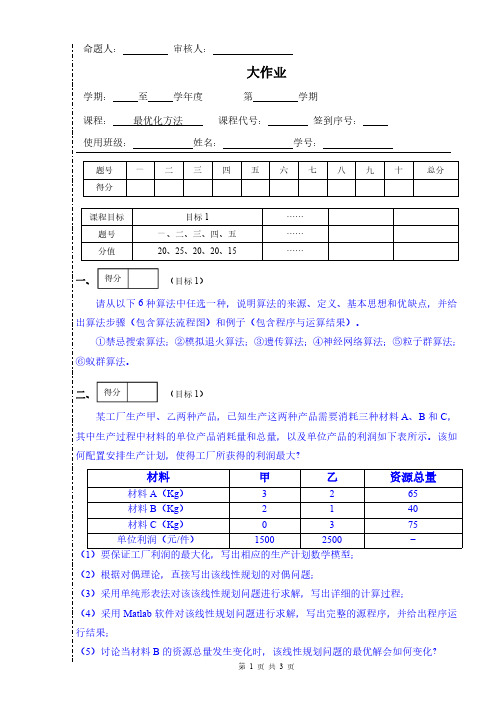
命题人:审核人:大作业学期:至学年度第学期课程:最优化方法课程代号:签到序号:使用班级:姓名:学号:题号一二三四五六七八九十总分得分一、(目标1)请从以下6种算法中任选一种,说明算法的来源、定义、基本思想和优缺点,并给出算法步骤(包含算法流程图)和例子(包含程序与运算结果)。
①禁忌搜索算法;②模拟退火算法;③遗传算法;④神经网络算法;⑤粒子群算法;⑥蚁群算法。
二、(目标1)某工厂生产甲、乙两种产品,已知生产这两种产品需要消耗三种材料A 、B 和C ,其中生产过程中材料的单位产品消耗量和总量,以及单位产品的利润如下表所示。
该如何配置安排生产计划,使得工厂所获得的利润最大?材料甲乙资源总量材料A (Kg )3265材料B (Kg )2140材料C (Kg )0375单位利润(元/件)15002500-(1)要保证工厂利润的最大化,写出相应的生产计划数学模型;(2)根据对偶理论,直接写出该线性规划的对偶问题;(3)采用单纯形表法对该该线性规划问题进行求解,写出详细的计算过程;(4)采用Matlab 软件对该线性规划问题进行求解,写出完整的源程序,并给出程序运行结果;(5)讨论当材料B 的资源总量发生变化时,该线性规划问题的最优解会如何变化?课程目标目标1……题号一、二、三、四、五……分值20、25、20、20、15……得分得分三、(目标1)求解下列无约束非线性规划问题(1)采用黄金分割法求解:min 4()24f x x x =++。
初始区间为[-1.0],精度为ε=10-4。
(要求:采用黄金分割法进行Matlab 编程求解,写出源程序,并给出运行结果,列出迭代过程的数据表格)(2)采用阻尼牛顿法求解:222121212min (,)4f x x x x x x =+-。
分别取两个初始点:x A =(1,1)T ,x B =(3,4)T 。
(要求:采用阻尼牛顿法进行Matlab 编程求解,并给出运行结果,列出迭代过程的数据表格)四、(目标1)求解下列约束非线性规划问题:22112212121212min ()23532..00f x x x x x x x x x x x s t x x =-+--+≤⎧⎪-≤⎪⎨≥⎪⎪≥⎩(1)采用罚函数法进行求解,需写出具体计算过程;(2)采用二次规划方法进行求解,需写出具体计算过程,并进行MATLAB 编程,写出源程序和运算结果;五、(目标1)(1)某商店在未来的4个月里,准备利用它的一个仓库来专门经营某种商品,仓库的最大容量为1000单位,而且该商店每月只能出卖仓库现有的货。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
m=m+1; end x0=x0+rho^mk*d; val=feval(fun,x0); g0=g; d0=d; k=k+1; end x=x0; val=feval(fun,x);
//f(x)//
function f=fun(x) x1=[1 0]*x; x2=[0 1]*x; f=(1-x1)^2+100*(x2-x1^2)^2; //梯度函数// function g=gfun(x) x1=[1 0]*x; x2=[0 1]*x; g=[-2*(1-x1)-400*x1*(x2-x1^2); 200*(x2-x1^2)]; //运行过程// >> x0=[0 0]'
k=k+1; btaold=btak; x0=x; end f=feval(fun,x); output.fval=f; output.iter=k; output.inner_iter=ink; output.bta=btak;
//增广拉格朗日函数//
function psi=mpsi(x,fun,hf,gf,dfun,dhf,dgf,mu,lambda,sigma) f=feval(fun,x); he=feval(hf,x); gi=feval(gf,x); l=length(he); m=length(gi); psi=f; s1=0.0; for(i=1:l) psi=psi-he(i)*mu(i); s1=s1+he(i)^2; end psi=psi+0.5*sigma*s1; s2=0.0; for(i=1:m) s3=max(0.0, lambda(i) - sigma*gi(i)); s2=s2+s3^2-lambda(i)^2; end psi=psi+s2/(2.0*sigma); //增广拉格朗日函数// function dpsi=dmpsi(x,fun,hf,gf,dfun,dhf,dgf,mu,lambda,sigma) dpsi=feval(dfun,x); he=feval(hf,x); gi=feval(gf,x); dhe=feval(dhf,x); dgi=feval(dgf,x); l=length(he); m=length(gi); for(i=1:l) dpsi=dpsi+(sigma*he(i)-mu(i))*dhe(:,i); end for(i=1:m) dpsi=dpsi+(sigma*gi(i)-lambda(i))*dgi(:,i); end //f(x)// function f=f1(x) f=4*x(1)-x(2)^2-12; //等式约束// function he=h1(x) he=25-x(1)^2-x(2)^2;
//f(x)//
function f=f(x) x1=[1 0]*x; x2=[0 1]*x; f=(1-x1)^2+100*(x2-x1^2)^2; //梯度函数// function g=g(x) x1=[1 0]*x; x2=[0 1]*x; g=[-2*(1-x1)-400*x1*(x2-x1^2); 200*(x2-x1^2)]; //运行过程//
lls=x; sll=f(x); fprintf('after %d iterations,obtain the optimal solution.\n\nThe optimal solution is %f.\n\n The optimal "x" is "ans".\n',k,sll); //f(x)// function f=f(x) x1=[1 0]*x; x2=[0 1]*x; f=(1-x1)^2+100*(x2-x1^2)^2; //梯度函数// function g=g(x) x1=[1 0]*x; x2=[0 1]*x; g=[-2*(1-x1)-400*x1*(x2-x1^2); 200*(x2-x1^2)]; //hess 阵// function h=h(x) x1=[1 0]*x; x2=[0 1]*x; h=[ 2+1200*x1^2-400*x2-400*x1; -400*x1 200]; //运行过程// >> x=[0;0]
while (k>=0&&k<100) if norm(g0)<eps break; else lanmed=10;c=0.1;i=0; while (i>=0&&i<100) x=x0+lanmed*s0; if f(x)>(f(x0)+c*lanmed*g0'*s0) lanmed=lanmed/2; i=i+1; else break; end end x=x0+lanmed*s0; dete_x=x-x0; dete_g=g(x)-g0; miu=1+dete_g'*H0*dete_g/(dete_x'*dete_g); H=H0+(miu*dete_x*dete_x'-H0*dete_g*dete_x'-dete_x*dete_g'*H0)/(dete_x '*dete_g); s=-H*g(x); x0=x; s0=s; H0=H; g0=g(x); k=k+1; end end lls=x; sll=f(x); fprintf('after %d iterations,obtain the optimal solution.\n\nThe optimal solution is %f.\n\n The optimal "x" is "ans".\n',k,sll);
x=
0 0
>> di1tinewton(x) after 2 iterations,obtain the optimal solution.
The optimal solution is 0.000000.
The optimal "x" is "ans".
ans =
1.0000 1.0000 3°BFGS 方法 //bfgs 主函数// function lls=di1tiBFGS(x) x0=x; eps=1e-4; k=0; g0=g(x0); H0=eye(2);s0=-H0*g0;
优化方法
期末上机大作业
姓 名:李岚松 学 部:电信学部电气工程 学 号:31609020
2016 年 11 月 9 日
1°最速下降法 //最速下降法主函数// function lls=di1titidu(x) x0=x; eps=1e-4; k=0; g0=g(x0); s0=-g0; while (k>=0) if norm(g0)<eps break; else lanmed=10;c=0.1;i=0; while i>=0&&i<100 x=x0+lanmed*s0; if f(x)>(f(x0)+c*lanmed*g0'*s0) lanmed=lanmed/2; i=i+1; else break; end end x=x0+lanmed*s0; x0=x; g0=g(x); s0=-g0; k=k+1; end end lls=x; sll=f(x); fprintf('after %d iterations,obtain the optimal solution.\n\nThe optimal solu is "ans".\n',k,sll);
x0 =
0 0
>> [x,val,k]=frcg('fun','gfun',x0)
x=
1.0001 1.0002
val =
7.2372e-09
k=
122
//增广拉格朗日法主函数// function [x,mu,lambda,output]=multphr(fun,hf,gf,dfun,dhf,dgf,x0) maxk=500; sigma=2.0; eta=2.0; theta=0.8; k=0; ink=0; epsilon=1e-4; x=x0; he=feval(hf,x); gi=feval(gf,x); n=length(x); l=length(he); m=length(gi); mu=0.1*ones(l,1); lambda=0.1*ones(m,1); btak=10; btaold=10; while(btak>epsilon & k<maxk) [x,ival,ik]=bfgs('mpsi','dmpsi',x0,fun,hf,gf,dfun,dhf,dgf,mu,lambda,s igma); ink=ink+ik; he=feval(hf,x); gi=feval(gf,x); btak=0.0; for i=1:l, btak=btak+he(i)^2; end for i=1:m temp=min(gi(i),lambda(i)/sigma); btak=btak+temp^2; end btak=sqrt(btak); if btak>epsilon if(k>=2 & btak > theta*btaold) sigma=eta*sigma; end for i=1:l, mu(i)=mu(i)-sigma*he(i); end for i=1:m lambda(i)=max(0.0,lambda(i)-sigma*gi(i)); end end
x=
0 0
>> di1titidu(x) after 4574 iterations,obtain the optimal solution.
