基于动态加权Bagging矩阵分解的推荐系统模型
基于矩阵分解的情景感知个性化推荐法研究
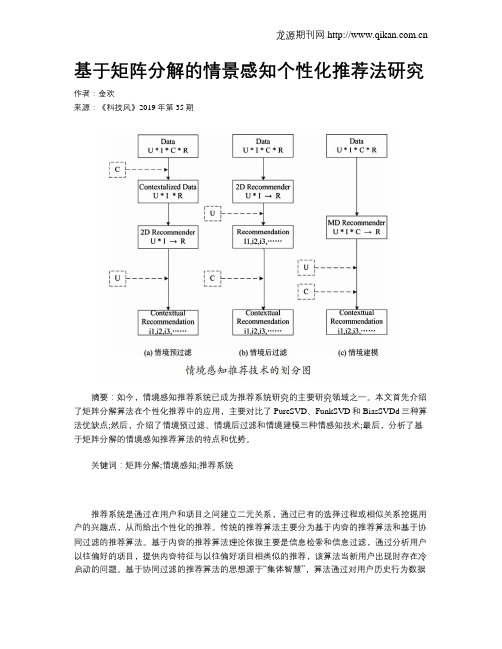
基于矩阵分解的情景感知个性化推荐法研究作者：金欢来源：《科技风》2019年第35期摘要：如今，情境感知推荐系统已成为推荐系统研究的主要研究领域之一。
本文首先介绍了矩阵分解算法在个性化推荐中的应用，主要对比了PureSVD、FunkSVD和BiasSVDd三种算法优缺点;然后，介绍了情境预过滤、情境后过滤和情境建模三种情感知技术;最后，分析了基于矩阵分解的情境感知推荐算法的特点和优势。
关键词：矩阵分解;情境感知;推荐系统推荐系统是通过在用户和项目之间建立二元关系，通过已有的选择过程或相似关系挖掘用户的兴趣点，从而给出个性化的推荐。
传统的推荐算法主要分为基于内容的推荐算法和基于协同过滤的推荐算法。
基于内容的推荐算法理论依据主要是信息检索和信息过滤，通过分析用户以往偏好的项目，提供内容特征与以往偏好项目相类似的推荐，该算法当新用户出现时存在冷启动的问题。
基于协同过滤的推荐算法的思想源于“集体智慧”，算法通过对用户历史行为数据的挖掘发现用户的偏好，基于不同的偏好对用户进行群组划分并推荐品味相似的商品。
协同过滤算法同样也存在冷启动的问题，当没新用户数据时，无法给出较好的推荐。
没有考虑情境的差异，比如不同根据季节的不同，给用户推荐与季节相适应的服饰。
基于以上问题，研究人员提出了基于矩阵分解的情境感知推荐法。
1 矩阵分解算法在个性化推荐中的应用矩阵分解的核心思想是将用户评分矩阵分解为低秩的矩阵，使其乘积尽可能接近原始评分矩阵，使得预测的矩阵与原始矩阵之间的误差平方最小。
奇异值分解（Singular Value Decomposition，以下简称SVD）在机器学习领域得到了广泛的应用，因为它不仅可以用于降维算法中的特征分解，还能用于推荐算法。
如果将m个用户和n个项目对应的评分看做一个矩阵M，本文将用矩阵分解来解决该问题。
1.1 PureSVD算法PureSVD（传统的奇异值分解）在降维中的应用，将用户和项目对应的m×n矩阵M进行SVD分解，通过选择部分较大的奇异值进行降维分解为：Mm×n=Um×k∑k×kVTk×n（1）其中k是矩阵M中的奇异值的个数，一般会小于用户数和项目数。
bagging,boosting,stacking基本流程
bagging,boosting,stacking基本流程
以下是bagging、boosting、stacking三种集成学习方法的流程：
1. Bagging：
从原始样本集中使用Bootstraping方法随机抽取n个训练样本，共进行k 轮抽取，得到k个训练集（k个训练集之间相互独立，元素可以有重复）。
对于抽取的k个训练集，可以训练出k个模型。
对于分类问题，由投票表决产生的分类结果。
2. Boosting：
对训练集中的每个样本建立权值wi，表示每个样本的权重。
在随后的运算中，对于被错误分类的样本，权重会在下一轮的分类中获得
更大的权重。
对于误差率较小的弱学习器，加大权值，使其在表决中起到更大的作用。
对于误差率较大的弱学习器，减小权值，使其在表决中起到较小的作用。
Boosting算法基于错误提升模型性能，根据前面分类器分类错误的样本，调整训练集中各个样本的权重，构建新的分类器。
其训练过程是呈阶梯状的，后一个基模型会在前一个基模型的基础上进行学习，最终以某种综合方式，比如加权法，对所有模型的预测结果进行加权来产生最终的结果。
3. Stacking：
将训练数据D划分为两个不相交的子集D1，D2。
用训练集的第一部分D1训练多个不同的基模型。
将多个基模型用于预测训练集的第二部分D2。
将基模型的预测结果当作输入，D2的样本标签当作学习目标，训练一个高层的模型。
以上是三种集成学习方法的基本流程，请注意这些方法各有特点，适用于不同的情况和问题类型。
在实际应用中需要根据具体需求和数据特点来选择合适的方法。
《基于矩阵分解的鲁棒推荐算法研究》范文
《基于矩阵分解的鲁棒推荐算法研究》篇一一、引言随着互联网技术的飞速发展，网络数据呈现爆炸式增长，用户面临着信息过载的问题。
为了解决这一问题，推荐系统应运而生，成为了一种有效的信息过滤工具。
其中，基于矩阵分解的推荐算法是当前研究的热点之一。
本文旨在研究基于矩阵分解的鲁棒推荐算法，以提高推荐系统的准确性和稳定性。
二、背景及意义推荐系统通过分析用户的行为数据，为用户提供个性化的信息推荐服务。
基于矩阵分解的推荐算法是推荐系统中的一种重要方法，其核心思想是将用户-项目评分矩阵分解为用户矩阵和项目矩阵，从而捕捉用户和项目的潜在特征。
然而，传统的矩阵分解算法在处理稀疏数据和噪声数据时，容易出现准确性下降和稳定性差的问题。
因此，研究基于矩阵分解的鲁棒推荐算法具有重要意义。
三、相关文献综述近年来，关于矩阵分解的推荐算法研究取得了丰富的成果。
研究者们从不同角度对算法进行了改进和优化，如引入额外信息、考虑时间因素、处理数据稀疏性等。
然而，现有研究在处理噪声数据和保证算法鲁棒性方面仍有待加强。
因此，本研究旨在针对这一问题展开深入研究。
四、基于矩阵分解的鲁棒推荐算法研究（一）算法原理本研究提出的基于矩阵分解的鲁棒推荐算法，主要思想是在传统矩阵分解的基础上，引入鲁棒性优化方法，以提高算法在处理噪声数据时的准确性和稳定性。
具体而言，我们采用一种改进的梯度下降算法，通过引入正则化项和损失函数调整，使得算法在优化过程中能够更好地抵抗噪声数据的干扰。
（二）算法实现1. 数据预处理：对原始数据进行清洗、去重、归一化等处理，以便于后续的算法分析。
2. 矩阵分解：将用户-项目评分矩阵进行分解，得到用户矩阵和项目矩阵。
3. 鲁棒性优化：在传统矩阵分解的基础上，引入鲁棒性优化方法，通过调整损失函数和正则化项，提高算法的鲁棒性。
4. 预测与推荐：根据用户的历史行为数据和其他相关信息，预测用户对项目的评分，并为用户提供个性化的推荐服务。
（三）实验与分析我们采用真实数据集对算法进行实验验证。
bagging分类回归算法的基本原理及例子
Bagging分类回归算法的基本原理及例子1. 介绍Bagging分类回归算法是一种集成学习算法，它通过对多个模型的预测进行组合来提高预测准确性。
本文将深入探讨Bagging算法的基本原理，以及通过例子来说明其应用。
2. 基本原理2.1 Bagging的概念Bagging算法的全称是Bootstrap Aggregating，即自举聚集。
它通过对原始数据集进行有放回的随机抽样，生成多个子数据集，然后在每个子数据集上训练一个基学习器。
将每个基学习器的预测结果进行组合，得到Bagging模型的最终预测结果。
2.2 Bagging算法流程1.从原始数据集中随机有放回地抽样，生成多个子数据集。
2.在每个子数据集上训练一个基学习器，可以是决策树、神经网络等。
3.将每个基学习器的预测结果进行组合，可以取平均值（回归问题）或投票（分类问题）来得到Bagging模型的最终预测结果。
3. 例子说明3.1 Bagging在决策树中的应用以分类问题为例，假设我们有一个包含1000个样本的数据集，每个样本有10个特征。
我们想要使用决策树进行分类预测。
我们从原始数据集中有放回地抽样，生成10个子数据集，每个子数据集包含800个样本。
然后在每个子数据集上训练一个决策树模型。
将10个决策树的预测结果进行投票，得到Bagging模型的最终分类预测结果。
3.2 Bagging在神经网络中的应用以回归问题为例，假设我们有一个包含10000个样本的数据集，每个样本有20个特征。
我们想要使用神经网络进行回归预测。
同样地，我们从原始数据集中有放回地抽样，生成5个子数据集，每个子数据集包含2000个样本。
然后在每个子数据集上训练一个神经网络模型。
将5个神经网络的预测结果取平均值，得到Bagging模型的最终回归预测结果。
4. 总结通过本文的介绍和例子可以看出，Bagging算法通过对多个基学习器的预测结果进行组合，可以显著提高模型的预测准确性，尤其是在降低方差方面有很好的效果。
电商行业：智能推荐系统优化解决方案
电商行业：智能推荐系统优化解决方案第一章：智能推荐系统概述 (2)1.1 推荐系统的定义与发展 (2)1.2 推荐系统的类型与特点 (3)第二章：用户行为数据挖掘与分析 (3)2.1 用户行为数据采集 (3)2.2 用户行为数据分析方法 (4)2.3 用户画像构建 (4)第三章：推荐算法研究与优化 (4)3.1 常见推荐算法介绍 (5)3.1.1 内容推荐算法 (5)3.1.2 协同过滤算法 (5)3.1.3 深度学习推荐算法 (5)3.2 算法优化策略 (5)3.2.1 减少冷启动问题 (5)3.2.2 提高推荐质量 (6)3.2.3 提高推荐多样性 (6)3.3 模型融合与集成 (6)第四章：推荐系统评估与评价指标 (6)4.1 推荐系统评估方法 (6)4.2 评价指标体系 (7)4.3 评估指标优化 (7)第五章：冷启动问题解决方案 (8)5.1 冷启动问题分析 (8)5.2 冷启动解决方案 (8)5.3 冷启动效果评估 (8)第六章：多样性与新颖性优化 (9)6.1 多样性与新颖性定义 (9)6.2 多样性与新颖性优化策略 (9)6.2.1 策略一：基于用户行为数据的多样性优化 (9)6.2.2 策略二：基于内容的多样性优化 (9)6.2.3 策略三：基于时间的多样性优化 (9)6.2.4 策略四：基于新颖性的优化 (9)6.3 优化效果评估 (10)6.3.1 多样性评估 (10)6.3.2 新颖性评估 (10)6.3.3 用户满意度评估 (10)6.3.4 推荐效果评估 (10)第七章：实时推荐系统设计与实现 (10)7.1 实时推荐系统架构 (10)7.1.1 系统整体架构 (10)7.1.2 关键组件 (11)7.2 实时数据处理与推荐算法 (11)7.2.1 实时数据处理 (11)7.2.2 推荐算法 (11)7.3 实时推荐系统优化 (11)7.3.1 数据处理优化 (11)7.3.2 推荐算法优化 (11)7.3.3 系统功能优化 (12)7.3.4 用户反馈优化 (12)第八章：跨域推荐系统研究 (12)8.1 跨域推荐系统概述 (12)8.2 跨域推荐算法与应用 (12)8.3 跨域推荐系统优化 (13)第九章：推荐系统在电商行业的应用案例 (13)9.1 电商行业推荐系统需求分析 (13)9.2 典型应用案例解析 (14)9.3 案例效果评估与优化 (14)第十章：未来发展趋势与展望 (15)10.1 推荐系统技术发展趋势 (15)10.2 电商行业推荐系统发展前景 (15)10.3 面临的挑战与应对策略 (16)第一章：智能推荐系统概述1.1 推荐系统的定义与发展推荐系统是一种信息过滤技术，旨在根据用户的历史行为、偏好、兴趣以及其他相关因素，向用户推荐可能感兴趣的商品、服务或内容。
bagging的算法及案例
bagging的算法及案例转载声明原⽂作者：Datawhale学习社区原⽂链接：参考资料：著作权归作者所有，任何形式的转载都请联系作者。
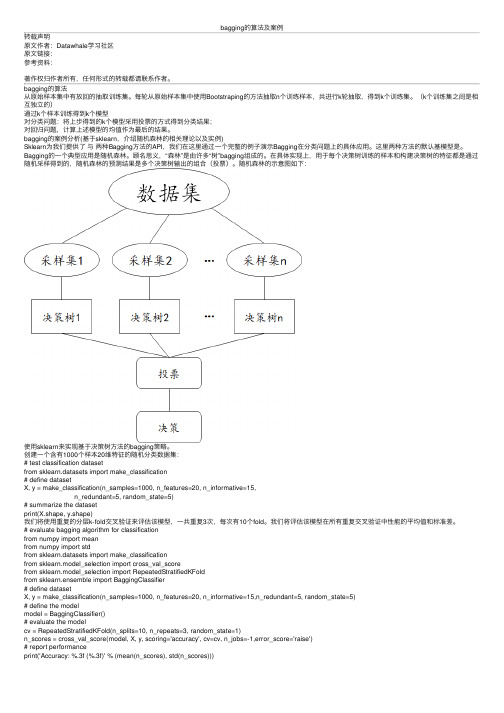
bagging的算法从原始样本集中有放回的抽取训练集。
每轮从原始样本集中使⽤Bootstraping的⽅法抽取n个训练样本，共进⾏k轮抽取，得到k个训练集。
（k个训练集之间是相互独⽴的）通过k个样本训练得到k个模型对分类问题：将上步得到的k个模型采⽤投票的⽅式得到分类结果；对回归问题，计算上述模型的均值作为最后的结果。
bagging的案例分析(基于sklearn，介绍随机森林的相关理论以及实例)Sklearn为我们提供了与两种Bagging⽅法的API，我们在这⾥通过⼀个完整的例⼦演⽰Bagging在分类问题上的具体应⽤。
这⾥两种⽅法的默认基模型是。
Bagging的⼀个典型应⽤是随机森林。
顾名思义，“森林”是由许多“树”bagging组成的。
在具体实现上，⽤于每个决策树训练的样本和构建决策树的特征都是通过随机采样得到的，随机森林的预测结果是多个决策树输出的组合（投票）。
随机森林的⽰意图如下：使⽤sklearn来实现基于决策树⽅法的bagging策略。
创建⼀个含有1000个样本20维特征的随机分类数据集：# test classification datasetfrom sklearn.datasets import make_classification# define datasetX, y = make_classification(n_samples=1000, n_features=20, n_informative=15,n_redundant=5, random_state=5)# summarize the datasetprint(X.shape, y.shape)我们将使⽤重复的分层k-fold交叉验证来评估该模型，⼀共重复3次，每次有10个fold。
智能推荐算法优化平台建设方案
智能推荐算法优化平台建设方案第1章项目背景与目标 (4)1.1 推荐系统概述 (4)1.2 项目背景分析 (4)1.3 建设目标与意义 (4)第2章推荐算法概述 (5)2.1 常用推荐算法简介 (5)2.1.1 协同过滤推荐算法 (5)2.1.2 基于内容的推荐算法 (5)2.1.3 混合推荐算法 (5)2.1.4 深度学习推荐算法 (6)2.2 推荐算法发展趋势 (6)2.2.1 面向多模态数据的推荐算法 (6)2.2.2 面向序列数据的推荐算法 (6)2.2.3 集成学习和迁移学习在推荐算法中的应用 (6)2.2.4 可解释性推荐算法 (6)2.3 推荐算法评估指标 (6)2.3.1 准确率（Accuracy） (6)2.3.2 F1分数（F1 Score） (6)2.3.3 平均倒数排名（Mean Reciprocal Rank，MRR） (6)2.3.4 覆盖率（Coverage） (7)2.3.5 新颖性（Novelty） (7)2.3.6 满意度（Satisfaction） (7)第3章智能推荐算法优化策略 (7)3.1 算法优化方向 (7)3.1.1 提高推荐准确度 (7)3.1.2 增强推荐多样性 (7)3.1.3 提升推荐实时性 (7)3.2 深度学习在推荐系统中的应用 (8)3.2.1 神经协同过滤 (8)3.2.2 序列模型 (8)3.2.3 多模态学习 (8)3.3 多模型融合策略 (8)3.3.1 集成学习 (8)3.3.2 多任务学习 (8)3.3.3 模型自适应融合 (8)第4章平台架构设计 (9)4.1 总体架构 (9)4.1.1 数据处理模块 (9)4.1.2 推荐算法模块 (9)4.1.3 应用接口模块 (9)4.1.4 平台管理模块 (9)4.2.1 数据预处理 (9)4.2.2 数据存储 (9)4.2.3 数据挖掘与分析 (9)4.3 推荐算法模块设计 (9)4.3.1 用户画像构建 (9)4.3.2 协同过滤算法 (10)4.3.3 内容推荐算法 (10)4.3.4 深度学习算法 (10)4.3.5 混合推荐算法 (10)第5章数据处理与分析 (10)5.1 数据来源与采集 (10)5.1.1 数据源选择 (10)5.1.2 数据采集方法 (10)5.2 数据预处理技术 (10)5.2.1 数据清洗 (10)5.2.2 数据集成 (11)5.2.3 数据转换 (11)5.3 特征工程 (11)5.3.1 特征提取 (11)5.3.2 特征编码 (11)5.3.3 特征选择 (11)5.3.4 特征变换 (11)5.3.5 特征组合 (11)第6章基于内容的推荐算法优化 (11)6.1 内容分析 (11)6.1.1 用户画像构建 (11)6.1.2 项目内容特征提取 (12)6.2 基于内容的推荐算法实现 (12)6.2.1 相似度计算 (12)6.2.2 推荐列表 (12)6.3 算法优化策略 (12)6.3.1 冷启动问题优化 (12)6.3.2 用户兴趣动态更新 (12)6.3.3 多维度特征融合 (12)6.3.4 模型调优与优化 (12)6.3.5 推荐结果多样性 (13)第7章协同过滤算法优化 (13)7.1 用户与物品相似度计算 (13)7.1.1 相似度度量方法 (13)7.1.2 相似度计算优化 (13)7.2 基于模型的协同过滤算法 (13)7.2.1 矩阵分解算法 (13)7.2.2 深度学习方法 (13)7.3.1 冷启动问题优化 (13)7.3.2 稀疏性问题优化 (13)7.3.3 多任务学习 (14)7.3.4 融合外部信息 (14)第8章深度学习推荐算法实现 (14)8.1 神经协同过滤算法 (14)8.1.1 算法概述 (14)8.1.2 模型构建 (14)8.1.3 损失函数与优化策略 (14)8.1.4 实验与分析 (14)8.2 序列化推荐模型 (14)8.2.1 序列化推荐概述 (14)8.2.2 基于循环神经网络的序列化推荐模型 (15)8.2.3 基于长短时记忆网络的序列化推荐模型 (15)8.2.4 实验与分析 (15)8.3 深度学习算法优化 (15)8.3.1 算法优化策略 (15)8.3.2 模型融合与集成 (15)8.3.3 实时推荐与在线学习 (15)8.3.4 实验与分析 (15)第9章多模型融合推荐策略 (15)9.1 模型融合技术概述 (15)9.1.1 模型融合的基本概念 (15)9.1.2 模型融合在推荐系统中的应用 (16)9.2 多模型融合方法 (16)9.2.1 线性融合 (16)9.2.2 非线性融合 (16)9.2.3 深度融合 (16)9.3 融合策略优化 (16)9.3.1 模型选择与组合 (16)9.3.2 特征级融合 (16)9.3.3 超参数优化 (17)9.3.4 模型动态调整 (17)9.3.5 融合策略的评价 (17)第10章系统评估与优化 (17)10.1 系统功能评估 (17)10.1.1 功能指标体系 (17)10.1.2 评估方法 (17)10.1.3 评估结果与分析 (17)10.2 推荐效果评估 (17)10.2.1 推荐效果评价指标 (17)10.2.2 评估方法与实验设计 (17)10.2.3 评估结果与分析 (17)10.3.1 算法优化 (18)10.3.2 系统架构优化 (18)10.3.3 数据处理与特征工程优化 (18)10.3.4 用户交互与体验优化 (18)10.3.5 安全与隐私保护优化 (18)第1章项目背景与目标1.1 推荐系统概述推荐系统作为信息过载时代下的关键技术，通过分析用户行为与兴趣偏好，为用户推荐个性化的内容、商品或服务，从而提高用户体验，促进信息的有效传递与价值最大化。
《基于矩阵分解的鲁棒推荐算法研究》范文
《基于矩阵分解的鲁棒推荐算法研究》篇一一、引言在信息爆炸的时代，如何从海量的数据中为用户提供个性化的推荐成为了互联网服务的关键问题。
推荐算法作为一种有效的手段，已经被广泛应用于各大互联网平台。
其中，基于矩阵分解的推荐算法因其良好的可扩展性和准确性而备受关注。
然而，传统的矩阵分解推荐算法在处理数据稀疏性和噪声干扰时仍存在一定的问题。
因此，本文提出了一种基于矩阵分解的鲁棒推荐算法，以提高推荐系统的准确性和稳定性。
二、矩阵分解推荐算法概述矩阵分解是一种常用的推荐算法技术，其基本思想是将用户-项目评分矩阵分解为用户矩阵和项目矩阵，通过分析这两个矩阵来预测用户对项目的评分。
在传统的矩阵分解推荐算法中，通常采用随机梯度下降等方法进行优化，但这种方法在处理数据稀疏性和噪声干扰时效果并不理想。
三、鲁棒性问题的提出在现实应用中，推荐系统常常面临数据稀疏性和噪声干扰等问题。
数据稀疏性指的是用户对项目的评分数据不足，导致推荐算法难以准确预测用户的偏好；而噪声干扰则是指数据中存在的错误或异常值，这些因素都会影响推荐系统的准确性和稳定性。
因此，如何在处理这些问题的同时保持算法的鲁棒性成为了推荐算法研究的重要方向。
四、基于矩阵分解的鲁棒推荐算法针对上述问题，本文提出了一种基于矩阵分解的鲁棒推荐算法。
该算法在传统的矩阵分解基础上，引入了鲁棒性优化策略，包括数据预处理、正则化项和损失函数优化等方面。
首先，在数据预处理阶段，我们采用了一种基于奇异值分解的降维方法，对原始的用户-项目评分矩阵进行预处理，以降低数据稀疏性对算法的影响。
其次，在正则化项方面，我们引入了L1和L2正则化项，以防止过拟合和提高算法的稳定性。
最后，在损失函数优化方面，我们采用了鲁棒损失函数来处理噪声干扰问题。
五、实验与分析为了验证本文提出的鲁棒推荐算法的有效性，我们进行了大量的实验。
实验结果表明，与传统的矩阵分解推荐算法相比，本文提出的鲁棒推荐算法在处理数据稀疏性和噪声干扰方面具有更好的性能。
基于矩阵分解的图书推荐算法研究
September2020No418TotalNo44602020年9月第18期总第460期内蒙古科技与经济Inner Mongolia Science Technology & Economy基于苑阵5解）團齐E 爲算法12任杰麟，陈力平，高燕琼，李显志（西南石油大学图书馆，四川成都610500$摘 要：为了提高基于矩阵分解的推荐算法精度，解决传统矩阵分解结果出现负数和运算量大的问 题，提出了改进的基于矩阵分解的推荐算法，在推荐模型中引进Sigmoid 函数，该函数能够控制分解结 果的值域，提高推荐算法评分的可理解性，消除矩阵分解结果出现负数的情况；在推荐模型中利用系数 控制推荐算法中不同部分权重，能够使得算法更加的灵活，利用交替梯度下降法实现计算结果的部分分 离，为分布式计算奠定了基础，通过实验验"，提出的推荐算法提高了评分的准确度，并增强了推荐算法的可扩展性％关键词：推荐系统；矩阵分解；潜语义模型；函数；偏置中图分类号:G250 文献标识码:A 文章编号1007—6921（2020）18—0119—03随着互联网的快速发展，网络信息量急剧增长#人们很容易就被一些无关的信息干扰（日益增多的电子商务产品，成千上万的视频音乐资源，人们在获 得海量的信息的同时，也越来越难以分辨筛选有用 的推送信息。
推荐算法能够根据用户的习惯和行为 方式获取用户大致的喜好，从而自动推荐给用户喜 欢、相关的物品（这就需要高精确的信息获取，能正 确分析用户的行为习惯（在电子商务、音乐平台、视 频网站等行业，推荐算法得到了普遍的应用，但同时也存在着较多的缺点。
例如协同过滤推荐算法，它通过相似度的计算发掘一个选择范围进行推荐，但 由于数据的不完整，相似度计算不准确等原因，推荐 的精度不高（其中算法，它常被用作数据压缩，进行 数据特征的提取工作，其计算量较大，导致它只能用 于理论研究而无法应用于工程实践（笔者将采用LFM 算法进行矩阵分解模型改进，并针对其分解结果存在负数，计算量较大且集中等问题做出相应的改进，进而实现一个高效、准确的推荐算法（1 矩阵分解算法1. 1 基本矩阵分解SVD 是矩阵分解的基本模型，常常被用于数据降维等场景,1-（矩阵A 是一个的矩阵，则矩阵A 的 SVD 为：A = U S V T （1$其中U 是一个的正交矩阵，则具有正交矩阵的性质：矩阵的每行都是单位向量，矩阵的逆矩阵还是 正交矩阵（%是一个的矩阵，除了主对角线上的元 素以外全为0,主对角线上的每个元素都称为奇异 值 V 是一个的矩阵。
基于加权与动态选择的不平衡数据流分类算法
基于加权与动态选择的不平衡数据流分类算法1. 内容概述随着信息技术的迅猛发展，数据流处理已成为当前研究的热点问题。
在众多应用场景中，不平衡数据流分类作为一个重要研究方向，对于维护系统的稳定性和提高资源利用率具有重要意义。
传统分类算法在处理不平衡数据时存在一定的局限性，如分类精度下降、计算复杂度高等。
为了解决这一问题，本文提出了一种基于加权与动态选择的不平衡数据流分类算法。
该算法的核心思想是在保证分类精度的同时，充分考虑数据流的动态变化特性，通过引入加权机制和动态选择策略，实现对不同数据流的差异化处理。
我们首先对数据流进行预处理，提取其特征信息；然后，根据特征信息计算每个数据流的权重值，权重值的大小反映了数据流的重要性；接着，在分类过程中，根据权重值动态选择待分类的数据流，优先处理权重较高的数据流；结合动态选择策略和传统分类算法，实现对不平衡数据流的分类。
本算法的创新之处在于：一方面，通过引入加权机制，使得算法能够根据数据流的实际重要性进行差异化处理，从而提高了分类精度；另一方面，通过动态选择策略，有效降低了计算复杂度，提高了算法的实时性。
本算法还具有较好的适应性，能够适应不同类型的数据流和不同的应用场景。
本文提出的基于加权与动态选择的不平衡数据流分类算法，旨在解决传统分类算法在处理不平衡数据时存在的局限性，提高分类精度和计算效率。
相信该算法在未来的实际应用中，将为相关领域的研究和应用带来有益的启示和参考。
1.1 背景介绍随着互联网的发展，网络流量日益增长，其中不平衡数据流的分类成为一个亟待解决的问题。
在不平衡数据流中，某一类别的数据量可能远远大于其他类别，导致分类器在训练过程中产生偏见，从而影响分类性能。
为了解决这一问题，本文提出了一种基于加权与动态选择的不平衡数据流分类算法。
在不平衡数据流分类问题中，传统的分类方法往往无法取得良好的效果，因为它们通常只关注多数类，而忽略了少数类的重要性。
传统方法在处理不平衡数据时，往往采用简单的权重设置或者采样方法，这些方法在某些情况下可能无法有效地提高分类性能。
bagging方法
bagging方法Bagging方法是一种有效的机器学习算法，用于预测和分类数据。
这种技术强调在使用多个模型进行预测或分类时获得的预测能力。
它的主要特点是使用一组预测器来结合诸如“bagging”，也称为“voting ensemble”（投票集成）的技术，其中每个预测器都仅以少量数据（如随机抽样）作为输入，并估计出不同的预测结果。
Bagging方法也可用于减少由于过拟合造成的较差的模型性能。
这种技术也可用于提高模型性能，如集成学习。
集成学习是指利用多个分类器构建一个分类模型，其中每个分类器对同一个分类任务分别做出自己独立的预测，最后将这些预测结果结合在一起，以得出最终的预测结果。
【Bagging法的工作原理】Bagging方法的工作原理非常简单，它是将原始数据集合分解成更多的子集，每个子集上都构建一个模型，最后将这些子模型的预测结果合并在一起，以得出最终的预测结果。
Bagging方法通常用“bootstrap aggregating”（bootstrap聚合）来实现，即以一种随机方式从原始数据集中选择数据来构建多个模型，并且每个模型都以放回式采样的方式选取多个数据样本，以防止过度拟合的情况发生。
【Bagging法的优势】Bagging方法的优势在于可以在降低模型复杂性的同时，有效地减少过拟合的风险。
因为每个模型构建者都在少量的随机数据上进行构建，因此，模型本身就没有特别多的复杂度。
此外，由于每个模型者都是独立的，因此它们可以从不同角度来看待问题，从而减少过拟合的风险。
【Bagging法的应用】Bagging方法在机器学习中有着广泛的应用，其常见的应用场景包括分类、预测和回归等。
它可以提高模型的准确性，减少过拟合的风险，并改善模型的稳定性。
例如，在支持向量机（SVM）中，Bagging可以提高模型的健壮性，减少模型的受噪音的影响；在决策树中，Bagging可以减少过拟合的风险，并提高模型的准确性；在人脸识别中，Bagging可以提高泛化能力，并减少识别错误率。
基于Bagging集成方法的互联网金融信用风险评估
基于Bagging集成方法的互联网金融信用风险评估
陈凯玥
【期刊名称】《应用数学进展》
【年(卷),期】2022(11)4
【摘要】互联网金融是对传统金融模式的延伸,但由于部分借款人在借款后无法按期、足额还款,使得互联网金融平台面临着信用风险。
对借款人的信用风险进行准确评估,可以降低风险,并且能够在一定程度上为互联网金融行业的稳定发展提供保障。
数据分析方法在信用风险评估领域已有广泛应用。
本文从国内某互联网金融平台借款人的个人、资产、借款信息三类数据提取特征,研究了数据分析方法中Logistic回归的衍生方法逐步Logistic回归、弹性网络和Bagging集成方法的代表Bagging、极端随机树和随机森林。
研究发现随机森林与逐步Logistic回归分别在F1-score、Accuracy、FPR和AUC指标下效果最优,且筛选出的重要特征也保持一致。
【总页数】11页(P1657-1667)
【关键词】信用风险评估;LOGISTIC回归;Bagging集成;特征重要性
【作者】陈凯玥
【作者单位】河北工业大学理学院
【正文语种】中文
【中图分类】F83
【相关文献】
1.基于Logistic回归模型的互联网金融信用风险评估
2.基于BP神经网络模型的互联网金融信用风险评估研究
3.基于Bagging神经网络集成的燃料电池性能预测方法
4.LGB-BAG在P2P网贷借款者信用风险评估中的应用
5.基于改善Bagging-SVM集成多样性的网络入侵检测方法
因版权原因，仅展示原文概要，查看原文内容请购买。
《基于矩阵分解的鲁棒推荐算法研究》范文
《基于矩阵分解的鲁棒推荐算法研究》篇一一、引言随着互联网技术的飞速发展，信息过载问题日益严重，推荐系统应运而生，成为解决这一问题的有效手段。
在众多推荐算法中，基于矩阵分解的推荐算法因其准确性和有效性受到了广泛关注。
然而，传统的矩阵分解推荐算法在处理数据稀疏性和用户偏好变化等实际问题时，往往表现出一定的脆弱性。
因此，本文提出了一种基于矩阵分解的鲁棒推荐算法，以提高推荐系统的稳定性和准确性。
二、相关研究概述矩阵分解是推荐系统中的一种常用技术，通过分析用户-项目评分矩阵，提取出用户的潜在特征和项目的潜在特征，从而进行推荐。
近年来，许多研究者对矩阵分解技术进行了深入研究，提出了许多改进的算法。
然而，这些算法在处理数据稀疏性和用户偏好变化等问题时，仍存在一定的局限性。
因此，研究鲁棒的矩阵分解推荐算法具有重要的现实意义。
三、基于矩阵分解的鲁棒推荐算法（一）算法原理本文提出的基于矩阵分解的鲁棒推荐算法，主要思路是在传统的矩阵分解基础上，引入鲁棒性优化方法。
具体来说，通过在损失函数中加入正则化项和约束条件，使得算法在处理数据稀疏性和用户偏好变化等问题时，能够更好地保持稳定性。
同时，通过优化算法的迭代过程，提高算法的收敛速度和准确性。
（二）算法实现1. 数据预处理：对用户-项目评分矩阵进行预处理，包括数据清洗、缺失值填充等操作，以提高数据的完整性和质量。
2. 矩阵分解：采用传统的矩阵分解技术，对用户-项目评分矩阵进行分解，提取出用户的潜在特征和项目的潜在特征。
3. 鲁棒性优化：在损失函数中加入正则化项和约束条件，对算法进行鲁棒性优化。
具体来说，通过调整正则化参数和约束条件，使得算法在处理数据稀疏性和用户偏好变化等问题时，能够更好地保持稳定性。
4. 迭代优化：采用优化算法对损失函数进行迭代优化，直至达到收敛。
（三）算法优势本文提出的基于矩阵分解的鲁棒推荐算法具有以下优势：1. 鲁棒性强：通过引入鲁棒性优化方法，使得算法在处理数据稀疏性和用户偏好变化等问题时，能够更好地保持稳定性。
电商行业：智能推荐系统优化升级方案
电商行业：智能推荐系统优化升级方案第1章智能推荐系统概述 (4)1.1 推荐系统的基本原理 (4)1.1.1 用户行为分析：收集并分析用户的历史行为数据，如浏览、购买、评价等，以获取用户的兴趣偏好。
(4)1.1.2 项目特征提取：提取项目（商品）的各类属性信息，如类别、价格、品牌等，以便进行项目之间的相似度计算。
(4)1.1.3 相似度计算：基于用户或项目的特征，采用余弦相似度、皮尔逊相关系数等方法计算相似度。
(4)1.1.4 推荐算法：结合相似度计算结果，采用不同的推荐算法（如协同过滤、基于内容的推荐、混合推荐等）为用户个性化推荐列表。
(4)1.2 智能推荐系统的优势 (4)1.2.1 提高用户满意度：通过精准地为用户提供感兴趣的商品，提高用户购物体验，提升用户满意度和留存率。
(4)1.2.2 促进销售：智能推荐系统有助于提高商品转化率，增加销售额，为企业带来更高收益。
(5)1.2.3 算法优化：采用先进的机器学习算法，不断优化推荐结果，适应不同场景和用户需求。
(5)1.2.4 实时性：智能推荐系统能够实时收集用户行为数据，快速响应用户需求，为用户提供最新的推荐结果。
(5)1.3 当前推荐系统存在的问题 (5)1.3.1 冷启动问题：新用户或新商品缺乏足够的用户行为数据，导致推荐效果不佳。
51.3.2 算法偏见：推荐算法可能过于依赖历史数据，导致推荐结果出现偏见，忽视了用户潜在的兴趣。
(5)1.3.3 稀疏性：用户商品评分矩阵往往非常稀疏，影响推荐系统的准确性。
(5)1.3.4 可解释性差：部分推荐算法缺乏可解释性，用户难以理解推荐原因，从而降低推荐效果。
(5)1.3.5 隐私问题：收集用户行为数据可能涉及隐私问题，如何在保护用户隐私的同时提高推荐效果，是当前亟待解决的问题。
(5)第2章推荐系统技术架构升级 (5)2.1 基于大数据的推荐算法优化 (5)2.1.1 升级协同过滤算法 (5)2.1.2 深度学习算法的应用 (5)2.1.3 多模型融合推荐 (5)2.1.4 实时推荐算法优化 (6)2.2 分布式计算框架的应用 (6)2.2.1 基于Spark的分布式计算 (6)2.2.2 融合Flink流处理技术 (6)2.2.3 参数服务器分布式训练 (6)2.3 云计算与边缘计算在推荐系统中的融合 (6)2.3.1 云计算资源调度优化 (6)2.3.2 边缘计算在推荐系统中的应用 (6)第3章用户画像优化 (7)3.1 用户行为数据分析 (7)3.1.1 数据收集 (7)3.1.2 数据预处理 (7)3.1.3 数据分析 (7)3.2 用户画像构建方法 (7)3.2.1 用户特征提取 (7)3.2.2 用户标签体系 (7)3.2.3 用户画像建模 (7)3.3 用户画像更新与维护 (7)3.3.1 实时更新策略 (7)3.3.2 离线更新机制 (7)3.3.3 用户画像维护 (8)3.3.4 用户画像评估 (8)第4章商品画像构建 (8)4.1 商品属性挖掘 (8)4.1.1 数据预处理 (8)4.1.2 属性提取 (8)4.1.3 属性归一化 (8)4.1.4 属性权重计算 (8)4.2 商品关联关系分析 (8)4.2.1 基于规则的关联分析 (8)4.2.2 基于聚类的关联分析 (8)4.2.3 基于深度学习的关联分析 (9)4.3 商品画像在推荐系统中的应用 (9)4.3.1 冷启动问题解决 (9)4.3.2 用户兴趣建模 (9)4.3.3 推荐结果优化 (9)4.3.4 实时推荐 (9)4.3.5 跨域推荐 (9)第五章深度学习技术在推荐系统中的应用 (9)5.1 深度学习模型概述 (9)5.2 常用深度学习推荐算法 (9)5.3 深度学习推荐模型的优化与改进 (10)第6章多通道融合推荐 (11)6.1 多通道推荐系统架构 (11)6.1.1 数据采集模块 (11)6.1.2 特征工程模块 (11)6.1.3 多通道融合模块 (11)6.2 离线多通道特征融合 (11)6.2.1 多通道特征提取 (11)6.2.2 多通道特征权重分配 (11)6.2.3 多通道特征融合 (11)6.3.1 用户行为实时分析 (12)6.3.2 推荐权重动态调整 (12)6.3.3 推荐结果排序优化 (12)第7章融合社会化信息的推荐系统 (12)7.1 社会化信息挖掘与分析 (12)7.1.1 用户社交行为数据收集 (12)7.1.2 社会化信息预处理 (13)7.1.3 社会化信息分析 (13)7.2 社交网络在推荐系统中的应用 (13)7.2.1 社交关系推荐 (13)7.2.2 社交影响推荐 (13)7.2.3 社交内容推荐 (13)7.3 融合社会化信息的推荐算法 (13)7.3.1 基于协同过滤的融合算法 (13)7.3.2 基于内容的融合算法 (14)7.3.3 深度学习融合算法 (14)第8章智能推荐系统冷启动问题解决策略 (14)8.1 冷启动问题概述 (14)8.2 基于内容的推荐算法在冷启动中的应用 (14)8.2.1 物品特征提取 (14)8.2.2 用户偏好建模 (14)8.2.3 利用用户行为数据 (14)8.3 利用社会化信息解决冷启动问题 (14)8.3.1 社交关系推荐 (15)8.3.2 信任网络构建 (15)8.3.3 利用群体智慧 (15)第9章推荐系统评估与优化 (15)9.1 推荐系统评估指标体系 (15)9.1.1 准确性指标 (15)9.1.2 覆盖率指标 (15)9.1.3 多样性指标 (15)9.1.4 新颖性指标 (15)9.2 推荐算法功能分析 (16)9.2.1 协同过滤算法 (16)9.2.2 深度学习算法 (16)9.2.3 混合推荐算法 (16)9.3 推荐系统优化策略 (16)9.3.1 数据预处理优化 (16)9.3.2 推荐算法优化 (16)9.3.3 推荐结果优化 (16)9.3.4 系统架构优化 (16)第10章推荐系统应用实践与未来发展 (16)10.1 推荐系统在各领域的应用案例 (17)10.1.2 视频网站领域 (17)10.1.3 社交媒体领域 (17)10.2 推荐系统面临的挑战与机遇 (17)10.2.1 数据稀疏与冷启动问题 (17)10.2.2 用户隐私保护 (17)10.2.3 模型可解释性 (17)10.2.4 多样化需求与场景适配 (18)10.3 推荐系统的未来发展展望 (18)10.3.1 更深层次的个性化推荐 (18)10.3.2 集成学习与迁移学习 (18)10.3.3 融合知识与推理的推荐系统 (18)10.3.4 隐私保护与安全 (18)10.3.5 可解释性与透明度 (18)10.3.6 跨平台与多模态推荐 (18)10.3.7 个性化交互式推荐 (18)第1章智能推荐系统概述1.1 推荐系统的基本原理推荐系统作为信息过滤的一种手段，旨在解决信息过载问题，通过分析用户的历史行为、兴趣偏好以及项目（商品）的特征，向用户推荐可能感兴趣的项目。
回归分析中的Bagging回归模型应用技巧(Ⅲ)
回归分析是数据科学领域的重要工具，它用于预测变量之间的关系，并找出影响因变量的自变量。
在回归分析中，Bagging回归模型是一种常用的技术，它通过组合多个模型的预测结果来提高预测准确性。
在本文中，我们将探讨Bagging回归模型的应用技巧，以及如何在实际数据分析中使用它来提高预测的准确性和稳定性。
Bagging回归模型基本原理Bagging回归模型是基于Bagging技术的一种回归分析方法。
Bagging技术是指通过对训练数据集进行有放回抽样，生成多个子数据集，然后分别用子数据集训练出多个模型。
最后，将这些模型的预测结果进行平均或投票来得到最终的预测结果。
在回归分析中，Bagging模型可以用于提高单个模型的预测准确性，并且可以减少模型的方差。
Bagging回归模型的应用技巧在实际应用中，Bagging回归模型有一些技巧和注意事项需要注意。
首先，选择合适的基本回归模型非常重要。
通常来说，Bagging模型适用于任何类型的回归模型，但是在选择基本模型时需要考虑到模型的稳定性和泛化能力。
其次，确定子数据集的大小和数量也是关键。
子数据集的大小和数量会影响模型的稳定性和准确性。
一般来说，子数据集的大小可以选择为原始数据集的70%到80%，子数据集的数量可以选择为10到20个。
另外，还需要考虑到子模型之间的相关性。
如果子模型之间的相关性过高，会导致Bagging模型的效果不佳。
因此，可以通过调整抽样方法或者引入随机性来减少子模型之间的相关性。
在实际数据分析中使用Bagging回归模型在实际数据分析中，使用Bagging回归模型可以提高预测的准确性和稳定性。
首先，需要准备好数据集，并对数据进行预处理和特征工程。
然后，可以选择合适的基本回归模型，并通过交叉验证等方法来确定子数据集的大小和数量。
接下来，可以使用Bagging技术来训练多个子模型，并将它们的预测结果进行平均或投票，得到最终的预测结果。
最后，需要评估模型的性能，并根据需要对模型进行调优和改进。
基于动态权值最优加权法的移动网络流量预测
= β j 1=j 1 =j 1
（1）
p
式中：λ
为非负正则化参数，
λ∑ j =1
|β
j
|
为惩罚项。同时当
λ
值
越大，保留的变量会随之减少，其惩罚力度也随之增加，反
之亦然。
1.2 BP 神经网络预测模型 BP 神经网络模型 [9] 具有良好的通用性、非线性逆映射
处理能力、鲁棒性和自动学习处理能力。因此，BP 神经网络 系统模型往往被广泛选用为分类模型。但是 ,BP 神经网络模 型仍然有一些不足之处 , 如可能陷入局部最优、收敛与信息 反映率等收敛性能依赖于初始参数设定等问题。
图 1 神经网络模型 BP 神经网络是借助最快梯度下降法的学习过程，通过不 断地进行反向传播从而对隐含层的阈值以及权值进行改变， 能够得到最小的期望输出实际输出的误差平方和。此算法包 含两个阶段：第一个阶段是输入学习样本，借助设置的隐含 层参数以及其网络结构，向后计算各神经元的输出，如果得 到的期望输出对比其实际输出有很大的出入，那么就会开始 第二阶段通过从最后一层逐步向前展开计算，记录各个层的 阈值以及权重的误差是否会有较大的影响，然后在最后一层 开始借助最快梯度下降法矫正其权值以及阈值的误差。通过 不断进行这两个阶段的过程，直至收敛。
测得到结果分别为 y1, y2 ,...., yn ，设单一模型的权值分别为 最小较优权值系数进行综合分配后的计算公式 , 就已经得到
w1, w2 ,...., wn 则融合后的 y 值为：
可以直接求出 tk 次数的加权与融合时的最优权值：
_
n
∑ y = wi xi
i =1
（2）
∧
= wi (k)
∧
（16） （17）
基于自适应动态加权图的会话推荐系统
TECHNOLOGY AND INFORMATION科学与信息化2023年10月下 77基于自适应动态加权图的会话推荐系统姜宜鑫 吴杰（通讯作者）辽宁科技大学计算机与软件工程学院 辽宁 鞍山 114051摘 要 会话推荐系统可以通过对话交互的方式获取用户对物品和属性的偏好，并且可以有效预测出用户偏好。
基于自适应动态加权图的会话推荐系统主要解决了3个问题：拓展性、通用性及稳定性。
文章将会话推荐系统的3个决策问题统一成1个决策策略，提出一种基于动态加权的强化学习策略，在每个会话回合中增加询问属性和推荐项因子。
实验结果表明，该方法不仅显著优于现有方法，而且提高了会话推荐系统的可扩展性和稳定性。
关键词 会话推荐系统；强化学习；图表示学习Conversational Recommender System Based on Self-adaption Dynamic Weighted Graph Jiang Yi-xin, Wu Jie (corresponding author)School of Computer Science and Software Engineering, University of Science and Technology Liaoning, Anshan 114051, Liaoning Province, ChinaAbstract The conversational recommender system can obtain the user’s preference for items and attributes through conversational interaction, and can effectively predict the user’s preference. The conversational recommender system based on self-adaption dynamic weighted graph mainly solves three problems: scalability, versatility and stability. This paper unifies the three decision problems of the conversational recommender system into one decision strategy, and proposes a reinforcement learning strategy based on dynamic weighting, which increases the inquiry attribute and recommendation factor in each conversational round. Experimental results show that this method not only significantly outperforms the existing methods, but also improves the scalability and stability of the conversational recommender system.Key words conversational recommender system; reinforcement learning; graph representation learning引言对话推荐系统（CRS ）的目标是通过互动对话的方式了解用户的喜好并推荐。