外啮合不完全齿轮机构1的主要参数计算
机械设计基础 第4章齿轮机构(4-56)讲解
刀具刀号的选择——按被加工齿轮的m、α、z 。
这种切齿方法简单,不需要专用机床,但生产率低、精度差, 故仅适用于单件生产及精度要求不高的场合。
2、拉刀(broaching tool)拉齿
拉刀拉齿主要用来拉削内齿轮,拉刀的形状与齿轮齿 槽形状相同。因拉刀的制造成本高,故它适用于批量生产 的情况。
2、切削过程中的运动(以插齿为例) 1)范成运动
齿条插刀:刀具的节线与被加工齿轮齿坯的分度圆相 切并作纯滚动的运动——刀具移动v =ωr = ωm z / 2。
齿轮插刀:刀具的节圆与齿坯节圆相切并作纯滚动的 运动—— i =ω0 /ω= z /z0)
2)切削运动(↑↓):刀具沿齿轮毛坯轴向的切齿运动。 3)让刀运动(←→):插齿刀具返回时,为避免擦伤已
∵ 分度圆与中线作纯滚动,且刀具分度线上s=e=πm/2;
∴ 切出的齿轮: s=e=πm/2;
ቤተ መጻሕፍቲ ባይዱ
1
ω1
∴ 被切的齿轮
是标准齿轮。 ra1r1'==r1
rb1
h a* m
N1
α '=α
P V2
N 2∞
2 )切制非标准齿轮时,刀具的加工节线与被加工齿轮的 分度圆相切,刀具的加工节线与中线不重合。
∵ 刀具的加工节线上s≠e; ∴ 被切的齿轮是非标准齿轮。
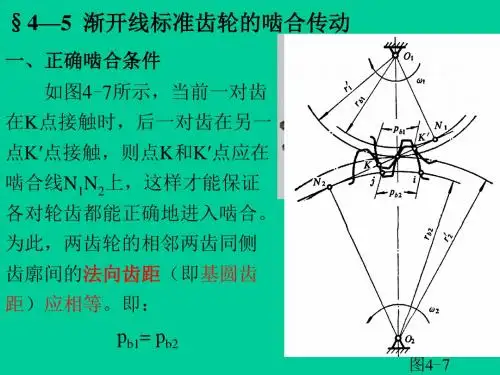
§4—5 渐开线标准齿轮的啮合传动
一、正确啮合条件 如图4-7所示,当前一对齿
在K点接触时,后一对齿在另一 点K′点接触,则点K和K′点应在 啮合线N1N2上,这样才能保证 各对轮齿都能正确地进入啮合。 为此,两齿轮的相邻两齿同侧 齿廓间的法向齿距(即基圆齿 距)应相等。即:
外啮合圆柱齿轮几何计算公式

求出啮合角α'后,由上式求(x1+x2)值,再进行分配
中心距变动系数y
y=(a'-a)/m
=(z1+z2)(cosα/cosα'-1)/2
yn=(a'-a)/mn
=(z1+z2)(cosαt/cosαt'-1)
/(2cosβ)
yt=ynconβ
外啮合圆柱齿轮几何计算公式
名称及代号
计算公式及说明
直齿轮
斜齿及人字齿轮
由强度计算或结构设计确定,
并取标准值
法向模数mn取标准值。
端面模数:mt=mncosβ
β=0
两轮螺旋角相等,方向相反
α=20°
αn=20°
tanαt=tanαn/cosβ
d=mz
d=mtz
a=(d1+d2)/2
=(z1+z2)m/2
变位后的中心距a'
a'=a+ym=acosα/cosα'
a'=a+ytmt=a+ynmn=acosαt/cosαt'
齿根圆直径df
df=d-2(ha+c-xm)
df=d-2(han+cn-xnmn)
齿顶圆直径da
da1=2a'-df2-2c
da2=2a'-df1-2c
da1=2a'-df2-2cn
da2=2a'-df1-2cn
纵向重合度εβ
εβ=0
εβ=bsinβ/(mnπ)
b——齿轮宽度
总重合度εγ
εγ=εα
εγ=εα+εβ
注:角标n为法面,t为端面;1为小齿轮,2为大齿轮。
a=(d1+d2)/2
齿轮基本参数计算

1.齿轮相关参数计算基本参数:齿形角 α/°齿顶高系数h a*顶缝隙系数c*2010.25齿形角(弧度)0.3490661.1.标准齿轮计算模数m/m n齿数z1齿数z2分度圆直径d1/mm分度圆直径d2/mm 8100106800848齿顶圆d a齿根圆d f齿根高h f齿高h中心距a △h a*外啮合ha1ha2h f1h f2h1h20.0712148810101818内啮合ha1ha2h f1h f2h1h287.430291*********.4303基本参数:齿形角 α/°齿顶高系数h a*顶缝隙系数c*2010.25齿形角(弧度)0.3490661.2.高变位齿轮计算模数m/m n齿数z1齿数z2分度圆直径d1/mm分度圆直径d2/mm 810074800592齿顶圆d a齿根圆d f中心距a基圆直径d b△h a*外啮合ha1ha2h f1h f2h1h20.1020091246141810内啮合ha1ha2h f1h f2h1h21211.183932661817.1839基本参数:齿形角 α/°齿顶高系数h a*顶缝隙系数c*2010.25齿形角(弧度)0.349066invαt=0.0149041.3.1 角变位齿轮计算模数m/m n齿数z1齿数z2分度圆直径d1/mm分度圆直径d2/mm121510618012721.3.1 已知x 滚齿法加工齿顶圆d a齿根圆d f中心距a基圆直径d b△h a*外啮合ha1ha2h f1h f2h1h20.07121417.3626417.3626459926.3626426.3626y/y n0.946887△y0.053113内啮合ha1ha2h f1h f2h1h29.4545414.5454692118.4545423.5455y/y n0.7121217△y0.712122滚齿参数:h a、h f、h、d a、d f 。
不完全齿轮机构和凸轮式间歇机构
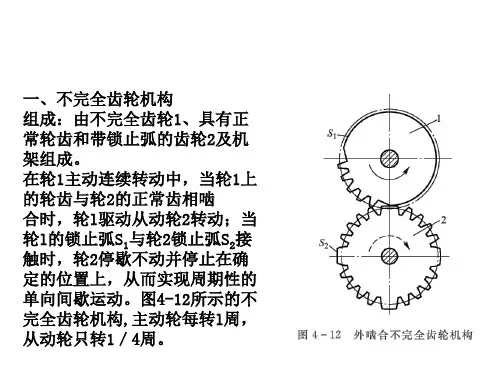
外啮合不完全齿轮机构
内啮合不完全齿轮机构
常用外啮合的形式
二、凸轮式间歇机构ห้องสมุดไป่ตู้
图4-14所示是一种圆柱凸轮式间歇运动机构。这种机构的主动 轮l为具有曲线沟槽的圆柱凸轮,从动件2则为均布有柱销3的圆 盘。当主动轮1转动时,拨动柱销3,使从动圆盘2作间歇运动。 这种机构常用在轻载情况下的间歇运动(如火柴包装机),间歇 运动的频率每分钟可高达1500次左右。
齿轮参数及配合设计

• 两齿廓保证连续相切传动,即不干涉又不脱开的基本条件为:
vk 2k1 n 0 ---齿廓啮合的基本方程式
o1
ω1
n
vk2
vk2k1 vk1
k p
vk n
n
ω2 o2
• 2. 齿廓啮合基本定律
o1
ω1
n
vk2
vp12 1o1 p 202 p
vk2k1 vk1
k p
• 刀具不标准
2.变位齿轮问题的提出
1)z<zmin时又要不根切; 2)a’≠a;
3)ρ小<ρ大, σ小>σ大, u小>u大,
• 3.刀具的变位 1)正变位 2)负变位 • 4. 变位传动
1)零变位齿轮传动:∑x=0,α’=α, a’=a • x1=x2=0 标准齿轮传动 x1=-x2 等移距变位齿轮传动 • 2)非零变位齿轮传动:∑x≠0,α’≠α, a’≠a
2
cos '
• 3)变位齿轮传动的中心距及齿顶高变动系数Δy
• 无侧隙啮合时:a’=a+ym=m(z1+z2)/2+ym • 具有标准顶隙时(c=c*m时): • a’’=ra1+c+rf2= m(z1+z2)/2+(x1+x2)m
Δy m=a’’-a’=(x1+x2)-ym Δy = (x1+x2)-y ha=(ha*+x*- Δy)m
α
r
α N1
xm ha m
p
Q
• 2. 变位齿轮的几何计算
• m、a由强度计算确定,α、z、d、db不变化 • h高a和、齿h厚f 、的d变a化、 df、s 、e 、α’都将变化,而关键是齿
不完全齿轮——精选推荐

5.3不完全齿轮机构不完全渐开线齿轮机构能将主动轮的等速连续转动转换为从动轮的间歇运动。
其动停时间比不受机构结构的限制,制造方便,但是从动轮在每次间歇运动的始末有剧烈冲击,故一般只用于低速,轻载及机构冲击不影响正常工作的场所。
若设置缓冲结构可改善机构的动力性能。
5.3.1基本型式与啮合特性不完全齿轮机构分外啮合与内啮合两类(图4-2-82、4-2-83)。
机构由三部分组成:主动轮1与2;一对锁止弧3,主动轮上的凸弧和从动轮上的凹弧可以直接切出或装配而成,也可单独制成一对锁止弧;缓冲结构,用以缓和或消除间歇涌动始.末时的剧烈冲击,改善机构的动力性能。
本节只讨论没有缓冲结构的运动分析与尺寸设计。
不完全齿轮的啮合特性:每一次简谐运动,可以只由一对齿啮合来完成,也可以由若干对齿来完成。
不完全齿轮机构首.末二对齿的啮合过程与完全齿轮机构不同,而中间各对齿的啮合过程与完全齿轮相同。
首对齿:从动轮所处的静止位置,应使主动轮旋转时其首齿S能顺利地通过二轮顶圆右侧交点G,从动轮具有锁止弧的齿K啮合(图4-2-84a、b)。
首啮点E由从动轮的静止位置决定,它可能位于从动轮齿顶圆弧GB1上(图b)或啮合线段B1P上(图a)。
首齿开始推动从动轮.锁止弧恰好脱开。
轮齿在GB1段啮合时,从动轮变速转动;E点离B1点越远,则开始啮合时冲击越大;齿轮在B1B2段啮合时,从动轮匀速转动。
如所选参数满足连续传动条件,则第一对齿到B2点终止啮合时,第二对齿已进入啮合。
末对齿:末对齿啮合至B2点时,因无后续齿所以并不立即脱齿,而以主动齿顶尖角与从动末齿根部啮合,经圆弧B2F,最终于二顶圆左侧交点F处分离。
在B2F段啮合过程中,从动轮角速度逐渐降低。
在F点终止啮合时,锁止弧恰好锁住,从动轮突然停止。
中间各对齿开始啮合与B1点,终止啮合于B2点。
仅由一对齿啮合来完成一次间歇运动时,啮合轨迹的前半段EB1P(或EP)与首对齿的前半段相同;后半段PB2F与末对齿的后半段相同。
齿轮参数计算
da2 d2 2ha m( z2 2had f 1 d1 2h f
m(z1
* 2ha
2c* )
d f 2 d2 2hf m( z2 2ha* 2c* )
分 度 圆 齿 距 p p=m
s 1 m
分度圆齿厚 s
2
基
圆
齿
距
pb
pb=1mcos
中
心
距
a
a 2 m(z2 z1 )
传递交错轴运动 蜗杆涡轮
准双曲面齿轮
二、渐开线齿廓的形成及其啮合特性
1. 渐开线的形成
如图,当一直线n-n沿一个半
径为rb的圆的圆周作纯滚动 时,该直线上任一点K的轨迹 AK称为该圆的渐开线。这个 圆称为基圆,该直线称为渐 开线的发生线。渐开线上任 一点K的向径与起始点A的向 径的夹角<AOK( < AOK= θk)称为渐开线(AK段)的展 角。
三弧
基圆(d b和
齿齿厚距spii 齿槽宽ei
rb)齿顶高ha 齿根高hf
同一圆上pi si ei
rf rb
ra r ri
o
三高 齿齿顶根高高hhaf 齿全高h
h ha hf
分度圆 齿顶圆 基圆 齿根圆
任务1:
从手中的齿轮中,找出所有名称所对应部 分
思考题
1、是不是任意两个齿轮都能正确啮合? 2、若齿轮损坏,需测绘哪些数据? 3、对一些需要知道却无法测量的参数,该
国家标准规定齿轮分度圆 α=20°为标准值 某些场合:α=14.5°、15°、22.5°、25°。 分度圆就是齿轮上具有标准模数和标准压力角 的圆。
齿数、模数、压力角为渐开线齿轮的三个最基本 参数。
4)、齿顶高系数和顶隙(径向间隙)系数
齿轮各参数计算公式
模数齿轮计算公式:名称代号计算公式模数数)齿距齿数分度圆直径齿顶圆直径齿根圆直径齿顶高齿根高齿高齿厚中心距跨测齿数公法线长度m m=p/ n =d/z=da/ (z+2) (d为分度圆直径,z为齿p p二兀m= n d/zz=d/m=兀d/pd d=mz=da-2mda da=m (z+2) =d+2m=p (z+2) / ndf df二d-2. 5m=m(z-2. 5)=da-2h=da-4. 5mha ha=m=p/nhf hf=l. 25mh h=2.25ms s=p/2= m/2a a=(zl+z2)m/2=(dl+d2)/2k k=z/9+0.5w w=m[2. 9521 (k-0. 5) +0. 014z]13-1什么是分度圆?标准齿轮的分度圆在什么位這上?13-2 一渐开线,其基圆半径rb=40mm,试求此渐开线压力角«=20°处的半径r和曲率半径p的大小。
13-3有一个标准渐开线宜齿圆柱齿轮,测疑其齿顶圆直径da = 106.40 mm,齿数z=25,问是哪一种齿制的齿轮,基本参数是多少?13-4两个标准直齿圆柱齿轮,已测得齿数爲=22、Z2 = 98,小齿轮齿顶圆直径d a i=240 mm,大齿轮全齿高h = 22.5 mm,试判断这两个齿轮能否正确啮合传动?13-5有一对正常齿制渐开线标准直齿圆柱齿轮,它们的齿数为z】 = 19、Z2 = 81,模数m = 5mm,压力角&=20。
若将其安装成J =250 mm的齿轮传动,问能否实现无侧隙啮合?为什么?此时的顶隙(径向间隙)C是多少?13-6已知C6150车床主轴箱内一对外啮合标准直齿圆柱齿轮,其齿数zi=21、Z2 = 66,模数m = 3.5 mm,压力角«=20°,正常齿。
试确左这对齿轮的传动比、分度圆直径、齿顶圆直径、全齿髙、中心距、分度圆齿厚和分度圆齿槽宽。
13-7已知一标准渐开线直齿圆柱齿轮,其齿顶圆直径dai = 77.5mm,齿数zx=29。
外啮合齿轮参数计算(完美整理版)
相目公式中间过程数据齿数Z1设计时选定(满足强度及传动比等)齿数Z2设计时选定(根据传动比等要求)模数Mn设计选定(满足强度要求等)中心距a'实际中心距(或计算所得)齿宽b设计选定(满足强度要求等)螺旋角β设计选定(满足强度要求等)0.235619449齿顶高系数ha*设计选定(一般标准值为1)法向压力角αn 设计选定(满足强度要求等)0.34906585顶隙系数cn*设计选定(按标准一般取0.25,0.35,0.4等)1分度圆直径d1d1=Mn*Z1/cosβ10.798359532分度圆直径d2d2=Mn*Z2/cosβ84.844253483未变位时中心距a a=(d1+d2)/2=Mn*(Z1+Z2)/2cosβ47.821306514中心距变动系数Yn Yn=(a'-a)/Mn0.7857956635端面压力角αttan(αt)=tan(αn)/cos β0.374312519αt=arctan(αt)0.3581678116啮合角αwt a'*cos(αwt)=a*cos(αt)0.914012228αwt=arccos(αwt)0.4177299397总变位系数Xninv(αwt)=tan(αwt)-αwt 0.026122587inv(αt)=tan(αt)-αt0.016144708Xn=(Z1+Z2)*(invαwt-invαt)/(2*tanαn)0.8498339558变位系数分配Xn1 Xn2Xn1 取值0.300Xn2=Xn-Xn10.5509齿顶高变动系数ΔYn ΔYn =Xn-Yn0.06410齿顶高ha1 ha2ha1=(ha*+Xn1-ΔYn)*Mn 1.853942562ha2=(ha*+Xn2-ΔYn)*Mn 2.22869349511齿根高hf1 hf2hf1=(ha*+cn*-Xn1)*Mn 1.65hf2=(ha*+cn*-Xn2)*Mn 1.27524906712全齿高 h1 h2h1=ha1+hf1 3.504h2=ha2+hf2 3.50413齿顶圆直径da1 da2da1=d1+2*ha114.50624466da2=d2+2*ha289.3016404714齿根圆直径df1 df2df1=d1-2*hf17.498359533df2=d2-2*hf282.29375534公法线计算Wk1 Wk215当量齿数 Z*1 Z*2Z*1=Z1*invαt/invαn7.582531652Z*2=Z2*invαt/invαn59.57703441 16跨测齿数 k1 k2(1+2*Xn/Z*)*(1+2*Xn/Z*) 1.1645199261.037256527cosan*cosan0.883022222SQRT0.5305635730.392726757k1 1.757262977 k28.142981876 W*1 W*2W*=cos(PI(K-0.5)+Z**invαn) 4.53439459222.9753942217Wk1Wk1=(W*1+2*Xn1*sinαn)*Mn7.109410017 Wk2Wk1=(W*2+2*Xn2*sinαn)*Mn35.02725419变位后的中心距(验算值)a′=a×cos(αt)/cos(αwt)49备注: 1、绿色为输入数据,黄色为结果数据2、根据C12数值选择C13单元参数(一般C12≯1,C13=0.5、或C13=0.5C12)3、C7单元参数输入角度数值4、该程序适用于外啮合齿轮的传动计算外啮合变位圆柱齿轮,已知变位系数,求中心距:1.先算未变位时中心距 a=m(z1+z2)/22.再求变为后的啮合角 invα′=2(x1+x2)×tanα/(z1+z2)+invα3.计算变位后的中心距 a′=a×cosα/cosα′如果是斜齿轮,那么:a=m(z1+z2)/(2cosβ)invαt′=2(xn1+xn2)×tanαn/(z1+z2)+invαta′=a×cosαt/cosαt′invα就是渐开线函数,就是渐开线上那一点的展开角(弧度)。
不完全齿轮机构知识讲解
脱离啮合时,从动轮停歇不动。因此,当主 动轮连续转动时,从动轮获得时动时停的间 歇运动。
图5-12a所示为
外啮合不完全齿轮
机构,其主动轮1
转动一周时,从动
轮2转动六分之一
周,从动轮每转一
周停歇6次。当从
图 5- 12
动轮停歇时,主动
轮上的锁止弧与从
动轮上的锁止弧互相配合锁住,以保证从动轮停
歇在预定位置。图b为内啮合不完全齿轮机构。
t2 K(z2)
t1 K 2z
由于运动系数 应小于1,即z2
增加径向槽数z可以增加机构运动的平稳 性,但是机构尺寸随之增大,导致惯性力增 大。所以一般取 z =4~8。
槽轮机构中拨盘上的圆销数、槽轮上的
径向槽数以及径向槽的几何尺寸等均视运动 要求的不同而定。每一个圆销在对应的径向 槽中相当于曲柄摆动导杆机构。因此,该机 构为分析槽轮的速度、加速度带来了方便, 有兴趣的同学可以下去自学。
作业布置
❖ P93 6-2、6-4
此课件下载可自行编辑修改,仅供参考! 感谢您的支持,我们努力做得更好!谢谢
不完全齿轮机构
它由带有圆 销的主动拨盘1、 具有径向槽从动 槽轮2和机架所组 成。
5 -1 0
当拨盘1以等角速度连 续转动,拨盘上的圆销A 没进入槽轮的径向槽时, 槽轮上的内凹锁止弧被 拨盘上的外凸弧mm卡住, 槽轮静止不动。当拨盘 上的圆销刚开始进入槽 轮径向槽时,锁止弧nn 也刚好被松开槽轮在圆 销A的推动下开始转动。
如图所示为不完全齿轮齿条机构, 当主动轮连续转动时,从动轮作时动时 停的往复移动。
不完全齿轮机构 1
不完全齿轮机构 2
与普通渐开线齿轮机构一样,当主动 轮匀速转动时,其从动轮在运动期间也保 持匀速转动,但在从动轮运动开始和结束 时,即进入啮合和脱离啮合的瞬时,速度 是变化的,故存在冲击。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
τ
(当
, )=0.5043
外啮合不完全齿轮机构 2 的主要参数计算
序
参数
号
符号
计算式及结果
1 假想齿数
z1’
z1’=50
z2’
2 模数
m
3 压力角
α
4
主,从动轮齿顶高系数 ha1*
z2’=50 m=1.5 α=20° ha1*=1
5 中心距
ha2* ha2*=1 a
6
主动轮转一周,从动轮 的间歇运动次数
序
参数
号
符号
计算式及结果
1 假想齿数
z1’
z1’=50
z2’
2 模数
m
3 压力角
α
4
主,从动轮齿顶高系数 ha1*
z2’=50 m=1.5 α=20° ha1*=1
5 中心距
ha2* ha2*=1 a
6
主动轮转一周,从动轮 的间歇运动次数
N
1
7
主,从动轮齿顶压力角 αa1
αa2
°
8
从动轮顶圆齿间所对应 的中心角
2γ
9
在一次间歇运动中,从 动轮转过的角度所包含
z2
10
的齿距数
10
在一次间歇运动中,主 动轮仅一个齿时,从动
K
3
轮转过角度所包含的齿
距数
11
从动轮相邻两锁止弧间 的齿槽数,即在一次间
z1
歇运动中,主动轮转过
的齿数
12
在一尺间歇运动中,从 动轮的转角
δ
δ’
13 主动轮末齿齿顶高系数 ham*
14 主动轮首齿齿顶高系数 has*
N
1
7
主,从动轮齿顶压力角 αa1
αa2
8
从动轮顶圆齿间所对应 的中心角
2γ
9
在一次间歇运动中,从 动轮转过的角度所包含
z2
30
的齿距数
10
在一次间歇运动中,主 动轮仅一个齿时,从动
K
3
轮转过角度所包含的齿
距数
11
从动轮相邻两锁止弧间 的齿槽数,即在一次间
z1
歇运动中,主动轮转过
的齿数
12
在一尺间歇运动中,从 动轮的转角
14 主动轮首齿齿顶高系数 has*
15
主动轮首齿和末齿的齿 顶压力角
αas
αam
16 首齿重合度
ε
17 锁止弧半径
R
=13.5456°
=23.3221 =0.4622 has*< ham*=0.3500
6 16.1088
18 主动轮齿顶圆半径
ra1
19 主动轮首齿齿顶圆半径 ras1
20 主动轮末齿齿顶圆半径 ram1
E 的向径 与首齿中线
(3)
间的夹角
(4)
(2)
16.7133° =1.4933
24 过主动轮锁止弧起始点 QS
S 的向径 与末齿中线间
的夹角
25 主动轮的运动角
β
β’
26 动停比和运动系数
κ
τ
(当
)
(当
)
(当
,)
外啮合不完全齿轮机构 1 的主要参数计算
序
参数
号
符号
计算式及结果
1 假想齿数
z1’
z1’=50
z2’
2 模数
m
3 压力角
α
4
主,从动轮齿顶高系数 ha1*
z2’=50 m=1.5 α=20° ha1*=1
5 中心距
ha2* ha2*=1 a
6
主动轮转一周,从动轮 的间歇运动次数
N
1
7
主,从动轮齿顶压力角 αa1
αa2
8
从动轮顶圆齿间所对应 的中心角
2γ
9
在一次间歇运动中,从 动轮转过的角度所包含
z2
25
的齿距数
10
在一次间歇运动中,主 动轮仅一个齿时,从动
K
3
轮转过角度所包含的齿
距数
11
从动轮相邻两锁止弧间 的齿槽数,即在一次间
z1
歇运动中,主动轮转过
的齿数
12
在一尺间歇运动中,从 动轮的转角
δ
δ’
13 主动轮末齿齿顶高系数 ham*
ra2
=39
22
主动轮首末两齿中心线 间的夹角
ψ
23 过主动轮锁止弧中心点 QE
E 的向径 与首齿中线
(2)
间的夹角
(2)
24 过主动轮锁止弧起始点 QS
S 的向径 与末齿中线间
的夹角
25 主动轮的运动角
β
°
(当
)
β’
26 动停比和运动系数
κ
(当
)
τ
(当
,)
外啮合不完全齿轮机构 3 的主要参数计算
15
主动轮首齿和末齿的齿 顶压力角
αas
αam
16 首齿重合度
ε
17 锁止弧半径
R
has*< ham*=0.3500
18 主动轮齿顶圆半径
ra1
19 主动轮首齿齿顶圆半径m1
=36.5926
21 从动轮齿顶圆半径
ra2
22
主动轮首末两齿中心线 间的夹角
ψ
23 过主动轮锁止弧中心点 QE
21 从动轮齿顶圆半径
ra2
22
主动轮首末两齿中心线 间的夹角
ψ
23 过主动轮锁止弧中心点 QE
E 的向径 与首齿中线
间的夹角
(1) 由于
(2)
=9.2110
24 过主动轮锁止弧起始点 QS
S 的向径 与末齿中线间
的夹角
25 主动轮的运动角
β
(当
)
β’
26 动停比和运动系数
κ
(当 =1.1074
)=181.5525°
δ
δ’
13 主动轮末齿齿顶高系数 ham*
14 主动轮首齿齿顶高系数 has*
15
主动轮首齿和末齿的齿 顶压力角
αas
αam
16 首齿重合度
ε
17 锁止弧半径
R
has*< ham*=0.3500
°
18 主动轮齿顶圆半径
ra1
19 主动轮首齿齿顶圆半径 ras1
20 主动轮末齿齿顶圆半径 ram1
21 从动轮齿顶圆半径
