【考前三个月】(江苏专用)高考数学 压轴大题突破练 概率与统计
压轴题07 统计与概率压轴题压轴题(解析版)--2023年高考数学压轴题专项训练(全国通用-理)

压轴题07统计与概率压轴题题型/考向一:计数原理与概率题型/考向二:随机变量及其分布列题型/考向三:统计与成对数据的统计分析一、计数原理与概率热点一排列与组合解决排列、组合问题的一般步骤(1)认真审题弄清楚要做什么事情;(2)要做的事情是分步还是分类,还是分步分类同时进行,确定分多少步及多少类;(3)确定每一步或每一类是排列(有序)问题还是组合(无序)问题,元素总数是多少及取出多少元素.热点二二项式定理1.求(a+b)n的展开式中的特定项一般要应用通项公式T k+1=C k n a n-k b k(k=0,1,2,…,n).2.求两个因式积的特定项,一般对某个因式用通项公式,再结合因式相乘,分类讨论求解.3.求三项展开式的特定项,一般转化为二项式求解或用定义法.4.求解系数和问题应用赋值法.热点三概率1.古典概型的概率公式P (A )=事件A 中包含的样本点数试验的样本点总数.2.条件概率公式设A ,B 为随机事件,且P (A )>0,则P (B |A )=P (AB )P (A ).3.全概率公式设A 1,A 2,…,A n 是一组两两互斥的事件,A 1∪A 2∪…∪A n =Ω,且P (A i )>0,i =1,2,…,n ,则对任意的事件B ⊆Ω,有P (B )=∑ni =1P (A i )P (B |A i ).○热○点○题○型一计数原理与概率一、单选题1.现将甲乙丙丁四个人全部安排到A 市、B 市、C 市三个地区工作,要求每个地区都有人去,则甲乙两个人至少有一人到A 市工作的安排种数为()A .12B .14C .18D .22【答案】D【详解】若甲乙两人中的1人到A 市工作,有12C 种选择,其余3人到另外两个地方工作,先将3人分为两组,再进行排列,有2232C A 安排种数,故有12223212C C A =种;若甲乙两人中的1人到A 市工作,有12C 种选择,丙丁中一人到A 市工作,有12C 种选择,其余2人到另外两个地方工作,有22A 种选择,故安排种数有112222C C A 8=种;若安排甲乙2人都到A 市工作,其余丙丁2人到另外两个地方工作,安排种数有22A 2=种,故总共有12+8+2=22种.故选:D2.世界数学三大猜想:“费马猜想”、“四色猜想”、“哥德巴赫猜想”,其中“四色猜想”和“费马猜想”已经分别在1976年和1994年荣升为“四色定理”和“费马大定理”.281年过去了,哥德巴赫猜想仍未解决,目前最好的成果“1+2”由我国数学家陈景润在1966年取得.哥德巴赫猜想描述为:任何不小于4的偶数,都可以写成两个质数之和.在不超过17的质数中,随机选取两个不同的数,其和为奇数的概率为()A .14B .27C .13D .253.在2x x y -+的展开式中,项7x y 的系数为()A .60B .30C .20D .60-【答案】D【详解】由()()6622x x y x x y ⎡⎤-+=-+⎣⎦,可得其二项展开式()61216C ,0,1,2,3,4,5,6rrr r T x x y r -+=-=,若先满足项7x y 中y 的次数,则1r =,可得()()55112226C 6T x x y x x y =-=-,其中()52x x -展开式的通项为()()()52210155C 1C ,0,1,2,3,4,5rrrr r rr T x x x r --+=-=-=,令107r -=,得3r =,可得()32377451C 10T x x =-=-,故项7x y 的系数为()61060⨯-=-.故选:D.4.在)7311⎛⋅ ⎝的展开式中,含1x 的项的系数为()A .21B .35C .48D .56择,每个志愿者只能选其中一个小区.则每个小区至少有一名志愿者,且甲不在A 小区的概率为()A .193243B .100243C .23D .59至少有一个白球”,事件:B “3个球中至少有一个红球”,事件:C “3个球中有红球也有白球”,下列结论不正确的是()A .事件A 与事件B 不为互斥事件B .事件A 与事件C 不是相互独立事件C .()3031P C A =D .()()P AC P AB >的社团.目前话剧社团、书法社团、摄影社团、街舞社团分别还可以再接收1名学生,恰好含甲、乙的4名同学前来教务科申请加入,按学校规定每人只能加入一个社团,则甲进街舞社团,乙进书法社团或摄影社团的概率为()A .14B .15C .16D .183月5日和3月4日胜利召开,为实现新时代新征程的目标任务汇聚智慧和力量.某市计划开展“学两会,争当新时代先锋”知识竞赛活动.某单位初步推选出3名党员和5名民主党派人士,并从中随机选取4人组成代表队参赛.在代表队中既有党员又有民主党派人士的条件下,则党员甲被选中的概率为()A .12B .1115C .713D .27【答案】C【详解】记“随机选取4人”为事件Ω,“代表队中既有党员又有民主党派人士”为事件A ,“党二、多选题9.在9x ⎛+ ⎝的展开式中,下列结论正确的是()A .第6项和第7项的二项式系数相等B .奇数项的二项式系数和为256C .常数项为84D .有理项有2项10.已知01239252222x a a x a x a x a x -=+-+-+-++- ,则下列结论成立的是()A .20911a a a a ++++=LB .3672a =C .9012393a a a a a -+-+-= D .123912398=++++ a a a a 【答案】ABD【详解】()()()()()9929012925122222x x a a x a x a x --+-=+⎣=-+-++-⎡⎤⎦,展开式的通项为()()()()99199C 125C 125r rrrrr rr T x x --+=--=-⋅⋅-⎡⎤⎣⎦,对选项A :令3x =,可得()901292351a a a a ++++=⨯-= ,正确;对选项B :()33498C 2T x =-,所以3398C 672a ==,正确;对选项C :令1x =,可得901293a a a a -+--=- ,错误;对选项D :()()()()()923901239252222x a a x a x a x a x -=+-+-+-++- ,两边同时求导,得()()()()82812391825223292x a a x a x a x -=+-+-++- ,令3x =,123912398=++++ a a a a ,正确.故选:ABD11.甲箱中有5个红球,2个白球和3个黑球,乙箱中有4个红球,3个白球和3个黑球.先从甲箱中随机取出一球放入乙箱中,分别以1A ,2A ,3A 表示由甲箱中取出的是红球,白球和黑球的事件;再从乙箱中随机取出一球,以B 表示由乙箱中取出的球是红球的事件,则下列结论正确的是()A .()25P B =B .()1511P B A =C .事件B 与事件1A 相互独立D .1A 、2A 、3A 两两互斥表演分为“燃爆竹、放烟花、辞旧岁、迎新春”4个环节.小光按照以上4个环节的先后顺序进行表演,每个环节表演一次.假设各环节是否表演成功互不影响,若每个环节表演成功的概率均为34,则()A.事件“成功表演燃爆竹环节”与事件“成功表演辞旧岁环节”互斥B.“放烟花”、“迎新春”环节均表演成功的概率为9 16C.表演成功的环节个数的期望为3D.在表演成功的环节恰为3个的条件下“迎新春”环节表演成功的概率为3 4热点一分布列的性质及应用离散型随机变量X的分布列为X x1x2…x i…x nP p1p2…p i…p n 则(1)p i≥0,i=1,2,…,n.(2)p1+p2+…+p n=1.(3)E(X)=x1p1+x2p2+…+x i p i+…+x n p n.(4)D (X )=∑ni =1[x i -E (X )]2p i .(5)若Y =aX +b ,则E (Y )=aE (X )+b ,D (Y )=a 2D (X ).热点二随机变量的分布列1.二项分布一般地,在n 重伯努利试验中,设每次试验中事件A 发生的概率为p (0<p <1),用X 表示事件A 发生的次数,则X 的分布列为P (X =k )=C k n p k (1-p )n -k,k =0,1,2,…,n .E (X )=np ,D (X )=np (1-p ).2.超几何分布一般地,假设一批产品共有N 件,其中有M 件次品,从N 件产品中随机抽取n 件(不放回),用X 表示抽取的n 件产品中的次品数,则X 的分布列为P (X =k )=C k M C n -k N -M C n N,k =m ,m +1,m +2,…,r .其中n ,N ,M ∈N *,M ≤N ,n ≤N ,m =max{0,n -N +M },r =min{n ,M },E (X )=n ·M N .热点三正态分布解决正态分布问题的三个关键点(1)对称轴x =μ.(2)样本标准差σ.(3)分布区间:利用3σ原则求概率时,要注意利用μ,σ分布区间的特征把所求的范围转化为3σ的特殊区间.○热○点○题○型二随机变量及其分布列一、单选题1.某班级有50名学生,期末考试数学成绩服从正态分布()2120,N σ,已(140)0.2P X >=,则[100,140]X ∈的学生人数为()A .5B .10C .20D .30【答案】D【详解】因为期末考试数学成绩服从正态分布()2120,N σ,所以期末考试数学成绩关于120μ=对称,则(140)(100)0.2P X P X >=<=,所以(100140)0.6P X ≤≤=,所以[100,140]X ∈的学生人数为:0.65030⨯=人.故选:D.2.在某个独立重复实验中,事件A ,B 相互独立,且在一次实验中,事件A 发生的概率为p ,事件B 发生的概率为1p -,其中()0,1p ∈.若进行n 次实验,记事件A 发生的次数为X ,事件B 发生的次数为Y ,事件AB 发生的次数为Z ,则下列说法正确的是()A .()()()1pE X p E Y =-B .()()()1p D X pD Y -=C .()()E ZD Y =D .()()()2D Z D X D Y=⋅⎡⎤⎣⎦【答案】C【详解】由已知,(),X B n p ,∴()E X np =,()()1D X np p =-,(),1Y B n p ~-,∴()()1E Y n p =-,()()()()1111D Y n p p np p ⎡⎤=---=-⎣⎦,∵事件A ,B 相互独立,∴一次实验中,A ,B 同时发生的概率()()()()1P AB P A P B p p ==-,∴()(),1Z B n p p ~-,∴()()1E Z np p =-,()()()()()211111D Z np p p p np p p p ⎡⎤=---=--+⎣⎦,对于A ,()2pE X np =,()()()211p E Y n p -=-,()()()1pE X p E Y =-不一定成立,故选项A 说法不正确;对于B ,()()()211p D X np p -=-,()()21pD Y np p =-,()()()1p D X pD Y -=,不一定成立,故选项B 说法不正确;对于C ,()()1E Z np p =-,()()1D Y np p =-,()()E Z D Y =成立,故选项C 说法正确;对于D ,()()()22222211D Z n p p p p ⎡⎤=--+⎣⎦,()()()2221D X D Y n p p ⋅=-,()()()2D Z D X D Y =⋅⎡⎤⎣⎦不一定成立,故选项D 说法不正确.故选:C.3.新能源汽车具有零排放、噪声小、能源利用率高等特点,近年来备受青睐.某新能源汽车制造企业为调查其旗下A 型号新能源汽车的耗电量(单位:kW·h/100km )情况,随机调查得到了1200个样本,据统计该型号新能源汽车的耗电量2(13,)N ξσ ,若()12140.7P ξ<<=,则样本中耗电量不小于14kW h /100km ⋅的汽车大约有()A .180辆B .360辆C .600辆D .840辆4.设1122,这两个正态分布密度曲线如图所示.下列结论中正确的是()A .对任意实数t ,()()P X t P Y t ≥≥≥B .对任意实数t ,()()P X t P Y t ≤≥≤C .()()21P Y P Y μμ≥≥≥D .()()21P X P X σσ≤≤≤..A .两个随机变量的线性相关性越强,相关系数的绝对值越接近于1B .设()21N ξσ~,,且(0)0.2P ξ<=,则(12)0.2P ξ<<=C .线性回归直线ˆˆˆybx a =+一定经过样本点的中心(),x y D .随机变量()B n p ξ~,,若()()3020E D ξξ==,,则90n =从正态分布()272,8N ,则数学成绩位于[80,88]的人数约为()参考数据:()0.6827P X μσμσ-≤≤+≈,()220.9545P X μσμσ-≤≤+≈,()330.9973P X μσμσ-≤≤+≈.A .455B .2718C .6346D .95457.某种品牌手机的电池使用寿命X (单位:年)服从正态分布,且使用寿命不少于2年的概率为0.9,则该品牌手机电池至少使用6年的概率为()A .0.9B .0.7C .0.3D .0.1面包店的面包师声称自己所出售的面包的平均质量是1000g ,上下浮动不超过50g .这句话用数学语言来表达就是:每个面包的质量服从期望为1000g ,标准差为50g 的正态分布.假设面包师的说法是真实的,记随机购买一个面包的质量为X ,若()2~,X N μσ,则买一个面包的质量大于900g 的概率为()(附:①随机变量η服从正态分布()2,N μσ,则()0.6827μσημσ-≤≤+=,(22)0.9545P μσημσ-≤≤+=,(33)0.9973P μσημσ-≤≤+=;)A .0.84135B .0.97225C .0.97725D .0.99865二、多选题9.已知随机变量X 服从二项分布29,3B ⎛⎫⎪⎝⎭,随机变量21Y X =+,则下列说法正确的是()A .随机变量X 的数学期望()6E X =B .512(2)93P X ⎛⎫==⨯ ⎪⎝⎭C .随机变量X 的方差()2D X =D .随机变量Y 的方差()4D Y =10.随机变量且20.5P X ≤=,随机变量3,Y B p ,若E Y E X =,则()A .2μ=B .()22D x σ=C .23p =D .()36D Y =坐公交车和骑自行车所花的时间,经数据分析得到:坐公交车平均用时30分钟,样本方差为36;自行车平均用时34分钟,样本方差为4.假设坐公交车用时X 和骑自行车用时Y 都服从正态分布,则()A .P (X >32)>P (Y >32)B .P (X ≤36)=P (Y ≤36)C .李明计划7:34前到校,应选择坐公交车D .李明计划7:40前到校,应选择骑自行车【答案】BCD【详解】A.由条件可知()230,6X N ,()234,2Y N ~,根据对称性可知()()320.532P Y P X >>>>,故A 错误;B.()()36P X P X μσ≤=≤+,()()36P Y P Y μσ≤=≤+,所以()()3636P X P Y ≤=≤,故B 正确;C.()340.5P X ≤>=()34P Y ≤,所以()()3434P X P Y ≤>≤,故C 正确;D.()()()40422P X P X P X μσ≤<<=<+,()()403P Y P Y μσ≤=≤+,所以()()4040P X P Y ≤<≤,故D 正确.故选:BCD12.假设某厂有两条包装食盐的生产线甲、乙,生产线甲正常情况下生产出来的包装食盐质量服从正态分布()2500,5N (单位:g ),生产线乙正常情况下生产出来包装食盐质量为x g ,随机变量x 服从正态密度函数()2200(1000)x x ϕ--=,其中x ∈R ,则()附:随机变量2(,)N ξμσ-,则()0.683P μσξμσ-<<+=,()220.954P μσξμσ-<<+=,()330.997P μσξμσ-<<+=.A .正常情况下,从生产线甲任意抽取一包食盐,质量小于485g 的概率为0.15%B .生产线乙的食盐质量()2~1000,100x N C .生产线乙产出的包装食盐一定比生产线甲产出的包装食盐质量重D .生产线甲上的检测员某天随机抽取两包食盐,称得其质量均大于515g ,于是判断出该生产线出现异常是合理的三、解答题13.学校要从12名候选人中选4名同学组成学生会,已知有4名候选人来自甲班,假设每名候选人都有相同的机会被选到.(1)求恰有1名甲班的候选人被选中的概率;(2)用X 表示选中的候选人中来自甲班的人数,求()3P X ≥;(3)求(2)中X 的分布列及数学期望.()012344954954954954953E X =⨯+⨯+⨯+⨯+⨯=.14.网购生鲜蔬菜成为很多家庭日常消费的新选择.某小区物业对本小区三月份参与网购生鲜蔬菜的家庭的网购次数进行调查,从一单元和二单元参与网购生鲜蔬菜的家庭中各随机抽取10户,分别记为A 组和B 组,这20户家庭三月份网购生鲜蔬菜的次数如下图:假设用频率估计概率,且各户网购生鲜蔬菜的情况互不影响·(1)从一单元参与网购生鲜蔬菜的家庭中随机抽取1户,估计该户三月份网购生鲜蔬菜次数大于20的概率;(2)从一单元和二单元参与网购生鲜蔬菜的家庭中各随机抽取1户,记这两户中三月份网购生鲜蔬菜次数大于20的户数为X ,估计X 的数学期望()E X ;(3)从A 组和B 组中分别随机抽取2户家庭,记1ξ为A 组中抽取的两户家庭三月份网购生鲜蔬菜次数大于20的户数,2ξ为B 组中抽取的两户家庭三月份网购生鲜蔬菜次数大于20的户数,比较方差()1D ξ与()2D ξ的大小.(结论不要求证明)高科技体验.现有A,B两种型号的小型家庭生活废品处理机器人,其工作程序依次分为三个步骤:分捡,归类,处理,每个步骤完成后进入下一步骤.若分捡步骤完成并且效能达到95%及以上,则该步骤得分为20分,若归类步骤完成并且效能达到95%及以上,则该步骤得分为30分,若处理步骤完成并且效能达到95%及以上,则该步骤得分为50分.若各步骤完成但效能没有达到95%,则该步骤得分为0分,在第三个步骤完成后,机器人停止工作.现已知A款机器人完成各步骤且效能达到95%及以上的概率依次为45,35,13,B款机器人完成各步骤且效能达到95%及以上的概率均为12,每款机器人完成每个步骤且效能是否达到95%及以上都相互独立.(1)求B款机器人只有一个步骤的效能达到95%及以上的概率;(2)若准备在A,B两种型号的小型家庭生活废品处理机器人中选择一款机器人,从最后总得分的期望角度来分析,你会选择哪一种型号?则()416226802030507575257575E X =⨯+⨯+⨯+⨯+14380015270801002525753⨯+⨯+⨯==.设B 款机器人完成所有工作总得分为Y ,则Y 的可能取值为0,20,30,50,70,80,100,所以()()3110,20,30,70,80,10028P Y ξξ⎛⎫==== ⎪⎝⎭,()31150224P Y ⎛⎫==⨯= ⎪⎝⎭,所以Y 的分布列为:Y02030507080100P18181814181818则()11111020305088848E Y =⨯+⨯+⨯+⨯+11400708010050,888⨯+⨯+⨯==因为152503>,所以()()E X E Y >,所以从最后总得分的期望角度来分析,应该选择A 种型号的机器人.三、统计与成对数据的统计分析热点一用样本估计总体1.频率分布直方图中相邻两横坐标之差表示组距,纵坐标表示频率组距,频率=组距×频率组距.2.在频率分布直方图中各小长方形的面积之和为1.3.利用频率分布直方图求众数、中位数与平均数.(1)最高的小长方形底边中点的横坐标即众数.(2)中位数左边和右边的小长方形的面积和相等.(3)平均数是频率分布直方图的“重心”,等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和.热点二回归分析求经验回归方程的步骤(1)依据成对样本数据画出散点图,确定两个变量具有线性相关关系(有时可省略).(2)计算出x -,y -,∑n i =1x 2i ,∑n i =1x i y i 的值.(3)计算a ^,b ^.(4)写出经验回归方程.热点三独立性检验独立性检验的一般步骤(1)根据样本数据列2×2列联表;(2)根据公式χ2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d ),计算χ2的值;(3)查表比较χ2与临界值的大小关系,作统计判断.χ2越大,对应假设事件H 0成立(两类变量相互独立)的概率越小,H 0不成立的概率越大.○热○点○题○型三统计与成对数据的统计分析一、单选题1.已知一组数据1231,31,,31n x x x --- 的方差为1,则数据12,,,n x x x 的方差为()A .3B .1C .13D .19抽取部分员工体检,已知该企业营销部门和研发部门的员工人数之比是4:1且被抽到参加体检的员工中,营销部门的人数比研发部门的人数多72,则参加体检的人数是()A .90B .96C .102D .120【答案】D绩的频率分布直方图如图所示,则下列说法正确的是()A .频率分布直方图中a 的值为0.004B .估计这20名学生考试成绩的第60百分位数为75C .估计这20名学生数学考试成绩的众数为80D .估计总体中成绩落在[)60,70内的学生人数为150【答案】D【详解】由()10237621a a a a a ⨯++++=可得0.005a =,故A 错误;前三个矩形的面积和为()102370.6a aa ⨯++=,所以这20名学生数学考试成绩的第60百分位数为80,故B 错误;这20名学生数学考试成绩的众数为75,故C 错误;总体中成绩落在[)60,70内的学生人数为3101000150a ⨯⨯=,故D 正确.故选:D4.如图,一组数据123910,,,,,x x x xx ⋅⋅⋅,的平均数为5,方差为21s ,去除9x ,10x 这两个数据后,平均数为x ,方差为22s ,则()A .5x >,2212s s >B .5x <,2212s s <C .5x =,2212s s <D .5x =,2212s s >根据食品安全管理考核指标对抽到的企业进行考核,并将各企业考核得分整理成如下的茎叶图.由茎叶图所给信息,可判断以下结论中正确是()A .若2a =,则甲地区考核得分的极差大于乙地区考核得分的极差B .若4a =,则甲地区考核得分的平均数小于乙地区考核得分的平均数C .若5a =,则甲地区考核得分的方差小于乙地区考核得分的方差D .若6a =,则甲地区考核得分的中位数小于乙地区考核得分的中位数A .将总体划分为2层,通过分层随机抽样,得到两层的样本平均数和样本方差分别为12,x x 和2212,s s ,且已知12x x =,则总体方差()2221212s s s =+B .在研究成对数据的相关关系时,相关关系越强,相关系数r 越接近于1C .已知随机变量X 服从正态分布()2,N μσ,若()()151P X P X -+= ,则2μ=D .按从小到大顺序排列的两组数据:甲组:27,30,37,,40,50m ;乙组:24,,33,44,48,52n ,若这两组数据的第30百分位数、第50百分位数都分别对应相等,则67m n +=1,2,…,10A .数据141x +,241x +,…,1041x +的平均数为9B .10120i i x ==∑C .数据13x ,23x ,…,103x 的方差为D .102170i i x ==∑1制动距离(2d ,单位:m )之和.如图为某实验所测得的数据,其中“KPH”表示刹车时汽车的初速度v (单位:km/h ).根据实验数据可以推测,下面四组函数中最适合描述1d ,2d 与v 的函数关系的是()A .1d v α=,2d =B .1d v α=,22d v β=C .1d =,2d v β=D .1d =,22d vβ=【答案】B【详解】设()()1d v f v =,()()2d v g v =.由图象知,()()1d v f v =过点()40,8.5,()50,10.3,()60,12.5,()70,14.6,()80,16.7,()90,18.7,()100,20.8,()110,22.9,()120,25,()130,27.1,()140,29.2,()150,31.3,()160,33.3,()170,35.4,()180,37.5.作出散点图,如图1.由图1可得,1d 与v 呈现线性关系,可选择用1d v α=.()()2d v g v =过点()40,8.5,()50,16.2,()60,23.2,()70,31.4,()80,36,()90,52,()100,64.6,()110,78.1,()120,93,()130,108.5,()140,123,()150,144.1,()160,164.3,()170,183.6,()180,208.作出散点图,如图2.由图2可得,2d 与v 呈现非线性关系,比较之下,可选择用22d v β=.故选:B.二、多选题9.下列说法正确的是()A .数据5,7,8,11,10,15,20的中位数为11B .一组数据7,8,8,9,11,13,15,17,20,22的第80百分位数为18.5C .从1,2,3,4,5中任取3个不同的数,则这3个数能构成直角三角形三边长的概率为0.1D .设随机事件A 和B ,已知0.8)PA =(,0.6|PB A =(),(|)0.1P B A =,则()0.5P B =故选:BCD.10.为了加强学生对党的二十大精神的学习,某大学开展了形式灵活的学习活动.随后组织该校大一学生参加二十大知识测试(满分:100分),随机抽取200名学生的测试成绩,这200名学生的成绩都在区间[]60,100内,将其分成5组:[)60,68,[)68,76,[)76,84,[)84,92,[]92,100,得到如下频率分布直方图.根据此频率分布直方图,视频率为概率,同一组中的数据用该组区间的中点值为代表,则()A .该校学生测试成绩不低于76分的学生比例估计为76%B .该校学生测试成绩的中位数估计值为80C .该校学生测试成绩的平均数大于学生测试成绩的众数D .从该校学生中随机抽取2人,则这2人的成绩不低于84分的概率估计值为0.16到该地旅游的游客中随机抽取10000位游客进行调查,得到各年龄段游客的人数和旅游方式,如图所示,则()A .估计2022年到该地旅游的游客中中年人和青年人占游客总人数的80%B .估计2022年到该地旅游的游客中选择自助游的游客占游客总人数的26.25%C .估计2022年到该地旅游且选择自助游的游客中青年人超过一半D .估计2022年到该地旅游的游客中选择自助游的青年人比到该地旅游的老年人还要多【答案】ABC【详解】设2022年到该地旅游的游客总人数为a ,由题意可知游客中老年人、中年人、青年人的人数分别为0.2a ,0.35a ,0.45a ,其中选择自助游的老年人、中年人、青年人的人数分别为0.04a ,0.0875a ,0.135a ,所以2022年到该地旅游的游客中中年人和青年人的人数为0.350.450.8a a a +=,所以A 正确;因为2022年到该地旅游的游客选择自助游的人数0.040.08750.1350.2625a a a a ++=,所以B 正确;因为2022年到该地旅游且选择自助游的游客的人数为0.2625a ,其中青年人的人数为0.135a ,所以C 正确;因为2022年到该地旅游的游客中选择自助游的青年人的人数为0.135a ,而到该地旅游的老年人的人数为0.2a ,所以D 错误.故选:ABC.12.如图为国家统计局于2022年12月27日发布的有关数据,则()A .营业收入增速的中位数为9.1%B .营业收入增速极差为13.6%C .利润总额增速越来越小D .利润总额增速的平均数大于6%【答案】ABD【详解】由表中数据易知营业收入增速的中位数为9.1%,故选项A 正确;营业收入增速的极差为20.3% 6.7%13.6%-=,故选项B 正确;利润总额增速2022年1-3月累计比2022年1-2月累计上升,故选项C 错误;利润总额增速的平均数(38.0%34.3% 5.0%8.5% 3.5% 1.0% 1.0% 1.1%++++++-2.1% 2.3% 3.0% 3.6%)12 6.6%----÷=,故选项D 正确;故选:ABD .三、解答题13.为了检测某种抗病毒疫苗的免疫效果,需要进行动物与人体试验.研究人员将疫苗注射到200只小白鼠体内,一段时间后测量小白鼠的某项指标值,按[)[)[)[)[]0,20,20,40,40,60,60,80,80,100分组,绘制频率分布直方图如图所示,实验发现小白鼠体内产生抗体的共有160只,其中该项指标值不小于60的有110只,假设小白鼠注射疫苗后是否产生抗体相互独立.抗体指标值合计小于60不小于60有抗体没有抗体合计(1)填写下面的2×2列联表,并根据列联表及0.05a =的独立性检验,判断能否认为注射疫苗后小白鼠产生抗体与指标值不小于60有关.(单位:只)(2)为检验疫苗二次接种的免疫抗体性,对第一次注射疫苗后没有产生抗体的40只小白鼠进行第二次注射疫苗,结果又有20只小自鼠产生抗体.(i )用频率估计概率,求一只小白鼠注射2次疫苗后产生抗体的概率p ;(ii )以(i )中确定的概率p 作为人体注射2次疫苗后产生抗体的概率,进行人体接种试验,记n 个人注射2次疫苗后产生抗体的数量为随机变量X .试验后统计数据显示,当X =99时,P (X )取最大值,求参加人体接种试验的人数n .参考公式:22()()()()()n ad bc x a b c d a c b d -=++++(其中n a b c d =+++为样本容量)20()P x k ≥0.500.400.250.150.1000.0500.0250k 0.4550.7081.3232.0722.7063.8415.024零假设为0根据列联表中数据,得220.05200(502020110) 4.945 3.8411604070130x x ⨯⨯-⨯=≈>=⨯⨯⨯,根据0.05α=的独立性检验,推断0H 不成立,即认为注射疫苗后小白鼠产生抗体与指标值不小于60有关,此推断犯错误的概率不大于0.05.(2)(i )令事件A =“小白鼠第一次注射疫苗产生抗体”,事件B =“小白鼠第二次注射疫苗产生抗体’’,事件C =“小白鼠注射2次疫苗后产生抗体”,记事件A ,B ,C 发生的概率分别为(),(),()P A P B P C ,则160()0.8200P A ==,20(|)0.540P B A ==,()1()1()(|)10.20.50.9P C P AB P A P B A =-=-=-⨯=,所以一只小白鼠注射2次疫苗后产生抗体的概率0.9p =,(ii )由题意,知随机变量~(,0.9)X B n ,()C 0.90.1(0,1,2,)k k n kn P X k k n -==⨯⨯= ,因为(99)P X =最大,所以999999989898999999100100100C 0.90.1C 0.90.1C 0.90.1C 0.90.1n n n n n n nn ----⎧⨯⨯≥⨯⨯⎨⨯⨯≥⨯⨯⎩,解得1109110,9n ≤≤n Q 是整数,所以109n =或110n =,∴接受接种试验的人数为109或110.14.某地经过多年的环境治理,已将荒山改造成了绿水青山.为估计一林区某种树木的总材积量,随机选取了10棵这种树木,测量每棵树的根部横截面积(单位:2m )和材积量(单位:3m ),得到如下数据:样本号i12345678910平均值根部横截面积0.040.060.040.080.080.05a b c 0.070.06ix 材积量i y 0.250.410.220.540.530.340.350.390.430.440.39其中a ,b ,c 为等差数列,并计算得:610.146i i i xy ==∑0.044≈,0.303≈.(1)求b的值;(2)若选取前6个样本号对应数据,判断这种树木的根部横截面积与材积量是否具有很强的线性相关性,并求该林区这种树木的根部横截面积与材积量的回归直线方程(若0.250.75r ≤≤,则认为两个变量的线性相关性一般;若0.75r>,则认为两个变量的线性相关性很强);附:相关系数n i i x y nx yr -=∑回归直线y bx a =+$$$中,1221n i i i n ii x y nx y b xnx ==-=-∑∑ ,a y bx =-$$.(3)根据回归直线方程估计a ,c 的值(精确到0.01).。
压轴题08 概率与统计的综合运用(解析版)-2023年高考数学压轴题专项训练(江苏专用)

压轴题08概率与统计的综合运用概率统计在高考中扮演着很重要的角色,概率统计解答题是新高考卷及多数省市高考数学必考内容,考查热点为古典概型、相互独立事件的概率、条件概率、超几何分布、二项分布、正态分布、统计图表与数字特征、回归分析、离散型随机变量的分布列、期望与方差的实际应用等.回顾近几年的高考试题,可以看出概率统计解答题,大多紧密结合社会实际,以现实生活为背景设置试题,注重知识的综合应用与实际应用,作为考查实践能力的重要载体,命题者要求考生会收集,整理、分析数据,能从大量数据中抽取对研究问题有用的信息,建立数学模型,再应用数学原理和数学工具解决实际问题.考向一:概率与其它知识的交汇问题考向二:递推概率考向三:与体育比赛规则有关的概率问题考向四:决策型问题考向五:条件概率、全概率公式、贝叶斯公式(一)涉及的概率知识层面主要考查随机变量的概率分布与数学期望,一定要根据有关概念,判断是等可能事件、互斥事件、相互独立事件还是独立重复试验,以便选择正确的计算方法,进行概率计算及离散型随机变量的分布列和数学期望的计算,也要掌握几种常见常考的概率分布模型:离散型有二项分布、超几何分布,连续型有正态分布.考查运用概率知识解决简单实际问题的能力,1、离散型随机变量的期望与方差一般地,若离散型随机变量X 的分布列为称1122()n n E X x p x p x p =+++ 为随机变量X 的均值或数学期望,它反映了离散型随机变量取值的平均水平.称()21()()ni i i D X x E X p ==-∑为随机变量X 的方差,它刻画了随机变量X 与其均值()E XX 的标准差.(1)离散型随机变量的分布列的性质①0(1,2,,)i p i n = ;②121n p p p +++= .(2)均值与方差的性质若Y aX b =+,其中,a b 为常数,则Y 也是随机变量,且2()();()()E aX b aE X b D aX b a D X +=++=(3)分布列的求法①与排列、组合有关分布列的求法.由排列、组合、概率知识求出概率,再求出分布列.②与频率分布直方图有关分布列的求法.可由频率估计概率,再求出分布列.③与互斥事件有关分布列的求法.弄清互斥事件的关系,利用概率公式求出概率,再列出分布列.④与独立事件(或独立重复试验)有关分布列的求法.先弄清独立事件的关系,求出各个概率,再列出分布列.(4)常见的离散型随机变量的概率分布模型①二项分布;②超儿何分布.2、常见的连续型概率分布模型正态分布.(二)概率分布与不同知识背景结合考查对实际问题的解决能力1、与数列结合的实际问题2、与函数导数结合的实际问题3、与分段函数求最值、解不等式结合的实际问题4、与统计结合的实际问题5、与其他背景结合的实际问题一、单选题1.(2023·福建·统考模拟预测)已知()2,X N μσ ,则()0.6827P X μσμσ-≤≤+≈,()220.9545P X μσμσ-≤≤+≈,()330.9973P X μσμσ-≤≤+≈.今有一批数量庞大的零件.假设这批零件的某项质量指标引单位:毫米)服从正态分布()25.40,0.05N ,现从中随机抽取N 个,这N 个零件中恰有K 个的质量指标ξ位于区间()5.35,5.55.若45K =,试以使得()45P K =最大的N 值作为N 的估计值,则N 为()A .45B .53C .54D .90【答案】B【解析】由已知可得,()()5.35 5.55 5.400.05 5.4030.05P P ξξ<<=-<<+⨯()3P X μσμσ=-<<+.又()()()3332P X P X P X μσμσμσμσμσμσ-<<++-<<+-<<+=0.68270.99730.842+≈=,所以,(),0.84K B N :,()45454545C 0.840.16N N P K -==⋅⋅.设()454545C 0.840.16x x f x -=⋅⋅,则()()45454414545451C 0.840.16C 0.840.16x x x x f x f x -+-+⋅⋅=⋅⋅()()()1!44!45!10.160.161!4445!45!x x x x x x +-+=⋅=⋅>--,所以,110452.521x <=,所以()()5352f f >.()()4545454545461C 0.840.161C 0.840.16x x x x f x f x ---⋅⋅=-⋅⋅()()()!45!45!0.160.1611!4546!45!x x x x x x -=⋅=⋅<---,所以,37545377x >=+,所以()()5354f f >.所以,以使得()45P K =最大的N 值作为N 的估计值,则N 为53.故选:B.2.(2023·贵州·统考模拟预测)信息熵是信息论中的一个重要概念.设随机变量X 所有可能的取值为1,2,,n ,且()()01,2,,i P X i p i n ==>=⋅⋅⋅,11ni i p ==∑,定义X 的信息熵()21log ni i i H X p p ==-∑,若2n m =,随机变量Y 所有可能的取值为1,2,,m ⋅⋅⋅,且()()211,2,,j m j P Y j p p j m +-==+=⋅⋅⋅,则()A .()()H X H Y ≥B .()()H X H Y ≤C .()()H X H Y <D .()()H X H Y >【答案】D【解析】依题意知,()121m P Y p p ==+,()2212m P Y p p -==+,()3223m P Y p p -==+,…,()1m m P Y m p p +==+,∴()H Y =()()()()()()122122212221121log log log m m m m m m m m p p p p p p p p p p p p --++-++++++⋅⋅⋅+++⎡⎤⎣⎦,又()()1212222222log log log log m m m m H X p p p p p p p p =-++⋅⋅⋅++⋅⋅⋅+,∴()()2121222221222112log log log m m m m m p p p H Y H X p p p p p p p p p --=++⋅⋅⋅++++,又1121mp p p <+,22211m p p p -<+,…,2121m mp p p <+,∴()()0H Y H X -<,∴()()H X H Y >.故选:D.3.(2023·云南·高三校联考阶段练习)一枚质地均匀的正方体骰子,其六个面分别刻有1,2,3,4,5,6六个数字,投掷这枚骰子两次,A 表示事件“第一次向上一面的数字是1”,B 表示事件“第二次向上一面的数字是2”,C 表示事件“两次向上一面的数字之和是7”,D 表示事件“两次向上一面的数字之和是8”,则()A .C 与D 相互独立B .A 与D 相互独立C .B 与D 相互独立D .A 与C 相互独立【答案】D【解析】由题意知()()()()11615,,6636636P A P B P C P D ====,()()()0P CD P C P D =≠,所以C 与D 不相互独立,()()()0P AD P A P D =≠,所以A 与D 不相互独立,()()()136P BD P B P D =≠,所以B 与D 不相互独立,()()()136P AC P A P C ==,所以A 与C 相互独立,故选:D二、多选题4.(2023·辽宁沈阳·沈阳二中校考三模)已知数列{}n a 的前n 项和为n S ,且1i a =或2i a =的概率均为()11,2,3,2i =⋅⋅⋅.设n S 能被3整除的概率为n P ,则()A .21P =B .314P =C .113411024P =D .当25n ≥时,13n P <【答案】BC【解析】由题意可知:11a =或22a =,则11S =或12S =,即13S ≠,故10P =;∵*n S ∈N ,则n S 被3整除的余数为0,1,2,若n S 被3整除的余数为0,由11n a +=或12n a +=,可得1n S +不能被3整除;若n S 被3整除的余数为1,则取12n a +=,可得1n S +被3整除;若n S 被3整除的余数为2,则取11n a +=,可得1n S +被3整除;综上所述:()1112n n P P +=-,可得1111323n n P P +⎛⎫-=-- ⎪⎝⎭,且110133P =-≠-,故数列13n P ⎧⎫-⎨⎩⎭是以首项11133P -=-,公比12q =-的等比数列,则1111332n n P -⎛⎫⎛⎫-=-⨯- ⎪ ⎪⎝⎭⎝⎭,故1111332n n P -⎛⎫=-⨯- ⎪⎝⎭.可得2111113322P ⎛⎫=-⨯-=≠ ⎪⎝⎭,2311113324P ⎛⎫=-⨯-= ⎪⎝⎭,11103411113321024P ⎛⎫-⨯-= ⎪⎝⎭=,A 错误,B 、C 正确;当n 为偶数时,则1n -为奇数,可得1102n -⎛⎫-< ⎪⎝⎭,故111113323n n P -⎛⎫=-⨯-> ⎪⎝⎭;当n 为奇数时,则1n -为偶数,可得1102n -⎛⎫-> ⎪⎝⎭,故111113323n n P -⎛⎫=-⨯-< ⎪⎝⎭;可得当25n ≥时,13n P <不成立,故D 错误.故选:BC.5.(2023·福建泉州·统考三模)某商场设有电子盲盒机,每个盲盒外观完全相同,规定每个玩家只能用一个账号登陆,且每次只能随机选择一个开启.已知玩家第一次抽盲盒,抽中奖品的概率为27,从第二次抽盲盒开始,若前一次没抽中奖品,则这次抽中的概率为12,若前一次抽中奖品,则这次抽中的概率为13.记玩家第n 次抽盲盒,抽中奖品的概率为n P ,则()A .21942P =B .数列37n P ⎧⎫-⎨⎬⎩⎭为等比数列C .1942n P ≤D .当2n ≥时,n 越大,n P 越小【答案】ABC【解析】记玩家第()N i i *∈次抽盲盒并抽中奖品为事件i A ,依题意,127P =,()113n n P A A -=,()112n n P A A -=,()n n P P A =,对于A 选项,()()()()()221211212121191737242P P A P A P A A P A P A A ⎛⎫==+=⨯+-⨯= ⎪⎝⎭,A 对;对于B 选项,()()()()()1111n n n n n n n P A P A P A A P A P A A ----=+,所以,()111111113262n n n n P P P P ---=+-=-+,所以,1313767n n P P -⎫⎛-=-- ⎪⎝⎭,又因为127P =,则131077P -=-≠,所以,数列37n P ⎧⎫-⎨⎬⎩⎭是首项为17-,公比为16-的等比数列,B 对;对于C 选项,由B 选项可知,1311776n n P -⎛⎫-=-⋅- ⎪⎝⎭,则1311776n n P -⎛⎫=-- ⎪⎝⎭,当n 为奇数时,131319776742n n P -=-<<⋅,当n 为偶数时,131776n n P -=+⋅,则n P 随着n 的增大而减小,所以,21942nP P ≤=.综上所述,对任意的n *∈N ,1942n P ≤,C 对;对于D 选项,因为1311776n n P -⎛⎫=-- ⎪⎝⎭,则数列{}n P 为摆动数列,D 错.故选:ABC.6.(2023·山西大同·大同市实验中学校考模拟预测)如图,已知正方体1111ABCD A B C D -顶点处有一质点Q ,点Q 每次会随机地沿一条棱向相邻的某个顶点移动,且向每个顶点移动的概率相同.从一个顶点沿一条棱移动到相邻顶点称为移动一次.若质点Q 的初始位置位于点A 处,记点Q 移动n 次后仍在底面ABCD 上的概率为n P ,则下列说法正确的是()A .259P =B .12133n n P P +=+C .点Q 移动4次后恰好位于点1C 的概率为0D .点Q 移动10次后仍在底面ABCD 上的概率为10111()232+【答案】ACD【解析】在正方体中,每一个顶点由3个相邻顶点,其中两个在同一底面,所以当点Q 在下底面时,随机移动一次仍在下底面的概率为23,在上底面时,随机移动一次回到下底面的概率为13,所以222115+=33339P =⨯⨯,故A 正确,12111(1)=3333n n n n P P P P +=+-+,故B 错误,点Q 由点A 移动到点1C 处最少需要3次,任意折返都需要2次移动,所以移动4次后不可能到达点1C ,故C 正确,由于1111111()33232n n n n P P P P ++=+⇒-=-且11211326P P =⇒-=,所以1111111()=(263232n n n n P P --=⨯⇒+,所以1010111=()232P +,故D 正确.故选:ACD.7.(2023·山东烟台·高二统考阶段练习)甲、乙两人进行()*2N n n ∈局羽毛球比赛(无平局),每局甲获胜的概率均为12.规定:比赛结束时获胜局数多的人贏得比赛.记甲贏得比赛的概率为()P n ,假设每局比赛互不影响,则()A .()114P =B .()11316P =C .()221C 122n nnP n +=-D .()P n 单调递增【答案】ACD【解析】由题意知:要使甲赢得比赛,则甲至少赢1n +局,()()21222221CC C 2nn n n nn n P n ++⎛⎫=+++ ⎪⎝⎭L .∵011122222222C C C C C C 2n n n n nn n n n n n -++++++++=L L ,又011122122222222C C C C C C C n n n n nn n n n n n n -++-+++=++++L L ,∴201112212222222222C C C CCCCC 2n nn n n n n nn n nnnnn-++--+++=++++=L L ,∴()2222212C C 112222n n n nn n n P n +-=⋅=-,故C 正确;∴()123C 111224P =-=,故A 正确;()367C 11132232P =-=,故B 错误;∵()22212C C 1112222n n n n n n P n ⎛⎫=-=- ⎪⎝⎭+,∴()12222C 11122n n n P n +++⎛⎫+=- ⎪⎝⎭,又∵()()()()()()()()2222112222222!C 441214C !!2122!C C 22212121!1!n n n n n n n n n n n n n n n n n n n n n +++++⋅++====>++++++,∴1222222C C 22n n n n n n +++>,∴()()1P n P n <+,即P (n )单调递增,故D 正确.故选:ACD .三、填空题8.(2023·河南信阳·校联考模拟预测)在ABC 中,内角,,A B C 的对边分别为,,a b c.若c =,2b =,π3C =,AD 是BC 边上的高线,点D 为垂足.点E 为线段BD 上一点,点B 关于直线AE 的对称点为点M .从四边形BACM 中任取一点,该点来自ABC 的概率记为()P A ,则()P A 的最小值为______.【答案】12/0.5【解析】由余弦定理知:2222cos a b ab C c +-=,即24212a a +-=,解得:4a =,222b c a ∴+=,ABC ∴ 为直角三角形,AB AC ⊥,设BM AE F = ,作MG BC ⊥于点G,bcAD a==,1CD ∴==,13BD a =-=,要使得()P A 最小,则BMC △面积最大,即点M 到BC 的距离MG 最大.设DEA θ∠=,则FEB θ∠=,AD = ,3BD =,DE ∴=,3BE =cos 3cos tan EF BE θθθ⎛⎫∴==- ⎪ ⎪⎝⎭,MGB ∽EFB △,MG MBEF BE∴=,22sin 23cos sin 3sin 2cos tan MG EF θθθθθθ⎛⎫∴==-=- ⎪ ⎪⎝⎭π3sin 2226θθθ⎛⎫==- ⎪⎝⎭则当ππ262θ-=,即π3θ=时,sin 26πθ⎛⎫- ⎪⎝⎭取得最大值1,max MG ∴=,此时MBC ABC S S =△△,()min 12ABC ABC MBC S P A S S ∴==+ .故答案为:12.9.(2023·山东枣庄·统考二模)一个袋子中有100个大小相同的球,其中有40个黄球,60个白球.采取不放回摸球,从中随机摸出22个球作为样本,用X 表示样本中黄球的个数.当()P X k =最大时,()E X k +=____________.【答案】17.8/4175【解析】不放回的摸球,每次实验结果不独立,为超几何分布()P X k ==22406022100C C 012...22C k k k -=,,,,()P X k =最大时,即224060C C k k-最大,超几何分布最大项问题,利用比值求最大项设()C C C s m s k n ks mn a P X s --===则111C C C C C C s m s ms k n kn ms m s s n k n ka a +--+---=⋅()()()()()()()()()!!1!1!1!1!!!!!!!n k k s k s m s n k m s k n k s k s m s n k m s -+------++=⋅-----+()()()()11k s m s s n k m s --=+--++令()()()()111k s m s s n k m s -->+--++()()()()11k s m s s n k m s ⇒-->+--++()()2221s k m s km s n k m s n k m ⇒-++>++--++--()()21km n s n m k ⇒>+++--()()()1211km m k n s n ⇒+++>++++()()1112k m s n ++⇒<-+故当()()112k m s n ++≤+时,()P X s =严格增加,当()()1112k m s n ++≥-+时,()P X s =严格下降,即9k =时取最大值,此题中1002240n m k s k ====,,,,根据超几何分布的期望公式可得()40228.8100⨯⨯===k m E X n ,()8.8917.8+=+=E X k故答案为:17.810.(2023·浙江金华·浙江金华第一中学校考模拟预测)定义:如果甲队赢了乙队,乙队赢了丙队,而丙队又赢了甲队,则称甲乙丙为一个“友好组”.如果20支球队参加单循环比赛,则友好组个数的最大值为__________.【答案】330【解析】当m 为偶数时,令2m n =,则总共有22C n 场比赛.不妨设有x 个友好组,考虑其反面,若甲乙丙三对为非友好组,不妨设甲队赢了乙队和丙队,此时,记甲队为非友好组的组长.对甲队而言,可以在赢的所有队伍中任意选择两队构成非友好组.因此,若队()1,2,,2i A i n = 在比赛中赢了i k 场,则2221C ni n i k ==∑,且以i A 为组长的非友好组有2C ik 个(补充定义:)2201C C 0==,于是所有非友好组的个数为221C i nk i =∑.下求221C i nk i =∑最小值.若在122,,,n k k k 中,有2j i k k -≥.则令**1,1i i j j k k k k =+=-,其余*(12j i k k l n =≤≤且,)l i j ≠,**2222222211C 1C C C C C C C i j i j i j ijk k k k k k i j k k k k +-+-=+-=-+--≤-,故调整后221C i nk i =∑的总和变小.重复上述操作,直至任意两个数的差最多为1.不妨设有y 个,2a n y -个1a +,则有()()()222121,n ya n y a C n n +-+==-整理有()1122y a n n -=--.由于121y n ≤≤-,故()0,12yn∈.由等式两边对应相等可知,1,a n y n =-=,即调整后有n 个1,n n -个n .此时的值221C i nk i =∑为2(1)n n -,则()()32211(1)3C n n n n x n n -+≤--=,故友好组个数的最大值为()()113n n n -+,即()()2224m m m -+.下面为取到最大值的例子:设在122,,,n A A A .共2n 支球队中,当1i n ≤≤时,队i A 胜12,,i i i n A A A +++ ;当12n i n +≤≤时,队i A 胜121,,,i i i n A A A +++- ,下标均是在模2n 的意义下.综上所述,当m 为偶数时,友好组个数的最大值为()()2224m m m -+.故如果20支球队参加单循环比赛,友好组个数的最大值为330.故答案为:33011.(2023·上海黄浦·高二上海市大同中学校考阶段练习)已知正三角形ABC ,某同学从A 点开始,用掷骰子的方法移动棋子.规定:①每掷一次骰子,把一枚棋子从三角形的一个顶点移动到另一个顶点.②棋子移动的方向由掷骰子(点数为16-)决定,若掷出骰子的点数大于3,则按逆时针方向移动;若掷出骰子的点数不大于3,则按顺时针方向移动.设掷骰子n 次时,棋子移动到,,A B C 处的概率分别为()n P A ,()n P B ,()n P C .例如:掷骰子一次时,棋子移动到,,A B C 处的概率分别为1()0P A =,11((1))2P B P C ==.当掷骰子7次时,棋子移动到A 处的概率7()P A 值为___________.【答案】2164【解析】设()n n P A a =,()n n P B b =,()n n P C c =,则1112b c ==,由于棋子移动的方向由掷骰子决定,若掷出骰子的点数大于3,则按逆时针方向移动;若掷出骰子的点数不大于3,则按顺时针方向移动,即顺时针与逆时针移动是等可能的,所以n n b c =,掷骰子n 次时,棋子共有移动到,,A B C 三种情况,故1n n n a b c ++=;∵n n b c =,即11,(2)n n b c n --=≥,又由题意可知111()2n n n b a c --=+,∴2n ≥时111111,()()22n n n n n b a c a b ----=+=+,又∵1111n n n a b c ---++=,即1112n n a b --=-,可得121n n b b -+=,即11122n n b b -=-+,故11111111()322323n n n b b b ---=-+-=--,可得数列1{}3n b -是首项为11136b -=,公比为12-的等比数列,所以1111()362n n b --=⋅-,即1111()362n n b -=+-,所以11111111212[.()][1()]36232n n n n a b --=-=-+-=--,故6711211()3264a ⎡⎤=--=⎢⎥⎣⎦,即721()64P A =,故答案为:216412.(2023·天津·统考一模)一袋中有大小相同的4个红球和2个白球若从中任取3球,则恰有一个白球的概率是__________,若从中不放回的取球2次,每次任取1球,记“第一次取到红球”为事件A ,“第二次取到红球”为事件B ,则()|P B A =__________.【答案】3535【解析】恰有一个白球的概率12243635C C P C ==;由题可知A =“第一次取到红球”,B =“第二次取到红球”,则()23P A =,()432655P AB ⨯==⨯,所以()()()3|5P AB P B A P A ==.故答案为:35,35.13.(2023·山东烟台·高二山东省招远第一中学校考期中)现有一款闯关游戏,共有4关,规则如下:在第n 关要抛掷骰子n 次,每次观察向上面的点数并做记录,如果这n 次抛掷所出现的点数之和大于2n n +,则算过第n 关.假定每次过关互不影响,则直接挑战第2关并过关的概率为__________,若直接挑战第4关,则过关的概率为__________.【答案】712351296【解析】第一空,直接挑战第二关过关需两次点数之和大于222=6+,两次点数满足要求的有如下几种情况:(1,6),(2,5),(2,6),(3,4)……(6,5),(6,6),则概率为:12345676612+++++=⨯;第二空,直接挑战第四关过关需四次点数之和大于424=20+,四次点数满足要求的有如下几种情况:(5,5,5,6)四种,(4,5,6,6)十二种,(5,5,6,6)六种,(3,6,6,6)四种,(4,6,6,6,)四种,(5,6,6,6)四种,(6,6,6,6)一种,合计35种,故概率为:4353561296=.故答案为:712,35129614.(2023·山东潍坊·统考一模)乒乓球被称为我国的“国球”.甲、乙两名运动员进行乒乓球比赛,其中每局中甲获胜的概率为34,乙获胜的概率为14,每局比赛都是相互独立的.①若比赛为五局三胜制,则需比赛五局才结束的概率为__________.②若两人约定其中一人比另一人多赢两局时比赛结束,则需要进行的比赛局数的数学期望为__________.附:当01q <<时,lim 0n n q →+∞=,lim 0n n n q →+∞⋅=.【答案】27128/0.2109375165【解析】①需比赛五局才结束,则说明前四局双方为2:2,概率为22243127C 44128⎛⎫⎛⎫⋅=⎪⎪⎝⎭⎝⎭.②假设比赛局数为随机变量X ,由已知,需比赛局数为偶数,则X 可取2,4,6,,2,n L L()*n ∈N .则()2222223152C C 448P X ⎛⎫⎛⎫==+= ⎪ ⎪⎝⎭⎝⎭,当2n ≥时,双方前22n -局战为平局,且任意前2m (11m n ≤≤-,且*m ∈N )局双方均战为平局,则()121211122313311532C C 44444488n n n P X n ---⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫==⨯⨯⨯+⨯⨯⨯=⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,显然1n =,满足该式.设()153288n n a P X n -⎛⎫===⨯ ⎪⎝⎭,则有115338885388nn n n a a +-⎛⎫⨯ ⎪⎝⎭==⎛⎫⨯ ⎪⎝⎭,所以,{}n a 是以158a =为首项,38q =为公比的等比数列.设2n n b na =,则15348n n n b -⎛⎫=⨯ ⎪⎝⎭.设{}n b 的前n 项和为n S ,则2112353331234888n n n S b b b b n -⎡⎤⎛⎫⎛⎫⎛⎫=++++=+⨯+⨯++⋅⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦L L ,2335333323848888nn S n ⎡⎤⎛⎫⎛⎫⎛⎫=+⨯+⨯++⋅⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦L ,作差可得,213533331848888n nn n S S n -⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-=++++-⋅⎢⎥⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦L311855335322344884818n n nnn n ⎡⎤⎛⎫⨯-⎢⎥⎪⎝⎭⎢⎥⎛⎫⎛⎫⎛⎫⎣⎦=⨯-⋅=-⋅-⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭-,整理可得,16163345588n nn S n ⎛⎫⎛⎫=-⋅-⋅ ⎪ ⎪⎝⎭⎝⎭.由题意可得,163lim 058n n →∞⎡⎤⎛⎫⋅=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦,3lim 408n n n →∞⎡⎤⎛⎫⋅=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦.则()()()()()222222232322E X P X P X P X n P X n =⋅=+⨯⋅=⨯+⨯⋅=⨯++⋅=+L L161633lim lim 45588n nn n n S n →∞→∞⎡⎤⎛⎫⎛⎫==-⋅-⋅⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦16163316lim lim lim 455885n n n n n n →∞→∞→∞⎡⎤⎡⎤⎛⎫⎛⎫=-⋅-⋅=⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦.故答案为:27128;165.四、解答题15.(2023·江西·校联考模拟预测)某企业对生产设备进行优化升级,升级后的设备控制系统由()21k k *-∈N 个相同的元件组成,每个元件正常工作的概率均为()01p p <<,各元件之间相互独立.当控制系统有不少于k 个元件正常工作时,设备正常运行,否则设备停止运行,记设备正常运行的概率为k p (例如:2p 表示控制系统由3个元件组成时设备正常运行的概率;3p 表示控制系统由5个元件组成时设备正常运行的概率).(1)若23p =,当2k =时,求控制系统中正常工作的元件个数X 的分布列和数学期望,并求3p ;(2)已知设备升级前,单位时间的产量为a 件,每件产品的利润为1元,设备升级后,在正常运行状态下,单位时间的产量是原来的4倍,且出现了高端产品,每件产品成为高端产品的概率为14,每件高端产品的利润是2元.记设备升级后单位时间内的利润为Y (单位:元).(i )请用k p 表示()E Y ;(ii )设备升级后,在确保控制系统中元件总数为奇数的前提下,分析该设备能否通过增加控制系统中元件的个数来提高利润.【解析】(1)因为2k =,所以控制系统中正常工作的元件个数X 的可能取值为0,1,2,3;因为每个元件的工作相互独立,且正常工作的概率均为23p =,所以23,3X B ⎛⎫⎪⎝⎭,所以()03032110C 3327P X ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,()12132121C 339P X ⎛⎫⎛⎫=== ⎪⎪⎝⎭⎝⎭()21232142C 339P X ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,()30332183C 3327P X ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,所以控制系统中正常工作的元件个数X 的分布列为X123P1272949827控制系统中正常工作的元件个数X 的数学期望为()2323E X =⨯=,324153453555212121C C C 333333P ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭8080321926424324324324381=++==;(2)(i )升级改造后单位时间内产量的分布列为产量4a 0设备运行概率kp 1kp -所以升级改造后单位时间内产量的期望为4k ap ;所以产品类型高端产品一般产品产量(单位:件)kap 3kap 利润(单位:元)21设备升级后单位时间内的利润为235k k k ap ap ap +=,即()5k E Y ap =;(ii )因为控制系统中元件总数为奇数,若增加2个元件,则第一类:原系统中至少有1k +个元件正常工作,其概率为()()1211C 1k k kk k p p p p --=--;第二类:原系统中恰好有k 个元件正常工作,新增2个元件中至少有1个正常工作,其概率为()()()()()121122212C 111C 12k k k kk k k k p p p p p p p --+--⎡⎤=-⋅--=--⎣⎦;第三类:原系统中有1k -个元件正常工作,新增2个元件全部正常工作,其概率为()()()1121121213C 1C 1kkk k k k k k p pp p p p ---+--=-⋅=-;所以()()()()111111212121C 1C 12C 1k k kk k k k k k k k k k k p p p p pp p p p --+-++---=--+--+-()()21C 121kk kk k p p p p -=+--,则()()121C 121kk k k k k p p p p p +--=--,所以当12p >时,10k k p p +->,k p 单调递增,即增加元件个数设备正常工作的概率变大,当12p ≤时,10k k p p +-≤,即增加元件个数设备正常工作的概率没有变大,又因为()5k E Y ap =,所以当12p >时,设备可以通过增加控制系统中元件的个数来提高利润;当12p ≤时,设备不可以通过增加控制系统中元件的个数来提高利润.16.(2023·浙江杭州·统考二模)马尔科夫链是概率统计中的一个重要模型,也是机器学习和人工智能的基石,在强化学习、自然语言处理、金融领域、天气预测等方面都有着极其广泛的应用.其数学定义为:假设我们的序列状态是…,2t X -,1t X -,t X ,1t X +,…,那么1t X +时刻的状态的条件概率仅依赖前一状态t X ,即()()1211,,,t t t t t t P X X X X P X X +--+⋅⋅⋅=.现实生活中也存在着许多马尔科夫链,例如著名的赌徒模型.假如一名赌徒进入赌场参与一个赌博游戏,每一局赌徒赌赢的概率为50%,且每局赌赢可以赢得1元,每一局赌徒赌输的概率为50%,且赌输就要输掉1元.赌徒会一直玩下去,直到遇到如下两种情况才会结束赌博游戏:一种是手中赌金为0元,即赌徒输光;一种是赌金达到预期的B 元,赌徒停止赌博.记赌徒的本金为()*N ,A A A B ∈<,赌博过程如下图的数轴所示.当赌徒手中有n 元(0n B ≤≤,N n ∈)时,最终输光的概率为........()P n ,请回答下列问题:(1)请直接写出()0P 与()P B 的数值.(2)证明(){}P n 是一个等差数列,并写出公差d .(3)当100A =时,分别计算200B =,1000B =时,()P A 的数值,并结合实际,解释当B →∞时,()P A 的统计含义.【解析】(1)当0n =时,赌徒已经输光了,因此()01P =.当n B =时,赌徒到了终止赌博的条件,不再赌了,因此输光的概率()0P B =.(2)记M :赌徒有n 元最后输光的事件,N :赌徒有n 元上一场赢的事件,()()(|)()(|)P M P N P M N P N P M N =+,即11()(1)(1)22P n P n n =-++,所以()()()()11P n P n P n P n --=+-,所以(){}P n 是一个等差数列,设()()1P n P n d --=,则()()()()1210P n P n d P P d ---=-=,, ,累加得()(0)P n n P d -=,故()(0)P B P Bd -=,得1d B=-,(3)100A =,由()()0P n P nd -=得()()0P A P Ad -=,即()1A P A B=-,当200B =时,()50%P A =,当1000B =时,()90%P A =,当B →∞时,()1P A →,因此可知久赌无赢家,即便是一个这样看似公平的游戏,只要赌徒一直玩下去就会100%的概率输光.17.(2023·吉林·统考三模)2022年11月20日,卡塔尔足球世界杯正式开幕,世界杯上的中国元素随处可见.从体育场建设到电力保障,从赛场内的裁判到赛场外的吉祥物都是中国制造,为卡塔尔世界杯提供了强有力的支持.国内也再次掀起足球热潮.某地足球协会组建球队参加业余比赛,该足球队教练组为了考查球员甲对球队的贡献,作出如下数据统计(甲参加过的比赛均分出了输赢):球队输球球队赢球总计甲参加23032甲未参加81018总计104050(1)根据小概率值0.005α=的独立性检验,能否认为该球队赢球与甲球员参赛有关联;(2)从该球队中任选一人,A 表示事件“选中的球员参赛”,B 表示事件“球队输球”.()()||P B A P B A 与()()||P B A P B A 的比值是选中的球员参赛对球队贡献程度的一项度量指标,记该指标为R .①证明:()()()()||||P A B P A B R P A B P A B =⋅;②利用球员甲数据统计,给出()|P A B ,()|P A B 的估计值,并求出R 的估计值.附:()()()()()22n ad bc a b c d a c b d χ-=++++.参考数据:a 0.050.010.0050.001ax 3.8416.6357.87910.828【解析】(1)零假设为0H :该球队胜利与甲球员参赛无关.()2250210308302510.50310403218288χ⨯⨯-⨯==≈⨯⨯⨯,因为27.879χ>,所以依据0.005α=的独立性检验,我们推断0H 不成立,所以认为该球队胜利与甲球员参赛有关,此推断犯错误的概率不大于0.005.(2)①证明:()()()()()()()()()()()()()()()()||||P AB P AB P B A P A P AB P B A P A P AB R P B A P AB P AB P B A P AB P AB P A P A =⋅=⋅=⋅()()()()()()()()()()()()()()()()()()()()||||P AB P AB P AB P AB P A B P B P B P B P B P A B P AB P AB P A B P AB P AB P A B P B P B P B P B =⋅=⋅=⋅②()1|5P A B =,()3|4P A B =,()()()()()()()()11|1|||154431|12|||54P A B P A B P A B P A B R P A B P A B P A B P A B ⨯-=⋅=⋅==-⨯.18.(2023·全国·模拟预测)2022年11月4日上午,福建省福州市教育局对2023年初中毕业生体育考试抽考类、抽选考类项目进行摇号抽签,最终确定排球对墙垫球为抽考项目,立定跳远、50米跑、双手头上前掷实心球三项为抽选考项目(考生从这三个项目中自选两项考试).此外,体育中考还有必考项目:1000米跑(男)、800米跑(女)或200米游泳(泳姿不限),考生按性别从2个项目中自选1项考试.若某初三男生参加中考体育测试的项目为排球对墙垫球、立定跳远、双手头上前掷实心球、1000米跑.为了提高成绩,该男生决定每天进行多次训练(一次练一项),第一次,在4个项目中等可能地随机选一项开始训练,从第二次起,每次都是从上一次未训练的3个项目中等可能地随机选1项训练.(1)若该男生某天进行了3次训练,求第三次训练的是“排球对墙垫球”的概率;(2)若该男生某天进行了5次训练,4个项目都有训练,且第一次训练的是“1000米跑”,前后训练项目不同视为不同的训练顺序,设5次训练中选择“1000米跑”的次数为X ,求X 的分布列及数学期望.【解析】(1)第一次训练的是“排球对墙垫球”,且第三次训练的是“排球对墙垫球”的概率为1131111C 43312P =⨯⨯⨯=,第一次训练的不是“排球对墙垫球”,且第三次训练的是“排球对墙垫球”的概率为112321111=C C 4336P ⨯⨯⨯⨯=,所以第三次训练的是“排球对墙垫球”的概率为121111264P P P =+=+=.(2)由题意知“1000米跑”最多训练2次,所以X 的所有可能取值为1,2.①1X =说明后4次训练中除“1000米跑”外的3项中有1项训练了2次,余下的2项都各训练一次,从除“1000米跑”外的3项中选一项训练2次有13C 种方法,不妨设训练了2次“排球对墙垫球”,可分为以下两类:第一类,第二次训练的是“排球对墙垫球”,则第四次或第五次也训练了“排球对墙垫球”,有1222C A 种方法;第二类,第三次训练的是“排球对墙垫球”,则第五次也训练了“排球对墙垫球”,有22A 种方法,因此共有()12122322C 1C A A 8+=种方法.②2X =说明“1000米跑”训练了2次,第三次或第四次或第五次也训练了“1000米跑”,故有1333C A 18=种方法.所以()181118182P X ===+,()181218182P X ===+.所以X 的分布列为:X12P1212所以()11312222E X =⨯+⨯=.19.(2023·福建莆田·统考二模)互花米草是禾本科草本植物,其根系发达,具有极高的繁殖系数,对近海生态具有较大的危害.为尽快消除互花米草危害,2022年10月24日,市政府印发了《莆田市互花米草除治攻坚实施方案》,对全市除治攻坚行动做了具体部署.某研究小组为了解甲、乙两镇的互花米草根系分布深度情况,采用按比例分层抽样的方法抽取样本.已知甲镇的样本容量12m =,样本平均数18x =,样本方差2119s =;乙镇的样本容量18n =,样本平均数36y =,样本方差2270s =.(1)求由两镇样本组成的总样本的平均数z 及其方差2S ;(2)为营造“广泛发动、全民参与”的浓厚氛围,甲、乙两镇决定进行一次“互花米草除治大练兵”比赛,两镇各派一支代表队参加,经抽签确定第一场在甲镇举行.比赛规则:每场比赛直至分出胜负为止,胜方得1分,负方得0分,下一场在负方举行,先得2分的代表队获胜,比赛结束.当比赛在甲镇举行时,甲镇代表队获胜的概率为35,当比赛在乙镇举行时,甲镇代表队获胜的概率为12.假设每场比赛结果相互独立.甲镇代表队的最终得分记为X ,求()E X .参考数据:2222212183888,183623328,28.8829.44,1210.81399.68,187.2933.12⨯=⨯==⨯=⨯=.【解析】(1)根据题意,得121821833628.812185x y z +⨯+⨯===+,因为()()()()()121212222111212i i i i i i x x x z x x x x x z x z ===-+-=-+--+-∑∑∑()()()()()12121222221112121212i i i i i i x x x z x x x z x x x z ===⎛=-+--+-=-+- ⎝⎭∑∑∑,同理()()()18182221112i i i i y y y z y y y z ==-+-=-+-∑∑,所以()()121822211130i i i i S x z y z ==⎡⎤=-+-⎢⎥⎣⎦∑∑()()12182211130i i i i x x x z y y y z ==⎡⎤=-+-+-+-⎢⎥⎣⎦∑∑()()()()12182222111121230i i i i x x x z y y y z ==⎡⎤=-++-+-⎢⎥⎣⎦∑∑22221211212()1818(30S x z S y z ⎡⎤=+-++-⎣⎦()22112191210.81870187.230=⨯⨯+⨯+⨯+⨯127.36 =,所以总样本的平均数为28.8z =,方差2127.36S =.(2)依题意可知,X 的所有可能取值为0,1,2,设“第i 场比赛在甲镇举行,甲镇代表队获胜”为事件i A ,“第i 场比赛在乙镇举行,甲镇代表队获胜”为事件, 1,2,3i B i =,则()()31,52i i P A P B ==,所以()21234(0)1525P X P A A ⎛⎫===-= ⎪⎝⎭,()()()1231231231233133316(1)1152555225P X P A B A A A B P A B A P A B ⎛⎫⎛⎫==+=+=⨯⨯-+-⨯⨯= ⎪ ⎪⎝⎭⎝⎭,15(2)1(0)(1)25P X P X P X ==-=-==,所以461536()01225252525E X =⨯+⨯+⨯=.20.(2023·浙江·模拟预测)2022年卡塔尔世界杯决赛圈共有32队参加,其中欧洲球队有13支,分别是德国、丹麦、法国、西班牙、英格兰、克罗地亚、比利时、荷兰、塞尔维亚、瑞士、葡萄牙、波兰、威尔士.世界杯决赛圈赛程分为小组赛和淘汰赛,当进入淘汰赛阶段时,比赛必须要分出胜负.淘汰赛规则如下:在比赛常规时间90分钟内分出胜负,比赛结束,若比分相同,则进入30分钟的加时赛.在加时赛分出胜负,比赛结束,若加时赛比分依然相同,就要通过点球大战来分出最后的胜负.点球大战分为2个阶段.第一阶段:前5轮双方各派5名球员,依次踢点球,以5轮的总进球数作为标准(非必要无需踢满5轮),前5轮合计踢进点球数更多的球队获得比赛的胜利.第二阶段:如果前5轮还是平局,进入“突然死亡”阶段,双方依次轮流踢点球,如果在该阶段一轮里,双方都进球或者双方都不进球,则继续下一轮,直到某一轮里,一方罚进点球,另一方没罚进,比赛结束,罚进点球的一方获得最终的胜利.下表是2022年卡塔尔世界杯淘汰赛阶段的比赛结果:淘汰赛比赛结果淘汰赛比赛结果1/8决赛荷兰3:1美国1/4决赛克罗地亚4112():()巴西阿根廷2:1澳大利亚荷兰3224():()阿根廷法国3:1波兰摩洛哥10:葡萄牙英格兰30:塞内加尔英格兰1:2法国日本1113():()克罗地亚半决赛阿根廷30:克罗地亚巴西4:1韩国法国20:摩洛哥摩洛哥3000():()西班牙季军赛克罗地亚2:1摩洛哥葡萄牙61:瑞士决赛阿根廷4332():()法国注:“阿根廷4332():()法国”表示阿根廷与法国在常规比赛及加时赛的比分为33:,在点球大战中阿根廷42:战胜法国.(1)请根据上表估计在世界杯淘汰赛阶段通过点球大战分出胜负的概率.(2)根据题意填写下面的22 列联表,并通过计算判断是否能在犯错的概率不超过0.01的前提下认为“32支决赛圈球队闯入8强”与是否为欧洲球队有关.欧洲球队其他球队合计闯入8强未闯入8强合计。
考前三个月新高考数学(文)二轮冲刺中档大题强化练——概率与统计(含答案详析)

中档大题加强练 —— 概率与统计1.(2013·标全国课 Ⅱ )经销商经销某种农产品,在一个销售季度内,每售出1 t该产品赢利润 500 元,未售出的产品,每1 t 损失 300 元.依据历史资料,获取销售季度内市场需求量的频次散布直方图, 以下图. 经销商为下一个销售季度购进了130 t 该农产品. 以X(单位: t,100≤ X ≤ 150)表示下一个销售季度内的市场需求量,T(单位:元 )表示下一个销售季度内经销该农产品的收益.(1)将 T 表示为 X 的函数; (2)依据直方图预计收益 T 许多于 57 000 元的概率.解(1)当 X ∈ [100,130) 时,T = 500X -300(130 - X)=800X - 39 000. 当 X ∈ [130,150] 时, T = 500× 130=65 000.800X - 39 000, 100≤ X<130,因此T =65 000 , 130≤ X ≤ 150.(2)由 (1)知收益T 许多于57 000 元当且仅当120≤ X ≤ 150.由直方图知需求量X ∈ [120,150] 的频次为 0.7,因此下一个销售季度内的收益T 许多于57 000 元的概率的预计值为0.7.2. 一袋中装有四个形状大小同样的球,球的编号分别为1,2,3,4.(1)从袋中随机抽取一个球, 将其编号记为 a ,而后从袋中余下的三个球中再随机抽取一22个球,将其编号记为b ,求对于 x 的一元二次方程 x + 2ax + b = 0 有实根的概率;(2)先从袋中随机取一个球,该球的编号记为m.将球放回袋中,而后再从袋中随机取一x - y ≥ 0, 个球,该球的编号记为n.若以 (m ,n)作为点 P 的坐标,求点P 落在地区 内x + y - 5<0的概率.解 (1)设事件 A 为 “ 方程 x 2+ 2ax + b 2= 0 有实根 ”. 当 a>0 ,b>0 时,方程 x 2+ 2ax +b 2= 0 有实根的充要条件为 a ≥b.以下第一个数表示 a 的取值,第二个数表示 b 的取值.基本领件共 12 个:(1,2),(1,3),(1,4) ,(2,1),(2,3),(2,4),(3,1),(3,2) ,(3,4) ,(4,1),(4,2),(4,3).事件 A 中包含 6 个基本领件: (2,1) ,(3,1), (3,2) ,(4,1), (4,2), (4,3) .事件 A 发生的概率为P(A)=6 112 = .2(2)先从袋中随机取一个球,放回后再从袋中随机取一个球,点P(m ,n)的全部可能状况为:(1,1),(1,2),(1,3),(1,4) ,(2,1) ,(2,2),(2,3),(2,4),(3,1),(3,2) ,(3,3) ,(3,4),(4,1),(4,2), (4,3), (4,4),共 16 个.x -y ≥ 0,落在地区 内的有 (1,1), (2,1) ,(2,2) , (3,1),共 4 个,x +y - 5<0x - y ≥ 0, 1因此点 P 落在地区 内的概率为x + y - 5<04.3. 某学校高一、高二、高三的三个年级学生人数以下表:高三高二 高一 女生 100 150 z男生300450600按年级分层抽样的方法评比优异学生 50 人,此中高三有10 人.(1)求 z 的值;(2)用分层抽样的方法在高一学生中抽取一个容量为 5 的样本,将该样本当作一个整体,从中任取 2 人,求起码有 1 名女生的概率;(3) 用随机抽样的方法从高二女生中抽取 8 人,经检测她们的得分以下:9.4,8.6,9.2,9.6,8.7,9.0,9.3,8.2 ,把这 8 人的总分看作一个整体,从中任取一个数,求该数与样本均匀数之差的绝对值不超出0.5 的概率.解 (1)设该校总人数为 n 人,50 10由题意得 n = 100+ 300,因此 n = 2 000,z = 2 000- 100-300- 150- 450- 600= 400.(2)设所抽样本中有 m 个女生,因为用分层抽样的方法在高一学生中抽取一个容量为5的样本,因此400 = m,解得 m = 2.也就是抽取了 2 名女生, 3 名男生,分别记作S ,1 000 51S 2; B 1 ,B 2, B 3,则从中任取 2 个的全部基本领件为 (S 1, B 1) ,(S 1,B 2) ,(S 1,B 3), (S 2,B 1), (S 2, B 2 ), (S 2, B 3 ), (S 1, S 2), (B 1,B 2), (B 2, B 3), (B 1, B 3),共 10 个,此中起码有 1 名女生的基本领件有 7 个: (S 1, B 1),(S 1,B 2),(S 1, B 3),(S 2,B 1), (S 2,B 2), (S 2,7B 3), (S 1, S2),因此从中任取 2 人,起码有 1 名女生的概率为 10.1 (3)样本的均匀数为x = 8(9.4+ 8.6+ 9.2+ 9.6+ 8.7+ 9.0+ 9.3+ 8.2)=9,那么与样本均匀数之差的绝对值不超出0.5 的数为 9.4,8.6,9.2,8.7,9.0,9.3 这 6 个数,总的个数为 8,因此该数与样本均匀数之差的绝对值不超出0.5 的概率为 6= 3 .8 44. (2013 北·京 )某小组共有 A ,B ,C ,D ,E 五位同学, 他们的身高 ( 单位:米 )及体重指标 (单位:千克 /米 2) 以下表所示:AB C D E 身高 1.69 1.73 1.75 1.79 1.82 体重指标19.225.118.523.320.9(1)从该小组身高低于 1.80 的同学中任选 2 人,求选到的 2 人身高都在 1.78 以下的概率;(2) 从该小组同学中任选2 人,求选到的 2 人的身高都在 1.70 以上且体重指标都在[18.5,23.9) 中的概率.解 (1)从身高低于 1.80 的 4 名同学中任选 2 人,其全部可能的结果构成的基本领件有:(A ,B), (A , C),(A ,D ),(B , C), (B ,D ),(C ,D )共 6 个.设 “ 选到的 2 人身高都在 1.78 以下 ” 为事件 M ,其包含事件有 3 个,故 P(M)=3= 1.6 2(2)从小组 5 名同学中任选 2 人,其全部可能的结果构成的基本领件有: (A , B), (A ,C) , (A , D), (A , E), (B ,C), (B ,D ), (B , E), (C , D), (C , E), (D , E)共 10 个. 设 “ 选到的 2 人的身高都在 1.70 以上且体重指标都在 [18.5,23.9) ”为事件 N ,且事件 N包含事件有: (C , D),( C , E), (D , E)共 3 个. 则 P(N)=310.5. 某饮料企业对一名职工进行测试以便确立其考评级别,企业准备了两种不一样的饮料共5杯,其颜色完整同样,而且此中 3 杯为 A 饮料,此外 2 杯为 B 饮料,企业要求此职工一一品味后,从 5 杯饮猜中选出3 杯 A 饮料.若该职工 3 杯都选对,则评为优异;若3杯选对 2 杯,则评为优异;不然评为合格.假定这人对A 和B 两种饮料没有鉴识能力.(1)求这人被评为优异的概率;(2)求这人被评为优异及以上的概率.解 将 5 杯饮料编号为 1,2,3,4,5,编号 1,2,3 表示 A 饮料,编号 4,5 表示 B 饮料, 则从 5杯饮猜中选出 3 杯的全部可能状况为(123), (124),(125) ,(134), (135) , (145) ,(234),(235), (245) , (345),可见共有 10 种.令 D 表示这人被评为优异的事件, E 表示这人被评为优异的事件,F 表示这人被评为良好及以上的事件,则1(1)P(D )=10.37(2)P(E)= 5, P(F)= P(D)+ P(E)= 10.6. 某生物兴趣小组,在学校生物园地栽种了一批名贵树苗,为认识树苗的生长状况,从这批树苗中随机地丈量了此中 50 棵树苗的高度 (单位:厘米 ),并把这些高度列成了以下的频数散布表:组别 [40,50)[50,60)[60,70) [70,80)[80,90)[90,100]频数231415124(1)在这批树苗中任取一棵,其高度在 85 厘米以上的概率大概是多少?(2)这批树苗的均匀高度大概是多少?(3)为了进一步获取研究资料,现从[40,50) 组中移出一棵树苗, [90,100] 组中移出两棵树苗,进行试验研究,则 [40,50) 组中的树苗 A 和 [90,100] 组中的树苗 C 同时被移出的概率是多少?解(1)因为 [80,90) 的中间值是85,故树苗高度在(85,90)的棵数约为6,高度在85 厘米以上的树苗的棵数约为6+ 4= 10,因此在这批树苗中任取一棵,其高度在85 厘米以上的概率大概是10= 0.2.50(2)依据样本预计整体的思想,能够使用各组的组中值取代各组的树苗高度,则这批树苗的均匀高度约为45× 2+ 55× 3+ 65×14+ 75× 15+ 85×12+ 95×450 =3 690= 73.8( 厘米 ) ,50即这批树苗的均匀高度约为73.8 厘米.(3)记 [40,50) 组中的树苗为 A , B ,[90,100] 组中的树苗为 C , D , E ,F ,则基本领件是:(A , C ,D ), ( A ,C , E), (A , C , F) , (A , D , E), (A , D , F), (A , E , F), (B , C ,D) ,(B , C , E), (B , C , F) ,(B , D , E), (B ,D ,F), (B , E , F),合计 12 个基本领件.此中随机事件 “[40,50) 组中的树苗 A 和 [90,100] 组中的树苗 C 同时被移出 ”有 (A , C ,D) ,(A , C ,E),(A ,C ,F),共 3 个,故所求的概率是3= 0.25.即 [40,50) 组中的树P =12 苗 A 和 [90,100] 组中的树苗 C 同时被移出的概率是 0.25.。
高考数学江苏(理)考前三个月配套文档 专题8 概率与统计 第35练 Word版含解析

第35练二项式定理的两类重点题型——求指定项与求和[题型分析·高考展望]二项式定理的应用,是理科高考的考点之一,考查频率较高,一般为填空题,题目难度不大,为低、中档题.主要考查两类题型,一是求展开式的指定项,二是求各项和或系数和,只要掌握两类题型的常规解法,该部分题目就能会做.体验高考1.(2015·课标全国Ⅰ改编)(x 2+x +y )5的展开式中,x 5y 2的系数为________. 答案30解析方法一利用二项展开式的通项公式求解. (x 2+x +y )5=[(x 2+x )+y ]5,含y 2的项为T 3=C 25(x 2+x )3·y 2. 其中(x 2+x )3中含x 5的项为C 13x 4·x =C 13x 5. 所以x 5y 2的系数为C 25C 13=30.方法二利用组合知识求解.(x 2+x +y )5为5个x 2+x +y 之积,其中有两个取y ,两个取x 2,一个取x 即可,所以x 5y 2的系数为C 25C 23C 11=30.2.(2016·四川改编)设i 为虚数单位,则(x +i)6的展开式中含x 4的项为________. 答案 -15x 4解析由题可知,含x 4的项为C 26x 4i 2=-15x 4.3.(2015·安徽)⎝⎛⎭⎫x 3+1x 7的展开式中x 5的系数是________.(用数字填写答案) 答案35解析⎝⎛⎭⎫x 3+1x 7的展开式的第r +1项为T r +1=C r 7(x 3)7-r ·⎝⎛⎭⎫1x r =C r 7·x 21-4r,令21-4r =5,得r =4,∴T 5=C 47x 5=35x 5.4.(2016·上海)在(3x -2x )n 的二次项式中,所有项的二项式系数之和为256,则常数项等于________. 答案112解析2n =256,n =8,通项T r +1=C r 8·83r x -·(-2x)r =C r 8(-2)r·843,rx -取r =2,常数项为C 28(-2)2=112.高考必会题型题型一求展开项例1(1)(x 2+1x2-2)3展开式中的常数项为________.(2)(2016·山东)若⎝⎛⎭⎫ax 2+1x 5的展开式中x 5的系数为-80,则实数a =________. 答案(1)-20(2)-2解析(1)二项式(x 2+1x 2-2)3可化为(x -1x )6,展开式的通项公式为T r +1=C r 6·(-1)r ·x 6-2r . 令x 的幂指数6-2r =0,解得r =3, 故展开式中的常数项为-C 36=-20.(2)∵T r +1=C r 5(ax 2)5-r⎝⎛⎭⎫1x r =a 5-r C r 5x 5102r -, ∴10-52r =5,解得r =2,∴a 3C 25=-80,解得a =-2. 点评应用通项公式要注意四点(1)T r +1是展开式中的第r +1项,而不是第r 项;(2)公式中a ,b 的指数和为n ,且a ,b 不能随便颠倒位置; (3)要将通项中的系数和字母分离开,以便于解决问题; (4)对二项式(a -b )n 展开式的通项公式要特别注意符号问题.变式训练1(1)(9x -13x )n (n ∈N *)的展开式的第3项的二项式系数为36,则其展开式中的常数项为________.(2)(1-12x )(1+2x )5展开式中x 2的系数为________.答案(1)84(2)60解析(1)第3项的二项式系数为C 2n =n ·(n -1)2=36,n =9, 其通项公式为T r +1=(-13)r C r 9(9x )9-rx -12r=(-13)r 99-r C r 9x 9-32r , 当9-32r =0,r =6时,为常数项,常数项为(-13)699-6C 69=84.(2)因为(1+2x )5展开式的通项公式为T r +1=C r 5·2r ·x r2, 所以(1-12x )(1+2x )5展开式中x 2的系数为1×C 45×24-12×C 25×22=60. 题型二赋值法求系数之和例2(1)对任意的实数x ,有(2x -3)6=a 0+a 1x +a 2x 2+a 3x 3+a 4x 4+a 5x 5+a 6x 6,则a 1+2a 2+3a 3+4a 4+5a 5+6a 6=________.(2)若(2x -1)2013=a 0+a 1x +a 2x 2+…+a 2013x 2013(x ∈R ),则12+a 222a 1+a 323a 1+…+a 201322013a 1=________.答案(1)-12(2)14026解析(1)由(2x -3)6=a 0+a 1x +a 2x 2+a 3x 3+a 4x 4+a 5x 5+a 6x 6,两侧求导,得a 1+2a 2x +3a 3x 2+4a 4x 3+5a 5x 4+6a 6x 5=12(2x -3)5, 令x =1,则a 1+2a 2+3a 3+4a 4+5a 5+6a 6 =12(2×1-3)5=-12.(2)因为(2x -1)2013=a 0+a 1x +a 2x 2+…+a 2013x 2013(x ∈R ),令x =0,则a 0=-1,a 1=2C 20122013(-1)2012=2C 20122013;令x =12,则a 0+a 12+a 222+…+a 201322013=0,所以12+a 222a 1+a 323a 1+…+a 201322013a 1=1a 1(a 12+a 222+a 323+…+a 201322013)=1a 1(a 0+a 12+a 222+a 323+…+a 201322013)-a 0a 1 =12C 20122013(2×12-1)2013+12C 20122013 =14026. 点评(1)“赋值法”普遍适用于恒等式,是一种重要的方法,对形如(ax +b )n 、(ax 2+bx +c )m (a ,b ∈R )的式子求其展开式的各项系数之和,常用赋值法,只需令x =1即可;对形如(ax +by )n (a ,b ∈R )的式子求其展开式各项系数之和,只需令x =y =1即可.(2)若f (x )=a 0+a 1x +a 2x 2+…+a n x n ,则f (x )展开式中各项系数之和为f (1),奇数项系数之和为a 0+a 2+a 4+…=f (1)+f (-1)2,偶数项系数之和为a 1+a 3+a 5+…=f (1)-f (-1)2.变式训练2(1)已知(1+x )+(1+x )2+(1+x )3+…+(1+x )n =a 0+a 1x +a 2x 2+…+a n x n ,且a 0+a 1+a 2+…+a n =126,那么(x -1x)n的展开式中的常数项为________. (2)若(1-5x )9=a 0+a 1x +a 2x 2+…+a 9x 9,那么|a 0|+|a 1|+|a 2|+…+|a 9|的值是________. 答案(1)-20(2)69解析(1)令x =1,得a 0+a 1+a 2+...+a n =2+22+ (2)=2×2n -12-1=2n +1-2=126⇒2n +1=128⇒2n +1=27⇒n =6,又T r +1=C r 6(x )6-r(-1x)r =C r 6(-1)r x 3-r, 所以由3-r =0得r =3,则常数项为-C 36=-20.(2)(1-5x )9展开式的通项公式为T r +1=C r 9(-5x )r =(-5)r C r 9x r ,所以当x 的指数为奇数时,其系数为负,所以在(1-5x )9=a 0+a 1x +a 2x 2+…+a 9x 9中令x =-1,得|a 0|+|a 1|+|a 2|+…+|a 9| =a 0-a 1+a 2-a 3+…+a 8-a 9=69.高考题型精练1.若(2x +3)4=a 0+a 1x +a 2x 2+a 3x 3+a 4x 4,则(a 0+a 2+a 4)2-(a 1+a 3)2=________. 答案1解析令x =1,得(2+3)4=a 0+a 1+a 2+a 3+a 4,又令x =-1,得(2-3)4=a 0-a 1+a 2-a 3+a 4, 所以(a 0+a 2+a 4)2-(a 1+a 3)2=(a 0+a 2+a 4+a 1+a 3)(a 0+a 2+a 4-a 1-a 3) =(2+3)4(2-3)4=14=1.2.设n ∈N *,则5C 1n +52C 2n +53C 3n +…+5n C nn 除以7的余数为________.答案0或5解析5C 1n +52C 2n +53C 3n +…+5n C n n =C 0n +5C 1n +52C 2n +53C 3n +…+5n C n n -C 0n=(1+5)n -1=(7-1)n -1=7M +(-1)n -1,M ∈Z , 当n 为奇数时,余数为5, 当n 为偶数时,余数为0.3.设a ≠0,n 是大于1的自然数,⎝⎛⎭⎫1+x a n 的展开式为a 0+a 1x +a 2x 2+…+a n x n .若点A i (i ,a i ) (i =0,1,2)的位置如图所示,则a =________. 答案3解析由题意知A 0(0,1),A 1(1,3),A 2(2,4). 故a 0=1,a 1=3,a 2=4.由⎝⎛⎭⎫1+x a n 的展开式的通项公式知T r +1=C r n ⎝⎛⎭⎫x a r (r =0,1,2,…,n ).故C 1n a =3,C 2n a 2=4,解得a =3.4.设m 为正整数,(x +y )2m 展开式的二项式系数的最大值为a ,(x +y )2m +1展开式的二项式系数的最大值为b ,若13a =7b ,则m =________. 答案6解析(x +y )2m 展开式中二项式系数的最大值为C m 2m ,∴a =C m 2m .同理,b =C m +12m +1. ∵13a =7b ,∴13·C m 2m =7·C m +12m +1,∴13·(2m )!m !m !=7·(2m +1)!(m +1)!m !,∴m =6.5.设(x 2+1)(2x +1)9=a 0+a 1(x +2)+a 2(x +2)2+…+a 11(x +2)11,则a 0+a 1+a 2+…+a 11的值为________. 答案-2解析令等式中x =-1可得a 0+a 1+a 2+…+a 11=(1+1)(-1)9=-2.6.设a ∈Z ,且0≤a <13,若512016+a 能被13整除,则a 的值为________. 答案12解析512016+a =(52-1)2016+a =C 02016×522016-C 12016×522015+…+C 20152016×52×(-1)2015+C 20162016×(-1)2016+a . 因为52能被13整除,所以只需C 20162016×(-1)2016+a 能被13整除, 即a +1能被13整除,因为0≤a <13,所以a =12.7.设f (x )是⎝⎛⎭⎫x 2+12x 6展开式的中间项,若f (x )≤mx 在区间⎣⎡⎦⎤22,2上恒成立,则实数m 的取值范围是____________. 答案[5,+∞)解析由于T r +1=C r 6⎝⎛⎭⎫12r x 12-3r ,故展开式中间的一项为T 3+1=C 36·⎝⎛⎭⎫123·x 3=52x 3,f (x )≤mx ⇔52x 3≤mx 在⎣⎡⎦⎤22,2上恒成立,即m ≥52x 2,又52x 2≤5,故实数m 的取值范围是m ≥5. 8.(x 2-x +1)10展开式中x 3项的系数为________. 答案-210解析(x 2-x +1)10=[1+(x 2-x )]10的展开式的通项公式为T r +1=C r 10(x 2-x )r,对于(x 2-x )r 通项公式为T m +1=C m r x 2r -2m (-x )m =(-1)m C m r x2r -m , 令2r -m =3且m ≤r ≤10,m ∈N ,r ∈N ,得r =2,m =1或r =3,m =3,(x 2-x +1)10的展开式x 3系数为C 210C 12·(-1)+C 310C 33·(-1)3=-210. 9.设⎝⎛⎭⎫5x -1x n的展开式的各项系数之和为M ,二项式系数之和为N ,若M -N =240,则展开式中x 的系数为________. 答案150解析M =⎝⎛⎭⎫5×1-11n =4n ,N =2n ⇒4n -2n =240⇒2n =16⇒n =4,T r +1=(-1)r C r 4·54-r ·x 342r-⇒r =2,则(-1)2C 24·52=150. 10.设a n (n =2,3,4,…)是(3-x )n的展开式中x 的一次项的系数,则32a 2+33a 3+…+318a 18=________. 答案17 解析令T n +1=C k n 3n -k(-x )k=C k n (-1)k ·3n -k2kx ,令k2=1,得k =2, ∴(3-x )n 的展开式中x 的一次项的系数为a n =C 2n (-1)2·3n -2=C 2n ·3n -2, 又C 2n =n (n -1)2, 则32a 2+33a 3+…+318a 18=32×(1C 22+1C 23+…+1C 218) =9×(22×1+23×2+…+218×17)=18×[(1-12)+(12-13)+…+(117-118)]=18×(1-118)=17.11.已知在n 的展开式中,第6项为常数项.(1)求n ;(2)求含x 2项的系数;(3)求展开式中所有的有理项.解(1)根据题意,可得n 的展开式的通项为T r +1=C r n (x 13)n -r 131()2r x - =(-12)r C rn23n r x -,又由第6项为常数项,则当r =5时,n -2r3=0,即n -103=0,解可得n =10.(2)由(1)可得,10231101()C ,2rr r r T x --+=令10-2r 3=2,可得r =2,所以含x 2项的系数为(-12)2C 210=454. (3)由(1)可得,10231101()C ,2rr r r T x --+=若T r +1为有理项,则有10-2r3∈Z ,且0≤r ≤10,分析可得当r =2,5,8时,10-2r3为整数,则展开式中的有理项分别为454x 2,-638,45256x -2. 12.已知⎝⎛⎭⎫12+2x n . (1)若展开式中第5项、第6项与第7项的二项式系数成等差数列,求展开式中二项式系数最大的项的系数;(2)若展开式前三项的二项式系数和等于79,求展开式中系数最大的项.解(1)因为C 4n +C 6n =2C 5n ,所以n 2-21n +98=0,解得n =7或n =14.当n =7时,展开式中二项式系数最大的项是T 4和T 5.所以T 4的系数为C 37⎝⎛⎭⎫12423=352, T 5的系数为C 47⎝⎛⎭⎫12324=70. 当n =14时,展开式中二项式系数最大的项是T 8. 所以T 8的系数为C 714⎝⎛⎭⎫12727=3432. (2)因为C 0n +C 1n +C 2n =79,所以n =12或n =-13(舍去). 设T r +1项的系数最大. 因为⎝⎛⎭⎫12+2x 12=⎝⎛⎭⎫1212(1+4x )12,所以⎩⎪⎨⎪⎧C r 124r ≥C r -1124r -1,C r 124r ≥C r +1124r +1,所以9.4≤r ≤10.4.又因为0≤r ≤12且r ∈N ,所以r =10. 所以展开式中系数最大的项为T 11. T 11=⎝⎛⎭⎫1212C 1012410x 10=16896x 10.。
2019版高考数学大一轮复习江苏专版文档:第十一章 统计高考专题突破六 含答案 精品
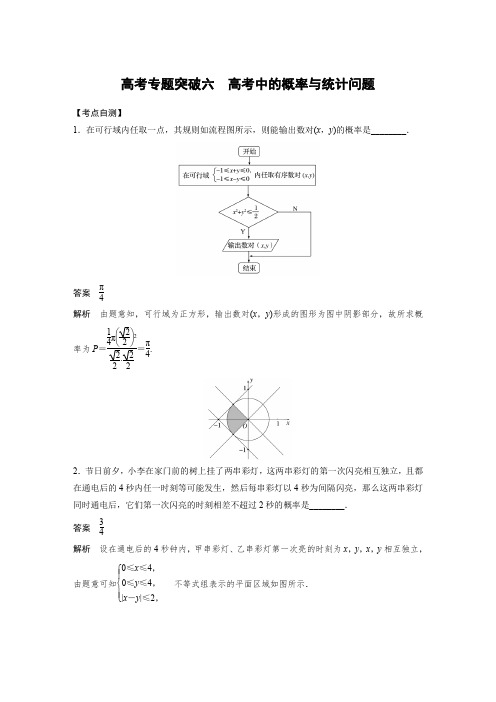
高考专题突破六 高考中的概率与统计问题【考点自测】1.在可行域内任取一点,其规则如流程图所示,则能输出数对(x ,y )的概率是________.答案 π4解析 由题意知,可行域为正方形,输出数对(x ,y )形成的图形为图中阴影部分,故所求概率为P =14π⎝⎛⎭⎫22222·22=π4.2.节日前夕,小李在家门前的树上挂了两串彩灯,这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒为间隔闪亮,那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过2秒的概率是________. 答案 34解析 设在通电后的4秒钟内,甲串彩灯、乙串彩灯第一次亮的时刻为x ,y ,x ,y 相互独立,由题意可知⎩⎪⎨⎪⎧0≤x ≤4,0≤y ≤4,|x -y |≤2,不等式组表示的平面区域如图所示.所以两串彩灯第一次亮的时间相差不超过2秒的概率为P (|x -y |≤2)=S 正方形-2S △ABCS 正方形=4×4-2×12×2×24×4=1216=34. 3.某班从4名男生、2名女生中选出3人参加志愿者服务,若选出的男生人数为ξ,则ξ的方差V (ξ)=________. 答案 25解析 从4名男生、2名女生中选出3人参加志愿者服务,选出的男生人数ξ可能为1,2,3,其中,P (ξ=1)=C 14C 22C 36=15,P (ξ=2)=C 24C 12C 36=35,P (ξ=3)=C 34C 02C 36=15.所以ξ的均值E (ξ)=1×15+2×35+3×15=2,V (ξ)=(1-2)2×15+(2-2)2×35+(3-2)2×15=25.4.已知高一年级某班有63名学生,现要选1名学生作为标兵,每名学生被选中的概率是相同的,若“选出的标兵是女生”的概率是“选出的标兵是男生”的概率的1011,则这个班男生的人数为________. 答案 33解析 根据题意,设该班的男生人数为x ,则女生人数为63-x ,因为每名学生被选中的概率是相同的, 根据古典概型的概率计算公式知,“选出的标兵是女生”的概率是63-x63,“选出的标兵是男生”的概率是x63,故63-x 63=1011×x 63,解得x =33,故这个班男生的人数为33. 5.在一次马拉松比赛中,35名运动员的成绩(单位:分钟)的茎叶图如图所示.若将运动员的成绩由好到差编为1~35号,再用系统抽样方法从中抽取7人,则其中成绩在区间[139,151]上的运动员人数是________. 答案 4 解析第一组(130,130,133,134,135),第二组(136,136,138,138,138),第三组(139,141,141,141,142),第四组(142,142,143,143,144),第五组(144,145,145,145,146),第六组(146,147,148,150,151),第七组(152,152,153,153,153).故成绩在[139,151]上的恰有4组,故有4人.题型一 古典概型与几何概型例1 (1)若函数f (x )=⎩⎪⎨⎪⎧e x ,0≤x <1,ln x +e ,1≤x ≤e ,在区间[0,e]上随机取一个实数x ,则f (x )的值不小于常数e 的概率是________. 答案 1-1e解析 当0≤x <1时,f (x )<e ,当1≤x ≤e 时,e ≤f (x )≤1+e ,∵f (x )的值不小于常数e ,∴1≤x ≤e ,∴所求概率为e -1e =1-1e.(2)现有2名女教师和1名男教师参加说题比赛,共有2道备选题目,若每位选手从中有放回地随机选出一道题进行说题,其中恰有一男一女抽到同一道题的概率为________. 答案 12解析 记两道题分别为A ,B ,所有抽取的情况为AAA ,AAB ,ABA ,ABB ,BAA ,BAB ,BBA ,BBB (其中第1个、第2个分别表示两个女教师抽取的题目,第3个表示男教师抽取的题目),共有8种;其中满足恰有一男一女抽到同一道题目的情况为ABA ,ABB ,BAA ,BAB ,共4种.故所求事件的概率为12.思维升华 几何概型与古典概型的本质区别在于试验结果的无限性,几何概型经常涉及的几何度量有长度、面积、体积等,解决几何概型的关键是找准几何测度;古典概型是命题的重点,对于较复杂的基本事件,列举时要按照一定的规律进行,做到不重不漏.跟踪训练1 (1)已知函数f (x )=13x 3+ax 2+b 2x +1,若a 是从1,2,3中任取的一个数,b 是从0,1,2中任取的一个数,则该函数有两个极值点的概率为________. 答案 23解析 f ′(x )=x 2+2ax +b 2,要使函数f (x )有两个极值点,则有Δ=(2a )2-4b 2>0,即a 2>b 2. 由题意知所有的基本事件有9个,即(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2),其中第一个数表示a 的取值,第二个数表示b 的取值.满足a 2>b 2的有6个基本事件,即(1,0),(2,0),(2,1),(3,0),(3,1),(3,2), 所以所求事件的概率为69=23.(2)如图所示,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角θ=π6.现在向该正方形区域内随机地投掷一枚飞镖,则飞镖落在小正方形内的概率是________.答案2-32解析 易知小正方形的边长为3-1, 故小正方形的面积为S 1=(3-1)2=4-23, 又大正方形的面积为S =2×2=4,故飞镖落在小正方形内的概率P =S 1S =4-234=2-32.题型二 求离散型随机变量的均值与方差例2 (2017·南京模拟)《最强大脑》是江苏卫视推出的国内首档大型科学类真人秀电视节目.该节目集结了国内外最顶尖的脑力高手,堪称脑力界的奥林匹克.某校为了增强学生的记忆力和辨识力也组织了一场类似《最强大脑》的PK 赛,A ,B 两队各由4名选手组成,每局两队各派一名选手PK ,除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛两队选手获胜的概率均为0.5,且各局比赛结果相互独立. (1)求比赛结束时A 队的得分高于B 队得分的得分的概率; (2)求比赛结束时B 队得分X 的概率分布和均值. 解 (1)记第i 局A 队胜为事件A i (i =1,2,3,4), 比赛结束时A 队得分高于B 队得分的事件记为C , 则P (C )=P (A 1A 2A 3A 4)+P (A 3)[1-P (A 1A2A 4)]=12.(2)X 的可能取值为0,1,2,3,4,5. 则P (X =0)=P (A 1A 2A 3A 4)=116,P (X =1)=C 13⎝⎛⎭⎫124=316,P (X =2)=P (A 1A 2A 3A 4)+C 23⎝⎛⎭⎫124=14, P (X =4)=C 23⎝⎛⎭⎫124=316, P (X =5)=116,P (X =3)=1-116-316-14-116-316=14.X 的概率分布为E (X )=0×116+1×316+2×14+3×14+4×316+5×116=52.思维升华 离散型随机变量的均值和方差的求解,一般分两步:一是定型,即先判断随机变量的分布是特殊类型,还是一般类型,如两点分布、二项分布、超几何分布等属于特殊类型;二是定性,对于特殊类型的均值和方差可以直接代入相应公式求解,而对于一般类型的随机变量,应先求其概率分布然后代入相应公式计算,注意离散型随机变量的取值与概率的对应. 跟踪训练2 受轿车在保修期内维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关.某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年.现从该厂已售出的两种品牌轿车中各随机抽取50辆,统计数据如下:将频率视为概率,解答下列问题:(1)从该厂生产的甲品牌轿车中随机抽取一辆,求其首次出现故障发生在保修期内的概率; (2)若该厂生产的轿车均能售出,记生产一辆甲品牌轿车的利润为X 1,生产一辆乙品牌轿车的利润为X 2,分别求X 1,X 2的概率分布;(3)该厂预计今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一种品牌的轿车.若从经济效益的角度考虑,你认为应生产哪种品牌的轿车?请说明理由.解 (1)设“甲品牌轿车首次出现故障发生在保修期内”为事件A ,则P (A )=2+350=110.(2)由题意得,X 1的概率分布为X 2的概率分布为(3)由(2)得E (X 1)=1×125+2×350+3×910=14350=2.86(万元),E (X 2)=1.8×110+2.9×910=2.79(万元).因为E (X 1)>E (X 2),所以应生产甲品牌轿车. 题型三 概率与统计的综合应用例3 2018年6月14日至7月15日,第21届世界杯足球赛将于俄罗斯举行,某大学为世界杯组委会招收志愿者,被招收的志愿者需参加笔试和面试,把参加笔试的40名大学生的成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示:(1)分别求出成绩在第3,4,5组的人数;(2)现决定在笔试成绩较高的第3,4,5组中用分层抽样抽取6人进行面试. ①已知甲和乙的成绩均在第3组,求甲或乙进入第二轮面试的概率;②若从这6名学生中随机抽取2名学生接受考官D 的面试,设第4组中有X 名学生被考官D 面试,求X 的概率分布和均值. 解 (1)由频率分布直方图知: 第3组的人数为5×0.06×40=12. 第4组的人数为5×0.04×40=8. 第5组的人数为5×0.02×40=4.(2)利用分层抽样,在第3组、第4组、第5组中分别抽取3人、2人、1人. ①设“甲或乙进入第二轮面试”为事件A ,则 P (A )=1-C 310C 312=511,所以甲或乙进入第二轮面试的概率为511.②X 的所有可能取值为0,1,2,P (X =0)=C 24C 26=25,P (X =1)=C 12C 14C 26=815,P (X =2)=C 22C 26=115.所以X 的概率分布为E (X )=0×25+1×815+2×115=1015=23.跟踪训练3 经销商经销某种农产品,在一个销售季度内,每售出1 t 该产品获得利润500元,未售出的产品,每1 t 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130 t 该农产品.以X (单位: t,100≤X ≤150)表示下一个销售季度内的市场需求量,T (单位:元)表示下一个销售季度内经销该农产品的利润.(1)将T 表示为X 的函数;(2)根据直方图估计利润T 不少于57 000元的概率;(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若需求量X ∈[100,110),则取X =105,且X =105的概率等于需求量落入[100,110)的频率),求T 的均值. 解 (1)当X ∈[100,130)时,T =500X -300(130-X )=800X -39 000. 当X ∈[130,150]时,T =500×130=65 000.所以T =⎩⎪⎨⎪⎧800X -39 000,100≤X <130,65 000,130≤X ≤150.(2)由(1)知利润T 不少于57 000元当且仅当120≤X ≤150.由直方图知需求量X ∈[120,150]的频率为0.7,所以下一个销售季度内的利润T 不少于57 000元的概率的估计值为0.7.(3)依题意可得T 的概率分布为所以E (T )=45 000×0.1+53 000×0.2+61 000×0.3+65 000×0.4=59 400.1.在不等式组⎩⎪⎨⎪⎧x -y +1≥0,x +y -2≤0,y ≥0所表示的平面区域内随机地取一点P ,则点P 恰好落在第二象限的概率为________. 答案 29解析 画出不等式组⎩⎪⎨⎪⎧x -y +1≥0,x +y -2≤0,y ≥0表示的平面区域(如图中阴影部分所示),因为S △ABC =12×3×32=94,S △AOD =12×1×1=12,所以点P 恰好落在第二象限的概率为S △AOD S △ABC =1294=29. 2.某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.(1)根据茎叶图计算样本平均值;(2)日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人?(3)从该车间12名工人中,任取2人,求恰有1名优秀工人的概率. 解 (1)样本平均值为17+19+20+21+25+306=1326=22.(2)由(1)知样本中优秀工人占的比例为26=13,故推断该车间12名工人中有12×13=4(名)优秀工人.(3)设事件A :“从该车间12名工人中,任取2人,恰有1名优秀工人”,则P (A )=C 14C 18C 212=1633.3.(2014·江苏)盒中共有9个球,其中有4个红球、3个黄球和2个绿球,这些球除颜色外完全相同.(1)从盒中一次随机取出2个球,求取出的2个球颜色相同的概率P .(2)从盒中一次随机取出4个球,其中红球、黄球、绿球的个数分别记为x 1,x 2,x 3,随机变量X 表示x 1,x 2,x 3中的最大数.求X 的概率分布和均值E (X ). 解 (1)取到的2个颜色相同的球可能是2个红球、2个黄球或2个绿球,所以P =C 24+C 23+C 22C 29=6+3+136=518. (2)随机变量X 所有可能的取值为2,3,4.{X =4}表示的随机事件是“取到的4个球是4个红球”, 故P (X =4)=C 44C 49=1126;{X =3}表示的随机事件是“取到的4个球是3个红球和1个其他颜色的球,或3个黄球和1个其他颜色的球”,故P (X =3)=C 34C 15+C 33C 16C 49=20+6126=1363; 于是P (X =2)=1-P (X =3)-P (X =4)=1-1363-1126=1114.所以随机变量X 的概率分布如下表:因此随机变量X 的均值E (X )=2×1114+3×1363+4×1126=209.4.某食品企业一个月内被消费者投诉的次数用ξ表示,据统计,随机变量ξ的概率分布如下:(1)求a 的值和ξ的均值;(2)假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率.解 (1)由概率分布的性质得0.1+0.3+2a +a =1, 解得a =0.2. ∴ξ的概率分布为∴E (ξ)=0×0.1+1×0.3+2×0.4+3×0.2=1.7.(2)设事件A 表示“两个月内共被投诉2次”,事件A 1表示“两个月内有一个月被投诉2次,另一个月被投诉0次”;事件A 2表示“两个月内每月均被投诉1次”,则 P (A 1)=2×0.4×0.1=0.08, P (A 2)=0.3×0.3=0.09,∴P (A )=P (A 1)+P (A 2)=0.08+0.09=0.17.故该企业在这两个月内共被消费者投诉2次的概率为0.17.5.一次考试共有12道选择题,每道选择题都有4个选项,其中有且只有一个是正确的.评分标准规定:“每题只选一个选项,答对得5分,不答或答错得零分”.某考生已确定有8道题的答案是正确的,其余题中有两道题都可判断两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只好乱猜.请求出该考生: (1)得60分的概率;(2)所得分数X 的概率分布和均值.解 (1)设“可判断两个选项是错误的”两道题之一选对为事件A , “有一道题可以判断一个选项是错误的”选对为事件B , “有一道题不理解题意”选对为事件C , ∴P (A )=12,P (B )=13,P (C )=14,∴得60分的概率为P =12×12×13×14=148.(2)X 可能的取值为40,45,50,55,60. P (X =40)=12×12×23×34=18;P (X =45)=C 12×12×12×23×34+12×12×13×34+12×12×23×14=1748;P (X =50)=12×12×23×34+C 12×12×12×13×34+C 12×12×12×23×14+12×12×13×14=1748; P (X =55)=C 12×12×12×13×14+12×12×23×14+12×12×13×34=748; P (X =60)=12×12×13×14=148.故X 的概率分布为E (X )=40×18+45×1748+50×1748+55×748+60×148=57512.6.为了评估天气对某市运动会的影响,制定相应预案,该市气象局通过对最近50多年气象数据资料的统计分析,发现8月份是该市雷电天气高峰期,在31天中平均发生雷电14.57天(如图所示).如果用频率作为概率的估计值,并假定每一天发生雷电的概率均相等,且相互独立.(1)求在该市运动会开幕(8月12日)后的前3天比赛中,恰好有2天发生雷电天气的概率(精确到0.01);(2)设运动会期间(8月12日至23日,共12天),发生雷电天气的天数为X ,求X 的均值和方差.解 (1)设8月份一天中发生雷电天气的概率为p ,由已知,得p =14.5731=0.47.因为每一天发生雷电天气的概率均相等,且相互独立,所以在运动会开幕后的前3天比赛中,恰好有2天发生雷电天气的概率P =C 23×0.472×(1-0.47)=0.351 231≈0.35.(2)由题意,知X ~B (12,0.47). 所以X 的均值E (X )=12×0.47=5.64, X 的方差V (X )=12×0.47×(1-0.47)=2.989 2.7.将某质地均匀的正十二面体玩具的十二个面上分别标记数字1,2,3,…,12.抛掷该玩具一次,记事件A :向上的面标记的数字是完全平方数(即能写成整数的平方形式的数,如9=32,9是完全平方数).(1)甲、乙二人利用该玩具进行游戏,并规定:①甲抛掷该玩具一次,若事件A 发生,则向上一面的点数的6倍为甲的得分;若事件A 没有发生,则甲得0分;②乙抛掷该玩具一次,将向上的一面对应数字作为乙的得分. (ⅰ)甲、乙二人各抛掷该玩具一次,求二人得分的均值; (ⅱ)甲、乙二人各抛掷该玩具一次,求甲的得分不低于乙的概率;(2)抛掷该玩具一次,记事件B :向上一面的点数不超过k (1≤k ≤12).若事件A 与B 相互独立,试求出所有的整数k .解 (1)设甲、乙二人抛掷该玩具后,得分分别为X ,Y . (ⅰ)易得X ,Y 的概率分布分别为故E (X )=7,E (Y )=132.(ⅱ)P =P (X =6,1≤Y ≤6)+P (X =24)+P (X =54) =112×612+112+112=524. (2)易知抛掷该玩具一次,基本事件总数为12,事件A 包含3个基本事件(1点,4点,9点). 记n (AB ),n (B )分别表示事件AB ,B 包含的基本事件数,由P (AB )=P (A )P (B )及古典概型, 得n (AB )12=312·n (B )12,所以n (B )=4n (AB ),① 故B 事件包含的基本事件数必为4的倍数, 即k ∈{4,8,12},当k =4时,n (B )=4,AB ={1,4},n (AB )=2,不符合①,当k=8时,n(B)=8,AB={1,4},n(AB)=2,符合①,当k=12时,n(B)=12,AB={1,4,9},n(AB)=3,符合①,故k的所有可能值为8或12.。
高考数学 考前三个月抢分训练30 概率与统计 试题

训练(xùnliàn)30概率与统计(推荐(tuījiàn)时间是:60分钟)1.关于(guānyú)x的一元二次方程x2-2(a-2)x-b2+16=0.(1)假设(jiǎshè)a、b是一枚骰子先后投掷两次所得到的点数,求方程有两个正实数根的概率;(2)假设a∈[2,6],b∈[0,4],求一元二次方程没有实数根的概率.2.某校高三年级进展了一次数学测验,随机从甲、乙两班各抽取6名同学,所得分数的茎叶图如下图.(1)根据茎叶图判断哪个班的平均分数较高,并说明理由;(2)现从甲班这6名同学中随机抽取两名同学,求他们的分数之和大于165分的概率.3.某校从参加某次“亚运〞知识竞赛的同学中,选取60名同学将其成绩(百分制)(均为整数)分成6组后得到如下图局部频率分布直方图.观察图形的信息,答复以下问题:(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;(3)假设从60名学生中随机抽取2人,抽到的学生成绩在[40,70)记0分,在[70,100]记1分,用ξ表示抽取完毕以后的总记分,求ξ的概率分布和数学期望.4.在某组织的一次篮球定点投篮训练中,规定(guīdìng)每人最多投3次;在A 处每投进一球得3分,在B 处每投进一球得2分;假如前两次得分之和超过3分即停顿投篮,否那么(nà me)投第三次.某同学在A 处的命中率q 1为0.25,在B 处的命中率为q 2.该同学(tóng xué)选择先在A 处投一球,以后(yǐhòu)都在B 处投,用ξ表示该同学投篮训练完毕以后所得的总分,其概率分布表为(1)求q 2的值;(2)求随机变量ξ的数学期望E (ξ);(3)试比拟该同学选择都在B 处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.答案1.解 (1)根本领件(a ,b )一共有36个,用a ,b ∈{1,2,3,4,5,6},方程有两个正实数根等价于a -2>0,16-b 2>0,Δ≥0,即a >2,-4<b <4,(a -2)2+b 2≥16.设“一元二次方程有两个正实数根〞为事件A ,那么事件A 所包含的根本领件数为(6,1),(6,2),(6,3),(5,3)一共4个,故所求的概率为P (A )=436=19. (2)试验的全部结果构成区域Ω={(a ,b )|2≤a ≤ 6,0≤b ≤4},其面积为S (Ω)=16. 设“一元二次方程无实根〞为事件B ,那么构成事件B 的区域为B ={(a ,b )|2≤a ≤6,0≤b ≤4,(a -2)2+b 2<16},其面积为S (B )=14×π×42=4π,故所求的概率为P (B )=4π16=π4.2.解 (1)因为乙班的成绩集中在80分,且没有低分,所以乙班的平均分比拟高.(2)设从甲班中任取两名同学,两名同学分数之和超过165分为事件A .从甲班6名同学中任取两名同学,那么根本(gēnběn)领件空间中包含15个根本领件,而事件A 中包含(bāohán)4个根本领件,所以(suǒyǐ),P (A )=415. 故从甲班中任取两名同学,两名同学分数之和超过(chāoguò)165分的概率为415. 3.解 (1)设分数在[70,80)内的频率为x ,根据频率分布直方图,那么有(0.01+0.015×2+0.025+0.005)×10+x =1,可得x =0.3,所以频率分布直方图如下图.(2)平均分为:x =45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71.(3)学生成绩在[40,70)的有0.4×60=24人,在[70,100]的有0.6×60=36人.并且ξ的可能取值是0,1,2.那么P (ξ=0)=C 224C 260=46295; P (ξ=1)=C 124C 136C 260=144295; P (ξ=2)=C 236C 260=105295. 所以ξ的概率分布表为 ξ 0 1 2E (ξ)=0×46295+1×144295+2×295=295. 4.解 (1)由题设知,“ξ=0”对应的事件为“在三次(sān cì)投篮中没有一次投中〞,由对立事件和互相HY 事件性质可知P (ξ=0)=(1-q 1)(1-q 2)2=0.03,解得q 2=0.8.(2)根据(gēnjù)题意p 1=P (ξ=2)=(1-q 1)C 12(1-q 2)q 2=0.75×2×0.2×0.8=0.24.p 2=P (ξ=3)=q 1(1-q 2)2=0.25×(1-0.8)2=0.01.p 3=P (ξ=4)=(1-q 1)q 222=0.48. p 4=P (ξ=5)=q 1q 2+q 1(1-q 2)q 2=0.25×0.8+0.25×0.2×0.8=0.24.因此(yīncǐ)E (ξ)=0×0.03+2×0.24+3×0.01+4×0.48+5×0.24=3.63.(3)用C 表示事件“该同学(tóng xué)选择第一次在A 处投,以后都在B 处投,得分超过3分〞,用D 表示事件“该同学选择都在B 处投,得分超过3分〞,那么P (C )=P (ξ=4)+P (ξ=5)=p 3+p 4=0.48+0.24=0.72.P (D )=q 22+C 12q 2(1-q 2)q 22+2×0.8×0.2×0.8=0.896.故P (D )>P (C ).即该同学选择都在B 处投篮得分超过3分的概率大于该同学选择第一次在A 处投篮以后都在B 处投篮得分超过3分的概率.内容总结(1)训练30概率与统计(推荐时间是:60分钟)1.关于x的一元二次方程x2-2(a-2)x-b2+16=0.(1)假设a、b是一枚骰子先后投掷两次所得到的点数,求方程有两个正实数根的概率。
2021新高考数学(江苏专用)一轮复习课件:第十章 高考专题突破六 高考中的概率与统计问题

概率与统计案例的综合应用常涉及相互独立事件同时发生的概率、独立重 复实验、超几何分布、二项分布、独立性检验、线性回归等知识,考查学 生的阅读理解能力、数据处理能力、运算求解能力及应用意识.
跟踪训练2 某商场营销人员进行某商品M市场营销调查发现,每回馈消费者 一定的点数,该商品每天的销量就会发生一定的变化,经过试点统计得到下表:
30
20
10
①求这200位拟购买该商品的消费者对返还点数的心理预期值X的样本平均数 及中位数的估计值(同一区间的预期值可用该区间的中点值代替;估计值精 确到0.1);
解 根据题意,这 200 位拟购买该商品的消费者对返还点数的心理预期值 X 的 样本平均数 x 为 x =2×0.1+4×0.3+6×0.3+8×0.15+10×0.1+12×0.05=6, 中位数的估计值为 5+2×100-6200-60=5+32≈5.7.
所以Y的概率分布为
Y0 1 2 3 4
P
16 81
32 81
8 27
8 81
1 81
所以X的概率分布为
X 0 300 600 900 1 200
P
16 81
32 81
8 27
8 81
1 81
由 E(Y)=4×13=43, 得X的均值E(X)=300E(Y)=400.
思维升华
SI WEI SHENG HUA
(2)若将频率视为概率,从该企业生产的这种产品中随机抽取3件,记这3件 产品中质量指标值位于[45,75)内的产品件数为X,求X的概率分布与均值.
解 从该企业生产的该种产品中随机抽取3件,相当于进行了3次独立重复试验, 所以X服从二项分布B(n,p),其中n=3. 由(1)得,落在区间[45,75)内的频率为0.3+0.2+0.1=0.6,将频率视为概率得p =0.6. 因为X的所有可能取值为0,1,2,3, 则 P(X=0)=C03×0.60×0.43=0.064, P(X=1)=C31×0.61×0.42=0.288, P(X=2)=C32×0.62×0.41=0.432, P(X=3)=C33×0.63×0.40=0.216,
专题12 概率与统计 专项突破(解析版)

(2)设企业可获利润为X(万元),则X的可能取值为0,100,120,220,
因
故所求的分布列为
X
0
100
120
220
P
所以数学期望为
8.把编号为1,2,3,4,5的五个大小、形状相同的小球,随机放入编号为1,2,3,4,5的五个盒子里.每个盒子里放入一个小球.
(1)求恰有两个球的编号与盒子的编号相同的概率;
【解析】(1)记“该生考上大学”的事件为事件A,其对立事件为 ,每次测试通过与否互相独立,则
所以 ,所以该学生考上大学的概率为 .
(2)参加测试次数X的可能取值为2,3,4,5,则
, , ,
.
所以X的概率分布为:
X
2
3
4
5
P
所以X的数学期望为 .
4.(江苏省淮安市2020届高三数学模拟测试卷)
乒乓球台面被网分成甲、乙两部分,如图,
因为60=20×3=40+10+10,
所以 .
2.(江苏省苏北七市2020届高三第二次调研考试 )
小丽在同一城市开的2家店铺各有2名员工.节假日期间的某一天, 每名员工休假的概率都是 ,且是否休假互不影响,若一家店铺的员工全部休假,而另一家无人休假,则调剂1人到该店维持营业,否则该店就停业.
(1)求发生调剂现象的概率;
(1)小明的两次回球的落点中恰有一次的落点在乙上的概率;
(2)两次回球结束后,小明得分之和 的分布列与数学期望.
【解析】(1)设恰有一次的落点在乙上这一事件为
(2)
0
1
2
3
4
6
.
5.( 南通市2020届高三年级第二学期高考模拟试卷)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中档大题规范练——概率与统计
1.第12届全运会已于2013年8月31日在辽宁沈阳举行,组委会在沈阳某大学招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如图所示的茎叶图(单位:cm),身高在175 cm 以上(包括175 cm)定义为“高个子”,身高在175 cm 以下(不包括175 cm)定义为“非高个子”.
(1)如果用分层抽样的方法从“高个子”和“非高个子”中共抽取5人,再从这5人中选2人,求至少有一人是“高个子”的概率;
(2)若从身高180 cm 以上(包括180 cm)的志愿者中选出男、女各一人,求这2人身高相差5 cm 以上的概率.
解 (1)根据茎叶图知,“高个子”有12人,“非高个子”有18人,
用分层抽样的方法,每个人被抽中的概率是530=16,
所以抽取的5人中,“高个子”有12×16=2人,“非高个子”有18×16=3人.
“高个子”用A ,B 表示,“非高个子”用a ,b ,c 表示,则从这5人中选2人的情况有(A ,B),(A ,a),(A ,b),(A ,c),(B ,a),(B ,b),(B ,c),(a ,b),(a ,c),(b ,c),共10种,
至少有一名“高个子”被选中的情况有(A ,B),(A ,a),(A ,b),(A ,c),(B ,a),(B ,b),(B ,c),共7种.
因此,至少有一人是“高个子”的概率是P =710.
(2)由茎叶图知,有5名男志愿者身高在180 cm 以上(包括180 cm),身高分别为181 cm,182 cm,184 cm,187 cm,191 cm ;有2名女志愿者身高为180 cm 以上(包括180 cm),身高分别为180 cm,181 cm.抽出的2人用身高表示,则有(181,180),(181,181),(182,180),(182,181),(184,180),(184,181),(187,180),(187,181),(191,180),(191,181),共10种情况,
身高相差5 cm 以上的有(187,180),(187,181),(191,180),(191,181),共4种情况,故这2人
身高相差5 cm 以上的概率为410=25.
2.(2013·北京)如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
(1)求此人到达当日空气质量优良的概率;
(2)求此人在该市停留期间只有1天空气重度污染的概率;
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
解 (1)在3月1日至3月13日到达这13天中,1日,2日,3日,7日,12日,13日共6天的空气质量优良.
所以,此人到达当日空气质量优良的概率P =613.
(2)事件“此人在该市停留期间只有1天空气重度污染”发生,则该人到达日期应在4日,5日,7日或8日.
所以,只有一天空气重度污染的概率P =413.
(3)从3月5日开始连续三天的空气质量指数方差最大.
3.先后随机投掷2枚正方体骰子,其中x 表示第1枚骰子出现的点数,y 表示第2枚骰子出现的点数.
(1)求点P(x ,y)在直线y =x -2上的概率;
(2)求点P(x ,y)满足y2<2x 的概率.
解 每枚骰子出现的点数都有6种情况,
所以,基本事件总数为6×6=36(个).
(1)记“点P(x ,y)在直线y =x -2上”为事件A ,
则事件A 有4个基本事件:(3,1),(4,2),(5,3),(6,4),
所以,P(A)=436=19.
(2)记“点P(x ,y)满足y2<2x”为事件B ,
则事件B 有12个基本事件:(1,1),(2,1),(3,1),(3,2),(4,1),(4,2),(5,1),(5,2),(5,3),(6,1),(6,2),(6,3),
所以,P(B)=1236=13.
4
(1)根据频数分布表计算苹果的重量在[90,95)的频率;
(2)用分层抽样的方法从重量在[80,85)和[95,100)的苹果中共抽取4个,其中重量在[80,85)的有几个?
(3)在(2)中抽出的4个苹果中,任取2个,求重量在[80,85)和[95,100)中各有1个的概率.
解 (1)苹果的重量在[90,95)的频率为2050=0.4.
(2)重量在[80,85)的有55+15
×4=1个. (3)设[80,85)段中的苹果为A ,[95,100)段中的苹果为B 、C 、D ,从中任取两个,其一切可能的基本事件有(A ,B),(A ,C),(A ,D),(B ,C),(B ,D),(C ,D)共6种,设“重量在[80,85)和[95,100)中各有1个”为事件E ,其包括(A ,B),(A ,C),(A ,D)共3种.
则P(E)=36=12.
5.有编号为1,2,3的三个白球,编号为4,5,6的三个黑球,这六个球除编号和颜色外完全相同,
现从中任意取出两个球.
(1)求取得的两个球颜色相同的概率;
(2)求取得的两个球颜色不相同的概率.
解 从六个球中取出两个球的基本事件有
(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6)共计15个基本事件.
(1)记事件A 为“取出的两个球是白球”,则这个事件包含的基本事件的是(1,2),(1,3),(2,3),共
计3个基本事件,故P(A)=315=15.
记事件B 为“取出的两个球是黑球”,同理可得P(B)=15.
记事件C 为“取出的两个球的颜色相同”,则C =A +B ,且A ,B 互斥,根据互斥事件的概率加
法公式,得P(C)=P(A +B)=P(A)+P(B)=25.
(2)记事件D 为“取出的两个球的颜色不相同”,则事件C ,D 互斥,根据互斥事件概率之间的关
系,得P(D)=1-P(C)=1-25=35.
6.(2014·福建)根据世行2013年新标准,人均GDP 低于1 035美元为低收入国家;人均GDP 为1 035~4 085美元为中等偏下收入国家;人均GDP 为4 085~12 616美元为中等偏上收入国家;人均GDP 不低于12 616美元为高收入国家.某城市有5个行政区,各区人口占该城市人口比例及人均GDP 如下表:
(1)判断该城市人均GDP 是否达到中等偏上收入国家标准;
(2)现从该城市5个行政区中随机抽取2个,求抽到的2个行政区人均GDP 都达到中等偏上收入国家标准的概率.
解 (1)设该城市人口总数为a ,则该城市人均GDP 为1a (8 000×0.25a +4 000×0.30a +6 000×0.15a
+3 000×0.10a +10 000×0.20a)=6 400.
因为6 400∈[4 085,12 616),
所以该城市人均GDP 达到了中等偏上收入国家标准.
(2)“从5个行政区中随机抽取2个”的所有的基本事件是{A ,B},{A ,C},{A ,D},{A ,E},{B ,C},{B ,D},{B ,E},{C ,D},{C ,E},{D ,E},共10个.
设事件“抽到的2个行政区人均GDP 都达到中等偏上收入国家标准”为M ,
则事件M 包含的基本事件是:{A ,C},{A ,E},{C ,E},共3个,所以所求概率为P(M)=310.。
