【100所名校】河北省定州中学2017-2018学年高二(承智班)下学期期中考试地理试题(解析版)
河北省定州中学2017-2018学年高二(承智班)下学期期中考试物理试题

高二年级第二学期承智班期中考试物理试题一、选择题1. 如图所示,两个线圈套在同一个铁芯上,线圈的绕向如图甲所示,左线圈连着正方形线框abcd,线框所在区域存在变化的磁场,取垂直纸面向外为正,磁感应强度随时间变化如图乙所示,不计线框以外的感生电场,右侧线圈连接一定值电阻R,下列说法中正确的是A. 设t1、t3时刻ab边中电流大小分别为i1、i3,则有i1<i3,定值电阻R中有电流B. t3~t4时间内通过ab边电量为0,定值电阻R中无电流C. t1时刻ab边中电流方向由,e点电势高于f点D. t5时刻ab边中电流方向由,f点电势高于e点【答案】D【解析】根据法拉第电磁感应定律,t1时刻磁感应强度的变化率小于t3时刻的变化率,故E3>E1,i3>i1。
由于E3,E1大小均不变,由法拉第电磁感应定律可知,副线圈中不会有感应电流出现,故A错误;t3~t4时间内有恒定感应电流,通过ab电量不为0,由于副线圈磁通量不变,定值电阻R中无电流,通过R的电量为0,故B错误;t1时刻磁场方向向里且均匀增加,根据楞次定律,ab边中电流方向由a→b,原线圈中电流值恒定,副线圈中不产生感应电动势,e点电势等于f点电势,故C错误;t5时刻磁场均匀减少,根据楞次定律,ab边中电流方向由b→a;原线圈中电流变化,副线圈中产生感应电动势(感应电动势上正下负),因此e点电势高于f点,故D正确。
2. 如图所示,在水平连线MN和PQ间有竖直向上的匀强电场,在MN上方有水平向里的匀强磁场。
两个质量和带电量均相等的带正电的粒子A、B,分别以水平初速度v0、2v0从PQ连线上O点先后进入电场,带电粒子A、B第一次在磁场中的运动时间分别为t A和t B,前两次穿越连线MN时两点间的距离分别为d A,和d B,粒子重力不计,则A. t A一定小于t B,d A一定等于d BB. t A一定小于t B,d A可能小于d BC. t A可能等于t B,d A一定等于d BD. t A可能等于t B,d A可能小于d B【答案】A【解析】两带正电粒子先在电场中做类平抛运动后在磁场中做匀速圆周运动,设类平抛的速度偏向角为α,则匀速圆周运动的圆心角为,因,,B粒子的水平速度大,则类平抛的时间短,较小,则α角较小,故圆周运动的圆心角较大,由可知时间较长,即;磁场中穿过的距离构成弦长,,,联立可得,因两粒子做类平抛的水平初速度不等,但沿着电场线方向的做功相同,速度相同,故和推得.综上可知A正确。
2017-2018学年河北省定州中学高二(承智班)下学期期中考试地理试题 Word版
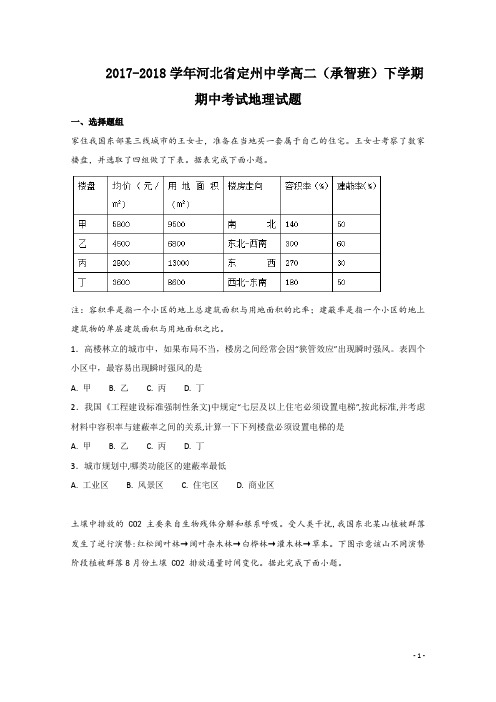
2017-2018学年河北省定州中学高二(承智班)下学期期中考试地理试题一、选择题组家住我国东部某三线城市的王女士,准备在当地买一套属于自己的住宅。
王女士考察了数家楼盘,并选取了四组做了下表。
据表完成下面小题。
注:容积率是指一个小区的地上总建筑面积与用地面积的比率;建蔽率是指一个小区的地上建筑物的单层建筑面积与用地面积之比。
1.高楼林立的城市中,如果布局不当,楼房之间经常会因“狭管效应”出现瞬时强风。
表四个小区中,最容易出现瞬时强风的是A. 甲B. 乙C. 丙D. 丁2.我国《工程建设标准强制性条文)中规定“七层及以上住宅必须设置电梯”,按此标准,并考虑材料中容积率与建蔽率之间的关系,计算一下下列楼盘必须设置电梯的是A. 甲B. 乙C. 丙D. 丁3.城市规划中,哪类功能区的建蔽率最低A. 工业区B. 风景区C. 住宅区D. 商业区土壤中排放的 CO2 主要来自生物残体分解和根系呼吸。
受人类干扰,我国东北某山植被群落发生了逆行演替:红松阔叶林→阔叶杂木林→白桦林→灌木林→草本。
下图示意该山不同演替阶段植被群落8月份土壤 CO2 排放通量时间变化。
据此完成下面小题。
4.该山植被群落从红松阔叶林向草本逆行演替过程中A. 草本物种数逐渐增B. 植被覆盖率逐渐下降C. 地上生物量逐渐减少D. 群落内光照逐渐减弱5.该时段土壤CO2 排放通量受士壤温度影响最小的森林群落是A. 红松阔叶林B. 阔叶杂木林C. 百桦林D. 灌木林6.下列因素中,与图中土壤CO2 排放通量的时空变化相关性最小的是A. 土壤微生物B. 地下生物量C. 表层凋落物D. 土壤含水量当强冷空气经过渤海上空时,受海水加热加湿促使空气中的水汽凝华,形成“冷流云”,继而在山东半岛北部形成“冷流雪”,12 月是月冷流雪量最多的月份。
据此完成下面小题。
7.山东半岛南部冷流雪量远少于北部的主要原因是A. 距海较远B. 地形阻挡C. 气温较高D. 地势低平8.冷空气南下时,山东半岛北部12 月比2 月更易产生冷流雪的原因主要是A. 海陆气温差异较大B. 南下冷空气较频繁C. 渤海表层水温较高D. 半岛上空尘埃较多地处美国某山脉的马尾瀑布是一条季节性瀑布(下图),隐蔽于群山之间,夏季几乎断流。
2017-2018学年河北省定州中学高二(承智班)下学期期中考试语文试题(Word版含解析)

2017-2018学年河北省定州中学高二(承智班)下学期期中考试语 文注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
第I 卷(选择题)一、选择题1.下列各句中加点成语的使用,全都不正确的一项是( )①促进科研成果转移转化是实施创新驱动发展战略的重要任务,我们应该制订一套行之有效....的激励机制和创新协同机制。
②小庄从小就对机器人玩具特别感兴趣,上学后喜欢收集机器人模型,通过各种途径得到的模型已经汗牛充栋....,整整一间屋都摆满了。
③约翰逊的学术方法虽比较新颖,但其学术成果得到学术界公认的却不是很多,再加上其随者大都等而下之....,以致他的学术地位一直不高。
④张家界独特的自然景观被列入《世界自然遗产名录》,徜徉其间,峰峦叠嶂,峪壑幽深,溪流澄碧,让人乐.不思蜀...。
⑤近年来,有关部门采取了一系列措施强化虚假广告的监管,使得滥竽充数....的广告得到了一定程度的遏制。
⑥丹·罗斯嘉德发明的“雾霾塔”是一种利用静电吸附尘粒原理的环保装置,脏空气滔滔不绝....地从塔顶进入后,能在塔中间得到净化。
A. ①③⑤B. ①④⑥C. ②③④D. ②⑤⑥ 2.下列各句中,没有语病的一句是( )A. 在实施全面二孩政策之后,新生人口必然会增长,这一方面将会改变现有的家庭结构,另一方面也会减轻适龄劳动人口赡养老年人的负担和职责。
B. 起源于中国的“石头、剪刀、布”游戏,随着亚欧贸易的不断开展,近百年来越来越多的欧洲人参与其中,玩得不亦乐乎。
C. 经过数千年的探索和实践,中国先民在乡村社会礼法并用,构建出了一套庞杂的治理和教化体系,其中,“乡约制度”尤为引人瞩目。
2017-2018年河北省保定市定州中学承智班高二(下)期中数学试卷和答案

2017-2018学年河北省保定市定州中学承智班高二(下)期中数学试卷一、单选题1.(3分)正方体ABCD﹣A1B1C1D1棱长为3,点E在边BC上,且满足BE=2EC,动点M在正方体表面上运动,并且总保持ME⊥BD1,则动点M的轨迹的周长为()A.B.C.D.2.(3分)如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,点E、F是棱BC、CC1的中点,P是底面ABCD上(含边界)一动点,满足A1P⊥EF,则线段A1P长度的取值范围是()A.B.C.D.3.(3分)如图,在单位正方体ABCD﹣A1B1C1D1中,点P在线段AD1上运动,给出以下四个命题:①异面直线A1P与BC1间的距离为定值;②三棱锥D﹣BPC1的体积为定值;③异面直线C1P与直线CB1所成的角为定值;④二面角P﹣BC1﹣D的大小为定值.其中真命题有()A.1个B.2个C.3个D.4个4.(3分)现有两个半径为2的小球和两个半径为3的小球两两相切,若第五个小球和它们都相切,则这个小球的半径是()A.B.C.D.5.(3分)设a,b是异面直线,则以下四个命题:①存在分别经过直线a和b 的两个互相垂直的平面;②存在分别经过直线a和b的两个平行平面;③经过直线a有且只有一个平面垂直于直线b;④经过直线a有且只有一个平面平行于直线b.其中正确的个数有()A.1B.2C.3D.46.(3分)已知l1,l2分别是函数f(x)=|lnx|图象上不同的两点P1,P2处的切线,l1,l2分别与y轴交于点A,B,且l1与l2垂直相交于点P,则△ABP的面积的取值范围是()A.(0,1)B.(0,2)C.(0,+∞)D.(1,+∞)7.(3分)已知F1,F2分别为双曲线的左焦点和右焦点,过F2的直线l与双曲线的右支交于A,B两点,△AF1F2的内切圆半径为r1,△BF1F2的内切圆半径为r2,若r1=2r2,则直线l的斜率为()A.1B.C.2D.8.(3分)设A,B为双曲线同一条渐近线上的两个不同的点,若向量,且,则双曲线的离心率为()A.2或B.3或C.D.39.(3分)已知双曲线x2﹣=1,直线l的斜率为﹣2,与双曲线交于A,B,若在双曲线上存在异于A,B的一点C,使直线AB,BC,AC的斜率满足+ +=3,若D,E,H三点为AB,BC,AC的中点,则k OE+k OH=()A.﹣6B.5C.6D.710.(3分)已知抛物线C:x2=4y,直线l:y=﹣1,PA,PB为抛物线C的两条切线,切点分别为A,B,则“点P在l上”是“PA⊥PB”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件11.(3分)已知双曲线C:的两条渐近线是l1,l2,点M是双曲线C 上一点,若点M到渐近线l1距离是3,则点M到渐近线l2距离是()A.B.1C.D.312.(3分)已知函数f(x)=(x﹣m)2+(ae x﹣3m)2(m∈R)的最小值为,则正实数a=()A.3B.3e﹣2C.3e2D.3或3e﹣2二、填空题13.(3分)菱形ABCD边长为6,∠BAD=60°,将△BCD沿对角线BD翻折使得二面角C﹣BD﹣A的大小为120°,已知A、B、C、D四点在同一球面上,则球的表面积等于.14.(3分)如图,等腰△PAB所在平面为α,PA⊥PB,AB=6.G是△PAB的重心.平面α内经过点G的直线l将△PAB分成两部分,把点P所在的部分沿直线l翻折,使点P到达点P'(P'∉平面α).若P'在平面α内的射影H恰好在翻折前的线段AB上,则线段P'H的长度的取值范围是.15.(3分)过双曲线的焦点与双曲线实轴垂直的直线被双曲线截得的线段的长称为双曲线的通径,其长等于,(a、b分别为双曲线的实半轴长与虚半轴长).已知双曲线(a>0)的左、右焦点分别为F1、F2,若点M 是双曲线C上位于第四象限的任意一点,直线l是双曲线的经过第二、四象限的渐近线,MQ⊥l于点Q,且|MQ|+|MF1|的最小值为3,则双曲线C的通径为.16.(3分)已知直三棱柱ABC﹣A1B1C1的侧棱长为6,且底面是边长为2的正三角形,用一平面截此棱柱,与侧棱AA1,BB1,CC1分别交于三点M,N,Q,若△MNQ为直角三角形,则该直角三角形斜边长的最小值为三、解答题17.四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,侧面PAD⊥底面ABCD,∠BCD=60°,,E是BC中点,点Q在侧棱PC上.(Ⅰ)求证:AD⊥PB;(Ⅱ)是否存在Q,使平面DEQ⊥平面PEQ?若存在,求出,若不存在,说明理由.(Ⅲ)是否存在Q,使PA∥平面DEQ?若存在,求出.若不存在,说明理由.18.如图,四棱锥P﹣ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形.(Ⅰ)证明:AD⊥PB;(Ⅱ)若四棱锥P﹣ABCD的体积等于,问:是否存在过点C的平面CMN,分别交PB,AB 于点M,N,使得平面CMN∥平面PAD?若存在,求出△CMN 的面积;若不存在,请说明理由.19.已知抛物线E:y2=4x的焦点为F,过点F的直线l与抛物线交于A,B两点,交y轴于点C,O为坐标原点.(1)若k OA+k OB=4,求直线l的方程;(2)线段AB的垂直平分线与直线l,x轴,y轴分别交于点D,M,N,求的最小值.20.已知抛物线C:y2=2x的焦点为F,平行于x轴的两条直线l1,l2分别交C于A,B两点,交C的准线于P,Q两点.(Ⅰ)若F在线段AB上,R是PQ的中点,证明AR∥FQ;(Ⅱ)若△PQF的面积是△ABF的面积的两倍,求AB中点的轨迹方程.2017-2018学年河北省保定市定州中学承智班高二(下)期中数学试卷参考答案与试题解析一、单选题1.(3分)正方体ABCD﹣A1B1C1D1棱长为3,点E在边BC上,且满足BE=2EC,动点M在正方体表面上运动,并且总保持ME⊥BD1,则动点M的轨迹的周长为()A.B.C.D.【解答】解:由正方体的特点可知BD1⊥平面ACB1,在AB,BB1上分别取点P,Q,使得BP=2PA,BQ=2QB1,连接PE,PQ,EQ,则PE∥AC,EQ∥B1C,∴平面AB1C∥平面PEQ,∴BD1⊥平面PEQ,∴M的轨迹为△PEQ.∵正方体棱长为3,∴AC=3,∴PE==2,∴△PEQ的周长为3PE=6.故选:A.2.(3分)如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,点E、F是棱BC、CC1的中点,P是底面ABCD上(含边界)一动点,满足A1P⊥EF,则线段A1P长度的取值范围是()A.B.C.D.【解答】解:如图,连接BC1,A1D,可得EF∥BC1,A1D⊥BC1,∴A1D⊥EF,又DC⊥EF,可得EF⊥平面A1DC,则A1C⊥EF,∴当P在线段CD上运动时,有A1P⊥EF,当P与D重合时,A1P有最小值为,当P与C重合时,A1P有最大值为.∴线段A1P长度的取值范围是[].故选:D.3.(3分)如图,在单位正方体ABCD﹣A1B1C1D1中,点P在线段AD1上运动,给出以下四个命题:①异面直线A1P与BC1间的距离为定值;②三棱锥D﹣BPC1的体积为定值;③异面直线C1P与直线CB1所成的角为定值;④二面角P﹣BC1﹣D的大小为定值.其中真命题有()A.1个B.2个C.3个D.4个【解答】解:对于①三棱锥D﹣BPC1的体积还等于三棱锥的体积P﹣DBC1的体积,而平面DBC1为固定平面且大小一定,又因为P∈AD1,而AD1∥平面BDC1,所以点A到平面DBC1的距离即为点P到该平面的距离,所以三棱锥的体积为定值,所以①正确;对于②三棱锥的底面DBC1为定值,因为AD1∥BC1,所以AD1∥平面DBC1,P⊂AD1,所以P到平面DBC1的距离是定值,所以三棱锥D﹣BPC1的体积为定值;故②正确;对于③因为在棱长为1的正方体ABCD﹣A1B1C1D1中,点P在线段AD1上运动,有正方体及题意易有B1C⊥平面ABC1D1,而C1P⊂平面ABC1D1,所以B1C⊥C1P,故这两个异面直线所成的角为定值90°,故③正确;对于④因为二面角P﹣BC1﹣D的大小,实质为平面ABC1D1与平面BDC1所成的二面角,而这两个平面为固定的不变的平面所以夹角也为定值,故④正确;故选:D.4.(3分)现有两个半径为2的小球和两个半径为3的小球两两相切,若第五个小球和它们都相切,则这个小球的半径是()A.B.C.D.【解答】解:如图所示,A,B是半径为2的球的球心,C、D是半径为3的球的球心,O是第五个球的球心,由题得CE===DE,EF==2,OF==,∵AB⊥CE,AB⊥D,∴AB⊥平面BEC,∴AB⊥EO,OF==,∴OE=2﹣,∵AB⊥CE,AB⊥ED,∴AB⊥平面BEC,∴AB⊥EO,在直角△AEO中,(r+2)2=22+(2﹣)2,解得r=.故选:A.5.(3分)设a,b是异面直线,则以下四个命题:①存在分别经过直线a和b 的两个互相垂直的平面;②存在分别经过直线a和b的两个平行平面;③经过直线a有且只有一个平面垂直于直线b;④经过直线a有且只有一个平面平行于直线b.其中正确的个数有()A.1B.2C.3D.4【解答】解:对于①:可以在两个互相垂直的平面中,分别画一条直线,当这两条直线异面时,可判断①正确对于②:可在两个平行平面中,分别画一条直线,当这两条直线异面时,可判断②正确对于③:当这两条直线不是异面垂直时,不存在这样的平面满足题意,可判断③错误对于④:假设过直线a有两个平面α、β与直线b平行,则面α、β相交于直线a,过直线b做一平面γ与面α、β相交于两条直线m、n,则直线m、n相交于一点,且都与直线b平行,这与“过直线外一点有且只有一条直线与已知直线平行”矛盾,所以假设不成立,所以④正确故选:C.6.(3分)已知l1,l2分别是函数f(x)=|lnx|图象上不同的两点P1,P2处的切线,l1,l2分别与y轴交于点A,B,且l1与l2垂直相交于点P,则△ABP的面积的取值范围是()A.(0,1)B.(0,2)C.(0,+∞)D.(1,+∞)【解答】解:设P1(x1,y1),P2(x2,y2)(0<x1<1<x2),当0<x<1时,f′(x)=﹣,当x>1时,f′(x)=,∴l1的斜率k1=﹣,l2的斜率k2=,∵l1与l2垂直,且x2>x1>0,∴k1•k2=﹣•=﹣1,即x1x2=1.直线l1:y=﹣(x﹣x1)﹣lnx1,l2:y=(x﹣x2)+lnx2.取x=0分别得到A(0,1﹣lnx1),B(0,﹣1+lnx2),|AB|=|1﹣lnx1﹣(﹣1+lnx2)|=|2﹣(lnx1+lnx2)|=|2﹣lnx1x2|=2.联立两直线方程可得交点P的横坐标为x=,∴S=|AB|•|x P|=×2×=,△PAB∵函数y=x+在(0,1)上为减函数,且0<x1<1,∴x1+>1+1=2,则0<<,∴0<<1.∴△PAB的面积的取值范围是(0,1).故选:A.7.(3分)已知F1,F2分别为双曲线的左焦点和右焦点,过F2的直线l与双曲线的右支交于A,B两点,△AF1F2的内切圆半径为r1,△BF1F2的内切圆半径为r2,若r1=2r2,则直线l的斜率为()A.1B.C.2D.【解答】解:记△AF1F2的内切圆圆心为C,边AF1、AF2、F1F2上的切点分别为M、N、E,易见C、E横坐标相等,则|AM|=|AN|,|F1M|=|F1E|,|F2N|=|F2E|,由|AF1|﹣|AF2|=2a,即|AM|+|MF1|﹣(|AN|+|NF2|)=2a,得|MF1|﹣|NF2|=2a,即|F1E|﹣|F2E|=2a,记C的横坐标为x0,则E(x0,0),于是x0+c﹣(c﹣x0)=2a,得x0=a,同样内心D的横坐标也为a,则有CD⊥x轴,设直线的倾斜角为θ,则∠OF2D=,∠CF2O=90°﹣,在△CEF2中,tan∠CF2O=tan(90°﹣)=,在△DEF2中,tan∠DF2O=tan=,由r1=2r2,可得2tan=tan(90°﹣)=cot,解得tan=,则直线的斜率为tanθ===2,故选:D.8.(3分)设A,B为双曲线同一条渐近线上的两个不同的点,若向量,且,则双曲线的离心率为()A.2或B.3或C.D.3【解答】解:∵,则在y轴上的射影长为﹣1而|AB|=3,因此A、B点所在的渐近线与y轴的夹角的余弦值为,正切值为2.∴渐近线的斜率k=,故当λ>0时.,e=.当λ<0时,,e=.故选:B.9.(3分)已知双曲线x2﹣=1,直线l的斜率为﹣2,与双曲线交于A,B,若在双曲线上存在异于A,B的一点C,使直线AB,BC,AC的斜率满足+ +=3,若D,E,H三点为AB,BC,AC的中点,则k OE+k OH=()A.﹣6B.5C.6D.7【解答】解:由题意得:++==3,∴,设B、C、E的坐标分别为(x B,y B),(x C,y C),(x E,y E),则,两式相减,得:﹣=(x B+x C)(x B﹣x C)•=0,整理,得=k BC•k OE=2,∴,∴,∴k OE+k OH==2()=2×=7.故选:D.10.(3分)已知抛物线C:x2=4y,直线l:y=﹣1,PA,PB为抛物线C的两条切线,切点分别为A,B,则“点P在l上”是“PA⊥PB”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【解答】解:由x2=4y,对其求导得.设A,B,则直线PA,PB的斜率分别为k PA=,k PB=.由点斜式得PA,PB的方程分别为:y﹣=.=(x﹣x2),联立解得P,因为P在l上,所以=﹣1,所以k PA•k PB==﹣1,所以PA⊥PB.反之也成立.所以“点P在l上”是“PA⊥PB”的充要条件.故选:C.11.(3分)已知双曲线C:的两条渐近线是l1,l2,点M是双曲线C 上一点,若点M到渐近线l1距离是3,则点M到渐近线l2距离是()A.B.1C.D.3【解答】解:双曲线C:的两条渐近线为:2x±3y=0,设M(x1,y1)为双曲线上的点,则4x12﹣9y12=36,由M到双曲线的渐近线的距离乘积为k===是常数,点M到渐近线l1距离是3,则点M到渐近线l2距离是:=.故选:A.12.(3分)已知函数f(x)=(x﹣m)2+(ae x﹣3m)2(m∈R)的最小值为,则正实数a=()A.3B.3e﹣2C.3e2D.3或3e﹣2【解答】解:(x﹣m)2+(ae x﹣3m)2表示点A(x,ae x)与点B(m,3m)的距离的平方,点A在曲线y=ae x上,点B在曲线y=3x上,如图,可得a>0,设与y=3x平行的直线与曲线y=ae x相切于点P(x0,ae).∵y′=ae x,∴,…①点A(x,ae x)与点B(m,3m)的距离的平方的最小值等于点P(x0,ae)到直线y=3x的距离.∴,∴…②结合①②得x0=0,a=3故选:A.二、填空题13.(3分)菱形ABCD边长为6,∠BAD=60°,将△BCD沿对角线BD翻折使得二面角C﹣BD﹣A的大小为120°,已知A、B、C、D四点在同一球面上,则球的表面积等于84π.【解答】解:设BD∩AC=H,球半径为R,∵菱形ABCD边长为6,∠BAD=60°,∴HB=3,AH=3.AH⊥BD.∵二面角C﹣BD﹣A的大小为120°,∴∠BHD=120°,设M为△ABC的外心,O为球心,∴OM⊥面ABC.根据对称性,O一定在面BHD上,且OB=OD=R,∴OH平分∠BHD,在△HOM中,HM=.∠OHM=60°,∴OM=3,在△OBM中,R=OB=.∴球的表面积等于4πR2=84π.⇒故答案为:84π.14.(3分)如图,等腰△PAB所在平面为α,PA⊥PB,AB=6.G是△PAB的重心.平面α内经过点G的直线l将△PAB分成两部分,把点P所在的部分沿直线l翻折,使点P到达点P'(P'∉平面α).若P'在平面α内的射影H恰好在翻折前的线段AB上,则线段P'H的长度的取值范围是(0,] .【解答】解:以AB的中点为原点,以AB为x轴建立平面坐标系如图所示:过P作直线l的垂线,交直线l于M,交AB于H,∵AB=6,∴OP=3,即P(0,3),∵G是△PAB的重心,∴G(0,1),设直线l的方程为:y=kx+1,即kx﹣y+1=0,∴PM=,直线PH的方程为:y=﹣x+3,∴H(3k,0),MH=.∴P′H2=PM2﹣MH2==﹣9(k2+1)+.令k2+1=t,f(t)=﹣3t+(t≥1),则f(t)为减函数,∴当t=1即k=0时,f(t)取得最大值3,又H落在线段AB上,故而PM>MH,∴f(t)>0,∴0<P′H≤.故答案为:.15.(3分)过双曲线的焦点与双曲线实轴垂直的直线被双曲线截得的线段的长称为双曲线的通径,其长等于,(a、b分别为双曲线的实半轴长与虚半轴长).已知双曲线(a>0)的左、右焦点分别为F1、F2,若点M 是双曲线C上位于第四象限的任意一点,直线l是双曲线的经过第二、四象限的渐近线,MQ⊥l于点Q,且|MQ|+|MF1|的最小值为3,则双曲线C的通径为2.【解答】解:根据题意,已知双曲线(a>0)中,b=1,其渐近线为y=±x,即x±ay=0,右焦点坐标为(c,0),其左、右焦点分别为F1、F2,点M是双曲线C上位于第四象限的任意一点,则|MF1|﹣|MF2|=2a,则|MQ|+|MF1|=|MQ|+2a+|MF2|=2a+|MQ|+|MF2|,分析可得:当Q、M、F三点共线时,|MQ|+|MF2|取得最小值,且|MQ|+|MF2|的最小值为|F2Q|,又由|F2Q|==b=1,则|MQ|+|MF1|的最小值为2a+1=3,解可得a=1,则双曲线C的通径=2;故答案为:2.16.(3分)已知直三棱柱ABC﹣A1B1C1的侧棱长为6,且底面是边长为2的正三角形,用一平面截此棱柱,与侧棱AA1,BB1,CC1分别交于三点M,N,Q,若△MNQ为直角三角形,则该直角三角形斜边长的最小值为【解答】解:如图,不妨设N在B处,AM=h,CQ=m,则MB2=h2+4,BQ2=m2+4,MQ2=(h﹣m)2+4,由MB2=BQ2+MQ2,得h2+4=m2+4+(h﹣m)2+4,∴m2﹣hm+2=0,∴△=h2﹣8≥0,解得h2≥8,∴该直角三角形斜边长MB=≥,∴该直角三角形斜边长的最小值为2.故答案为:2.三、解答题17.四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,侧面PAD⊥底面ABCD,∠BCD=60°,,E是BC中点,点Q在侧棱PC上.(Ⅰ)求证:AD⊥PB;(Ⅱ)是否存在Q,使平面DEQ⊥平面PEQ?若存在,求出,若不存在,说明理由.(Ⅲ)是否存在Q,使PA∥平面DEQ?若存在,求出.若不存在,说明理由.【解答】(本小题满分13分)证明:(Ⅰ)取AD中点O,连接OP,OB,BD.因为PA=PD,所以PO⊥AD.因为菱形ABCD中,∠BCD=60°,所以AB=BD.所以BO⊥AD.因为BO∩PO=O,且BO,PO⊂平面POB,所以AD⊥平面POB.所以AD⊥PB.解:(Ⅱ)由(Ⅰ)可知,BO⊥AD,PO⊥AD,因为侧面PAD⊥底面ABCD,且平面PAD∩底面ABCD=AD,所以PO⊥底面ABCD.以O为坐标原点,如图建立空间直角坐标系O﹣xyz.则,A(1,0,0),设.设Q(x,y,z),则,又因为,所以,即.,=(﹣1,,﹣1),=(﹣2λ,,﹣λ),设平面DEQ的法向量=(x,y,z),则,所以平面DEQ的法向量为,设平面PEQ的法向量为,则,取y=1,得=(0,1,),因为平面DEQ⊥平面PEQ,所以=0×(1﹣λ)+1×0+(2λ﹣1)=0,解得λ=,故Q为PC中点时,平面DEQ⊥平面PEQ.(Ⅲ)设由(Ⅱ)可知.设Q(x,y,z),则,又因为,所以,即.所以在平面DEQ中,,所以平面DEQ的法向量为,又因为PA∥平面DEQ,所以,即(1﹣λ)+(﹣1)(2λ﹣1)=0,解得.所以当,即PQ=PC时,PA∥平面DEQ.18.如图,四棱锥P﹣ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形.(Ⅰ)证明:AD⊥PB;(Ⅱ)若四棱锥P﹣ABCD的体积等于,问:是否存在过点C的平面CMN,分别交PB,AB 于点M,N,使得平面CMN∥平面PAD?若存在,求出△CMN 的面积;若不存在,请说明理由.【解答】(Ⅰ)证明:取AD的中点G,连接PG、GB、BD∵PA=PD,∴PG⊥AD.(2分)∵AB=AD,且∠DAB=60°,∴△ABD是正三角形,∴BG⊥AD,又∵PG∩BG=G,PG、BG⊂平面PGB∴AD⊥平面PGB.∴AD⊥PB.(5分)(Ⅱ)解:存在,理由如下:分别取PA、AB的中点M、N,连结CM、MN、NC,则MN∥PA;∵ABCD是梯形,且DC平行且等于AB,∴DC平行且等于AN,于是,四边形ANCD为平行四边形,∴平面CMN∥平面PAD.由(Ⅰ)知,MN=1,CN=2,在△PBC与在△CBM中:,∴△PBC∽△CBM,得CM=,∴△CBM是直角三角形,∴.…(12分)19.已知抛物线E:y2=4x的焦点为F,过点F的直线l与抛物线交于A,B两点,交y轴于点C,O为坐标原点.(1)若k OA+k OB=4,求直线l的方程;(2)线段AB的垂直平分线与直线l,x轴,y轴分别交于点D,M,N,求的最小值.【解答】解:(1)F(1,0),设直线l的方程为x=my+1,A(,y1),B(,y2),由得y2﹣4my﹣4=0,∴y1+y2=4m,y1y2=﹣4.∴k OA+k OB=+==﹣4m=4.∴m=﹣1,所以l的方程为x+y﹣1=0.(2)由(1)可知,m≠0,C(0,﹣),D(2m2+1,2m).∴直线MN的方程为:y﹣2m=﹣m(x﹣2m2﹣1),则M(2m2+3,0),N(0,2m3+3m),=•|NC|•|x D|=•|2m3+3m+|•(2m2+1)=,∴S△NDCS△FDM=•|FM|•|y D|=•(2m2+2)•2|m|=2|m|(m2+1),∴==m2++1≥2,当且仅当m2=,即m2=时取等号.所以,的最小值为2.20.已知抛物线C:y2=2x的焦点为F,平行于x轴的两条直线l1,l2分别交C于A,B两点,交C的准线于P,Q两点.(Ⅰ)若F在线段AB上,R是PQ的中点,证明AR∥FQ;(Ⅱ)若△PQF的面积是△ABF的面积的两倍,求AB中点的轨迹方程.【解答】(Ⅰ)证明:连接RF,PF,由AP=AF,BQ=BF及AP∥BQ,得∠AFP+∠BFQ=90°,∴∠PFQ=90°,∵R是PQ的中点,∴RF=RP=RQ,∴△PAR≌△FAR,∴∠PAR=∠FAR,∠PRA=∠FRA,∵∠BQF+∠BFQ=180°﹣∠QBF=∠PAF=2∠PAR,∴∠FQB=∠PAR,∴∠PRA=∠PQF,∴AR∥FQ.(Ⅱ)设A(x1,y1),B(x2,y2),F(,0),准线为x=﹣,S△PQF=|PQ|=|y1﹣y2|,设直线AB与x轴交点为N,∴S=|FN||y1﹣y2|,△ABF∵△PQF的面积是△ABF的面积的两倍,∴2|FN|=1,∴x N=1,即N(1,0).设AB中点为M(x,y),由得=2(x1﹣x2),又=,∴=,即y2=x﹣1.∴AB中点轨迹方程为y2=x﹣1.。
河北省定州中学2017-2018学年高二承智班下学期期中考试数学试题 含答案 精品

河北定州中学2017-2018学年第二学期高二数学承智班期中考试试题一、单选题1.正方体1111ABCD A BC D -棱长为3,点E 在边BC 上,且满足2BE EC =,动点M 在正方体表面上运动,并且总保持1ME BD ⊥,则动点M 的轨迹的周长为( )A. B. C. D.2.如图,在棱长为1的正方体1111ABCD A BC D -中,点E 、F 是棱BC 、1CC 的中点, P 是底面ABCD 上(含边界)一动点,满足1A P EF ⊥,则线段1A P 长度的取值范围是( )A. ⎡⎢⎣⎦B. 32⎤⎥⎣⎦C. ⎡⎣D. 3.如图,在单位正方体1111ABCD A BC D -中,点P 在线段1AD 上运动,给出以下四个命题:①异面直线1A P 与1BC 间的距离为定值; ②三棱锥1D BPC -的体积为定值;③异面直线1C P 与直线1CB 所成的角为定值; ④二面角1P BC D --的大小为定值.其中真命题有( )A. 1个B. 2个C. 3个D. 4个4.现有两个半径为2的小球和两个半径为3的小球两两相切,若第五个小球和它们都相切,则这个小球的半径是 ( ) A.611 B. 311 C. 411 D. 5115.设是异面直线,则以下四个命题:①存在分别经过直线和的两个互相垂直的平面;②存在分别经过直线和的两个平行平面;③经过直线有且只有一个平面垂直于直线;④经过直线有且只有一个平面平行于直线,其中正确的个数有( )A. B. C. D.6.已知12,l l 分别是函数()ln f x x =图像上不同的两点12,P P 处的切线, 12,l l 分别与y 轴交于点,A B ,且1l 与2l 垂直相交于点P ,则ABP ∆的面积的取值范围是( ) A. ()0,1 B. ()0,2 C. ()0,+∞ D. ()1,+∞7.已知1F , 2F 分别为双曲线22221(0,0)x y a b a b-=>>的左焦点和右焦点,过2F 的直线l 与双曲线的右支交于A , B 两点, 12AF F ∆的内切圆半径为1r , 12BF F ∆的内切圆半径为2r ,若122r r =,则直线l 的斜率为( )A. 1B.C. 2D. 8.设A , B 为双曲线()22220x y a bλλ-=≠同一条渐近线上的两个不同的点,若向量()0,2n =, 3AB =且1AB nn⋅=-,则双曲线的离心率为( )A. 2B. 32C. 25D. 3 9.已知双曲线22x 12y -=,直线l 的斜率为-2,与双曲线交于A ,B ,若在双曲线上存在异于A ,B 的一点C ,使直线AB ,BC ,AC 的斜率满足111k AB BC ACk k ++=3,若D ,E ,H 三点为AB ,BC ,AC 的中点,则k OE +k OH =( ) A. -6 B. 5 C. 6 D. 710.已知抛物线C: 24x y =,直线:1l y =-,PA,PB 为抛物线C 的两条切线,切点分别为A,B ,则“点P 在直线l 上”是“PA ⊥PB ”的( )条件A. 必要不充分B. 充分不必要C. 充要D. 既不充分也不必要11.已知双曲线C : 22194x y -=的两条渐近线是1l , 2l ,点M 是双曲线C 上一点,若点M 到渐近线1l 距离是3,则点M 到渐近线2l 距离是 A.1213 B. 1 C. 3613D. 3 12.已知函数()()()()223x f x x m ae mm R =-+-∈的最小值为910,则正实数a =( ) A. 3 B. 23e - C. 23e D. 3或23e -二、填空题13.菱形ABC D 边长为6, 60BAD ∠=,将BC D ∆沿对角线BD 翻折使得二面角C BD A --的大小为120,已知A 、B 、C 、D 四点在同一球面上,则球的表面积等于__________.14.如图,等腰PAB 所在平面为α, PA PB ⊥, 6AB =. G 是PAB ∆的重心.平面α内经过点G 的直线l 将PAB 分成两部分,把点P 所在的部分沿直线l 翻折,使点P 到达点'P ('P ∉平面α).若'P 在平面α内的射影H 恰好在翻折前的线段AB 上,则线段'P H 的长度的取值范围是__________.15.过双曲线的焦点与双曲线实轴垂直的直线被双曲线截得的线段的长称为双曲线的通径,其长等于22b a(a 、b 分别为双曲线的实半轴长与虚半轴长).已知双曲线222:1x C y a -=(0a >)的左、右焦点分别为1F 、2F ,若点M 是双曲线C 上位于第四象限的任意一点,直线l 是双曲线的经过第二、四象限的渐近线, MQ l ⊥于点Q ,且1M Q M F +的最小值为3,则双曲线C 的通径为__________.16.已知直三棱柱111ABC A B C -的侧棱长为6,且底面是边长为2的正三角形,用一平面截此棱柱,与侧棱1AA , 1BB , 1CC 分别交于三点M , N , Q ,若MNQ ∆为直角三角形,则该直角三角形斜边长的最小值为____________三、解答题17.四棱锥P A B C D -中,底面A B C D 是边长为2的菱形,侧面PAD ⊥底面A B C D ,BCD ∠=60°, PA PD == E 是BC 中点,点Q 在侧棱PC 上.(Ⅰ)求证: AD PB ⊥;(Ⅱ)是否存在Q ,使平面DEQ ⊥平面PEQ ?若存在,求出,若不存在,说明理由. (Ⅲ)是否存在Q ,使//PA 平面DEQ ?若存在,求出.若不存在,说明理由.18.如图,四棱锥中,底面是直角梯形,,,,侧面底面,且是以为底的等腰三角形.(Ⅰ)证明:(Ⅱ)若四棱锥的体积等于.问:是否存在过点的平面分别交,于点,使得平面平面?若存在,求出的面积;若不存在,请说明理由.19.已知抛物线2:4E y x =的焦点为F ,过点F 的直线l 与抛物线交于,A B 两点,交y 轴于点,C O 为坐标原点.(1)若4OA OB k k +=,求直线l 的方程;(2)线段AB 的垂直平分线与直线,l x 轴, y 轴分别交于点,,D M N ,求N D CFDMS S ∆∆ 的最小值. 20.已知抛物线C :y 2=2x 的焦点为F ,平行于x 轴的两条直线l 1,l 2分别交C 于A ,B 两点,交C 的准线于P ,Q 两点.(1)若F 在线段AB 上,R 是PQ 的中点,证明:AR∥FQ;(2)若△PQF 的面积是△ABF 的面积的两倍,求AB 中点的轨迹方程.参考答案ADDAC ADBDC 10.C 11.A 12.D 13.84π14.(15.216.17.(I )详见解析;(II )详见解析;(III )详见解析. (Ⅰ)取AD 中点O ,连接,,OP OB BD . 因为PA PD =,所以PO AD ⊥.因为菱形ABCD 中, 60BCD ∠=,所以AB BD =. 所以BO AD ⊥.因为BO PO O ⋂=,且,BO PO ⊂平面POB ,所以AD ⊥平面POB . 所以AD PB ⊥.(Ⅱ)由(Ⅰ)可知, ,BO AD PO AD ⊥⊥,因为侧面PAD ⊥底面ABCD ,且平面PAD ⋂底面ABCD AD =,所以PO ⊥底面ABCD .以O 为坐标原点,如图建立空间直角坐标系O xyz -. 则()()()()1,0,0,,0,0,1,D E P C ---,因为Q 为PC 中点,所以12Q ⎛⎫- ⎪ ⎪⎝⎭. 所以()10,3,0,0,2DE DQ ⎛⎫== ⎪ ⎪⎝⎭,所以平面DEQ 的法向量为()11,0,0n =. 因为()311,3,0,0,2DC DQ ⎛⎫=-= ⎪ ⎪⎝⎭,设平面DQC 的法向量为()2,,n x y z =,则220{0DC n DQ n ⋅=⋅=,即301022x yy z -+=+=. 令3x =,则1,y z ==即(23,1,n =.所以12121221cos ,7n n n n n n ⋅==. 由图可知,二面角E DQ C --为锐角, (Ⅲ)设()01PQ PC λλ=≤≤由(Ⅱ)可知()()2,3,1,1,0,1PC PA =--=-. 设(),,Qx y z ,则(),,1PQ x y z =-,又因为()2,PQ PC λλλ==--,所以2{ 1x y z λλ=-==-+,即()2,1Qλλ--+.所以在平面DEQ 中, ()()0,3,0,12,1DE DQ λλ==--, 所以平面DEQ 的法向量为()11,0,21n λλ=--, 又因为//PA 平面DEQ ,所以10PA n ⋅=, 即()()()11210λλ-+--=,解得23λ=.所以当23λ=时,//PA平面DEQ18.(Ⅰ)见解析;(Ⅱ).(Ⅰ)证明:取的中点,连接,∵,∴.∵且,∴是正三角形,且,又∵,平面∴平面,且平面∴(Ⅱ)解:存在,理由如下:分别取的中点,连接,则;∵是梯形,且,∴且,则四边形为平行四边形,∴又∵平面,平面 ∴平面,平面且平面,∴平面平面∵侧面,且平面平面由(Ⅰ)知,平面,若四棱锥的体积等于,则,所以在和中,∴,则∴是直角三角形,则.19.(1)10x y +-=;(2)2(1)设直线l 的方程为x =my +1,A (x 1,y 1),B (x 2,y 2), 由24{1y x x my ==+得y 2-4my -4=0,y 1+y 2=4m ,y 1y 2=-4.所以k OA +k OB =()121212444y y y y y y ++==-4m =4. 所以m =-1,所以l 的方程为x +y -1=0. (2)由(1)可知,m ≠0,C (0,-1m),D (2m 2+1,2m ). 则直线MN 的方程为y -2m =-m (x -2m 2-1),则M (2m 2+3,0),N (0,2m 3+3m ),F (1,0),S △NDC =12·|NC |·|x D |=12·|2m 3+3m +1m |·(2m 2+1)=()2221)212||m m m ++(,S △FDM =12·|FM |·|y D |=12·(2m 2+2)·2|m |=2|m | (m 2+1), 则NDCFDMS S ∆∆=()2222221144m m m m+=++1≥2, 当且仅当m 2=214m ,即m 2=12时取等号. 所以,NDCFDMS S ∆∆的最小值为2. 20.(1)见解析;(2)21y x =- (1)证明 由题意可知F,设l 1:y =a ,l 2:y =b ,且ab≠0,A ,B,P,Q,R.记过A ,B 两点的直线为l ,则l 的方程为2x -(a +b)y +ab =0. 因为点F 在线段AB 上,所以ab +1=0, 记直线AR 的斜率为k 1,直线FQ 的斜率为k 2,所以k 1=,k 2==-b ,又因为ab +1=0, 所以k 1=====-b ,所以k 1=k 2,即AR∥FQ.(2)解 设直线AB 与x 轴的交点为D(x 1,0), 所以S △ABF =|a -b|FD =|a -b|,又S △PQF =,所以由题意可得S △PQF =2S △ABF 即:=2××|a-b|·,解得x 1=0(舍)或x 1=1.设满足条件的AB 的中点为E(x ,y). 当AB 与x 轴不垂直时, 由k AB =k DE 可得= (x≠1).又=,所以y2=x-1(x≠1).当AB与x轴垂直时,E与D重合,所以,所求轨迹方程为y2=x-1.。
河北省定州中学2017-2018学年高二(承智班)下学期期中

河北定州中学高二承智班期中考试政治试卷一、单选题1.2017年6月,我国科学家利用“墨子号”量子科学实验卫星在国际上率先成功实现了千公里级的星地双向量子纠缠分发,这为未来开展大尺度量子网络和量子通信实验研究,以及开展外太空广义相对论、量子引力等物理学基本原理的实验检验奠定了可靠的技术基础。
“量子纠缠”现象虽然未被完全认知,但这仍然能够说明①物质世界的联系具有客观性和普遍性,实践活动具有能动性②世界总有一些秘密不能为人所理解,科学研究始终站在接近真理的路上③认识具有反复性,认识依赖于实践,要在实践中检验和发展真理④实践具有社会历史性,尚未探测到的事物迟早要为实践证实其存在A. ①②B. ③④C. ②④D. ①③2.我国《关于实行以增加知识价值为导向分配政策的若干意见》明确指出,在保障基本工资水平正常增长的基础上,逐步提高体现科研人员履行岗位职责、承担政府和社会委托任务等的基础性绩效工资水平,对社会科学研究机构和智库,推行政府购买服务制度。
这有利于①健全社会保障体系,促进初次分配公平②创新财政支出方式,激发经济社会发展活力③政府资源由行政配置转为市场配置,提高服务效率④完善收入分配制度,让创造社会财富的源泉充分涌流A. ①②B. ①③C. ③④D. ②④3.自2017年7月1日起降低中国人民银行征信中心服务收费标准。
商业银行等机构查询企业信用报告基准服务费标准由每份60元降低至40元,查询个人信用报告基准服务费标准由每份5元降低至4元。
下列对这一政策的传导路径分析正确的是①降低收费标准→扩大征信查询业务量→增加央行的利润→确保国家财政收入②降低收费标准→金融机构节省成本→更多使用征信系统→防范金融风险③降低收费标准→减少被查询对象负担→降低企业运营成本→提高企业经济效益④降低收费标准→有利于扩大征信服务→科学评估企业信用状况→企业加强诚信建设A. ①②B. ①③C. ②④D. ③④4.下列与“路漫漫其修远兮,吾将上下而求索”蕴含的民族精神一致的是①昭君出塞,修睦安邦②孔明诫子,俭以养德③越王勾践,卧薪尝胆④孙子膑脚,兵法修列A. ①②B. ①④C. ②③D. ③④5.“世界上最遥远的距离,莫过于我们坐在一起,你却在玩手机。
河北省定州中学17-18学年高二英语下学期第一次月考试题(承智班)
河北省定州中学2017-2018学年高二英语下学期第一次月考试题(承智班)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,时间120分钟。
第Ⅰ卷 (共100分)第一部分:听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)1. How will the woman get home?A. By bikeB. By busC. By car2. What is the weather like?A. RainyB. HotC. Cold3. What does the woman mean?A. She often plays chess.B. She hates playing chess.C. She is weak in playing chess.4. What will the speakers do?A. Wait for a short while.B. Call the service center.C. Press the emergency button.5. What are the speakers talking about?A. A houseB. An earthquakeC. A fire第二节(共15小题;每小题1.5分,满分22.5分)听第6段材料,回答第6、7题。
6. Which place is the cleaner’s next to?A. A parkB. A supermarketC. A video store7. What does the man ask the woman to do in the end?A. Buy him a DVD.B. Recommend a movie to him.C. Fetch the shopping list for him.听第7段材料,回答第8、9题。
8. What does the man think of the book?A. It’s worth reading.B. It’s too difficult.C. It’s popular.9. What does the man suggest doing?A. Asking April and Charle s for help.B. Borrowing references from the professor.C. Getting some background knowledge first.听第8段材料,回答第10至12题。
河北省定州中学2017-2018学年高二(承智班)下学期期中考试历史试题
定州中学2017--2018年度第一学期期中考试高二承智班历史试题一、单选题1.古代雅典官员任职期间,“任何公民都可因他行为不敬或侵占公款、叛国,共谋或其他严重犯罪活动而启动一种‘指控程序’来反对他,如果情况属实,他就被判处死刑。
案件首先由议事会来判决,但更严重的案件通常由议事会交由陪审法庭来做最终判决,极其严重的案件,像叛国罪,由公民大会来审问”。
这说明古代雅典A. 对政治权力实行严格的制约B. 公民大会是最高司法机构C. 直接民主能够确保司法公正D. 司法审判程序缺乏合理性2.第一次议会改革前英国内阁集体辞职的典型先例发生在1782年,但它毕竟是一次例外。
从1783年小皮特第一次组阁到1830年格雷上台之间,没有一届内阁是因在下院中就立法或征税等重大问题遭到挫折而集体辞职的。
导致上述现象出现的主要原因是英国第一次议会改革前A. 工业资产阶级还未崛起B. 责任制内阁仍不太成熟C. 内阁专横现象比较突出D. 政府工作得到社会承认3.美国学者波内克斯说:古欧洲有好几个里程碑式的变革,智者学派恰好产生于这些变革中期的希腊文化背景之中。
这些变革包括伯里克利民主改革,这次改革把一个人或者少数人统治的规则转变为多数人统治的规则,雅典由此从一个小城邦变为一个海洋帝国。
材料表明A. 雅典成为地跨欧亚非大帝国B. 思想变革得益于政治民主化C. 智者学派的产生植根于经济D. 伯里克利改革完善民主政治4.马克思·书伯认为,传统的天主教鄙视世俗劳动……但在新教那里,世俗生活中职业具有神圣的意义……是侍奉上帝的手段和荣誉……与此同时,新教徒拒绝享受他们创造的财富……这样在新教徒那里,狂热的劳动态度和谋利冒险精神与节俭精神结合起来……导致资本的积累。
作者旨在强调A. 新教理论推动了资本主义发展B. 新教废除禁欲主张任意享乐C. 新教教义尊奉上帝的至高无上D. 新教信仰必须借助特定仪式5.毛泽东曾在一篇文章中指出:“(中国)不是一个独立的民主国家,而是一个半殖民地的半封建的国家,在内部没有民主制度,在外部没有民族独立,而是受帝国主义压迫。
河北省定州中学2017-2018学年高二(承智班)下学期期中考试物理试题Word版含答案
河北省定州中学2017-2018学年高二(承智班)下学期期中考试物理试题物理注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
第I 卷(选择题)一、单选题1.关于万有引力定律的发现,符合历史事实的是 ( ) A. 开普勒通过分析第谷的天文观测数据发现了万有引力定律 B. 牛顿发现了万有引力定律,卡文迪许测出了万有引力常量 C. 牛顿发现了万有引力定律,笛卡儿测出了万有引力常量 D. 牛顿发现了万有引力定律并测出了万有引力常量2.某物体在几个恒力作用下保持平衡状态,若其中的一个力突然消失,其他力保持不变,则物体在此过程中,运动情况描述正确的是: ( )A. 物体一定做曲线运动B. 物体一定做直线运动C. 物体的加速度一定恒定D. 物体的速度一定增加3.如图是一汽车在平直路面上启动的速度—时间图象,从t 1时刻起汽车的功率保持不变,由图象可知()①0~t 1时间内,汽车的牵引力增大,加速度增大,功率不变②0~t 1时间内,汽车的牵引力不变,加速度不变,功率增大③t 1~t 2时间内,汽车的牵引力减小,加速度减小 ④t 1~t 2时间内,汽车的牵引力不变,加速度不变 A. ①③ B. ①④ C. ②③ D. ②④4.我国发射的风云一号气象卫星是极地卫星,周期为12h 。
风云二号气象卫星是地球同步卫星,周期是24h 。
与风云二号相比较,风云一号( )A. 距地面较近B. 角速度较小C. 线速度较小D. 受到地球的万有引力较小5.一水平抛出的小球落到一倾角为ө的斜面上时,其速度方向与斜面垂直,运动轨迹如图中虚线所示。
【配套K12】[学习]河北省定州中学2017-2018学年高二数学下学期期末考试试题(承智班)
河北省定州中学2017-2018学年高二数学下学期期末考试试题(承智班)一、单选题1.已知函数,在区间上任取三个数均存在以为边长的三角形,则的取值范围是()A. B. C. D.2.在长方体中,底面是边长为的正方形,侧棱为矩形内部(含边界)一点,为中点,为空间任一点且,三棱锥的体积的最大值记为,则关于函数,下列结论确的是()A. 为奇函数B. 在上不单调;C. D.3.已知函数(,),若,则的取值范围是()A. B. C. D.4.已知四面体的四个顶点都在半径为的球面上,是球的直径,且,则四面体的体积为()A. B. C. D.5.已知平面向量,,当时,的最小值是()A. B. C. D.6.设函数,其中表示中的最小者.下列说法错误的()A. 函数为偶函数 B. 若时,有C. 若时,D. 若时,7.设,,且为偶函数,为奇函数,若存在实数,当时,不等式成立,则的最小值为( )A. B. C. D.8.若函数有两个极值点,则实数的取值范围是( )A. B. C. D.9.设函数是定义在上的函数的导函数,有,若,,则的大小关系是( ) A.B.C.D.10.已知函数,若不等式在上恒成立,则的最小值是( )A. B. C. D.11.的展开式中,的系数为( ) A.B.C.D.12.如图,网格纸上小正方形的边长为,粗实线及粗虚线画出的是某多面体的三视图,则该多面体的表面积为( )A. B. C. D.二、填空题13.如图,在边长为1的正方形ABCD中,E为AB的中点,P为以A为圆心,AB为半径的圆弧(在正方形内,包括边界点)上的任意一点,则的取值范围是________;若向量,则的最小值为_________.14.如图,已知为中点,以为直径在同侧作半圆,分别为两半圆上的动点,(不含端点),且,则的最大值为__________.15.已知实数满足,则______.16.已知抛物线的参数方程为(为参数),其中,焦点为,准线为,过抛物线上一点作的垂线,垂足为.若,点的横坐标为3,则__________.三、解答题17.如图,焦点在轴上的椭圆与焦点在轴上的椭圆都过点,中心都在坐标原点,且椭圆与的离心率均为.(Ⅰ)求椭圆与椭圆的标准方程;(Ⅱ)过点M的互相垂直的两直线分别与,交于点A,B(点A、B不同于点M),当的面积取最大值时,求两直线MA,MB斜率的比值.18.已知函数,其中常数.(1)当时,讨论的单调性;(2)当时,是否存在整数使得关于的不等式在区间内有解?若存在,求出整数的最小值;若不存在,请说明理由.参考数据:,.19.在平面直角坐标系中,曲线与坐标轴的交点都在圆上.(1)求圆的方程;(2)若圆与直线交于,两点,且,求的值.20.已知椭圆:()经过点,且两个焦点,的坐标依次为和.(1)求椭圆的标准方程;(2)设,是椭圆上的两个动点,为坐标原点,直线的斜率为,直线的斜率为,若,证明:直线与以原点为圆心的定圆相切,并写出此定圆的标准方程.参考答案DDDBC DABAB11.B12.A13.14.15.16.2.17.(1),(2)(Ⅰ)依题意得对:,,得:;同理:.(Ⅱ)设直线的斜率分别为,则MA:,与椭圆方程联立得:,得,得,,所以同理可得.所以,从而可以求得因为,所以,不妨设,所以当最大时,,此时两直线MA,MB斜率的比值.18.(1) f(x)在(0,1)↑,(1,+∞)↓(2) −1解:(1) 求导,设明显g(x)在(0,+∞)↓,且g(1)=0故f (x)在(0,1)↑,(1,+∞)↓当时,设,,在 ,且注意F′()=−3<0,F′()=e3(1−ln2−e−2)≈0.1e3>0故在(0,)内,$唯一x0∈(,),使得lnx0=x0−2并且F(x)在(0,x0)↓,(x0,e)↑,(e,+∞)↓当x∈(0,e)时,F(x)min =F(x0)=e3(x0lnx0−x+x0)=e3(x−x0)因$∈(0,e),使2m≥F(x)成立,故需2m≥F (x)min=e3(x−x0)当x0∈(,)时,F(x)min=e3(x−x0)∈(−,−e)≈(−3.32,−2.51)因2m为偶数,故需2m≥−2Þm≥−1,即m的最小整数值为−119.(1);(2).(1)曲线与轴的交点为,与轴的交点为.故可设的圆心为,则有,解得.则圆的半径为,所以圆的方程为.(2)设,,其坐标满足方程组消去,得方程.由已知可得,判别式,且,.由于,可得.又,所以. 由 得,满足,故.20.(1);(2).(1)由椭圆定义得,即,又,所以,所以椭圆的标准方程为. (2)设直线的方程为,,,直线的方程与椭圆方程联立,消去得,当时,得,,由已知,即,因为点,在直线上,所以,整理得,即,化简得,原点到直线的距离,,所以直线与一个定圆相切,定圆的标准方程为.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河北省定州中学2017-2018学年高二(承智班)下学期期中考试地理试题地理注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
第I 卷(选择题)家住我国东部某三线城市的王女士,准备在当地买一套属于自己的住宅。
王女士考察了数家楼盘,并选取了四组做了下表。
据表完成下面小题。
注:容积率是指一个小区的地上总建筑面积与用地面积的比率;建蔽率是指一个小区的地上建筑物的单层建筑面积与用地面积之比。
1.高楼林立的城市中,如果布局不当,楼房之间经常会因“狭管效应”出现瞬时强风。
表四个小区中,最容易出现瞬时强风的是A. 甲B. 乙C. 丙D. 丁2.我国《工程建设标准强制性条文)中规定“七层及以上住宅必须设置电梯”,按此标准,并考虑材料中容积率与建蔽率之间的关系,计算一下下列楼盘必须设置电梯的是A. 甲B. 乙C. 丙D. 丁3.城市规划中,哪类功能区的建蔽率最低A. 工业区B. 风景区C. 住宅区D. 商业区土壤中排放的 CO2 主要来自生物残体分解和根系呼吸。
受人类干扰,我国东北某山植被群落发生了逆行演替:红松阔叶林→阔叶杂木林→白桦林→灌木林→草本。
下图示意该山不同演替阶段植被群落8月份土壤 CO2 排放通量时间变化。
据此完成下面小题。
4.该山植被群落从红松阔叶林向草本逆行演替过程中 A. 草本物种数逐渐增 B. 植被覆盖率逐渐下降 C. 地上生物量逐渐减少 D. 群落内光照逐渐减弱5.该时段土壤 CO2 排放通量受士壤温度影响最小的森林群落是 A. 红松阔叶林 B. 阔叶杂木林 C. 百桦林 D. 灌木林 6.下列因素中,与图中土壤 CO2 排放通量的时空变化相关性最小的是 A. 土壤微生物 B. 地下生物量 C. 表层凋落物 D. 土壤含水量地处美国某山脉的马尾瀑布是一条季节性瀑布(下图),隐蔽于群山之间,夏季几乎断流。
每年2 月中下旬,当夕阳照射在瀑布上时,水流染上橙色的光芒,如同岩浆沿着高崖倾泻而下,因此被称为“火瀑布”。
这一奇景在其他日期难以看到。
据此完成下面小题。
此卷只装订不密封班级 姓名 准考证号 考场号 座位号7.推断马尾瀑布位于图中的A. 甲地附近B. 乙地附近C. 丙地附近D. 丁地附近8.马尾瀑布面朝A. 西南B. 西北C. 东南D. 东北9.该地10 月中下旬无法观赏到“火瀑布”奇景的原因主要是A. 晴天少云层多B. 地形阻挡夕阳C. 瀑布水量不足D. 水色浑浊不清下图为我国某地(40°N,112°E)南坡的植树造林整地模式示意图,右图为沿图中P-M线所作的剖面图。
该模式是先在山坡上沿等高线挖沟,将沟内挖出的底土在沟前培埂(右图中A处),再用沟上沿的活土回填到沟的下方(右图中B处),最后在内斜坡一例(图中C坡)栽种小树苗,根据图文材料完成下列问题。
10.右图中A埂的作用是A. 改变沟内光照B. 拦蓄地表径流C. 升高沟内温度D. 增加地表粗糙度11.一年中正午时分,右图中沟内小树苗能全部被阳光照射的时间约为A. 60天B. 100天C. 180天D. 340天策勒河位于塔里木盆地南缘,河上的恰哈桥(下图)是315国道上的重要交通设施.该路段存在持续的过境风沙流。
2011年,历时三年工期的恰哈新桥建成,自新桥投入使用以来,受路基和护栏形态等因素的影响,桥面风沙堆积成为困扰交通的一大问题。
为减轻沙害,交通管理部门在桥面道路北侧设置高立式芦苇沙障,结果路面积沙日趋严重,随后沙障被拆除。
据此完成下列各题。
12.恰哈新桥修建的主要目的是()A. 规避风沙危害B. 降低道路坡度C. 增加通行能力D. 促进矿产开发13.导致新旧桥路面积沙差异的主要原因是()A. 透风护栏增加了进入桥面的沙量B. 不透风护栏阻滞沙流C. 平面路基减弱风速D. 阶梯状路基增强风速14.拆除芦苇沙障的主要目的是()A. 增强通过桥面道路的风速B. 扩大路面驾驶视野C. 降低桥面道路的维护成本D. 增加光照,减轻冻土厚度我国东部沿海某省区,所辖范围内岛屿众多,自然岸线(包括大陆岸线与岛岸线)曲折绵长。
近年来,填海造陆等方式的开发利用强度不断加大,岸线曲折度变小。
下图为1985-2015年该省区岸线长度与海岸人工化强度关系图。
据此完成下面小题。
15.图中分别对应海岸人工化强度、自然岸线、人工岸线、整体岸线的是A. ②③④①B. ②④③①C. ③④①②D. ①③②④16.随着全球气候变暖,对该省沿海地区的影响是A. 岛屿岸线变长B. 陆地岸线变长C. 改变地质构造D. 地下水质变差读“某景区等高线地形图”,完成下列各题。
17.若图中急流段相对高差为26m,则图中甲地与乙地高差约为()A. 104mB. 126mC. 146mD. 150m18.乙地河床上有鹅卵石与细沙共存现象,是因该河段()A. 流速急,搬运能力强B. 降水变化大,流速变化大C. 流量大,河流侵蚀能力强D. 地势起伏小,沉积作用显著当强冷空气经过渤海上空时,受海水加热加湿促使空气中的水汽凝华,形成“冷流云”,继而在山东半岛北部形成“冷流雪”,12 月是月冷流雪量最多的月份。
据此完成下面小题。
19.山东半岛南部冷流雪量远少于北部的主要原因是A. 距海较远B. 地形阻挡C. 气温较高D. 地势低平20.冷空气南下时,山东半岛北部12 月比2 月更易产生冷流雪的原因主要是A. 海陆气温差异较大B. 南下冷空气较频繁C. 渤海表层水温较高D. 半岛上空尘埃较多2017年中央“一号文件”首次提出了“田园综合体”这一新概念。
该发展模式建议有条件的乡村以农民合作社为主要载体,建设集现代农业、休闲旅游、田园社区为一体的特色小镇和乡村。
读“田园综合体”功能结构图,完成下面各题。
21.发展“田园综合体”模式的主要意义有()A. 促进土地流转、集约化经营B. 提高农产品产量C. 推动工业化、城镇化进程D. 促进大城市向田园型城市发展22.下列地区可以优先发展“田园综合体”模式的是()A. 黑龙江小麦种植区B. 浙江舟山渔村C. 太湖平原农耕区D. 新疆天山牧区第II卷(非选择题)23.阅读图文资料,完成下列问题。
温哥华岛西南部分布着大面积的温带雨林。
温带雨林是地球上中纬度高雨量地区的针叶树或阔叶树森林,冬季气温极少低于0℃。
温哥华岛曾受过冰川影响,目前冰川仅存留于山顶地区。
下图为温哥华岛简图。
(1)温哥华岛西南侧海岸线比较曲折,描述其形成的外力作用过程。
(2)判断温哥华岛位于大陆板块还是大洋板块,并说出判断理由。
(3)从气温和降水两方面,具体分析温带雨林多分布在温哥华岛西南部的原因。
24.阅读图文材料,完成下列要求。
材料一:塔希提岛是南太平洋上的波利尼西亚群岛118个岛中最大的一个岛屿,为一火山岛,面积1042平方千米,人口12.27万。
该岛南部湿润,年降雨量2500毫米以上;北部较干燥,年降雨量约1800毫米,全岛大部分降雨在12月至次年3月。
许多热带花卉生长在岛上整个岛屿的空气中弥漫着花香。
塔希提已成了重要的花卉基地。
材料二:下图示意塔希提岛位置、地形和河流分布。
(1)分析塔希提岛降雨南部多于北部且集中于每年12月至翌年3月的主要原因。
(2)简析塔希提岛的地形对河流水系的影响。
(3)阐释塔希提岛成为重要热带花卉基地的有利自然条件。
河北省定州中学2017-2018学年高二(承智班)下学期期中考试地理试题地理答案1.B2.C3.B【解析】1.我国东部城市是季风气候,夏季盛行东南风,冬季盛行西北风;甲丙两个小区楼房走向为南北和东西走向,不利于“狭管效应”的形成;乙、丁两楼的走向与风向一致辞,都有可能存在“狭管效应”;乙地的建蔽率较高,不利于通风,瞬间强风出现的可能性增强。
选B正确。
2.容积率是指一个小区的地上总建筑面积与用地面积的比率;建蔽率是指一个小区的地上建筑物的单层建筑面积与用地面积之比;由此可知,甲小区的单层建筑面积为9500×50%㎡,地上总建筑面积9500×140%㎡,甲小区楼层数量为140%÷50%,即容积率/建蔽率;可以测算甲乙丙丁四座楼盘的楼层数分别为2.8层、5层、9层、3.6层;只有丙地楼盘符合条文中的规定。
选C正确。
3.城市建设中风景区绿地面积广,建筑面积相对小且分散,建蔽率最小。
选B正确。
【点晴】当气流由开阔地带流入地形构成的峡谷时,由于空气质量不能大量堆积,于是加速流过峡谷,风速增大;当流出峡谷时,空气流速又会减缓,这种地形峡谷对气流的影响;称为“狭管效应”。
“狭管效应”也叫“峡谷效应”,就像峡谷里的风总比平原风猛烈一样,城市高楼间的狭窄地带风力也特强,易造成灾害。
一些楼间窄地的瞬间风力就大大超过七级,以至于行驶的汽车都会打晃;由狭管效应而增大的风,称为峡谷风或穿堂风,地球上山地的许多风口和许多地方出现的地形雨都与气流经过狭窄地形密切相关。
4.C5.A6.D【解析】4.该山植被群落从红松阔叶林向草本逆行演替过程中,草本植物是在林木树种之后出现的,并非逐渐增,植被覆盖率也不是逐渐下降;但从红松阔叶林向草本逆行演替过程中,地上生物量逐渐减少,群落内因地上生物量的减少,光照逐渐增强。
5.图中曲线显示,该时段红松阔叶林随时间变化,土壤CO2 排放通量变化不大,因此红松阔叶林受士壤温度影响最小,选A。
6.土壤CO2 排放通量与生物有关,而与土壤的含水量关联度相对较小,据此选D。
7.B8.A9.C【解析】7.根据材料信息,火瀑布是出现于2月中下旬的夕照,此时夕阳应在西南方向,根据材料,瀑布还应位于群山之间,且有丰沛的流水,据此推断选B。
8.火瀑布是出现于2月中下旬的夕照,此时夕阳应在西南方向,因此马尾瀑布面朝西南,选A。
9.10 月中下旬与2月中下旬的夕阳位置相当,但无法观赏到“火瀑布”奇景的原因则不会是来自夕阳,也不会是来自地形地势,应是水量不足无法形成瀑布奇景的问题,据此选C。
10.A11.B【解析】10.由材料可知,图中A埂是将沟内挖出的底土在沟前培成,位于南面,可以减少正午阳光对沟内小苗的照射,有利于成活,故A正确。
树苗种在沟内,沟本身就有拦截地表径流的作用,没有必要再培土作梗,而且若积水过多,树苗不易成活,故B错误。
A埂遮挡了光照,因此沟内温度偏低,故C错误。
增加地表粗糙度主要是为了防风,A埂对风力影响不大,故D错误。
