同济大学材料力学全套精品课件推荐
合集下载
《材料力学》课程讲解课件第八章组合变形
强度条件（简单应力状态）——
max
对有棱角的截面，最大的正应力发生在棱角点处，且处于单向应力状态。
max
N A
M zmax Wz
M ymax Wy
x
对于无棱角的截面如何进行强度计算——
1、确定中性轴的位置；
y
F z
M z F ey M y F ez
ez F ey z
y
zk yk z
y
x
1、荷载的分解
F
Fy F cos
Fz F sin
z
2、任意横截面任意点的“σ”
x
F
y
（1）内力： M z (x) Fy x F cos x
M y (x) Fz x F sin x
（2）应力：
Mz k
M z yk Iz
My k
M y zk Iy
（应力的 “＋”、“－” 由变形判断）
F
1， 首先将斜弯曲分解
为两个平面弯曲的叠加 Fy F cos
z
L2
L2
Fz F sin
z
2， 确定两个平面弯曲的最大弯矩
y
Mz
Fy L 4
M
y
Fz L 4
3， 计算最大正应力并校核强度
max
My Wy
Mz Wz
217.8MPa
查表： Wy 692.2cm3
4， 讨论 0
y
Wz 70.758cm3
的直径为d3，用第四强度理论设计的直径为d4，则d3 ___＝__ d4。
（填“＞”、“＜”或“＝”）
因受拉弯组合变形的杆件，危险点上只有正应力，而无切应力，
r3 1 3 2 4 2
r4
材料力学课件PPT
梁的剪力与弯矩
1
梁的剪力
解析剪力对梁的影响和剪切应力。
2
梁的弯曲
讨论梁的弯曲行为和弯曲应力。
3
横截面性能
探索截面形状对梁的强度和刚度的影响。
梁的挠度
1 挠度与刚度
2 梁的支撑条件
3 挠度计算
研究梁的弯曲变形和挠度。
解释梁的不同支撑条件对 挠度的影响。
介绍计算梁挠度的工程方 法。
杆件的稳定性
1
稳定性概念
材料力学课件PPT
材料力学课件PPT是一个全面的教学工具，涵盖了力学基础、应力与变形、杆 件的轴向受力、梁的剪力与弯矩、梁的挠度、杆件的稳定性以及结构稳定裂 解和破坏形态。
力学基础
1
牛顿力学原理
解释物体运动和力的相互作用。
2
力的向量和标量
了解力量的方向和大小。
3
运动和加速度
讨论物体的运动和加速度。
应力与变形
应力
探讨物体所受力的影响。
塑性变形
讲解材料在超出弹性范围时的塑性行为。
弹性变形
解析材料的弹性性质和应变量。
断裂
探索材料的破裂过程和强度。
杆件的轴向受力
拉力
描述由拉力引起的变形和破坏。
压力
研究由压力引起的压缩变形和破坏。
剪力
解释由剪切力引起的变形和破坏。
扭矩
探讨由扭转力引起的变形和破坏。
介绍杆件的稳定性和失稳行为。
2
纯压杆件
研究纯压杆件的稳定性和临界长度。
பைடு நூலகம்
3
压弯杆件
探讨压弯杆件的稳定性和稳定方程。
结构稳定裂解和破坏形态
稳定性裂解
解释结构在突然失去稳定性时的裂解过程。
材料力学PPT课件
A—截面面积
位移
构件在外力作用下，其变形的大小用位移和应变
来度量。 如图：
AA’连线称为A点的线位移
θ角度称为截面m-m的角位移，简称转角
注意，单元K的形状也有所改变
应变
分析单元K 单元原棱长为△x，△u为绝对伸长量，其相对伸长 △u/ △x的极限称为沿x方向的正应变ε。
材料力学的基本知识
变形
构件在载荷作用下，其形状和尺寸发生变化的现
象；变形固体的变形通常可分为两种：
弹性变形---载荷解除后变形随之消失的变形 塑性变形---载荷解除后变形不能消失的变形
材料力学研究的主要是弹性变形，并且只限于弹
性小变形，即变形量远远小于其自身尺寸的变形
变形固体的基本假设 连续性假设
• FNx使杆件延x方向产生轴向拉压变形，称为轴力 • FQy,FQz使杆件延y,z方向产生剪切变形，称为剪力 • Mx 使杆件绕x轴发生扭转变形，称为扭矩 • My、Mz使得杆件分别绕y z轴产生弯曲变形，称为弯矩
横截面上内力计算--截面法
截面法求内力步骤 将杆件在欲求内力的截面处假想的切开； 取其中任一部分并在截面上画出相应内力； 由平衡条件确定内力大小。
时衡量材料塑性的一个重要指标70ppt学习交流低碳钢和铸铁压缩时的力学性能低碳钢压缩铸铁压缩71ppt学习交流名义屈服极限对于没有明显屈服阶段的塑性材料在工程上常以卸载后产生02的残余应变的应力作为屈服应力称为名义屈服极限用p02来表示对于这种对材料预加塑性变形而使其比例极限或弹性极限提高塑性变形减小的现象称之为冷作硬化
2.当：a≤x2≤2a 时,即CD段
FQ2=11q.a/6-q.x2 ，直线 x2 =a；FQ2 = 5q.a/6 （= FQ1 ） x2 =2a；FQ2 = -q.a/6 （= FQ3 ）
材料力学课件共377页PPT
33、如果惧怕前面跌宕的山岩，生命 就永远 只能是 死水一 潭。 34、当你眼泪忍不住要流出来的时候 ，睁大 眼睛， 千万别 眨眼!你会看到 世界由 清晰变 模糊的 全过程 ，心会 在你泪 水落下 的那一 刻变得 清澈明 晰。盐 。注定 要融化 的，也 许是用 眼泪的 方式。
35、不要以为自己成功一次就可以了 ，也不 要以为 过去的 光荣可 以被永 远肯定 。
材料力学课件
31、别人笑我太疯癫，我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣，抱怨者 的牢骚 ，这是 羊群中 的瘟疫 ，我不 能被它 传染。 我要尽 量避免 绝望， 辛勤耕 耘，忍 受苦楚 。我一 试再试 ，争取 每天的 成功， 避免以 失败收 常在别 人停滞 不前时 ，我继 续拼搏 。
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂，怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最
35、不要以为自己成功一次就可以了 ，也不 要以为 过去的 光荣可 以被永 远肯定 。
材料力学课件
31、别人笑我太疯癫，我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣，抱怨者 的牢骚 ，这是 羊群中 的瘟疫 ，我不 能被它 传染。 我要尽 量避免 绝望， 辛勤耕 耘，忍 受苦楚 。我一 试再试 ，争取 每天的 成功， 避免以 失败收 常在别 人停滞 不前时 ，我继 续拼搏 。
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂，怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最
材料力学优秀课件
最大应力通常与截面形状，内力图形状有关。 a 脆性材料的最大应力与截面形状有关
由于脆性材料抗压不抗拉， 通常将梁做成T形、倒T形等 关于中性轴不对称的截面。
梁内最大拉应力与最大压应力分别发生在 离中性轴最远的最上边缘与最下边缘。
b 脆性材料的最大应力与内力图有关
① 脆性材料梁的危险截面与危险点
上压下拉
4KNm 52 zc
88
应用公式 My
Iz
t,max
4103 52103 7.64 106
27.2MPa
c,max
4103 88103 7.64 106
46.1MPa
9KN
A
CB
4KN C截面应力计算 C截面应力分布
FA 1m 1m
F1Bm
2.5KNm
M
应用公式
My
Iz
4KNm
t,max
FBY
3、C 截面上K点正应力
弯矩 M C 901 601 0.5 60kN m
公式
K
MC IZ
yK
60 103 60 103 5.832 105
61.7MPa （压应力）
4、C 截面上最大正应力
Cmax
M C ymax IZ
60 103 90 103 5.832 105
92.55MPa
3、静力学关系
横截面上没有切应力 只有正应力。
弯曲正应力的 分布规律和计算公式
变形与应变 观察在竖直平面内发生纯弯曲的梁，研究其表面变形情况
<1>. 弯曲前画在梁的侧面上相邻横向线mm和nn间的 纵向直线段aa和bb，在梁弯曲后成为弧线，靠近梁的顶面 的线段aa缩短，而靠近梁的底面的线段bb则伸长；
由于脆性材料抗压不抗拉， 通常将梁做成T形、倒T形等 关于中性轴不对称的截面。
梁内最大拉应力与最大压应力分别发生在 离中性轴最远的最上边缘与最下边缘。
b 脆性材料的最大应力与内力图有关
① 脆性材料梁的危险截面与危险点
上压下拉
4KNm 52 zc
88
应用公式 My
Iz
t,max
4103 52103 7.64 106
27.2MPa
c,max
4103 88103 7.64 106
46.1MPa
9KN
A
CB
4KN C截面应力计算 C截面应力分布
FA 1m 1m
F1Bm
2.5KNm
M
应用公式
My
Iz
4KNm
t,max
FBY
3、C 截面上K点正应力
弯矩 M C 901 601 0.5 60kN m
公式
K
MC IZ
yK
60 103 60 103 5.832 105
61.7MPa （压应力）
4、C 截面上最大正应力
Cmax
M C ymax IZ
60 103 90 103 5.832 105
92.55MPa
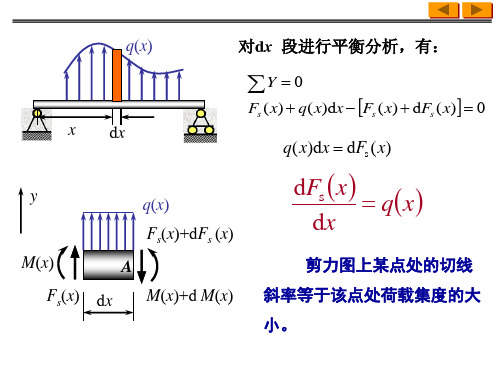
3、静力学关系
横截面上没有切应力 只有正应力。
弯曲正应力的 分布规律和计算公式
变形与应变 观察在竖直平面内发生纯弯曲的梁，研究其表面变形情况
<1>. 弯曲前画在梁的侧面上相邻横向线mm和nn间的 纵向直线段aa和bb，在梁弯曲后成为弧线，靠近梁的顶面 的线段aa缩短，而靠近梁的底面的线段bb则伸长；
材料力学PPT课件
通常用
MPa＝N/mm2 ＝ 10 6 Pa
有些材料常数 GPa＝ kN/mm2 ＝ 10 9 Pa
工程上用 kg/cm2 ＝ 0.1 MPa
正应力s
剪应力
二、轴向拉压时横截面上应力
dA
dN dA •s
N
s dN
N dN s dA
A
A
求应力，先要找到应力在横截面上的分布情况。
应力是内力的集度，而内力与变形有关，所以
绘轴力图
（2）求应力 AB段：A1＝240240mm＝57600mm2
BC段：A2＝370370mm＝136900mm2
s1
N1 A1
50 103 57600
0.87 N
/ mm 2
0.87MPa
s2
N2 A2
150 103 136900
1.1N
/ mm 2
1.1MPa
应力为负号表示柱受压。正应力的正负号与轴力N相同。
Nl
A
l
————虎克定律（Hooke)
EA
l Pl
EA
计算中用得多
lE——N——弹性s横量（Mpa,
Gpa)
s
E
l EA E
实验中用得多
计算变形的两个实例：
1.一阶梯轴钢杆如图，AB段A1＝200mm2，BC和CD段截面积相同A2＝A3＝ 500mm2；l1= l2= l3=100mm。弹性模量E＝200GPa，荷载P1＝20kN，P2 ＝40kN 。试求：（1）各段的轴向变形；（2）全杆AD的总变形；
N1＝-20kN（压） N2＝-10kN（压） N3＝+30kN（拉）
§3 应力
一、应力：
内力在杆件截面上某一点的密集程度
同济大学材料研究方法精品课程
第四章的高速电子束轰击样品表射线波谱仪或能谱仪检测从试样表面有限深度和侧向扩展的微区体积内产生的特征μ m3电子探针仪的镜筒构造和扫描电镜大体相似，扫描电扫描电镜电子束相对于样品表面的入入射电子束流强度较低，一-12A，能使入射电子束斑直径小于10-5~10-13A。
为屏蔽系数。
Z为原子序数射线强度与该元素在样品中的浓度成比例射线的入射角固定，对样品进行微区扫描，即可得到某一元素的线分布或面射线谱仪用的波谱仪有多旋转式波谱仪用磨制的弯晶(分光晶体)，将光源(电子束在样品上的照射点)发射出的射线束会聚在X射线探测器的接收狭缝处。
通过将弯晶沿聚焦圆转动来改变角的大小，探测器也随着在聚焦圆上作同步运动。
光源、弯晶反射面和接收狭缝始终落在聚焦圆的圆周上。
图4.73 旋转式波谱仪，则出射较为ϕ2的透路程较长，其强度较低，计算时须增加修正系数，比较直进式波谱仪它的特点是x射线出射角 固定不变。
弥补了旋转式波谱仪的缺点。
因此虽然结构上比较复杂，但它是目前常用的一种谱仪。
弯晶在某一方向上作直线运动并转动，探测器也随着运动。
聚焦圆半径不变，圆心在以光源为中心的圆周上运动，光源、弯晶和接收狭缝也都始终落在聚焦圆的圆周上。
图4.74 直进式波谱仪存在着简单的线性关系。
因此，只要读出谱仪上的20~223.5~11.913.724~4024~3737~6551~92检测器将所有波长(能量射线光子几乎同时接收进来，每一能量为E的为产生一对电子空穴对所需要的能量=3.8eV)检测器将它们接收后经过数据能谱仪示意图图4.75 能谱仪电子束流小，束斑尺寸小，对样品的污染作用小，；而波谱仪大分钟内完成元素定性全分析能谱仪工作时，不需要象波谱仪那样聚焦，因而不（波谱仪可达~ U921000；（图护费用高，用超纯锗探测器虽无此缺点，但其分辨能谱仪与波谱仪的比较(b) 波谱仪(a)能谱仪 (b)图4.81 角闪石定点元素全分析I-λ记录曲线样品表面须具有良好的导电性。
同济大学课件工程力学第五章弯曲内力
轴线
FR B
A
MM 图图
O
② 符号规定
M－使杆微段愈弯的弯矩为正 FS，FN－正负符号规定同前
③ 画弯矩图
与弯矩相对应的 点，画在横截面 弯曲时受拉一侧
10kN/m 4m
2.5m
RB 解：1、支反力
B
Y 0, RA RB 20 10 4 0
MB 0, 10 4 2 205 40 RA4 0
RA 35 (kN); RB 25 (kN).
2、画内力图
x CA段：剪力图为一条水平线；
25
弯矩图为一条斜直线
AB段：剪力图为斜向下的斜直线； 弯矩图为下凸的二次曲线。
3、简易法作内力图：
利用微分关系定形，利用特殊点的内力值来定值 利用积分关系定值
基本步骤： 1、确定梁上所有外力（求支座反力）；
2、分段 3、利用微分规律判断梁各段内力图的形状； 4、确定控制点内力的数值大小及正负； 5、画内力图。
控制点:端点、分段点（外力变化点）和驻点（极值点）等。
作图时应注意结合以下几点 * 集中力处——剪力图有突变，突变值等于集中力的大小；弯矩图有折角。
-qa2/2
M
x
解：求支反力 FAY
qa ; 2
FDY
qa 2
左端点A：
F
qa ;M 0
s2
B点左：
F s
qa 2
;M
1 2
qa 2
B点右： F qa ; M 1 qa2
s2
2
C点左： F
qa ;M
1
qa 2
s2
2
M 的驻点：F 0 ; M 3 qa2
s
8
C点右：F qa ; M 1 qa2