Vehicles PEMFC Power System Mathematical Model for Integrated Design
Mathematica 函数集

最接近的整数 不大于 x 的最大整数 不小于 x 的最小 绝对值 取符号函数 取整数部分 小数 多个数或数组的最大值 最小值
复变量 Re[z] Im[z] Comjugate[z] Abs[z] Arg[z]
z=x+I y 取实部 虚部 共轭 模 幅角
实数或虚数 Exp[z] Log[z] Log[b,z] Sin[z],Cos[z],Tan[z],Cot[z], Csc[z],Sec[z] ArcSin[z],ArcCos[z],Arctan[z],Arccot[z], ArcCsc[z],ArcSec[z] Sinh[z],Cosh[z],Tanh[z],Coth[z], Csch[z],Sech[z] ArcSinh[z],ArcCosh[z],……
Reduce[方程, 变量]:什么情况下方城有解,尽量化简方程并保留方程所有解
Eliminate[方程 s, 变量 s]:消去变量并重组方程组 如:eqns = {x= =1+a/2,y= =1+2 x};
Eliminate[eqns,x]
2.2.4 不等式方程和递归方程
InequalitySolve[ineq,x] InequalitySolve[{ineq1,ineq2},{x,y}
抽象函数的导数表示 f[x_]:=Sin[x^2] 定义函数 f[x] f[x]+f’[x]+f’’[x] 一阶导,二阶导
D[x g[2x],x]
全微分 df
全导数 df dx
多重全导数 全导数,说明 c1,c2, ……为常数
置 dy =0 dx
D[h[x,y],x,x,y]
计算
∂ ∂x2
∂ ∂y
h(3) (x,
mathematica 到底有多厉害

Mathematica 到底有多厉害?我拿来玩比较多……正经计算少,已经完全不是编程、计算工具类。
首先,绘图。
以前用数学函数plot 坐标轴绘制的皮卡丘。
那么我们就可以依据这个特征来制作动画。
有屏幕的地方就有东方Project的Bad apple。
视频点击/v/ac1709546然后我们来玩下乐器演奏功能。
mathematica里面内置了估计又100种左右的音色,具体请自行查找关于SoundNote的信息。
另外还不止这些,它除了可以输出超低音C-1到高音B9,还可以输出半音那种东西,像上面写的C#,Cb这些,所以只要稍微有点了解音乐乐谱和mathematica的话,就可以拿它来演出音乐了~为了方便后面的演奏,我们需要写个简单的函数先,可以输出从指定的一个音,比如说C4,往上数或者往下数n个音的那个音符,比如C4+7=C5,C4+1=D4,C4-1=B3这种:Letter2Num[letter_] :=Switch[ToUpperCase[letter], "C", 1, "D", 2, "E", 3, "F", 4, "G", 5,"A", 6, "B", 7];Number2Letter[num_] :=Switch[num, 1, "C", 2, "D", 3, "E", 4, "F", 5, "G", 6, "A", 7, "B"];GetTone[base_, idx_] :=Module[{tone = Characters[base][[1]], step =Characters[base][[2]]},Number2Letter[Mod[Letter2Num[tone] - 1 + Mod[idx, 7], 7] + 1] <>ToString[ToExpression[step] + Floor[idx/7]]]实践测试《一闪一闪亮晶晶》GetMusicSingleTone[i_] :=Module[{},If[i == 0, Play[0, {t, 0, 1}], SoundNote[GetTone["C4", i], 1]]];(*一闪一闪亮晶晶*)xingxing = Flatten[Riffle[{IntegerDigits[1155665],IntegerDigits[4433221],IntegerDigits[5544332],IntegerDigits[5544332],IntegerDigits[11556654433221]}, 0]];Sound[Table[GetMusicSingleTone[#[[i]]], {i, 1, Length[#]}], 20] &[xingxing]第一人称视角模拟游戏Mathematica 3D 视角这是一个叫Vespa的博主做的一个游戏。
mathematic使用指南
第一章Mathematica的启动的运行Mathematica是美国Wolfram公司生产的一种数学分析型的软件,以符号计算见长,也具有高精度的数值计算功能和强大的图形功能。
目前最新版本是Mathematica4.0,本附录仅介绍Mathematica4.0的一些常用功能,须深入掌握Mathematica的读者可查阅相关书籍。
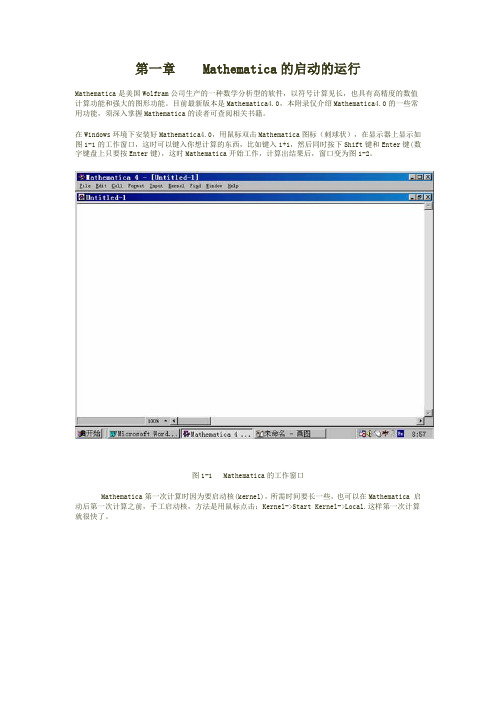
在Windows环境下安装好Mathematica4.0,用鼠标双击Mathematica图标(刺球状),在显示器上显示如图1-1的工作窗口,这时可以键入你想计算的东西,比如键入1+1,然后同时按下Shift键和Enter键(数字键盘上只要按Enter键),这时Mathematica开始工作,计算出结果后,窗口变为图1-2。
图1-1 Mathematica的工作窗口Mathematica第一次计算时因为要启动核(kernel),所需时间要长一些,也可以在Mathematica 启动后第一次计算之前,手工启动核,方法是用鼠标点击:Kernel->Start Kernel->Local.这样第一次计算就很快了。
图1-2 完成运算后的Mathematica的窗口图1-2中的“In[1]:=”表示第一个输入;“Out[1]=”表示第一个输出结果。
接下来可键入第二个输入,按这样的方式可利用Mathematica进行“会话式”计算。
要注意的是:“In[1]:= ”和“Out[1]=”是系统自动添加的,不需用户键入。
Mathematica还提供“批处理”运行方式,即可以将Mathematica作为一种算法语言,编写程序,让计算机执行,这在第七章将会作简要介绍。
第二章 Mathematica的基本运算功能2.1 算术运算Mathematica最基本的功能是进行算术运算,包括加(+),减(-),乘(*),除(/),乘方(^),阶乘(!)等。
注意:1 在Mathematica中,也可用空格代表乘号;数字和字母相乘,乘号可以省去,例如:3*2可写成3 2,2*x可写成2x,但字母和字母相乘,乘号不能省去。
Mathematic在数学中的应用

五、四种软件的比较
选用何种数学软件? 如果仅仅是要求一般的计算或者是普通用户日常使用, 首选的是MathCAD,它在高等数学方面所具有的能力,足 够一般客户的要求,而且它的输入界面也特别友好。 如果要求计算精度、符号计算和编程方面的话,最好同 时使用Maple和Mathematica,它们在符号处理方面各具特 色,有些Maple不能处理的,Mathematica却能处理,诸如 某些积分、求极限等方面,这些都是比较特殊的。 如果要求进行矩阵方面或图形方面的处理,则选择 MATLAB,它的矩阵计算和图形处理方面则是它的强项,同 时利用MATLAB的NoteBook功能,结合Word6.0/7.0的编辑 功能,可以很方便地处理科技文章。
比较如下的输入方式
若采用浮点数输入,则计算结果为近似值 (1)1./3+2/5 (2)2^100 (3)2.^100
一个是精确计算2的100次方,一个是近似计算2 的100次方
2:常数与函数
Mathematica软件中提供了数学上通用的一些常 数,下表中给出了其中一部分常数 常数 Pi E I 数学含义 圆周率 常数 Infinity 数学含义 正无穷大
Mathematica的进一步说明
它吸取了不同类型软件的一些优点: (1)具有BASIC的简单易学的交互式方法 (2)具有MathCAD\Matlab那样强的数值计算能力 (3)具有Maple的和SMP那样的符号计算能力 (4)具有APL和LISP那样的人工智能列表处理能力 (5)像C和PASCAL那样的结构化设计语言 Mathematica的开发者 Stephen Wolfram是Mathematica的创始人,并被公认为是 当今科学计算的先驱。 Wolfram1959年出生于伦敦。他曾在 牛津大学和加州理工学院接受教育,15岁发表了第一篇科技 论文,1979年20岁时在加州理工学院获得理论物理学博士学 位。 他从1973年开始使用计算机,1981年主持开发了第一个计算 机代数系统SMP。
数学专业词汇(M)

mach angle 马赫角mach cone 马赫锥mach number 马赫数machine computation 机破算machine computing 机破算machine equation 机平程machine language 机骑言machine word 计算机语mackey topology 麦基拓扑maclaurin expansion 马克劳林展开maclaurin formula 马克劳林公式macro instruction 广义指令macrooperation 大运算macroparameter 宏观参数macrostatistics 宏观统计学magic circle 幻圆magic cube 幻立方magic figure 幻图magic square 纵横图magnetic head 磁头magnetic store 磁存储器magnetic tape 磁带magnetohydrodynamics 磁铃力学magnitude 量main diagonal 衷角线main program 痔序major axis 长轴major cycle 大循环major premise 大前提major term 大词majorant 强级数majorant criterion 比较检验majorant series 强级数majority 多数majority decision function 多数判定函数majority function 强函数majority game 强对策majorized sequence 优化序列majorized series 优化级数mal posed problem 不适定问题malfunction 错误动作maltiple classification 廖分类manifold 廖manifold classification 廖分类manifold of flags 旗廖manifold without boundary 无边廖manipulation 操作mannheim curve 曼海姆曲线mantissa 尾数many body problem 多体问题many dimentional sepce 多维空间many valued composition law 多值合成律many valued function 多值函数many valued logic 多值逻辑many valued mapping 多值映射map 映射map coloring problem 地图着色问题map projection 地图投影mapping 映射mapping cone 映射锥mapping cylinder 映射柱mapping function 映射函数mapping norm 映射范数mapping of sets 集映射mapping of the boundary 边缘映射mapping space 映射空间mapping theorem 映射定理mapping transformation 映射变换marginal density 边缘密度marginal distribution 边缘分布marginal distribution density function 边缘分布密度函数marginal distribution function 边缘分布函数mark 记号market model 市场模型marking function 标记函数markoff chain 马尔可夫链markov chain 马尔可夫链markov decision process 马尔可夫决策过程markov matrix 马尔可夫矩阵markov process 马尔可夫过程markov transform 马尔可夫变换marriage problem 配对问题mass 质量master program 痔序master sample 标准样本matching 匹配matching theorems 匹配定理material implication 实质蕴涵mathematical 数学的mathematical analysis 数学分析mathematical approximation 数学近似法mathematical constant 数学常数mathematical expectation 期望值mathematical formula 数学公式mathematical induction 数学归纳法mathematical logic 数理逻辑mathematical model 数学模型mathematical pendulum 数学摆mathematical physics 数学物理mathematical programming 数学规划mathematical random sample 数学随机样本mathematical statistics 数理统计mathematics 数学mathieu equation 马提厄方程mathieu function 马提厄函数mathieu group 马提厄群matricial rank 矩阵的秩matrix 矩阵matrix algebra 矩阵代数matrix analysis 矩阵分析matrix calculation 矩阵计算matrix element 矩阵元matrix equation 矩阵方程matrix factorization method 矩阵因子分解方法matrix form 矩阵形式matrix function 矩阵函数matrix game 矩阵对策matrix group 矩阵群matrix inversion 矩阵求逆matrix norm 矩阵范数matrix of coefficients 系数矩阵matrix of the transformation 变换矩阵matrix operator 矩阵算子matrix power series 矩阵幂级数matrix product 矩阵积matrix representation 阵表示matrix ring 矩阵环matrix semigroup 矩阵半群matrix series 矩阵级数matrix solution 矩阵解matrix transformation 矩阵变换matrix tree theorem 矩阵狮理matrix unit 矩阵单位matroid 矩阵胚maximal abelian extension 最大阿贝耳扩张maximal chain 连通链maximal element 极大元maximal equivalent orber 极大整环maximal hermitian operator 最大埃尔米特算子maximal ideal 极大理想maximal ideal space 极大理想空间maximal operator 最大算子maximal order 极大整环maximal principle 最大值原理maximal separable extension 极大可分扩张maximal strip 极大带maximal tree 最大树生成树maximality 极大性maximin 极大极小maximization 极大化maximizing sequence 极大化序列maximum 最大maximum condition 极大条件maximum deviation 最大偏差maximum ergodic theorem 极大遍历定理maximum likelihood equations 极大似然方程maximum likelihood estimating function 极大似然估计量maximum likelihood estimator 极大似然估计量maximum likelihood method 极大似然法maximum likelihood principle 极大似然法maximum matching 极大匹配maximum modulus principle 最大模原理maximum number 最大数maximum of a function 函数最大maximum or minimum condition 极大或极小条件maximum point 最大点maximum principle 最大值原理maximum problem 极大值问题maximum solution 最大解maximum term 极大项maximum value 绝对极大值maxwell boltzmann distribution law 麦克斯韦玻耳兹曼分布律maxwell's distributlon law 麦克斯事分布律maxwell's equations 麦克斯事方程meager set 贫集mean 平均mean continuity 中数连续性mean convergence 平均收敛mean convergence of p th order p阶平均收敛mean curvature 平均曲率mean curvature of surface 曲面的平均曲率mean density 平均密度mean derivative 平均微商mean deviation 平均偏差mean difference 平均差mean error 平均误差mean life 平均寿命mean number 平均数mean ordinate 平均纵坐标mean pay off 平均支付mean proportional 比例中项mean square 均方mean square contingency 均方列联mean square deviation 方差mean square of error 误差的均方mean square value 均方值mean term 内项mean type 平均型mean value 平均值mean value method 平均值法mean value theorem 平均值定理mean vector 均值向量measurability 可测性measurable 可测的measurable function 可测函数measurable mapping 可测映射measurable set 可测集measure 测度measure of dispersion 离差的度量measure of skewness 偏度measure preserving transformation 保测变换measure space 测度空间measure theory 测度论measure zero 零测度measurement 测量measuring error 测量误差measuring rule 量尺mechanics 力学mechanism 机构median 中位数median line 中线median point 中点mediant 中间数medium 媒体meet 交meet homomorphic image 保交同态像meet irreducible element 交不可约元素mega 兆member 项member of an equation 方程的端边memory 存储器memory capacity 存储容量memory cell 存储单元memory register 存储寄存器mental arithmetic 心算meridian 子午线meromorphic differential 亚纯微分meromorphic function 亚纯函数meromorphic function element 亚纯函数元素meromorphic mapping 亚纯映射meromorphism 亚纯映射meromorphy 亚纯mesh point 网格点mesh size 网格大小mesokurtic distribution 常峰态分布meta axiom of choice 亚选择公理metabelian group 亚交换群metacompact space 亚紧空间metaharmonic function 亚低函数metalanguage 元语言metalogic of predicates 谓词元逻辑metatheorem 元定理meter 米method of approximation 近似法method of artificial variables 人工变量法method of balayage 扫除法method of characteristic curves 特者法method of comparison 比较法method of conjugate gradients 共轭梯度法method of difference 差分法method of elimination 消元法method of estimation 估计法method of exhaustion 穷竭法method of false position 试位法method of finite elements 有限元法method of fractional steps 分步法method of integration of partial differential equations 偏微分方程的积分法method of iteration 迭代法method of partial fractions 部分分数法method of perturbation 扰动法method of potentials 起脚石法method of power series 幂级数法method of principal axes 轴法method of principal components 种量法method of regularization 正则化法method of residues 剩余法method of runge kutta type 朗格库塔型的方法method of steepest ascent 最速上升法method of steepest descent 最速下降法method of successive approximation 逐次近似法method of undetermined coefficients 比较法metre 米metric 度量metric coefficient 度量系数metric connection 度量联络metric form 度量形式metric normal form of quadratic form 二次形式的度量标准形式metric space 度量空间metric subspace 度量子空间metric tensor 基本张量metric topology 度量拓扑metrically convex subset 度量凸子集metrically dense 度量的稠密metrizability 可度量性metrizable 可度量化的metrizable group 可度量化群metrizable uniform space 可度量化一致空间metrization 度量化metrization theorem of urysohn 乌里申度量化定理microlocal analysis 微局部分析mid square method 平方取中法middle term 中项midperpendicular 中垂线midpoint 中点midrange 中列数millimeter 毫米million 百万minimal automaton 极小自动机minimal basis 极小基minimal disjunctive normal form 极小析取范式minimal element 极小元素minimal generating set 不可约生成集minimal graph 极小图形minimal manifold 极小簇minimal model 极小模型minimal polynomial 极小多项式minimal propositional calculus 极小命题演算minimal solution 极小解minimal submanifold 极小子廖minimal sufficient estimator 最小充分估计量minimal sufficient statistic 最小充分统计量minimal surface 极小曲面minimal type 极小类型minimal variety 极小簇minimality 极小性minimax 极小极大minimax decision function 极小极大判决函数minimax inequality 极小极大不等式minimax principle 极小极大原理minimax solution 极小极大解minimax strategy 极小极大策略minimax theorem 极小极大定理minimization 极小化minimizing method 极小化法minimizing sequence 极小化序列minimum 最小minimum condition 极小条件minimum covering 极小覆盖minimum density 极小密度minimum integral 极小解minimum modulus 最小模minimum modulus principle 最小模原理minimum number 最小数minimum of a function 函数的最小minimum point 极小点minimum principle 极小原理minimum problem 极小问题minimum solution 极小解minimum value 最小值minimum with a condition 条件极小minimum with a constraint 条件极小minkowski approximation theorem 闵可夫斯基逼近定理minkowski inequalities 闵可夫斯基不等式minkowskian addition 闵可夫斯基加法minkowskian linear combination 闵可夫斯基线性组合minkowskian space 闵可夫斯基空间minor 子式minor arc 劣弧minor axis 短轴minor cycle 小循环minor determinant 子行列式minor premise 小前提minor term 小词minorant 弱函数minorant function 弱函数minuend 被减数minus infinity 负无穷大minus mark 负号minute 分miscalculation 计算误差;计算误差missing plot technique 缺区补救技术missing value 缺少值mistake 错误mix 混合mixed area 混合面积mixed concomitant 混合相伴式mixed differential parameter 混合微分参数mixed distribution 混合分布mixed graph 混合图形mixed group 混合群mixed ideal 混合理想mixed number 带分数mixed partial derivative 混合偏导数mixed problem 混合问题mixed side condition 混合边条件mixed strategy 混合策略mixed tensor 混合张量mixed type 混合型mixed vertex 混合顶点mixing problem 混合问题mixing ratio 混合比mixture 混合mnemonic 助记的mnemonic device 助记装置mnemonics 助记mobility 可动性modal class 众数组modal proposition 模态命题modal system 模态系统modal value 最常见的值modality logics 模态逻辑mode 众数mode of vibration 振动模式model 模型model of moving means 移动平均模型model test 模型试验model theory 模型理论modern geometry 近世几何学modification 变形modified bessel function 修正贝塞耳函数modified newton method 修正牛顿法modular 模的modular category 模范畴modular character 模特征modular equation 模方程modular figure 模图modular form 模形式modular function 模函数modular group 模群modular lattice 模格modular matrix 模矩阵modular substitution 模置换modular variety 模簇module 模module of boundaries 边界模module of homomorphisms 同态模module of program 程序的模module of quotients 商模moduli space 参模空间modulo 模modulus 绝对值;模modulus of a congruence 同余模modulus of elasticity 弹性模数modulus of periodicity 周期的模modulus of rigidity 刚性模量modus tollens 否定式moment 矩moment generating function 矩量母函数moment matrix 矩量矩阵moment of distribution 分布矩moment of force 力矩moment of inertia 惯性矩moment of momentum 动量矩moments method 矩量法momentum 动量monad 单子monge cone 蒙日锥monic 首一的monic polynomial 首一多项式monitor 监督程序monocyclic system 单循环系monodromy 单值monodromy group 单值群monodromy theorem 单值定理monogenic 单演的monogenic function 单演函数monogenic module 循环模monogyre 一次对称轴monoid 单式半群monoidal representation 单项表示monoidal transformation 单项变换monomial 单项式monomial equation 单项方程monomial factor 单项因子monomial form 单项形式monomial group 单项群monomial representation 单项表示monomorphism 单一同态monotone approximation 单灯近monotone class 单掂monotone decreasing 单递减的monotone decreasing function 单递减函数monotone function 单弹数monotone increasing function 单递增函数monotone numbering 单掂号monotone sequence 单凋列monotonic function 单弹数monotonic system of sets 单掂monotonic transformation 单典换monotonically decreasing sequence 单递减序列monotonically increasing sequence 单递增序列monotonicity 单翟monotony interval 单跌间monte carlo method 蒙特卡罗法monte carlo simulation 蒙特卡罗模拟montel space 空间moore smith convergence 穆尔史密斯收敛morphism 射morse inequalities 莫尔斯不等式morse theory 莫尔斯理论mortality rate 死亡率mortality table 死亡率表most powerful test 最大功效检定most probable duration 最可能持续时间most probable value 最常见的值most stringent test 最紧迫检验motion 运动motion equation 运动方程movable singularity 可移奇点move 步着movement 运动moving arm 移动臂moving average 移动平均moving average method 移动平均法moving frame 活动标架moving trihedral 怜三面形moving trihedron 怜三面形mrkoff process 马尔可夫过程mu continuity 连续性mu continuous function 连续函数mu integrable 可积分mu measurable 可测的mu singular 奇异multi dimensional integral 多维积分multi modal distribution 多重模态分布multi person game 多人对策multi phase sampling 多相抽样法multi purpose computer 万能计算机multi stage game 多阶段对策multi stage sampling 多级抽样法multi valued mapping 多值映射multi valuedness 多值性multiaddress 多地址multicollinearity 多重共线性multidimensional space 多维空间multigraph 多重图multigroup 超群multilinear form 多重线性形式multilinear function 多重线性函数multinomial 多项式multinomial coefficient 多项式系数multinomial distribution 多项分布multinomial expansion 多项展开式multinomial series 多项级数multinomial theorem 多项式定理multiple 倍数multiple arc 多重弧multiple correlation coefficient 多重相关系数multiple decision problem 多重判定问题multiple edge 多重棱multiple fourier series 多重傅里叶级数multiple hypergraph 多重超图multiple markov process 多重马尔可夫过程multiple point 多重点multiple regression 多重回归multiple root 多重根multiple sequence 多重序列multiple series 多重级数multiple stratification 多层化multiple tangent 多重切线multiple test 多重检验multiple valued 多值的multiple valued function 多值函数multiplicand 被乘数multiplicand register 被乘数寄存器multiplication 乘multiplication operator 乘法算子multiplication ring 乘环multiplication sign 乘号multiplication table 九九表multiplication theorem 乘法定理multiplicative 乘法的multiplicative axiom 乘法公理multiplicative character 乘法特贞multiplicative group 乘法群multiplicative lattice 乘格multiplicative process 繁殖过程multiplicatively closed set 积闭集multiplicator 乘数multiplicity 重数multiplicity of a root 根的重数multiplier 乘数;乘群multiplier register 乘数寄存器multiply 乘multiply connected domain 多连通区域multiply connected region 多连通区域multiply connected sequence 多连通序列multiply connected space 多连通空间multiply monotone sequence 多重单凋列multiply periodic function 多重周期函数multiply transitive group 多重可迁群multipolar 多极的multiprogram processing 多级程序处理multistage programming 多阶段规划multistep method 多步方法multitude 多数multivalent 多叶的multivalent function 多叶函数multivalued decision 多值判断multivariate analysis 多元分析multivariate analysis of variance 多元方差分析multivariate distribution 多元分布multivariate distribution function 多元分布函数multivariate statistics 多元统计multivector 多重矢量mutual information 交互信息mutually disjoint 互不相交的mutually disjoint events 互不相交事件mutually disjoint subsets 互不相交子集mutually independent events 互相独立事件myria 万myriad 无数的myriads 无数。
MATHEMATICS(PUREANDAPPLIED):(纯粹数学和应用)

Professor & Head of DepartmentNT Bishop, MA(Cambridge), PhD(Southampton), FRASSenior LecturersJ Larena, MSc(Paris), PhD(Paris)D Pollney, PhD(Southampton)CC Remsing, MSc(Timisoara), PhD(Rhodes)Vacant LecturersEOD Andriantiana, PhD(Stellenbosch)V Naicker, MSc(KwaZulu-Natal)AL Pinchuck, MSc(Rhodes), PhD(Wits)Lecturer, Academic Development M Lubczonok, Masters(Jagiellonian)Mathematics (MA T) is a six-semester subject and Applied Mathematics (MAP) is a four-semester subject. These subjects may be taken as major subjects for the degrees of BSc, BA, BJourn, BCom, BBusSci, BEcon and BSocSc, and for the diploma HDE(SEC).To major in Mathematics, a candidate is required to obtain credit in the following courses: MAT1C; MAM2; MAT3. See Rule S.23.To major in Applied Mathematics, a candidate is required to obtain credit in the following courses: MAT1C, MAM2; MAP3. See Rule S.23.The attention of students who hope to pursue careers in the field of Bioinformatics is drawn to the recommended curriculum that leads to postgraduate study in this area, in which Mathematics is a recommended co-major with Biochemistry, and for which two years of Computer Science and either Mathematics or Mathematical Statistics are prerequisites. Details of this curriculum can be foundin the entry for the Department of Biochemistry, Microbiology and Biotechnology.See the Departmental Web Page http://www.ru.ac.za/departments/mathematics/ for further details, particularly on the content of courses.First-year level courses in MathematicsMathematics 1 (MAT1C) is given as a year-long semesterized two-credit course. Credit in MAT1C must be obtained by students who wish to major in certain subjects (such as Applied Mathematics, MATHEMATICS (PURE AND APPLIED)Physics and Mathematical Statistics) and by students registered for the BBusSci degree.Introductory Mathematics (MAT1S) is recommended for Pharmacy students and for Science students who do not need MAT1C or MAT1C1.Supplementary examinations may be recommended for any of these courses, provided that a candidate achieves a minimum standard specified by the Department.Mathematics 1L (MA T1L) is a full year course for students who do not qualify for entry into any of the first courses mentioned above. This is particularly suitable for students in the Social Sciences and Biological Sciences who need to become numerate or achieve a level of mathematical literacy. A successful pass in this course will give admission to MA T1C.First yearMAT1CThere are two first-year courses in Mathematics for candidates planning to major in Mathematics or Applied Mathematics. MAT1C1 is held in thefirst semester and MAT1C2 in the second semester. Credit may be obtained in each course separately and, in addition, an aggregate mark of at least 50%will be deemed to be equivalent to a two-creditcourse MAT1C, provided that a candidate obtains the required sub-minimum (40%) in each component. Supplementary examinations may be recommended in either course, provided that a candidate achieves a minimum standard specified by the department. Candidates obtaining less than 40% for MAT1C1 are not permitted to continue with MAT1C2.MAT1C1 (First semester course): Basic concepts (number systems, functions), calculus (limits,continuity, differentiation, optimisation, curvesketching, introduction to integration), propositional calculus, mathematical induction, permutations, combinations, binomial theorem, vectors, lines andplanes, matrices and systems of linear equations.MAT1C2 (Second semester course): Calculus (integration, applications of integration, improper integrals), complex numbers, differential equations, partial differentiation, sequences and series.MAT1S (Semester course: Introductory Mathematics) (about 65 lectures)Estimation, ratios, scales (log scales), change of units, measurements; Vectors, systems of equations, matrices, in 2-dimensions; Functions: Review of coordinate geometry, absolute values (including graphs); Inequalities; Power functions, trig functions, exponential functions, the number e (including graphs); Inverse functions: roots, logs, ln (including graphs); Graphs and working with graphs; Interpretation of graphs, modeling; Descriptive statistics (mean, standard deviation, variance) with examples including normally distributed data; Introduction to differentiation and basic derivatives; Differentiation techniques (product, quotient and chain rules); Introduction to integration and basic integrals; Modeling, translation of real-world problems into mathematics.MAT 1L: Mathematics Literacy This course helps students develop appropriatemathematical tools necessary to represent and interpret information quantitatively. It also develops skills and meaningful ways of thinking, reasoning and arguing with quantitative ideas in order to solve problems in any given context.Arithmetic: Units of scientific measurement, scales, dimensions; Error and uncertainty in measure values.Fractions and percentages - usages in basic science and commerce; use of calculators and spreadsheets. Algebra: Polynomial, exponential, logarithmic and trigonometric functions and their graphs; modelling with functions; fitting curves to data; setting up and solving equations. Sequences and series, presentation of statistical data.Differential Calculus: Limits and continuity; Rules of differentiation; Applications of Calculus in curvesketching and optimisation.Second Year Mathematics 2 comprises two semesterized courses,MAM201 and MAM202, each comprising of 65 lectures. Credit may be obtained in each course seperately. An aggregate mark of 50% will grant the two-credit course MAM2, provided a sub-minimumof 40% is achieved in both semesters. Each semester consists of a primary and secondary stream which are run concurrently at 3 and 2 lectures per week, respectively. Additionally, a problem-based course in Mathematical Programming contributes to the class record and runs throughout the academic year.MAM201 (First semester):Advanced Calculus (39 lectures): Partial differentiation: directional derivatives and the gradient vector; maxima and minima of surfaces; Lagrange multipliers. Multiple integrals: surface and volume integrals in general coordinate systems. Vector calculus: vector fields, line integrals, fundamental theorem of line integrals, Green’s theorem, curl and divergence, parametric curves and surfaces.Ordinary Differential Equations (20 lectures): First order ordinary differential equations, linear differential equations of second order, Laplace transforms, systems of equations, series solutions, Green’s functions.Mathematical Programming 1 (6 lectures): Introduction to the MATLAB language, basic syntax, tools, programming principles. Applicationstaken from MAM2 modules. Course runs over twosemesters.MAM202 (Second semester):Linear Algebra (39 lectures): Linear spaces, inner products, norms. Vector spaces, spans, linear independence, basis and dimension. Linear transformations, change of basis, eigenvalues, diagonalization and its applications.Groups and Geometry (20 lectures): Number theory and counting. Groups, permutation groups, homomorphisms, symmetry groups in 2 and 3 dimensions. The Euclidean plane, transformations and isometries. Complex numbers, roots of unity and introduction to the geometry of the complex plane.Mathematical Programming 2 (6 lectures): Problem-based continuation of Semester 1.Third-year level courses inMathematics and Applied Mathematics Mathematics and Applied Mathematics are offered at the third year level. Each consists of four modules as listed below. Code TopicSemester Subject AM3.1 Numerical analysis 1 Applied MathematicsAM3.2 Dynamical systems 2 Applied Mathematics AM3.4 Partial differentialequations 1 Applied Mathematics AM3.5 Advanced differentialequations 2 Applied MathematicsM3.1 Algebra 2 MathematicsM3.2 Complex analysis 1 MathematicsM3.3 Real analysis 1 MathematicsM3.4 Differential geometry 2 Mathematics Students who obtain at least 40% in all of the above modules will be granted credit for both MAT3 and MAP3, provided that the average of the Applied Mathematics modules is at least 50% AND the average of the Mathematics modules is at least 50%. Students who obtain at least 40% for any FOUR of the above modules and with an average mark over the four modules of at least 50%, will be granted credit in either MAT3 or MAP3. If three or four of the modules are from Applied Mathematics then the credit will be in MAP3, otherwise it will be in MAT3.Module credits may be carried forward from year to year.Changes to the modules offered may be made from time-to-time depending on the interests of the academic staff.Credit for MAM 2 is required before admission to the third year courses.M3.1 (about 39 lectures) AlgebraAlgebra is one of the main areas of mathematics with a rich history. Algebraic structures pervade all modern mathematics. This course introduces students to the algebraic structure of groups, rings and fields. Algebra is a required course for any further study in mathematics.Syllabus: Sets, equivalence relations, groups, rings, fields, integral domains, homorphisms, isomorphisms, and their elementary properties.M3.2 (about 39 lectures) Complex Analysis Building on the first year introduction to complex numbers, this course provides a rigorous introduction to the theory of functions of a complex variable. It introduces and examines complex-valued functions of a complex variable, such as notions of elementary functions, their limits, derivatives and integrals. Syllabus: Revision of complex numbers, Cauchy- Riemann equations, analytic and harmonic functions, elementary functions and their properties, branches of logarithmic functions, complex differentiation, integration in the complex plane, Cauchy’s Theorem and integral formula, Taylor and Laurent series, Residue theory and applications. Fourier Integrals.M3.3 (about 39 lectures) Real AnalysisReal Analysis is the field of mathematics that studies properties of real numbers and functions on them. The course places great emphasis on careful reasoning and proof. This course is an essential basis for any further study in mathematics.Syllabus: Topology of the real line, continuity and uniform continuity, Heine-Borel, Bolzano-Weierstrass, uniform convergence, introduction to metric spaces.M3.4 (about 39 lectures) Differential Geometry Roughly speaking, differential geometry is concerned with understanding shapes and their properties in terms of calculus. This elementary course on differential geometry provides a perfect transition to higher mathematics and its applications. It is a subject which allows students to see mathematics for what it is - a unified whole mixing together geometry, calculus, linear algebra, differential equations, complex variables, calculus of variations and topology.Syllabus: Curves (in the plane and in the space), curvature, global properties of curves, surfaces, the first fundamental form, isometries, the second fundamental form, the normal and principal curvatures, the Gaussian and mean curvatures, the Gauss map, geodesics.AM3.1 (about 39 lectures) Numerical Analysis Many mathematical problems cannot be solved exactly and require numerical techniques. These techniques usually consist of an algorithm which performs a numerical calculation iteratively until certain tolerances are met. These algorithms can be expressed as a program which is executed by a computer. The collection of such techniques is called “numerical analysis”.Syllabus: Systems of non-linear equations, polynomial interpolation, cubic splines, numerical linear algebra, numerical computation of eigenvalues, numerical differentiation and integration, numerical solution of ordinary and partial differential equations, finite differences,, approximation theory, discrete Fourier transform.AM3.2 (about 39 lectures) Dynamical Systems This module is about the dynamical aspects of ordinary differential equations and the relations between dynamical systems and certain fields of applied mathematics (like control theory and the Lagrangian and Hamiltonian formalisms of classical mechanics). The emphasis is on the mathematical aspects of various constructions and structures rather than on the specific physical/mechanical models. Syllabus Linear systems; Linear control systems; Nonlinear systems (local theory); Nonlinear control systems; Nonlinear systems (global theory); Applications : elements of optimal control and/or geometric mechanics.AM3.4 (about 39 lectures) Partial Differential EquationsThis course deals with the basic theory of partial differential equations (elliptic, parabolic and hyperbolic) and dynamical systems. It presents both the qualitative properties of solutions of partial differential equations and methods of solution. Syllabus: First-order partial equations, classification of second-order equations, derivation of the classical equations of mathematical physics (wave equation, Laplace equation, and heat equation), method of characteristics, construction and behaviour of solutions, maximum principles, energy integrals. Fourier and Laplace transforms, introduction to dynamical systems.AM3.5 (about 39 lectures)Advanced differential equationsThis course is an introduction to the study of nonlinearity and chaos. Many natural phenomena can be modeled as nonlinear ordinary differential equations, the majority of which are impossible to solve analytically. Examples of nonlinear behaviour are drawn from across the sciences including physics, biology and engineering.Syllabus:Integrability theory and qualitative techniques for deducing underlying behaviour such as phase plane analysis, linearisations and pertubations. The study of flows, bifurcations, the Poincare-Bendixson theorem, and the Lorenz equations.Mathematics and Applied Mathematics Honours Each of the two courses consists of either eight topics and one project or six topics and two projects.A Mathematics Honours course usually requires the candidate to have majored in Mathematics, whilst Applied Mathematics Honours usually requires the candidate to have majored in Applied Mathematics. The topics are selected from the following general areas covering a wide spectrum of contemporary Mathematics and Applied Mathematics: Algebra; Combinatorics; Complex Analysis; Cosmology; Functional Analysis; General Relativity; Geometric Control Theory; Geometry; Logic and Set Theory; Measure Theory; Number Theory; Numerical Modelling; Topology.Two or three topics from those offered at the third-year level in either Mathematics or Applied Mathematics may also be taken in the case of a student who has not done such topics before. With the approval of the Heads of Department concerned, the course may also contain topics from Education, and from those offered by other departments in the Science Faculty such as Physics, Computer Science, and Statistics. On the other hand, the topics above may also be considered by such Departments as possible components of their postgraduate courses.Master’s and Doctoral degrees in Mathematics or Applied MathematicsSuitably qualified students are encouraged to proceed to these degrees under the direction of the staff of the Department. Requirements for these degrees are given in the General Rules.A Master’s degree in either Mathematics or Applied Mathematics may be taken by thesis only, or by a combination of course work and a thesis. Normally four examination papers and/or essays are required apart from the thesis. The whole course of study must be approved by the Head of Department.。
车辆横向稳定性自适应预测控制
2020年第9期【摘要】为解决利用车辆机理模型设计控制器时的自适应问题,针对非线性车辆动力学系统,提出一种基于数据驱动的横向稳定性控制策略。
利用递推子空间模型辨识算法设计预测器,根据预测器的形式并结合车辆横向稳定性控制提出一种具有模型自适应特性的预测控制器。
利用MATLAB/Simulink 建立7自由度整车动力学仿真模型,结合国际标准ISO/DIS 7401:2000以及ISO 3888:1999进行实车道路试验,并对仿真模型进行了数值验证,基于整车动力学模型,对自适应预测控制器的控制效果进行了数值仿真验证,证明了算法的有效性和鲁棒性。
主题词:车辆稳定性数据驱动子空间辨识预测控制标准道路试验数值仿真中图分类号:U461.1文献标识码:A DOI:10.19620/ki.1000-3703.20190297Adaptive and Predictive Control for Vehicle Lateral StabilityYang Weimiao,Zhang Jianwu,Feng Pengpeng(Shanghai Jiao Tong University,Shanghai 200240)【Abstract 】Targeted for nonlinear vehicle dynamic system,a data-driven stability control strategy is proposed,which aims to solve the problem of lacking self-adaptability of using vehicle mechanism model to design controller.Firstly,a predictor is designed by recursive subspace model identification algorithm,based on which a model-adaptive predictivecontroller for vehicle lateral stability control is proposed.Then,a 7-DOF vehicle dynamic simulation model is established using MATLAB/Simulink,and vehicle road test is performed according to ISO/DIS 7401:2000and ISO 3888:1999,mathematic verification is made to this simulation model.Based on the vehicle dynamic model,control effect of this self-adaptive and predictive controller is simulated and verified,the effectiveness and robustness of the algorithm are validated.Key words:Vehicle stability,Data-driven,Subspace model identification,Predictive control,Standard road test,Numerical simulation杨维妙张建武冯鹏鹏(上海交通大学,上海200240)*基金项目:国家自然科学基金项目(51175333)。
美国数学竞赛AMC8必须掌握的常用单词
美国数学竞赛AMC8必须掌握的常⽤单词美国数学竞赛AMC8必须掌握的常⽤单词(按字母顺序整理)⾮正态分布abnormal distribution ⾓angle平均数average 加plus(prep.), add(v.), addition(n.)振幅amplitude 反正弦arc sine 反余弦arc cosine 反正切arc tangent 反余切arc cotangent 反正割arc secant 反余割arc cosecant 被加数augend, summand 加数addend 轴axis 弧arc ⾯积area 算术arithmetic 公理axiom 代数algebra 锐⾓acute angle 锐⾓三⾓形acute triangle B ⼆进制binary system 折线统计图broken line graph 底base条形统计图bar graph重⼼barycentre(BrE, barycenter(AmE)C 全等congruent 曲线统计图curve diagram 进位carry 计算calculation 系数coefficient 三次⽅程cubic equation常量constant 微积分calculus 复数complex number 坐标系coordinates 组合combination 外切圆circumcircle 余割cosecant 余切cotangent 余弦cosine 圆周circumference 圆柱cylinder 圆锥cone 圆circle ⽴⽅体cube圆⼼centre(BrE), center(AmE)D ⼩数点decimal point ⼩数decimal ⾓度degree 除divided by (prep.), divide(v.), division(n.)被除数dividend 除数divisor 数字digit 分母denominator ⼗进制decimal system 微分differential 导数derivative 定积分definite integral ⾏列式determinant 分布distribution ⼗⾯体decahedron ⼗⼆⾯体dodecahedron ⼗⼆边形dodecagon ⼗边形decagon 直径diameter E 等于equals, is equal to, is equivalent to 等式,⽅程式equation 等边三⾓形equilateral trian gle 外⼼excentre(BrE), excenter(AmE)旁⼼escentre(BrE), escenter (AmE)正多边形equilateral polygon 九⾯体enneahedron 九边形enneagon 椭圆ellipse F 分数fraction公式formula, formulae(pl.)阶乘factorial 棱台frustum of a prism 圆台frustum of a cone G ⼏何geometry 图表graph H假设hypothesis, hypotheses(pl.)⼗⼀⾯体hendecahedron 六边形hexagon 七⾯体heptahedron 半球hemisphere 六⾯体hexahedron ⼗⼀边形hendecagon 七边形heptagon ⼗六进制hexadecimal system 柱形统计图histogram ⾼height 斜边hypotenuse 双曲线hyperbola I内⼼incentre(BrE), incenter(AmE)⼆⼗⾯体icosahedron图象imag ⽆穷⼤infinite(a.)infinity(n.)⽆穷⼩infinitesimal 积分integrale 等腰梯形isosceles trapezoid 不定积分indefinite integral 不等式inequation 整数integer ⼩于is lesser than ⼤于is greater than ⼤于等于is equal or greater than线line ⼩于等于is equal or lesser than ⽆效数字insignificant digit 相交intersect ⽆理数irrational number 虚数imaginary number 等腰三⾓形isosceles triangle 内切圆inscribed circle 极限limit 直⾓边leg 长length 轨迹locus, loca(pl.)M数学mathematics, maths(BrE), math(AmE)被减数minuend 被乘数multiplicand, 乘数multiplicator 单项式monomial 单调性monotonicity矩阵matrix N 正态分布normal distribution 数number ⾃然数natural number 分⼦numerator 负negative 零null, zero, nought, nil O运算符operator 运算operation 钝⾓obtuse angle 钝⾓三⾓形obtuse triangle 垂⼼orthocentre(BrE), orthocenter(AmE)原点origin ⼋⾯体octahedron⼋边形octagon P抛物线parabola 五⾯体pentahedron 平⾏六⾯体parallelepiped 相位phase周期period证明prove命题proposition 积product 正positive 多项式polynomial, multinomial 奇偶性parity 周期性periodicity点point ⾯plane 平⾏parallel 周⾓perigon平⾏四边形parallelogram 勾股定理Pythagorean theorem扇形统计图pie diagram 概率,或然率probability排列permutation ⽐例propotion 百分⽐percent百分点percentage 百分位数percentile 多⾯体polyhedron 圆周率p i 棱锥pyramid 棱柱prism 周长perimeter五边形pentagon 多边形polygon Q商quotient ⼆次⽅程quadratic equation 四次⽅程quartic equation 四边形quadrilateral R直⾓梯形right trapezoid 标准差root-mean-square deviation, standard deviation 差remainder⽐ratio 四舍五⼊round 下舍⼊round down 上舍⼊round up 值域range 有理数rational number 实数real number 直⾓right angle 射线radial 弧度radian 直⾓三⾓形right triangle 矩形rectangle 旋转rotation 菱形rhomb, rhombus, rhombi(pl.),diamond 环ring 半径radius S正⽅形square 有效数字significant digit ⼀次⽅程simple equation 体solid 线段segment 平⾓straight angle 边side不等边三⾓形scalene triangle 空间space 球sphere 正弦sine 统计statistics 和sum 减minus(prep.), subtract(v.), subtraction (n.)减数subtrahend 数列,级数series 正割secant表⾯积surface area 相似similar半圆semicircle 扇形sector T梯形trapezoid 截尾truncation 定理theorem乘times(prep.), multiply(v.), multiplication(n.)faciend三⾓形triangle 正切tangent 三⾓trigonometry四⾯体tetrahedron U未知数unknown, x-factor, y-factor, z-factor 底⾯undersurface 变量variable⽅差variance 体积volume W 权weight, significance宽width 加权平均数weighted average X 坐标轴x-axis, y-axis, z-axis 横坐标x-coordinate 纵坐标y-coordinate数学mathematics, maths(BrE), math(AmE)被除数dividend除数divisor 商quotient 等于equals, is equal to, is equivalent to ⼤于is greater than ⼩于is lesser than ⼤于等于is equal or greater than ⼩于等于is equal or lesser than 运算符operator数字digit 数number ⾃然数natural number 公理axiom定理theorem 计算calculation 运算operation 证明prove假设hypothesis, hypotheses(pl.)命题proposition 算术arithmetic 加plus(prep.), add(v.), addition(n.)被加数augend, summand 加数addend 和sum 减minus(prep.), subtract(v.), subtraction(n.)被减数minuend 减数subtrahend 差remainder 乘times(prep.), multiply(v.), multiplication(n.)被乘数multiplicand, faciend 乘数multiplicator 积product除divided by(prep.), divide(v.), division(n.)整数integer⼩数decimal ⼩数点decimal point 分数fraction分⼦numerator 分母denominator ⽐ratio正positive 负negative 零null, zero, nought, nil⼗进制decimal system ⼆进制binary system ⼗六进制hexadecimal system 权weight, significance进位carry 截尾truncation 四舍五⼊round下舍⼊round down 上舍⼊round up有效数字significant digit ⽆效数字insignificant digit代数algebra 公式formula, formulae(pl.)单项式monomial多项式polynomial, multinomial 系数coefficient未知数unknown, x-factor, y-factor, z-factor 等式,⽅程式equation⼀次⽅程simple equation ⼆次⽅程quadratic equation 三次⽅程cubic equation 四次⽅程quartic equation 不等式inequation阶乘factorial 对数logarithm 指数,幂exponent 乘⽅power⼆次⽅,平⽅square 三次⽅,⽴⽅cube 四次⽅the power of four, the fourth power n次⽅the power of n, the nth power开⽅evolution, extraction ⼆次⽅根,平⽅根square root三次⽅根,⽴⽅根cube root 四次⽅根the root of four, the fourth root n次⽅根the root of n, the nth root 集合aggregate元素element 空集void ⼦集subset 交集intersection 并集union 补集complement 映射mapping 函数function 定义域domain, field of definition 值域range 常量constant变量variable 单调性monotonicity 奇偶性parity周期性periodicity 图象image 数列,级数series 微积分calculus微分differential 导数derivative 极限limit⽆穷⼤infinite(a.)infinity(n.)⽆穷⼩infinitesimal积分integral 定积分definite integral不定积分indefinite integral 有理数rational number⽆理数irrational number 实数real number虚数imaginary number 复数complex number 矩阵matrix⾏列式determinant ⼏何geometry 点point 线line ⾯plane 体solid 线段segment 射线radial平⾏parallel 相交intersect ⾓angle ⾓度degree 弧度radian锐⾓acute angle 直⾓right angle 钝⾓obtuse angle 平⾓straight angle 周⾓perigon 底base 边side ⾼height 三⾓形triangle锐⾓三⾓形acute triangle 直⾓三⾓形right triangle 直⾓边leg斜边hypotenuse 勾股定理Pythagorean theorem 钝⾓三⾓形obtuse triangle 不等边三⾓形scalene triangle 等腰三⾓形isosceles triangle 等边三⾓形equilateral triangle 四边形quadrilateral平⾏四边形parallelogram 矩形rectangle长length 宽width 菱形rhomb, rhombus, rhombi(pl.), diamond正⽅形square 梯形trapezoid 直⾓梯形right trapezoid等腰梯形isosceles trapezoid 五边形pentagon 六边形hexagon 七边形heptagon ⼋边形octagon 九边形enneagon⼗边形decagon ⼗⼀边形hendecagon ⼗⼆边形dodecagon 多边形polygon 正多边形equilateral polygon 圆circle圆⼼centre(BrE), center(AmE)半径radius 直径diameter 圆周率pi 弧arc半圆semicircle 扇形sector 环ring 椭圆ellipse 圆周circumference 周长perimeter ⾯积area 轨迹locus, loca(pl.)相似similar 全等congruent 四⾯体tetrahedron 五⾯体pentahedron六⾯体hexahedron 平⾏六⾯体parallelepiped ⽴⽅体cube 七⾯体heptahedron ⼋⾯体octahedron 九⾯体enneahedron ⼗⾯体decahedron⼗⼀⾯体hendecahedron ⼗⼆⾯体dodecahedron ⼆⼗⾯体icosahedron多⾯体polyhedron 棱锥pyramid 棱柱prism 棱台frustum of a prism旋转rotation 轴axis 圆锥cone 圆柱cylinder 圆台frustum of a cone 球sphere 半球hemisphere 底⾯undersurface 表⾯积surface area 体积volume 空间space 坐标系coordinates 坐标轴x-axis,y-axis, z-axis 横坐标x-coordinate 纵坐标y-coordinate原点origin 双曲线hyperbola 抛物线parabola 三⾓trigonometry 正弦sine 余弦cosine 正切tangent 余切cotangent 正割secant 余割cosecant 反正弦arc sine 反余弦arc cosine 反正切arc tangent 反余切arc cotangent 反正割arc secant 反余割arc cosecant 相位phase 周期period 振幅amplitude 内⼼incentre(BrE), incenter (AmE)外⼼excentre(BrE), excenter(AmE)旁⼼escentre(BrE), escenter (AmE)垂⼼orthocentre(BrE),orthocenter(AmE)重⼼barycentre (BrE), barycenter(AmE)内切圆inscribed circle 外切圆circumcircle 统计statistics 平均数average 加权平均数weighted average⽅差variance 标准差root-mean-square deviation, standard deviation ⽐例propotion 百分⽐percent 百分点percentage 百分位数percentile 排列permutation 组合combination 概率,或然率probability 分布distribution 正态分布normal distribution⾮正态分布abnormal distribution 图表graph 条形统计图bar graph 柱形统计图histogram 折线统计图broken line graph 曲线统计图curve diagram。
mathematic求解薛定谔方程程序
5.编程求解薛定谔方程:BeginPackage["QuantumWell`"]Clear[PsiSym,PsiASym,Spectrum]PsiSym::usage="PsiSym[x_,k,a]determines the symmetric eigenfunctionfor a potential well of depth-V0.The input parameter k fixes the energy and2a the width of the well.Psisym is useful for a numerical representationof eigenfunctions."PsiASym::usage="PsiASym[x_,k_,a_]determines the antisymmetric eigenfunction for a potential well of depth-V0.The input parameter k fixes the energy and2a the width of the well. PsiASym is useful for a numerical representation of eigenfunctions."Spectrum::usage="Spectrum[V0_,a_]calculates the negative eigenvalues in a potential well.V0is the potential depth and2a the width of the well.The eigenvalues are returend as a list and are available in the variables lsymand lasym as replacement rules.The corresponding plots of eigenfunctions are stored in the variables Plsym and Plasym.The determining equation forthe eieenvalues is plotted."(*-一define global variables-一*)Plsym::usage="Variables containing the symmetric plots of the eigenfunctions."Plasym::usage="Variables containing the antisymmetric plots of the eigenfunctions."lsym::usage="List of symmetric eigenvalues."lasym::usage="List of antisymmetric eigenvalues."k::usage="Eigenvalue."Begin["`Private`"](*一symmetric eigenfunctions一*)Psisym[x,k,a]:=Module[{kapa,Al]},Kapa=k Tan[k a];(*一normalization constant一*)A1=1/Sqrt[a Exp[-2a kapa](1+1/(kapa a)+kapa/(k^2a)+Kapa^2/k^2)];(*一define the three domains of solution一一*)Which[-Infinity<x&&x<-a,A1Exp[kapa x],-a<=x&&x<=a,A1Exp[-kapa a]cos[kx]/Cos[k a],a<x&&x(Infinity,A1Exp[-kapa x]]](*---antisymmetric eigenfunctions---*)Pa iASym[x_,k_,a_]:=Module[{kapa,Al},Kapa=一k Cut[k a];(*一normalization constant一*)A1=1/Sqrt[a Exp[-2a kapa](1+1/(kapa a)+kapa/(k^2a)+Kapa^2/k^2)];(*一define the three domains of solution一*)Which[-Infinity<x&&x<-a,-Al Exp[kapa x],-a<=x&&x‘=a,A1Exp[-kapa a]Sin[k x]/Sin[k a],a<x&&x<Infinity,A1Exp[-kapa x]]](*一determination of the eigenvalues;plot of the eigenfunction:一*)Spectrum[V0_,a];=Module[{hbar=1,m=1,ymax,C2,rhs,lhssym,lhsasym,equatsym,equatasym,kmax,nsym,nasym, resultsym,resultasym},(*一define constants and the eigenvalue equation一*)C2=2m V0a^2/(hbar^2);Rhs=Tan[k a];Lhssym=Sqrt[C2-(k a)^2]/(k a);Lhsasym=-k a/Sqrt[C2-(k a)^2];equatsym=Sqrt[C2-(k a)^2]/(k a)一Tan[k a];equatasym=-k a/Sqrt[C2-(k a)^2]-Tan[k a];(*一location of the singularity in k一*)Kmax=Sqrt[C2/a^2];(*一number of symmetric eigenvalues一*)Nsym=Floor[N[kmax/(Pi/a)]]十1;(*一number of antisymmetric eigenvalues一*)nasym=Floor[N[(kmax一Pi/(2a))/(Pi/a)]]+1;(*-一initialize the lists for the eigenvalues一一*)Lsym={};lasym={};(*一calculate the symetric eigenvalue:一*)Do[resultsym=Chop[FindRoot[equatsym==0,{k,Pi/(2a)+0.1+(Pi/a)(i-1)}]];AppendTo[lsym,resultsym],{i,1,nsym}];(*一Chop[]replaces small numbers(<10^<(-10))by0一*)(*-一calculate he antisymmetric eigenvalues一*)Do[resultasym=Chop[FindRoot[equatasym=0,[k,Pi/(2a)+0.l+(Pi/a)(i-1)}]];AppendTo[lasym,resultasym],{i,1,nasym)];(*一plot the eigenvalue equation一*)Ymax=lhssym 1.5/.lsym[[1]];Off[Plot::plnr];Plot[{rhs,lhssym,lhsasym},{k,0.01,3kmax/2},P1otRange->{-ymax,ymax},Prolog->Thickness[0.001],PlotStyle->(RGBColor[1,0,0],Da shing[{}],Dashing[{1/60}]},AxesLabel->{"k",""}];On[Plot::plnr];(*一plot the symmetric eigenfunctions一*)Do[k1=k/.lsym[[i]];Plsym[i]=Plot[PsiSym[z,kl,a],{x,-2a,2a},AxesLabel->{"x","Psi_s"},P1otRange->All,Prolog->Thickness[0.001],P1otStyle->{Dashing[{1/(i20)}]}],(i,1,nsym)];(*一plot the antisymmetric eigenfunctions一*)Do[k1=k/.lasym[[i]];Plasym[i]=Plot[PsiASym[x,kl,a],[x,-2a,2a},AxesLabel->{"x","Psia"),P1otRange->All,Prolog->Thickness[0.001],Plotstyle->{Dashing[{1/(i 20)1]}],{i,1,nasym)];(*一print the eigenvalues一*)Print[""]:Print["---eigenvalues---’];Print["”];Do[k1=k/.lsym[[i]];If[i<=nasym,k2=k/.lasym[[i]],,k2="---"];Print["sym eigenvalue k",i,"=",k1,"asym eigenvalue k",i,"=",k2],{i,1,nsym}]]End[]EndPackage[]利用上面程序可以求解不同势阱高度和宽度的一维势阱薛定谔方程波函数和能量谱的程序包。
汽车专业英语试题及答案
汽车专业英语试题及答案一、选择题(每题2分,共20分)1. Which of the following is NOT a component of an internal combustion engine?A. CylinderB. PistonC. Spark plugD. AlternatorAnswer: D2. What is the primary function of a carburetor in a vehicle?A. To cool the engineB. To mix fuel and airC. To ignite the fuelD. To lubricate the engineAnswer: B3. What does the acronym ABS stand for in automotive technology?A. Anti-lock Braking SystemB. Automatic Brake SystemC. Advanced Braking SystemD. Auxiliary Braking SystemAnswer: A4. In a four-stroke engine, what is the term for the process where the piston moves down the cylinder to draw in air and fuel?A. Compression strokeB. Exhaust strokeC. Intake strokeD. Power strokeAnswer: C5. What is the purpose of a transmission in a vehicle?A. To generate electricityB. To control the speed and torqueC. To cool the engineD. To increase fuel efficiencyAnswer: B6. What is the term used to describe the ratio of the number of rotations of the drive wheels to the number of rotations of the engine?A. Gear ratioB. Speed ratioC. Drive ratioD. Torque ratioAnswer: B7. Which of the following is NOT a type of suspension system used in vehicles?A. Independent suspensionB. Dependent suspensionC. Semi-independent suspensionD. Non-suspensionAnswer: D8. What does the acronym HVAC stand for in a vehicle's climate control system?A. Heating, Ventilation, and CoolingB. High Voltage, Air ConditioningC. Hot Water, Ventilation, and CoolingD. Heavy Vehicle, Air ConditioningAnswer: A9. What is the main purpose of a catalytic converter in a vehicle's exhaust system?A. To reduce noiseB. To increase fuel efficiencyC. To reduce harmful emissionsD. To improve engine performanceAnswer: C10. What is the term for the system that helps a vehicle to stop by converting kinetic energy into thermal energy?A. Power steering systemB. Braking systemC. Suspension systemD. Engine cooling systemAnswer: B二、填空题(每空1分,共20分)1. The main components of an engine include the _______,_______, _______, and _______.Answer: block, head, crankshaft, camshaft2. In a vehicle, the _______ is responsible for converting the linear motion of the piston into rotational motion. Answer: crankshaft3. The _______ is a safety feature that prevents the wheels from locking up during hard braking, allowing the driver to maintain steering control.Answer: ABS4. The _______ is the system in a vehicle that provides power to the electrical components when the engine is not running. Answer: alternator5. The _______ is a type of suspension system where each wheel moves independently of the others, allowing for better handling and ride comfort.Answer: independent suspension6. The _______ is the part of the engine that controls the flow of air and fuel into the combustion chamber.Answer: intake manifold7. The _______ is the process by which a vehicle's engine converts the heat energy from combustion into mechanicalenergy.Answer: power stroke8. The _______ is the system in a vehicle that controls the temperature and quality of the air inside the cabin. Answer: HVAC9. The _______ is a device that reduces the amount of harmful gases and particulates released into the atmosphere by the vehicle's exhaust.Answer: catalytic converter10. The _______ is the system that allows a vehicle to change gears, adjusting the engine's speed and torque to match driving conditions.Answer: transmission三、简答题(每题10分,共20分)1. Explain the function of a radiator in a vehicle.Answer: A radiator in a vehicle is responsible for cooling the engine by dissipating the heat generated during combustion. It circulates coolant through a network of tubes and fins, allowing the coolant to absorb heat from the engine and then release it into the atmosphere, thus maintaining the engine at an optimal operating temperature.2. Describe the role of a differential in a vehicle's drivetrain.Answer: The differential is a gearbox located between the transmission and the drive wheels. Its primary role is to allow the wheels to rotate at different speeds when thevehicle is turning, as the outer wheel travels a greater distance than the inner wheel. This ensures that the wheels maintain traction and reduces wear on the tires, while also providing a smoother ride. Additionally, the differential can distribute torque between the wheels, which can be beneficial in situations where one wheel may lose traction,。
