20℃空气的热膨胀系数
水和水蒸汽及空气物性

kJ/kg #NAME?
50.00
查询时在
的框
饱和水蒸汽表(按压力排列,SI单位,1-20000kPa)
查询压力 kPaA 温度 ℃ 蒸汽比容 蒸汽密度 液体焓 蒸汽焓 汽化热
内输入状态参数即可。
欢迎使用,敬请反馈意见,
m3/kg #NAME?
kg/m3 #NAME?
kJ/kg #NAME?
kJ/kg #NAME?
W/mK #NAME?
cP #NAME?
10-5m2/s #NAME?
10-3/℃ #NAME?
mN/m #50℃)
查询温度 ℃ 绝对压力 蒸汽比容 蒸汽密度 液体焓 蒸汽焓 汽化热
说 kJ/kg #NAME?
明
本程序用以查询水、水蒸 汽和空气的基本物性数据。 请务必注意其有效温度范围。
kPaA #NAME?
m3/kg #NAME?
kg/m3 #NAME?
kJ/kg #NAME?
kJ/kg #NAME?
以便及时更正。
500.00
#NAME?
水的饱和蒸汽压(-20-100℃)
查询温度 饱和蒸汽压 ℃ 压力 查询温度 ℃
空气的重要物理性质(-50-1000℃)
密度 定压比热 导热系数 粘度 运动粘度
KPa
mmHg
kg/m3 #NAME?
kJ/kg℃ #NAME?
W/mK #NAME?
10-3cP #NAME?
10-6m2/s #NAME?
80.00
#NAME? #NAME?
-50.00
水的重要物理性质(0-350℃)
查询温度 ℃ 外压 密度 焓 比热 导热系数 粘度 运动粘度 V膨胀系数 表面张力
空气的体积膨胀系数表

空气的体积膨胀系数表全文共四篇示例,供读者参考第一篇示例:空气的体积膨胀系数是指单位温度变化下空气体积变化的比例系数。
在常规温度和压力下,空气的体积膨胀系数是一个固定的数值,可以帮助我们计算在不同温度下气体的体积变化情况。
下面将介绍一份关于空气的体积膨胀系数表。
空气的体积膨胀系数受温度的影响,通常在常温常压下,空气的体积膨胀系数约为1/273K。
这意味着当温度上升1摄氏度时,空气的体积将增加约1/273。
以下是一份常用的关于空气的体积膨胀系数表:温度(摄氏度)体积膨胀系数0 1/27310 1/26320 1/25330 1/24340 1/23350 1/22360 1/21370 1/20380 1/19390 1/183100 1/173根据上表,我们可以看到随着温度的升高,空气的体积膨胀系数也逐渐增加,即单位温度变化下空气的体积变化比例增大。
这表明在高温下,空气的体积变化会更为显著。
了解空气的体积膨胀系数对于工程、科学和日常生活中的一些实际问题都是非常重要的。
在工程领域,我们需要考虑气体在不同温度下的体积变化,以确保系统的正常运行。
在科学研究中,空气的体积膨胀系数也被广泛应用于热力学和气体状态方程等方面。
在日常生活中,了解气体的体积膨胀系数可以帮助我们理解一些现象,比如为什么气球在冷空气中收缩,而在热空气中膨胀。
第二篇示例:空气是我们日常生活中不可或缺的一部分,但是我们常常忽略了它的一些特性,比如它的体积膨胀系数。
空气的体积膨胀系数是指在一定温度范围内,单位温度变化时空气体积的变化量与初始体积的比值。
在工程领域和科学实验中,我们经常需要考虑到物体与空气之间的热胀冷缩关系,因此了解空气的体积膨胀系数是非常重要的。
让我们来了解一下空气的组成和性质。
空气主要由氧气、氮气和少量的二氧化碳、氩气等气体组成,其中氧气和氮气占比最大。
空气的化学性质稳定,不易燃烧,但能促进燃烧。
空气的物理性质包括密度、压力、温度等,而空气的体积膨胀系数则是描述其在温度变化时体积变化的性质。
第7章 高分子材料的热学性能

比定容热容(Cv)
Q 1 E 1 cv T v m T p m
式中:Q为热量,E为内能,H为焓
c p cv
c p cv V VmT /
2
材料科学与工程学院
5
高分子材料的热容随温度的变化
材料科学与工程学院
6
表7-1 一些工程材料的比热容
V
1 V V0 T
材料科学与工程学院
9
对于各向同性材料,体积膨胀系数αV和线膨胀系 数αL之间具有如下关系:
V
1 V 3 V T P
L
实际上固体材料的热膨胀系数通常随温度升高而加大
材料科学与工程学院
10
常见工程材料的热膨胀性能 金属材料热膨胀系数介于陶瓷和高分子之间,最
dT dt
d T
2
2
c p dx
热扩散率或导温系数
c p
18
材料科学与工程学院
二、热传导的微观机理
气体导热——质点间直接碰撞; 金属导热——自由电子间碰撞; 固体导热——晶格振动(格波,并且
格波分为声频支和光频支两类
材料科学与工程学院
19
热性能的物理本质:晶格热振动
弹性波(格波):包括振动频率低的声频支 振动频率高的光频支 声频支—相邻原子具有相同的振动方向,两种原子的 质量不同,振幅不同,两原子间有相对运动。
导电共轭高分子的热导率是普通非共轭高分子的2030倍,将导电高分子与普通高分子共混可提高材料热 导率
材料科学与工程学院
24
7.4 高聚物的形变-温度曲线
形 变
玻璃态 高弹态
粘流态
干空气物理性质表

(106 m2 /s)
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
40
42
44
46
48
50
52
54
56
70
72
74
76
78
80
82
84
86
88
90
92
94
96
98
100
∞
∞
∞
∞
02380
水的物理性质
温度
( ℃ )
饱和蒸汽压
(kPa)
密度
(kg/m 3 )
南京
73
郑州
67
玉门
39
洛阳
63
兰州
57
武汉
76
银川
60
长沙
78
青岛
70
南昌
79
济南
55
桂林
73
西安
66
南宁
76
延安
58
广州
75
太原
57
成都
79
大同
54
自贡
77
西宁
61
重庆
83
乌鲁木齐
56
昆明
71
包头
50
贵州
77
呼和浩特
52
遵义
79
哈尔宾
66
拉萨
42
长春
68
锦州
60
吉林
67
100度热空气的比热容

100度热空气的比热容比热容是物质吸收或释放热量的能力的度量,表示单位质量物质升高1度所需要的热量。
对于100度热空气来说,它的比热容是一个重要的物理性质,决定了它在吸热或放热过程中的表现。
我们来了解一下比热容的概念。
比热容是一个物质的固有属性,不同物质的比热容值是不同的。
比热容的大小取决于物质的种类以及物质的状态(固体、液体或气体)。
对于气体来说,比热容可以分为定压比热容和定容比热容。
定压比热容是在恒定压力下,单位质量物质增加1度温度所需要的热量。
对于100度热空气来说,如果我们以恒定的压力加热它,每增加1度温度,就需要提供一定的热量。
这个热量就是100度热空气的定压比热容。
定容比热容是在恒定容积下,单位质量物质增加1度温度所需要的热量。
对于100度热空气来说,如果我们以恒定的容积加热它,每增加1度温度,就需要提供一定的热量。
这个热量就是100度热空气的定容比热容。
那么,具体来说,100度热空气的比热容是多少呢?实际上,不同气体的比热容是不同的,而且还会随着温度的变化而变化。
对于大气中的主要成分氮气和氧气来说,它们在常温下的比热容约为1.0J/(g·℃)。
所以,可以认为100度热空气的比热容约为1.0 J/(g·℃)。
那么,100度热空气的比热容有什么作用呢?比热容决定了物质在吸热或放热过程中的温度变化情况。
在实际应用中,比热容的大小会影响到热力学系统的热平衡和热传导性能。
比热容的大小还与物质的状态有关。
对于气体来说,比热容通常比固体和液体要大,这是因为气体分子之间的空隙较大,分子的自由度较高,容易吸收和释放热量。
因此,在相同条件下,相同质量的气体比固体和液体吸热或放热的能力要强。
在实际应用中,我们常常利用比热容来计算物体所需的加热或冷却时间。
以100度热空气为例,如果我们需要将它冷却到室温,就可以利用比热容的计算公式来估算所需的冷却时间。
当然,在实际操作中还需要考虑其他因素,如传热介质的温度、传热方式等。
空气热膨胀系数计算公式

空气热膨胀系数计算公式
空气热膨胀系数公式是α=ΔV/(V*ΔT),物体由于温度改变而有胀缩现象。
其变化能力以等压(p一定)下,单位温度变化所导致的长度量值的变化,即热膨胀系数表示。
各物体的热膨胀系数不同,一般金属的热膨胀系数单位为1/度(摄氏)。
线胀系数是指固态物质当温度改变摄氏度1度时,其某一方向上的长度的变化和它在20℃(即标准实验室环境)时的长度的比值。
大多数情况之下,此系数为正值。
也就是说温度变化与长度变化成正比,温度升高体积扩大。
但是也有例外,如水在0到4摄氏度之间,会出现负膨胀。
而一些陶瓷材料在温度升高情况下,几乎不发生几何特性变化,其热膨胀系数接近0。
空气粘度表常用

空气粘度表(可以直接使用,可编辑优质资料,欢迎下载)空气粘度表水的黏度表(0~40℃)水的物理性质370 21040.9 450.5 1892.43 40.319 33.73 5.69 264 0.48 6.80 F3Viscosity decreases with pressure(at temperatures below 33°C)Viscous flow occurs by molecules moving through the voids that exist betweenthem. As the pressure increases, the volume decreases and the volume of thesevoids reduces, so normally increasing pressure increases the viscosity.Water's pressure-viscosity behavior [534] can be explained by the increasedpressure (up to about 150 MPa) causing deformation, so reducing the strength ofthe hydrogen-bonded network, which is also partially responsible for the viscosity.This reduction in cohesivity more than compensates for the reduced void volume. Itis thus a direct consequence of the balance between hydrogen bonding effects andthe van der Waals dispersion forces [558] in water; hydrogen bonding prevailing atlower temperatures and pressures. At higher pressures (and densities), the balancebetween hydrogen bonding effects and the van der Waals dispersion forces is tipped in favor of the dispersion forces and the remaining hydrogen bonds are stronger due to the closer proximity of the contributing oxygen atoms [655]. Viscosity, then, increases with pressure. The dashed line (opposite) indicates the viscosity minima.The variation of viscosity with pressure and temperature has been used as evidence that the viscosity is determined more by the extent of hydrogen bonding rather than hydrogen bonding strength.Self-diffusion is also affected by pressure where (at low temperatures) both the translational and rotational motion of water anomalously increase as the pressure increases.TWB 监测公司原始记录表 TWB/JL-CY-01-001环境空气采样原始记录表项目名称: 任务编号: 采样点名称: 采样日期: 采样器型号、名称: 采样器编号: 天气状况: 计算公式:V 0=111103.101273273V P t V P T ⨯⨯=+⨯⨯采样人员: 记录人员: 校核人员: 记录时间: 校核时间:第 页 共 页干空气物理性质表(101.33Pa)湿空气的性质水的物理性质全国主要城市年平均温度及湿度表。
材料属性
热传递有三种基本形式:热传导、热对流和辐射。
在本论文中,因为辐射而散失的热量与其他两种热传递方式相比可以忽略,因此只考虑热传导和热对流。
各材料相应的力学性质和物理性质视为定值,这里考虑材料的导热系数和线胀系数两项数值随温度变化进行分析。
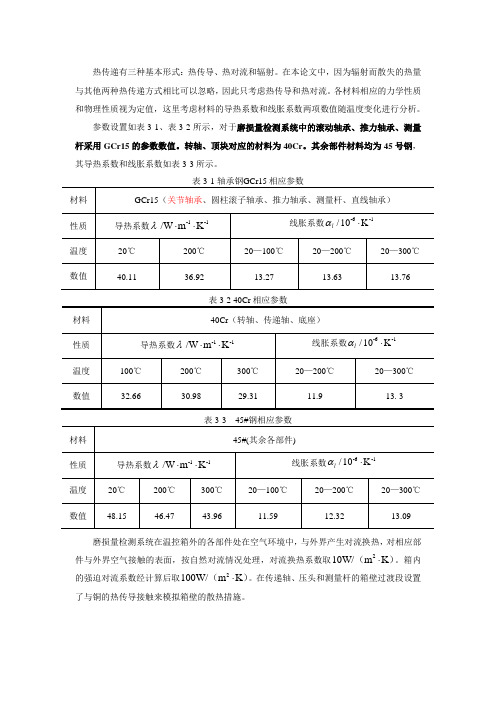
参数设置如表3-1、表3-2所示,对于磨损量检测系统中的滚动轴承、推力轴承、测量杆采用GCr15的参数数值。
转轴、顶块对应的材料为40Cr 。
其余部件材料均为45号钢,其导热系数和线胀系数如表3-3所示。
表3-1 轴承钢GCr15相应参数材料 GCr15(关节轴承、圆柱滚子轴承、推力轴承、测量杆、直线轴承)性质 导热系数λ-1-1/W m K ⋅⋅线胀系数-6-1/10K l α⋅温度 20℃ 200℃ 20—100℃ 20—200℃ 20—300℃ 数值40.1136.9213.2713.6313.76表3-2 40Cr 相应参数材料 40Cr (转轴、传递轴、底座)性质 导热系数λ-1-1/W m K ⋅⋅ 线胀系数-6-1/10K l α⋅ 温度 100℃ 200℃ 300℃ 20—200℃ 20—300℃ 数值32.6630.9829.3111.913. 3表3-3 45#钢相应参数材料 45#(其余各部件)性质 导热系数λ-1-1/W m K ⋅⋅ 线胀系数-6-1/10K l α⋅温度 20℃ 200℃ 300℃ 20—100℃ 20—200℃ 20—300℃ 数值48.1546.4743.9611.5912.3213.09磨损量检测系统在温控箱外的各部件处在空气环境中,与外界产生对流换热,对相应部件与外界空气接触的表面,按自然对流情况处理,对流换热系数取210W/m K ⋅()。
箱内的强迫对流系数经计算后取2100W/m K ⋅()。
在传递轴、压头和测量杆的箱壁过渡段设置了与铜的热传导接触来模拟箱壁的散热措施。
张丹论文材料参数 表3-2 材料参数衬垫为高分子材料,其热膨胀系数和导热率随温度变化,如表3-3,表3-4所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
20℃空气的热膨胀系数
首先,我们需要了解什么是热膨胀系数以及它是如何计算的。
热膨胀系数(α)是描述物体在温度变化时其体积如何变化的一个参数。
它通常用以下的数学公式表示:
α= (ΔV/V) / (ΔT/T)
其中,ΔV是物体体积的变化,ΔT是温度的变化,V是物体的原始体积,T是物体的原始温度。
对于空气,我们通常使用理想气体模型,这样我们就可以用波义尔定律来描述空气的体积和压力之间的关系。
但在这个问题中,我们假设空气在20℃时的热膨胀系数是一个已知的常数。
实际上,空气的热膨胀系数会随着温度和压力的变化而变化,但我们这里只关心20℃时的热膨胀系数。
为了解决这个问题,我们需要查找已知的20℃时空气的热膨胀系数的数据。
计算结果为:20℃时空气的热膨胀系数是3.6e-05 K^-1。
所以,20℃空气的热膨胀系数是3.6e-05 K^-1。
