热膨胀力计算
热膨胀系数
热膨胀量=温度差X热胀系数X长度=5.802X长度(mm)长度单位: m参考资料：GB/T20801.2-2006 表B.1(东北大学，辽宁沈阳 110006)2.2 材料的其它性能①机械强度如上所述，系统的器壁必须承受得住大气的压力。
因此它必须满足最低机械强度和刚度的要求，应考虑相应尺寸的结构所能承受的总压力(当然，容器结构形状也有较大的影响。
例如，圆柱形和球面形结构的强度就大于平面形结构的强度)。
②热学性能许多真空系统要承受温度的变化，如加热和冷却或二者兼备。
因而必须对所用材料的热学性能十分熟悉。
不仅要考虑到熔点，还要考虑到强度随温度的变化。
例如，铜的机械性能远在低于熔点温度之前就开始下降，因而不宜用铜制做真空容器的承压器壁。
另外，真空系统的材料除了受到温度缓慢变化的影响外，还会受到温度突变的影响。
因此，还要考虑材料的抗热冲击的特性。
③电磁性能许多真空系统中的部件必须具备能完成某项功能或工序所要求的电性能，同时这些性能又不能与真空系统的要求相矛盾。
例如，元件在真空室中工作，是靠辐射放热冷却的，因此元件的工作温度将会很高，使得元件的电性能可能受到影响，因此在选材及结构设计上要考虑工作部件的耐高温及冷却问题。
在许多真空系统中，往往要应用带电粒子束。
但这些带电粒子束往往容易受到某些不必要磁场的干扰。
因此在有电子束或离子束的系统中，必须认真考虑系统材料的磁性能，在某些情况下，即使很小的磁场也可能造成很严重的问题。
因此必须考虑用非磁性材料。
④其它性能光学性能(例观察窗)、硬度、抗腐蚀性、热导率和热膨胀等性能也常常起着十分重要的作用。
2.3 真空材料的选材原则2.3.1 对真空容器壳体及内部零件材料的要求①有足够的机械强度和刚度来保证壳体的承压能力。
②气密性好。
要保持一个完好的真空环境，器壁材料不应存在多孔结构、裂纹或形成渗漏的其它缺陷。
有较低的渗透速率和出气速率。
③在工作温度和烘烤温度下的饱和蒸气压要足够低(对超高真空系统来说尤其重要)。
管子热膨胀量计算公式与举例
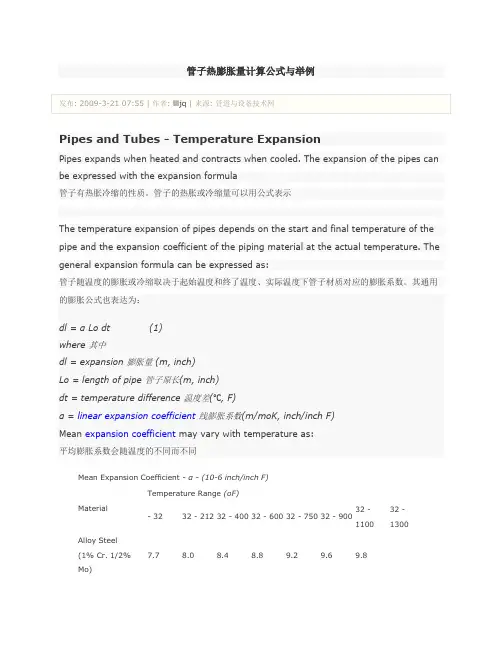
管子热膨胀量计算公式与举例Pipes and Tubes - Temperature ExpansionPipes expands when heated and contracts when cooled. The expansion of the pipes can be expressed with the expansion formula管子有热胀冷缩的性质。
管子的热胀或冷缩量可以用公式表示The temperature expansion of pipes depends on the start and final temperature of the pipe and the expansion coefficient of the piping material at the actual temperature. The general expansion formula can be expressed as:管子随温度的膨胀或冷缩取决于起始温度和终了温度、实际温度下管子材质对应的膨胀系数。
其通用的膨胀公式也表达为：dl = α Lo dt (1)where 其中dl = expansion 膨胀量 (m, inch)Lo = length of pipe 管子原长(m, inch)dt = temperature difference 温度差(℃, F)α = linear expansion coefficient线膨胀系数(m/moK, inch/inch F)Mean expansion coefficient may vary with temperature as:平均膨胀系数会随温度的不同而不同Mean Expansion Coefficient - α - (10-6 inch/inch F)Material Temperature Range (oF)- 32 32 - 212 32 - 400 32 - 600 32 - 750 32 - 90032 -110032 -1300Alloy Steel(1% Cr. 1/2%Mo)7.7 8.0 8.4 8.8 9.2 9.6 9.8Mild Steel7.1 7.8 8.3 8.7 9.0 9.5 9.7(0.1 - 0.2% C)Stainless Steel10.8 11.1 11.5 11.8 12.1 12.4 12.6 12.8(18% Cr. 8% Ni)Formula (1) can also be used with SI units. The expansion coefficient must be adjusted to ℃.公式（1）也可以用SI单位表示，膨胀系数需要转化为℃。
一般材料的热膨胀系数
一般材料的热膨胀系数热膨胀系数（Coefficient of Thermal Expansion，简称CTE）是一种衡量材料在温度变化下长度变化的物理性质，通常用于工程和材料科学中的热应力分析和设计。
热膨胀系数的定义是材料在单位温度变化下的长度变化与原始长度的比值。
它通常由单位温度变化对应的线性热膨胀的长度变化与起始长度的比值表示。
热膨胀系数可以是正值、负值或零值，这取决于材料的热性质。
正值表示材料在加热时会膨胀，负值表示在加热时会收缩，零值表示材料在温度变化时不发生体积变化。
不同材料的热膨胀系数存在很大差异。
以下是一些常见材料的热膨胀系数范围：1.金属材料：-铝：23.1×10^(-6)/°C-铜：16.5×10^(-6)/°C-钢铁：10.8-13.0×10^(-6)/°C-钠：71×10^(-6)/°C2.陶瓷材料：-石英：0.55×10^(-6)/°C-石墨：8.1×10^(-6)/°C-球墨铸铁：10.4×10^(-6)/°C-高纯度氧化铝陶瓷：7-10×10^(-6)/°C3.聚合物材料：-聚乙烯：100-200×10^(-6)/°C-聚丙烯：100-200×10^(-6)/°C-聚氯乙烯：70-190×10^(-6)/°C-聚四氟乙烯（PTFE）：120-200×10^(-6)/°C需要注意的是，材料的热膨胀系数不仅与材料的种类有关，还与温度的变化范围和使用条件有关。
热膨胀系数通常以线性近似表示，即在一定温度范围内认为热膨胀系数是恒定的。
在实际工程中，需要注意考虑温度变化对材料性能和结构稳定性的影响。
热膨胀系数的知识在工程设计和材料选择中非常重要。
常见材料热膨胀系数
常见材料热膨胀系数引言材料的热膨胀系数是指材料在温度变化时，单位温度变化下材料长度、面积或体积的变化量。
热膨胀系数是一个重要的物理参数，对于工程设计、材料选择和热力学计算等方面都有重要的影响。
本文将介绍常见材料的热膨胀系数，包括金属材料、陶瓷材料、塑料材料和复合材料等。
我们将分别介绍这些材料的定义、热膨胀原理以及具体的热膨胀系数数值。
一、金属材料金属材料是一类常见的工程材料，具有良好的导热性和导电性。
金属材料的热膨胀系数一般较大，因此在温度变化较大的情况下，金属结构往往需要考虑热膨胀的影响。
常见金属材料的热膨胀系数如下：•铁（Fe）：12.0 × 10^-6 /℃•铝（Al）：23.1 × 10^-6 /℃•铜（Cu）：16.6 × 10^-6 /℃•镍（Ni）：13.3 × 10^-6 /℃•钛（Ti）：8.6 × 10^-6 /℃二、陶瓷材料陶瓷材料是一类具有高硬度、高耐磨性和耐高温性能的材料。
陶瓷材料的热膨胀系数一般较小，因此在高温条件下，陶瓷材料往往能够保持较好的尺寸稳定性。
常见陶瓷材料的热膨胀系数如下：•氧化铝（Al2O3）：8.0 × 10^-6 /℃•氮化硅（Si3N4）：3.2 × 10^-6 /℃•硼化硅（SiC）：4.0 × 10^-6 /℃•氧化锆（ZrO2）：9.0 × 10^-6 /℃•氧化锆陶瓷（ZTA）：10.0 × 10^-6 /℃三、塑料材料塑料材料是一类具有良好的绝缘性能、耐腐蚀性和可塑性的材料。
塑料材料的热膨胀系数一般较大，因此在温度变化较大的情况下，塑料制品往往需要考虑热膨胀的影响。
常见塑料材料的热膨胀系数如下：•聚乙烯（PE）：100 × 10^-6 /℃•聚丙烯（PP）：90 × 10^-6 /℃•聚氯乙烯（PVC）：60 × 10^-6 /℃•聚苯乙烯（PS）：80 × 10^-6 /℃•聚四氟乙烯（PTFE）：125 × 10^-6 /℃四、复合材料复合材料是一类由两种或两种以上的材料组成的材料。
管道热膨胀计算解析
管道专业施工相关热力计算
第一部分管道热推力的计算
一、管道热伸长计算
管道的热伸长量的大小与管材的种类、管段的长度及温差数值有关。
ΔL=αLΔt=αL(t2-t1) 公式一
式中ΔL——管段的热伸长量（m）；
α——管材的线膨胀系数[m/(m•)]；在附表1中查询
L——管段长度（m）；
t1 ——安装时环境温度（℃）；
t2 ——管内介质最高温度（℃）；
二、管道的热应力计算
管道受热时所产生的热应力大小与管材的性质、管段长度及热伸长量有关。
δ=E(ΔL/L) 公式二
式中δ——管道受热产生的热应力（MPa）；
E——管道的弹性模量（MPa）；在附表2中查询
ΔL——管段的热伸长量（m）；（由公式一得出）
L——管段长度（m）；
当管道受热时的应力知道后，乘以管道截面积，就是整个截面积所产生的总的热推力，即：
P=106δF 公式三
式中P——管道的热推力（N）
F——管道截面积（㎡）
δ——管道热应力（MPa）
附表1：常用钢材的线膨胀系数(×10-6m/m·℃)
附表2：不同温度下不同材料的弹性模量
第二部分相关补偿器的计算
一、管道的自然补偿
1、L形直角弯自然补偿；L形自然补偿管段如图。
热膨胀系数的测量与计算
热膨胀系数的测量与计算热膨胀系数是物体在温度变化时线膨胀或者体膨胀的程度，在工程设计和材料研究中具有重要的意义。
本文将对热膨胀系数的测量与计算进行探讨。
测量热膨胀系数的方法主要有拉伸法、差热法和干涉法。
拉伸法是将待测物体固定住，在温度变化时通过测量其长度的变化来计算热膨胀系数。
这种方法适用于线膨胀系数的测量，但对于体膨胀系数的测量有一定的局限。
差热法是将待测物体与参比物体置于同一温度条件下，然后通过测量两者间的温度差来计算热膨胀系数。
这种方法适用于大部分材料的热膨胀系数测量，但需要考虑到温度梯度和传热问题。
干涉法是利用光的相位差来测量热膨胀系数，通过干涉仪或干涉条纹方法来实现。
这种方法精确度高，适用于各种材料的热膨胀系数测量，但设备复杂，操作要求高。
除了测量方法，计算热膨胀系数也是十分重要的。
根据热膨胀系数的定义，可得到其计算公式为ΔL/L0=α*ΔT，其中ΔL为温度变化引起的长度变化，L0为初始长度，α为热膨胀系数，ΔT为温度变化量。
对于材料的体膨胀系数，可通过加权平均法或基于理论模型的计算方法来求取。
加权平均法是根据不同晶向的膨胀系数以及晶体的晶向构造来计算体膨胀系数，这种方法适用于单晶材料。
基于理论模型的计算方法则是利用分子动力学模拟或经验公式来计算体膨胀系数，这种方法适用于非晶态材料。
在实际工程和研究中，热膨胀系数的测量和计算可以帮助我们预测材料在温度变化下的形变和变形情况。
例如，在航空航天领域，热膨胀系数的准确测量和计算有助于设计和制造航天器的构件，确保其在极端温度条件下的正常运行。
在建筑领域，根据材料的热膨胀系数，可以合理选择与搭配建筑材料，防止建筑物在温度变化下产生不均匀的应力和变形，从而影响结构的安全性和使用寿命。
此外，热膨胀系数还可以用于材料的热膨胀补偿和应力分析。
在电子设备制造中，为了保证电子元件的稳定性和可靠性，通常会采用热膨胀系数匹配的方法，将材料的热膨胀系数与其他部件相匹配，以减少因温度变化引起的应力和变形。
热力管道的热膨胀及其补偿
热力管道的热膨胀及其补偿摘要：热力管道输送的介质温度很高，投入运行后，将引起管道的热膨胀，使管壁内或某些焊缝上产生巨大的应力，如果此应力超过了管材或焊缝的强度极限，就会使管道造成破坏。
本文就热力管道的热膨胀、热应力、轴向推力的理论分析计算，针对各种补偿器的选用原则和安装要点进行了简述。
关键词：热力管道热膨胀热应力热补偿补偿器预拉伸1 管道的热膨胀及热应力计算1.1 管道的热膨胀计算管段的热膨胀量按下式计算：ΔL=ɑ.L.Δt=2.L.(t2-t1)式中：ΔL——管段的热膨胀量（mm）；ɑ——管材的线膨胀系数，即温度每升高1℃每米管子的膨胀量（mm/m.℃）；L——管段长度（m）；Δt——计算温差，即管道受热时所升高的温度，它等于管道输送介质的最高工作温度t2与管道安装时的环境温度t1之差（℃）。
对于一般碳钢管ɑ=12×10-4mm/m.℃，则ΔL=0.012.L.Δt。
在施工中，为了迅速估算碳钢管道的热膨胀量，可按每米管道在升温100℃时，其膨胀量为1.2mm计算。
1.2 管道的热应力计算管道受热时所产生的应力的大小可按下式计算：σ=E. ε= E. = ■ E. ■ =E.ɑ.Δt式中：σ——管道受热时所产生的应力（kg/cm2）；E——管材的弹性模量（kg/cm2）；ε——管道的相对变形量，它等于管道的热膨胀量ΔL（mm）与管道原长L（m）之比，即ε=■常用钢材的弹性模量E=2×10-6（kg/cm2），一般碳钢管的线膨胀系数ɑ=12×10-6（mm/m.℃），则热应力的计算公式可简化为σ=2×106×12×10-6×Δt=24.Δt（kg/cm2）。
利用此式，可以很容易地计算出钢管道热膨胀受到限制时产生的热应力。
由此可见，管道受热时所产生的应力的大小，与管子直径及管壁厚度无关。
它是由管子材料的弹性模量、线膨胀系数和管道受热时所升高的温度来决定的。
铝合金热膨胀计算公式
铝合金热膨胀计算公式以铝合金热膨胀计算公式为标题，我们来探讨一下铝合金的热膨胀性质及其计算方法。
铝合金是一种常用的材料，其具有较低的密度、良好的导热性和机械性能等优点，因此在许多领域得到广泛应用。
然而，材料在受热或受冷过程中会发生热膨胀或热收缩，这可能对工程设计和实际应用造成影响。
因此，我们需要了解材料的热膨胀性质，并能够准确计算其热膨胀系数。
热膨胀是指物体在温度变化时发生的体积变化现象。
铝合金的热膨胀系数是指在单位温度变化下，单位长度的材料长度变化的比例。
一般情况下，铝合金的热膨胀系数是一个常数，可以通过实验测量或查阅资料获得。
铝合金的热膨胀计算公式如下：ΔL = α * L0 * ΔT其中，ΔL表示长度变化量，α表示热膨胀系数，L0表示原始长度，ΔT表示温度变化量。
在使用该计算公式时，我们需要注意以下几点：1. 温度的单位应保持一致。
如果温度使用摄氏度，则计算结果也是以摄氏度为单位的长度变化量。
2. 热膨胀系数的单位与长度单位相互匹配。
如果长度以米为单位，则热膨胀系数应为每摄氏度的米数。
3. 原始长度应与温度变化量在同一温度下测量。
如果温度变化是从初始温度到最终温度，那么原始长度应在初始温度下测量。
以一个具体的例子来说明热膨胀计算的过程。
假设一根铝合金杆的原始长度为1米，热膨胀系数为0.0000225/℃，温度变化量为100℃。
我们可以使用上述公式计算出长度变化量。
ΔL = 0.0000225/℃ * 1米* 100℃ = 0.00225米 = 2.25毫米因此，当铝合金杆受热100℃时，其长度将增加2.25毫米。
需要注意的是，热膨胀计算公式只适用于温度变化较小的情况下。
如果温度变化较大，材料可能会发生相变或其他复杂的热力学行为，这就需要考虑更加复杂的计算方法。
铝合金的热膨胀计算公式是一个重要的工具，可以帮助我们预测和解决材料在温度变化下的行为。
合理应用热膨胀计算公式可以为工程设计和实际应用提供有价值的参考数据，确保材料的使用安全和性能稳定。
金属热胀冷缩力学计算公式
金属热胀冷缩力学计算公式引言。
金属是一种常见的材料，广泛应用于工程领域。
在工程设计和制造过程中，金属的热胀冷缩特性是一个重要的考虑因素。
热胀冷缩力学计算公式可以帮助工程师预测金属在不同温度下的尺寸变化和应力分布，从而指导工程设计和制造过程。
本文将介绍金属热胀冷缩力学计算公式的基本原理和应用。
一、金属热胀原理。
金属在受热时会膨胀，受冷时会收缩，这是由于金属的分子在受热时振动加剧，分子间的距离增加，从而导致金属的体积扩大；而在受冷时，分子的振动减弱，分子间的距离减小，金属的体积收缩。
这种热胀冷缩特性是金属材料的固有属性，也是金属在工程应用中需要考虑的重要因素。
二、金属热胀冷缩力学计算公式。
金属的热胀冷缩力学计算公式可以用来计算金属在不同温度下的线膨胀系数、体积膨胀系数以及由此引起的应力分布。
以下是金属热胀冷缩力学计算公式的基本形式：1. 线膨胀系数。
线膨胀系数是描述金属在单位长度上的膨胀量随温度变化的比例关系。
常用的线膨胀系数计算公式为：ΔL = αL0ΔT。
其中，ΔL表示金属在温度变化ΔT下的长度变化量，α表示金属的线膨胀系数，L0表示金属在参考温度下的长度。
2. 体积膨胀系数。
体积膨胀系数是描述金属在单位体积上的膨胀量随温度变化的比例关系。
常用的体积膨胀系数计算公式为：ΔV = βV0ΔT。
其中，ΔV表示金属在温度变化ΔT下的体积变化量，β表示金属的体积膨胀系数，V0表示金属在参考温度下的体积。
3. 应力分布。
金属在受热或受冷时会产生内部应力，这些应力会影响金属的力学性能和稳定性。
金属热胀冷缩力学计算公式可以用来计算金属在不同温度下的应力分布，以指导工程设计和制造过程。
三、金属热胀冷缩力学计算公式的应用。
金属热胀冷缩力学计算公式在工程领域有着广泛的应用。
以下是金属热胀冷缩力学计算公式的一些应用场景：1. 工程设计。
在工程设计中，金属的热胀冷缩特性需要被充分考虑。
工程师可以利用金属热胀冷缩力学计算公式来预测金属在不同温度下的尺寸变化和应力分布，从而确定合适的尺寸和结构设计方案。
热膨胀力计算
热膨胀力计算
热膨胀力是物体由于温度变化而产生的力。
它可以通过以下公式计算：
热膨胀力 = 热膨胀系数 ×温度变化量 ×物体的初始长度
其中，热膨胀系数表示物体的热膨胀性能，通常用α表示；温度变化量表示物体的温度变化，用ΔT表示；物体的初始长度用L0表示。
需要注意的是，热膨胀力的方向与温度变化量的方向相反。
也就是说，当物体受热膨胀时，热膨胀力的方向与温度变化量的方向相反，当物体受冷缩小时，热膨胀力的方向与温度变化量的方向相同。
另外，热膨胀力只是作用在物体上的一种内力，不会引起物体的整体运动。
金属和合金热膨胀系数计算法
金属和合金热膨胀系数计算法
金属和合金的热膨胀系数是指材料在温度变化时长度、面积或体积发生的变化，是材料热膨胀特性的重要参数。
热膨胀系数的计算可以采用数学模型、实验方法或经验公式等多种方法。
其中，基于数学模型的计算方法是最常用的，其基本思路是通过对材料的结构、晶格和能量状态等进行建模，然后利用热力学理论和统计力学方法求出材料的热膨胀系数。
具体而言，金属和合金的热膨胀系数可以采用以下数学模型进行计算：
1.自由原子模型：该模型假设金属中的原子是自由的，且它们在温度变化时可以沿着三个坐标轴自由运动。
在此基础上，可以得出金属的热膨胀系数公式。
2.简单晶格模型：该模型假设金属中的原子是排列成规则晶格结构的，且它们在温度变化时可以沿着晶格的各个方向运动。
在此基础上，可以得出晶体的热膨胀系数公式。
3.电子气模型：该模型考虑了电子在金属中的运动，并将其纳入了热膨胀系数的计算中。
该模型还可以用于研究金属的热导率、电导率等其他热学性质。
除了数学模型外，金属和合金的热膨胀系数还可以通过实验方法进行测量。
常用的实验方法包括线膨胀法、光栅法、差动热分析法等，其中线膨胀法是最为常用的方法之一。
此外，还有一些经验公式可以用于估算金属和合金的热膨胀系数，例如Debye-Einstein公式、
Gruneisen公式、Klemens公式等。
总之，金属和合金热膨胀系数的计算方法多种多样，每种方法都有其适用范围和优缺点。
在实际应用中，应根据具体情况选择最为合适的方法进行计算。
热学解题技巧热膨胀和热传导的计算
热学解题技巧热膨胀和热传导的计算热学解题技巧：热膨胀和热传导的计算热学是物理学的重要分支，研究能量传递和转换的规律。
在热学问题解题过程中，热膨胀和热传导是两个重要的计算内容。
本文将介绍有关热膨胀和热传导计算的一些技巧和方法。
热膨胀的计算：热膨胀是指物体由于温度升高而引起的尺寸变化。
在计算热膨胀问题时，我们首先需要了解两个重要的物理量，即热膨胀系数和温度变化量。
热膨胀系数是描述物体膨胀或收缩程度的物理量，通常用符号α表示。
不同物质的热膨胀系数存在差异，因此在计算之前需要查阅相关资料或者题目中已给出。
热膨胀系数的单位是1/℃（开尔文）。
温度变化量是指物体温度的变化程度，通常用符号ΔT表示。
将物体的初温度记为T1，末温度记为T2，则温度变化量ΔT等于T2减去T1的差。
在计算物体的热膨胀量时，我们可以使用如下公式：ΔL = αL0ΔT 其中，ΔL表示物体的长度变化量，α是物体的热膨胀系数，L0是物体的初始长度，ΔT是温度变化量。
这个公式可以用于计算线性膨胀、面积膨胀和体积膨胀的情况。
在实际计算时，需要根据题目中给出的具体条件选择适当的公式进行计算。
热传导的计算：热传导是指物体内部或不同物体之间发生的热量传递过程。
在计算热传导问题时，我们需要了解几个重要的物理量，包括热传导系数、面积、厚度和温度差。
热传导系数是描述物质导热性能的物理量，通常用符号λ表示。
不同物质的热传导系数也存在差异，因此在计算之前需要查阅相关资料或者题目中已给出。
热传导系数的单位是W/(m·℃)（瓦特/米·开尔文）。
面积是指热传导过程中参与传热的物体或物体表面的面积。
通常用符号A表示，其单位是平方米（m^2）。
厚度是指热传导物体的厚度，通常用符号d表示，其单位是米（m）。
温度差是指热传导过程中参与传热的物体（或者不同物体之间）的温度差，通常用符号ΔT表示。
在计算热传导问题时，我们可以使用如下公式：Q = λAΔT/d其中，Q表示传热速率或单位时间内传热的热量，λ是物质的热传导系数，A是热传导面积，ΔT是传热物体之间的温度差，d是传热物体的厚度。
可逆过程中膨胀功,技术功的计算公式
可逆过程中膨胀功,技术功的计算公式
（最新版）
目录
1.可逆过程中的膨胀功和技术功的定义
2.膨胀功和技术功的计算公式
3.应用实例与注意事项
正文
在热力学中，可逆过程是指系统在经历某个过程时，其状态参数的变化是可以恢复到原始状态的。
在这个过程中，系统所做的功可以分为膨胀功和技术功两部分。
膨胀功是指在可逆过程中，由于系统体积的膨胀而对外做的功。
膨胀功的计算公式为：W_v = -p_ext * ΔV，其中 W_v 表示膨胀功，p_ext 表示系统外部的压力，ΔV 表示系统体积的变化。
技术功是指在可逆过程中，系统从高温热源吸收的热量减去向低温热源释放的热量。
技术功的计算公式为：W_t = Q_h - Q_l，其中 W_t 表示技术功，Q_h 表示从高温热源吸收的热量，Q_l 表示向低温热源释放的热量。
在实际应用中，膨胀功和技术功的计算公式可以帮助我们分析热力学系统的性能和效率。
需要注意的是，在计算膨胀功时，要确保系统的压力是外部压力，而不是系统内部的压力。
在计算技术功时，要确保热量的正负号正确，从高温热源吸收的热量为正，向低温热源释放的热量为负。
总之，可逆过程中的膨胀功和技术功的计算公式是热力学中重要的概念，可以帮助我们分析系统的性能和效率。
第1页共1页。
铝热膨胀量计算公式
铝热膨胀量计算公式引言：在热力学中，热膨胀是指物体在温度变化时体积或长度发生的变化。
铝是一种常见的金属材料，其热膨胀量可以通过公式来计算。
本文将介绍铝热膨胀量的计算公式，以及相关的背景知识和实际应用。
一、铝热膨胀量的背景知识铝是一种具有良好导电性和导热性的金属材料，广泛应用于工业和建筑领域。
当铝材料受热时，由于分子热运动的增加，分子之间的距离会增大，从而导致铝材料的体积或长度发生变化。
这种现象称为热膨胀。
二、铝热膨胀量的计算公式铝的热膨胀量可以通过以下公式来计算：ΔL = αL0ΔT其中，ΔL表示铝材料的长度变化量，α表示铝的线膨胀系数，L0表示铝材料的初始长度，ΔT表示温度变化量。
三、铝热膨胀量的实际应用铝热膨胀量的计算公式在工程设计和实际生产中具有重要的应用价值。
例如，在建筑领域，当设计一个大型的铝合金结构时，需要考虑铝材料在不同温度下的热膨胀量，以确保结构的稳定性和安全性。
此外，在航空航天领域，铝材料的热膨胀量也是设计和制造飞机零部件时必须考虑的因素之一。
四、铝热膨胀量计算公式的应用注意事项在使用铝热膨胀量计算公式时，需要注意以下几点：1. 温度单位的选择：公式中的温度变化量ΔT应使用摄氏度（℃）作为单位。
2. 线膨胀系数的确定：铝的线膨胀系数α是一个物理常数，可以通过实验测定得到，也可以在相关资料中查找。
3. 初始长度的测量：公式中的初始长度L0应使用与线膨胀系数α相对应的长度单位进行测量。
五、总结铝热膨胀量的计算公式ΔL = αL0ΔT可以帮助工程师和科学家预测和解决与铝材料热膨胀相关的问题。
在实际应用中，我们需要准确测量初始长度、选择合适的温度单位，并确定铝的线膨胀系数。
通过合理使用铝热膨胀量计算公式，可以提高铝材料的设计和制造的准确性和可靠性，为工程和科研工作提供有力支持。
热膨胀系数与应力
热膨胀系数与应力热膨胀是指物体在温度变化时体积发生变化的现象。
当物体受热时，分子的热运动增强，分子间的平均距离增大，导致物体体积膨胀。
热膨胀系数是衡量物体对温度变化的敏感程度的物理量，它描述了单位温度变化时物体的体积变化率。
热膨胀系数可以用来计算物体在温度变化下的体积变化量。
设物体的初始体积为V0，初始温度为T0，温度变化为ΔT，热膨胀系数为α，则物体温度变化后的体积V可以由下式计算得到：V = V0 * (1 + α * ΔT)热膨胀系数与应力之间存在着密切的关系。
应力是物体受到的内部或外部力的作用下产生的一种物理量，它与物体的形变密切相关。
当物体受到应力时，其形状和体积都会发生变化。
当物体受到温度变化引起的热膨胀时，会产生内部应力。
这是因为物体的不同部分由于受热程度不同，会出现不同的膨胀程度，从而产生内部的应力。
这种应力会对物体的性能和结构产生重要影响，特别是在工程领域中。
在工程设计中，需要考虑热膨胀对结构的影响。
如果结构的热膨胀系数与应力不匹配，就会导致结构变形、裂纹和破坏。
因此，在设计中需要合理选择材料和考虑热膨胀系数，以保证结构的稳定性和安全性。
热膨胀系数的大小取决于材料的性质。
不同材料的热膨胀系数有很大的差异。
例如，金属的热膨胀系数一般较大，而玻璃等非金属材料的热膨胀系数较小。
这也是为什么在工程中常常使用复合材料，以充分利用不同材料的性质来抵消热膨胀带来的影响。
热膨胀系数还可以用于解释一些日常生活中的现象。
例如，在冬天，当我们用热水冲洗冻住的自来水管道时，由于水管受热膨胀系数较大，会导致水管破裂。
这就是因为水管受热膨胀产生的应力超过了其所能承受的极限。
热膨胀系数是描述物体对温度变化的敏感程度的物理量，它与应力之间存在着密切的关系。
热膨胀系数可以用来计算物体在温度变化下的体积变化量，也可以用来解释一些日常生活中的现象。
在工程中，需要合理选择材料和考虑热膨胀系数，以保证结构的稳定性和安全性。
液体热膨胀系数
液体热膨胀系数液体热膨胀系数是指液体在温度变化时体积的变化率。
它是描述液体热膨胀特性的重要物理量，对于工程设计和实际应用具有重要意义。
本文将从液体热膨胀系数的概念、计算方法、影响因素以及应用等方面进行阐述。
一、概念液体热膨胀系数是指单位温度变化下液体体积的变化率。
通常用符号β表示，单位是℃^-1或K^-1。
液体热膨胀系数的大小与液体的性质有关，不同液体的热膨胀系数也不同。
二、计算方法液体热膨胀系数的计算方法有多种，其中常用的是线膨胀系数和体膨胀系数。
1. 线膨胀系数线膨胀系数是指液体在单位长度上的膨胀量与温度变化之间的比值。
它可以通过实验测量得到，也可以通过理论计算获得。
线膨胀系数的计算公式如下：β = ΔL/(L0ΔT)其中，β为线膨胀系数，ΔL为液体长度的变化量，L0为初始长度，ΔT为温度的变化量。
2. 体膨胀系数体膨胀系数是指液体在单位体积上的膨胀量与温度变化之间的比值。
它可以通过实验测量得到，也可以通过理论计算获得。
体膨胀系数的计算公式如下：β = ΔV/(V0ΔT)其中，β为体膨胀系数，ΔV为液体体积的变化量，V0为初始体积，ΔT为温度的变化量。
三、影响因素液体热膨胀系数的大小受到多种因素的影响，主要包括以下几个方面：1. 液体的性质：不同液体的分子结构和相互作用力不同，因此其热膨胀系数也不同。
一般来说，液体的分子间作用力较强的，其热膨胀系数较小。
2. 温度变化范围：液体的热膨胀系数一般随温度的升高而增大，但不同液体的变化趋势有所不同。
在一定温度范围内，液体的热膨胀系数可以近似看作常数。
3. 压力变化：液体的热膨胀系数还受到压力的影响。
一般情况下，液体的热膨胀系数随着压力的增大而减小。
四、应用液体热膨胀系数在工程设计和实际应用中具有重要作用，主要体现在以下几个方面：1. 设计容器和管道：在设计容器和管道时，需要考虑液体在温度变化下的膨胀量，以避免因温度变化引起的破裂或泄漏问题。
2. 温度补偿：在一些仪器和设备中，液体热膨胀系数的变化会影响测量和控制的准确性。