管道热膨胀量计算
热膨胀系数
热膨胀量=温度差X热胀系数X长度=5.802X长度(mm)长度单位: m参考资料：GB/T20801.2-2006 表B.1(东北大学，辽宁沈阳 110006)2.2 材料的其它性能①机械强度如上所述，系统的器壁必须承受得住大气的压力。
因此它必须满足最低机械强度和刚度的要求，应考虑相应尺寸的结构所能承受的总压力(当然，容器结构形状也有较大的影响。
例如，圆柱形和球面形结构的强度就大于平面形结构的强度)。
②热学性能许多真空系统要承受温度的变化，如加热和冷却或二者兼备。
因而必须对所用材料的热学性能十分熟悉。
不仅要考虑到熔点，还要考虑到强度随温度的变化。
例如，铜的机械性能远在低于熔点温度之前就开始下降，因而不宜用铜制做真空容器的承压器壁。
另外，真空系统的材料除了受到温度缓慢变化的影响外，还会受到温度突变的影响。
因此，还要考虑材料的抗热冲击的特性。
③电磁性能许多真空系统中的部件必须具备能完成某项功能或工序所要求的电性能，同时这些性能又不能与真空系统的要求相矛盾。
例如，元件在真空室中工作，是靠辐射放热冷却的，因此元件的工作温度将会很高，使得元件的电性能可能受到影响，因此在选材及结构设计上要考虑工作部件的耐高温及冷却问题。
在许多真空系统中，往往要应用带电粒子束。
但这些带电粒子束往往容易受到某些不必要磁场的干扰。
因此在有电子束或离子束的系统中，必须认真考虑系统材料的磁性能，在某些情况下，即使很小的磁场也可能造成很严重的问题。
因此必须考虑用非磁性材料。
④其它性能光学性能(例观察窗)、硬度、抗腐蚀性、热导率和热膨胀等性能也常常起着十分重要的作用。
2.3 真空材料的选材原则2.3.1 对真空容器壳体及内部零件材料的要求①有足够的机械强度和刚度来保证壳体的承压能力。
②气密性好。
要保持一个完好的真空环境，器壁材料不应存在多孔结构、裂纹或形成渗漏的其它缺陷。
有较低的渗透速率和出气速率。
③在工作温度和烘烤温度下的饱和蒸气压要足够低(对超高真空系统来说尤其重要)。
管道膨胀量及弯管计算
主管道存在热膨胀时，为避免系统产生过大应力，连接在主管道上的支管应具有一个最 小无 约束长度，计算如下表(支管最小为DN20)： 支管的影响 直管段总膨胀量 e/mm 516.52 e/in 20.34 支管最小公称直径 D/mm 20 D/in 0.79 最小无约束长度 Lmin/M 12.20
此直管段上各支管的无约束长度要大于计算所得最小无约束长度则视为允许。
计 算 直管段长度 L/M 直管段总膨胀 直管段总膨胀量 量 e/in e/mm 98间管线总膨胀量 计算系数 参考系数 U/ft 321.52 E/mm 516.52 E/in 20.34 7.44 0.03
两固定点间直线距离
弯管宽度 W/M 9.80
对于一般管系，可不进行全面应力分析以节省费用，而进行快速核算来判断未经详细应力分析的管系弹性是否合适 弯管长度快速核算 初始温度 T1/℃ 20 操作温度 T2/℃ 400 d/mm 101.6 管子外径 d/in 4 L1/ft 160.76 分管段长度 L1/M 49.00
实际的弯管高度和宽度大于所要求的最小高度和宽度则视为补偿后的管系符合要求。
胀量和补偿弯管长度计算如
上。 变形，管廊立柱加防火涂料
易燃易爆管线在上层（越危
经详细应力分析的管系弹性是否合适，对于弯管型膨胀节，快速核算如下表：
速核算 弯管最小高度 Hmin/ft 9.89 Hmin/M 3.01 弯管最小宽度 Wmin/ft 4.94 Wmin/M 1.51
要求。
以管道引出点为基准点，采用下表计算 主 管 道 热 膨 胀 量 计 算 初始温度 T1/℃ 20 操作温度 平均膨胀系数 T2/℃ α 400 0.01156 膨胀系数 α 1 0.01167 膨胀系数 α 2 0.01376 每米管长膨胀量 Δ L/mm 5.27
物体的膨胀与热膨胀系数的计算
物体的膨胀与热膨胀系数的计算物体的膨胀是指物体在受热或受冷时发生的体积变化。
膨胀是一个普遍存在的现象，我们可以通过热膨胀系数来计算物体的膨胀程度。
一、膨胀与热膨胀系数的概念热膨胀系数是一个用于衡量物体在温度变化下的膨胀程度的物理量。
它表示单位温度变化时物体相对于其原始长度或体积的变化比例。
膨胀系数通常用α表示，单位是1/℃或℃^-1。
对于长度膨胀，我们用线膨胀系数α_l表示；对于体积膨胀，我们用体积膨胀系数α_v表示。
二、线膨胀系数的计算公式线膨胀系数α_l可以通过以下公式进行计算：α_l = ΔL / (L * ΔT)其中，ΔL表示长度变化量，L表示原始长度，ΔT表示温度变化量。
三、体积膨胀系数的计算公式体积膨胀系数α_v可以通过以下公式进行计算：α_v = ΔV / (V * ΔT)其中，ΔV表示体积变化量，V表示原始体积，ΔT表示温度变化量。
四、膨胀系数的实际应用膨胀系数在工程学、物理学等领域有着广泛的应用。
例如，建筑工程中，膨胀系数的计算可以帮助我们预测建筑材料在不同温度下的膨胀和收缩，从而避免因温度变化引起的损害；在热力学研究中，膨胀系数可以用来计算物体在热力学循环中的温度变化和体积变化。
膨胀系数还可以用于设计热膨胀补偿装置，例如管道系统中的膨胀节，用来克服由于温度变化而引起的管道的热膨胀。
五、常见物体的膨胀系数不同物体的膨胀系数各不相同，下面是一些常见物体的线膨胀系数α_l的范围：- 铝：23×10^-6/℃- 铜：16×10^-6/℃- 黄铜：18×10^-6/℃- 钢：12×10^-6/℃- 玻璃：8×10^-6/℃- 混凝土：7×10^-6/℃对于体积膨胀系数α_v，可以通过以下公式与线膨胀系数α_l之间进行转换：α_v = 3α_l六、总结物体的膨胀是受热或受冷时发生的体积变化现象，可以通过热膨胀系数来计算物体的膨胀程度。
管道膨胀及流量要点
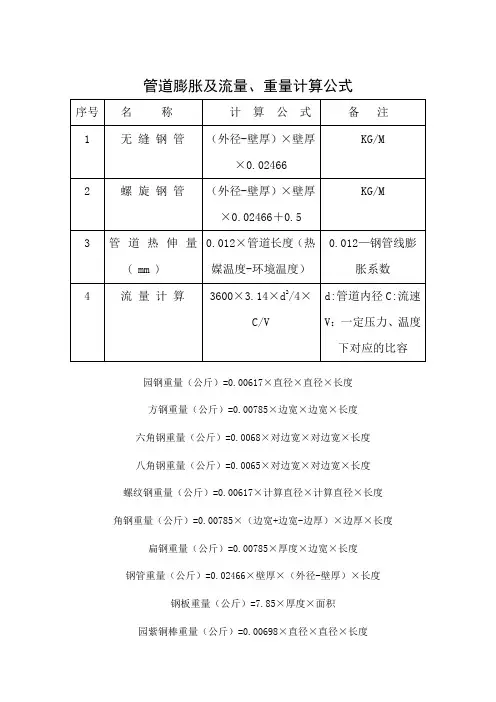
管道膨胀及流量、重量计算公式园钢重量（公斤）=0.00617×直径×直径×长度方钢重量（公斤）=0.00785×边宽×边宽×长度六角钢重量（公斤）=0.0068×对边宽×对边宽×长度八角钢重量（公斤）=0.0065×对边宽×对边宽×长度螺纹钢重量（公斤）=0.00617×计算直径×计算直径×长度角钢重量（公斤）=0.00785×（边宽+边宽-边厚）×边厚×长度扁钢重量（公斤）=0.00785×厚度×边宽×长度钢管重量（公斤）=0.02466×壁厚×（外径-壁厚）×长度钢板重量（公斤）=7.85×厚度×面积园紫铜棒重量（公斤）=0.00698×直径×直径×长度园黄铜棒重量（公斤）=0.00668×直径×直径×长度园铝棒重量（公斤）=0.0022×直径×直径×长度方紫铜棒重量（公斤）=0.0089×边宽×边宽×长度方黄铜棒重量（公斤）=0.0085×边宽×边宽×长度方铝棒重量（公斤）=0.0028×边宽×边宽×长度六角紫铜棒重量（公斤）=0.0077×对边宽×对边宽×长度六角黄铜棒重量（公斤）=0.00736×边宽×对边宽×长度六角铝棒重量（公斤）=0.00242×对边宽×对边宽×长度紫铜板重量（公斤）=0.0089×厚×宽×长度黄铜板重量（公斤）=0.0085×厚×宽×长度铝板重量（公斤）=0.00171×厚×宽×长度园紫铜管重量（公斤）=0.028×壁厚×（外径-壁厚）×长度园黄铜管重量（公斤）=0.0267×壁厚×（外径-壁厚）×长度园铝管重量（公斤）=0.00879×壁厚×（外径-壁厚）×长度注：公式中长度单位为米，面积单位为平方米，其余单位均为毫米。
管道热膨胀量计算
管道热膨胀量计算管道是工业生产、建筑供水、供气等领域中广泛应用的管状构件，而温度的变化会引起管道的热膨胀量。
因此，对于管道的热膨胀量进行准确的计算是非常重要的。
管道的热膨胀量是由温度变化引起的长度变化。
当管道受到热膨胀时，管道的长度会增加；而当管道受到热收缩时，管道的长度会减少。
因此，我们需要计算管道在不同温度下的热膨胀量，以便在设计、施工等过程中进行合理的管道布置和固定，以避免管道的过度应力。
那么，如何计算管道的热膨胀量呢？一般来说，管道的热膨胀量可以使用下述公式进行计算：ΔL=α*L0*(T1-T0)其中，ΔL表示管道在温度变化下的长度变化量，α表示管道的线膨胀系数，L0表示管道在初始温度T0下的长度，T1表示管道的最终温度。
在计算过程中，我们需要注意以下几点：1.管道的线膨胀系数α是一个常数，表示单位温度变化引起的长度变化与初始长度的比例。
不同材料的管道具有不同的线膨胀系数，可以通过查询相关资料获得。
2.初始温度T0和最终温度T1的单位应保持一致，一般为摄氏度。
如果有需要，可以进行单位转换。
3.计算过程中的长度单位也应保持一致，比如可以选择使用米作为长度单位。
接下来，我们以其中一种材料的管道为例进行热膨胀量的计算。
即该管道在温度从20摄氏度变化到80摄氏度时，长度会增加0.06米。
需要注意的是，这只是一个简单的计算示例，实际的计算可能会更为复杂，需要考虑更多的因素，比如管道的支撑方式、周围环境的温度变化等等。
在实际工程中，我们应根据具体情况进行计算，并采取相应的措施来控制管道的热膨胀量，保证工程的安全和稳定运行。
总之，管道热膨胀量的计算对于工程设计和施工具有重要意义。
通过合理的计算和控制，可以避免管道因温度变化而产生的过度应力，确保管道的正常运行。
管道膨胀系数
管道膨胀系数
管道膨胀系数是指管道由于热胀冷缩而引起的长度变化与温度变化之间的比值。
它代表了每度温度变化时管道单位长度的变化量。
管道膨胀系数可以用来计算管道在温度变化时的长度变化。
一般情况下，管道材料的膨胀系数（也称为热膨胀系数）在设计过程中已经确定。
常见的管道材料如钢、铜、塑料等都有不同的膨胀系数。
例如，钢的膨胀系数比较大，塑料的膨胀系数较小。
根据管道的材料和温度变化范围，可以通过膨胀系数计算出管道在温度变化时的长度变化。
这对于管道的设计和安装非常重要，可以避免管道因温度变化而发生破裂、变形等问题。
管道热膨胀计算
第一部分管道热推力的计算
一、管道热伸长计算
管道的热伸长量的大小与管材的种类、管段的长度及温差数值有关。
ΔL=αLΔt=αL(t2-t1)公式一
式中ΔL——管段的热伸长量（m）；
α——管材的线膨胀系数[m/(m?)]；在附表1中查询
L——管段长度（m）；
t1——安装时环境温度（℃）；
t2——管内介质最高温度（℃）；
二、管道的热应力计算
管道受热时所产生的热应力大小与管材的性质、管段长度及热伸长量有关。
δ=E(ΔL/L)公式二
式中δ——管道受热产生的热应力（MPa）；
E——管道的弹性模量（MPa）；在附表2中查询
ΔL——管段的热伸长量（m）；（由公式一得出）
L——管段长度（m）；
当管道受热时的应力知道后，乘以管道截面积，就是整个截面积所产生的总的热推力，即：
1．92
1．87
1．69
2
20G
2．09
2．06
1．97
1．91
1．83
1．74
3
12Cr1MoV
2．14
2．11
2．06
1．95
1．87
1．79
4
15CrMo
2．12
2．10
2．04
1．97
1．87
1．77
第二部分相关补偿器的计算
一、管道的自然补偿
1、L形直角弯自然补偿；L形自然补偿管段如图
350
360
370
380
390
400
410
420
430
440
14
450
14
460
14
470
管道热膨胀计算解析
管道专业施工相关热力计算
第一部分管道热推力的计算
一、管道热伸长计算
管道的热伸长量的大小与管材的种类、管段的长度及温差数值有关。
ΔL=αLΔt=αL(t2-t1) 公式一
式中ΔL——管段的热伸长量（m）；
α——管材的线膨胀系数[m/(m•)]；在附表1中查询
L——管段长度（m）；
t1 ——安装时环境温度（℃）；
t2 ——管内介质最高温度（℃）；
二、管道的热应力计算
管道受热时所产生的热应力大小与管材的性质、管段长度及热伸长量有关。
δ=E(ΔL/L) 公式二
式中δ——管道受热产生的热应力（MPa）；
E——管道的弹性模量（MPa）；在附表2中查询
ΔL——管段的热伸长量（m）；（由公式一得出）
L——管段长度（m）；
当管道受热时的应力知道后，乘以管道截面积，就是整个截面积所产生的总的热推力，即：
P=106δF 公式三
式中P——管道的热推力（N）
F——管道截面积（㎡）
δ——管道热应力（MPa）
附表1：常用钢材的线膨胀系数(×10-6m/m·℃)
附表2：不同温度下不同材料的弹性模量
第二部分相关补偿器的计算
一、管道的自然补偿
1、L形直角弯自然补偿；L形自然补偿管段如图。
蒸汽管道的膨胀与处理
蒸汽管道的膨胀与处理所有的管道都是在环境温度下安装，但是当用来输送热的流体，例如热水或者蒸汽时，管道运行在高温状态。
从环境温度升至工作温度时管道会膨胀，特别是长的管道情况更加严重。
膨胀的长度可以用以下的公式计算所得。
在有些情况下，蒸汽主管道的疏水阀将冷凝水排放至回收管(沿蒸汽管道并排布置)。
此时必须记住两根管道的热膨胀是不同的。
蒸汽主管道的温度要远高于冷凝水回收管道的温度，在系统起机阶段，两个连接点能互相移动。
这可以通过固定两部分管道，并且在自由膨胀的部分安装适当的膨胀设备(例如全环、波纹管等)。
在长距离的蒸汽管道时通过安装特别的管道连接件来产生膨胀余量(如工厂内)。
在建筑物内，管道本身具有很多弯头，其自然特性能补偿膨胀，因此不需要特别的连接件。
如果知道了管道内蒸汽的温度和周围的环境温度，确定管道的膨胀长度具有足够的精度。
其它材料也有自己相应的图表，但输送蒸汽的管道通常使用低碳钢。
管道布置必须足够灵活以吸收由于加热引起的管道移动。
在很多情况下，管道布置有其自然的灵活性，例如利用管道的长度和很多的弯头，以确保没有很大的应力积聚。
而在另外一些安装中则必须采取措施以达到灵活的要求。
管道膨胀的计算膨胀(∆) =L o x∆t xa(mm)其中：L o =支撑点之间的距离(m)∆t =温度差o Cα=膨胀系数⨯10－3蒸汽疏水阀管道必须有一定的柔性，以避免支管连接应力过大。
移动的位置被管道所占据，任何辅助的设施可以通过冷态收缩减小。
首先计算每一固定支撑点之间的管道膨胀总量。
管道缩短一半的膨胀总长，通过法兰连接之间的拉伸螺栓冷态伸长，这样管道在冷态下单方向受应力。
当管道加热到一半温度时，管道膨胀一半，管道将不受应力。
在工作温度下，管道全部膨胀，管道将在相反的方向受压。
在实际应用中，管道配有隔离件，其长度为管道总膨胀的一半，装在两片法兰之间。
当管道全部安装完毕并固定后，撤离隔离件，连接被拉紧。
如果剩余的膨胀不能被管道的自然柔性所吸收，则必须使用膨胀件。
热膨胀和热膨胀系数的计算
热膨胀和热膨胀系数的计算热膨胀是指物体在受热时体积会增大的现象，是由于物体分子内部的热运动引起的。
而热膨胀系数则是表示物体在温度变化下体积变化程度的物理量，通常用符号α表示。
本文将介绍热膨胀的基本原理和热膨胀系数的计算方法。
一、热膨胀的原理当物体受热时，其分子内部的热运动会增加，分子之间的相互作用力也会增强，导致物体整体体积增大。
这种现象被称为热膨胀。
热膨胀是普遍存在的，几乎所有的物体在受热时都会出现膨胀现象。
二、热膨胀系数的定义热膨胀系数α，用于衡量物体在温度变化下体积增加的程度。
它定义为单位温度变化下单位长度的线膨胀量，通常以℃⁻¹或K⁻¹作为单位，表示为α = ΔL / (L0 × ΔT) ，其中ΔL表示长度变化量，L0表示初始长度，ΔT表示温度变化量。
三、固体的热膨胀系数计算在大多数情况下，固体的热膨胀系数可以通过测量线膨胀量和温度变化量来计算。
具体操作如下：1. 准备一个测量装置：可以使用游标卡尺等工具测量材料的长度变化量。
2. 测量温度变化量：使用温度计或红外线测温仪等工具，测量材料的温度变化量。
3. 测量线膨胀量：将材料加热或降温到一定温度，测量它的线膨胀量。
可以通过测量两个温度点下的长度差来计算线膨胀量。
4. 计算热膨胀系数：根据热膨胀系数的定义，将线膨胀量、初始长度和温度变化量代入公式α = ΔL / (L0 × ΔT) ，即可计算得到热膨胀系数。
需要注意的是，不同材料的热膨胀系数是不同的，同一种材料在不同温度范围内的热膨胀系数也会有所差异。
因此，在实际计算中，应该参考相关资料或实验数据以获取准确的热膨胀系数。
四、液体的热膨胀系数计算与固体相比，液体的热膨胀系数计算相对简单，可以通过公式α =β / V 来进行估算，其中β表示液体的体膨胀系数，V表示液体的体积。
液体的热膨胀系数一般是通过实验测量得到的。
在实验中，可以测量液体在不同温度下的体积，然后根据公式α = β / V 计算得到热膨胀系数。
管材的线膨胀及伸缩量的计算
第一节 管材的线膨胀及伸缩量的计算一、热膨胀量的计算管道安装完毕投入运行时，常因管内介质的温度与安装时环境温度的差异而产生伸缩。
另外，由于管道本身工作温度的高低，也会引起管道的伸缩。
实验证明，温度变化而引起管道长度成比例的变化。
管道温度升高，由于膨胀，长度增加；温度下降，则由于收缩，长度缩短。
温度变化1度相应的长度成比例变化量称为管材的线膨胀系数。
不同材质的材料线膨胀系数也不同。
碳素钢的线膨胀系数为12×10—6／℃，而硬质聚氯乙烯管的线膨胀系数为80X10—6／℃，约为碳素钢的七倍。
管材受热后的线膨胀量，按下式进行计算：()L t t L 21-=∆α式中△L ——管道热膨胀伸长量(m)；α——管材的线膨胀系数(1／K)或(1／℃)； t 2——管道运行时的介质温度(℃)；t l ——管道安装时的温度(℃)，安装在地下室或室内时取t 1=—5℃；当室外架空敷设时，t 1应取冬季采暖室外计算温度；L ——计算管段的长度(m)。
不同材质管材的。
值见表2—1。
表2—1不同材质管材的线膨胀系数在管道工程中，碳素钢管应用最广，其伸长量的计算公式为()L t t L 2161012-⨯=∆-式中12×10—6——常用钢管的线膨胀系数(1／)。
根据式(2—2)制成管道的热伸长量△L 表(见表2—2)，由表中可直接查出不同温度下相应管长的热伸长量。
例有一段室内热水采暖碳素钢管道，管长70m ，输送热水温度为95℃，试计算此段管道的热伸长量。
解根据钢管的热膨胀伸长量计算式(2—2)△L=12×10—6(t 1—t 2)L=12×10—6（95+5）×70=0.084m由已知管长及送水温度，直接查表2—2，也可得管道的热伸长量△L 。
如果管道中通过介质的温度低于环境温度，则计算出来的是缩短量。
二、热应力计算如果管道两端不固定，允许它自由伸缩，则热伸缩量对管予的强度没有什么影响。
管道的热变形计算
三.管道的热变形计算：计算公式：X=a*L*△Tx 管道膨胀量a为线膨胀系数，取0.0133mm/mL补偿管线（所需补偿管道固定支座间的距离）长度△T为温差（介质温度-安装时环境温度）三.关于轴向型、横向型和角向型补偿器对管系及管架设计的要求（一）轴向型补偿器1、安装轴向型补偿器的管段，在管道的盲端、弯头、变截面处，装有截止阀或减压阀的部们及侧支管线进入主管线入口处，都要设置主固定管架。
主固定管架要考虑波纹管静压推力及变形弹性力的作用。
推力计算公式如下：Fp=100*P*AFp-补偿器轴向压力推（N），A-对应于波纹平均直径的有效面积（cm2），P-此管段管道最高压力（MPa）。
轴向弹性力的计算公式如下：Fx=f*Kx*XFX-补偿器轴向弹性力（N），KX-补偿器轴向刚度（N/mm）；f-系数，当“预变形”（包括预变形量△X=0）时，f=1/2，否则f=1。
管道除上述部位外，可设置中间固定管架。
中间固定管架可不考虑压力推力的作用。
2、在管段的两个固定管架之间，仅能设置一个轴向型补偿器。
3、固定管架和导向管架的分布推荐按下图配置。
补偿器一端应靠近固定管架，若过长则要按第一导向架的设置要求设置导向架，其它导向架的最大间距可按下计算：LGmax-最大导向间距（m）；E-管道材料弹性模量（N/cm2）；i-tp 管道断面惯性矩（cm4）；KX-补偿器轴向刚度（N/mm），X0-补偿额定位移量（mm）。
当补偿器压缩变形时，符号“+”，拉伸变形时，符合为“-”。
当管道壁厚按标准壁厚设计时，LGmax可按有关标准选取。
（二）横向型及角向型补偿器1、装在管道弯头附近的横向型补偿器，两端各高一导向支座，其中一个宜是平面导向管座，其上、下活动间隙按下式计算：ε-活动间隙（mm）；L-补偿器有效长度（mm）；△Y-管段热膨胀量（mm）；△X-不包括L长度在内的垂直管段的热膨胀量（mm）；2、角向型补偿器宜两个或三个为一组配套使用，用以吸收管道的横向位移，对Z形和L形管段两个固定管架之间，只允许安装一个横向型补偿器或一组角向型补偿器。
管道常用计算公式
δ气=7.4mm＞管子的壁厚6.5 mm，不能用。 答：这批Q235 φ273×6.5的焊管能用在压力为6.4MPa的输油管线上，
但不能用在6.4MPa的输气管线上。
第七节 管线允许跨度的计算
管线的固定和支承，不管是跨沟过路，还是架空布线都涉及管线的跨 度问题。所谓跨度计算，就是在考虑1管重、2介质重、3管外防腐保温 材料重以及4雨雪影响，甚至维护时的5人、6物重量、7风力、8抗震影 响等因素,计算出两支承点的最大允许距离L。
例4．某段2Km供暖管线，施工温度20℃。最高工作温度60℃，试求热 膨胀量。
解：已知t2=60℃ t1=20℃ Δt=60-20=70℃ L=2000m，供热管一般为钢管α=1.2×10-5/℃
把数据带入
ΔL=α.L.Δt
=1.2×10-5×2000×（60-20）=0.96（m）
答：这段管的总膨胀量为0.96m.
2
24
再求σa = Eα（t1-t2）+μσn
=2.06×105×1.2×10-5×（12-70）+104×0.3 =-143.4+31.2=-112.2
MPa
代入计算公式
σ=σn-σa =104-（-112.2）=216.2 MPa
因[σ] =0.9σs=235×0.9=211.5 MPa
4
σt=α.E.Δt =1.2×10-5×2.06×105×50=123.6MPa 对罐的推力F=σt.A=123.6×2180=269448N=269.45KN 答：管的温度应力为123.6MPa，管对罐的推力F为269.45KN。
三、管的轴向应力σa（下册43页）。管的轴向应力是管的温度应力和 环向应力对轴向应力的影响之和，（对研究对象，拉为正，压为负。） 温度应力是热胀为负（压），冷缩为正（拉），环向应力影响是正 （拉），因为流体压力使管外胀，管有变短的倾向。
供热管道的热膨胀系数-概述说明以及解释
供热管道的热膨胀系数-概述说明以及解释1.引言1.1 概述概述部分的内容:热膨胀系数是描述物体在受热后体积、长度或面积等尺寸的变化程度的物理参数。
在供热管道系统中，热膨胀系数的重要性不言而喻。
热膨胀系数的准确计算和合理应用对于保证供热管道的正常运行、避免破裂与漏水等问题具有重要意义。
供热管道在工作过程中，热水或蒸汽通过管道输送到供热终端，由于温度的变化，管道的长度和体积会发生相应的变化。
这种长度或体积的变化称为热膨胀。
当热水从锅炉中流出，经过居民用水热交换后冷却后再返回锅炉，管道会发生热胀冷缩的现象，如果不加以合理的处理，就会对供热系统产生严重的影响。
文章的主要目的是通过对供热管道热膨胀系数的深入研究，探讨其对供热系统的影响以及如何合理应用热膨胀系数来解决相关问题。
在文章的后续部分，将详细介绍热膨胀系数的定义和作用，以及影响热膨胀系数的因素。
最后，结论部分将强调供热管道中热膨胀系数的重要性，并提出合理应用热膨胀系数的建议。
通过本文的阅读，读者将能够了解到供热管道热膨胀系数在供热系统中的重要性，同时也能够学习到如何通过合理使用热膨胀系数来解决供热管道在工作过程中出现的问题。
希望本文能给读者带来一定的启发，并对相关领域的从业人员有所帮助。
文章结构部分的内容可以从以下几个方面进行描述：1.2 文章结构文章采用以下结构进行组织和呈现：引言部分主要分为三个小节，分别是概述、文章结构和目的。
正文部分主要分为两个小节，分别是热膨胀系数的定义和作用以及影响热膨胀系数的因素。
结论部分主要分为两个小节，分别是供热管道中热膨胀系数的重要性以及如何合理应用热膨胀系数。
通过以上的结构安排，本文将全面介绍供热管道的热膨胀系数相关知识。
首先，在引言部分，将对热膨胀系数的概念进行简要介绍，同时阐述文章的结构和目的，为读者提供全局的认识和导引。
接着，在正文部分，将详细介绍热膨胀系数的定义和作用。
通过对热膨胀系数的解释，读者可以更好地了解热膨胀现象在供热管道中的表现以及其对管道性能的影响。
热力学中的热膨胀和线膨胀系数
热力学中的热膨胀和线膨胀系数热力学是研究能量转化和传递的科学，而热膨胀和线膨胀系数是热力学中的重要概念。
热膨胀指的是物体在温度变化时大小发生变化，而线膨胀系数则是描述物体线膨胀性质的一个参数。
本文将详细介绍热膨胀和线膨胀系数的概念、计算方法以及在工程应用中的重要性。
一、热膨胀的概念和原理热膨胀是指物体在温度变化的情况下，由于内部分子运动增加导致物体体积扩大的现象。
这是因为温度升高会增加物体内部分子的平均动能，使得分子之间的距离增大，从而导致物体的体积增加。
相反，当温度降低时，物体的体积会缩小。
热膨胀现象可以由以下公式描述：ΔL = αL₀ΔT其中，ΔL表示物体温度变化引起的长度变化，α为热膨胀系数，L₀为物体的原始长度，ΔT为温度变化。
二、线膨胀系数的计算方法线膨胀系数是用于描述物体线膨胀性质的一个重要参数，通常用符号β表示。
线膨胀系数可以通过以下公式计算：β = (1/L₀) * (dL/dT)其中，L₀为原始长度，dL/dT表示温度变化引起的长度变化率。
在实际计算中，线膨胀系数也可以通过利用已知材料的热膨胀系数来间接获得。
三、热膨胀和线膨胀系数的工程应用1. 材料选择和设计：在工程领域中，热膨胀和线膨胀系数是考虑材料选择和构件设计的重要因素。
不同材料具有不同的热膨胀和线膨胀系数，因此需要根据实际需求来选择合适的材料，以确保在温度变化时不会产生过大的变形或应力。
2. 钢铁结构设计：钢铁是常用的建筑材料，因其具有较大的线膨胀系数，在设计钢铁结构时需要考虑其热膨胀特性。
合理地估计热膨胀引起的长度变化，可以避免钢结构在温度变化时产生过大的变形和应力。
3. 焊接应用：焊接是常用的连接方法，但焊接过程中产生的高温会导致材料热膨胀。
需要在焊接设计中考虑热膨胀引起的变形和应力，以确保焊接后的构件稳定性和可靠性。
4. 管道设计：在管道系统中，由于流体传输中产生的温度变化，管道的长度也会发生变化。
因此，在管道设计中需要考虑热膨胀引起的长度变化，通过合理设置伸缩节等装置来补偿管道的线膨胀。
圆管热膨胀内径
圆管热膨胀内径
摘要：
1.圆管热膨胀的概念
2.圆管热膨胀的影响因素
3.圆管热膨胀的计算方法
4.圆管热膨胀的应用实例
正文：
一、圆管热膨胀的概念
圆管热膨胀是指在温度变化时，圆管的内径尺寸发生变化的现象。
当圆管受热时，其内部分子的热运动增强，导致管壁原子间距增大，进而使圆管的内径扩大。
相反，当圆管冷却时，其内径会缩小。
二、圆管热膨胀的影响因素
1.材料：不同的材料在不同温度下的热膨胀系数不同，因此材料的种类是影响圆管热膨胀的重要因素。
2.温度：温度的变化是引发圆管热膨胀的直接原因，温度变化范围越大，圆管热膨胀程度越明显。
3.管径和管壁厚度：管径和管壁厚度越大，圆管的热膨胀程度越明显。
三、圆管热膨胀的计算方法
圆管热膨胀的计算通常采用以下公式：
ΔL = L0 * α* ΔT
其中，ΔL 为圆管长度的变化，L0 为圆管的原始长度，α为材料的线膨胀系数，ΔT 为温度变化。
四、圆管热膨胀的应用实例
1.管道设计：在设计管道时，需要考虑到材料的热膨胀特性，以确保在温度变化时，管道能够正常工作，避免因热膨胀导致管道变形或泄漏。
2.工业生产：在工业生产过程中，圆管热膨胀的影响因素需要被充分考虑，以保证生产过程中的稳定性和安全性。
无缝钢管热膨胀系数表
无缝钢管热膨胀系数表1. 什么是无缝钢管热膨胀系数？无缝钢管热膨胀系数是指在不同温度下，无缝钢管长度的变化比例。
热膨胀系数是一个重要的物理参数，它可以帮助我们理解材料在温度变化下的性质和行为。
2. 为什么需要无缝钢管热膨胀系数表？无缝钢管在使用过程中，会受到温度的影响而发生热膨胀或热收缩。
了解无缝钢管的热膨胀系数可以帮助我们预测和计算在不同温度下钢管的变形情况，从而在设计和安装过程中做出合理的决策和调整。
3. 如何测量和计算无缝钢管的热膨胀系数？测量无缝钢管的热膨胀系数需要进行实验和数据记录。
以下是一种常见的测量方法：1.准备一段无缝钢管样品，并测量其初始长度。
2.将样品放置在恒温槽中，使其达到目标温度。
3.在不同温度下，测量样品的长度变化，并记录数据。
4.根据测量数据，计算出不同温度下的热膨胀系数。
4. 无缝钢管热膨胀系数表示方法无缝钢管热膨胀系数通常以线性形式表示，单位为1/℃（或ppm/℃）。
以下是一个示例无缝钢管热膨胀系数表：温度范围（℃）热膨胀系数（1/℃）-50 至 0 10.50 至 100 11.2100 至 200 12.8200 至 300 14.3300 至 400 15.95. 无缝钢管热膨胀系数表的应用无缝钢管热膨胀系数表的应用非常广泛。
以下是一些常见的应用场景：5.1 工程设计在工程设计过程中，无缝钢管热膨胀系数表可以帮助工程师预测和计算材料在不同温度下的变形情况。
通过合理使用热膨胀系数表，工程师可以选择合适的材料和结构设计，以确保在温度变化下系统的稳定性和安全性。
5.2 管道安装在管道安装过程中，无缝钢管热膨胀系数表可以帮助工人正确计算和安装管道的长度和支撑位置。
通过合理考虑热膨胀系数，可以避免管道在温度变化下发生过度应力和变形，从而保证管道的正常运行和使用寿命。
5.3 材料选择无缝钢管热膨胀系数表也可以用于材料选择过程中的比较和评估。
不同材料的热膨胀系数不同，通过比较不同材料的热膨胀系数，可以选择最适合特定应用的材料。
圆管热膨胀内径
圆管热膨胀内径热膨胀是物质受热后体积膨胀的现象，当物体受热时，分子的热运动增强，距离变远，导致物体体积增大。
热膨胀是一个普遍存在的现象，几乎所有物质都会发生热膨胀。
在工程应用中，特别是在圆管的设计和制造过程中，了解圆管的热膨胀内径是十分重要的。
圆管是一种常见的管道形式，它在许多领域都有广泛应用，如工业、建筑、航天等。
在使用过程中，由于温度的变化，圆管会发生热膨胀现象，这就需要对圆管的热膨胀内径进行计算和控制。
圆管的热膨胀内径是指圆管在受热膨胀后内径的变化情况。
为了计算圆管的热膨胀内径，我们首先需要知道圆管的材料特性，如热膨胀系数。
热膨胀系数是描述物质热膨胀性质的一个重要参数，它表示单位温度变化时物质体积的变化量与初始体积的比值。
以铜管为例，铜是一种常用的圆管材料，具有良好的导热性和热膨胀性。
对于铜管来说，其热膨胀系数是一个常数，可以通过实验测量得到。
在计算圆管的热膨胀内径时，我们可以利用热膨胀系数和圆管的初始内径来进行计算。
假设圆管的初始内径为D0，温度变化为ΔT，铜管的热膨胀系数为α。
根据热膨胀系数的定义，我们可以得到圆管的热膨胀内径的计算公式为：ΔD = α * D0 * ΔT其中，ΔD表示圆管的热膨胀内径的变化量。
通过这个计算公式，我们可以得到圆管在受热膨胀后内径的变化情况。
如果ΔD为正值，表示圆管的内径增大；如果ΔD为负值，表示圆管的内径减小。
根据计算结果，我们可以合理设计圆管的初始内径，以满足在不同温度下的使用需求。
除了圆管的热膨胀内径，还有其他与热膨胀相关的参数需要考虑，如圆管的长度膨胀、圆管的外径膨胀等。
这些参数的计算方法与圆管的热膨胀内径类似，只是需要考虑不同的物理量和几何参数。
在实际工程中，为了减小圆管的热膨胀对系统的影响，可以采取一些措施。
例如，可以在圆管的设计中留有一定的伸缩余量，以容纳圆管的热膨胀；还可以采用热膨胀节或补偿器等装置，来补偿圆管的热膨胀。
圆管的热膨胀内径是圆管设计和制造过程中需要考虑的重要参数之一。